Structure-Circuit Resistor Integrated Design Optimization of Piezoelectric Energy Harvester Considering Stress Constraints
Abstract
:1. Introduction
- To develop a reliable simulation model, model calibration is performed by comparing the initial configuration of the target PEH with the experiment.
- Topology optimization of PEH considering multi-physics is performed in order to obtain an intuition-independent conceptual design for maximum power generation in a given design area.
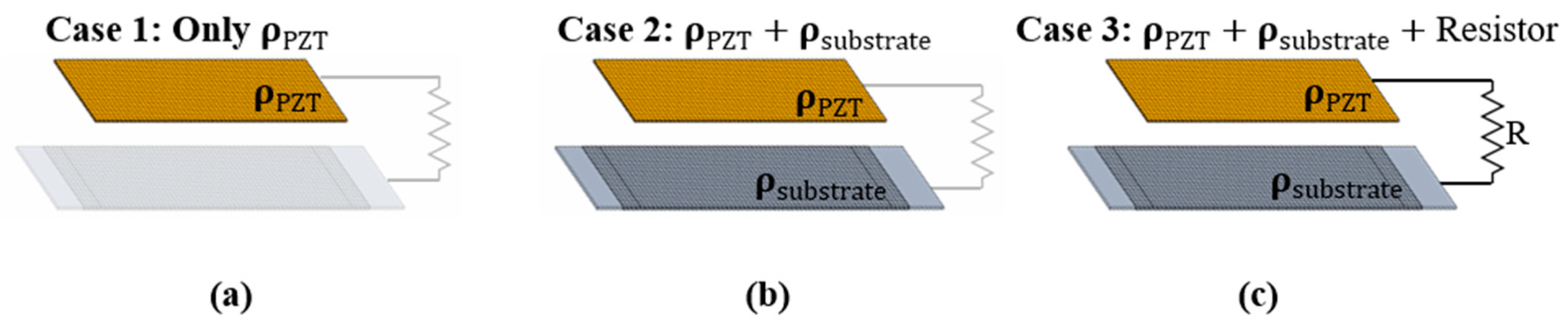
- In order to confirm the effect of the multi-physics effect of the piezoelectric material, substrate, and resistor on the result of the optimal design, case study is conducted while expanding the design domain: only PZT case, PZT and substrate case, and PZT, substrate and resistor case.
- Model simplification and size optimization are performed as a post-processing to obtain manufacturable design for the optimal topology optimization result.
- The optimal design obtained by the two-stage design process of topology optimization and size optimization considering stress constraints and multi-physics is compared with the recently performed design methods, and the excellence of the proposed method is confirmed.
2. PEH Modeling Considering Multi-Physics
2.1. Piezoelectric Effect of Piezoelectric Energy Harvester
2.2. PEH Simulation Model
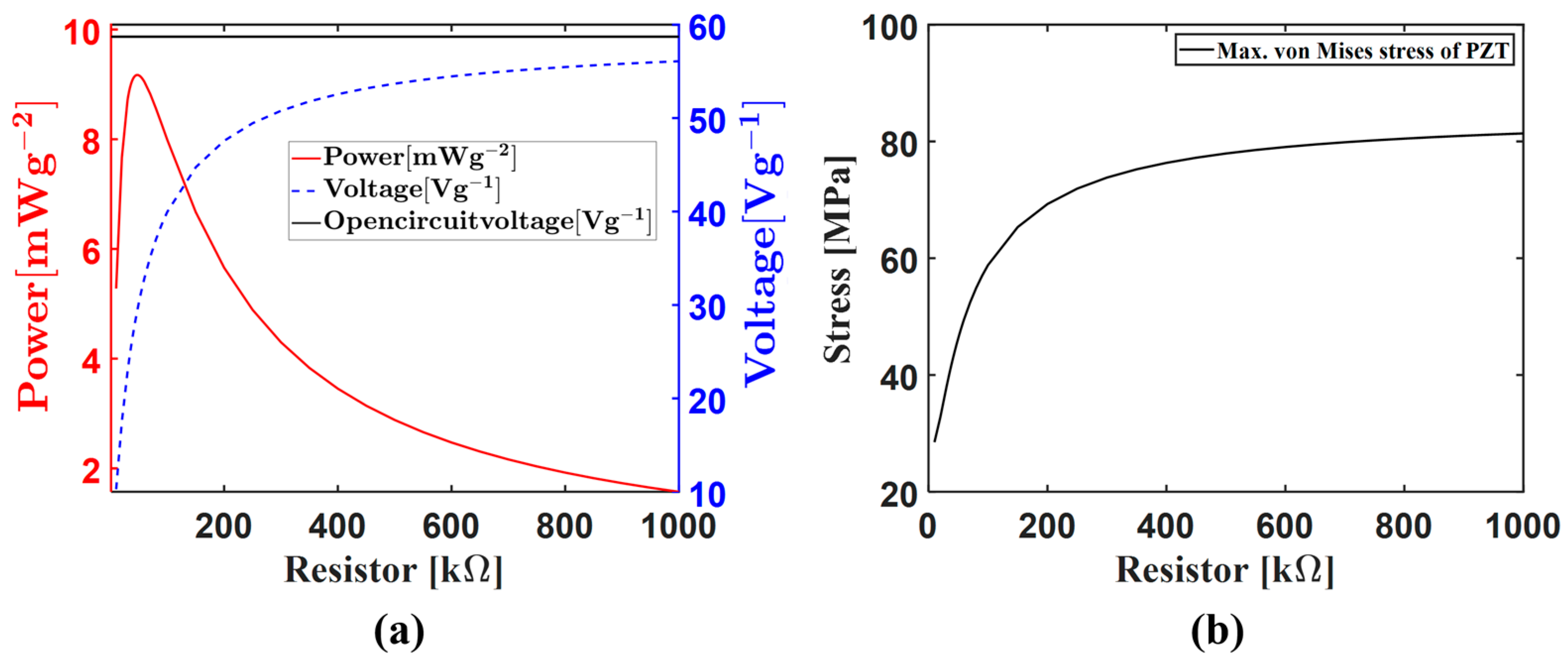
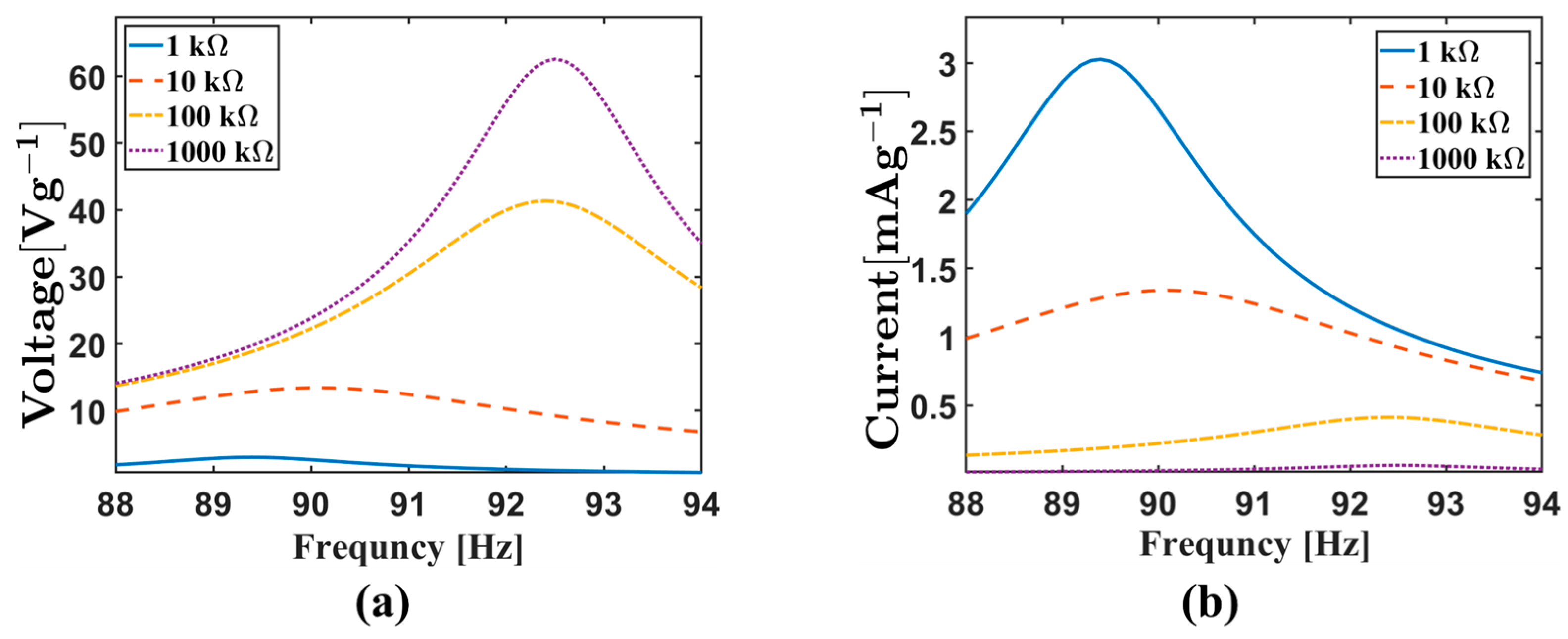
2.3. Circuit Resistor Influence on PEH Performance
3. Conceptual Design
3.1. Design Degree of Freedom Comparison
3.2. Density-Based Topology Optimization of PEH
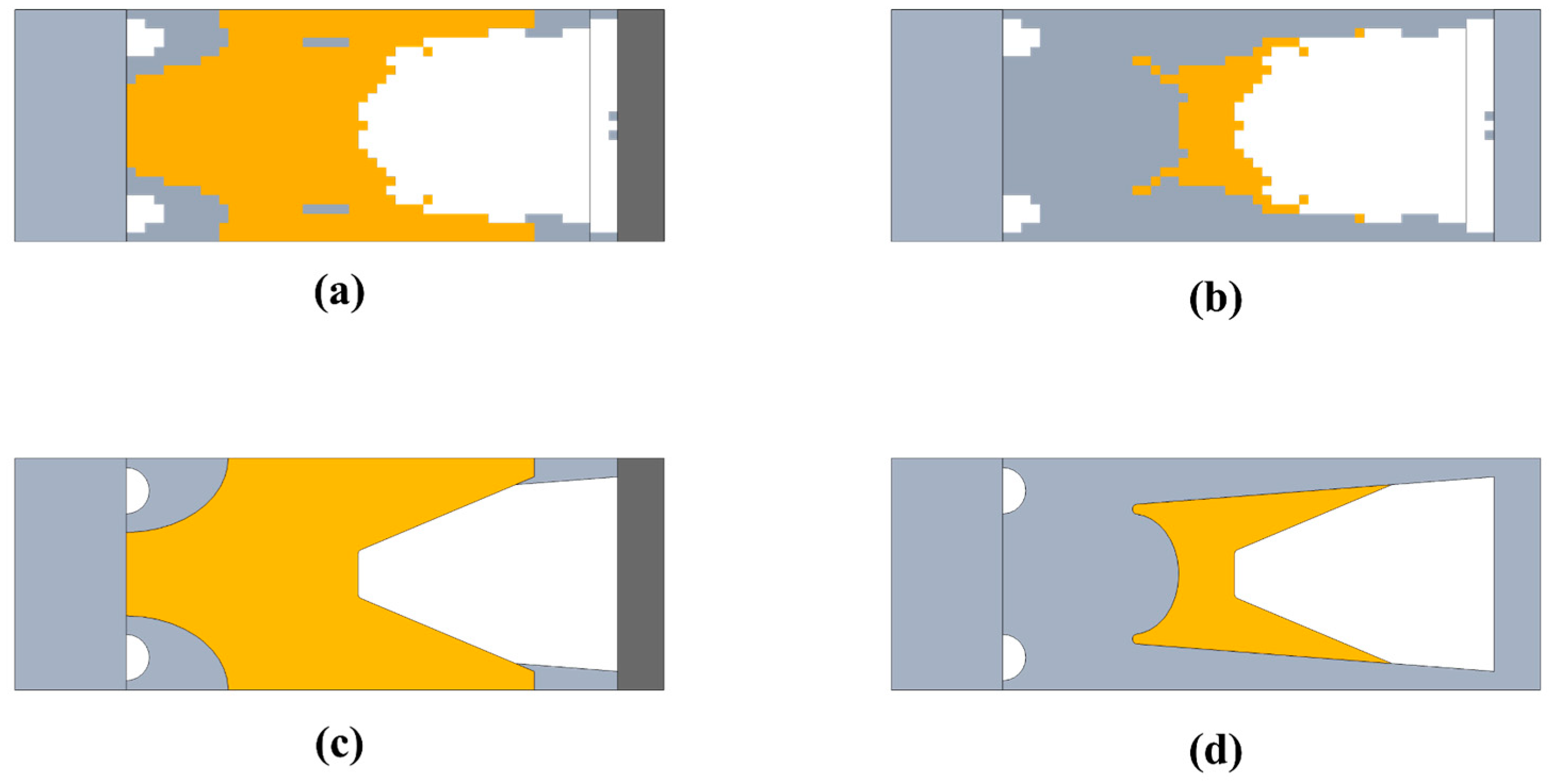
3.3. Topology Optimization Results
4. Detailed Design
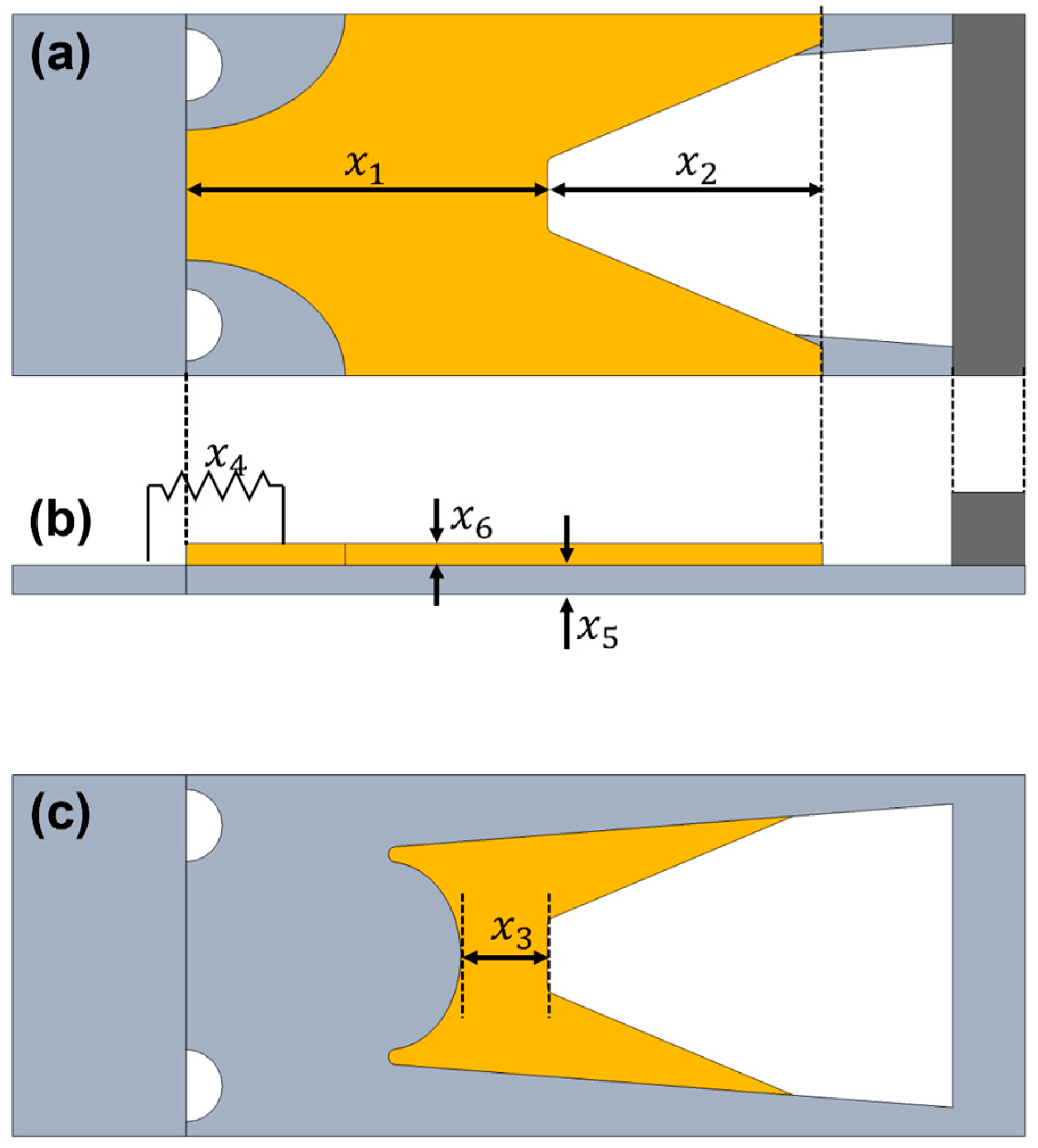
4.1. Size Optimization of Refined Optimal Topology Model
4.2. Results
5. Conclusions
Author Contributions
Data Availability Statement
Conflicts of Interest
References
- Farokhi, H.; Gholipour, A.; Ghayesh, M.H. Efficient Broadband Vibration Energy Harvesting Using Multiple Piezoelectric Bimorphs. J. Appl. Mech. Trans. ASME 2020, 87, 41001. [Google Scholar] [CrossRef]
- Panda, S.K.; Srinivas, J. Electro-Structural Analysis and Optimization Studies of Laminated Composite Beam Energy Harvester. Mech. Adv. Mater. Struct. 2021, 29, 4193–4205. [Google Scholar] [CrossRef]
- Hey, J.; Repaka, M.; Li, T.; Tan, J.L. Design Optimization of a Rotary Thermomagnetic Motor for More Efficient Heat Energy Harvesting. Energies 2022, 15, 6334. [Google Scholar] [CrossRef]
- Mohammadnia, A.; Rezania, A.; Ziapour, B.M.; Sedaghati, F.; Rosendahl, L. Hybrid Energy Harvesting System to Maximize Power Generation from Solar Energy. Energy Convers. Manag. 2020, 205, 112352. [Google Scholar] [CrossRef]
- Sheeraz, M.A.; Malik, M.S.; Rehman, K.; Elahi, H.; Butt, Z.; Ahmad, I.; Eugeni, M.; Gaudenzi, P. Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications. Energies 2021, 14, 2498. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, M.; Shirvanimoghaddam, K.; Abolhasani, M.M.; Farhangi, M.; Zahiri Barsari, V.; Liu, H.; Dohler, M.; Naebe, M. Towards a Green and Self-Powered Internet of Things Using Piezoelectric Energy Harvesting. IEEE Access 2019, 7, 94533–94556. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, A.; Kumar, R.; Vaish, R. Finite Element Study on Acoustic Energy Harvesting Using Lead-Free Piezoelectric Ceramics. J. Electron. Mater. 2018, 47, 1447–1458. [Google Scholar] [CrossRef]
- Kianpoor, A.; Jahani, K. Modeling and Analyzing of Energy Harvesting from Trapezoidal Piezoelectric Beams. Iran. J. Sci. Technol.-Trans. Mech. Eng. 2019, 43, 259–266. [Google Scholar] [CrossRef]
- Montazer, B.; Sarma, U. Design and Optimization of Quadrilateral Shaped Pvdf Cantilever for Efficient Conversion of Energy from Ambient Vibration. IEEE Sens. J. 2018, 18, 3977–3988. [Google Scholar] [CrossRef]
- Bath, D.; Salehian, A. A Novel 3D Folded Zigzag Piezoelectric Energy Harvester; Modeling and Experiments. Smart Mater. Struct. 2019, 28, 25011. [Google Scholar] [CrossRef]
- Fernandes, E.; Martin, B.; Rua, I.; Zarabi, S.; Debéda, H.; Nairn, D.; Wei, L.; Salehian, A. Design, Fabrication, and Testing of a Low Frequency MEMS Piezoelectromagnetic Energy Harvester. Smart Mater. Struct. 2018, 27, 35017. [Google Scholar] [CrossRef]
- Dhote, S.; Li, H.; Yang, Z. Multi-Frequency Responses of Compliant Orthoplanar Spring Designs for Widening the Bandwidth of Piezoelectric Energy Harvesters. Int. J. Mech. Sci. 2019, 157–158, 684–691. [Google Scholar] [CrossRef]
- Townsend, S.; Grigg, S.; Picelli, R.; Featherston, C.; Kim, H.A. Topology Optimization of Vibrational Piezoelectric Energy Harvesters for Structural Health Monitoring Applications. J. Intell. Mater. Syst. Struct. 2019, 30, 2894–2907. [Google Scholar] [CrossRef]
- Amlashi, A.H.; Mohand-ousaid, A.; Rakotondrabe, M. Topology Optimization of Piezoelectric Plate Energy Harvester Under External In-Plan Force Considering Different Boundary Conditions. In Proceedings of the 2019 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Helsinki, Finland, 1–5 July 2019. [Google Scholar]
- Thein, C.K.; Liu, J.S. Numerical Modeling of Shape and Topology Optimisation of a Piezoelectric Cantilever Beam in an Energy-Harvesting Sensor. Eng. Comput. 2017, 33, 137–148. [Google Scholar] [CrossRef]
- Uchino, K. Piezoelectric Energy Harvesting Systems—Essentials to Successful Developments. Energy Technol. 2018, 6, 829–848. [Google Scholar] [CrossRef]
- Hasan, N.; Muktadir, M.A.; Alam, M. Forces in Mechanics Comparative Study of Tapered Shape Bimorph Piezoelectric Energy Harvester via Finite Element Analysis. Forces Mech. 2022, 9, 100131. [Google Scholar] [CrossRef]
- Salas, R.A.; Reddy, J.N. A Topology Optimization Formulation for Transient Design of Multi-Entry Laminated Piezocomposite Energy Harvesting Devices Coupled with Electrical Circuit. Int. J. Numer. Methods Eng. 2018, 113, 1370–1410. [Google Scholar] [CrossRef]
- Kiyono, C.Y.; Silva, E.C.N.; Reddy, J.N. Optimal Design of Laminated Piezocomposite Energy Harvesting Devices Considering Stress Constraints. Int. J. Numer. Methods Eng. 2016, 105, 883–914. [Google Scholar] [CrossRef]
- Wang, Q.; Kim, K.B.; Woo, S.B.; Song, Y.; Sung, T.H. A Magneto-Mechanical Piezoelectric Energy Harvester. Energies 2021, 14, 2387. [Google Scholar] [CrossRef]
- Methods, C.; Mech, A.; Li, H.; Gao, L.; Li, H.; Li, X.; Tong, H. ScienceDirect Full-Scale Topology Optimization for Fiber-Reinforced Structures with Continuous Fiber Paths. Comput. Methods Appl. Mech. Eng. 2021, 377, 113668. [Google Scholar] [CrossRef]
- Zhu, J.; Cai, X.; Zhang, J.; Ni, X. Improved Structural Design of Wind Turbine Blade Based on Topology and Size Optimization. Int. J. Low-Carbon Technol. 2021, 17, 69–79. [Google Scholar] [CrossRef]
- Côté, F.; Masson, P.; Mrad, N.; Cotoni, V. Dynamic and Static Modelling of Piezoelectric Composite Structures Using a Thermal Analogy with MSC/NASTRAN. Compos. Struct. 2004, 65, 471–484. [Google Scholar] [CrossRef]
- Jung, B.C.; Yoon, H.; Oh, H.; Lee, G.; Yoo, M.; Youn, B.D.; Huh, Y.C. Hierarchical Model Calibration for Designing Piezoelectric Energy Harvester in the Presence of Variability in Material Properties and Geometry. Struct. Multidiscip. Optim. 2016, 53, 161–173. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; McAvoy, P. Basic Electric Circuit Theory: A One-Semester Text, 1st ed.; Academic Press: San Diego, CA, USA, 1997; ISBN 9780124808652. [Google Scholar]
- Platt, S.R.; Farritor, S.; Haider, H. On Low-Frequency Electric Power Generation with PZT Ceramics. IEEE/ASME Trans. Mechatron. 2005, 10, 240–252. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An Experimentally Validated Bimorph Cantilever Model for Piezoelectric Energy Harvesting from Base Excitations. Smart Mater. Struct. 2009, 18, 25009. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology Optimization Approaches: A Comparative Review. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Kögl, M.; Silva, E.C.N. Topology Optimization of Smart Structures: Design of Piezoelectric Plate and Shell Actuators. Smart Mater. Struct. 2005, 14, 387–399. [Google Scholar] [CrossRef]
- Hooker, W. Properties Ceramics of PZT-Based Piezoelectric and 250 °C; Technical Report for NASA; NASA: Langley, VR, USA, 1998.
- Anand, A.; Pal, S.; Kundu, S. Multi-Perforated Energy-Efficient Piezoelectric Energy Harvester Using Improved Stress Distribution. IETE J. Res. 2021, 1–16. [Google Scholar] [CrossRef]
- Pertin, O.; Guha, K.; Jakšić, O.; Jakšić, Z.; Iannacci, J. Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications. Micromachines 2022, 13, 1399. [Google Scholar] [CrossRef]
- Debnath, B.; Kumar, R. Design and Simulation Study of a New Flared-U Shaped Springs Based MEMS Piezoelectric Vibration Energy Harvester. In Proceedings of the 2020 IEEE International Conference on Computing, Power and Communication Technologies GUCON 2020, Greater Noida, India, 2–4 October 2020; pp. 101–105. [Google Scholar] [CrossRef]
- Hu, Y.; Yi, Z.; Dong, X.; Mou, F.; Tian, Y.; Yang, Q.; Yang, B.; Liu, J. High Power Density Energy Harvester with Non-Uniform Cantilever Structure Due to High Average Strain Distribution. Energy 2019, 169, 294–304. [Google Scholar] [CrossRef]
- Huang, Y.; Yi, Z.; Hu, G.; Yang, B. Data-Driven Optimization of Piezoelectric Energy Harvesters via Pattern Search Algorithm. Micromachines 2021, 12, 561. [Google Scholar] [CrossRef] [PubMed]
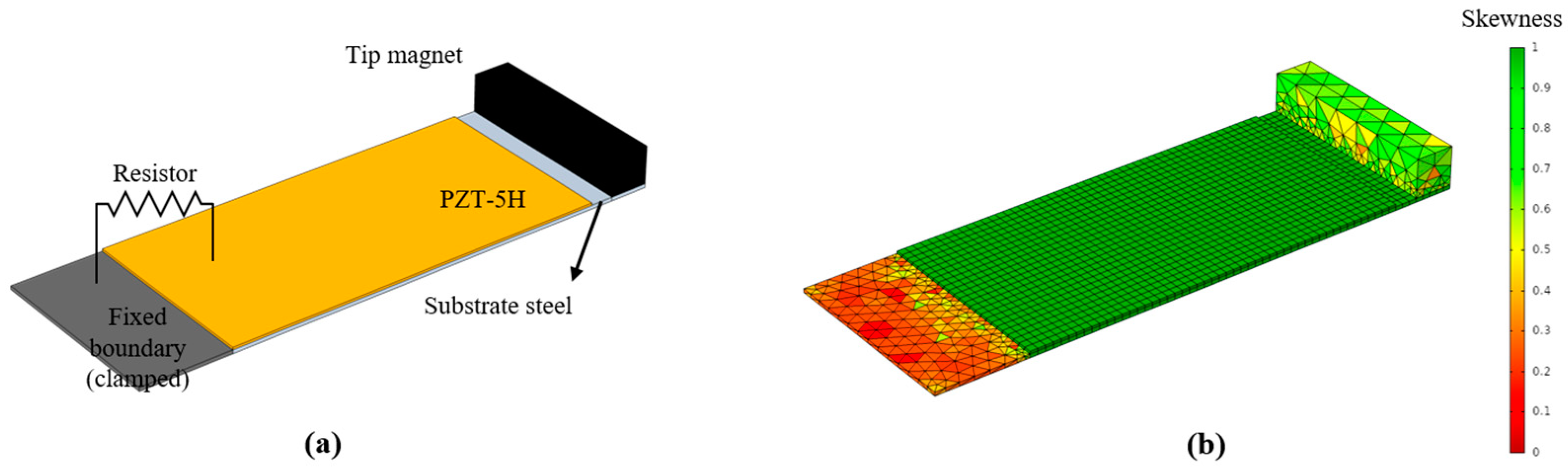
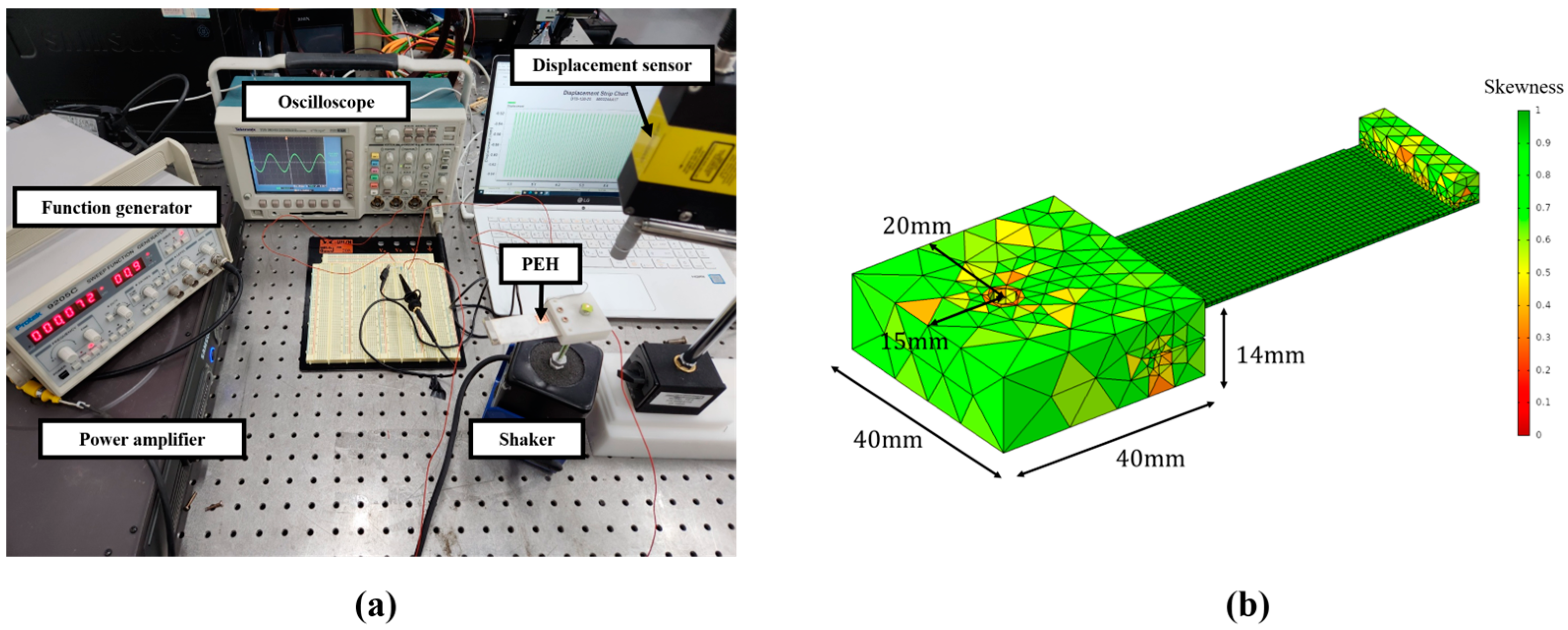
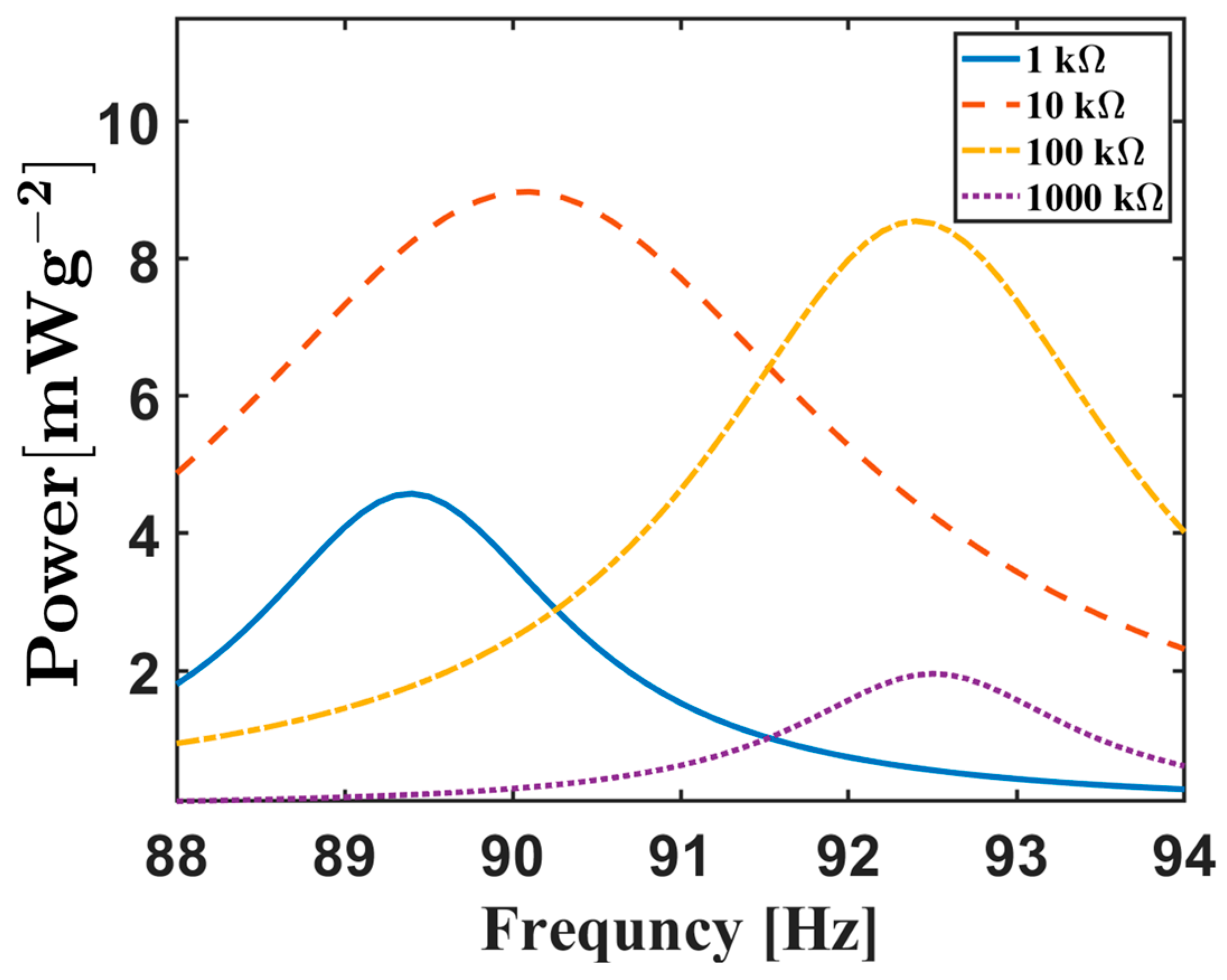

| Experiment | Calibrated Model | Error [%] | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | Mean | |||
| Resonance [Hz] | 75.5 | 76 | 75.2 | 75.1 | 74.1 | 75.18 | 75.52 | 0.45 |
| RMS voltage [V] | 33.6 | 33.2 | 34 | 32.8 | 32 | 33.12 | 33.24 | 0.36 |
| Component | Material Property | Value |
|---|---|---|
| PZT ceramic (PZT-5H) | Density () | |
| Dielectric constants: | ||
| Piezoelectric charge constants (): | ||
| Substrate steel | Density () | |
| Young’s modulus (): | ||
| Tip magnet | Density () | |
| Clamping jig | Young’s modulus (): | 2.0509 |
| Case No. | PZT Material | Substrate Material | Resistor |
|---|---|---|---|
| 1 | O | X | |
| 2 | O | O | |
| 3 | O | O | O |
| Case No. | PZT Domain | Substrate Domain |
|---|---|---|
| 1 |  | N/A |
| 2 |  |  |
| 3 |  |  |
| Performance | Case 1 | Case 2 | Case 3 |
| ] | 1.0124 | 3.3977 | 8.6929 |
| ] | 1.2071 | 4.5981 | |
| ] | 935 | 204 | 163 |
| ] | 105.68 | 70.32 | 87.75 |
| ] | 53.31 | 49.24 | 61.93 |
| Variable | Description | Lower Bound | Initial Design | Upper Bound |
|---|---|---|---|---|
| PZT center length | ||||
| PZT shaving length | ||||
| Space margin | ||||
| Resistor | ||||
| Substrate thickness, discrete | ||||
| PZT thickness, discrete |
| Variables | Simplified Model | Optimal Model |
|---|---|---|
| Power @ 60 Hz | ||
| Substrate stress @ 60 Hz | ||
| PZT stress @ 60 Hz |
| Reference | Piezoelectric Material | Resonance Frequency [Hz] |
Acceleration |
Volume |
Power |
Power Density |
|---|---|---|---|---|---|---|
| A. Anand et al. [32] | BaTiO3 | 98.59 | 1 | 4.31 | 7.15 | 1.66 |
| O. Pertin et al. [33] | PZT-5H | 150.3 | 0.9 | 753 | 3210 | 4.26 |
| B. Debnath et al. [34] | PZT-5H | 28.6 | 0.07 | 1.89 | 2.19 | 1.16 |
| Y. Hu et al. [35] | PZT | 45.37 | 2 | 32 | 241.25 | 7.54 |
| Y. Huang et al. [36] | PZT | 26.38 | 1 | 4.43 | 261.02 | 58.87 |
| This work | PZT-5H | 61.13 | 1 | 1264.1 | 8360 | 6.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Kim, J.; Lee, T.H. Structure-Circuit Resistor Integrated Design Optimization of Piezoelectric Energy Harvester Considering Stress Constraints. Energies 2023, 16, 3766. https://doi.org/10.3390/en16093766
Kim T, Kim J, Lee TH. Structure-Circuit Resistor Integrated Design Optimization of Piezoelectric Energy Harvester Considering Stress Constraints. Energies. 2023; 16(9):3766. https://doi.org/10.3390/en16093766
Chicago/Turabian StyleKim, Taekyun, Jihoon Kim, and Tae Hee Lee. 2023. "Structure-Circuit Resistor Integrated Design Optimization of Piezoelectric Energy Harvester Considering Stress Constraints" Energies 16, no. 9: 3766. https://doi.org/10.3390/en16093766





