Comparison on Hydraulic Characteristics of Vertical and Horizontal Air-Cushion Surge Chambers in the Hydropower Station under Load Disturbances
Abstract
:1. Introduction
2. Mathematical Model
2.1. One-Dimensional Model
- The inertia of the water body in the chamber was ignored;
- The turbine efficiency remained constant in the process of fluctuation;
- The power station ran separately.
2.2. Three-Dimensional Model
3. Case Study
3.1. Description of Case Study
3.2. Scenarios Set-Up
4. Results and Discussion
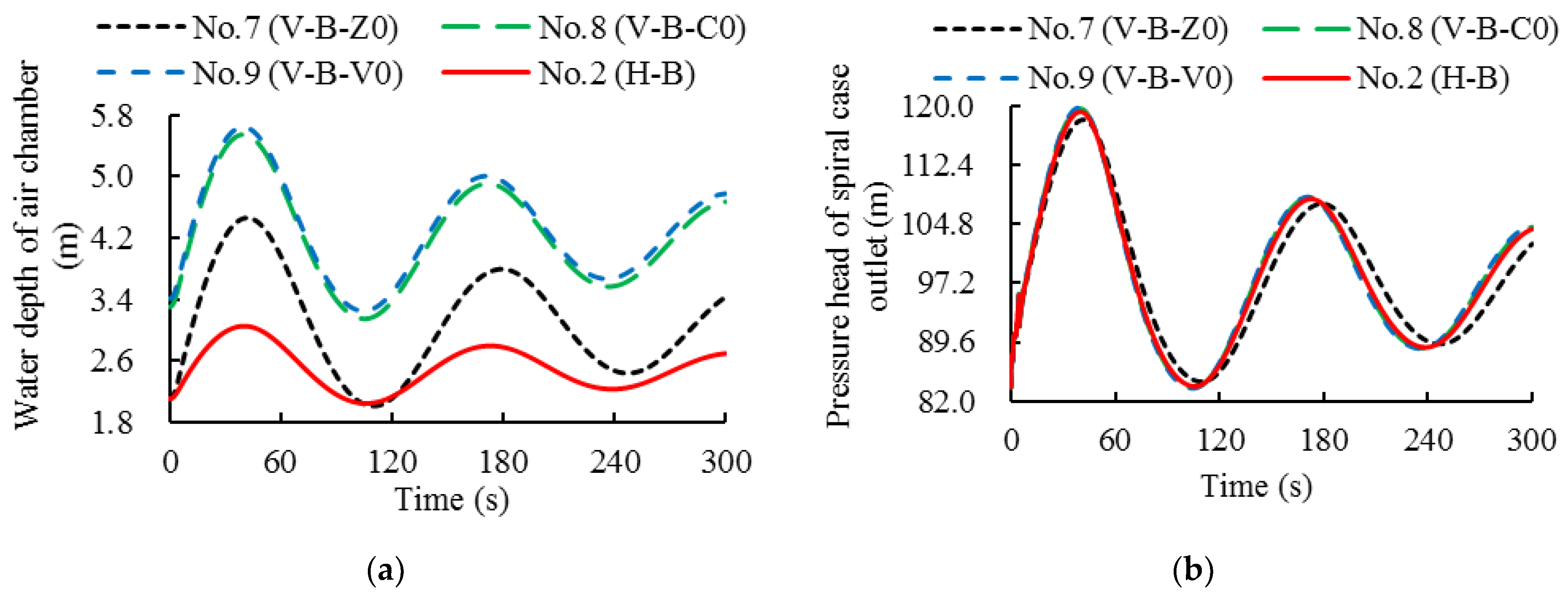
4.1. Large Load Disturbance
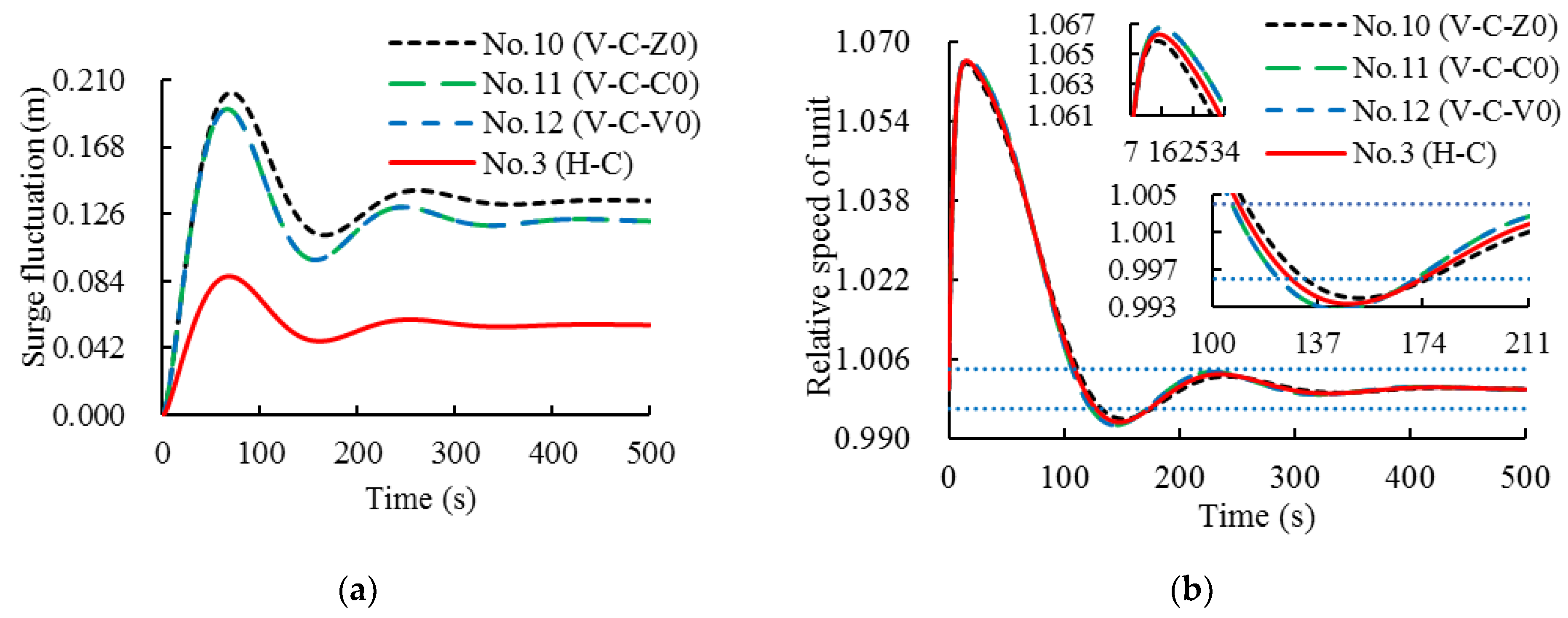
4.2. Small Load Disturbance
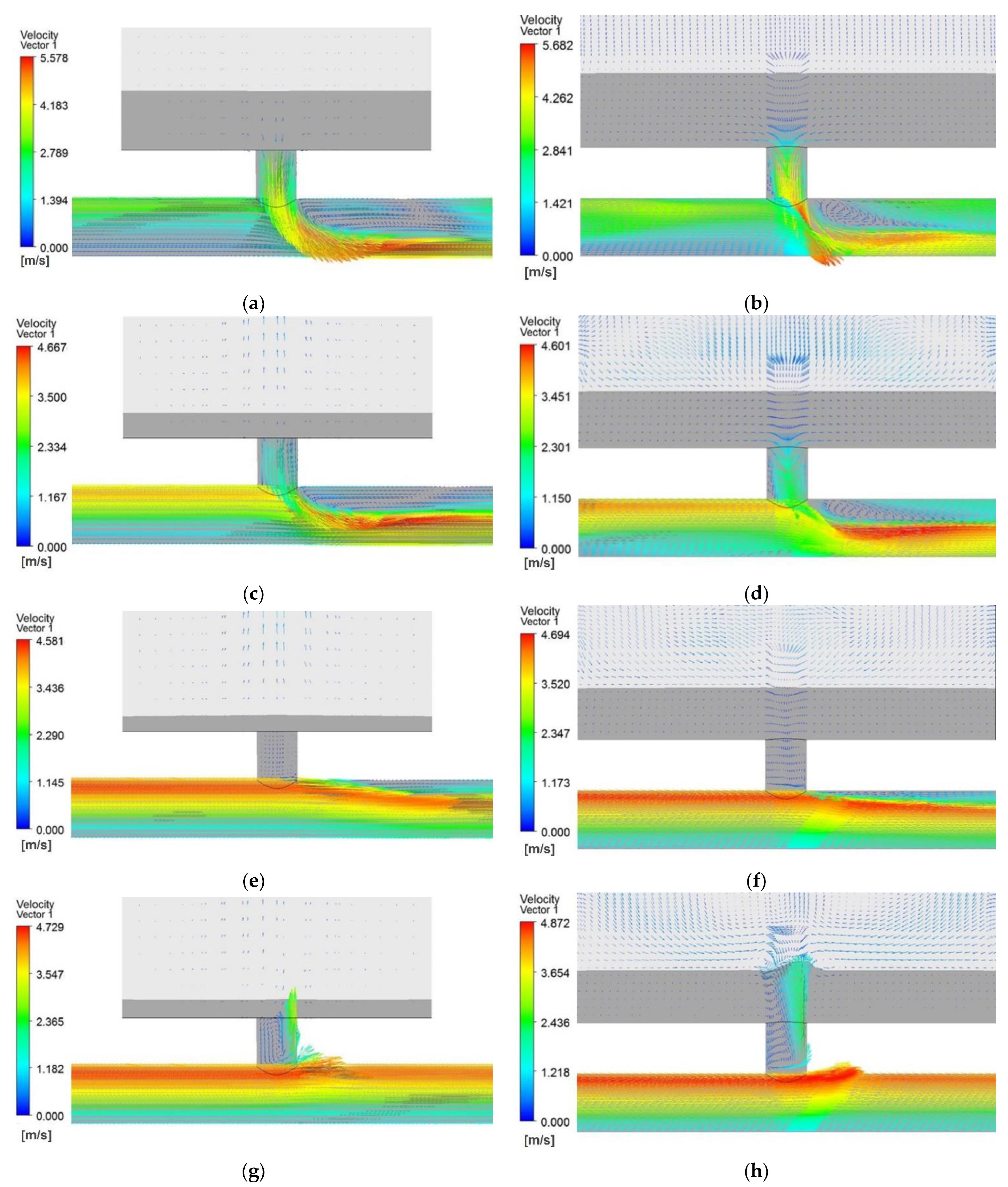
4.3. Flow Regime in the ACSC
5. Conclusions
- Both ACSCs could positively affect water hammer protection under proper initial parameters under LLD. Different implements of such cylinder ACSC had little influence on the water hammer protection. However, the surge and air pressure in the chamber varied considerably in their characteristics. The vertical ACSC with enough water volume had a better performance on safe water depth and smaller maximum air pressure under LLD.
- Both ACSCs had good stability under the transient SLD condition with similar unit speed oscillations. However, the horizontal ACSC was better than the vertical ACSC for its extensive water area to calm the SLD during the transient process and smaller fluctuation of the surge.
- The flow regime of the air–water surface of the horizontal ACSC was more complex than that of the vertical ACSC. It was difficult to form the air-trapped vertical vortices in the chamber for sufficient water depth. Only a surface vortex existed in the horizontal ACSC’s water.
- After a comprehensive comparison, the vertical ACSC was more advisable because of a safer operation under LLD during hydraulic transients.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stephenson, D. Simple Guide for Design of Air Vessels for Water Hammer Protection of Pumping Lines. J. Hydraul. Eng. 2002, 128, 792–797. [Google Scholar] [CrossRef]
- Yazdi, J.; Hokmabadi, A.; JaliliGhazizadeh, M.R. Optimal Size and Placement of Water Hammer Protective Devices in Water Conveyance Pipelines. Water Resour. Manag. 2018, 33, 569–590. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Ahmed, H.; Javed, M.B.; Shahid, U. Numerical analysis and parametric optimization of surge protection devices in a long up-pumping water pipeline. J. Mech. Sci. Technol. 2019, 33, 367–376. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014; 583p. [Google Scholar] [CrossRef]
- Wan, W.; Huang, W.; Li, C. Sensitivity Analysis for the Resistance on the Performance of a Pressure Vessel for Water Hammer Protection. J. Press. Vessel. Technol. Trans. Asme 2014, 136, 3464. [Google Scholar] [CrossRef]
- Lee, T.S. Effects of Air Entrainment on the Ability of Air Vessels in the Pressure Surge Suppressions. J. Fluids Eng. 2000, 122, 499–504. [Google Scholar] [CrossRef]
- Khurana, M. Temperature Distribution in Vertical and Horizontal High Pressure Vessels and its Impact On Food Safety. Ph.D. Thesis, The State University of New Jersey, New Brunswick, NJ, USA, 2012. [Google Scholar]
- Sun, Q.; Wu, Y.; Xu, Y.; Jang, T. Optimal Sizing of an Air Vessel in a Long-Distance Water-Supply Pumping System Using the SQP Method. J. Pipeline Syst. Eng. Pract. 2016, 7, 05016001. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, J.; Yu, X.; Chen, S. Water hammer protective performance of a spherical air vessel caused by a pump trip. Water Supply 2019, 19, 1862–1869. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, J.; Yu, X.-D.; Wang, X.-T.; Chen, X.-Y.; Zhang, Z.-X. Optimal volume selection of air vessels in long-distance water supply systems. J. Water Supply: Res. Technol. 2021, 70, 1053–1065. [Google Scholar] [CrossRef]
- Chaudhry, M.H.; Sabbah, M.A.; Fowler, J.E. Analysis and Stability of Closed Surge Tanks. J. Hydraul. Eng. 1985, 111, 1079–1096. [Google Scholar] [CrossRef]
- Guo, W.C.; Yang, J.D.; Chen, J.P.; Teng, Y. Study on the stability of waterpower-speed control system for hydropower station with air cushion surge chamber. IOP Conf. Series: Earth Environ. Sci. 2014, 22, 42004. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, J.; Chen, S.; He, W.; Yu, X.; Zhu, D.Z. Operational Stability of a Hydropower Plant with a Pipe-Shaped Air-Cushion Surge Chamber. J. Press. Vessel. Technol. 2021, 143, 044501. [Google Scholar] [CrossRef]
- Cai, F.; Cheng, Y.-G.; Xia, L.-S.; Jiang, Y.-Q. Mechanism of air-trapped vertical vortices in long-corridor-shaped surge tank of hydropower station and their elimination. J. Hydrodyn. 2017, 29, 845–853. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Cheng, Y.G.; Liu, K.; Wang, Q.; Yang, F. Optimization of surge tank structures in hydropower station based on VOF method. In Proceedings of the 2nd IAHR—Asia Symposium on Hydraulic Machinery and Systems, Busan, Republic of Korea, 24–25 September 2019. [Google Scholar]
- Vereide, K.; Lia, L.; Nielsen, T.K. Hydraulic scale modelling and thermodynamics of mass oscillations in closed surge tanks. J. Hydraul. Res. 2015, 53, 519–524. [Google Scholar] [CrossRef]
- Vereide, K.; Tekle, T.; Nielsen, T.K. Thermodynamic Behavior and Heat Transfer in Closed Surge Tanks for Hydropower Plants. J. Hydraul. Eng. 2015, 141, 06015002. [Google Scholar] [CrossRef]
- Kheav, K.; Duan, Y.; Egusquiza, M.; Xu, B.; Chen, D.; Egusquiza, E. Transient analysis to air chamber and orifice surge tanks in a hydroelectric generating system during the successive load rejection. Energy Convers. Manag. 2021, 244, 114449. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Aalami, M.T.; Ramos, H.M. Study of a Compressed Air Vessel for Controlling the Pressure Surge in Water Networks: CFD and Experimental Analysis. Water Resour. Manag. 2016, 30, 2687–2702. [Google Scholar] [CrossRef]
- Xia, L.; Cheng, Y.; Zhou, D. 3-D simulation of transient flow patterns in a corridor-shaped air-cushion surge chamber based on com-putational fluid dynamics. J. Hydrodyn. 2013, 25, 249–257. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Yu, X.; Xie, H. Study on Small Fluctuation Stability in Air Cushion Surge Chamber Based on State Space Method. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017. [Google Scholar]
- An, J.; Zhang, J.; Hazrati, A. Safe control of air cushion surge chambers in hydropower systems. Sci. Iran. A 2013, 20, 1605–1611. [Google Scholar]
- Xu, T.; Zhang, J. Study on control mode of operation parameter in hydropower air chamber. MATEC Web Conf. 2018, 246, 01038. [Google Scholar] [CrossRef]
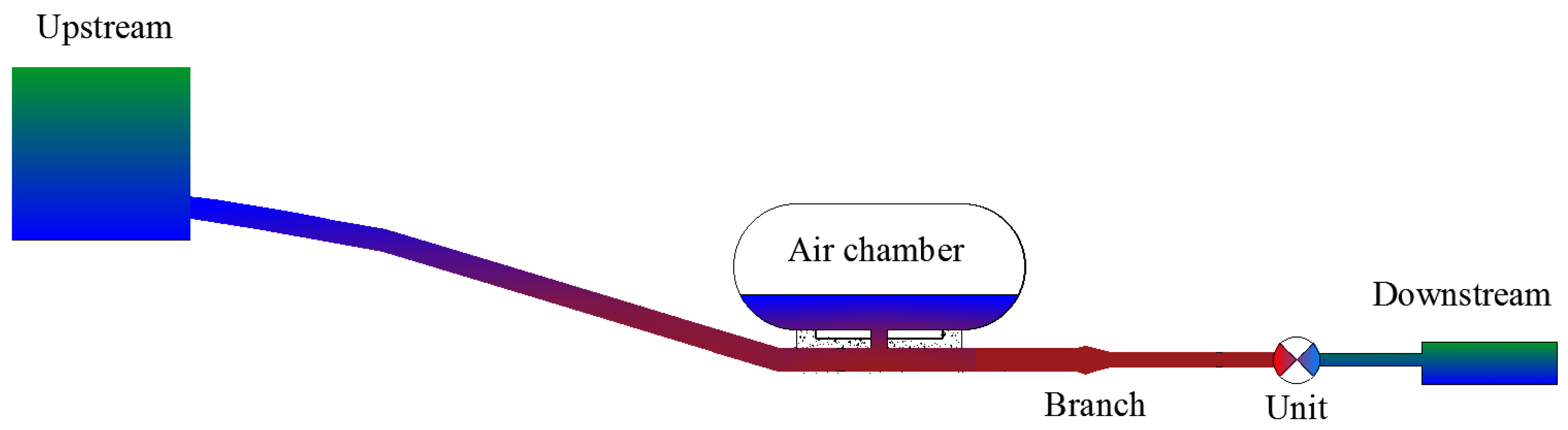



| Parameter | Value |
|---|---|
| Rated water head of the power station (m) | 84.4 |
| Inflow (m3/s) | 4.6 |
| Installed capacity (MW) | 2 × 1.5 |
| Length between upstream and ACSC (m) | 2047.97 |
| Length between ACSC and unit (m) | 31.37 |
| Length between unit and downstream (m) | 4.33 |
| Diameter of the pipe (m) | 1.4 |
| Bottom elevation of ACSC (m) | 1.9 * |
| Diameter of cross-section of ACSC (m) | 7.6 |
| Length of ACSC (m) | 10.0 |
| Diameter of impedance hole of ACSC (m) | 1.0 |
| Number of Cells (M) | Minimum Water Fraction | Time Point (s) | Absolute Relative Error (%) |
|---|---|---|---|
| 24 | 0.163 | 66.8 | |
| 32 | 0.163 | 67.7 | 0.05 |
| 41 | 0.163 | 66.9 | 0.05 |
| 68 | 0.164 | 66.9 | 0.59 |
| Time Steps (s) | Minimum Water Fraction | Time Point (s) | Absolute Relative Error (%) |
|---|---|---|---|
| 0.001 | 0.164 | 67.1 | |
| 0.005 | 0.163 | 66.9 | 0.41 |
| 0.01 | 0.163 | 67.7 | 0.16 |
| 0.02 | 0.152 | 67.4 | 7.03 |
| Condition | Upstream Water Level (m) | Downstream Water Level (m) | Variation of Discharge (m3/s) | Variation of Units |
|---|---|---|---|---|
| A | 98.133 * | 0.38 * | 0→4.6 | 0→2 in 30 s |
| B | 98.923 * | 0.38 * | 4.6→0 | 2→0 in 5 s |
| C | 98.133 * | 0.38 * | 5% load disturbance |
| No. | Condition | (m) | (m3) | ( m4) | Evaluation Index |
|---|---|---|---|---|---|
| 1 | H-A | 2.11 | 528.68 | 0.55 | |
| 2 | H-B | 2.11 | 528.68 | 6.06 | |
| 3 | H-C | 2.11 | 528.68 | 0.49 | |
| 4 | V-A-Z0 | 2.11 | 587.77 | 0.61 | 1D maximum surge in the chamber |
| 1D minimum water depth in the chamber | |||||
| 1D maximum and minimum pressure in the system | |||||
| 3D minimum water fraction in the chamber | |||||
| 3D local flow regime | |||||
| 5 | V-A-C0 | 3.28 | 534.73 | 0.55 | |
| 6 | V-A-V0 | 3.41 | 528.68 | 0.54 | 1D maximum surge in the chamber |
| 7 | V-B-Z0 | 2.11 | 587.78 | 7.03 | 1D minimum water depth in the chamber |
| 8 | V-B-C0 | 3.31 | 533.57 | 6.06 | 1D maximum and minimum pressure in the system |
| 9 | V-B-V0 | 3.41 | 528.68 | 5.98 | |
| 10 | V-C-Z0 | 2.11 | 587.77 | 0.54 | 1D maximum surge in the chamber |
| 11 | V-C-C0 | 3.31 | 534.73 | 0.49 | 1D response time, number of oscillations, maximum relative speed of the units, overshoot, attenuation degree |
| 12 | V-C-V0 | 3.41 | 528.68 | 0.49 |
| No. | First Surge (m) | Range of Absolute Air Pressure (m) | Maximum Head of Spiral Case Outlet (m) | Minimum Head of Draft Tube Inlet (m) |
|---|---|---|---|---|
| 1 | 1.04 | 87.47~103.35 | 95.43 | −1.87 |
| 2 | 0.94 | 91.78~126.07 | 119.22 | −2.36 |
| 4 | 2.15 | 88.66~103.35 | 95.43 | −1.86 |
| 5 | 2.06 | 87.00~102.18 | 95.43 | −1.87 |
| 6 | 2.04 | 86.81~102.04 | 95.43 | −1.86 |
| 7 | 2.35 | 92.40~123.63 | 118.19 | −2.26 |
| 8 | 2.23 | 90.32~124.03 | 119.77 | −2.26 |
| 9 | 2.24 | 90.49~123.99 | 119.63 | −2.26 |
| No. | Surge in Chamber (m) |
Response Time (s) | Number of Oscillations | Maximum Relative Unit Speed | Overshoot (%) |
Attenuation Degree (%) |
|---|---|---|---|---|---|---|
| 3 | 0.09 | 174.0 | 0.5 | 1.066 | 10.07 | 95.48 |
| 10 | 0.20 | 176.0 | 0.5 | 1.066 | 9.21 | 96.11 |
| 11 | 0.19 | 171.5 | 0.5 | 1.067 | 10.93 | 94.82 |
| 12 | 0.19 | 171.5 | 0.5 | 1.067 | 10.93 | 94.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Chen, S.; Zhang, J.; Yu, X.; Lyu, J.; Yan, H. Comparison on Hydraulic Characteristics of Vertical and Horizontal Air-Cushion Surge Chambers in the Hydropower Station under Load Disturbances. Energies 2023, 16, 1501. https://doi.org/10.3390/en16031501
Xu T, Chen S, Zhang J, Yu X, Lyu J, Yan H. Comparison on Hydraulic Characteristics of Vertical and Horizontal Air-Cushion Surge Chambers in the Hydropower Station under Load Disturbances. Energies. 2023; 16(3):1501. https://doi.org/10.3390/en16031501
Chicago/Turabian StyleXu, Tingyu, Sheng Chen, Jian Zhang, Xiaodong Yu, Jiawen Lyu, and Haibin Yan. 2023. "Comparison on Hydraulic Characteristics of Vertical and Horizontal Air-Cushion Surge Chambers in the Hydropower Station under Load Disturbances" Energies 16, no. 3: 1501. https://doi.org/10.3390/en16031501






