Water Entry of a Heated Axisymmetric Vertical Cylinder
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Quenching Experiment
| Temperature T, (K) | Heat Conductivity λ (W/mK) | Specific Heat c (kJ/kgK) | Density ρ (kg/m3) | Thermal Diffusivity a (mm2/s) |
|---|---|---|---|---|
| 300.15 | 14.80 | 0.4440 | 8420 | 3.9600 |
| 368.45 | 15.84 | 0.4801 | 3.9178 | |
| 468.95 | 17.36 | 0.5038 | 4.0925 | |
| 478.15 | 17.50 | 0.5038 | 4.1253 | |
| 619.75 | 19.77 | 0.5041 | 4.6583 | |
| 827.15 | 23.10 | 0.5453 | 5.0314 | |
| 869.15 | 23.80 | 0.5536 | 5.1059 | |
| 935.15 | 24.90 | 0.5958 | 4.9634 | |
| 1069.45 | 27.14 | 0.6817 | 4.7280 |
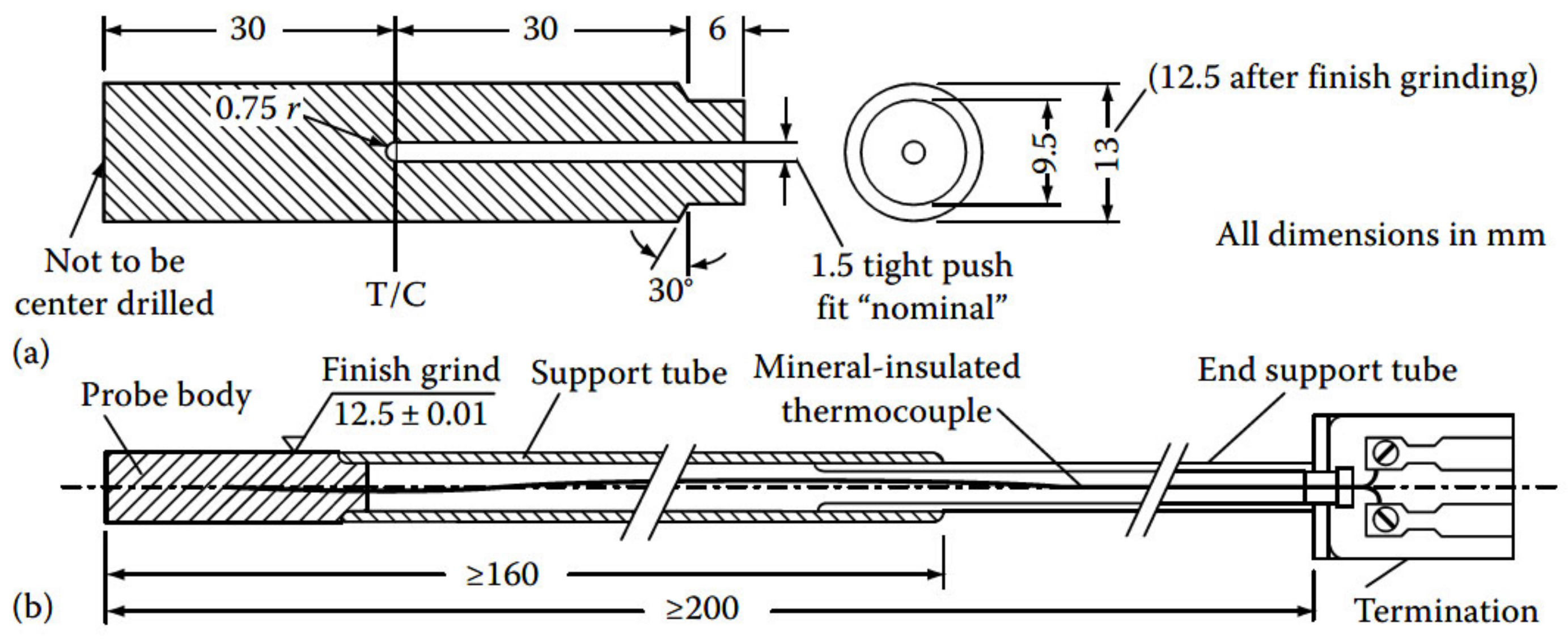
2.2. Mathematical Modeling of an Immersion Process
2.2.1. The Eulerian Two-Fluid VOF Model
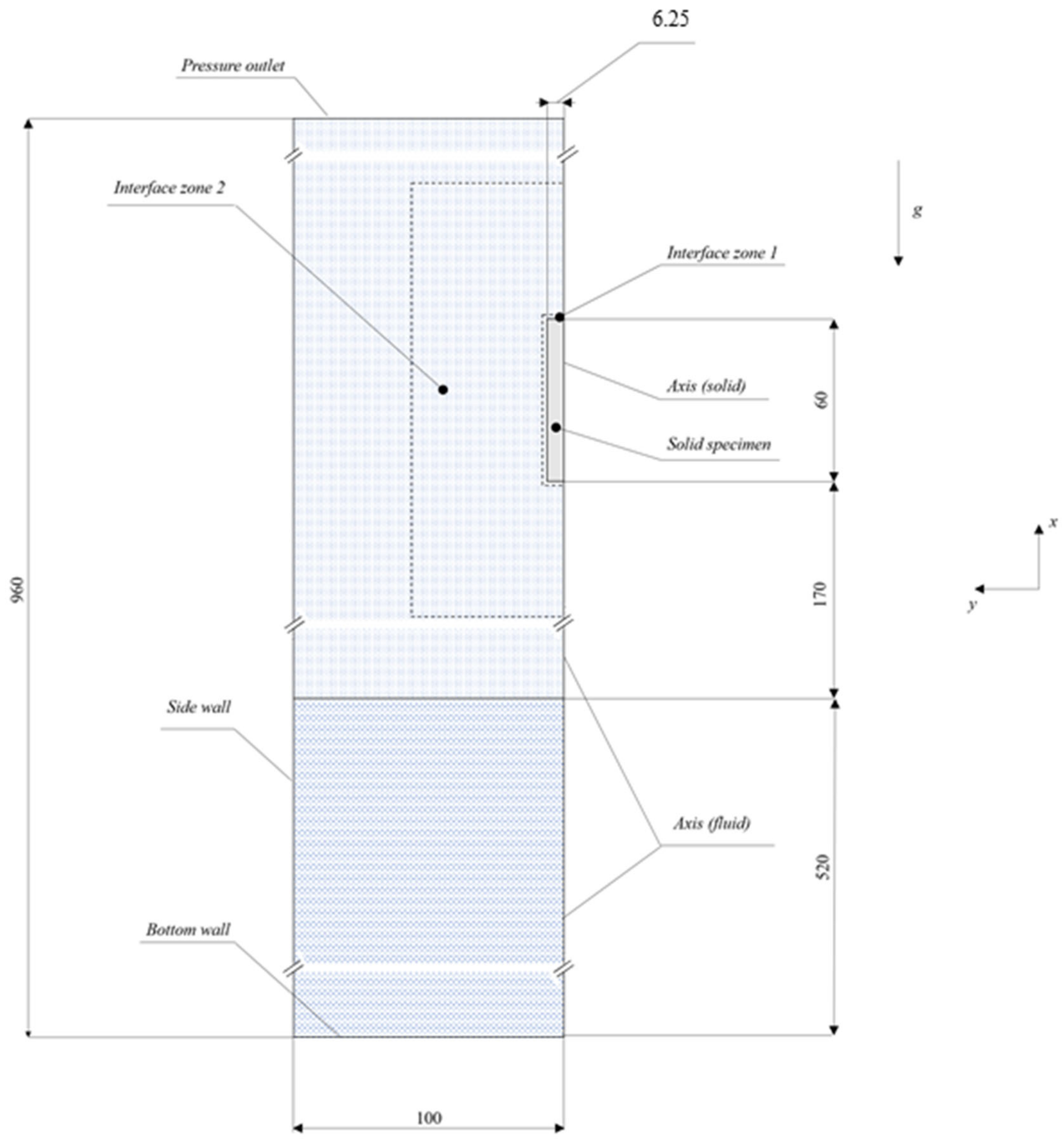
2.2.2. Geometry Domains
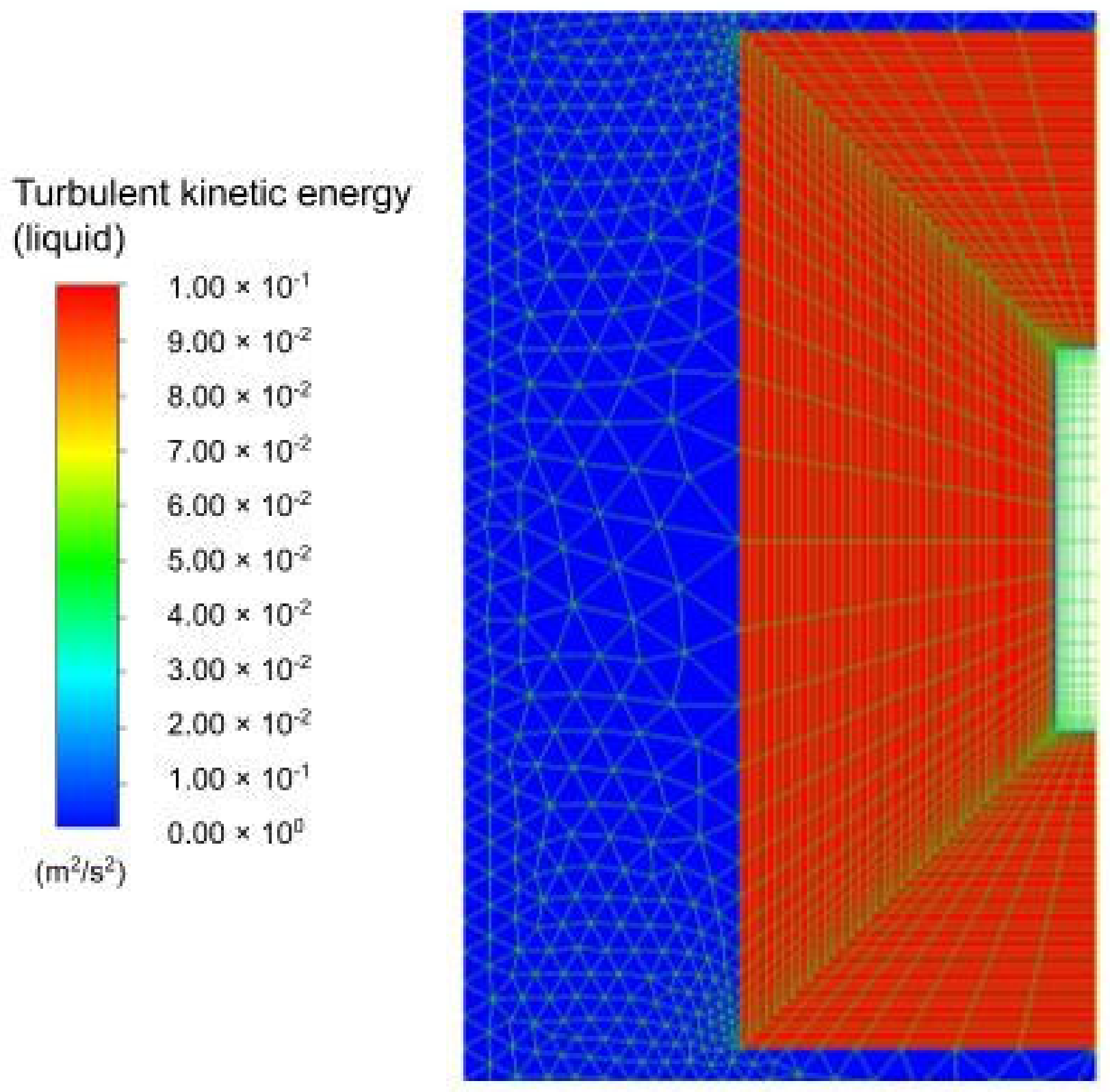
2.3. Generating a Finite Volume Mesh
2.4. Turbulence Modeling
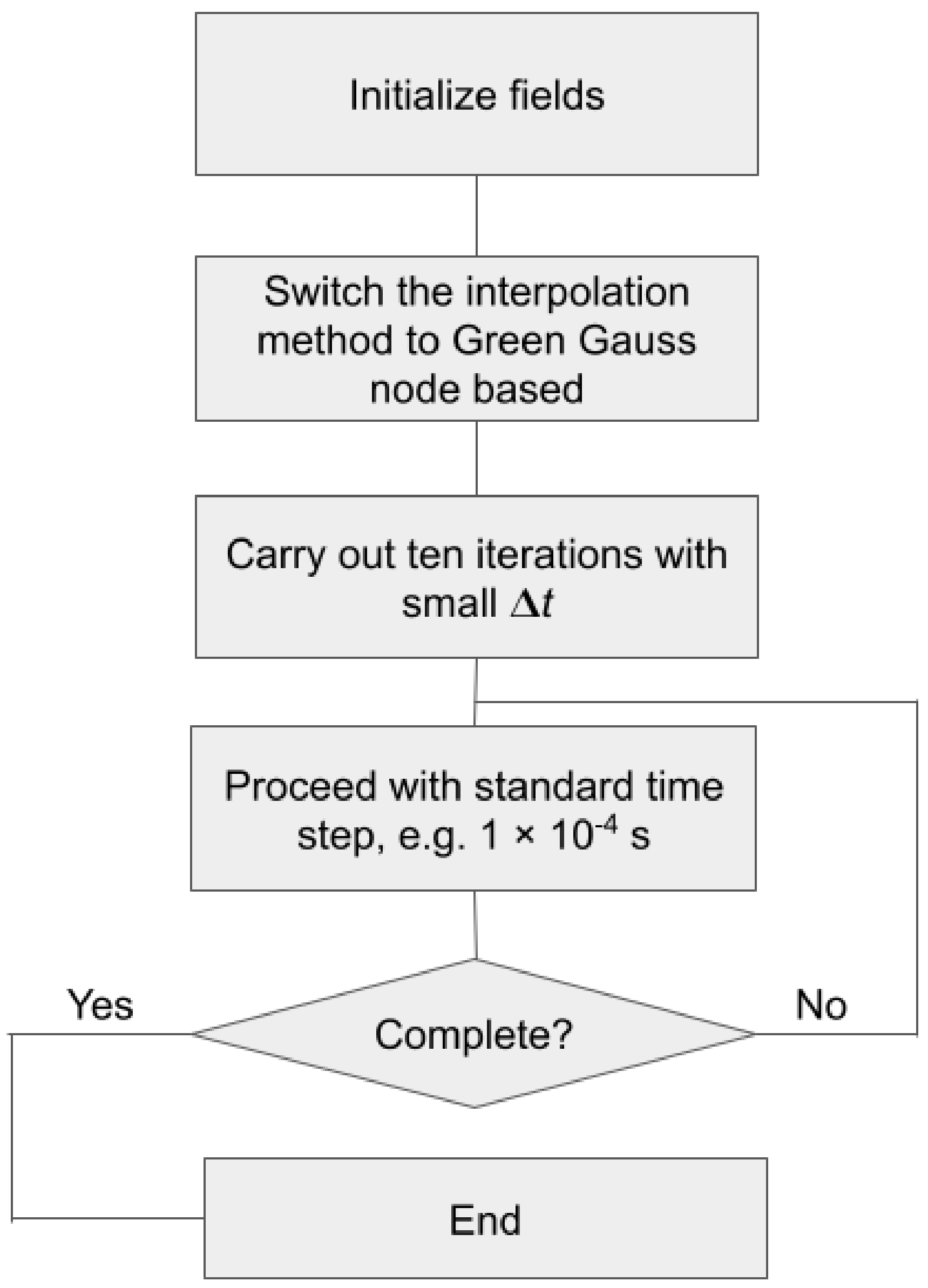
2.5. Solution Procedure
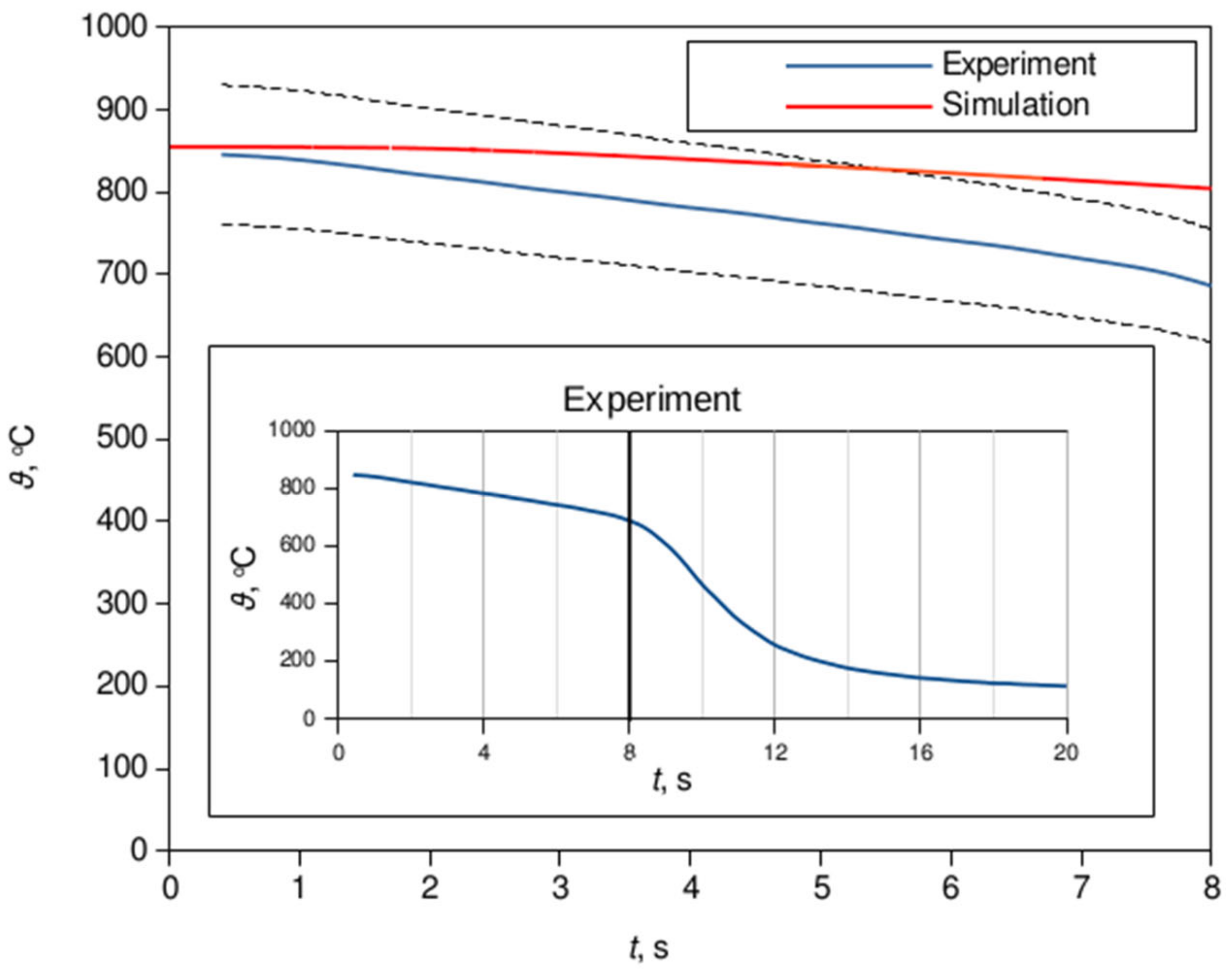
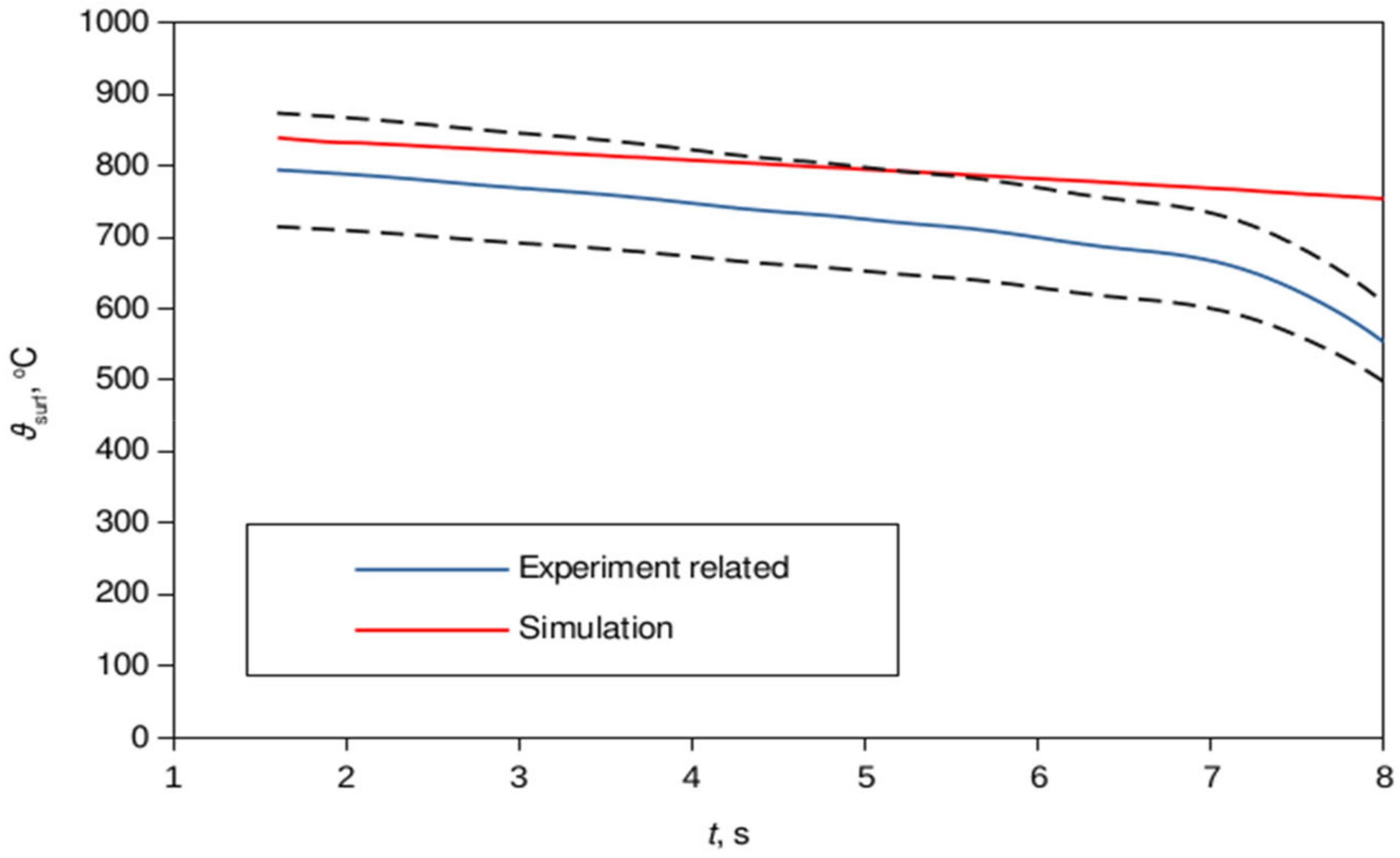
3. Results and Discussion
4. Conclusions
5. Future Work Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toso, N.R.S. Contribution to the Modelling and Simulation of Aircraft Structures Impacting on Water. (Beitrag zur Modellierung und Simulation von Luftfahrtstrukturen beim Wasseraufprall). Ph.D. Thesis, Stuttgart University, Stuttgart, Germany, 2009. [Google Scholar] [CrossRef]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid Based Simulation Method for Wave Impact Problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Bašić, J.; Degiuli, N.; Werner, A. Simulation of Water Entry and Exit of a Circular Cylinder Using the ISPH Method. Trans. FAMENA 2014, 38, 45–62. [Google Scholar]
- Yu, P.; Shen, C.; Zhen, C.; Tang, H.; Wang, T. Parametric Study on the Free-Fall Water Entry of a Sphere by Using the RANS Method. J. Mar. Sci. Eng. 2019, 7, 122. [Google Scholar] [CrossRef]
- Lu, Y.; Del Buono, A.; Xiao, T.; Iafrati, A.; Xu, J.; Deng, S.; Chen, J. Parametric Study on the Water Impacting of a Free-Falling Symmetric Wedge Based on the Extended von Karman’s Momentum Theory. Ocean. Eng. 2023, 271, 113773. [Google Scholar] [CrossRef]
- Li, J.-C.; Wei, Y.-J.; Wang, C.; Xia, W.-X. Cavity Formation during Water Entry of Heated Spheres. Chin. Phys. B 2018, 27, 094703. [Google Scholar] [CrossRef]
- Jetly, A.; Vakarelski, I.U.; Yang, Z.; Thoroddsen, S.T. Giant Drag Reduction on Leidenfrost Spheres Evaluated from Extended Free-Fall Trajectories. Exp. Therm. Fluid Sci. 2019, 102, 181–188. [Google Scholar] [CrossRef]
- Gylys, J.; Skvorčinskienė, R.; Paukštaitis, L. Peculiarities of the Leidenfrost Effect Application for Drag Force Reduction. Mechanics 2014, 20, 266–273. [Google Scholar] [CrossRef]
- Felde, I. Új Módszer Acélok Edzéséhez Használatos Hűtőközegek Hűtőképességének Minősítésére. Ph.D. Thesis, Miskolci Egyetem, Miskolc, Hungary, 2007. [Google Scholar]
- Demirel, C. Experimentelle Untersuchung und Simulation des Abschreckprozesses von Bauteilähnlichen Geometrien aus G-AlSi7Mg. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 2009. [Google Scholar]
- Landek, D.; Župan, J.; Filetin, T. A Prediction of Quenching Parameters Using Inverse Analysis. Matls. Perf. Charact. 2014, 3, 229–241. [Google Scholar] [CrossRef]
- Troell, E.; Kristoffersen, H.; Bodin, J.; Segerberg, S.; Felde, I. Unique Software Bridges the Gap between Cooling Curves and the Result of Hardening∗. HTM J. Heat Treat. Mater. 2007, 62, 110–115. [Google Scholar] [CrossRef]
- Landek, D. Models and Algorithms for Computer-Aided Planning of Induction Hardening Process. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2005. [Google Scholar]
- Tenzer, F.M. Heat Transfer during Transient Spray Cooling: An Experimental and Analytical Study. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2020. [Google Scholar]
- Jagga, S.; Vanapalli, S. Cool-down Time of a Polypropylene Vial Quenched in Liquid Nitrogen. Int. Commun. Heat Mass Transf. 2020, 118, 104821. [Google Scholar] [CrossRef]
- Afify, M.; Gentile, D.; Llory, M. Courbes d’ébullition en convection forcée. Deuxième partie: Effets paramétriques et corrélations. Houille Blanche 1986, 72, 463–474. [Google Scholar] [CrossRef][Green Version]
- ISO 9950:1995; Industrial Quenching Oils—Determination of Cooling Characteristics—Nickel-Alloy Probe Test Method. International Organization for Standardization: Geneva, Switzerland, 1995.
- Župan, J.; Landek, D.; Filetin, T. Cooling Characteristics of Water Based Nanofluids with Agitation. Mater. Perform. Charact. 2014, 3, 326–336. [Google Scholar] [CrossRef]
- Liščić, B.; Tensi, H.M.; Canale, L.C.F.; Totten, G.E. Quenching Theory and Technology; CRC Press & Taylor & Francis Group, LCC.: Boca Raton, FL, USA, 2010. [Google Scholar]
- Cukrov, A.; Sato, Y.; Boras, I.; Ničeno, B. A Solution to Stefan Problem Using Eulerian Two-Fluid VOF Model. Brodogr. Teor. Praksa Brodogr. Pomor. Teh. 2021, 72, 141–164. [Google Scholar] [CrossRef]
- Zhu, H.J.; Lin, Y.H.; Xie, L.H. FLUENT Fluid Analysis and Simulation Practical Tutorial; People’s Posts and Telecommunications Press: Beijing, China, 2010. [Google Scholar]
- Cukrov, A.; Sato, Y.; Boras, I.; Ničeno, B. Film Boiling around a Finite Size Cylindrical Specimen—A Transient Conjugate Heat Transfer Approach. Appl. Sci. 2023, 13, 9144. [Google Scholar] [CrossRef]
- Aubram, D. An Arbitrary Lagrangian-Eulerian Method for Penetration into Sand at Finite Deformation. Ph.D. Thesis, TU Berlin, Berlin, Germany, 2014. [Google Scholar]
- Hannoschöck, N. Wärmeleitung und -Transport: Grundlagen der Wärme- und Stoffübertragung; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-662-57571-0. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Grubišić, L.; Lacmanović, D.; Tambača, J. Preconditioning the Quad Dominant Mesh Generator for Ship Structural Analysis. Algorithms 2022, 15, 2. [Google Scholar] [CrossRef]
- Gauss, F.; Lucas, D.; Krepper, E. Grid Studies for the Simulation of Resolved Structures in an Eulerian Two-Fluid Framework. Nucl. Eng. Des. 2016, 305, 371–377. [Google Scholar] [CrossRef]
- Liu, Y.; Pointer, W.D. Eulerian Two-Fluid RANS-Based CFD Simulations of a Helical Coil Steam Generator Boiling Tube; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2017. [Google Scholar]
- Yoshikawa, M. A Study on Wind Load Estimation of High-Rise Buildings by Unstructured Grid LES. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2016. [Google Scholar]
- Kharangate, C.R.; Mudawar, I. Review of Computational Studies on Boiling and Condensation. Int. J. Heat Mass Transf. 2017, 108, 1164–1196. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Makris, C.V.; Memos, C.D.; Krestenitis, Y.N. Numerical Modeling of Surf Zone Dynamics under Weakly Plunging Breakers with SPH Method. Ocean. Model. 2016, 98, 12–35. [Google Scholar] [CrossRef]
- Čančarević, M. Približno rješavanje nelinearnih sustava (Newton–Raphsonova metoda). Poučak Čas. Metod. Nastavu Mat. 2010, 11, 64–72. [Google Scholar]
- Momoki, S.; Yamada, T.; Shigechi, T.; Kanemaru, K.; Yamaguchi, T. Film Boiling Around a Vertical Cylinder with Top and Bottom Horizontal Surfaces; American Society of Mechanical Engineers Digital Collection. In Proceedings of the ASME/JSME 2007 Thermal Engineering Heat Transfer Summer Conference, Vancouver, BC, Canada, 8–12 July 2007; pp. 611–619. [Google Scholar]
- Rohatgi, A. WebPlotDigitizer, Version 4.5; Pacifica, CA, USA. 2021. Available online: https://automeris.io/WebPlotDigitizer/ (accessed on 19 August 2022).
- Takamatsu, H.; Yamashiro, H.; Honda, H. Theoretical Analysis of the Stability of Vapor Film in Subcooled Film Boiling on a Horizontal Wire. Heat Transf. Jpn. Res. 1997, 26, 219–235. [Google Scholar] [CrossRef]
- Degiuli, N.; Farkas, A.; Martić, I.; Zeman, I.; Ruggiero, V.; Vasiljević, V. Numerical and Experimental Assessment of the Total Resistance of a Yacht. Brodogr. Teor. Praksa Brodogr. Pomor. Teh. 2021, 72, 61–80. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cukrov, A.; Landek, D.; Sato, Y.; Boras, I.; Ničeno, B. Water Entry of a Heated Axisymmetric Vertical Cylinder. Energies 2023, 16, 7926. https://doi.org/10.3390/en16247926
Cukrov A, Landek D, Sato Y, Boras I, Ničeno B. Water Entry of a Heated Axisymmetric Vertical Cylinder. Energies. 2023; 16(24):7926. https://doi.org/10.3390/en16247926
Chicago/Turabian StyleCukrov, Alen, Darko Landek, Yohei Sato, Ivanka Boras, and Bojan Ničeno. 2023. "Water Entry of a Heated Axisymmetric Vertical Cylinder" Energies 16, no. 24: 7926. https://doi.org/10.3390/en16247926
APA StyleCukrov, A., Landek, D., Sato, Y., Boras, I., & Ničeno, B. (2023). Water Entry of a Heated Axisymmetric Vertical Cylinder. Energies, 16(24), 7926. https://doi.org/10.3390/en16247926







