Numerical Tracking of Natural Gas Migration in Underground Gas Storage with Multilayered Sandstone and Fault-Bearing Caprocks
Abstract
:1. Introduction
2. Sealing Mechanism of Fault-Bearing Caprocks
3. Mathematical Models
4. Numerical Model Setup
4.1. Simplified Geological Model
4.2. Formation Properties, Initial and Boundary Conditions
4.3. Different Conditions in Sensitivity Case Studies
5. Results and Discussion
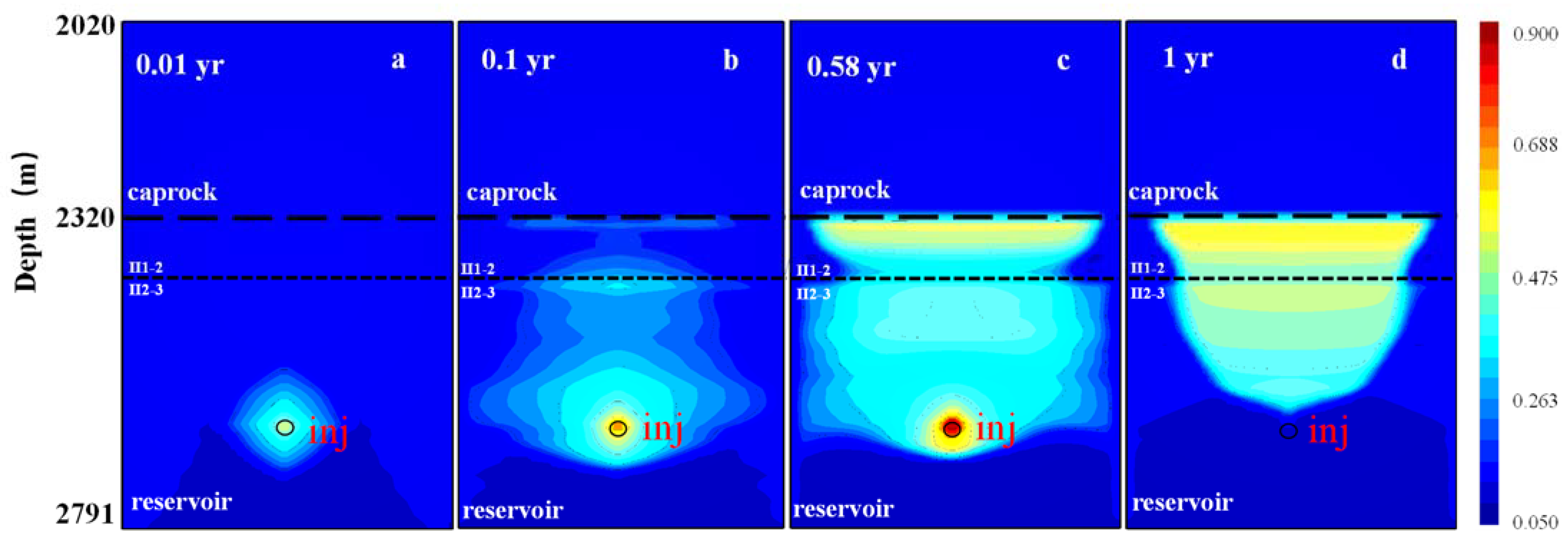
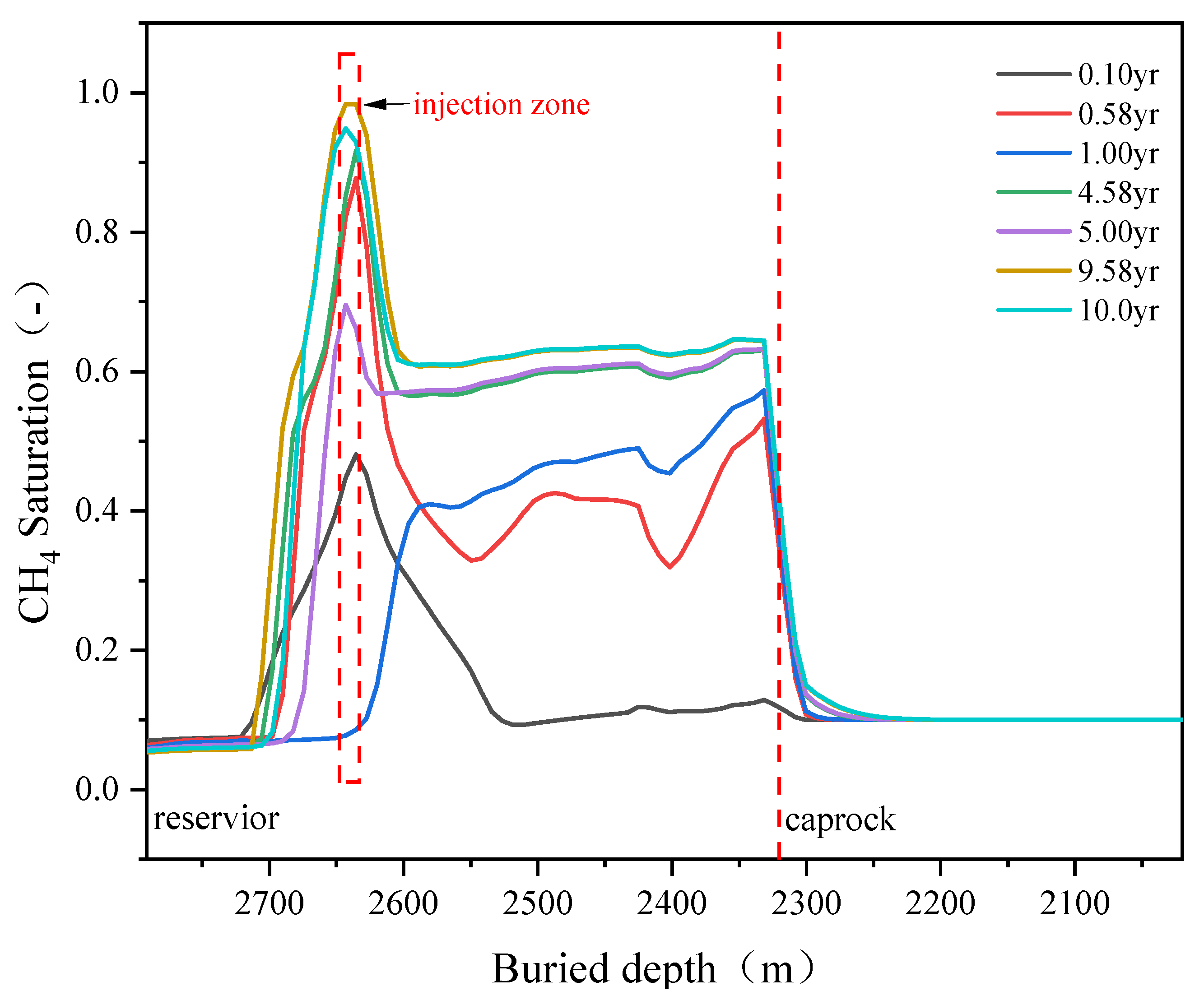
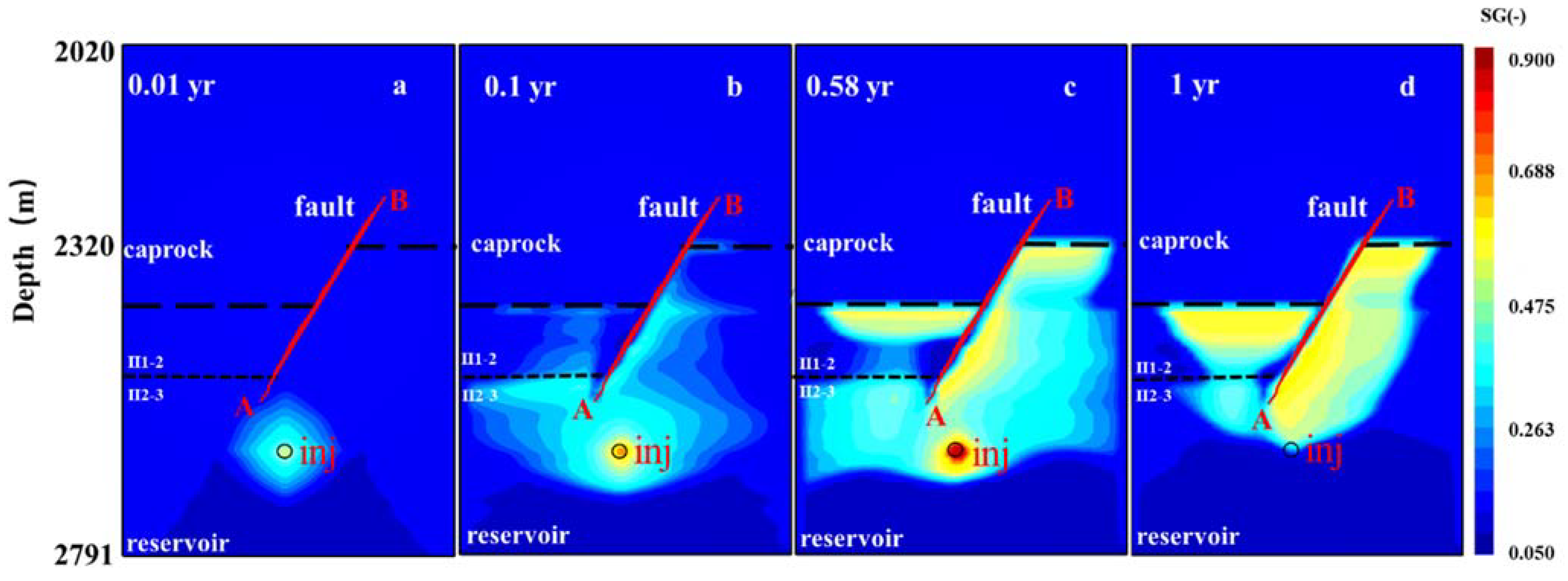
5.1. Natural Gas Migration in the UGS without Considering Faults
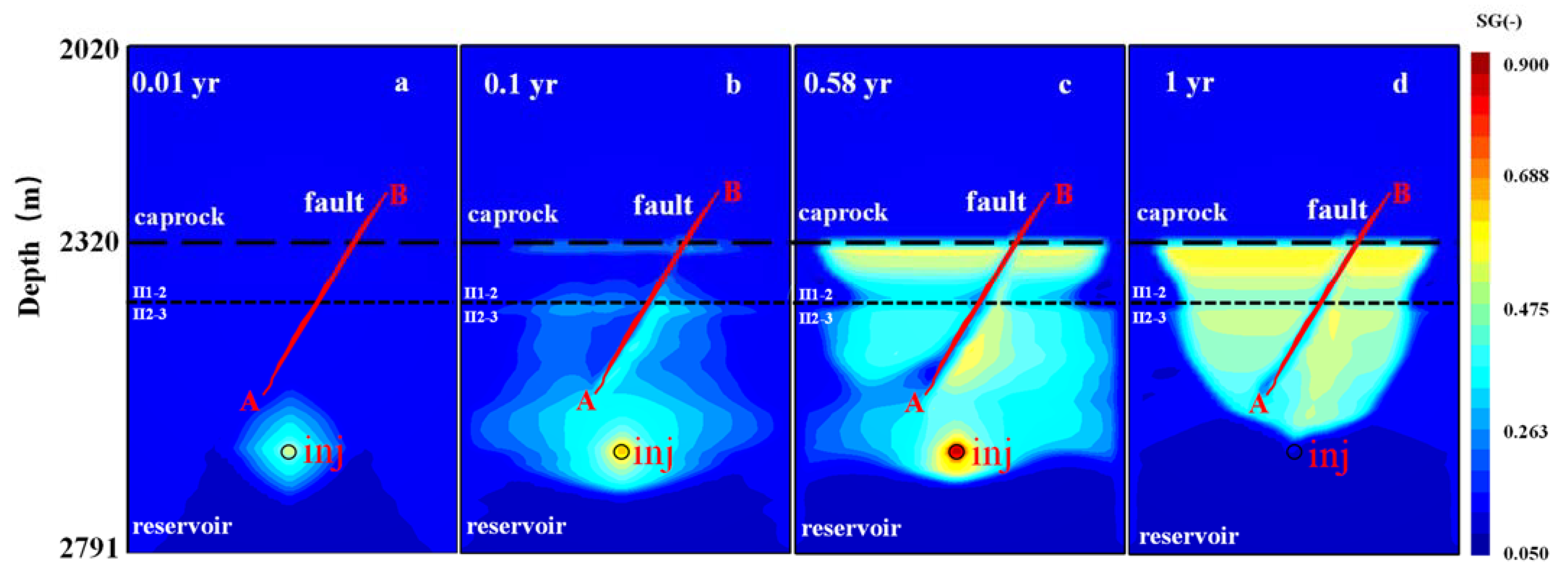
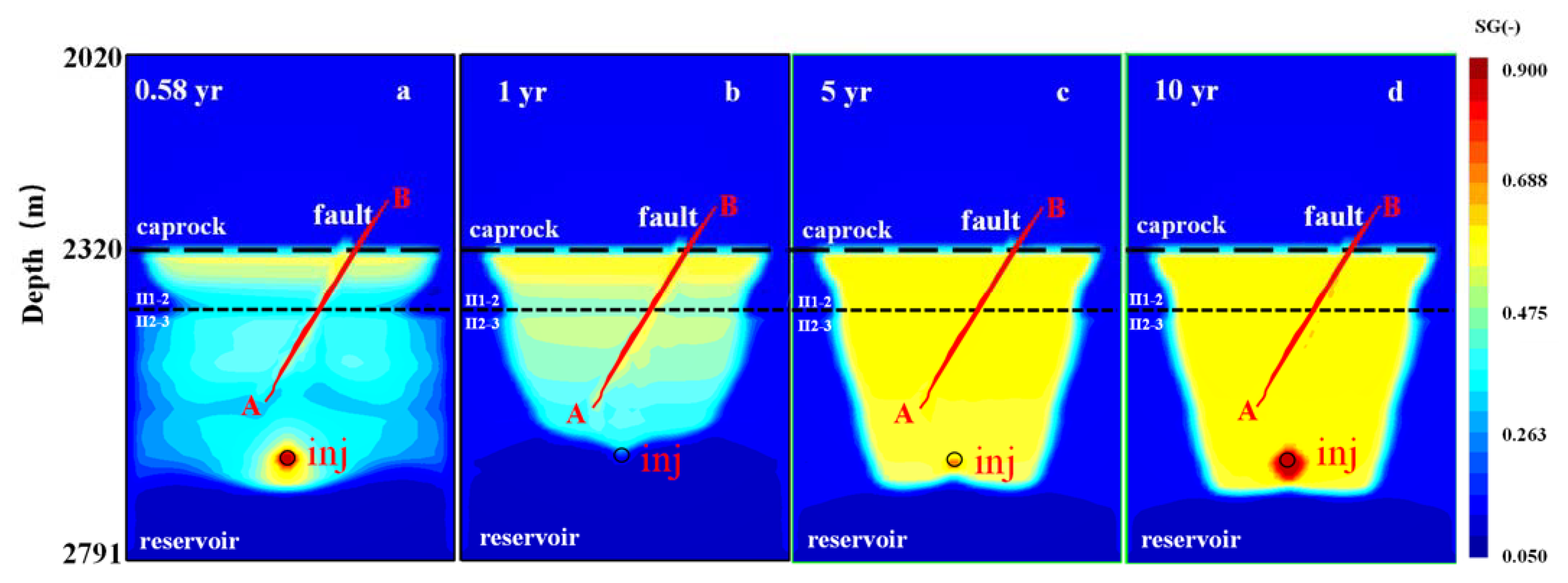
5.1.1. Spatial Distribution of Natural Gas during the Gas Injection and Production Process
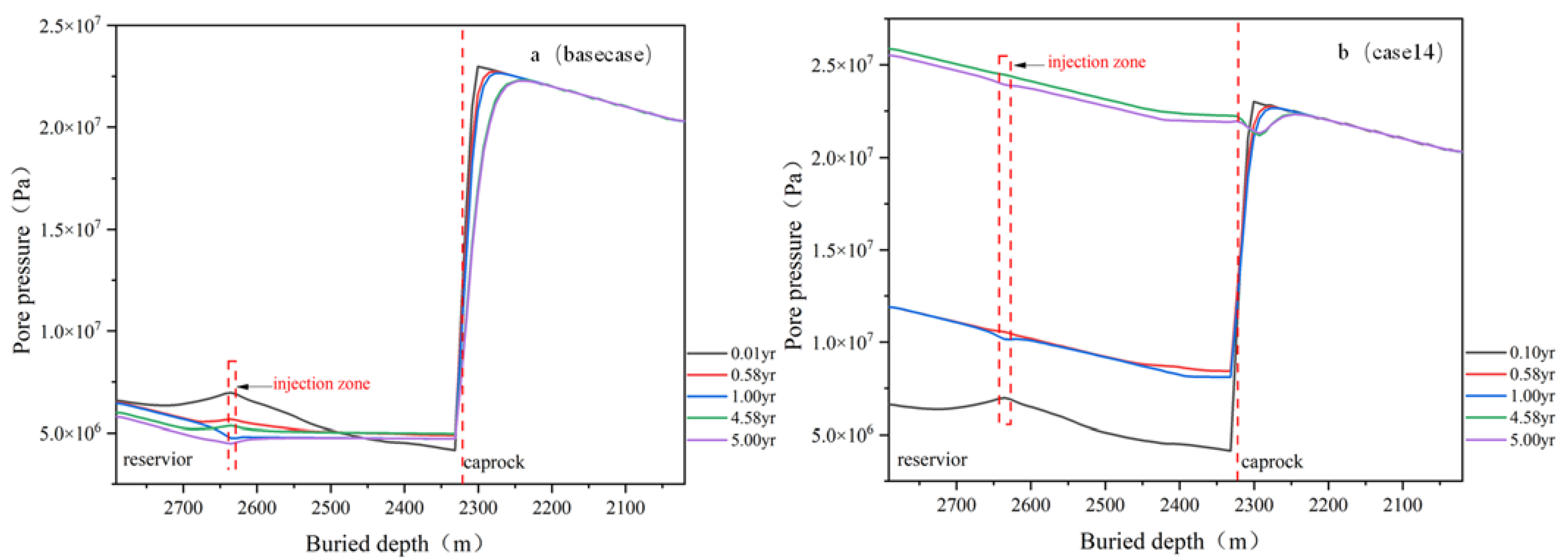
5.1.2. Pore Pressure Dissipation during the Gas Injection and Production Process
5.2. Migration of Natural Gas in UGSs with Internal Faults
5.2.1. Influence of Initial Permeability of Fault Zone
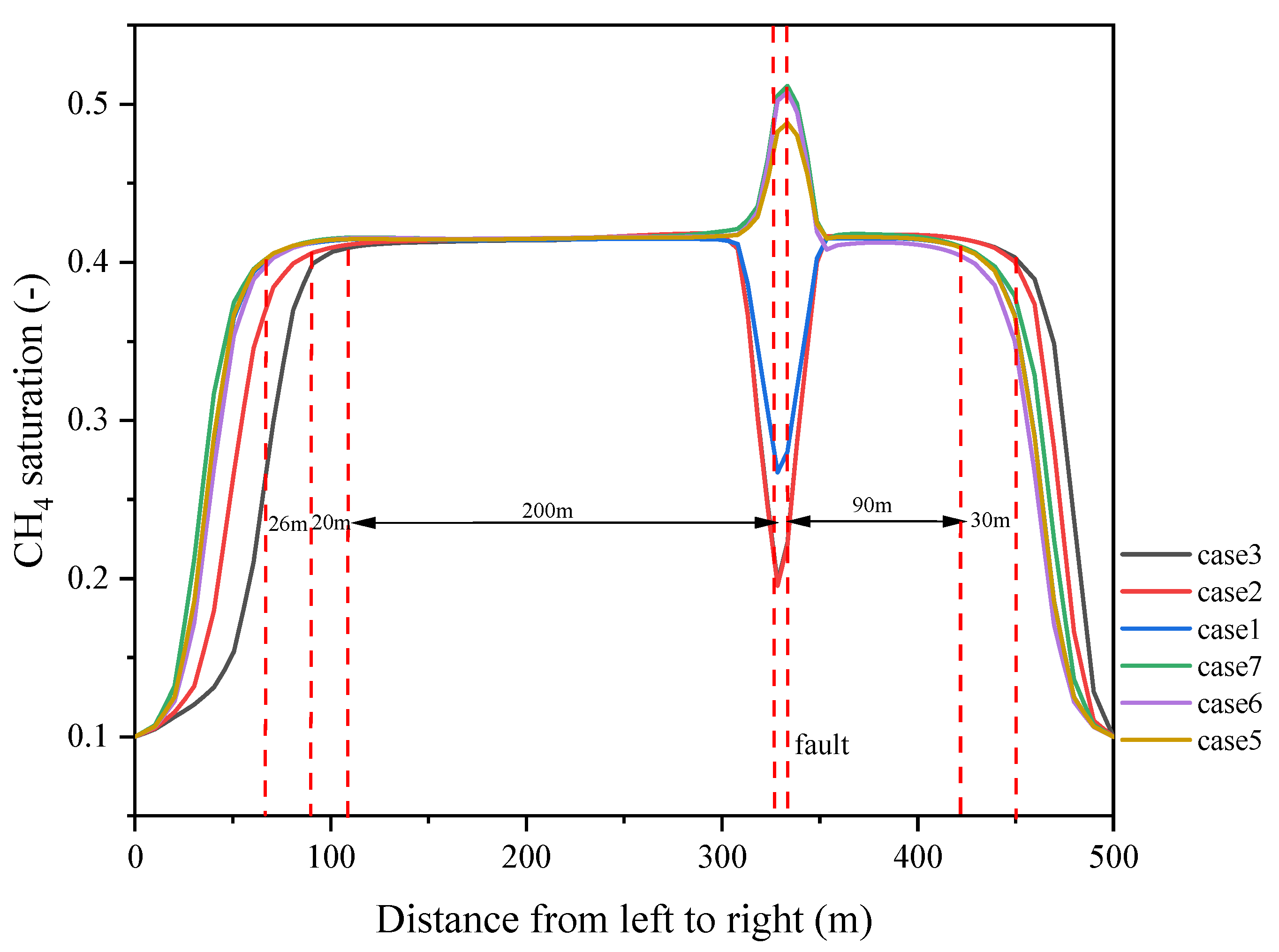
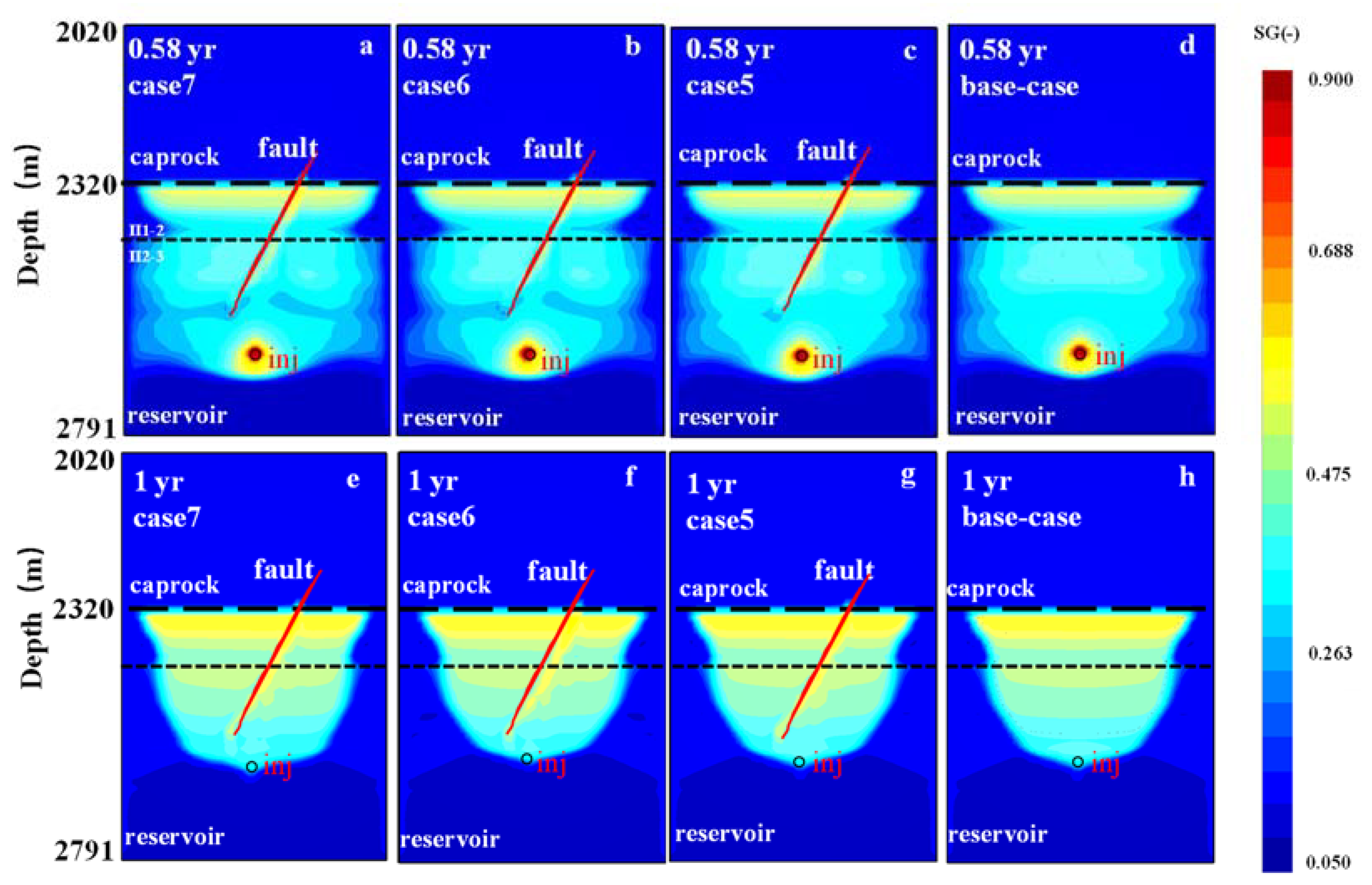
5.2.2. Influence of Fault Scale
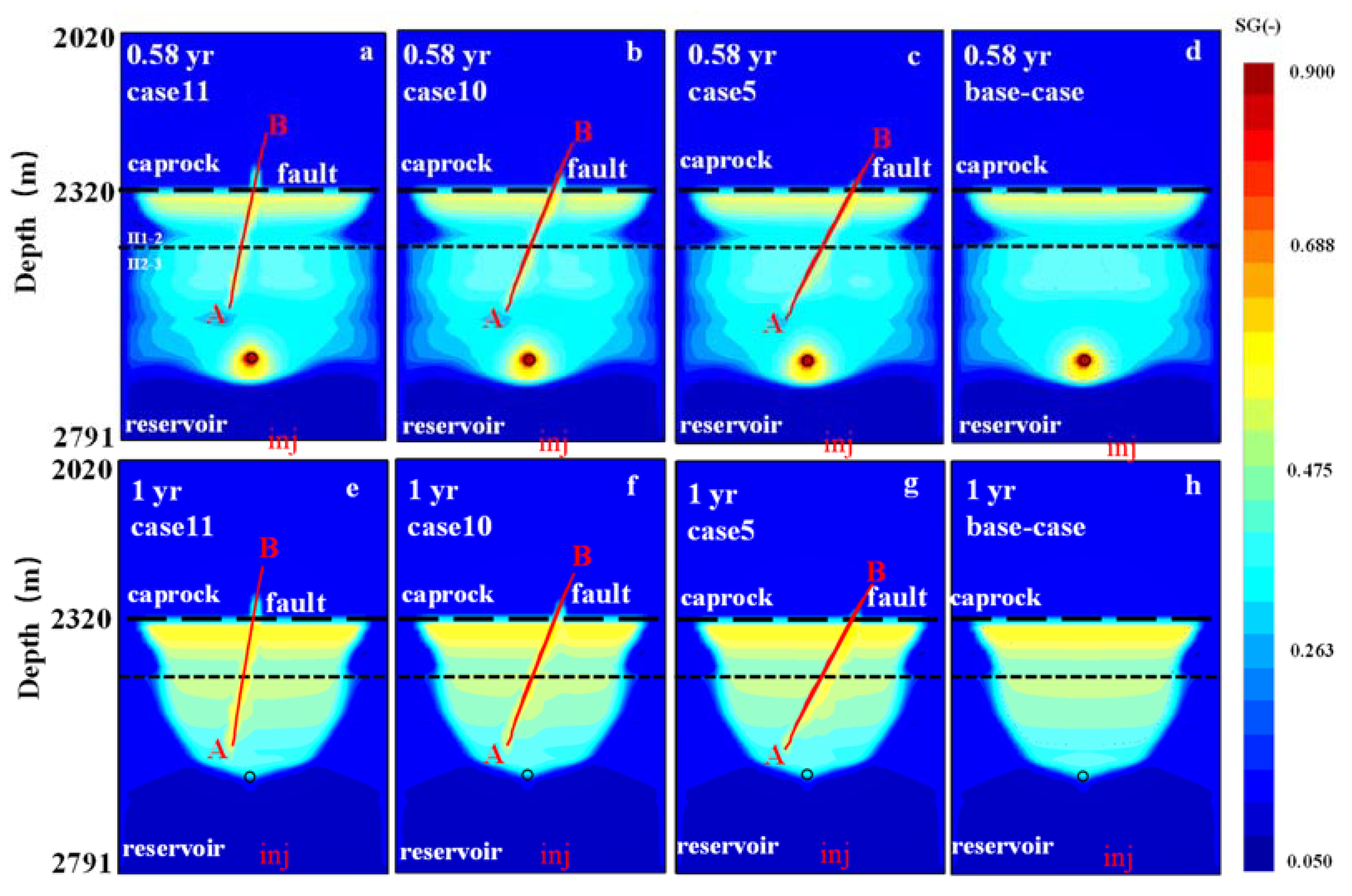
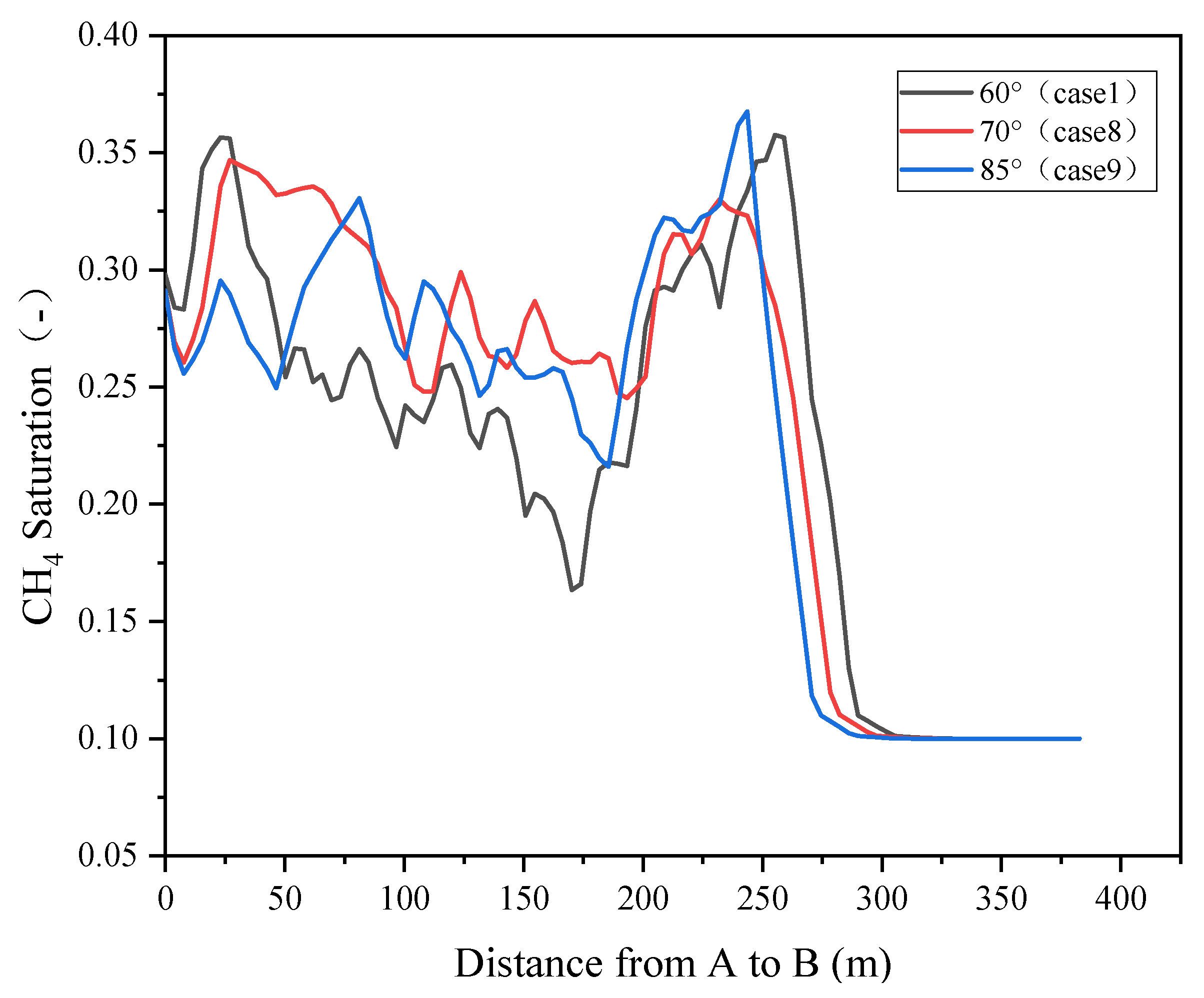
5.2.3. Influence of Fault Dip Angle
5.2.4. Influence of Fault Type
6. Conclusions
- Reservoir pressure is strongly disturbed during the cyclic high rate injection and production of natural gas in underground gas storage engineering, especially at the periphery of wells. Formation anisotropy leads to an obvious difference in the gas front in different layers, due to lateral and vertical migration of natural gas, which is strongly constrained by relatively low permeability layers.
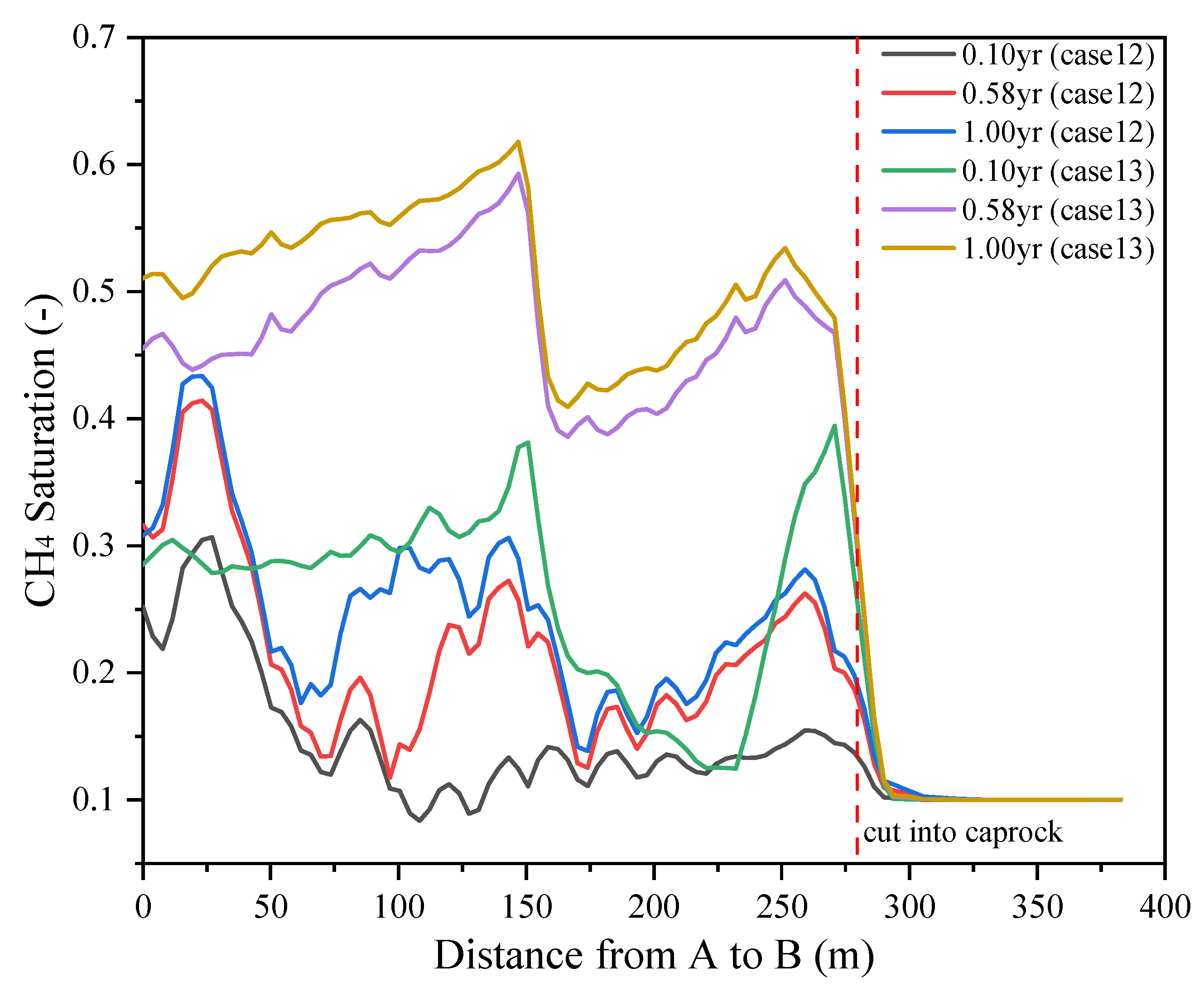
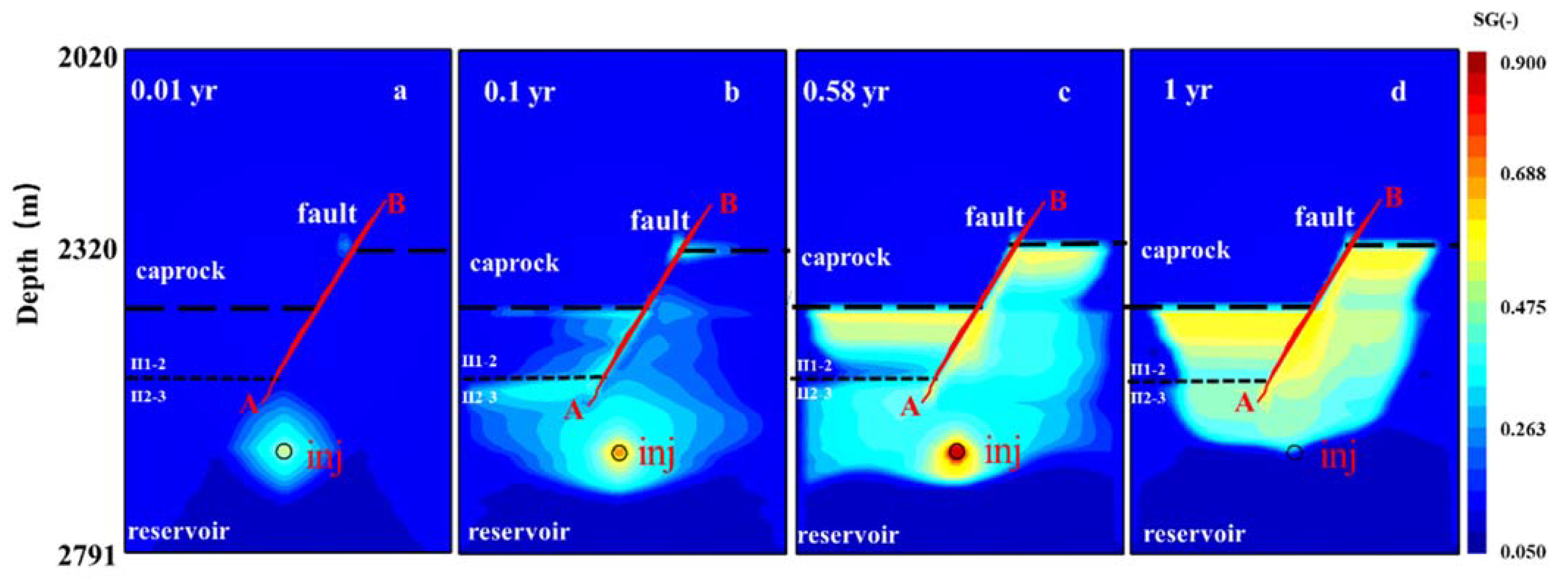
- Fault permeability is the most important factor controlling natural gas migration along the fault zone, causing the high concentration of natural gas distributed along the fault strike direction in the high permeability fault zone. Limited natural gas entering into the caprocks through the fault partially penetrating into the upper caprocks, which does not obviously deteriorate the sealing performance of the caprocks.
- Based on the gas saturation at the top of the fault zone in the caprocks (Y = 0 m, Z = −2320 m), when the dip angle of the fault with high permeability is in the range of 60° to 85°, the gas saturation varies from 0.4 to 0.55 at the end of injection of the first cycle. When the fault length is in the range of 10 m to 500 m and the dip angle of fault is 60°, the gas saturation varies from 0.45 to 0.5. The gas saturation does not change obviously when the normal fault with displacement is considered. This illustrates that fault permeability plays the most important role in controlling the gas breakthrough in caprocks affected by fault zones, followed by the fault dip angle, the fault length, etc.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, P.; Lv, Y.; Wen, W. The Low-Carbon Transition of Energy Systems: A Bibliometric Review from an Engineering Management Perspective. Engineering 2023. [Google Scholar] [CrossRef]
- Wang, X.; Economides, M.J. Purposefully built underground natural gas storage. J. Nat. Gas Sci. Eng. 2012, 9, 130–137. [Google Scholar] [CrossRef]
- Demirel, N.C.; Demirel, T.; Deveci, M.; Vardar, G. Location selection for underground natural gas storage using Choquet integral. J. Nat. Gas Sci. Eng. 2017, 45, 368–379. [Google Scholar] [CrossRef]
- Mohanty, U.S.; Ali, M.; Azhar, M.R.; Al-Yaseri, A.; Keshavarz, A.; Iglauer, S. Current advances in syngas (CO + H2) production through bi-reforming of methane using various catalysts: A review. Int. J. Hydrogen Energy 2021, 46, 32809–32845. [Google Scholar] [CrossRef]
- Wei, X.; Shi, X.; Hu, W.; Ban, S.; Li, Y.; Ma, H.; Li, P.; Yang, C. Dynamic tightness evaluation of salt cavern energy storage. J. Energy Storage 2023, 57, 106313. [Google Scholar] [CrossRef]
- Zhang, G.; Li, B.; Zheng, D.; Ding, G.; Wei, H.; Qian, P.; Li, C. Challenges to and proposals for underground gas storage (UGS) business in China. Nat. Gas Ind. B 2017, 4, 231–237. [Google Scholar] [CrossRef]
- Zhang, N.; Shi, X.; Zhang, Y.; Shan, P. Tightness analysis of underground natural gas and oil storage caverns with limit pillar widths in bedded rock salt. IEEE Access 2020, 8, 12130–12145. [Google Scholar] [CrossRef]
- Wang, T.; Li, J.; Jing, G.; Zhang, Q.; Yang, C.; Daemen, J.J.K. Determination of the maximum allowable gas pressure for an underground gas storage salt cavern—A case study of Jintan, China. J. Rock Mech. Geotech. Eng. 2019, 11, 251–262. [Google Scholar] [CrossRef]
- Iglauer, S.; Akhondzadeh, H.; Abid, H.; Paluszny, A.; Keshavarz, A.; Ali, M.; Giwelli, A.; Esteban, L.; Sarout, J.; Lebedev, M. Hydrogen Flooding of a Coal Core: Effect on Coal Swelling. Geophys. Res. Lett. 2022, 49, e2021GL096873. [Google Scholar] [CrossRef]
- Li, J. Development status and prospect of underground gas storage in China. Oil Gas Storage Transp. 2022, 41, 780–786. (In Chinese) [Google Scholar]
- Zhang, J.; Tan, Y.; Zhang, T.; Yu, K.; Wang, X.; Zhao, Q. Natural gas market and underground gas storage development in China. J. Energy Storage 2020, 29, 101338. [Google Scholar] [CrossRef]
- Zheng, Y.; Sun, J.; Qiu, X.; Lai, X.; Liu, J.; Guo, Z.; Wei, H.; Min, Z. Connotation and evaluation technique of geological integrity of UGSs in oil-gas fields. Nat. Gas Ind. 2020, 40, 94–103. [Google Scholar] [CrossRef]
- Wei, G.; Zheng, Y.; Qiu, X.; Sun, J.; Shi, L.; Lai, X. Geological theory and application of underground gas storage in China. Acta Pet. Sin. 2019, 40, 1519. [Google Scholar]
- Fu, X.F.; Yan, L.Y.; Meng, L.D.; Liu, X.B. Deformation Mechanism and Vertical Sealing Capacity of Fault in the Mudstone Caprock. J. Earth Sci. 2019, 30, 367–375. [Google Scholar] [CrossRef]
- Evans, D.J. A review of underground fuel storage events and putting risk into perspective with other areas of the energy supply chain. In Underground Gas Storage: Worldwide Experiences and Future Development in the UK and Europe; Special Publications; Evans, D.J., Chadwick, R.A., Eds.; The Geological Society: London, UK, 2009; Volume 313, pp. 173–216. [Google Scholar]
- Ingram, G.M.; Urai, J.L. Top-Seal Leakage through Faults and Fractures: The Role of Mudrock Properties; Special Publications; Geological Society: London, UK, 1999; Volume 158, pp. 125–135. [Google Scholar]
- Liu, B.; Fu, X.F.; Li, Z. Impacts of CO2-brine-rock interaction on sealing efficiency of sand caprock: A case study of Shihezi formation in Ordos basin. Adv. Geo-Energy Res. 2018, 2, 380–392. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, J.; Sun, G.; Song, Y.; Zhao, W. Operation risk and technical countermeasures of underground gas storage containing hydrogen sulfide in North China. Oil Gasfield Surf. Eng. 2020, 39, 56–63. (In Chinese) [Google Scholar]
- Muhammed, N.S.; Haq, M.B.; Al Shehri, D.A.; Al-Ahmed, A.; Rahman, M.M.; Zaman, E.; Iglauer, S. Hydrogen storage in depleted gas reservoirs: A comprehensive review. Fuel 2023, 337, 127032. [Google Scholar] [CrossRef]
- Fleury, M.; Pironon, J.; Le Nindre, Y.M.; Bildstein, O.; Berne, P.; Lagneau, V.; Vidal, O. Evaluating sealing efficiency of caprocks for CO2 storage: An overviewof the Geocarbone Integrity program and results. Energy Procedia 2011, 4, 5227–5234. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Yan, Y.; Sheng, Z.; Yan, X. Uncertainty failure risk quantitative assessments for underground gas storage near-wellbore area. J. Energy Storage 2021, 36, 102393. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Liu, J.; Guo, J.; Zhang, Y. A review on state-of-the-art of underground gas storage and causes of typical accidents. Hazard Control. Tunn. Undergr. Eng. 2019, 1, 49–58. [Google Scholar]
- Bruno, M.S.; Dewolf, G.; Foh, S. Geomechanical Analysis and Decision Analysis for Delta Pressure Operations in Gas Storage Reservoirs; Proc. AGA Operations Conf.: Denver, CO, USA, 2000; pp. 7–9. [Google Scholar]
- Tesei, T.; Collettini, C.; Viti, C.; Barchi, M.R. Fault architecture and deformation mechanisms in exhumed analogues of seismogenic carbonate-bearing thrusts. J. Struct. Geol. 2013, 55, 167–181. [Google Scholar] [CrossRef]
- Kirkham, C.; Cartwright, J.; Bertoni, C.; Van Rensbergen, P. The genesis of a giant mud canopy by catastrophic failure of a thick evaporite sealing layer. Geology 2020, 48, 787–791. [Google Scholar] [CrossRef]
- Bock, H.; Dehandschutter, B.; Martin, C.D.; Mazurek, M.; De Haller, A.; Skoczylas, F.; Davy, C. Self-Sealing of Fractures in Argillaceous Formations in the Context of Geological Disposal of Radioactive Waste; OECD: Paris, France; NEA: Philadelphia, PA, USA, 2010. [Google Scholar]
- Jolley, S.J.; Dijk, H.; Lamens, J.H.; Fisher, Q.J.; Manzocchi, T.; Eikmans, H.; Huang, Y. Faulting and fault sealing in production simulation models: Brent Province, northern North Sea. Pet. Geosci. 2007, 13, 321–340. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhu, Z.; Patrick, W.; Liu, J.; Lei, H.; Zhang, L. Pore-scale numerical simulation of supercritical CO2 migration in porous and fractured media saturated with water. Adv. Geo-Energy Res. 2020, 4, 419–434. [Google Scholar] [CrossRef]
- Liu, H.; Hou, Z.; Were, P.; Gou, Y.; Sun, X. Numerical investigation of the formation displacement and caprock integrity in the Ordos Basin (China) during CO2 injection operation. J. Pet. Sci. Eng. 2016, 147, 168–180. [Google Scholar] [CrossRef]
- Liu, H.; Shi, Y.; Fang, Z.; Liu, J.; Zhang, L.; Tong, R. Seepage characteristics of thermally and chemically treated Mesozoic granite from geothermal region of Liaodong Peninsula. Environ. Earth Sci. 2021, 80, 599. [Google Scholar] [CrossRef]
- Shipton, Z.K.; Evans, J.P.; Kirschner, D.; Kolesar, P.T.; Williams, A.P.; Heath, J. Analysis of CO2 Leakage through ‘Low-Permeability’ Faults from Natural Reservoirs in the Colorado Plateau, East-Central Utah; Special Publications; Geological Society: London, UK, 2004; Volume 233, pp. 43–58. [Google Scholar]
- Pio Rinaldi, A.; Rutqvist, J.; Jeanne, P.; Cappa, F.; Guglielmi, Y. Induced seismicity and CO2 leakage through fault zones during large-scale underground injection in a multilayered sedimentary system. Gen. Assem. Conf. Abstr. 2014, 16, 3164. [Google Scholar]
- Kang, K.; Huh, C.; Kang, S.-G. A numerical study on the CO2 leakage through the fault during offshore carbon sequestration. J. Korean Soc. Mar. Environ. Energy 2015, 18, 94–101. [Google Scholar] [CrossRef]
- Yehya, A.; Yang, Z.; Rice, J.R. Effect of fault architecture and permeability evolution on response to fluid injection. J. Geophys. Res. Solid Earth 2018, 123, 9982–9997. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Yang, R.; Geng, F.; Wang, L.; Wang, L.; Guo, J. Analyzing the Formation and Evolution of Strike-Slip Faults and Their Controlling Effects on Hydrocarbon Migration and Charging: A Case Study of Tahe Area, Tarim Basin. Energies 2023, 16, 2370. [Google Scholar] [CrossRef]
- Aoyagi, R.; Kitamura, O.; Itaoka, K.; Igawa, S.; Suzuki, S. Study on role of simulation of possible leakage from geological CO2 storage in sub-seabed for environmental impact assessment. Energy Procedia 2011, 4, 3881–3888. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Wang, Y.; Feng, D.; Gong, J.K. CO2 migration and distribution in multiscale-heterogeneous deep saline aquifers. Adv. Geo-Energy Res. 2021, 5, 333–346. [Google Scholar] [CrossRef]
- Lyu, X.; Yun, L.; Xu, J.; Liu, H.; Yu, X.; Peng, P.; Ouyang, M.; Luo, Y. Sealing capacity evolution of gypsum salt caprocks under multi-cycle alternating stress during operations of underground gas storage. J. Pet. Sci. Eng. 2023, 220, 111244. [Google Scholar] [CrossRef]
- Cappa, F.; Guglielmi, Y.; Barros, L.D. Transient evolution of permeability and friction in a slowly slipping fault activated by fluid pressurization. Nat. Commun. 2022, 13, 3039. [Google Scholar] [CrossRef]
- Yang, J. Numerical Simulation of Geologic Body Stress Field in Gas Storage Traps. Master’s Thesis, The Northeast Petroleum University, Daqing, China, 2022. (In Chinese). [Google Scholar]
- Liu, H.; Hou, Z.; Were, P.; Gou, Y.; Sun, X. Simulation of CO2 plume movement in multilayered saline formations through multilayer injection technology in the Ordos Basin, China. Environ. Earth Sci. 2014, 71, 4447–4462. [Google Scholar] [CrossRef]
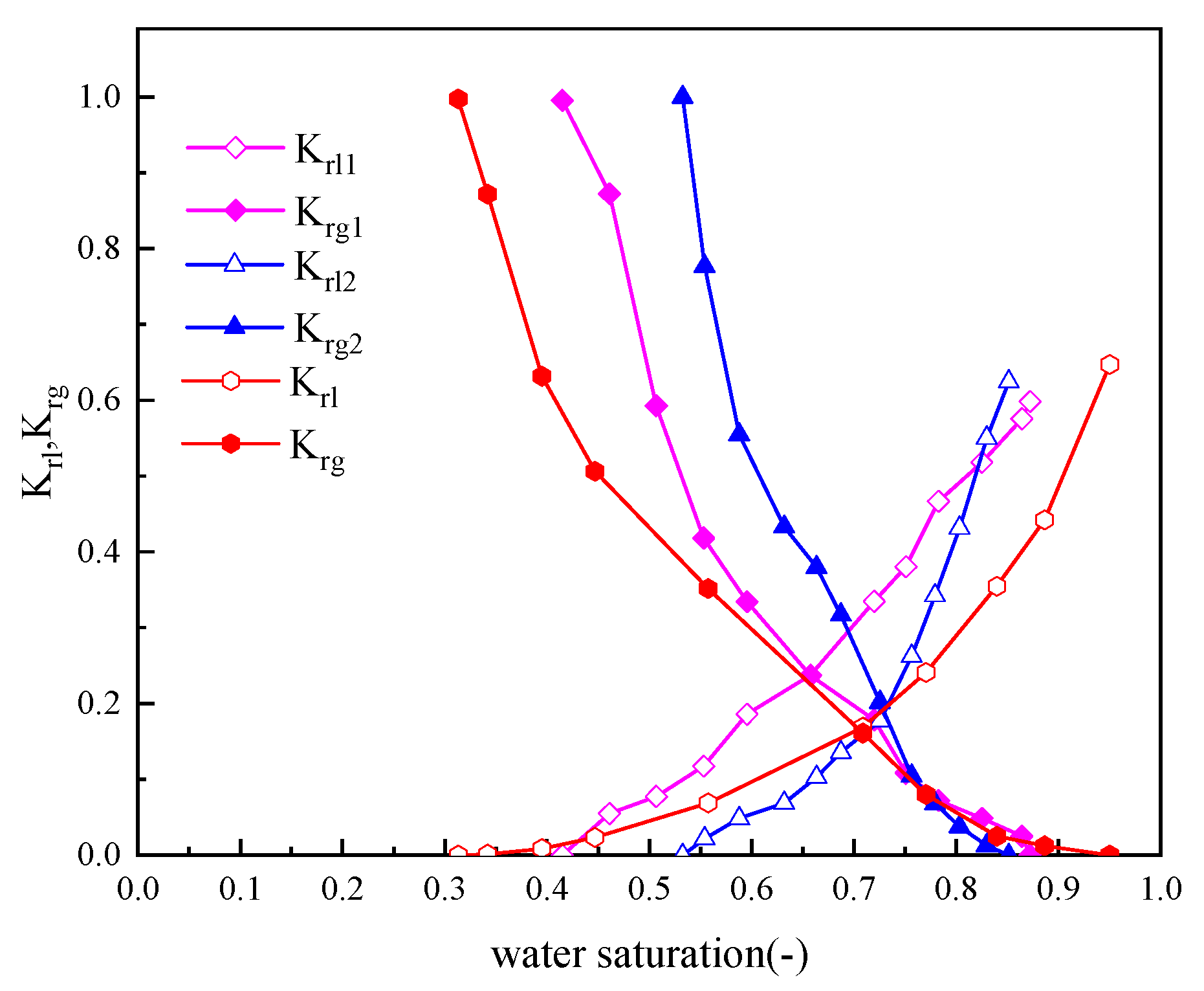
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 38–41. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Bu, F. Study on the Influence of Small Faults in Reservoir on the Spatial Distribution and Storage of CO2. Master’s Thesis, Jilin University, Changchun, China, 2015. [Google Scholar]
- Li, Y.; Xiao, F.; Xu, W.; Wang, J. Performance evaluation on water-producing gas wells based on gas & water relative permeability curves: A case study of tight sandstone gas reservoirs in the Sulige gas field, Ordos Basin. Nat. Gas Ind. B 2016, 3, 52–58. (In Chinese) [Google Scholar]
- Shi, F. Influence of Minor Faults within the Reservoir on CO2 Spatial Distribution and Storage. Master’s Thesis, Jilin University, Changchun, China, 2015. (In Chinese). [Google Scholar]
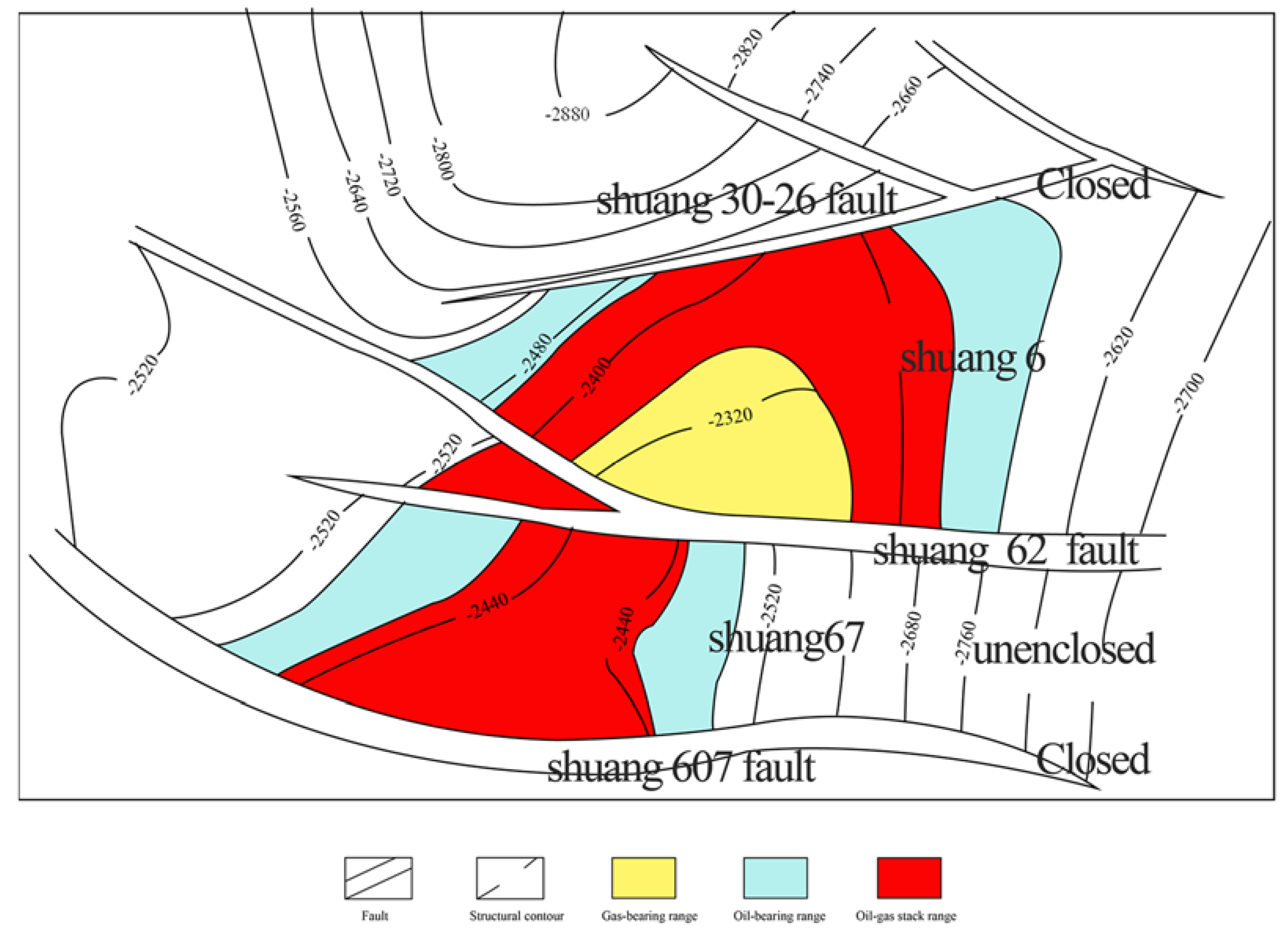
- Li, J.; Meng, L.; Fu, X.; Jin, Y.; Jiang, M.; Liu, C. Analysis of efficient operation conditions of the Shuang 6 gas storage in Shuangtaizi Oilfield, LiaoHe Basin, China. Arab. J. Geosci. 2022, 15, 1486. [Google Scholar] [CrossRef]
- Han, H. Study on Numerical Simulation of Shuang6 Block in Shuangtaizi Oilfield. China Pet. Chem. Stand. Qual. 2013, 33, 142–143. (In Chinese) [Google Scholar]
- Solomon, S. Criteria for Intermediate Storage of Carbon Dioxide in Geological Formations; The Bellona Foundation: Oslo, Norway, 2006; pp. 1–6. [Google Scholar]
- Watson, M.N.; Gibson-Poole, C.M. Reservoir Selection for Optimised Geological Injection and Storage of Carbon Dioxide: A Combined Geochemical and Stratigraphic Perspective; Conference Reservoir Selection for Optimised Geological Injection and Storage of Carbon Dioxide; National Energy Technology Laboratory, US Department of Energy: Alexandria, Egypt, 2005; pp. 2–5. [Google Scholar]
- Flett, M.; Gurton, R.; Taggart, I. Heterogeneous saline formations: Long-term benefits for geo-sequestration of greenhouse gases. In Greenhouse Gas Control Technologies 7; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2005; pp. 501–509. [Google Scholar]
- Birkholzer, J.T.; Zhou, Q.; Tsang, C.F. Large-scale impact of CO2 storage in deep saline aquifers: A sensitivity study on pressure response in stratified systems. Int. J. Greenh. Gas Control 2009, 3, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Xu, Y.; Zhang, K. Investigation of CO2 storage capacity in open saline aquifers with numerical models. Procedia Eng. 2012, 31, 886–892. [Google Scholar]
- Lu, C.; Sun, Y.; Buscheck, T.A.; Hao, Y.; White, J.A.; Chiaramonte, L. Uncertainty quantification of CO2 leakage through a fault with multiphase and nonisothermal effects. Greenh. Gases Sci. Technol. 2012, 2, 445–459. [Google Scholar] [CrossRef]
- Hu, Y.J.; Wang, Y.; Ren, J. Analysis of factors affecting the leakage of CO2 along the fault zone in deep saline aquifers. China Sci. 2016, 13, 1437–1444. (In Chinese) [Google Scholar]





| Small Layer Name | Formation Thickness (m) | Buried Bottom Depth (m) | Density (kg/m3) | Porosity (-) | Permeability (mD) |
|---|---|---|---|---|---|
| Caprock | 300 | 2320 | 2400 | 0.1 | 0.001 |
| I-1 | 33.4 | 2353.4 | 2050 | 0.2 | 64.5 |
| I-2 | 22.1 | 2375.5 | 2000 | 0.25 | 124.5 |
| II1-1 | 27.9 | 2403.4 | 2050 | 0.2 | 74.8 |
| II1-2 | 14 | 2417.4 | 2050 | 0.2 | 50.9 |
| II2-3 | 16 | 2433.4 | 2000 | 0.25 | 166 |
| II2-4 | 22 | 2455.4 | 2000 | 0.25 | 191.7 |
| II3-5 | 23.6 | 2479 | 2000 | 0.25 | 200.7 |
| II3-6 | 33 | 2512 | 2000 | 0.25 | 233.8 |
| III1-1 | 20.5 | 2532.5 | 2000 | 0.25 | 185.8 |
| III1-2 | 16.8 | 2549.3 | 2000 | 0.25 | 179 |
| III2-3 | 22 | 2571.3 | 2000 | 0.25 | 150.8 |
| III2-4 | 22.6 | 2593.9 | 2000 | 0.25 | 172.5 |
| III3-5 | 22.1 | 2616 | 2000 | 0.25 | 171.8 |
| III3-6 | 23.2 | 2639.2 | 2000 | 0.25 | 153.8 |
| III4-7 | 35 | 2674.2 | 2000 | 0.25 | 113.9 |
| III4-8 | 36.7 | 2710.9 | 2000 | 0.25 | 101.4 |
| III5-9 | 38.9 | 2749.8 | 2050 | 0.2 | 71.7 |
| III5-10 | 41.4 | 2791.2 | 2050 | 0.2 | 48 |
| Scenario | Porosity (-) | Permeability (mD) | Fault Geometry (Dip Angle, Strike Length, Width) | Boundary Type |
|---|---|---|---|---|
| Basecase | - | No fault | Open | |
| Case1 | 0.05 | 0.001 | 60°, 10 m, 10 m | Open |
| Case2 | 0.05 | 0.001 | 60°, 250 m, 10 m | Open |
| Case3 | 0.05 | 0.001 | 60°, 500 m, 10 m | Open |
| Case4 | 0.2 | 10 | 60°, 500 m, 10 m | Open |
| Case5 | 0.5 | 1000 | 60°, 10 m, 10 m | Open |
| Case6 | 0.5 | 1000 | 60°, 250 m, 10 m | Open |
| Case7 | 0.5 | 1000 | 60°, 500 m, 10 m | Open |
| Case8 | 0.05 | 0.001 | 70°, 10 m, 10 m | Open |
| Case9 | 0.05 | 0.001 | 85°, 10 m, 10 m | Open |
| Case10 | 0.5 | 1000 | 70°, 10 m, 10 m | Open |
| Case11 | 0.5 | 1000 | 85°, 10 m, 10 m | Open |
| Case12 | 0.5 | 1000 | 60°, 500 m, 10 m (normal fault) | Open |
| Case13 | 0.05 | 0.001 | 60°, 500 m, 10 m (normal fault) | Open |
| Case14 | -- | -- | No fault | Closed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ban, S.; Liu, H.; Mao, H.; Shi, X.; Qiu, X.; Liu, M.; Min, Z.; Song, Y.; Wei, X. Numerical Tracking of Natural Gas Migration in Underground Gas Storage with Multilayered Sandstone and Fault-Bearing Caprocks. Energies 2023, 16, 4936. https://doi.org/10.3390/en16134936
Ban S, Liu H, Mao H, Shi X, Qiu X, Liu M, Min Z, Song Y, Wei X. Numerical Tracking of Natural Gas Migration in Underground Gas Storage with Multilayered Sandstone and Fault-Bearing Caprocks. Energies. 2023; 16(13):4936. https://doi.org/10.3390/en16134936
Chicago/Turabian StyleBan, Shengnan, Hejuan Liu, Haijun Mao, Xilin Shi, Xiaosong Qiu, Mancang Liu, Zhongshun Min, Yujia Song, and Xinxing Wei. 2023. "Numerical Tracking of Natural Gas Migration in Underground Gas Storage with Multilayered Sandstone and Fault-Bearing Caprocks" Energies 16, no. 13: 4936. https://doi.org/10.3390/en16134936
APA StyleBan, S., Liu, H., Mao, H., Shi, X., Qiu, X., Liu, M., Min, Z., Song, Y., & Wei, X. (2023). Numerical Tracking of Natural Gas Migration in Underground Gas Storage with Multilayered Sandstone and Fault-Bearing Caprocks. Energies, 16(13), 4936. https://doi.org/10.3390/en16134936






