Optimization of Oil Productivity from the Ultra−Depth Strike−Slip Fault−Controlled Carbonate Reservoirs in Northwestern China
Abstract
:1. Introduction
2. Geological Background
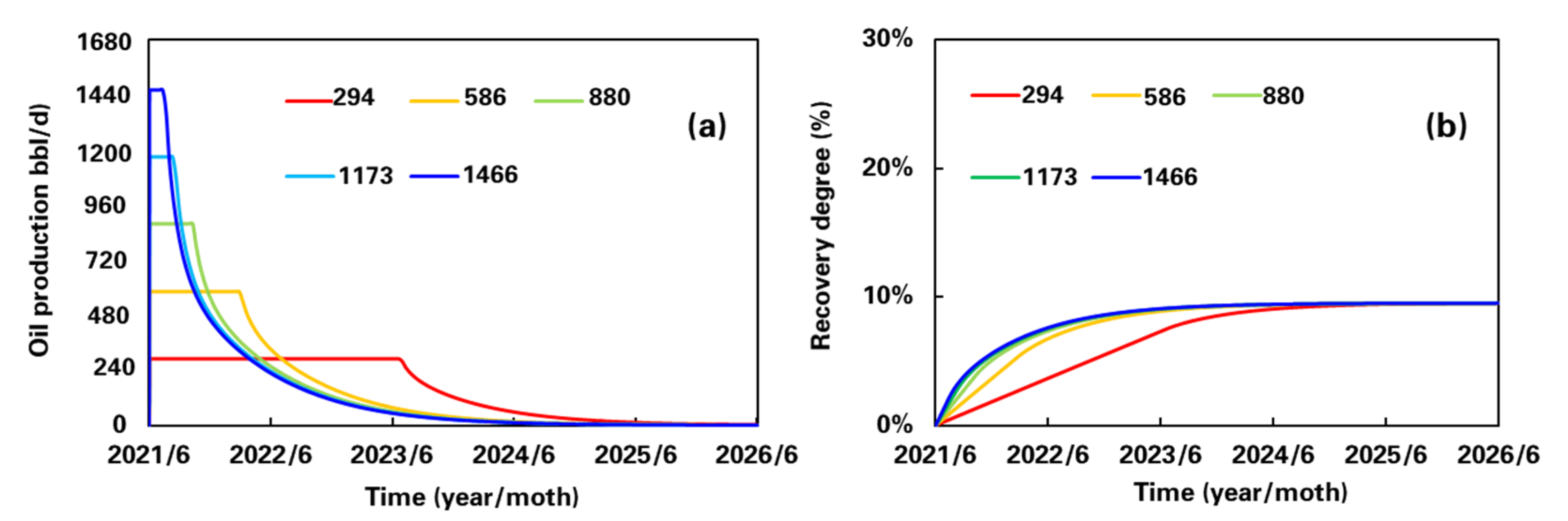
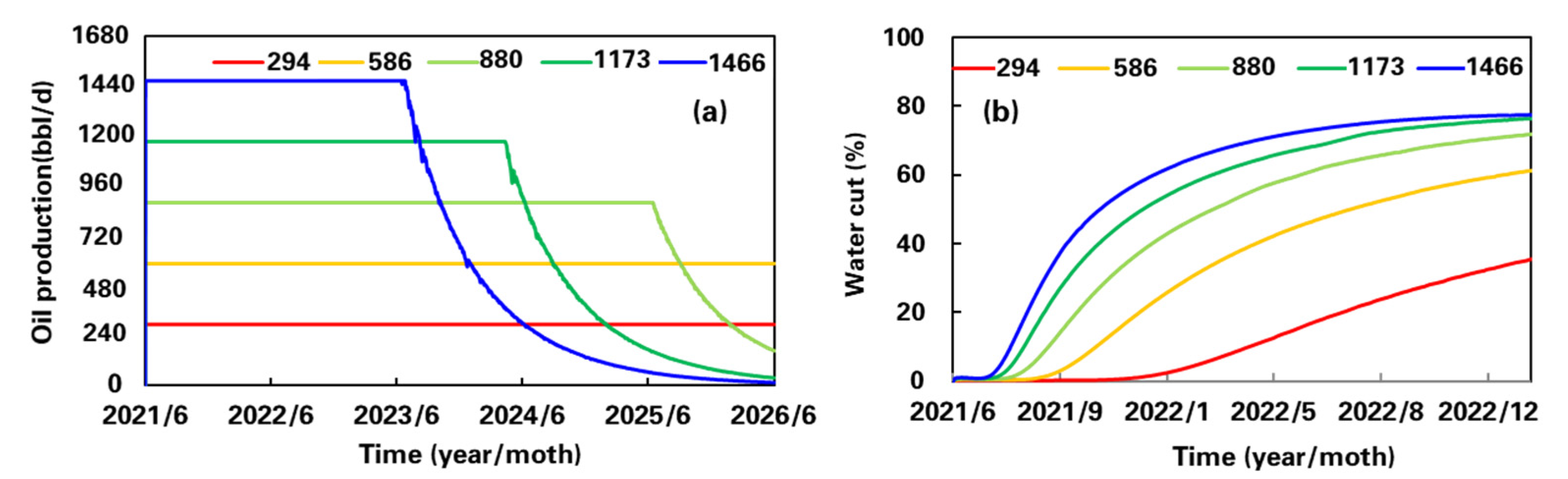
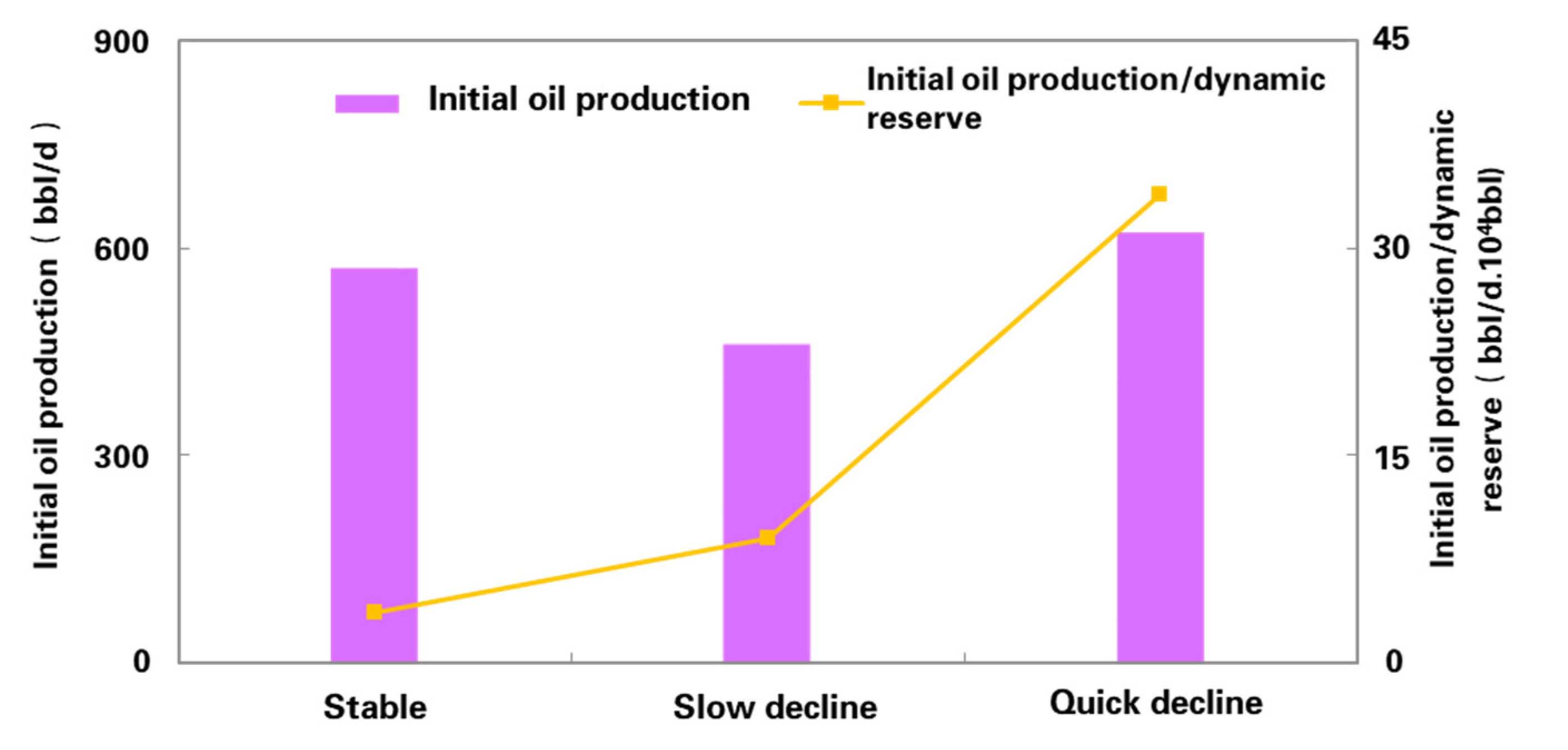
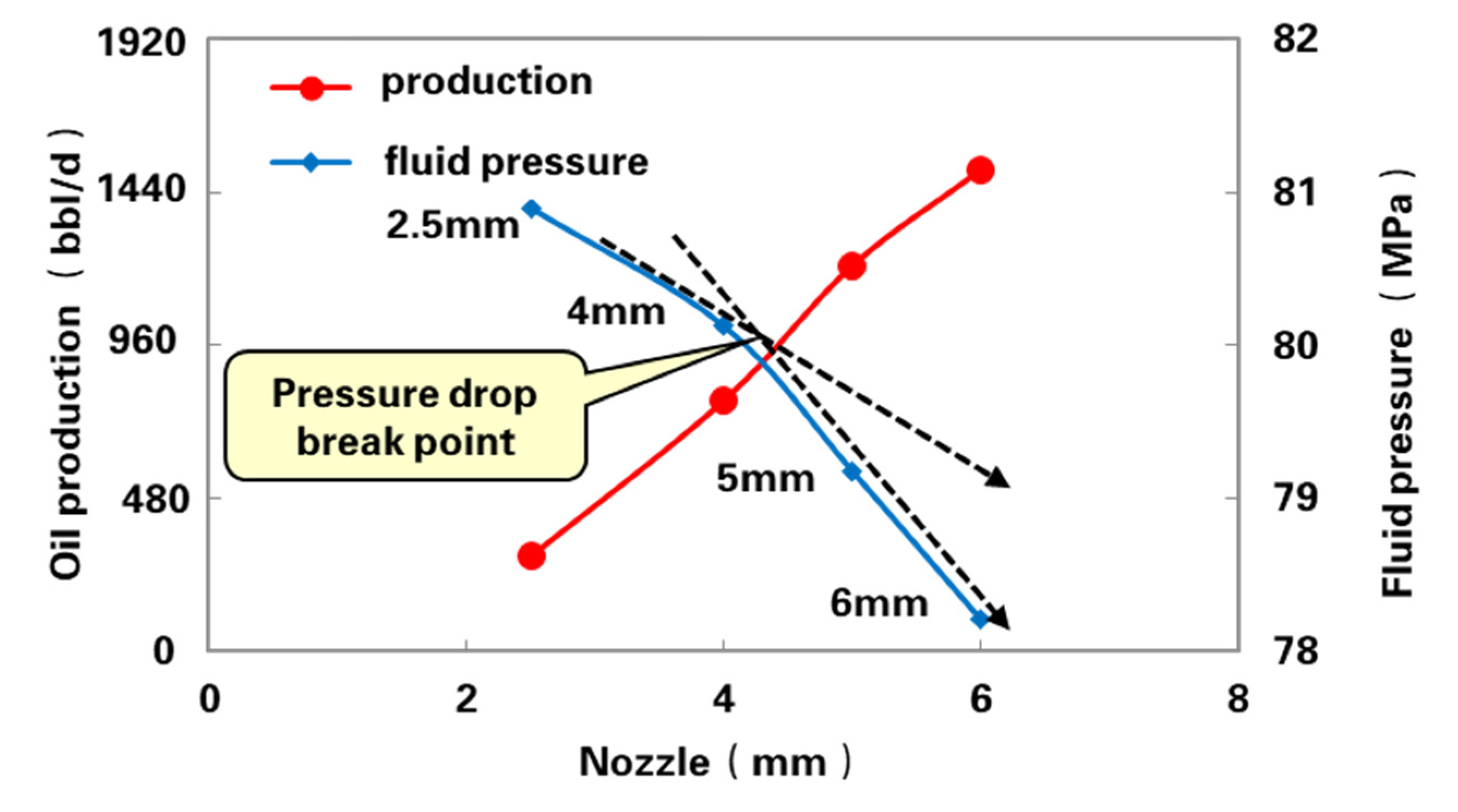
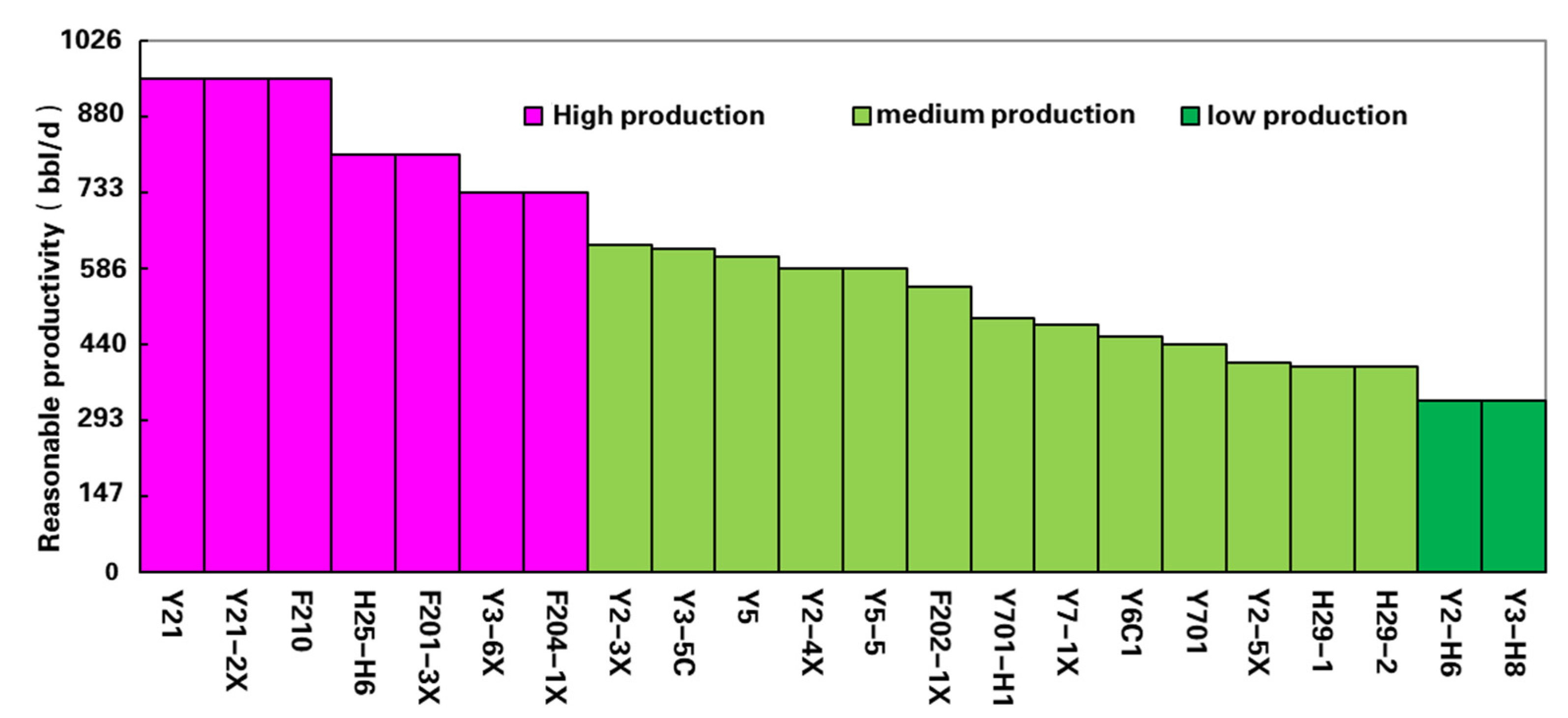
3. Influence of Productivity Rationality on Development Effect of Different Types of Wells
4. Relationship between Reasonable Productivity and Well Control Dynamic Reserves
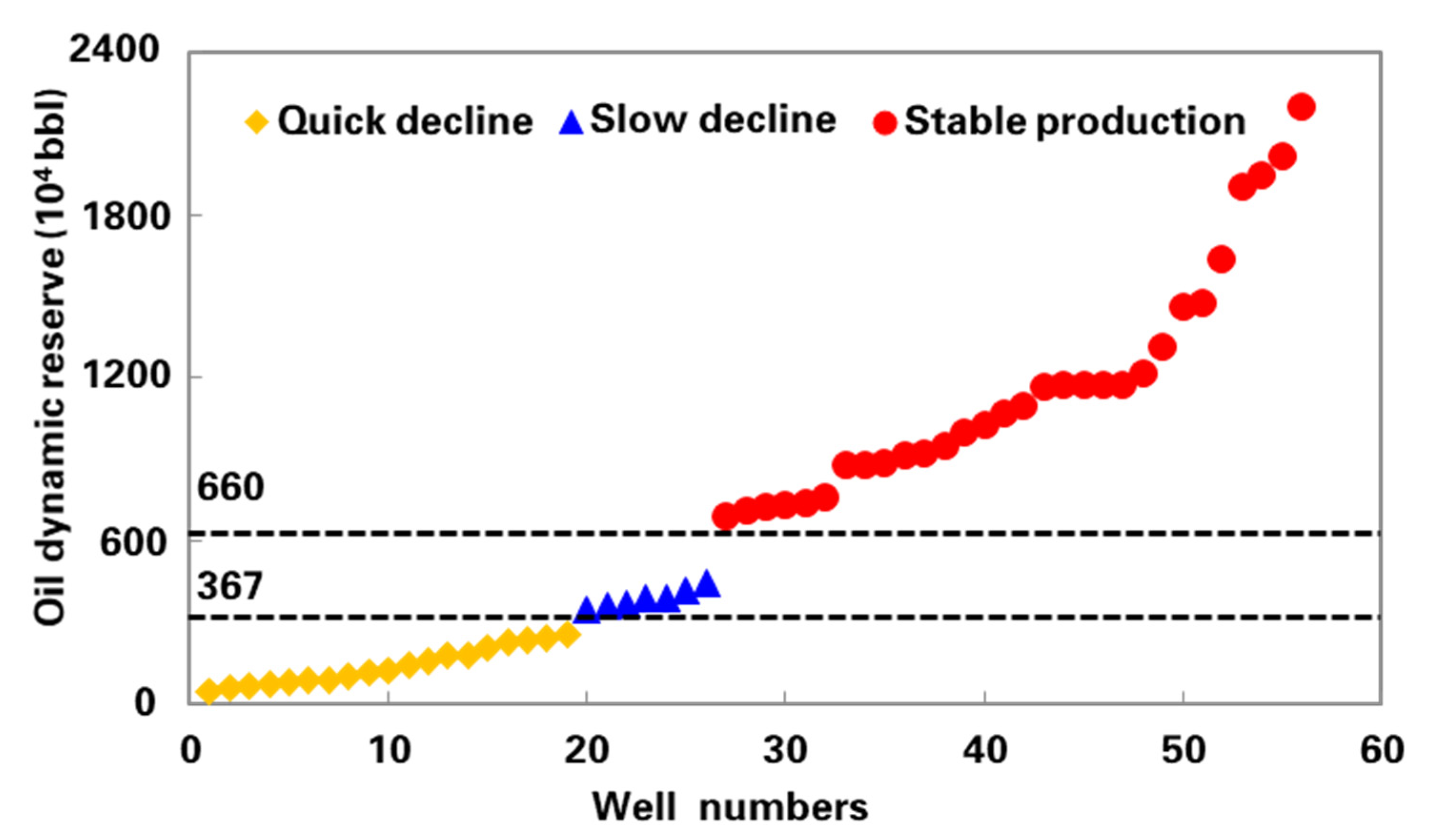
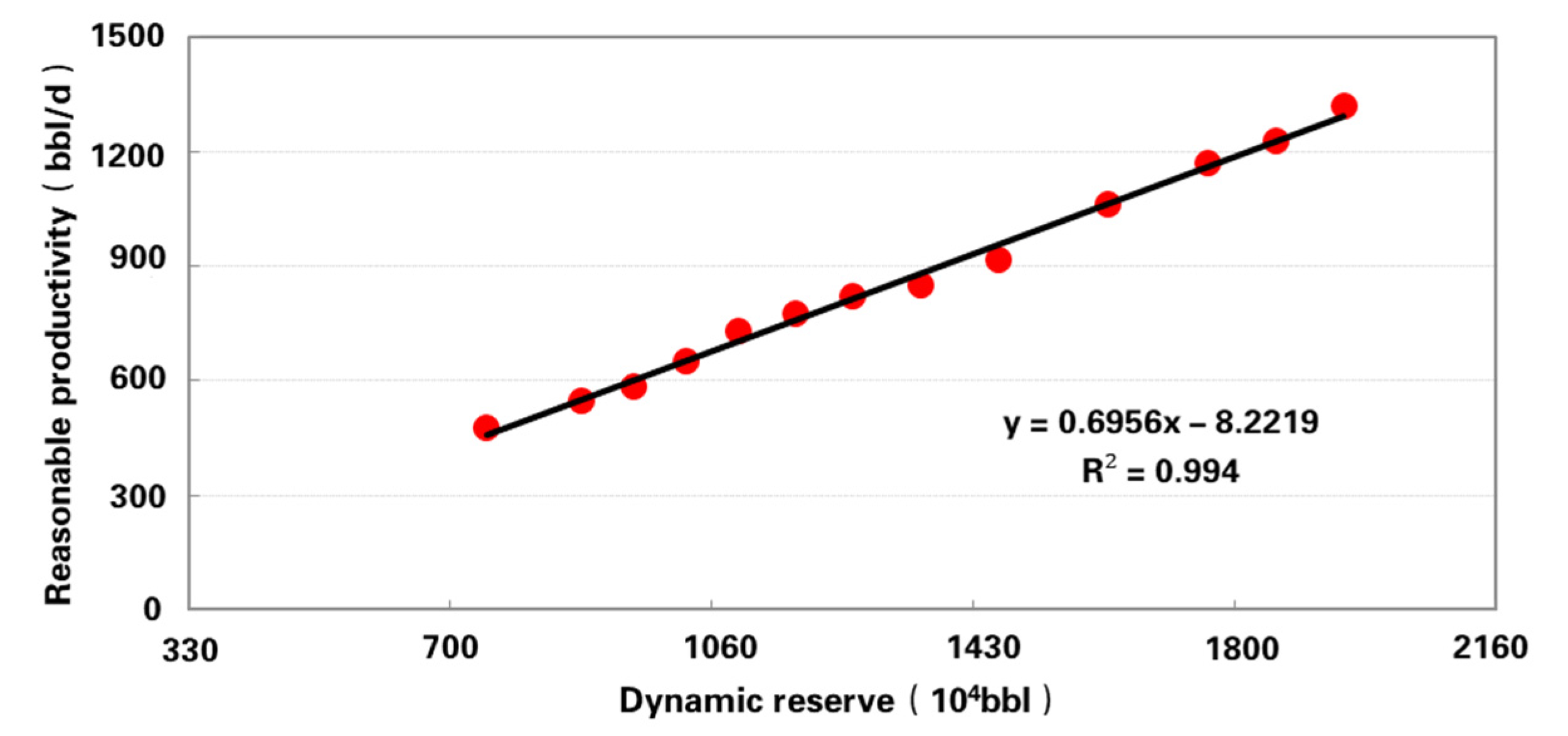
4.1. Relationship between Single Well Productivity and Well Control Dynamic Reserves
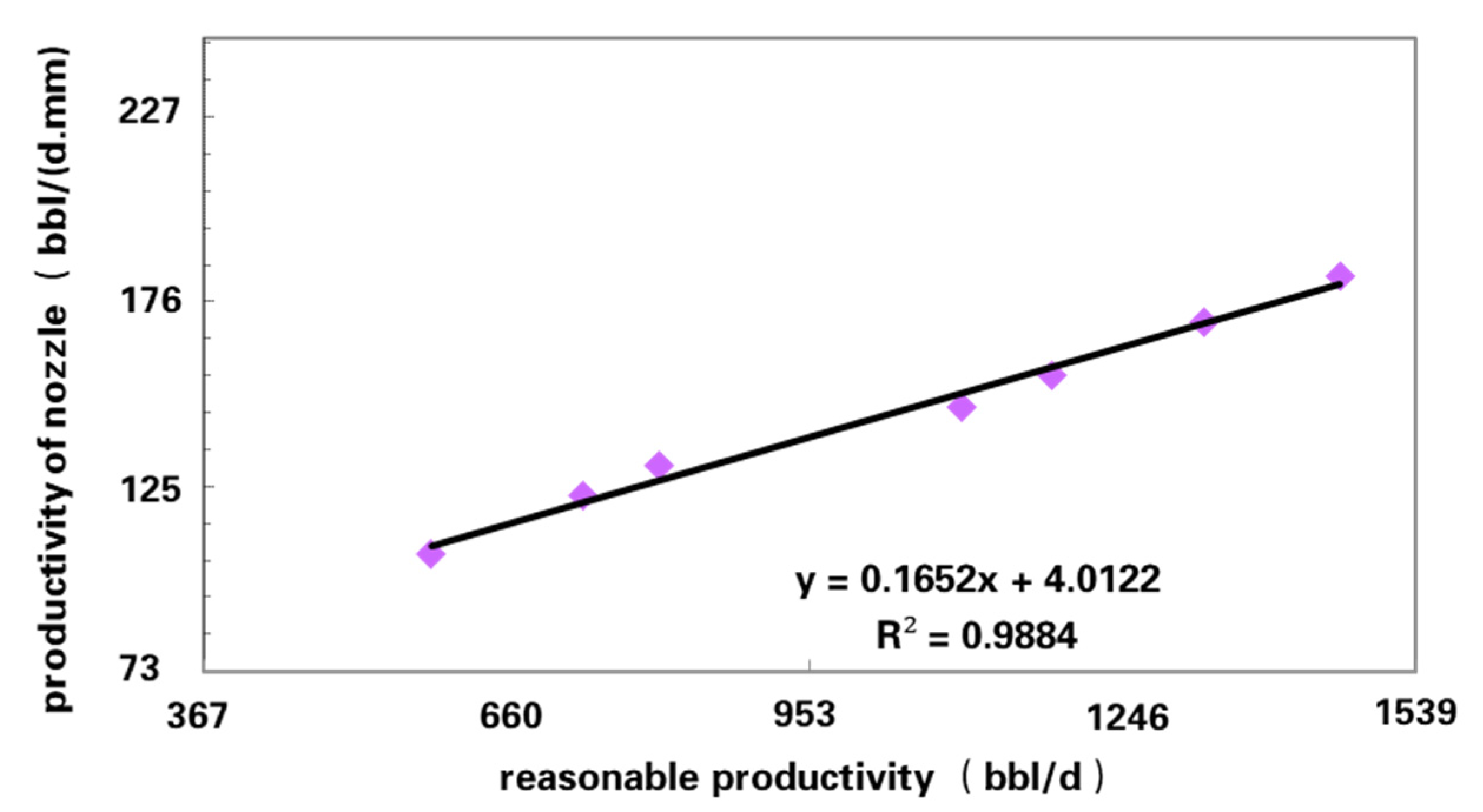
4.2. Reasonable Productivity−Well Control Dynamic Reserves Correlation
5. Applications
5.1. Reasonable Productivity Calibration
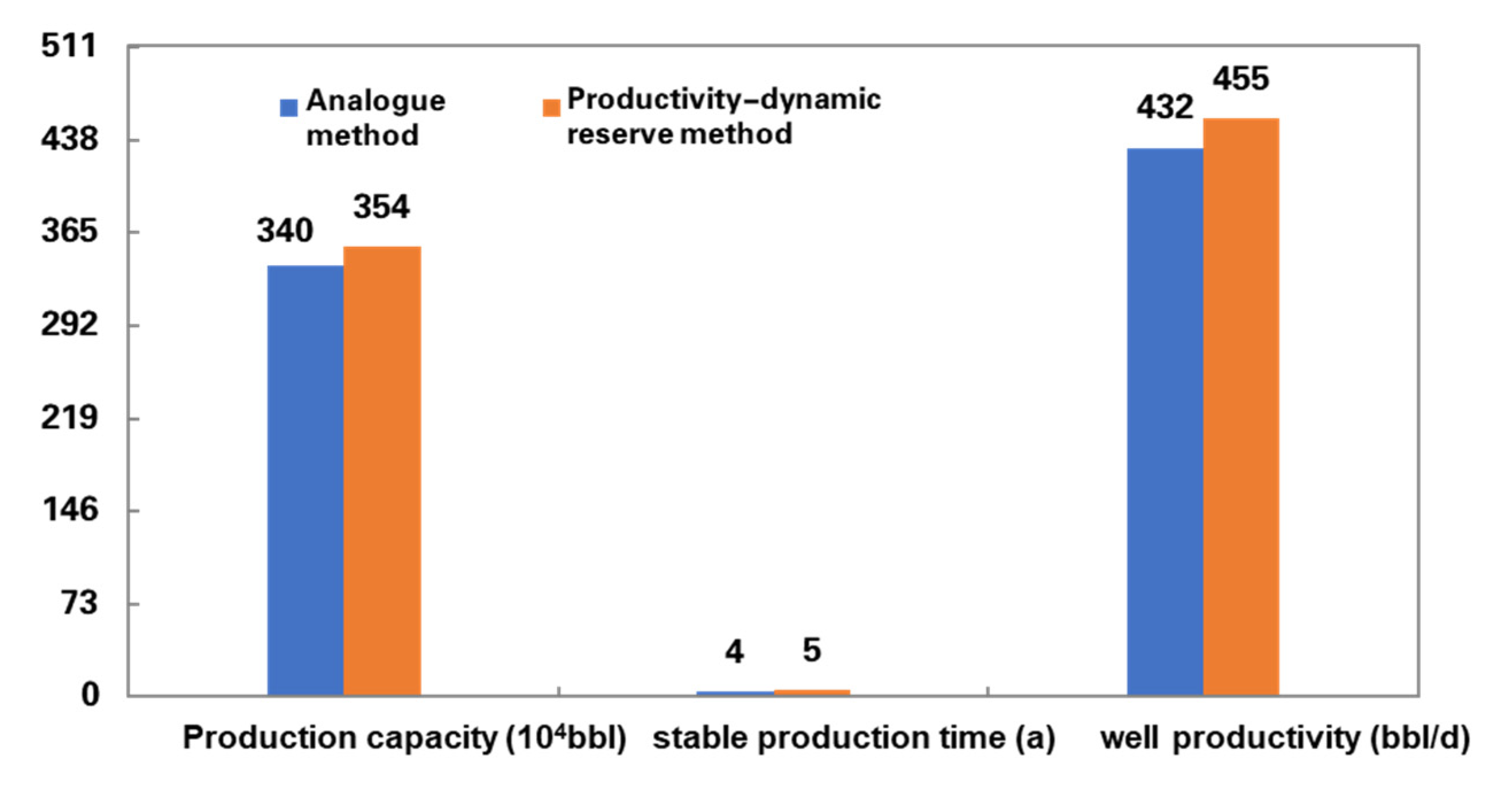
5.2. Prediction and Optimization of Development Indicators
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, L.D.; Zou, C.N.; Zhu, R.K.; Zhang, Y.H.; Zhang, S.C.; Zhang, B.M.; Zhu, G.Y.; Gao, Z.Y. Formation, distribution and potential of deep hydrocarbon resources in China. Pet. Explor. Dev. 2013, 40, 687–695. [Google Scholar] [CrossRef]
- Tong, X.G.; Zhang, G.Y.; Wang, Z.M.; Wen, Z.X.; Tian, Z.J.; Wang, H.J.; Ma, F.; Wu, Y.P. Distribution and potential of global oil and gas resources. Pet. Explor. Dev. 2018, 45, 779–789. [Google Scholar] [CrossRef]
- Sylvester, A.G. Strike-slip faults. Geol. Soc. Am. Bull. 1988, 100, 1666–1703. [Google Scholar] [CrossRef]
- Woodcock, N.H.; Schubert, V. Continental Strike-Slip Tec-Tonics; Pergamon Press: Oxford, UK, 1994; pp. 251–263. [Google Scholar]
- Cunningham, W.D.; Mann, P. Tectonics of strike-slip re-straining and releasing bends. Lond. Geol. Soc. 2007, 290, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Leighton, M.W.; Kolata, D.R.; Oltz, D.F.; Eidel, J.J. Interior Cratonic Basins. AAPG Mem. 1990, 51, 1–819. [Google Scholar]
- Mann, P. Comparison of structural styles and giant hydro-carbon occurrences within four active strike-slip regions: Cal-ifornia, Southern Caribbean, Sumatra, and East China. AAPG Mem. 2013, 100, 43–93. [Google Scholar]
- Yang, H.J.; Wu, G.H.; Han, J.F.; Su, Z. Structural analysis of strike-slip faults in the Tarim intracratonic Basin. Chin. J. Geol. 2020, 55, 1–16, (In Chinese with English Abstract). [Google Scholar]
- Yang, X.W.; Wang, R.J.; Deng, X.L.; Li, S.Y.; Zhang, H.; Yao, C. Theoretical exploration and practice of water injection gravity flooding oil in ultra-deep fault-controlled fractured-cavity carbonate reservoirs. Pet. Explor. Dev. 2022, 49, 133–143. [Google Scholar] [CrossRef]
- Deng, S.; Zhao, R.; Kong, Q.F.; Li, Y.T.; Li, B. Two distinct strike-slip fault networks in the Shunbei area and its surroundings, Tarim Basin: Hydrocarbon accumulation, distribution, and controlling factors. AAPG Bull. 2022, 106, 77–102. [Google Scholar] [CrossRef]
- Wu, G.H.; Zhao, K.Z.; Qu, H.Z.; Nicola, S.; Zhang, Y.T.; Han, J.F.; Xu, Y.F. Permeability distribution and scaling in multi-stages carbonate damage zones: Insight from strike-slip fault zones in the Tarim Basin, NW China. Mar. Pet. Geol. 2020, 114, 104208. [Google Scholar] [CrossRef]
- Wang, Q.H.; Yang, H.J.; Wang, R.J.; Li, S.Y.; Deng, X.L.; Li, Y.; Chang, L.J.; Wan, X.G.; Zhang, Y.T. Discovery and exploration technology of fault-controlled large oil and gas fields of ultra-deep formation in strike slip fault zone in Tarim Basin. China Pet. Explor. 2021, 26, 58–71, (In Chinese with English Abstract). [Google Scholar]
- Yang, S.; Wu, G.H.; Zhu, Y.F.; Zhng, Y.T.; Zhao, X.X.; Lu, Z.Y.; Zhang, B.S. Key oil accumulation periods of ultra-deep fault-controlled oil reservoir in northern Tarim Basin, NW China. Pet. Explor. Dev. 2022, 49, 285–289. [Google Scholar] [CrossRef]
- Barss, D.L.; Montandon, F.A. Sukunka-Bullmoose Gas Fields: Models for a Developing Trend in the Southern Foothills of Northeast British Columbia. SPG Bull. 1981, 29, 293–333. [Google Scholar]
- Camacho-Velázquez, R. Pressure-Transient and Decline-Curve Behaviors in Naturally Fractured Vuggy Carbonate Reservoirs. SPE Reserv. Eval. Eng. 2005, 8, 95–112. [Google Scholar] [CrossRef]
- Cao, P.; Chang, S.Y.; Dai, C.R.; Liu, J.L.; Luo, X.Y. Determination of reasonable work system for fractured-vuggy carbonate reservoir—Taking Lunguxi reservoir as example. J. Chongqing Univ. Sci. Technol. 2012, 14, 20–23, (In Chinese with English Abstract). [Google Scholar]
- Li, Y.; Kang, Z.J.; Xue, Z.J.; Zheng, S.Q. Theories and practices of carbonate reservoirs development in China. Pet. Explor. Dev. 2018, 45, 712–722. [Google Scholar] [CrossRef]
- Méndez, J.N.; Jin, Q.; González, M.; Zhang, X.D.; Lobo, C.; Boateng, C.; Zambrano, M. Fracture characterization and modeling of karsted carbonate reservoirs: A case study in Tahe oilfield, Tarim Basin (western China). Mar. Pet. Geol. 2020, 112, 104104. [Google Scholar] [CrossRef]
- Dong, J.X.; Shi, W.; Xu, M.Y. Numerical simulation of gas wells in different types of carbonate reservoirs. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012206. [Google Scholar] [CrossRef]
- Li, Y.J.; Yao, J.; Li, Y.C.; Yin, C.B.; Pan, B.; Lee, J.; Dong, M.Z. An equivalent continuum approach for modeling two-phase flow in fractured-vuggy media. Int. J. Multiscale Comput. Eng. 2017, 15, 79–98. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.X.; Xia, Z.Y. A Novel Semi-Analytical Model for Multi-branched Fractures in Naturally Fractured-Vuggy Reservoirs. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.Z. Tectonic Characteristics and Petroleum, Tarim Basin, China; Petroleum Industry Press: Beijing, China, 1997. [Google Scholar]
- Wu, G.H.; Pang, X.Q.; Li, Q.M.; Yang, H.J. The Structural Characteristics of Carbonate Rocks and their Effects on Hydrocarbon Exploration in Craton Basin: A Case Study of the Tarim Basin; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Deng, S.; Li, H.L.; Zhang, Z.P.; Zhang, J.B.; Yang, X. Structural characterization of intracratonic strike-slip faults in the central Tarim Basin. AAPG Bull. 2019, 103, 109–137. [Google Scholar] [CrossRef]
- Wu, G.H.; Ma, B.S.; Han, J.F.; Guan, B.Z.; Chen, X.; Yang, P.; Xie, Z. Origin and growth mechanisms of strike-slip faults in the central Tarim cratonic basin, NW China. Pet. Explor. Dev. 2021, 48, 595–607. [Google Scholar] [CrossRef]
- Lu, X.B.; Wang, Y.; Tian, F.; Li, X.H.; Yang, D.B.; Li, T.; Lv, Y.P.; He, X.M. New insights into the carbonate karstic fault system and reservoir formation in the Southern Tahe area of the Tarim Basin. Mar. Pet. Geol. 2017, 86, 587–605. [Google Scholar] [CrossRef]
- Han, J.F.; Su, Z.; Chen, L.X.; Guo, D.S.; Zhang, Y.T.; Ji, Y.G.; Zhang, H.F.; Yuan, J.Y. Reservoir-controlling and accumulation-controlling of strike-slip faults and exploration potential in the platform of Tarim Basin. Acta Pet. Sin. 2019, 40, 1296–1310, (In Chinese with English Abstract). [Google Scholar]
- Shen, W.B.; Chen, J.F.; Wang, Y.Y.; Zhang, K.; Chen, Z.Y.; Luo, G.P.; Fu, X. The origin, migration and accumulation of the Ordovician gas in the Tazhong III region, Tarim Basin, NW China. Mar. Pet. Geol. 2019, 101, 55–77. [Google Scholar] [CrossRef]
- Jiang, T.W.; Han, J.F.; Wu, G.H.; Yu, H.F.; Su, Z.; Xiong, C.; Chen, J.; Zhang, H.F. Differences and controlling factors of composite hydrocarbon accumulations in the Tazhong uplift, Tarim Basin, NW China. Pet. Explor. Dev. 2020, 47, 229–241. [Google Scholar] [CrossRef]
- Deng, X.L.; Yan, T.; Zhang, Y.T.; Wan, X.G.; Feng, K.; Yuan, A.Y.; Yao, C.; Xiao, C.Y. Characteristics and well location deployment ideas of strike-slip fault controlled carbonate oil and gas reservoirs: A case study of the Tarim Basin. Nat. Gas Ind. 2021, 41, 21–29, (In Chinese with English Abstract). [Google Scholar]
- Ding, Z.W.; Wang, R.J.; Chen, F.F.; Yang, J.P.; Zhu, Z.Q.; Yang, Z.M.; Sun, X.H.; Xian, B.; Li, E.P.; Shi, T.; et al. Origin, hydrocarbon accumulation and oil-gas enrichment of fault-karst carbonate reservoirs: A case study of Ordovician carbonate reservoirs in in South Tahe area of Halahatang oilfield, Tarim Basin. Pet. Explor. Dev. 2020, 47, 306–317. [Google Scholar] [CrossRef]
- Li, C.L. The Principles of Reservoir Engineering; Petroleum Industry Press: Beijing, China, 2010; pp. 426–428. [Google Scholar]


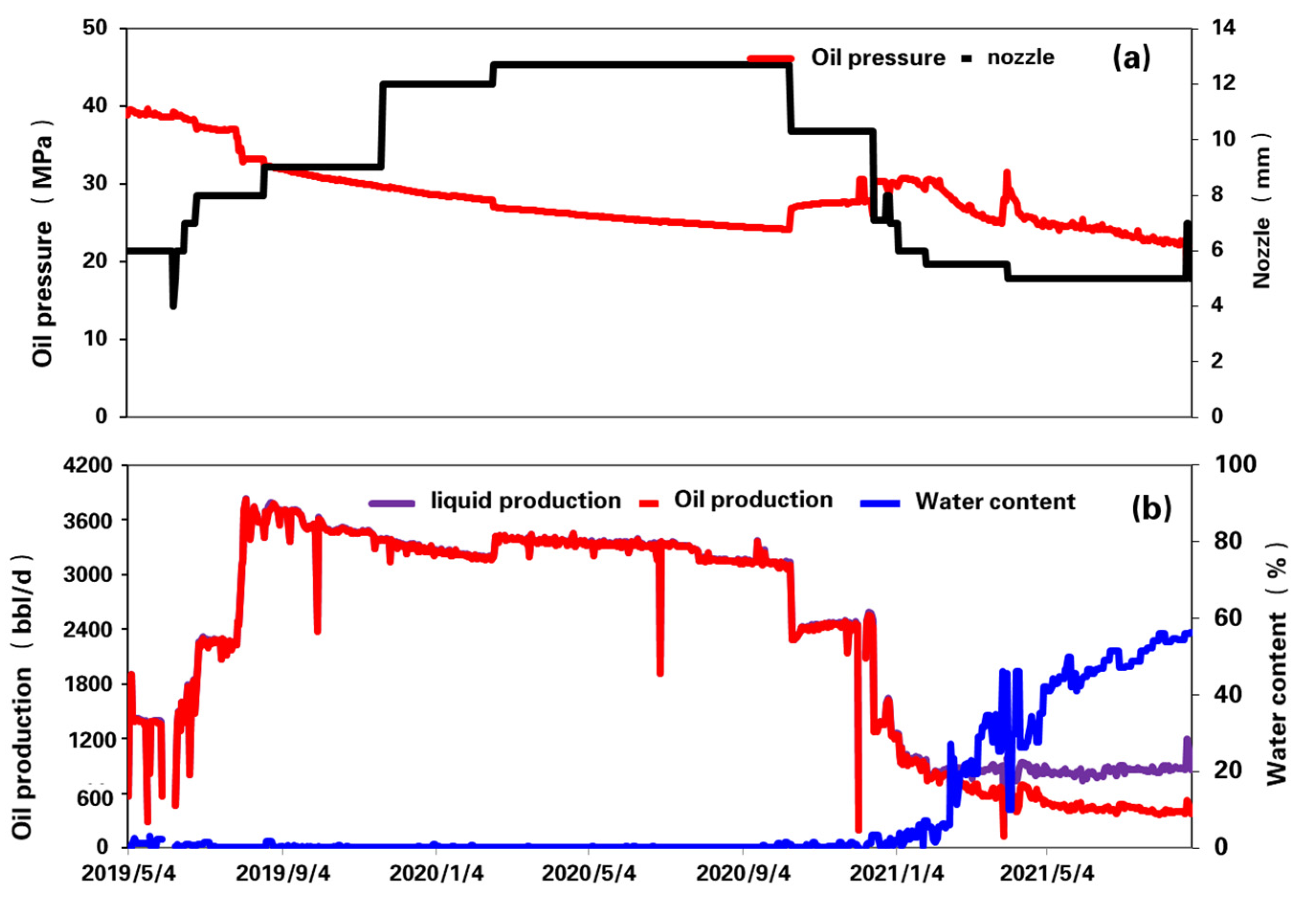





| Nozzle (mm) | Oil Pressure (MPa) | Stable Production (bbl/d) |
|---|---|---|
| 3 | 26.2 | 328 |
| 3.5 | 25.3 | 357 |
| 4 | 23.8 | 441 |
| 5 | 18.3 | 553 |
| Years | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Average well productivity in adjacent areas (bbl/d) | 513 | 462 | 425 | 388 | 352 |
| Plan to deploy new well static reserves (104 bbl) | 828~872 | 755~792 | 704~733 | 645~674 | 594~616 |
| Number of new wells to be deployed (wells) | 6 | 6 | 5 | 5 | 4 |
| Production by analogy (bbl/d) | 513 | 462 | 425 | 388 | 352 |
| Reasonable production (bbl/d) | 513~550 | 462~491 | 425~447 | 388~410 | 352~367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, R.; Yang, J.; Li, S.; Yao, C.; Wu, G. Optimization of Oil Productivity from the Ultra−Depth Strike−Slip Fault−Controlled Carbonate Reservoirs in Northwestern China. Energies 2022, 15, 3472. https://doi.org/10.3390/en15093472
He X, Wang R, Yang J, Li S, Yao C, Wu G. Optimization of Oil Productivity from the Ultra−Depth Strike−Slip Fault−Controlled Carbonate Reservoirs in Northwestern China. Energies. 2022; 15(9):3472. https://doi.org/10.3390/en15093472
Chicago/Turabian StyleHe, Xinxing, Rujun Wang, Jianping Yang, Shiyin Li, Chao Yao, and Guanghui Wu. 2022. "Optimization of Oil Productivity from the Ultra−Depth Strike−Slip Fault−Controlled Carbonate Reservoirs in Northwestern China" Energies 15, no. 9: 3472. https://doi.org/10.3390/en15093472





