An Optimization Study on the Operating Parameters of Liquid Cold Plate for Battery Thermal Management of Electric Vehicles
Abstract
:1. Introduction
2. Numerical Investigation
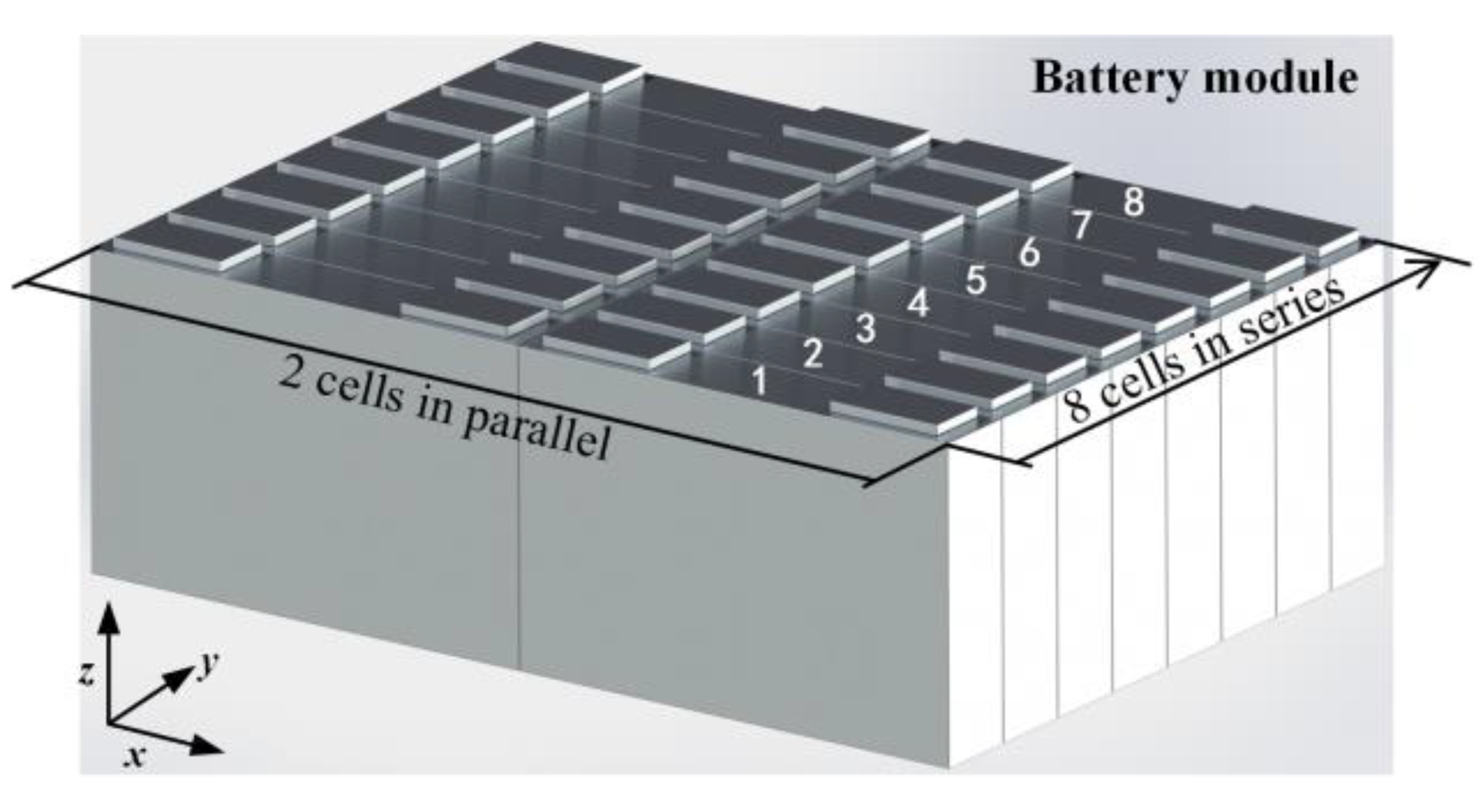
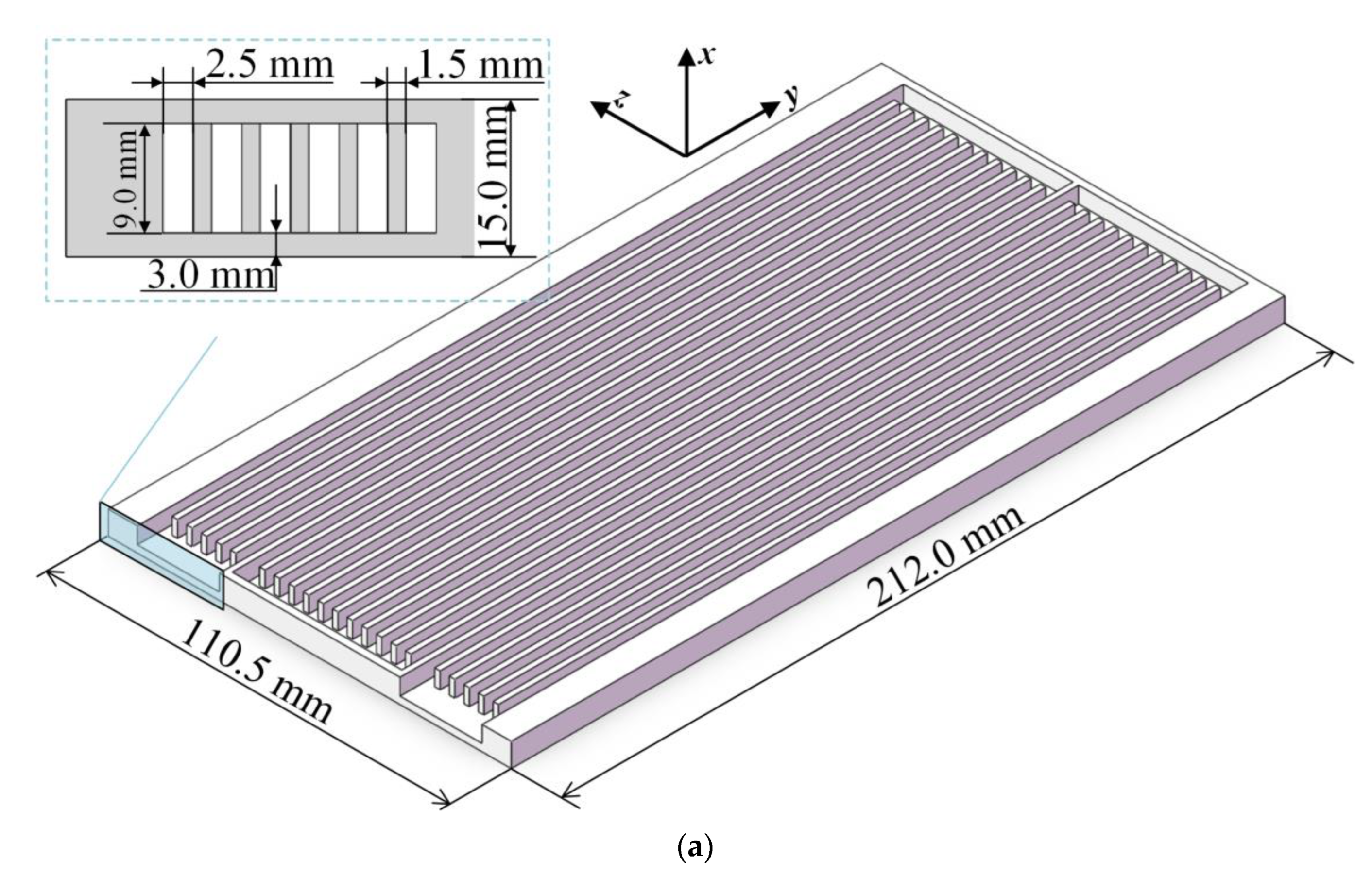
2.1. Configuration of Liquid Cooling System
2.2. Governing Equations and Boundary Conditions
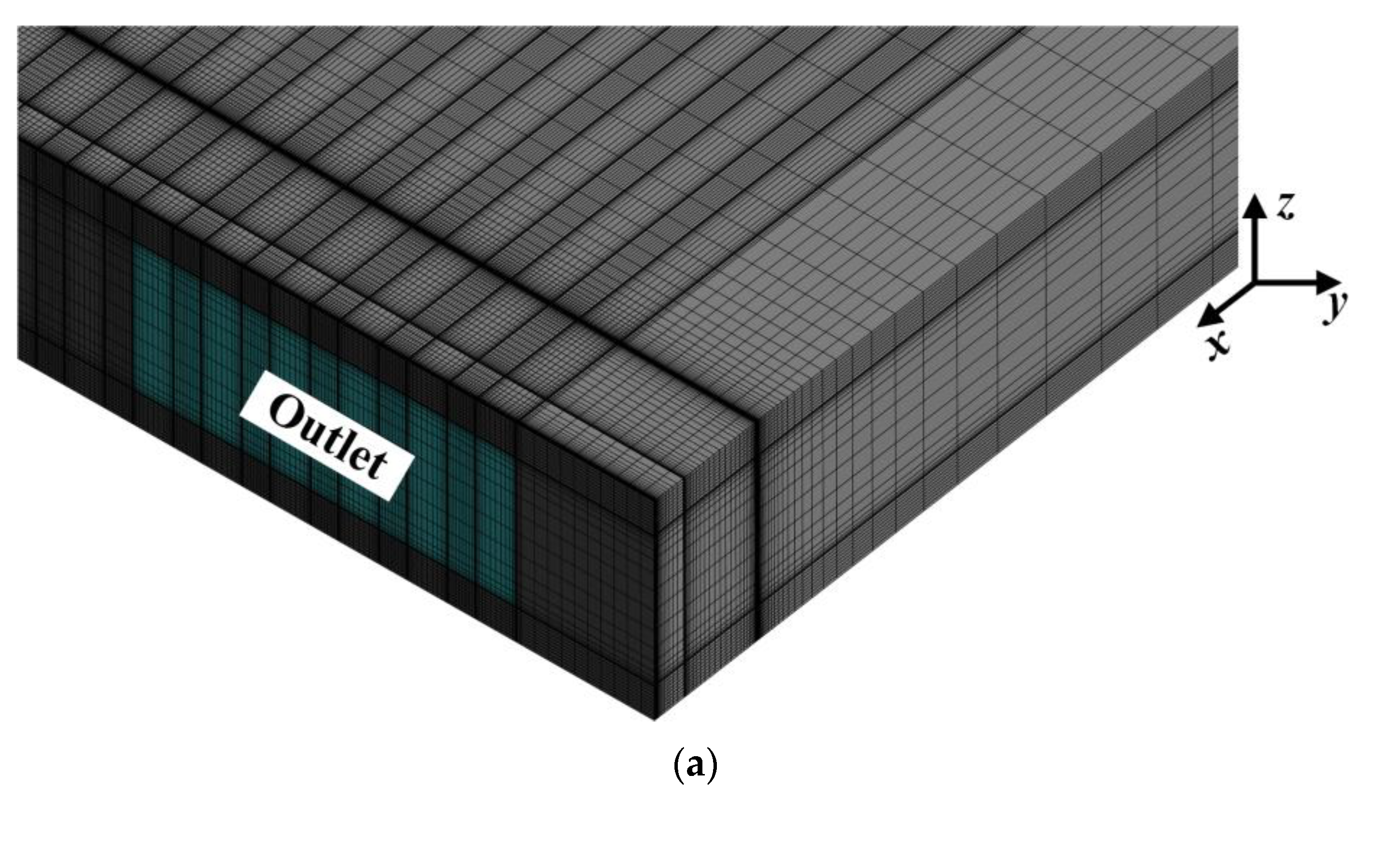
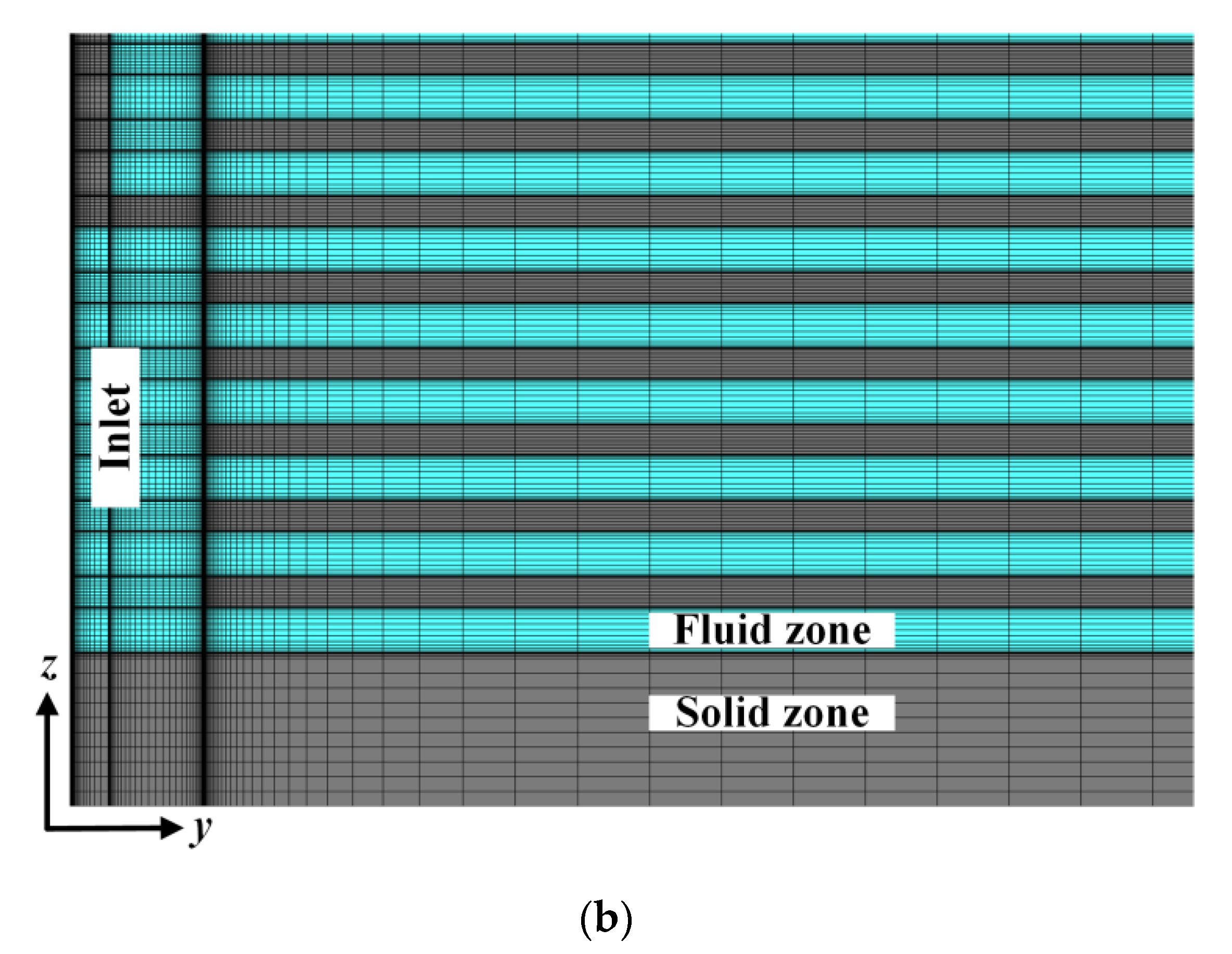
2.3. Numerical Scheme
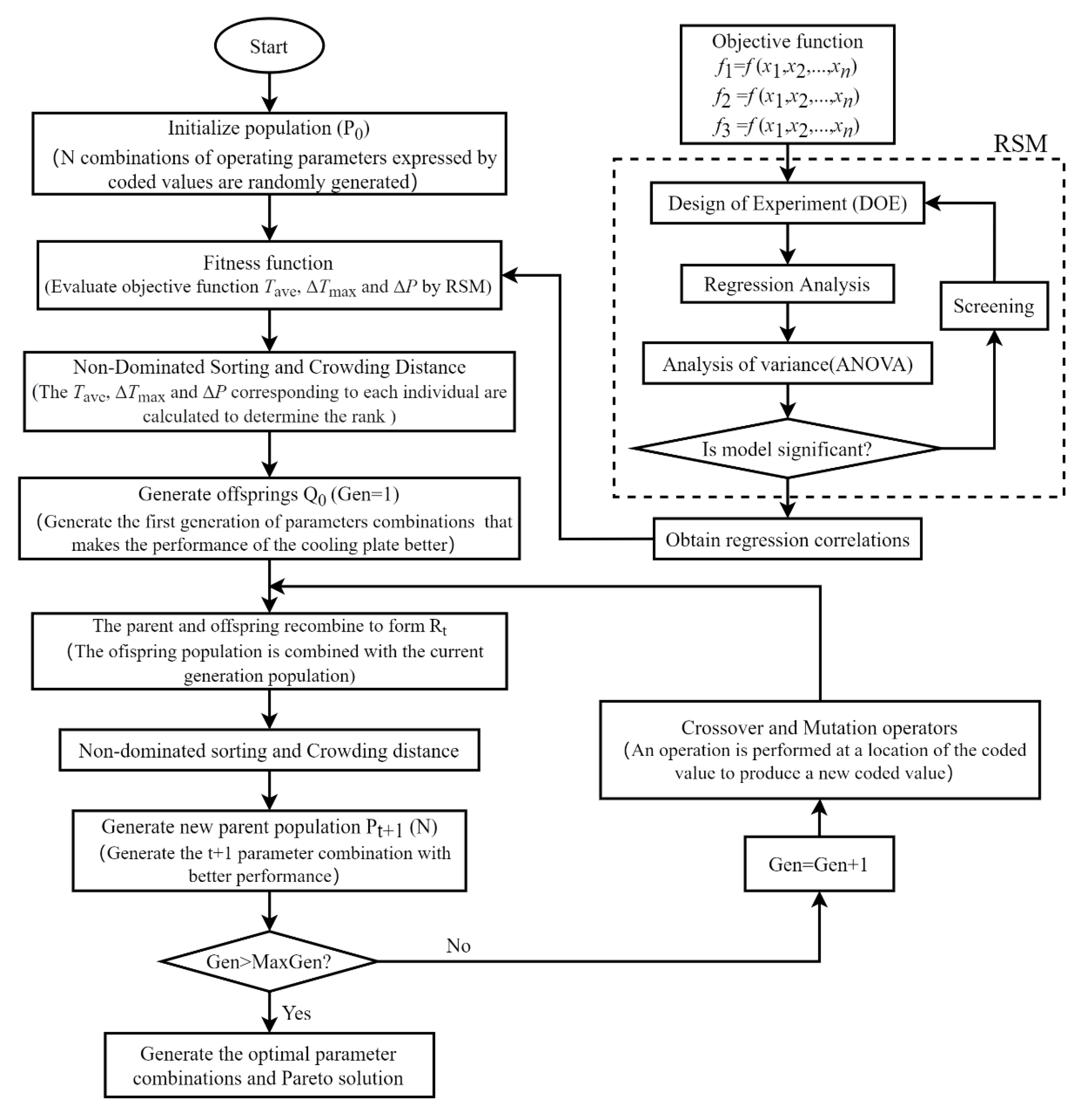
3. Optimization Method
3.1. Response Surface Methodology
3.2. NSGA-Ⅱ Algorithm
4. Results and Discussion
4.1. Numerical Analysis
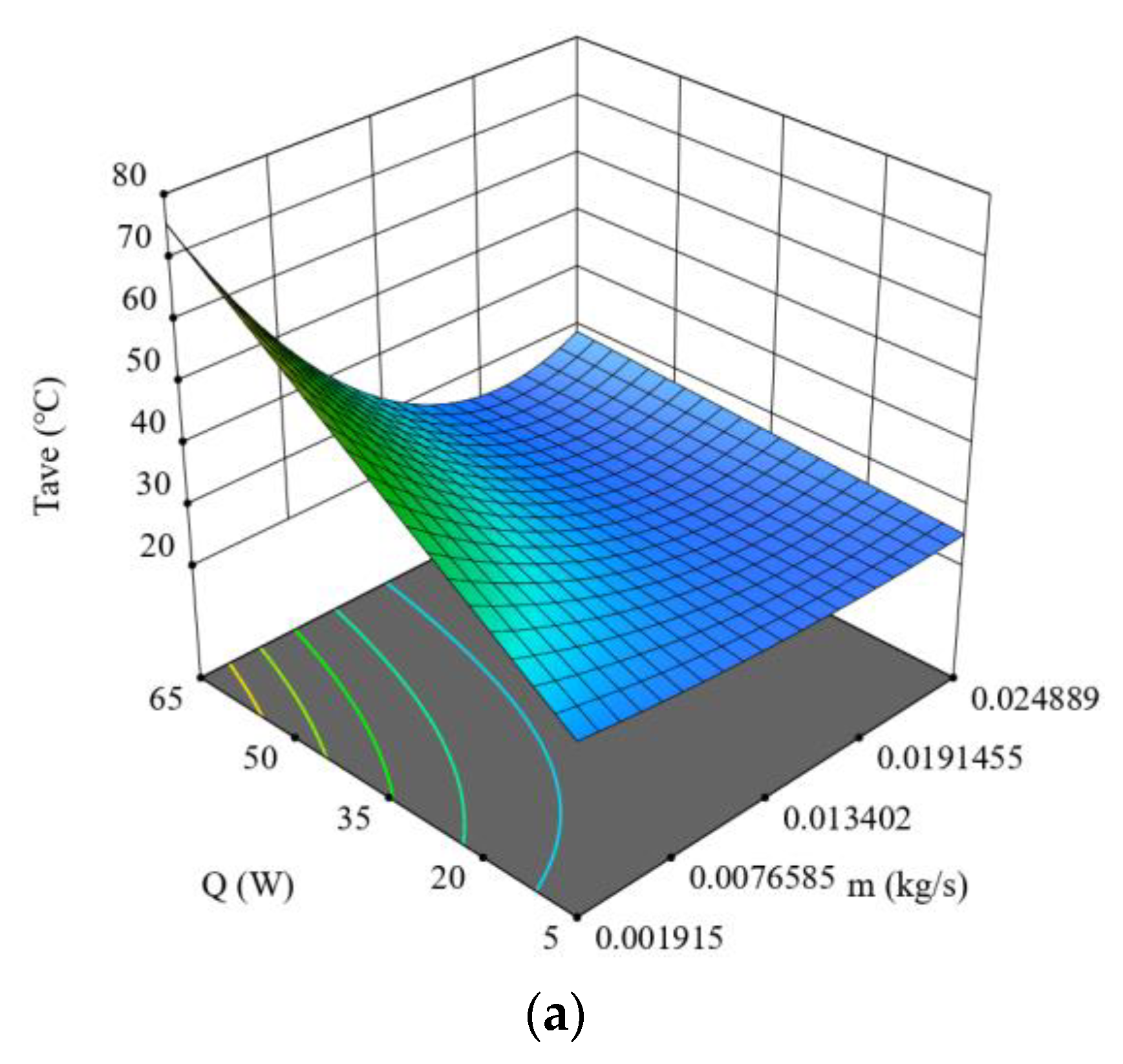
4.2. Response Surface Equations and Validations
4.3. Optimization Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| f | Response function |
| Mass flow rate (kg·s−1) | |
| n | Normal direction |
| P | Pressure (Pa) |
| ΔP | Pressure drop (Pa) |
| Q | Average heat generation (W) |
| R2 | Dimensionless distance |
| Radj2 | Thermal resistance (K·W−1) |
| T | Temperature (°C) |
| Tave | Average temperature (°C) |
| Tin | Inlet temperature (°C) |
| Tmax | Maximum temperature (°C) |
| ΔTmax | Maximum temperature difference (°C) |
| U | velocity vector (m·s−1) |
| u | velocity (m·s−1) |
| Xk | Design variable |
| x | x-coordinate |
| y | y-coordinate |
| z | z-coordinate |
| Greek: | |
| λ | Thermal conductivity (W·m−1K−1) |
| ρ | Density (kg·m−3) |
| ε | Residual error |
| Subscripts: | |
| k | Number of design variables |
| in | Inlet fluid |
| f | Fluid |
| s | Solid |
| out | Outlet fluid |
| x | x direction |
| y | y direction |
| z | z direction |
Appendix A
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Prob. > F |
|---|---|---|---|---|---|
| Model | 4626.93 | 11 | 420.63 | 4.273 × 109 | <0.0001 |
| 1568.31 | 1 | 1568.31 | 1.593 × 1010 | <0.0001 | |
| Q | 19.87 | 1 | 19.87 | 2.019 × 108 | <0.0001 |
| Tin | 49.51 | 1 | 49.51 | 5.030 × 108 | <0.0001 |
| ·Q | 923.81 | 1 | 923.81 | 9.385 × 109 | <0.0001 |
| ·Tin | 0.0006 | 1 | 0.0006 | 6222.22 | <0.0001 |
| Q·Tin | 0.0002 | 1 | 0.0002 | 2031.75 | <0.0001 |
| · | 385.68 | 1 | 385.68 | 3.918 × 109 | <0.0001 |
| Q·Q | 6.125 × 10−7 | 1 | 6.125 × 10−7 | 6.22 | 0.0373 |
| ·Q·Tin | 0.0002 | 1 | 0.0002 | 1645.71 | <0.0001 |
| 2·Q | 141.99 | 1 | 141.99 | 1.442 × 109 | <0.0001 |
| 2·Tin | 8.100 × 10−6 | 1 | 8.100 × 10−6 | 82.29 | <0.0001 |
| Residual | 7.875 × 10−7 | 8 | 9.844 × 10−8 | ||
| Lack of fit | 7.875 × 10−7 | 3 | 2.625 × 10−7 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| total | 4626.93 | 19 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4273.94 | 13 | 328.76 | 5.904 × 109 | <0.0001 |
| 302.85 | 1 | 302.85 | 5.439 × 109 | <0.0001 | |
| Q | 34.94 | 1 | 34.94 | 6.276 × 108 | <0.0001 |
| Tin | 0.0000 | 1 | 0.0000 | 323.27 | <0.0001 |
| ·Q | 892.30 | 1 | 892.30 | 1.602 × 1010 | <0.0001 |
| ·Tin | 0.0122 | 1 | 0.0122 | 2.199 × 105 | <0.0001 |
| Q·Tin | 0.0215 | 1 | 0.0215 | 3.866 × 105 | <0.0001 |
| · | 280.85 | 1 | 280.85 | 5.044 × 109 | <0.0001 |
| Q·Q | 2.784 × 10−7 | 1 | 2.784 × 10−7 | 5.00 | 0.0667 |
| Tin·Tin | 2.784 × 10−7 | 1 | 2.784 × 10−7 | 5.00 | 0.0667 |
| ·Q·Tin | 0.0174 | 1 | 0.0174 | 3.123 × 105 | <0.0001 |
| 2·Q | 120.35 | 1 | 120.35 | 2.161 × 109 | <0.0001 |
| 2·Tin | 0.0038 | 1 | 0.0038 | 68,640.45 | <0.0001 |
| ·Q·Q | 6.250 × 10−7 | 1 | 6.250 × 10−7 | 11.22 | 0.0154 |
| Residual | 3.341 × 10−7 | 6 | 5.568 × 10−8 | ||
| Lack of fit | 3.341 × 10−7 | 1 | 3.341 × 10−7 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| Cor total | 4273.94 | 19 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Prob. > F |
|---|---|---|---|---|---|
| Model | 4.748 × 106 | 4 | 1.187 × 106 | 6.154 × 105 | <0.0001 |
| 4.443 × 106 | 1 | 4.443 × 106 | 2.304 × 106 | <0.0001 | |
| Tin | 1043.63 | 1 | 1043.63 | 541.13 | <0.0001 |
| ·Tin | 357.98 | 1 | 357.98 | 185.62 | <0.0001 |
| · | 3.031 × 105 | 1 | 3.031 × 105 | 1.571 × 105 | <0.0001 |
| Residual | 28.93 | 15 | 1.93 | ||
| Lack of fit | 28.93 | 10 | 2.89 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| total | 4.748 × 106 | 19 |
References
- Amjad, S.; Neelakrishnan, S.; Rudramoorthy, R. Review of design considerations and technological challenges for successful development and deployment of plug-in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2020, 14, 1104–1110. [Google Scholar] [CrossRef]
- Leipzig, I.T.F. Reducing Transport Greenhouse Gas Emissions: Trends & Data. In Background for the 2010 International Transport Forum, Berlin; ITF: Paris, France, 2010. [Google Scholar]
- Andersen, P.H.; Mathews, J.A.; Rask, M. Integrating private transport into renewable energy policy: The strategy of creating intelligent recharging grids for electric vehicles. Energy Policy 2009, 37, 2481–2486. [Google Scholar] [CrossRef]
- Maja, M.; Morello, G.; Spinelli, P. A model for simulating fast charging of lead/acid batteries. J. Power Sources 1992, 40, 81–91. [Google Scholar] [CrossRef]
- Liu, J.; Gao, D.; Cao, J. Study on the effects of temperature on LiFePO4 battery life. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Leng, F.; Tan, C.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [Green Version]
- Cui, S.; Wei, Y.; Liu, T.; Deng, W.; Pan, F. Optimized Temperature Effect of Li-Ion Diffusion with Layer Distance in Li(Nix MnyCoz )O2 Cathode Materials for High Performance Li-Ion Battery. Adv. Energy Mater. 2016, 6, 1501309. [Google Scholar] [CrossRef]
- Liu, X.; Ren, D.; Hsu, H.; Feng, X.; Xu, G.; Zhuang, M.; Han, G.; Lu, L.; Han, X.; Chu, Z. Thermal Runaway of Lithium-Ion Batteries without Internal Short Circuit. Joule 2018, 2, 2047–2064. [Google Scholar] [CrossRef] [Green Version]
- Lei, Z.; Zhang, C.; Li, J.; Fan, G.; Lin, Z. A study on the low-temperature performance of lithium-ion battery for electric vehicles. Auto. Eng. 2013, 35, 927–933. [Google Scholar]
- Ren, D.; Xiang, L.; Feng, X.; Lu, L.; Ouyang, M.; Li, J.; He, X. Model-based thermal runaway prediction of lithium-ion batteries from kinetics analysis of cell components. Appl. Energ. 2018, 228, 633–644. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Li, X. Temperature rise prediction of lithium-ion battery suffering external short circuit for all-climate electric vehicles application. Appl. Energ. 2018, 213, 275–383. [Google Scholar] [CrossRef]
- Landini, S.; Leworthy, J.; O’Donovan, T.S. A Review of Phase Change Materials for the Thermal Management and Isothermalisation of Lithium-Ion Cells. J. Energy Stor. 2019, 25, 100887. [Google Scholar] [CrossRef]
- Jiang, Z.; Qu, Z. Lithium–ion battery thermal management using heat pipe and phase change material during discharge–charge cycle: A comprehensive numerical study. Appl. Energ. 2019, 242, 378–392. [Google Scholar] [CrossRef]
- Ling, Z.; Zhang, Z.; Shi, G.; Fang, X.; Wang, L.; Gao, X.; Fang, Y.; Xu, T.; Wang, S.; Liu, X. Review on thermal management systems using phase change materials for electronic components, Li-ion batteries and photovoltaic modules. Renew. Sustain. Energy Rev. 2014, 31, 427–437. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; He, R. Review on the heat dissipation performance of battery pack with different structures and operation conditions. Renew. Sustain. Energy Rev. 2014, 29, 301–315. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.-F.; Zhou, J.-G.; Xiong, X.; Zhang, C.-C.; Wang, Y.-P. Numerical simulation of hybrid battery thermal management system combining of thermoelectric cooler and phase change material. Energy Rep. 2022, 8, 1094–1102. [Google Scholar] [CrossRef]
- Saechan, P.; Dhuchakallaya, I. Numerical study on the air-cooled thermal management of Lithium-ion battery pack for electrical vehicles. Energy Rep. 2022, 8, 1264–1270. [Google Scholar] [CrossRef]
- Liang, G.; Li, J.; He, J.; Tian, J.; Chen, X.; Chen, L. Numerical investigation on a unitization-based thermal management for cylindrical lithium-ion batteries. Energy Rep. 2022, 8, 4608–4621. [Google Scholar] [CrossRef]
- Lyu, Y.; Siddique, A.R.M.; Majid, S.H.; Biglarbegian, M.; Gadsden, S.A.; Mahmud, S. Electric vehicle battery thermal management system with thermoelectric cooling. Energy Rep. 2019, 5, 822–827. [Google Scholar] [CrossRef]
- Intano, W.; Kaewpradap, A.; Hirai, S.; Masomtob, M. Thermal investigation of cell arrangements for cylindrical battery with forced air-cooling strategy. J. Res. Appl. Mech. Eng. 2020, 8, 11–21. [Google Scholar]
- Saw, L.H.; Ye, Y.H.; Tay, A.; Chong, W.T.; Kuan, S.H.; Yew, M.C. Computational fluid dynamic and thermal analysis of Lithium-ion battery pack with air cooling. Appl. Energ. 2016, 177, 783–792. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Xu, L.; Kong, J.; Yang, Q. Thermal performance of cylindrical Lithium-ion battery thermal management system based on air distribution pipe. Int J. Heat Mass Tran. 2019, 131, 984–998. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, X.; Wei, L.; Qiu, Y.; Zhang, L.; Meng, X.; Jin, L. Parametric study of forced air cooling strategy for lithium-ion battery pack with staggered arrangement. Appl. Therm. Eng. 2018, 136, 28–40. [Google Scholar] [CrossRef]
- Burban, G.; Ayel, V.; Alexandre, A.; Lagonotte, P.; Bertin, Y.; Romestant, C. Experimental investigation of a pulsating heat pipe for hybrid vehicle applications. Appl. Therm. Eng. 2013, 50, 94–103. [Google Scholar] [CrossRef]
- Tran, T.H.; Harmand, S.; Desmet, B.; Filangi, S. Experimental investigation on the feasibility of heat pipe cooling for HEV/EV lithium-ion battery. Appl. Therm. Eng. 2014, 63, 551–558. [Google Scholar] [CrossRef]
- Tran, T.H.; Harmand, S.; Sahut, B. Experimental investigation on heat pipe cooling for Hybrid Electric Vehicle and Electric Vehicle lithium-ion battery. J. Power Sources 2014, 265, 262–272. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery Thermal Management in EVs and HEVs: Issues and Solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Park, S.; Jung, D. Battery cell arrangement and heat transfer fluid effects on the parasitic power consumption and the cell temperature distribution in a hybrid electric vehicle. J. Power Sources 2013, 227, 191–198. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Kai, C.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; Jiaqiang, E.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Li, Y. Thermal performance of mini-channel liquid cooled cylinder based battery thermal management for cylindrical lithium-ion power battery. Energy Convers. Manag. 2015, 103, 157–165. [Google Scholar] [CrossRef]
- Gao, R.; Fan, Z.; Liu, S. A gradient channel-based novel design of liquid-cooled battery thermal management system for thermal uniformity improvement. J. Energy Storage 2022, 48, 104014. [Google Scholar] [CrossRef]
- Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Sohn, D.K.; Yeo, T. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system. Appl. Energ. 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Du, X.; Qian, Z.; Chen, Z.; Rao, Z. Experimental investigation on mini-channel cooling-based thermal management for Li-ion battery module under different cooling schemes. Int. J. Energy Res. 2018, 42, 2781–2788. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Yang, X. Optimization of liquid cooling technology for cylindrical power battery module. Appl. Therm. Eng. 2019, 162, 114200. [Google Scholar] [CrossRef]
- Zhao, Z.; Bermudez, S.Z.; Ilyas, A.; Muylaert, K.; Vankelecom, I.F.J. Optimization of negatively charged polysulfone membranes for concentration and purification of extracellular polysaccharides from Arthrospira platensis using the response surface methodology. Sep. Purif. Technol. 2020, 252, 117385. [Google Scholar] [CrossRef]
- Cai, M.; Wang, S.; Liang, H.H. Optimization of ultrasound-assisted ultrafiltration of Radix astragalus extracts with hollow fiber membrane using response surface methodology. Sep. Purif. Technol. 2012, 100, 74–81. [Google Scholar] [CrossRef]
- Salahi, A.; Noshadi, I.; Badrnezhad, R.; Kanjilal, B.; Mohammadi, T. Nano-porous membrane process for oily wastewater treatment: Optimization using response surface methodology. J. Environ. Eng. 2013, 1, 218–225. [Google Scholar] [CrossRef]
- Yi, S.; Su, Y.; Qi, B.; Su, Z.; Wan, Y. Application of response surface methodology and central composite rotatable design in optimizing the preparation conditions of vinyltriethoxysilane modified silicalite/polydimethylsiloxane hybrid pervaporation membranes. Sep. Purif. Technol. 2010, 71, 252–262. [Google Scholar] [CrossRef]
- Kumar, A.; Thakur, A.; Panesar, P.S. A comparative study on experimental and response surface optimization of lactic acid synergistic extraction using green emulsion liquid membrane. Sep. Purif. Technol. 2019, 211, 54–62. [Google Scholar] [CrossRef]
- Chanukya, B.S.; Kumar, M.; Rastogi, N.K. Optimization of lactic acid pertraction using liquid emulsion membranes by response surface methodology. Sep. Purif. Technol. 2013, 111, 1–8. [Google Scholar] [CrossRef]
- Song, T.; Yao, Y.; Ni, L. Response surface method to study the effect of conical surface and vortex-finder lengths on de-foulant hydrocyclone with reflux ejector. Sep. Purif. Technol. 2020, 253, 117511. [Google Scholar] [CrossRef]
- Zou, Y.; Wei, L.; Lu, Z.; Qin, S.; Cao, F. An optimal study of serpentine channel with various configurations based on response surface analysis. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; Volume 1074, p. 012016. [Google Scholar]
- Liebig, G.; Gupta, G.; Kirstein, U.; Schuldt, F.; Agert, C. Parameterization and validation of an electrochemical thermal model of a lithium-ion battery. Batteries 2019, 5, 62. [Google Scholar] [CrossRef] [Green Version]
- Lyu, P.; Huo, Y.; Qu, Z.; Rao, Z. Investigation on the thermal behavior of Ni-rich NMC lithium ion battery for energy storage. Appl. Therm. Eng. 2020, 166, 114749. [Google Scholar] [CrossRef]
- Abdul, Q.Y.; Laurila, T.; Karppinen, J.; Jalkanen, K.; Vuorilehto, K.; Skogström, L.; Paulasto-Kröckel, M. Heat generation in high power prismatic Li-ion battery cell with LiMnNiCoO2 cathode material. Int. J. Energy Res. 2014, 38, 1424–1437. [Google Scholar] [CrossRef]
- Liang, X.; Sun, Z.; Huang, Q. Study on the Channel and Heat Transfer Performance of Liquid Cold Plate Used for LED Module. China Light Lighting 2012, 1, 6–10. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. Lect. Notes Comput. Sci. 2000, 1917, 849–858. [Google Scholar]





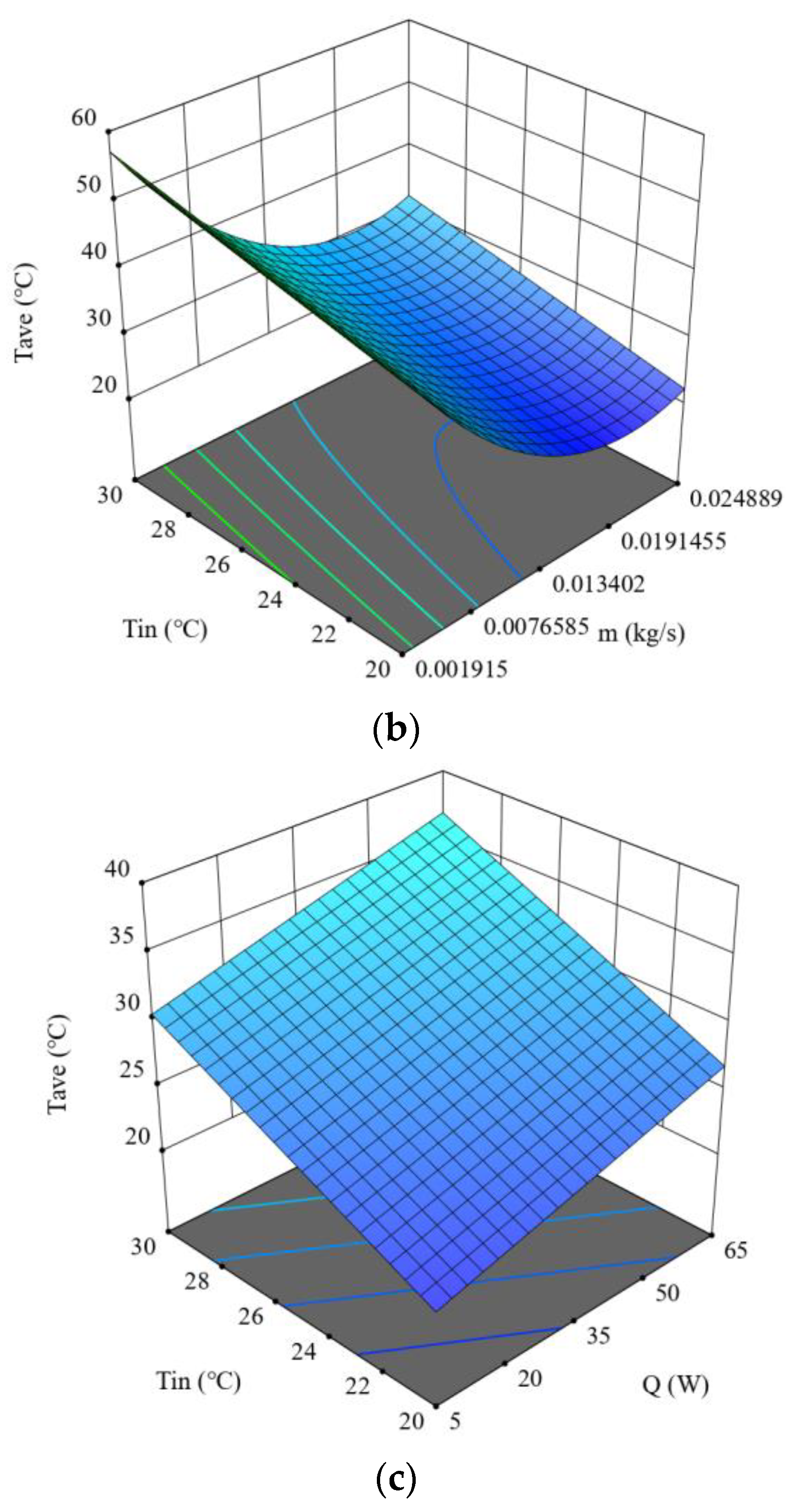
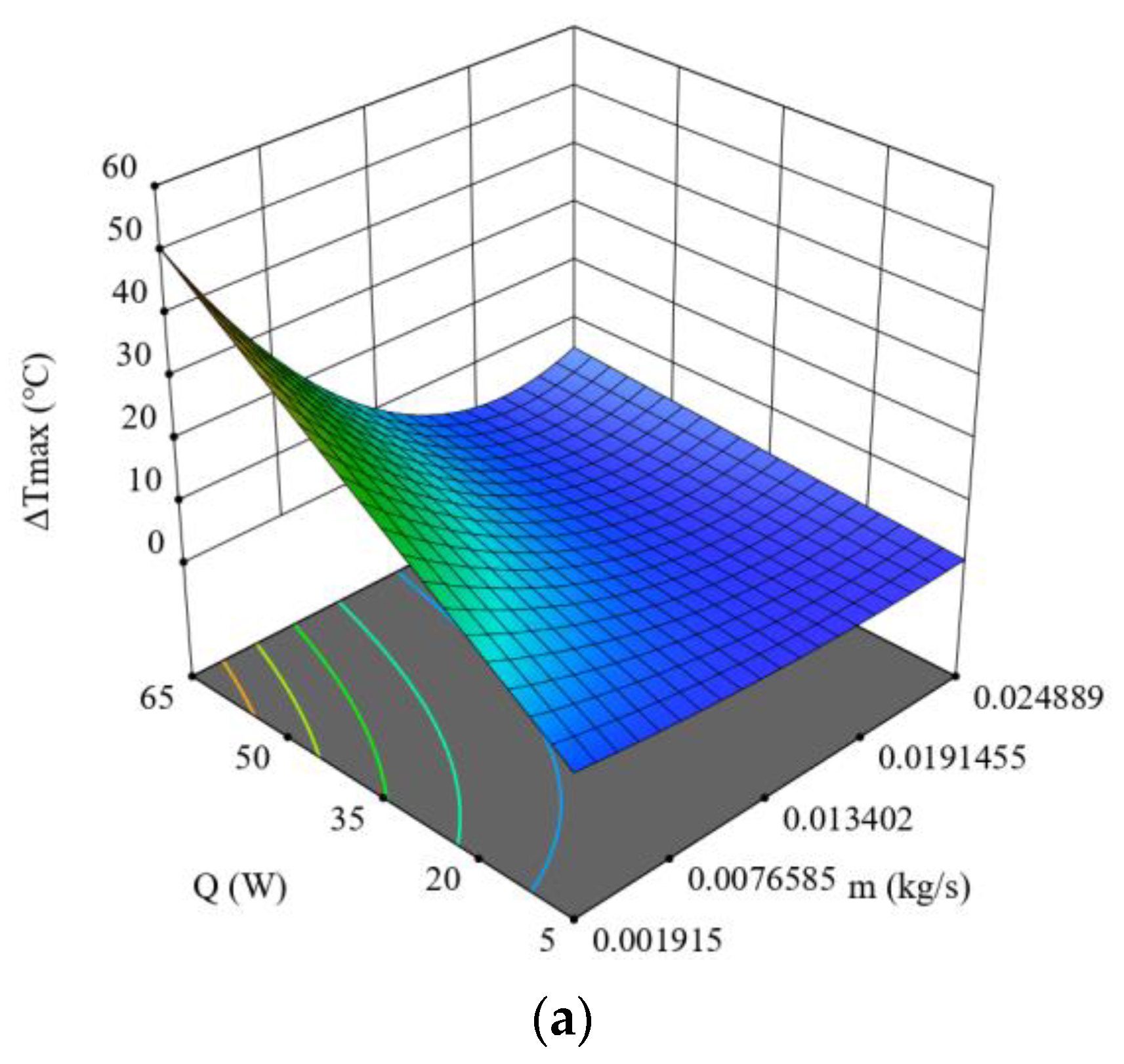

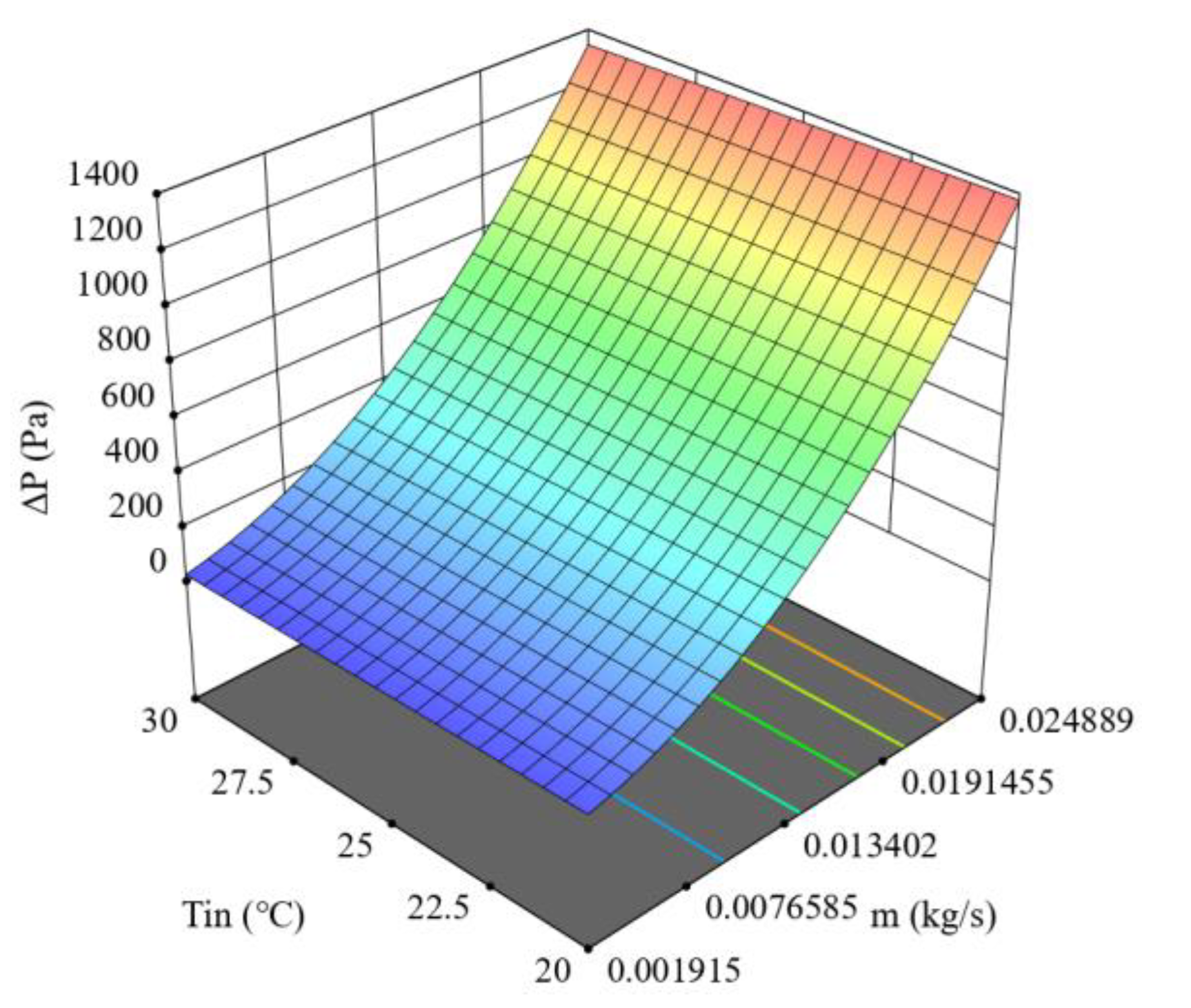
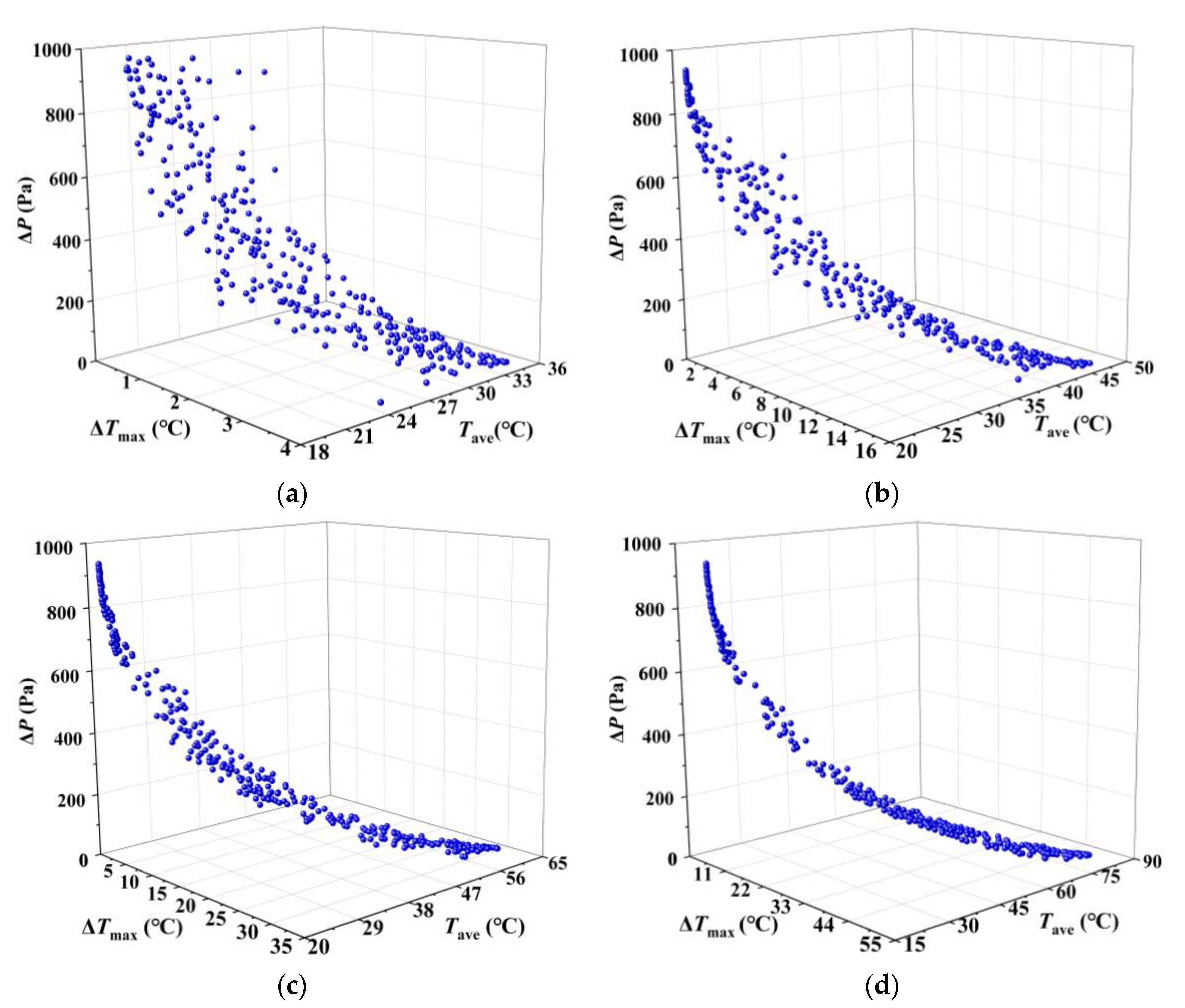
| S/No. | Design Variables | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| 1 | Flow rate, kg·s−1 | 0.0019 | 0.0134 | 0.0249 |
| 2 | Average heat generation rate, W | 5 | 35 | 65 |
| 3 | Inlet temperature, °C | 20 | 25 | 30 |
| Variables (Code) | Variables (Actual Value) | Response | |||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Q | Tin | , kg·s−1 | Q, W | Tin, °C | Tave, °C | ΔTmax, °C | ΔP, Pa | |
| case1 | −1 | −1 | −1 | 0.0019 | 5 | 20 | 23.89 | 3.89 | 30.45 |
| case2 | 1 | −1 | −1 | 0.0249 | 5 | 20 | 20.31 | 0.38 | 1377.06 |
| case3 | −1 | 1 | −1 | 0.0019 | 65 | 20 | 70.53 | 50.52 | 30.45 |
| case4 | 1 | 1 | −1 | 0.0249 | 65 | 20 | 23.98 | 4.95 | 1377.06 |
| case5 | −1 | −1 | 1 | 0.0019 | 5 | 30 | 33.83 | 3.86 | 25.09 |
| case6 | 1 | −1 | 1 | 0.0249 | 5 | 30 | 30.3 | 0.38 | 1344.95 |
| case7 | −1 | 1 | 1 | 0.0019 | 65 | 30 | 80.46 | 50.88 | 25.09 |
| case8 | 1 | 1 | 1 | 0.0249 | 65 | 30 | 33.93 | 4.98 | 1344.93 |
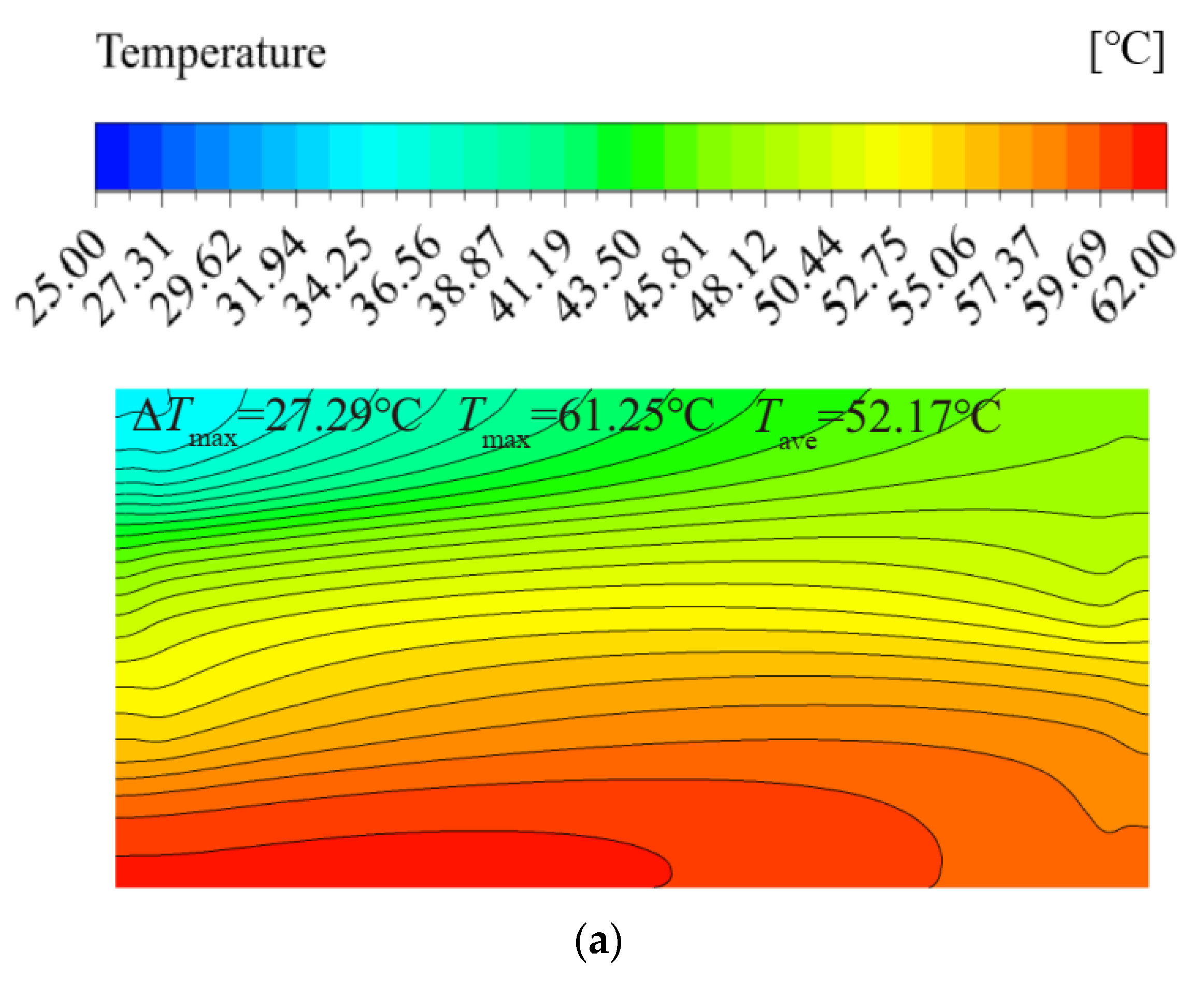
| case9 | −1 | 0 | 0 | 0.0019 | 35 | 25 | 52.17 | 27.29 | 27.77 |
| case10 | 1 | 0 | 0 | 0.0249 | 35 | 25 | 27.13 | 2.67 | 1360.47 |
| case11 | 0 | −1 | 0 | 0.0134 | 5 | 25 | 25.52 | 0.69 | 448.10 |
| case12 | 0 | 1 | 0 | 0.0134 | 65 | 25 | 31.83 | 9.05 | 448.10 |
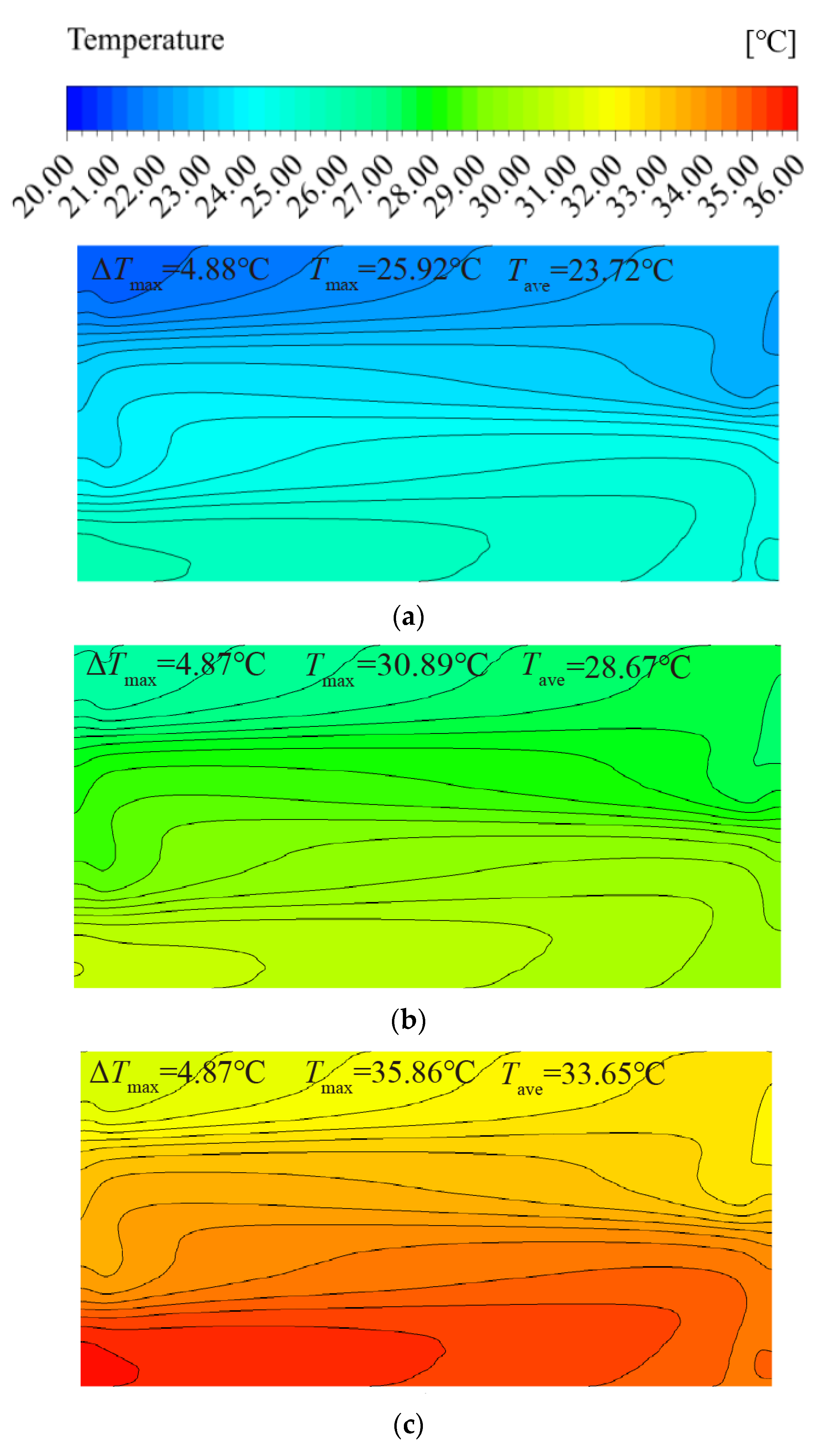
| case13 | 0 | 0 | −1 | 0.0134 | 35 | 20 | 23.72 | 4.88 | 461.87 |
| case14 | 0 | 0 | 1 | 0.0134 | 35 | 30 | 33.65 | 4.87 | 434.67 |
| case15 | 0 | 0 | 0 | 0.0134 | 35 | 25 | 28.67 | 4.87 | 448.10 |
| Parameters | Values |
|---|---|
| PopulationSize | 1000 |
| ParetoFraction | 0.3 |
| MaxGenerations | 200 |
| MaxStallGenerations | 200 |
| FunctionTolerance | 10−10 |
| Number of variables | 2 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4626.93 | 12 | 385.58 | 3.452 × 109 | <0.0001 |
| 1568.31 | 1 | 1568.31 | 1.404 × 1010 | <0.0001 | |
| Q | 19.87 | 1 | 19.87 | 1.779 × 108 | <0.0001 |
| Tin | 49.51 | 1 | 49.51 | 4.433 × 108 | <0.0001 |
| · Q | 923.81 | 1 | 923.81 | 8.271 × 109 | <0.0001 |
| · Tin | 0.0006 | 1 | 0.0006 | 5484.01 | <0.0001 |
| Q·Tin | 0.0002 | 1 | 0.0002 | 1790.70 | <0.0001 |
| · | 331.45 | 1 | 331.45 | 2.968 × 109 | <0.0001 |
| Q·Q | 5.682 × 10−7 | 1 | 5.682 × 10−7 | 5.09 | 0.0587 |
| Tin·Tin | 5.682 × 10−9 | 1 | 5.682 × 10−9 | 0.0509 | 0.8280 |
| · Q·Tin | 0.0002 | 1 | 0.0002 | 1450.47 | <0.0001 |
| 2· Q | 141.99 | 1 | 141.99 | 1.271 × 109 | <0.0001 |
| 2·Tin | 8.100 × 10−6 | 1 | 8.100 × 10−6 | 72.52 | <0.0001 |
| · Q·Q | 1.000 × 10−7 | 1 | 1.000 × 10−7 | 0.8800 | 0.3844 |
| Residual | 7.818 × 10−7 | 8 | 1.117 × 10−7 | ||
| Lack of fit | 7.818 × 10−7 | 3 | 3.909 × 10−7 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| Cor total | 4626.93 | 19 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4273.94 | 13 | 328.76 | 5.904 × 109 | <0.0001 |
| 302.85 | 1 | 302.85 | 5.439 × 109 | <0.0001 | |
| Q | 34.94 | 1 | 34.94 | 6.276 × 108 | <0.0001 |
| Tin | 0.0000 | 1 | 0.0000 | 323.27 | <0.0001 |
| · Q | 892.30 | 1 | 892.30 | 1.602 × 1010 | <0.0001 |
| ·Tin | 0.0122 | 1 | 0.0122 | 2.199 × 105 | <0.0001 |
| Q·Tin | 0.0215 | 1 | 0.0215 | 3.866 × 105 | <0.0001 |
| · | 280.85 | 1 | 280.85 | 5.044 × 109 | <0.0001 |
| Q·Q | 2.784 × 10−7 | 1 | 2.784 × 10−7 | 5.00 | 0.0667 |
| Tin·Tin | 2.784 × 10−7 | 1 | 2.784 × 10−7 | 5.00 | 0.0667 |
| ·Q·Tin | 0.0174 | 1 | 0.0174 | 3.123 × 105 | <0.0001 |
| 2·Q | 120.35 | 1 | 120.35 | 2.161 × 109 | <0.0001 |
| 2·Tin | 0.0038 | 1 | 0.0038 | 68,640.45 | <0.0001 |
| ·Q·Q | 6.250 × 10−7 | 1 | 6.250 × 10−7 | 11.22 | 0.0154 |
| Residual | 3.341 × 10−7 | 6 | 5.568 × 10−8 | ||
| Lack of fit | 3.341 × 10−7 | 1 | 3.341 × 10−7 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| Cor total | 4273.94 | 19 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4.748 × 106 | 9 | 5.275 × 105 | 1.833 × 105 | <0.0001 |
| 4.443 × 106 | 1 | 4.443 × 106 | 1.544 × 106 | <0.0001 | |
| Q | 0.0001 | 1 | 0.0001 | 0.0000 | 0.9955 |
| Tin | 1043.63 | 1 | 1043.63 | 362.74 | <0.0001 |
| ·Q | 0.0001 | 1 | 0.0001 | 0.0000 | 0.9950 |
| ·Tin | 357.98 | 1 | 357.98 | 124.43 | <0.0001 |
| · | 1.665 × 105 | 1 | 1.665 × 105 | 57,870.36 | <0.0001 |
| Q·Q | 0.0028 | 1 | 0.0028 | 0.0010 | 0.9756 |
| Tin·Tin | 0.1196 | 1 | 0.1196 | 0.0416 | 0.8425 |
| Residual | 28.77 | 10 | 2.88 | ||
| Lack of fit | 28.77 | 5 | 5.75 | ||
| Pure error | 0.0000 | 5 | 0.0000 | ||
| Cor total | 4.748 × 106 | 19 |
| Discharging Rate | Q kg·s−1 | Tin °C | Predicted/CFD Results of Tave, °C | Predicted/CFD Results of ΔTmax, °C | Predicted/ CFD Results of ΔP, Pa | Error of Tave % | Error of ΔTmax % | Error of ΔP % |
|---|---|---|---|---|---|---|---|---|
| 1.0 C | 0.0156 | 26.86 | 27.09/ 27.31 | 0.51/0.58 | 579.82/ 582.91 | −0.81 | −12.07 | −0.53 |
| 0.0057 | 28.29 | 30.68/ 29.68 | 2.46/2.49 | 108.95/ 105.79 | 3.37 | −1.20 | 2.99 | |
| 2.0 C | 0.0163 | 25.33 | 26.03/ 27.07 | 2.14/2.32 | 629.69/ 628.76 | −3.84 | −7.88 | 0.15 |
| 0.0118 | 28.00 | 31.18/ 29.85 | 3.36/3.12 | 356.27/ 356.58 | 4.46 | 7.63 | −0.09 | |
| 3.0 C | 0.0174 | 21.13 | 21.9/ 24.44 | 3.86/4.37 | 718.26/ 722.97 | −10.39 | −11.67 | −0.65 |
| 0.0158 | 25.54 | 27.34/ 29.14 | 4.05/4.79 | 593.37/ 593.15 | −6.18 | −15.50 | 0.04 | |
| 4.0 C | 0.0199 | 20.00 | 24.08/ 24.72 | 3.58/3.97 | 919.68/ 920.81 | −2.59 | −9.82 | −0.12 |
| 0.0203 | 20.23 | 23.60/ 23.25 | 3.42/3.87 | 743.05/ 743.85 | 1.51 | −11.63 | −0.11 |
| Discharging Rate | ΔTmax, °C | Tave, °C | ΔP, Pa |
|---|---|---|---|
| 1.0 C | 0.29~3.90 | 20.03~33.82 | 24.39~966.91 |
| 2.0 C | 1.11~15.66 | 20.07~45.40 | 24.44~941.94 |
| 3.0 C | 2.17~31.39 | 20.14~60.72 | 24.56~940.21 |
| 4.0 C | 3.43~50.92 | 20.22~80.22 | 24.53~936.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Zou, Y.; Cao, F.; Ma, Z.; Lu, Z.; Jin, L. An Optimization Study on the Operating Parameters of Liquid Cold Plate for Battery Thermal Management of Electric Vehicles. Energies 2022, 15, 9180. https://doi.org/10.3390/en15239180
Wei L, Zou Y, Cao F, Ma Z, Lu Z, Jin L. An Optimization Study on the Operating Parameters of Liquid Cold Plate for Battery Thermal Management of Electric Vehicles. Energies. 2022; 15(23):9180. https://doi.org/10.3390/en15239180
Chicago/Turabian StyleWei, Lichuan, Yanhui Zou, Feng Cao, Zhendi Ma, Zhao Lu, and Liwen Jin. 2022. "An Optimization Study on the Operating Parameters of Liquid Cold Plate for Battery Thermal Management of Electric Vehicles" Energies 15, no. 23: 9180. https://doi.org/10.3390/en15239180





