Optimization and Techno-Economic Appraisal of Parabolic Trough Solar Power Plant under Different Scenarios: A Case Study of Morocco

Abstract

Morocco is a country with a lack of fossil fuel resources and an increasing demand for energy. This inspired the country to increase the use of renewable energy in the energy mix. The objective of this study was to conduct an optimization and techno-economic appraisal of a concentrated solar power plant (CSP) using different scenarios that took Ouarzazate city in the south of Morocco as a case study. To achieve this, several parameters were assessed, including the impacts of solar collector assemblies (SCAs), receiver types, heat transfer fluids, cooling systems, solar multiples, and thermal storage hours, with regard to the profitability of the CSP plant. Then, performance and sensitivity analyses were conducted to select the best integration scenarios based on different economic indicators, including levelized cost of electricity (LCOE) and net present value (NPV). The findings revealed that the use of the Luz LS-3 as the collector/SCA, Solel UVAC 3 as receiver, and Dowtherm Q as heat transfer fluid exhibited the highest performance in terms of the annual energy production yield and capacity factor, as well as the lowest real and nominal LCOEs with a wet cooled condenser. Furthermore, the LCOE is extremely sensitive to changes in the number of hours of storage and the solar multiple, and the optimal real and nominal LCOEs are determined by a highly specific combination of the solar multiple and the number of hours of storage. As a consequence, the maximum and minimum net electricity outputs for the best configuration of the Parabolic Trough Collector (PTC) plant were 24.6 GWh and 7.4 GWh in May and December, respectively. Likewise, the capacity factor and the gross-to-net conversion factor for the optimized plant were found to be 47.9%, and 93.5%, respectively. Concerning the economic study, the expected energy cost was 0.1303 USD per kWh and the NPV value for Ouarzazate city was positive (more than USD 20 million), which indicates that the studied PTC plant was estimated to be financially and economically feasible. The results of this analysis are highly significant and may persuade decision makers, financiers, and solar energy industry players to increase their investments in the Kingdom of Morocco.

1. Introduction

Nowadays, shifting toward a green and sustainable society is a necessity for both countries with high fossil resources and those with a lack of these resources so that they can decrease CO₂ emissions on the one hand and decrease the energy bill on the other hand. Among the various renewable energy sources, solar energy presents one of the best solutions to drive this energy shift due to its high efficiency—in comparison to other resources [1]—and flexible adaptation for different applications, such as hydrogen production [2,3], seawater desalination [4], food drying [5], and industrial heat process [6], especially for locations with high solar irradiation [7,8].

Generally, when talking about solar energy, two main technologies come mind: photovoltaics (PV) and concentrated solar power (CSP). The first technology currently has the greatest installed capacity, with 194 GW in 2020 according to the IEA [9]. This installation is expected to increase significantly and reach 329.5 GW by 2026. This is largely due to the drop in investment costs—mainly in the price of the PV modules—as well as improvements in overall PV system efficiency [10]. However, the main inconvenience of PV technologies is storage. Indeed, PV produces electricity directly from the sun and, to store this electricity, lithium battery units are usually used. These batteries are still expensive and, for large-scale projects, the price of a kWh increases significantly when a storage scenario is used [11].

In contrast, storage is the main advantage of CSP technologies, for which the produced heat can be stored to be re-used during sunset or cloudy periods, ensuring better energy dispatch for CSP power plants [12].

However, CSP technologies are still not competitive in the energy market as the CAPEX for building a CSP power plant is high in comparison to other renewable technologies [13]. In addition, the operation of these plants is quite difficult, especially in desert locations (such as Ouarzazate in Morocco or the Atacama Desert in Chile) where the highest direct normal irradiation (DNI) values are recorded, as dust may lead to an important drop in the optical efficiency [14], attenuation of the intensity of the reflected irradiation [15], and degradation of the power plant components themselves [16].

In the face of weather conditions, solar irradiation, and hosting site specificities [17], optimization of power plant configurations is necessary to decrease the LCOE and increase the electricity production and profitability of solar plant projects [18]. Indeed, during the selection phase of a solar plant integration project, engineers must conduct different simulation runs taking into consideration different variables, such as the technology to be used, the area of the solar field, and the heat transfer fluid (HTF), as well as the type of cooling.

Then, a detailed economic study must be conducted to evaluate the feasibility of the project and calculate its cost-effectiveness from both technical and economic points of view. This step is usually difficult and the challenge relates to the stage of the choice of the configuration to be adapted especially for large-scale power plans where the investment costs are high, as CSP technology is still not competitive against conventional energy sources [19].

The goal of this study was to conduct an optimization and techno-economic evaluation of a concentrated solar power plant (CSP) using different scenarios that took Ouarzazate city in southern Morocco as a case study. To do so, we selected the parabolic trough collector (PTC) technology, as it is the most trustworthy and widely installed technology worldwide [20], and it has a 70% share of total CSP-based power generation [21]. Then, we developed seven scenarios in which we proposed several optimization processes for the plant’s components, including solar field size, TES time, heat transfer fluids, the types of receiver tubes, and the power block cooling technique. Next, for each one of the scenarios, we calculated the amount of electricity production, as well as the LCOE. Finally, the feasibility of the best configuration for a PTC power plant adaptable to the Moroccan context with a nominal capacity of 50 MWe was determined and compared with Andasol 1, SEGS VI, and other solar power plants from the literature.

This paper is structured as follows: the next section presents the methodology of the work, including a description of the selected power plant, the scenarios to be studied, and the mathematical and economic model. After that, we briefly describe the field of study and assess the solar resource. Finally, the results section summarizes the key finding of this study.

2. Methodology

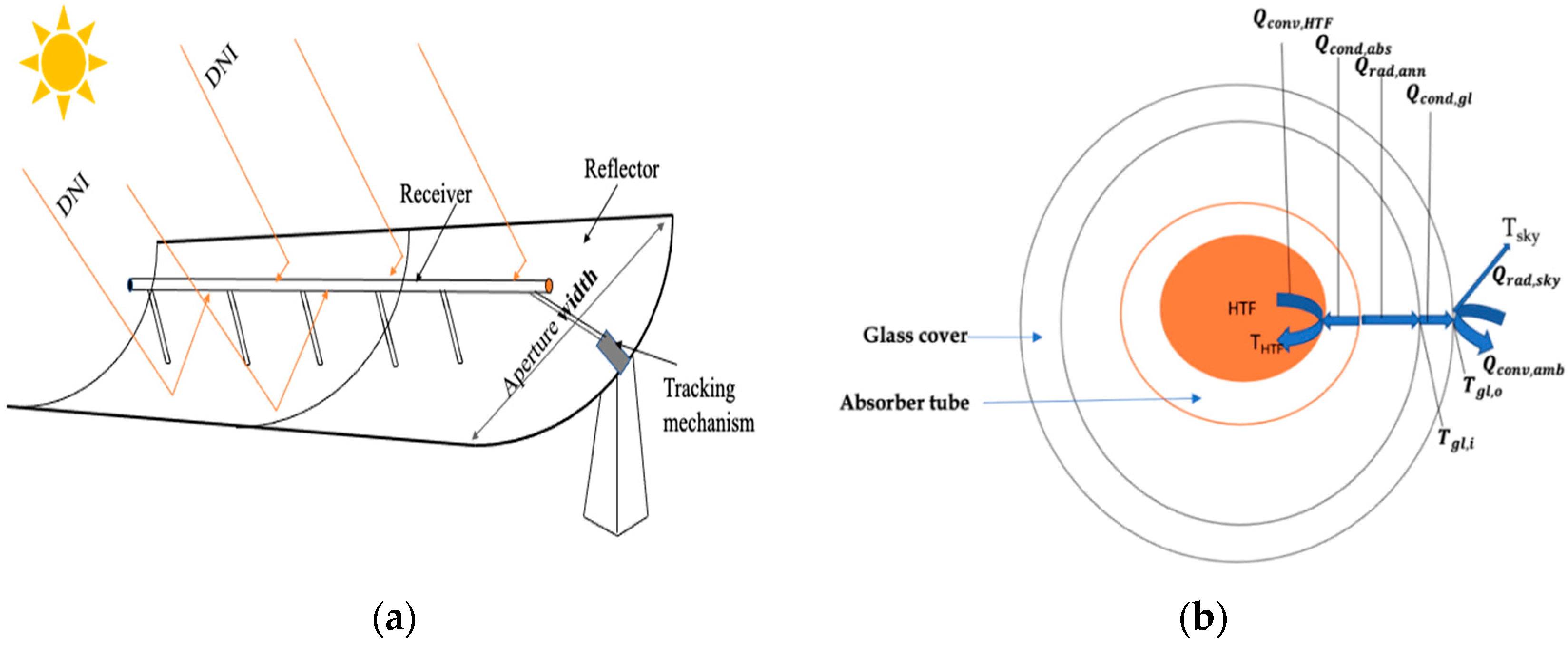
2.1. System Description and Modeling of PTC Plant

A 50 MWe PTC solar power facility was designed in order to evaluate the performance of the investigated plant in Morocco. The design was further optimized for seven different scenarios, including the solar multiple and full load hours of the thermal energy storage:

• Scenario 1: PTC facility with various solar collector assemblies (SCAs);
• Scenario 2: PTC facility with various receivers (HCEs);
• Scenario 3: PTC facility with various heat transfer fluids (HTFs);
• Scenario 4: PTC facility with various types of cooling options (Wet and Dry);
• Scenario 5: PTC facility with various solar multiple values (SM);
• Scenario 6: PTC facility with various thermal storage times (TES);
• Scenario 7: PTC best configuration and sensitivity analysis.

The proposed PTC system was subdivided into three main portions: (i) a solar field consisting of a series of mirrors that concentrate direct solar radiation in the receivers, which are filled with heat transfer fluid; (ii) a sensible thermal energy storage (TES) made up of a hot salt tank and a cold salt tank and consisting of a binary salt combining a sodium nitrate (NaNO₃) content of 60% and a potassium nitrate content of 40% (KNO₃)—the TES system is used to store additional thermal energy that can be used when sunlight is unavailable; (iii) a power block using the Rankine power cycle and comprised of a boiler/steam generator for the generation of electricity. Figure 1 displays a schematic diagram of the investigated PTC plant [22]. Lists of the various commercial collectors, receivers, and heat transfer fluids that were used for the simulations, along with their specifications and proprieties, are shown in

Table 1. Description of parameters for different various SCAs.

	Reflective Aperture Area (m2)	Aperture Width—Total Structure (m)	Length of Collector Assembly (m)	Length of a Single Module (m)	Number of Modules Per Assembly	Reflector Coating
ET150	817.5	5.75	150	12.5	12	Back silver-coated
Luz LS-2	235	5	49	8.16	6	Back silver-coated
Luz LS-3	545	5.75	100	8.33	12	Back silver-coated
SGX-1	470.3	5	100	8.33	12	Back silver-coated
AT150	817.5	5.774	150	12.5	12	Back silver-coated
Siemens Sunfield 6	545	5.776	95.2	11.9	8	-
SkyFuel SkyTrough	656	6	115	14.37	8	RelecTech Plus polymer film
FLABEG Ultimate Trough RP6	1720	7.53	247	24.7	10	Back silver-coated

,

Table 2. Description of different parabolic trough solar receiver HCEs available on the market.

	Absorber Flow Pattern	Absorber Tube Inner Diameter (m)	Absorber Tube Outer Diameter (m)	Glass Envelope Inner Diameter (m)	Glass Envelope Outer Diameter (m)
Schott PTR70	304 L	0.066	0.07	0.115	0.12
Schott PTR70-2008	304 L	0.066	0.07	0.115	0.12
Solel UVAC 3	304 L	0.066	0.07	0.115	0.121
Siemens UVAC 2010	216 L	0.066	0.07	0.109	0.115
Schott PTR80	304 L	0.076	0.08	0.115	0.12
Royal Tech CSP RTUVR 2014	321 H	0.066	0.07	0.119	0.125
TRX70-125	321 H	0.066	0.07	0.119	0.125

and

Table 3. Heat transfer fluid proprieties.

	Chemical Composition (%wt)	Field HTF Min Operating Temp	Field HTF Max Operating Temp	Min Field Flow Velocity	Max Field Flow Velocity	Ensity (kg m3) vs. Temperature (°C)
Hitec solar salt	NaNO3 (60%)/KNO3 (40%)	238	593	0.153546	1.90492	ρ = 2090 − 0.63·T
Caloria HT 43		−12	315	0.429685	5.77916
Hitec XL	NaNO3 (15%)/KNO3 (43%)/Ca (NO3)2 (42%)	120	500	0.14631	1.82992	ρ = 2240 − 0.827·T
Therminol VP1	Eutectic mixture of diphenyl oxide (DPO) and bipheny	12	400	0.356109	4.96554	$\begin{array}{c}\rho =1083.25-\\ 0.90797\cdot \mathrm{T}+\\ 0.00078116\cdot \mathrm{T}2\\ 2.367\cdot 10-6\cdot \mathrm{T}3\end{array}$
Hitec	NaNO3/KNO3/NaNO2 (7/53/40)	142	538	0.156709	1.95583	ρ = −0.9·T + 2269.4
Dowtherm Q	Mixture of diphenylethane and alkylated aromatics	−35	330	0.385166	5.12302
Therminol 59		−45	315	0.385278	5.23268

, respectively. The System Advisor Model (SAM) program [23] was used to study the effectiveness of the PTC/TES installation under the weather conditions of Morocco (Ouarzazate city) from technical and economic viewpoints in different scenarios. The solar power facility was based on parabolic trough technology. System Advisor Model is widely used for pre-feasibility studies [8,24,25,26,27]. It computes numerous economic performance parameters for renewable energy installations, including the system generated power, estimated annual capacity factor, net present value (NPV), and levelized cost of electricity (LCOE). We can note that NREL Laboratory has already validated the PTC model used in the SAM software [28]. Furthermore, the complete model used in this program is presented by Wagner and Gilman [29].

2.2. Mathematical Description

Among CSP systems for energy production, parabolic trough collectors have received more development and are better commercially demonstrated than others. PTC systems generally use a long, parabolic-shaped mirror to focus direct solar radiation on a receiving tube located at the parabola’s focal line. Large fields of collectors are used to drive a steam turbine, which in turn drives the electric generator. Figure 2 depicts a parabolic trough collector in cross-section. The absorber tube is formed of a metal tube covered in a glass envelope. The space between the glass envelope and the metal tube is either filled with air or comprised of a vacuum to allow for thermal expansion while limiting convective heat loss.

The reflected solar power can be obtained by the following equation [30]:

$$Q_{sol,sf}=DNI\ast \cos \mathsf{\theta }\ast A_{field}$$

(1)

where:

• DNI: direct normal irradiation (W/m²);
• $A_{field}$: total solar field aperture area;
• $\mathsf{\theta }$: incidence angle.

The power absorbed by the receiving tubes is obtained as follows [30]:

$$Q_{\mathrm{rec}}=Q_{sol,sf}\ast k\left({\theta }_{\mathrm{csp} }\right)\ast {\eta }_{\mathrm{shadow} }\ast {\eta }_{\mathrm{end} }\ast {\eta }_{\mathrm{track} }\ast {\eta }_{\mathrm{col} }\ast {\eta }_{\mathrm{rec} }$$

(2)

where $k\left({\theta }_{\mathrm{csp} }\right)$ is the incidence angle modifier, ${\eta }_{\mathrm{shadow}}$ is the shadowing factor, ${\eta }_{\mathrm{track} }$ is the tracking factor, ${\eta }_{\mathrm{end}}$ is the end loss factor, ${\eta }_{\mathrm{col}}$ is the collector efficiency, and ${\eta }_{\mathrm{rec}}$ is the receiver efficiency. The absorber tube, also known as the heat collector element (HCE), is an integral component of the parabolic trough comprised of a stainless-steel tube. To limit losses through convection and radiation to the outside, a glass envelope covers the absorber and creates a vacuum in the annular space. To decrease thermal radiation losses, a dark-colored selective coating (typically a cermet layer) is used to achieve strong radiation absorptance in the solar energy spectrum and low emittance in the long solar energy spectrum [31]. The following equation can be used to estimate heat transmission through convection from the absorber pipe’s inside surface to the HTF [31]:

$$Q_{conv,HTF}=h_{abs,HTF}\ast \pi \ast D_{abs,i}\ast \left(T_{abs,i}-T_{HTF}\right)$$

(3)

where:

• $h_{abs,HTF}:$HTF convection heat transfer coefficient;
• $D_{abs,i}:$absorber pipe’s inside diameter;
• $T_{abs,i}$: temperature of the absorber pipe’s inside surface;
• $T_{HTF}$: the HTF’s average temperature.

The heat transfer through conduction from the absorber’s outer surface to the absorbent’s inner surface can be stated as follows [31]:

$$Q_{cond,abs}=\frac{2\pi \ast k_{abs}\left(T_{abs,o}-T_{abs,i}\right)}{ln\left(\frac{D_{abs,o}}{D_{abs,i}}\right)}$$

(4)

where:

• k_abs: the absorber’s thermal conductivity at the average absorber temperature;
• $T_{abs,i}$: temperature of the absorber’s inner surface;
• $T_{abs,o}$: temperature of the exterior surface of the absorber;
• $D_{abs,i}$: absorber inside diameter;
• $D_{abs,o}$: absorber outside diameter.

The following equation is employed to calculate the heat transfer through radiation between the absorber and the glass envelope [21,32]:

$$Q_{rad,ann}=\frac{\sigma \ast \pi \ast D_{abs,o.}\left(T^4{}_{abs,o}-T^4{}_{gl,i}\right)}{\frac{1}{{\epsilon }_{abs}}+\frac{1-{\epsilon }_{gel}}{{\epsilon }_{gel}}\left(\frac{D_{abs,o}}{D_{gl,i}}\right)}$$

(5)

where:

• T_abs,o: temperature of the outer absorber surface in Kelvin;
• T_gl,i: surface temperature of the inside glass envelope in Kelvin;
• ε_abs: emissivity of absorber selective coating;
• ε_gl: glass surface emissivity;
• $D_{abs,o}$: outer absorber diameter;
• $D_{gl,i}$: inner glass envelope diameter;
• σ: Stefan–Boltzmann constant.

The heat transported via conduction through the glass envelope from the inner glass surface to the outer glass surface can be estimated with following equation:

$$Q_{cond,gl}=\frac{2\pi \ast k_{gl}\left(T_{gl,o}-T_{gl,i}\right)}{\ln \left(\frac{r_{gl,o}}{r_{gl,i}}\right)}$$

(6)

where:

• k_gl: glass thermal conductivity.

The heat transferred from the glass envelope to the environment through radiation can be estimated using the following formula [31]:

$$Q_{rad,sky}=\sigma \ast \pi \ast {\epsilon }_{gel}\ast D_{gl,o}\ast \left(T^4{}_{gl,o,kelvin}-T^4{}_{sky,Kelvin}\right)$$

(7)

where:

• $D_{gl,o}:$ glass envelope outer diameter;
• T_gl,o,Kelvin: glass envelope outer surface temperature;
• T_sky,Kelvin: sky temperature.

The sky temperature is obtained from the ambient temperature using the following formula [21,33]:

$$T_{sky}=0.0552\ast T_{amb}^{1.5}$$

(8)

2.2.1. Storage System

One of the primary benefits of solar thermal power plants is thermal energy storage (TES). It is low-cost and easier than the storage of electrical energy [34], and its application is very advantageous as it improves the annual solar share, reducing the plant’s operation under partial load while boosting its availability.

A two-tank molten salt system was used in this study. This technology is commercially viable and widely applied in PTC power plants around the world due to its high heat transfer coefficient and high thermal storage capacity. The technology is made up of a hot salt tank and a cold salt tank consisting of a binary salt combining a sodium nitrate (NaNO₃) content of 60% and a potassium nitrate content of 40% (KNO₃). In the charging phase, the salt is pumped through the heat exchanger from the cold tank to heat it up to a temperature of about 386 °C, and then it is pumped into the hot salt tank to be stored. In the discharge phase, the flow path is reversed, and heat is transferred from the hot salt to the PTC via the heat exchanger. A control system ensures that the salt temperature does not drop below 292–293 °C to prevent the salt from solidifying at a high temperature of around 220 °C [35]. The mass of each tank (hot and cold) is introduced in the following equations as a function of the mass flow rate [36]:

$$M_{HT}\left(t\right)={{\displaystyle \int }}_{t_0}^t{\dot{m}}_{CT}-{\dot{m}}_{HT}\left(t\right)dt+x_0$$

(9)

$$M_{CT}\left(t\right)={{\displaystyle \int }}_{t_0}^t{\dot{m}}_{HT}-{\dot{m}}_{CT}\left(t\right)dt+x_0$$

(10)

where:

• • M_HT: mass inside the hot tank;
  • M_CT: mass inside the cold tank;
  • ${\dot{m}}_{HT}$: outlet mass flow rate from the hot tank;
  • ${\dot{m}}_{CT}$: outlet mass flow rate from the cold tank;
  • t₀: The two tanks’ lowest limit;
  • t: The two tanks’ highest saturation limit.

The stored thermal energy in the TES system can be calculated using the following formula [37]:

$$Q_{stored}\left(MWh\right)=\frac{{10}^{-6}}{3600}{M}_{HT}\ast C_{P,HTF}\left(T_{HT,salt}\right)\ast \left(T_{HT,salt}-T_{CT,salt}\right)$$

(11)

where:

• • $T_{HT,salt}$: temperature of the salt in the hot tank;
  • $T_{CT,salt}$: temperature of the salt in the cold tank.

2.2.2. Solar Multiple (SM)

The SM is expressed as the ratio of the actual size of the solar field to the size of the solar field needed to power the turbine at nominal conditions [38] and is expressed by the following formula:

$${\mathrm{SM}}_{\mathrm{design}\text{\_}\mathrm{point} }={\frac{{\mathrm{Q}}_{\mathrm{th},\mathrm{solar}\text{\_}\mathrm{field} }}{{\mathrm{Q}}_{\mathrm{th},\mathrm{power}\text{\_}\mathrm{block} }}|}_{\mathrm{design}\text{\_}\mathrm{point} }$$

(12)

where:

• • ${\mathrm{Q}}_{\mathrm{th},\mathrm{solar}\text{\_}\mathrm{field} }$: thermal power generated in the solar field;
  • ${\mathrm{Q}}_{\mathrm{th},\mathrm{power}\text{\_}\mathrm{block} }$: thermal power demanded by the power block.

The SM is a crucial indicator in determining the size of a PTC plant and defining its optimal field and the amount of power to be stored. The SM fluctuates with the parabolic collectors’ overall surface area: with a larger SM (>1), the surface is larger, meaning that the power provided by the solar field increases and, hence, more power can be stored.

2.2.3. Capacity Factor CF

The CF is a crucial indicator for power plant generation. This metric describes the proportion of the electrical energy generated by the facility during a given period over the nominal electrical energy that could have been produced if the solar facility was working at full capacity during the same period. The annual capacity factor of the investigated PTC power plant was obtained with the following equation [39]:

$$CF=\frac{ \mathrm{annualgeneratedelectricity} }{ \mathrm{design}\text{-}\mathrm{capacity} \times 8760}$$

(13)

2.3. Economic Parameters and System Costs

2.3.1. Levelized Cost of Energy

According to the literature, the levelized cost of energy or electricity (LCOE) is the main figure tool for investors for the analysis of the economics of a solar thermal power plant. It is used to compare the kWh cost of different power system technologies and to justify the choice of installation types and locations. Assumptions and inputs, such as solar field cost, thermal energy storage cost, and operation and maintenance costs, can have a considerable impact on this factor. The economic investigation is carried out with the help of the SAM program, and the real and notional LCOEs are determined as follows [40,41]:

$$\mathrm{nominal} LCOE=\frac{{\sum }_{n=1}^N\frac{R_n}{{(1+D{R}_{\mathrm{nominal}})}^n}}{{\sum }_{n=1}^N\frac{Q_n}{{(1+D{R}_{\mathrm{nominal}})}^n}}$$

(14)

$$\mathrm{real} LCOE=\frac{{\sum }_{n=1}^N\frac{R_n}{{(1+D{R}_{\mathrm{nominal}})}^n}}{{\sum }_{n=1}^N\frac{Q_n}{{(1+D{R}_{\mathrm{real}})}^n}}$$

(15)

where $R_n$ is the necessary revenue from power sales in year n, $Q_n$ is the electricity generated in year n, ${DR}_{\mathrm{nominal}}$ is the nominal discount rate, and ${DR}_{\mathrm{real} }$ is the real discount rate. We can note that the nominal LCOE is a current dollar value more suitable for short-term analyses, while the real LCOE is a constant dollar (inflation-adjusted) value more suitable for long-term analyses.

2.3.2. Net Present Value

Another economic indicator used to evaluate the economic feasibility of a solar power plant project throughout the analysis period is the net present value (NPV). The NPV shows the absolute and dynamic index for the evaluation of the cost-effectiveness of solar power facility installations. It is comprised of both cost and revenue and can be estimated using the following formula [41]:

$$NPV=-C_o+\sum _{n=1}^N\frac{P{R}_n}{{(1+d_{nom})}^n}$$

(16)

where ${PR}_n$ represents the project’s after-tax returns in year $n$.

3. Site Location and Solar Resources

Since the potential of concentrated solar power plants is strongly affected by solar resources data, it is necessary to discuss the amount of solar resources received by our field of study. For this reason, we used typical meteorological year (TMY) data for Ouarzazate city from a one-hour interval dataset obtained from Meteonorm software [42]. Ouarzazate is positioned at 30.91° N latitude, −6.89° E longitude, at an elevation of 1113 m. It is located in the south of Morocco in the Draa-Tafilalet region, which is characterized by an arid and relatively warm climate that receives high solar radiation. Direct normal irradiation (DNI) was here given more weight, since it has the greatest impact on the net power output of a concentrated solar plant. Figure 3 illustrates the direct normal irradiation for the investigated location. As indicated in Figure 3a, the highest values for the DNI are between 11 AM and 5 PM. The highest average DNI was recorded in May, with a maximum value of 854 W/m², while the lowest values occurred in December. The sum of the DNI is 6.70 kWh/m²/day. Figure 3b presents the probability and cumulative distribution function (CDF) for the DNI at the Ouarzazate site; the DNI for the design was selected as 950 W/m² (~95% CDF). This value was used as the design point DNI for the solar field.

4. Results and Discussion

As previously mentioned, optimization and performance improvement strategies were developed in this work. Multiple analyses were performed as follows: (i) evaluation of the impact of collector assemblies on PTC effectiveness, (ii) evaluation of PTC plant designs with different commercial receivers (HCEs), (iii) assessment of the effects of different heat transfer fluids on PTC effectiveness, (vi) evaluation of an optimal dry cooling option for the PTC plant, (iv) optimization of the solar multiple, and (v) optimization of the thermal storage hours. Furthermore, a sensitivity analysis was used for the best scenario to determine the impact of several economic parameters, such as net present value and annual interest rate.

• Scenario 1: PTC facility with various solar collector assemblies (SCAs)

In the first scenario, we undertook a comparison including the yearly energy production, the capacity factor, and the LCOEs of the PTC plant with different types of solar collector assemblies (SCAs) using VP1 as the heat transfer fluid—the most widely used heat transfer fluid in parabolic trough solar power plants—and 7.5 h storage. According to the results revealed in Figure 4a, Luz LS-3 and Solargenix SGX-1 had the highest output power, with values of 168.8 GWh and 168.6 GWh, respectively, and a 42.8% capacity factor both collectors. Furthermore, the cost estimation showed that Luz LS-3 also had the lowest LCOE (see Figure 4b). Therefore, in accordance with the results, Luz LS-3 was selected in the study.

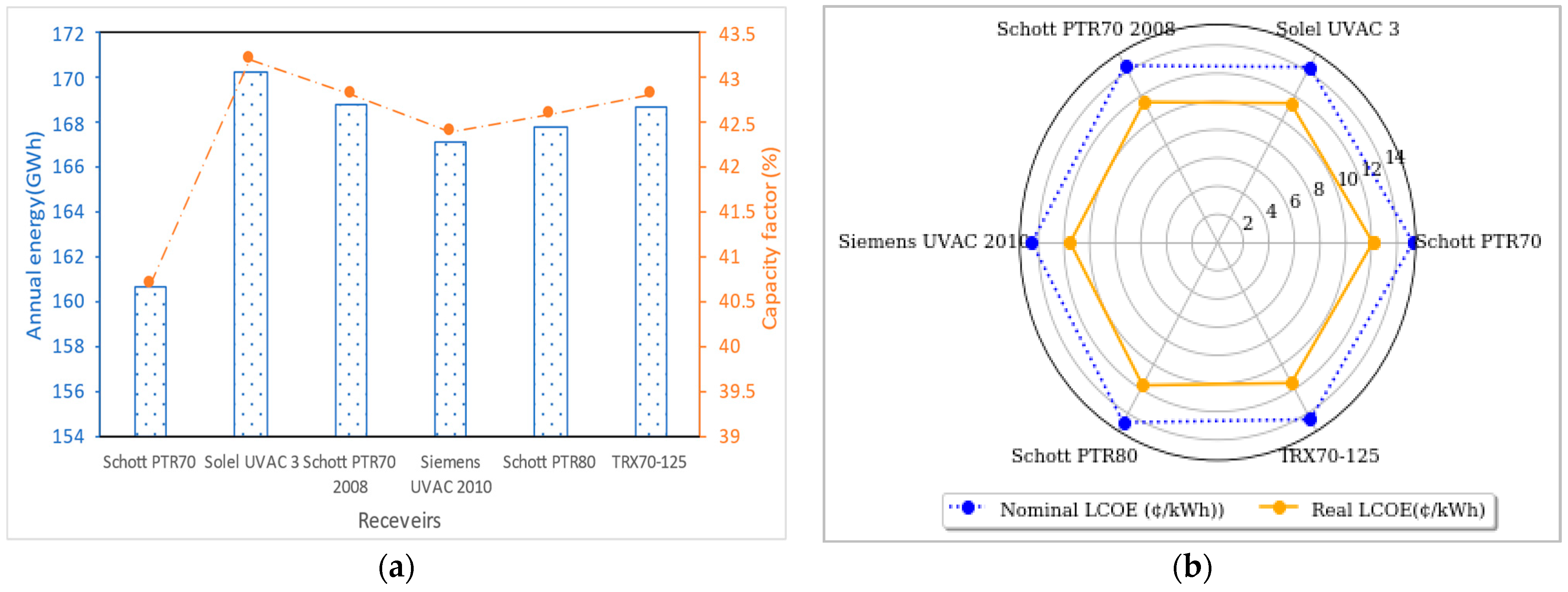
• Scenarios 2: PTC facility with various receivers (HCEs)

In the second scenario, the comparison included the yearly energy output, the capacity factor, and the LCOE of the PTC plant with different commercial receivers (see Table 2) using Luz LS-3 (selected from scenario 1), VP1 as the heat transfer fluid, and 7.5 h storage with a wet cooled condenser.

Figure 5a depicts the influence of the receiver type on the power output of a PTC plant with 7.5 h of thermal storage. The quality of the vacuum in the glass tube has a large impact on the performance of the receivers. As can be seen from the figure, among the six commercial receivers selected in this study, Solel UVAC 3 provided a high output power (170.21 GWh) and capacity factor (73.2%). Hence, it achieved the lowest real and nominal LCOEs with values of 0.1141 USD/kWh and 0.1437 USD/kWh, respectively, as shown in Figure 5b.

• Scenarios 3: PTC facility with various heat transfer fluid (HTFs)

The heat transfer fluid, which is regarded as one of the most significant components of CSP facilities, permits the transfer of thermal energy through a loop to power the power cycle. The most widely used heat transfer fluids in PTC plants are thermal oils due to the low vapor pressure and high thermal stability. In recent years, numerous other HTFs have been assessed, including molten salts and water/steam. Figure 6a shows the performances of seven different HTFs under the climatic conditions of Ouarzazate (arid climate). Except for the heat transfer fluids, all of the parameters and inputs were kept the same during this simulation in order to choose the optimal HTF to employ for the investigated PTC plant. We can observe that Therminol VP1 and Dowtherm Q were the most suitable HTFs for PTC systems, demonstrating the highest output powers with values of 170.1 GWh and 170.4 GWh, respectively, and a 43.2% capacity factor for both HTFs. Furthermore, the cost estimation showed that Dowtherm Q had the lowest LCOE of all of the selected HTFs (see Figure 6b), while the Hitec salts were unsuitable, demonstrating lower electrical production and a higher LCOE. Therefore, in accordance with the results, Dowtherm Q was selected in the study.

• Scenario 4: PTC facility with various types of cooling options (Wet and Dry)

A comparison of two cooling configurations for PTC plants applying synthetic oil VP1 as the heat transfer fluid is summarized in

Table 4. Results of simulations for the investigated PTC plant for both cooling modes.

Parameter	Wet Cooling	Dry Cooling	Diff. (%)
Annual energy (GWh)	170.4	158.35	+7
Gross-to-net conversion (%)	93.3	90.3	+3.2
Capacity factor (%)	43.2	40.2	+6.9
Annual water usage (m3)	607,215	33,701	+94
Real LCOE (USD/kWh)	0.1139	0.1223	−0.73
Nominal LCOE (USD/kWh)	0.1435	0.1541	−0.73
Internal rate of return (%)	11	11	-

. This study was based on the assessment of the thermodynamic yield, water usage, and the levelized cost of electricity. As can be seen in

Table 5. Simulation results for the optimized 50 MWe PTC plant.

Metric	Value
Annual energy	189 GWh
Gross-to-net conversion	93.5%
Capacity factor	47.9%
PPA price	0.1141 USD/kWh
Annual total water consumption	668,465 m3
Internal rate of return (IRR)	11%
NPV	USD 20,321,670

, the dry cooling mode significantly reduced water consumption by almost 94% in the PTC plant. However, the annual energy and capacity factor were reduced by more than 7% compared to the PTC plant with a wet cooling option. Moreover, the real and nominal LCOEs increased by 7.3% due to the increase in the equipment cost for the dry cooling mode. According to the findings, we can conclude that the wet cooling condenser with 50 MWe turbine gross output is more suitable than the dry one in terms of electricity yield and LCOE.

• Scenarios 5: PTC facility with various solar multiple (SM) values

As mentioned before, the SM factor changes with the total surface of the parabolic collectors: with a larger surface, more power is produced by the solar field and, hence, more power can be stored. However, having a large SM and, therefore, much more power than the generator demands but not enough storage capacity to store the surplus will result in power and investment loss. Figure 7a illustrates the yearly power generation and capacity factors for 16 different solar field times (SM) using 7.5 full-load thermal storage. As anticipated, the solar multiple increases the power generation and capacity factor. As can be seen in the figure, the annual electricity and the capacity factor increase nonlinearly with the SM: for small fields, it increases fast with the SM, whereas it rises relatively slowly for large fields. The curve thus found (Figure 7b) illustrates the variation in the LCOE as a function of the solar multiple (SM). As can be seen, the real and nominal LCOEs decrease with the increase in the solar field sizes up to an optimal value, then they start to grow. The optimal real and nominal LCOEs found were in the range of 0.112 USD/kWh and 0.1413 USD/kWh, respectively, corresponding to a solar multiple of 2.4.

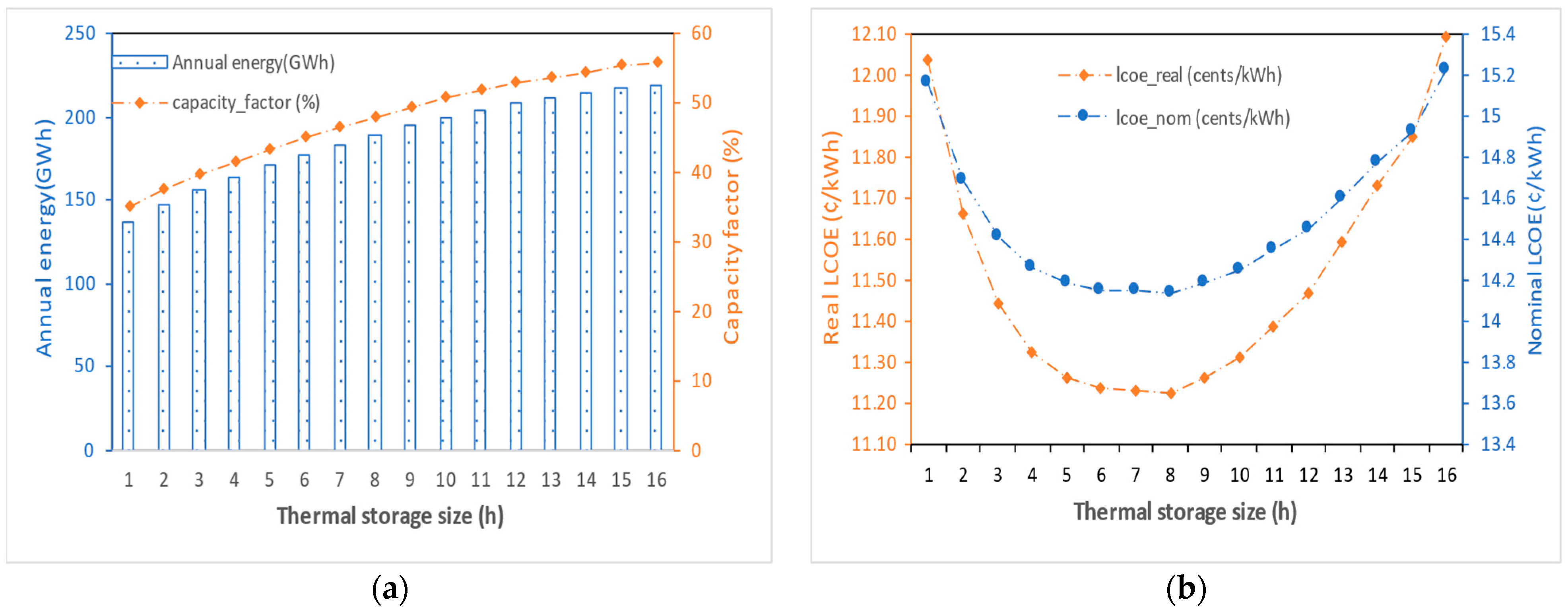
• Scenarios 6: PTC facility with various thermal storage times (TES)

Thermal energy storage is a technology employed in concentrated solar power facilities. It is particularly useful since it allows for the storage of a considerable amount of energy, which improves the yearly solar contribution, reduces partial load operation, and boosts plant availability. Thus, in the fifth scenario, we assessed a PTC facility with different thermal storage times (TES). Figure 8 illustrates the correlation between the duration of the thermal storage, annual energy, capacity factor, and cost of energy. As expected, Figure 8a shows that the solar plant’s energy production and capacity factor increase nonlinearly as the thermal storage times increases. They increase quickly with the low TES time and relatively slowly for large TES times. Concerning the cost of energy, as can be seen from Figure 8b, the LCOE was the maximum at one hour of storage and it began to decrease when the number of hours of storage was increased (TES capacity). This trend was followed until it reached a point where the optimal LCOE value was achieved, after which it began inversely increasing. The simulation indicated that the system achieved optimum performance at 189 GWh of annual energy per year and a 47.9% capacity factor. The results shown in Figure 8b demonstrate that the LCOE is extremely sensitive to changes in the number of hours of storage and the solar multiple and that the optimal LCOE is determined by a highly specific combination of the solar multiple and the number of hours of storage.

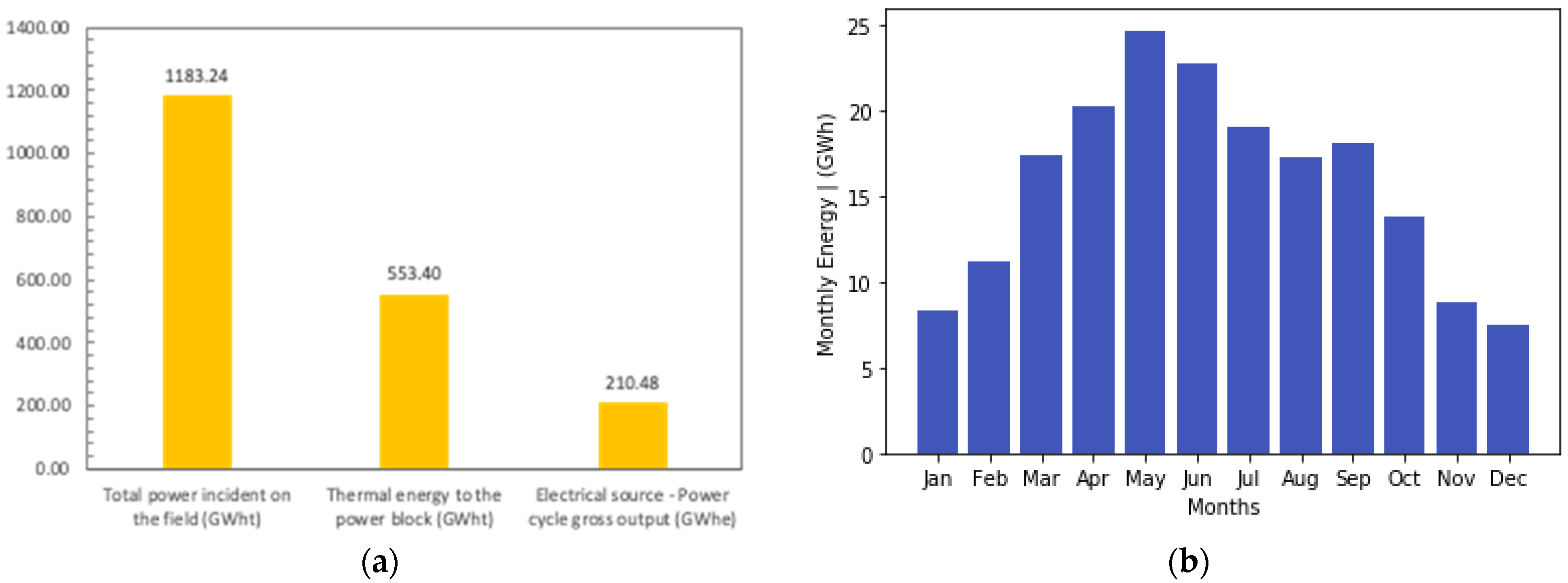
• Scenario 7: PTC best configuration and sensitivity analysis

In the last scenario, we chose the best configuration from the results obtained for the scenarios (scenarios 1 to 6) so that we had a higher yearly energy output and capacity factor and the lowest LCOEs. The configuration was as follows: collector—Luz LS3, receiver—Solel UVAC 3, HTF—Dowtherm Q, SM = 2.4, TES = 8, and wet cooled condenser.

Figure 9a displays the annual performance charts for each system element in the solar plant. The last bar presents the thermal power generated by the solar field with a value of 594,901 MWh_th/year, with the next one being 553,398 MWh_th/year, for the thermal energy to power block. The power cycle gross output (210,480 MWh/year) is represented by the first bar. The monthly net electric power produced that is ready to be fed to the grid by the optimized PTC facility is depicted in Figure 9b. This energy value recorded a maximum during the month of May, and the production surpassed the value of 24.6 GWh due to the duration of the sunshine period being the maximum in this month. The minimum production of 7.4 GWh for December was recorded during the winter months. This PTC facility was operating with a capacity factor of 47.9%, having a gross-to-net conversion of 93.5% and 668,465 m³ annual water usage for the cycle makeup and washing of the parabolic trough field. Concerning the economic study, the analysis results showed that the NPV value for the considered location (Ouarzazate city) was positive (more than USD 20 million), which indicated that the studied PTC plant was estimated to be financially and economically feasible (see Table 5).

A comparison of the hypothetical PTC plant with the Andasol (Spain) and SEGS VI (USA) plants described in previously published work is presented in

Table 6. Comparison with previously published work.

Authors, Reference	PTC Plant Capacity (MWe)	Annual Energy (GWh)	Capacity Factor (%)
Our work	50	189	47.9
Boukelia et al. [43]	50	118.45	27.30
Abbas et al. [44]	100	237	21.1
Bishoyi [45]	100	285.28	32.6
Ikhlefet al. [46]	25	82.46	41.8
Praveen et al. [47]	100	369.26	42.19
Tahir et al. [48]	100	294	33.6
Andasol 1 [49]	50	179.1	41.5
SEGS VI [50]	30	71.40	22.2

. From the results from other studies, it is clear that the results obtained from this study confirm that the Ouarzazate site has high potential for generating solar thermal electricity.

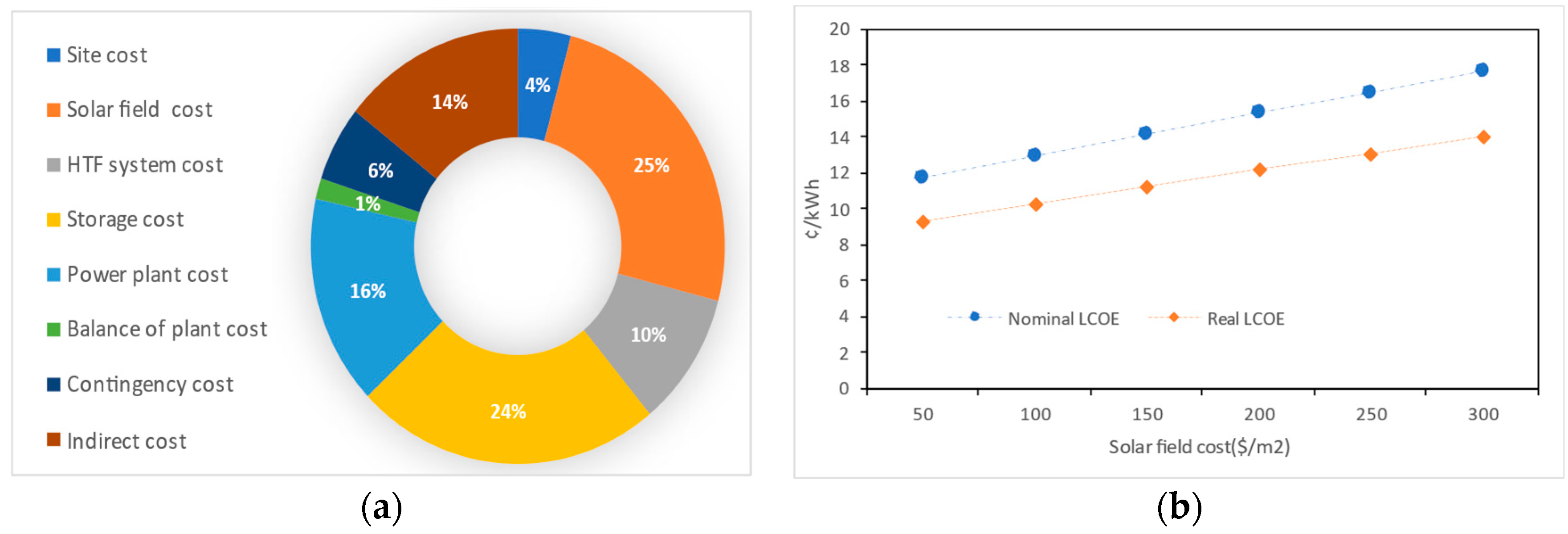
5. Sensitivity Analyses

As an economic analysis is critical in determining the profitability and viability of any project and the cost figures are subject to variations in the future, a sensitivity study demonstrating how specific costs affect the optimal design of the investigated PTC power plant was necessary. Therefore, the sensitivity analysis was based on two major factors: the LCOE and the NPV against the main financial model parameters.

Figure 10a depicts the relative contributions in the total investment cost of the optimized PTC facility, including the solar field cost, power plant cost, storage cost, HTF cost, and indirect costs. It can be noted that the solar field, which contains the mirrors, receivers, steel constructions, and trackers, is the largest cost component, with more than 25%. Furthermore, the installation of the thermal energy storage system accounts for the second-largest portion of the cost. Hence, an increase in different costs, especially in the field cost, increases the LCOE, as shown in Figure 10b.

Figure 11 illustrates the sensitivity of LCOE to the real discount rate and inflation rate. As can be observed from the figure, the notional LCOE increases linearly with these two factors, with different slopes indicating the degree of sensitivity. The real LCOE decreases when the analysis period and inflation rate are increased and increases when the real discount rate increases. Figure 12 displays the tornado charts, which show the influence of financial input parameters, including the solar field cost, storage cost, power plant cost, and heat transfer fluid cost, on the real and nominal LCOE. As revealed in Figure 12, an increase/decrease in different costs increases/decreases the LCOE. However, the uncertainty (+/−15%) in the cost of the solar field and the storage cost has the greatest impact on the LCOE, which is because the solar field and storage system are the most expensive parts of a PTC plant, as shown in Figure 10a.

Figure 13a depicts the sensitivity analysis for the NPV against the discount rate. As can be seen, the NPV is heavily influenced by the real discount rate; an increase of 10% in the discount rate causes a corresponding decrease in the net present value and verse versa. Furthermore, Figure 13b demonstrates that the annual interest rate has a significant impact on the NPV. A reduction in these costs could make the PTC plant more economically feasible.

6. Conclusions and Recommendations

In this work, the performance of a PTC/TES plant under the weather conditions of Morocco (Ouarzazate city) was evaluated from both a technical and a financial standpoint with different scenarios. Multiple analyses were undertaken as follows: (i) evaluation of the collector assemblies’ effects on PTC plant performance, (ii) evaluation of the PTC plant with different commercial receivers (HCEs), (iii) evaluation of the effects of different heat transfer fluids on performance, (vi) evaluation of an optimal dry cooling option for the PTC plant, (iv) optimization of the solar multiple, and (v) optimization of the thermal storage hours. Furthermore, a sensitivity analysis was used for the best scenario to determine the impact of several economic elements, such as LCOEs and net present value, on the PTC project’s performance and financial outputs. The main conclusion can be summarized as follows:

• The use of the Luz LS-3 as the collector/SCA, Solel UVAC 3 as receiver/HCE, and Dowtherm Q as heat transfer fluid showed higher performance in terms of yearly energy production yield and capacity factor, as well as the lowest real and nominal LCOEs;
• The annual energy and capacity factor using the wet cooling mode increased by almost 7% compared to the PTC facility with a dry cooling mode. However, the dry cooling system significantly reduced water consumption by almost 94% in the PTC plant;
• PTC plants with large storage capacity demonstrated better annual performance, such as net electricity output and capacity factor, but higher real and nominal LCOEs due to the high costs of TES systems. As a result, the number of full loads of storage must be optimized, otherwise the LCOE increases significantly;
• The optimal solar multiple value was 2.4, corresponding to the lowest real and nominal LCOE. Moreover, the duration of TES had significant effects on the annual performance simulations and LCOEs. The optimum investigated PTC plant TES was 8 h, for which the real and nominal LCOEs were estimated to be 0.112 USD/kWh and 0.141 USD/kWh, respectively;
• The maximum and minimum net electricity outputs for the best-configuration PTC plant were 24.6 GWh and 7.4 GWh in May and December, respectively. The capacity factor and the gross-to-net conversion factor for the optimized plant were found to be 93.5% and 47.9%, respectively;
• The sensitivity study of the PTC facility demonstrated ±15% and ±10% uncertainties in input parameters for the financial assessments. According to the sensitivity study, the collector cost was the key economic parameter affecting the real and nominal LCOE, and the increase of 10% in the discount rate caused a correspondent decrease in the NPV and verse versa.

Finally, the results determined that, when using solar energy for PTC plants, a choice must be made to enhance system performance and lower energy prices. Decision makers may pick parameters and components for CSP plants with the use of this study’s analysis of CSP technology. In our upcoming work, we will discuss other CSP technologies, such as central receiver concentrated solar thermal plants and linear Fresnel reflectors, and benchmark them with PTC power plants.

Therefore, for better integration of CSP technology in Morocco, we recommend that the government invest in the construction of collectors locally, which may contribute to decreasing the investment costs. In addition, we recommend the development of a flexible bankability model or governmental support to encourage investments in this promising technology, which may lead to a shift towards a sustainable society and create energy security and independence for Morocco.