Modal Analysis of Tubing Considering the Effect of Fluid–Structure Interaction
Abstract
:1. Introduction
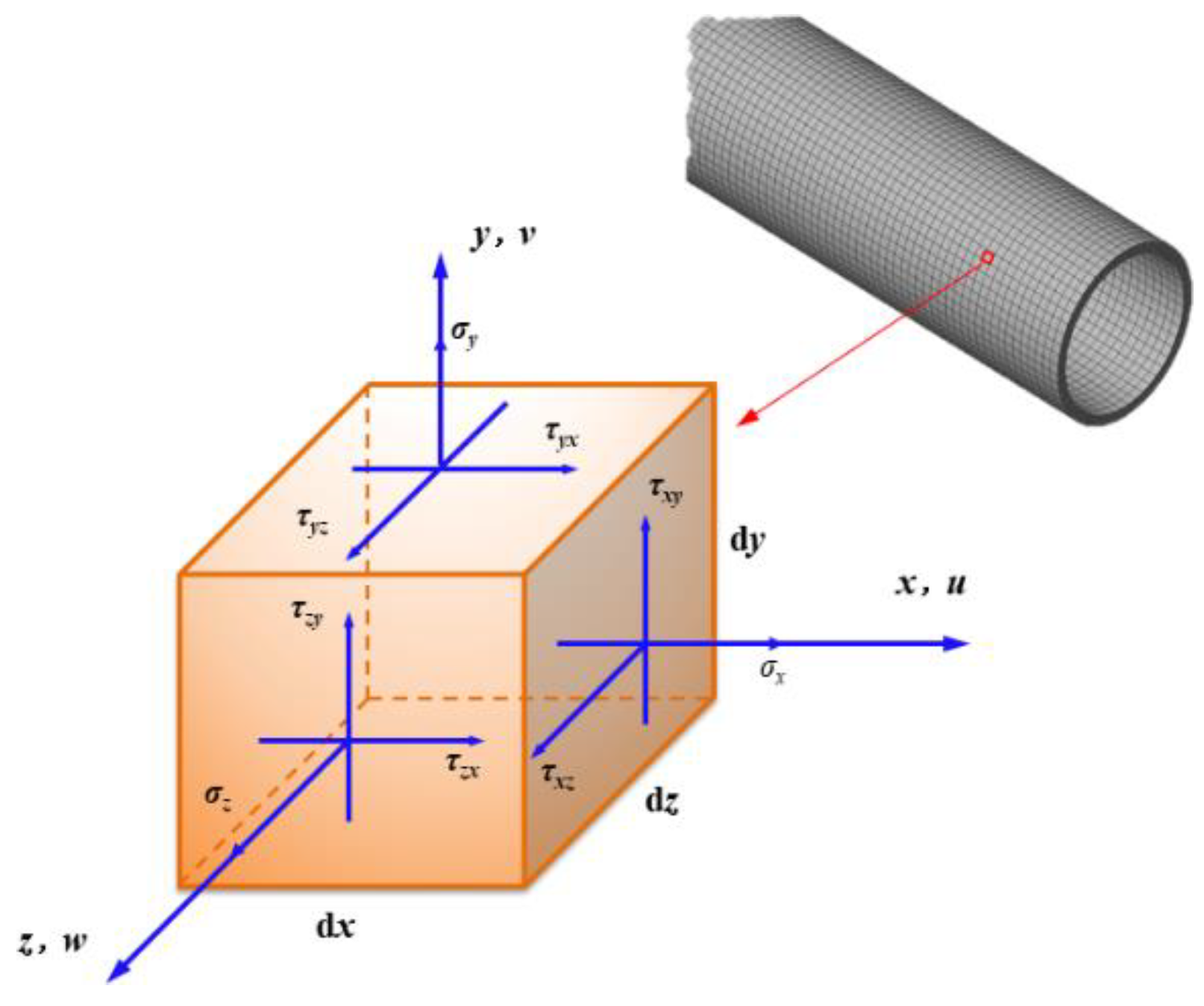
2. Vibration Mechanics Model of Tubing
3. Dry Mode Finite Element Analysis of Tubing
3.1. Establishment of Finite Element Mechanical Mode
3.2. Simulation
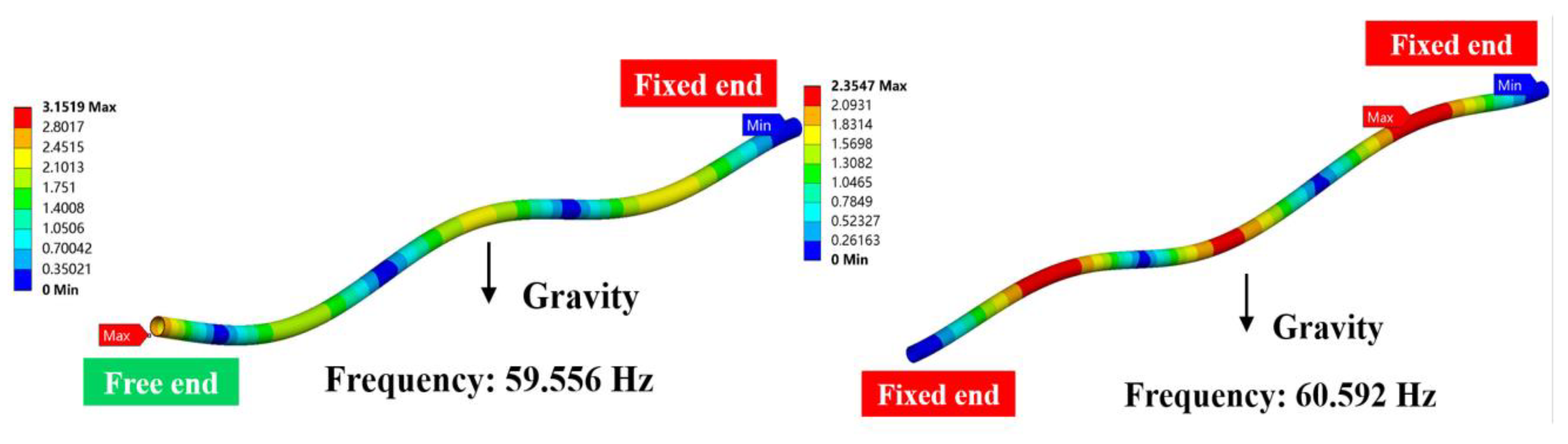
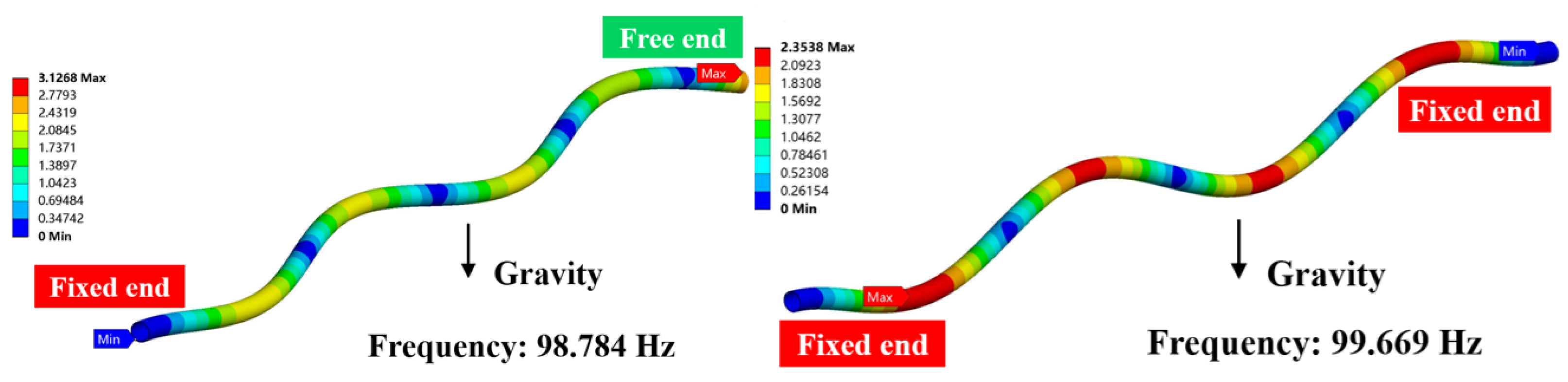
3.3. Dry Modal Analysis of Tubing
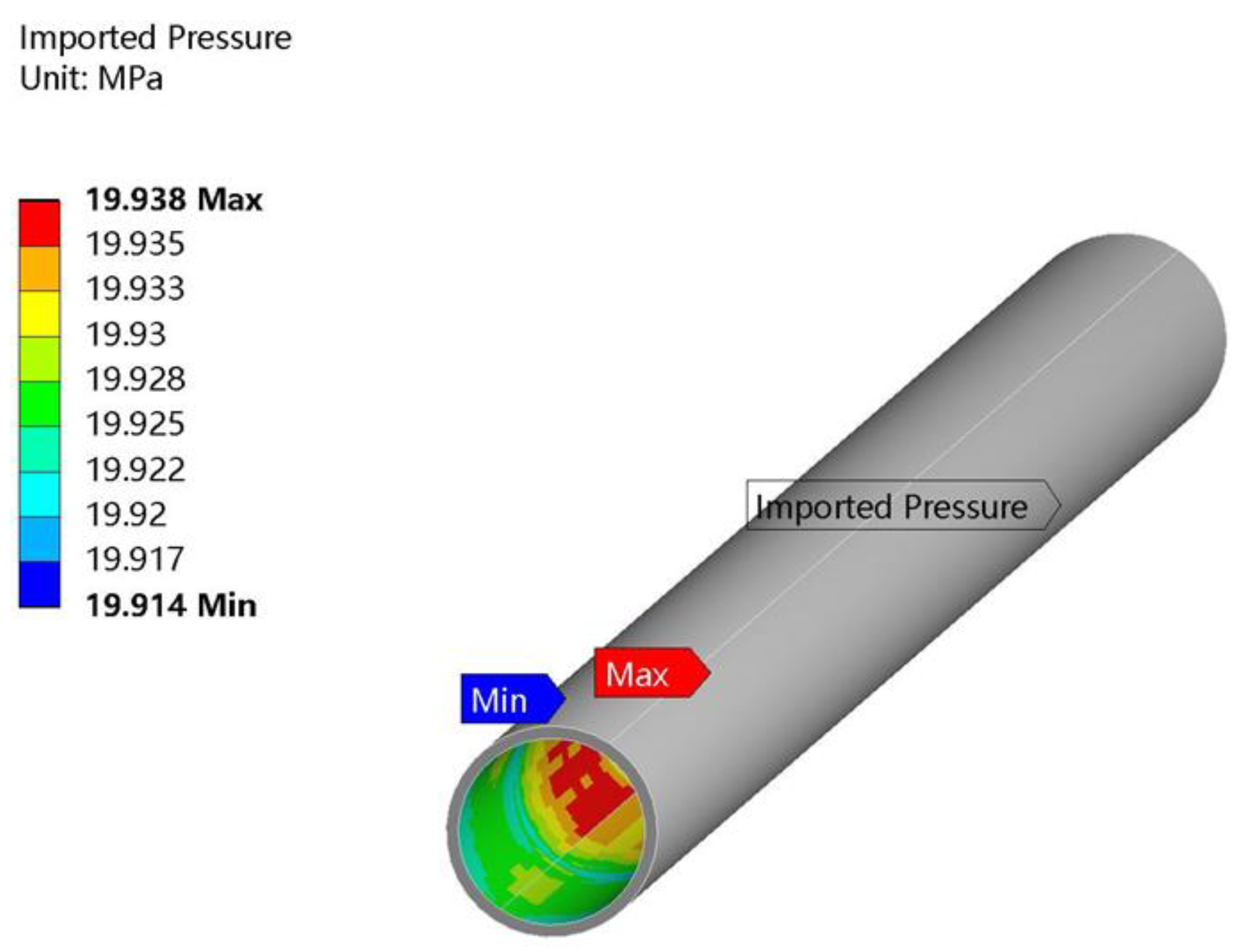
4. Wet Modal Finite Element Analysis of Tubing
5. Analysis of Influencing Factors of Tubing Mode
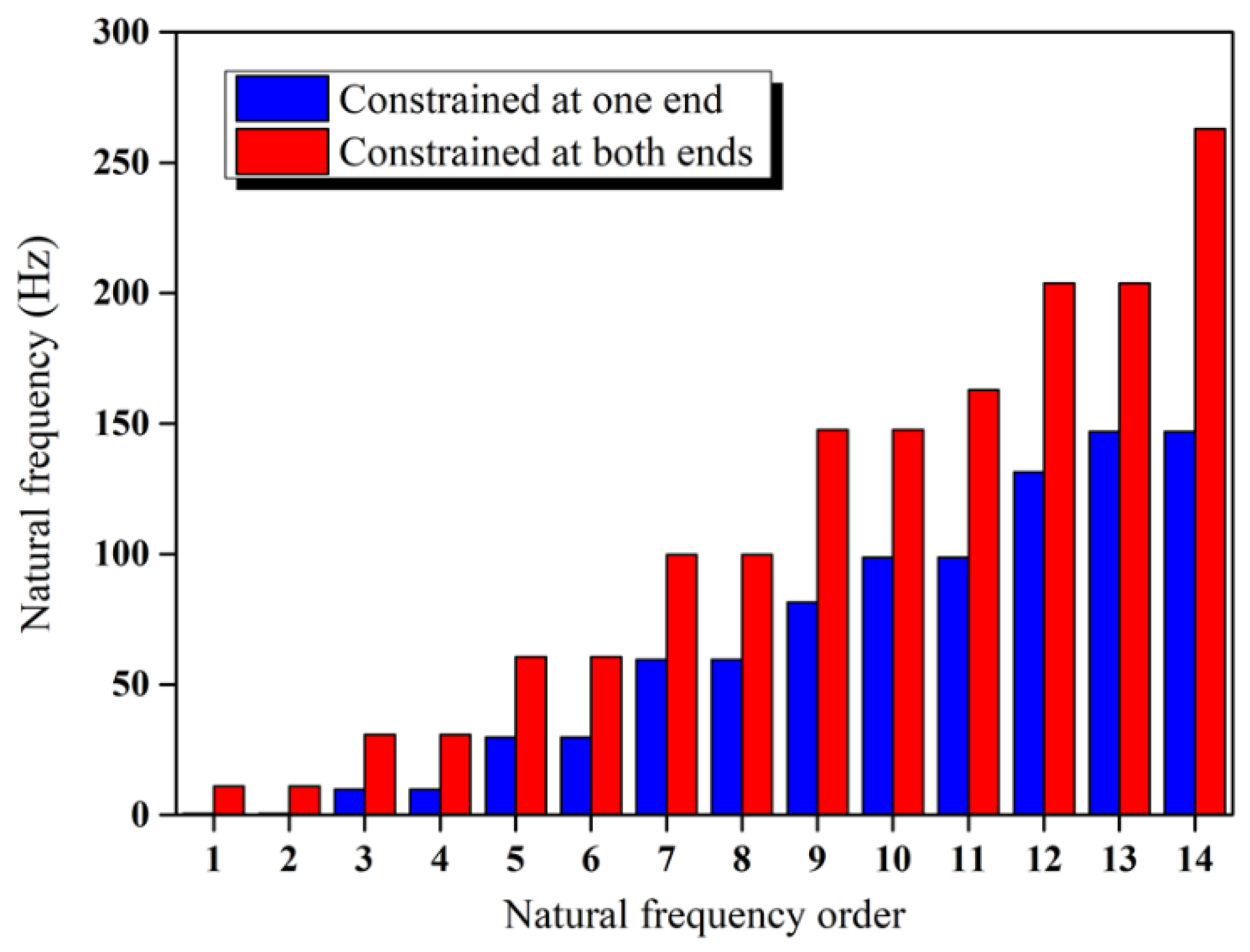
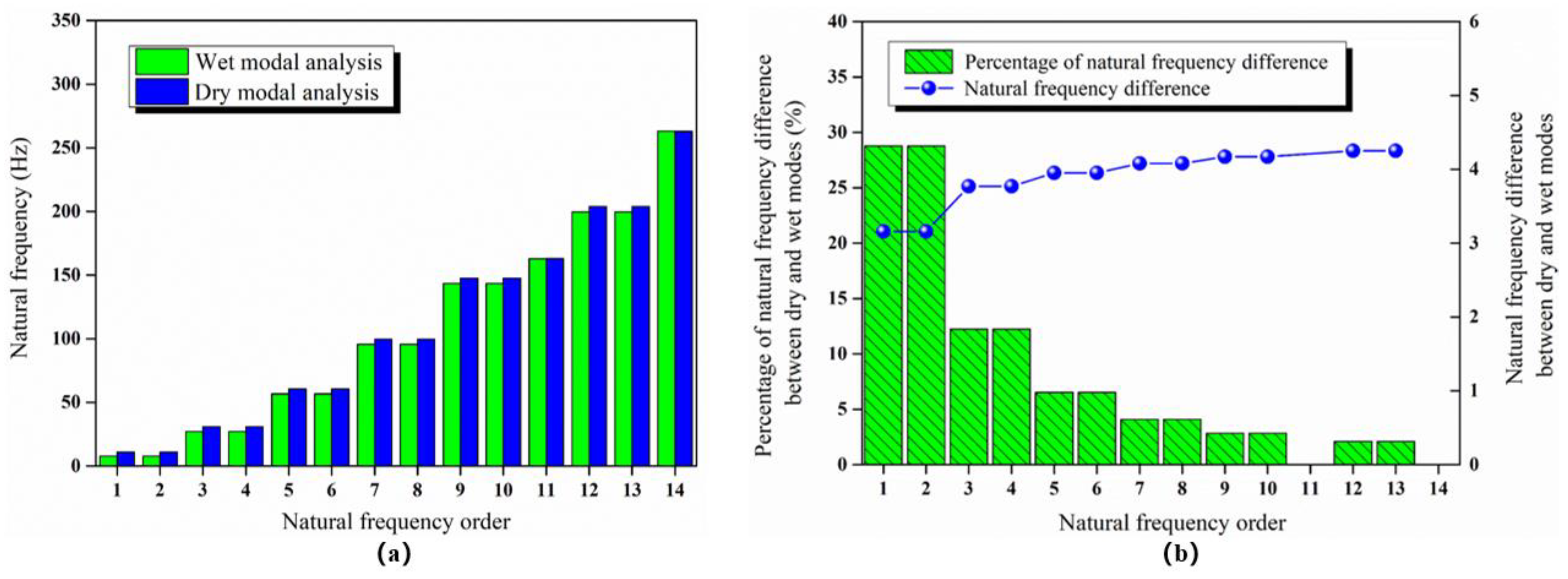
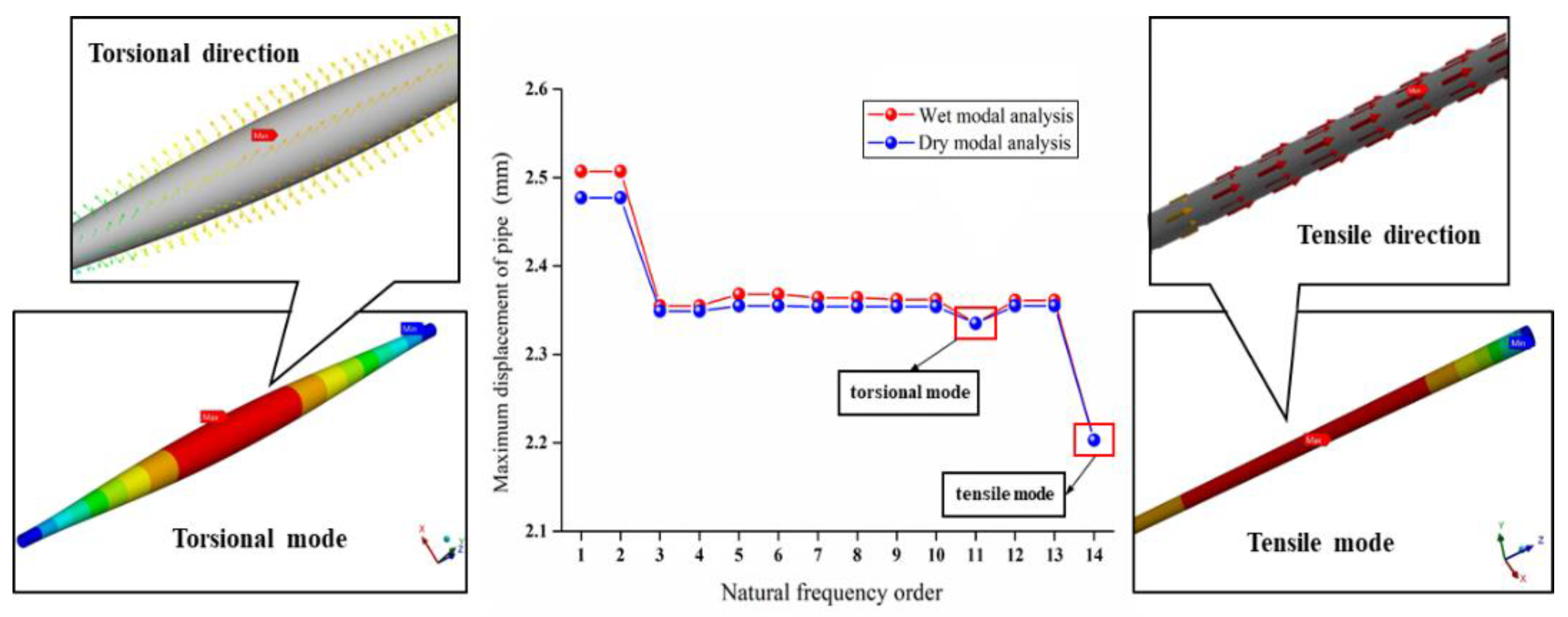
5.1. Influence of Fluid–Structure Interaction Effect on Tubing Mode
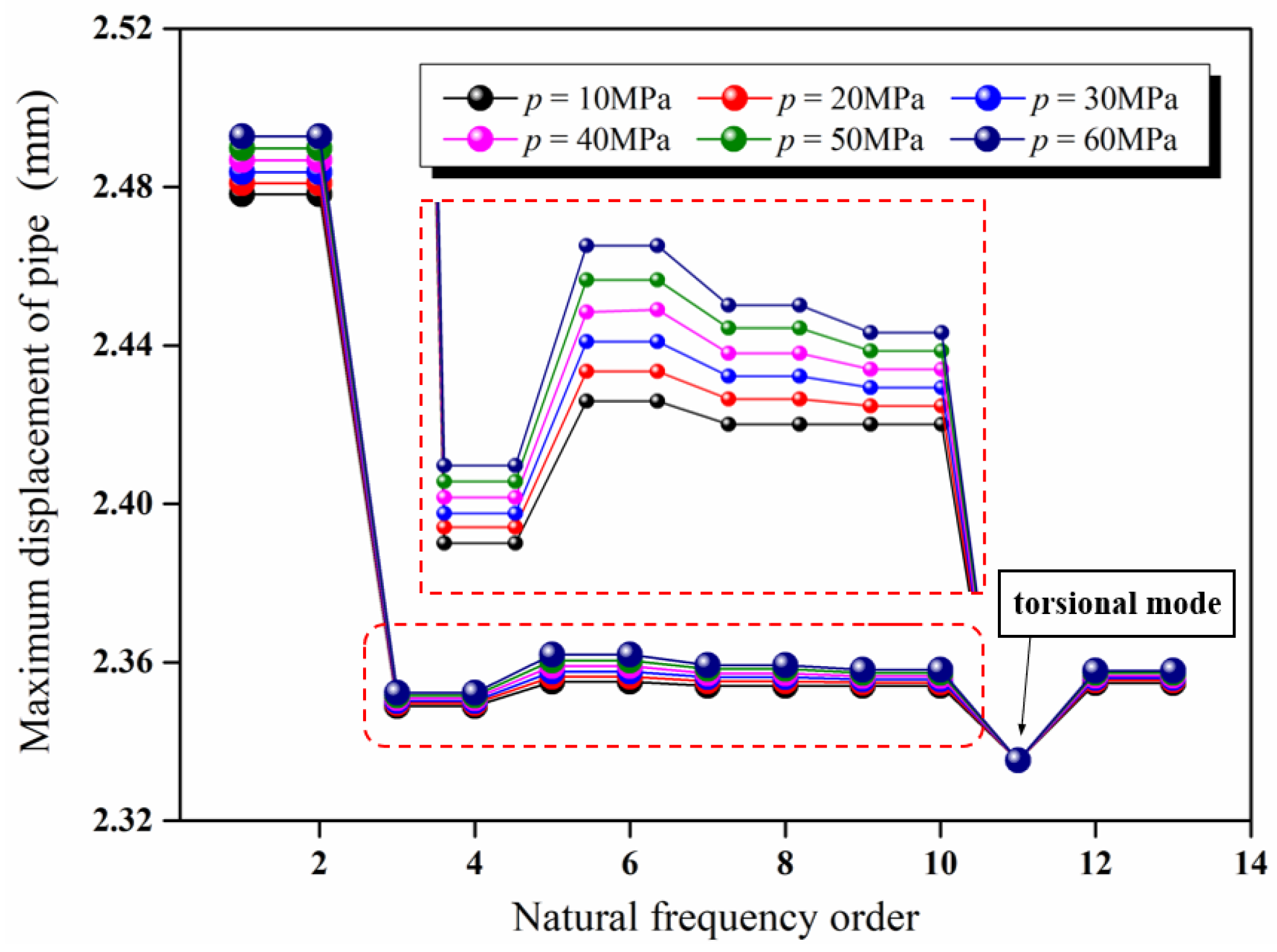
5.2. Influence of Inlet Pressure on Tubing Mode
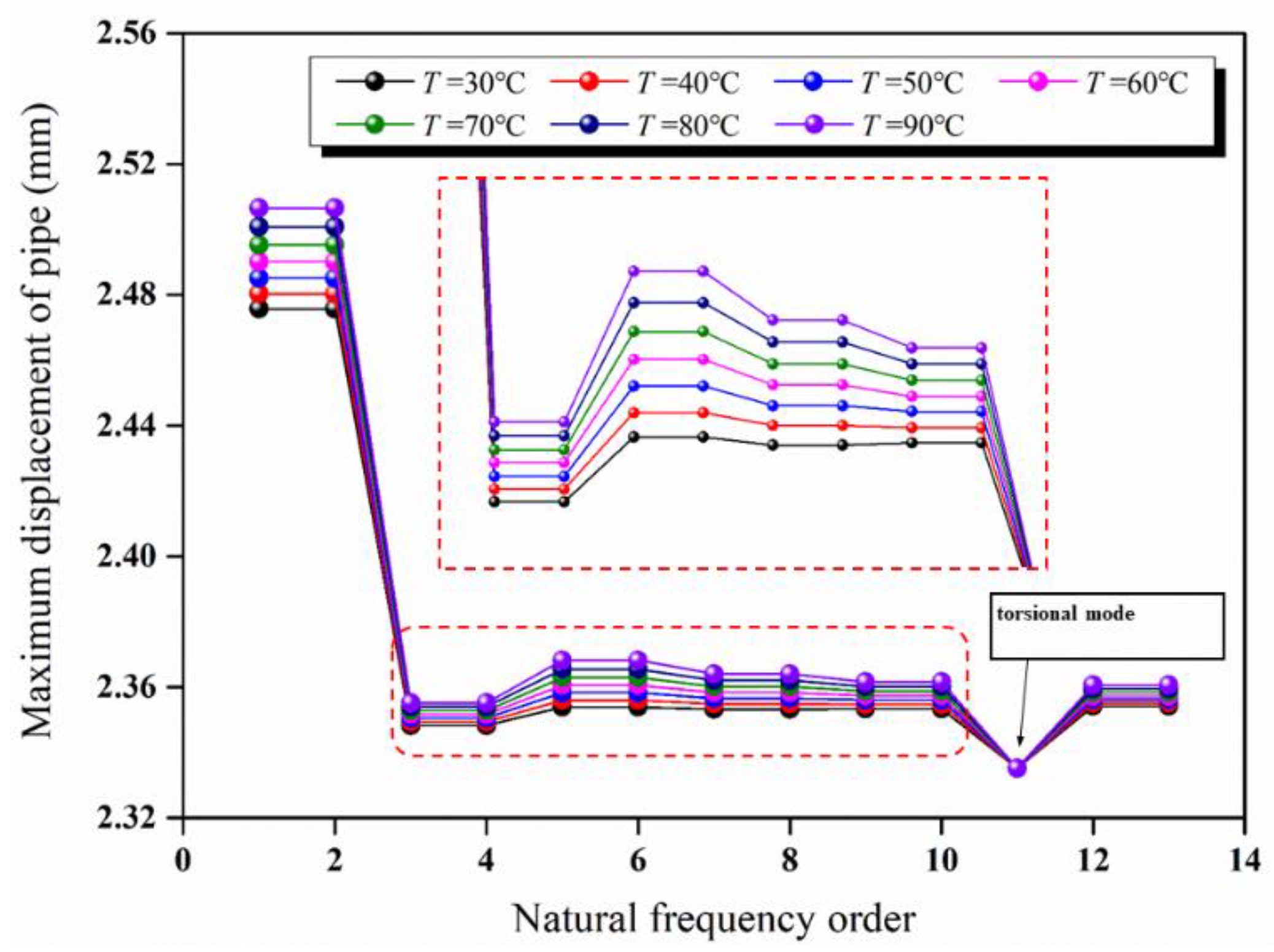
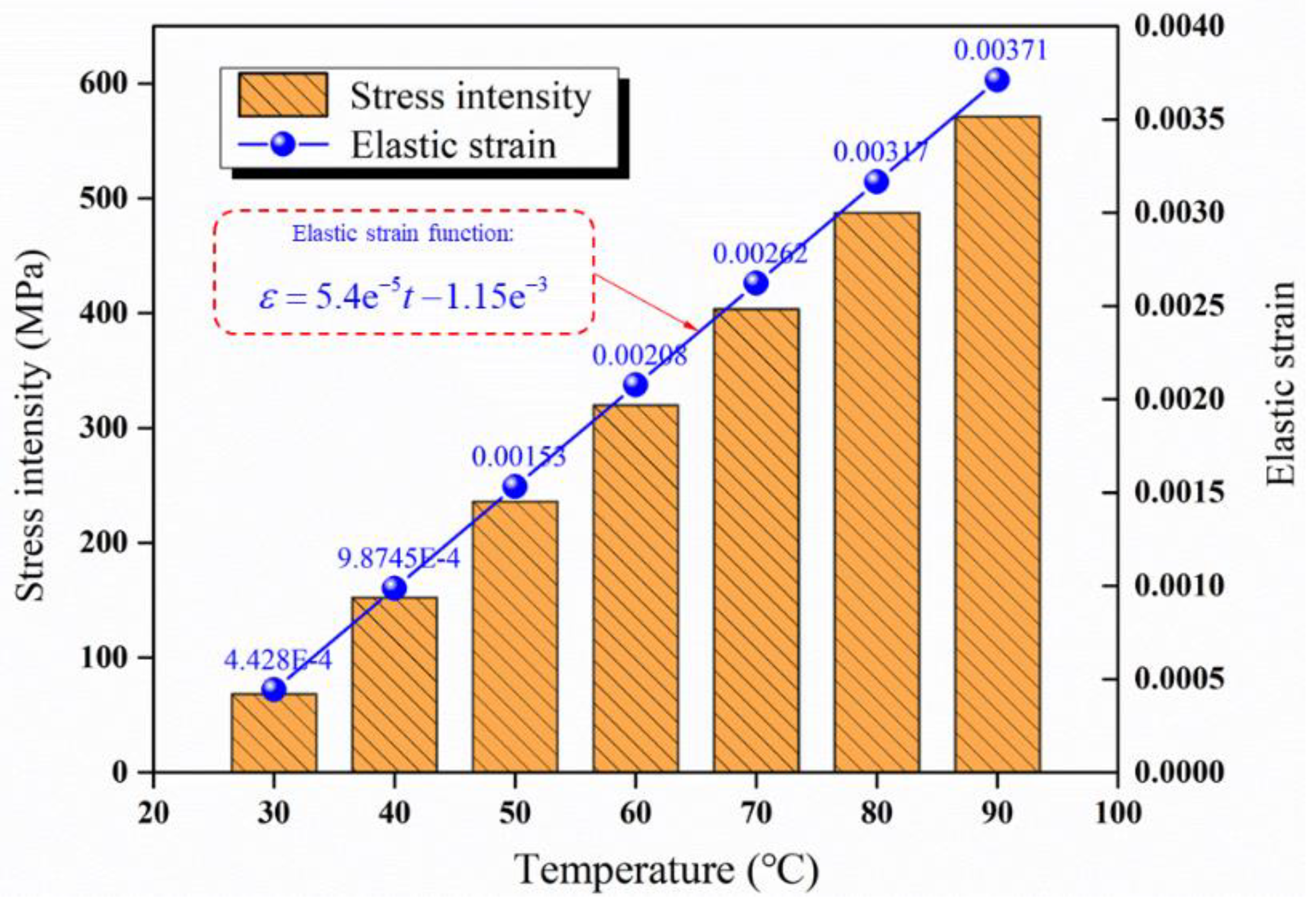
5.3. Effect of Temperature on Tubing Mode
6. Conclusions
- After considering the fluid–solid coupling effect, the research objects include tubings and natural gas in the tubing. The mass increases, so the natural frequency decreases, but the displacement is slightly larger. In the actual production process, the buckling and deformation damage of the tubing can be reduced by inducing the corresponding torsional or tensile mode.
- The greater the pressure in the tubing, the greater the equivalent stress on the tubing body, so the tubing is more prone to vibration, i.e., the natural frequency is lower. Furthermore, after considering the fluid–solid coupling effect, the pressure in the tubing is the true pulsating pressure of the fluid. The prestress applied to the tubing wall changes with time, and the pressures at different parts are different. At this time, the tubing is changed at different frequencies. Vibration is prone to occur, i.e., the natural frequency is smaller than the dry mode.
- The higher the temperature, the lower the rigidity of the tubing body and the faster the strength attenuation, so the tubing is more prone to vibration, i.e., the natural frequency is lower. Both the stress intensity and the elastic strain increase with the temperature, so the displacement of the tubing also increases. The influence of temperature on the tubing modal is slightly greater than that of pressure.
Author Contributions
Funding
Conflicts of Interest
References
- Alkhamis, M.; Imqam, A. A Simple Classification of Wellbore Integrity Problems Related to Fluids Migration. Arab. J. Sci. Eng. 2021, 46, 6131–6141. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; Yang, X.; Zhao, X. Evaluation of wellbore integrity for HTHP gas wells under solid-temperature coupling using a new analytical model. J. Nat. Gas Sci. Eng. 2015, 25, 347–358. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Li, Y.; Ming, L.; Zhang, C. Effects of instantaneous shut-in of high production gas well on fluid flow in tubing. Pet. Explor. Dev. 2020, 47, 642–650. [Google Scholar] [CrossRef]
- Kou, Z.; Wang, H. Transient Pressure Analysis of a Multiple Fractured Well in a Stress-Sensitive Coal Seam Gas Reservoir. Energies 2020, 13, 3849. [Google Scholar] [CrossRef]
- Jun, L.; Guo, X.; Wang, G.; Liu, Q.; Fang, D.; Huang, L.; Mao, L. Bi-nonlinear vibration model of tubing string in oil & gas well and its experimental verification. Appl. Math. Model. 2020, 81, 50–69. [Google Scholar]
- Liu, J.; Zeng, L.; Guo, X.; Dai, L.; Huang, X.; Cai, L. Nonlinear flow-induced vibration response characteristics of leaching tubing in salt cavern underground gas storage. J. Energy Storage 2021, 41, 102909. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Li, Y.; Liu, H.; Meng, W.; Li, L. Research on the influence of production fluctuation of high-production gas well on service security of tubing string. Oil Gas Sci. Technol. Revue d’IFP Energies Nouv. 2021, 76, 54. [Google Scholar] [CrossRef]
- Lenwoue, A.; Deng, J.; Feng, Y.; Li, H.; Oloruntoba, A.; Selabi, N.B.S.; Marembo, M.; Sun, Y. Numerical Investigation of the Influence of the Drill String Vibration Cyclic Loads on the Development of the Wellbore Natural Fracture. Energies 2021, 14, 2015. [Google Scholar] [CrossRef]
- Xu, J.; Mou, Y.; Xue, C.; Ding, L.; Wang, R.; Ma, D. The study on erosion of buckling tubing string in HTHP ultra-deep wells considering fluid–solid coupling. Energy Rep. 2021, 7, 3011–3022. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Yao, M.H.; Zhang, W.; Wen, B.C. Dynamical modeling and multi-pulse chaotic dynamics of cantilevered pipe conveying pulsating fluid in parametric resonance. Aerosp. Sci. Technol. 2017, 68, 441–453. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, L. Modal analysis of liquid-filled tubing under fluid-structure interaction by simulation and experiment methods. Vibroeng. Procedia 2018, 21, 42–47. [Google Scholar]
- Wróbel, J.; Blaut, J. Influence of Pressure Inside a Hydraulic Line on Its Natural Frequencies and Mode Shapes. In Proceedings of the International Scientific-Technical Conference on Hydraulic and Pneumatic Drives and Control, Staniszow, Poland, 21–23 October 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Xin, L.; Wang, S.; Ran, L. Modal Analysis of Two Typical Fluid-filled Pipes in Aircraft. In Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, Beijing, China, 17–20 August 2011; pp. 469–473. [Google Scholar]
- Lubecki, M.; Stosiak, M.; Bocian, M.; Urbanowicz, K. Analysis of selected dynamic properties of the composite hydraulic microhose. Eng. Fail. Anal. 2021, 125, 105431. [Google Scholar] [CrossRef]
- Chai, Q.; Zeng, J.; Ma, H.; Li, K.; Han, Q. A dynamic modeling approach for nonlinear vibration analysis of the L-type tubing system with clamps. Chin. J. Aeronaut. 2020, 33, 3253–3265. [Google Scholar] [CrossRef]
- Sekacheva, A.A.; Pastukhova, L.G.; Alekhin, V.N.; Noskov, A.S. Natural frequencies of a vertical tubing element. In Proceedings of the IV International Conference on Safety Problems of Civil Engineering Critical Infrastructures, Ekaterinburg, Russia, 4–5 October 2019; p. 481. [Google Scholar]
- Wu, Q.; Qi, G. Global dynamics of a pipe conveying pulsating fluid in primary parametrical resonance: Analytical and numerical results from the nonlinear wave equation. Phys. Lett. A 2019, 383, 1555–1562. [Google Scholar] [CrossRef]
- Guo, X.; Liu, J.; Wang, G.; Dai, L.; Fang, D.; Huang, L.; He, Y. Nonlinear flow-induced vibration response characteristics of a tubing string in HPHT oil & gas well. Appl. Ocean Res. 2020, 106, 102468. [Google Scholar]
- Jiang, N.; Zhu, B.; Zhou, C.; Li, H.; Wu, B.; Yao, Y.; Wu, T. Blasting vibration effect on the buried tubing: A brief overview. Eng. Fail. Anal. 2021, 129, 105709. [Google Scholar] [CrossRef]
- Tian, X.; Zhou, S.; Hu, L.; Li, W.; He, W. Vibration Fatigue Characteristic of High-Pressure Fuel Pipe Based on Fluid-Solid Coupling Model. J. Vib. Meas. Diagn. 2018, 38, 1234–1239. [Google Scholar]
- Xu, Y.; Zhang, H.; Guan, Z. Dynamic Characteristics of Downhole Bit Load and Analysis of Conversion Efficiency of Drill String Vibration Energy. Energies 2021, 14, 229. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, K.; Liu, J.; Mu, L.; Wang, F. The Study of Tubing Vibration Mechanism in High Pressure Gas Well. World J. Eng. Technol. 2021, 9, 128–137. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Wang, L.; Chu, S.; Tang, F.P.; Jiang, Y.; Xu, T.; Yu, J. Analysis of Strength and Modal Characteristics of a Full Tubular Pump Impeller Based on Fluid-Structure Interaction. Energies 2021, 14, 6395. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Fluid-structure interactions in a flexible pipe conveying two-phase flow. Int. J. Multiph. Flow 2021, 141, 103667. [Google Scholar] [CrossRef]
- Mohmmed, A.O.; Al-Kayiem, H.H.; Osman, A.B.; Sabir, O. One-way coupled fluid-structure interaction of gas-liquid slug flow in a horizontal pipe: Experiments and simulations. J. Fluids Struct. 2020, 97, 103083. [Google Scholar] [CrossRef]
- Huang, Z.; Li, L.; Hu, G. Fatigue Life Prediction of Tubing Strings in Natural Gas Wells; Chongqing University Press: Chongqing, China, 2012. [Google Scholar]
- Lee, G.; Jhung, M.; Bae, J.; Kang, S. Numerical Study on the Cavitation Flow and Its Effect on the Structural Integrity of Multi-Stage Orifice. Energies 2021, 14, 1518. [Google Scholar] [CrossRef]
- Lian, Z.; Mou, Y.; Liu, Y.; Xu, D. Buckling behaviors of tubing strings in HTHP ultra-deep wells. Nat. Gas Ind. 2018, 38, 89–94. [Google Scholar]
- Mou, Y.; Lian, Z.; Zhang, Q.; Lu, Z.; Li, J. Study on influence of centralizer on buckling behavior of tubing string in ultra-deep gas well. J. Saf. Sci. Technol. 2018, 14, 109–114. [Google Scholar]
- Bęben, D. The Influence of Temperature on Degradation of Oil and Gas Tubing Made of L80-1 Steel. Energies 2021, 14, 6855. [Google Scholar] [CrossRef]






| Order | 10 MPa | 20 MPa | 30 MPa | 40 MPa | 50 MPa | 60 MPa |
|---|---|---|---|---|---|---|
| 1 | 10.891 | 10.604 | 10.308 | 10.003 | 9.6872 | 9.3599 |
| 2 | 10.891 | 10.604 | 10.308 | 10.003 | 9.6872 | 9.3599 |
| 3 | 30.721 | 30.346 | 29.966 | 29.581 | 29.19 | 28.793 |
| 4 | 30.721 | 30.346 | 29.966 | 29.581 | 29.19 | 28.793 |
| 5 | 60.477 | 60.071 | 59.662 | 59.250 | 58.836 | 58.418 |
| 6 | 60.477 | 60.071 | 59.662 | 59.251 | 58.836 | 58.418 |
| 7 | 99.550 | 99.124 | 98.697 | 98.268 | 97.837 | 97.404 |
| 8 | 99.550 | 99.125 | 98.697 | 98.268 | 97.837 | 97.404 |
| 9 | 147.46 | 147.02 | 146.58 | 146.14 | 145.69 | 145.25 |
| 10 | 147.46 | 147.02 | 146.58 | 146.14 | 145.69 | 145.25 |
| 11 | 163.00 | 162.97 | 162.95 | 162.92 | 162.89 | 162.86 |
| 12 | 203.67 | 203.22 | 202.76 | 202.31 | 201.86 | 201.40 |
| 13 | 203.67 | 203.22 | 202.76 | 202.31 | 201.86 | 201.40 |
| 14 | 263.03 | 263.03 | 263.04 | 263.04 | 263.05 | 263.05 |
| Order | 10 MPa | 20 MPa | 30 MPa | 40 MPa | 50 MPa | 60 MPa |
|---|---|---|---|---|---|---|
| 1 | 11.249 | 10.973 | 10.688 | 10.395 | 10.093 | 9.7807 |
| 2 | 11.249 | 10.973 | 10.688 | 10.395 | 10.093 | 9.7807 |
| 3 | 31.198 | 30.829 | 30.455 | 30.077 | 29.693 | 29.303 |
| 4 | 31.198 | 30.829 | 30.455 | 30.077 | 29.693 | 29.303 |
| 5 | 60.994 | 60.592 | 60.187 | 59.779 | 59.368 | 58.954 |
| 6 | 60.994 | 60.592 | 60.187 | 59.779 | 59.368 | 58.954 |
| 7 | 100.09 | 99.669 | 99.244 | 98.817 | 98.388 | 97.958 |
| 8 | 100.09 | 99.669 | 99.244 | 98.817 | 98.388 | 97.958 |
| 9 | 148.02 | 147.58 | 147.14 | 146.70 | 146.26 | 145.82 |
| 10 | 148.02 | 147.58 | 147.14 | 146.70 | 146.26 | 145.82 |
| 11 | 163.01 | 162.98 | 162.95 | 162.93 | 162.90 | 162.87 |
| 12 | 204.24 | 203.79 | 203.34 | 202.89 | 202.43 | 201.98 |
| 13 | 204.24 | 203.79 | 203.34 | 202.89 | 202.43 | 201.98 |
| 14 | 263.01 | 263.02 | 263.02 | 263.03 | 263.04 | 263.04 |
| Order | 30 °C | 40 °C | 50 °C | 60 °C | 70 °C | 80 °C | 90 °C |
|---|---|---|---|---|---|---|---|
| 1 | 11.152 | 10.677 | 10.178 | 9.6502 | 9.0894 | 8.4884 | 7.8379 |
| 2 | 11.152 | 10.677 | 10.178 | 9.6502 | 9.0894 | 8.4884 | 7.8379 |
| 3 | 31.068 | 30.443 | 29.803 | 29.149 | 28.478 | 27.790 | 27.083 |
| 4 | 31.068 | 30.443 | 29.803 | 29.149 | 28.478 | 27.790 | 27.084 |
| 5 | 60.854 | 60.177 | 59.492 | 58.799 | 58.098 | 57.388 | 56.669 |
| 6 | 60.854 | 60.177 | 59.492 | 58.800 | 58.098 | 57.388 | 56.669 |
| 7 | 99.946 | 99.238 | 98.525 | 97.807 | 97.084 | 96.354 | 95.620 |
| 8 | 99.946 | 99.239 | 98.525 | 97.807 | 97.084 | 96.355 | 95.620 |
| 9 | 147.87 | 147.14 | 146.41 | 145.67 | 144.93 | 144.19 | 143.44 |
| 10 | 147.87 | 147.14 | 146.41 | 145.67 | 144.93 | 144.19 | 143.44 |
| 11 | 163.03 | 163.02 | 163.00 | 162.99 | 162.98 | 162.97 | 162.95 |
| 12 | 204.09 | 203.34 | 202.60 | 201.84 | 201.09 | 200.34 | 199.58 |
| 13 | 204.09 | 203.34 | 202.60 | 201.85 | 201.09 | 200.34 | 199.58 |
| 14 | 263.02 | 263.04 | 263.05 | 263.07 | 263.08 | 263.10 | 263.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Li, C.; Jin, J. Modal Analysis of Tubing Considering the Effect of Fluid–Structure Interaction. Energies 2022, 15, 670. https://doi.org/10.3390/en15020670
Duan J, Li C, Jin J. Modal Analysis of Tubing Considering the Effect of Fluid–Structure Interaction. Energies. 2022; 15(2):670. https://doi.org/10.3390/en15020670
Chicago/Turabian StyleDuan, Jiehao, Changjun Li, and Jin Jin. 2022. "Modal Analysis of Tubing Considering the Effect of Fluid–Structure Interaction" Energies 15, no. 2: 670. https://doi.org/10.3390/en15020670





