Effect of Overhead Contact Line Pre-Sag on the Interaction Performance with a Pantograph in Electrified Railways
Abstract
:1. Introduction
1.1. Problem Description
1.2. Literature Review
1.3. Contribution of This Paper
- (1)
- A nonlinear finite element approach is implemented to build the overhead contact line system by accurately describing the pre-sag of the contact line.
- (2)
- Through a nonlinear solution, the effect of contact line pre-sag on the interaction performance is quantified with different tension classes.
- (3)
- An optimisation procedure is implemented to obtain the optimal amount of pre-sag for different train speeds and tension classes.
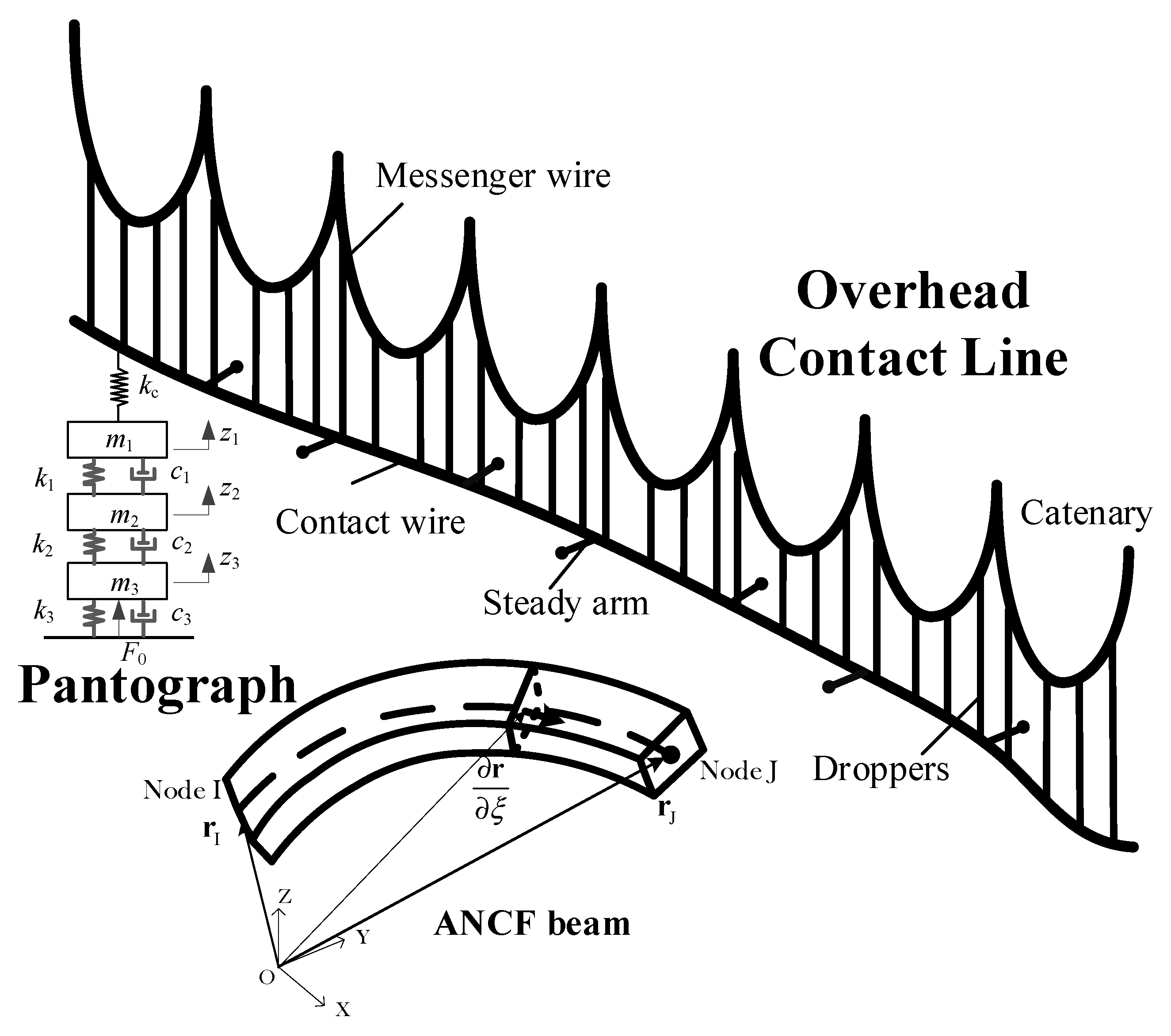
2. Modelling of Overhead Contact Line and Pantograph
2.1. Model of Overhead Contact Line
2.2. Modelling of Pantograph
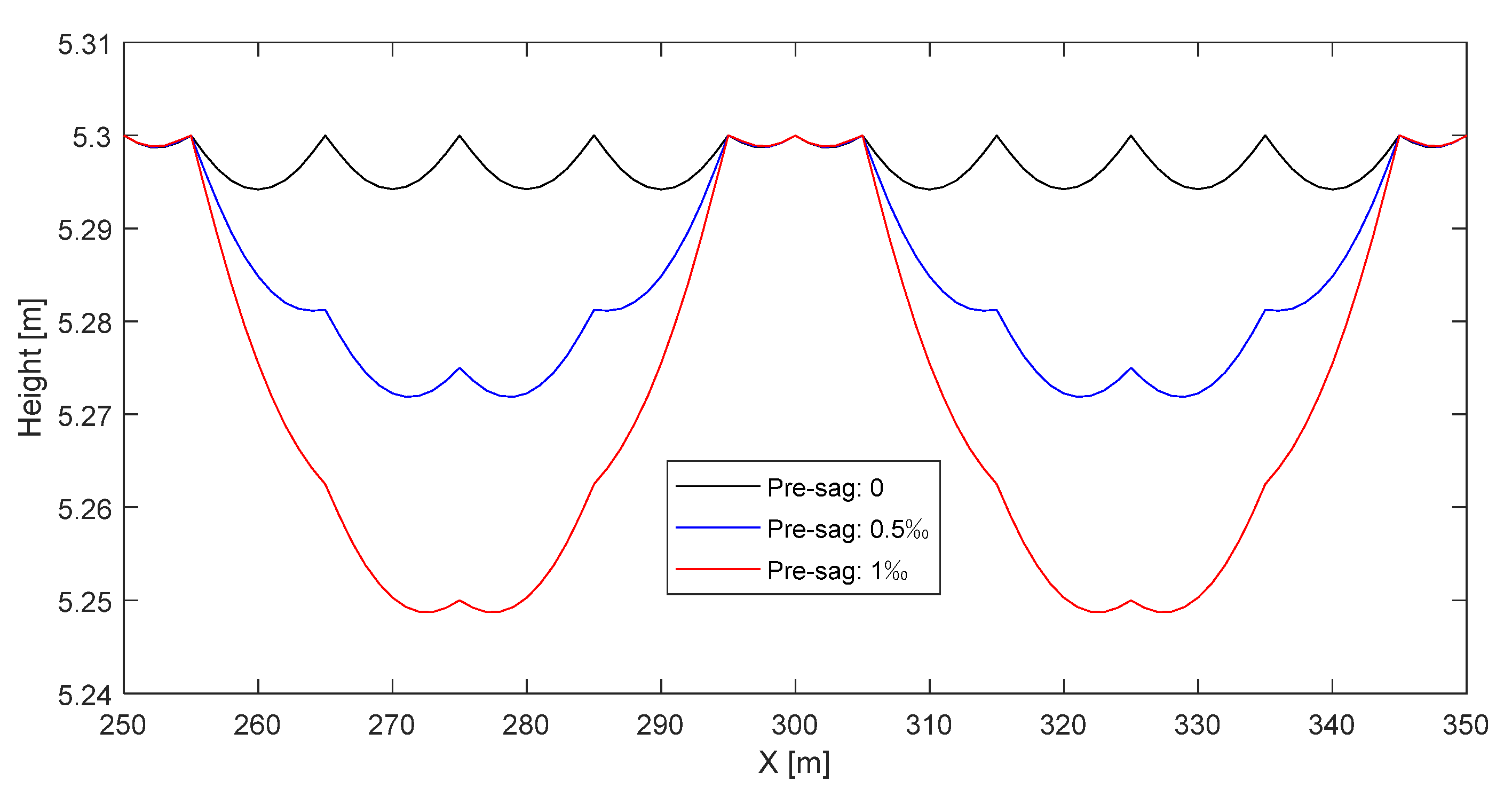
3. Analysis of Pre-Sag’s Effect
3.1. Evaluation of Contact Force with Different Speeds
3.2. Evaluation of Contact Force with Different Tension Classes
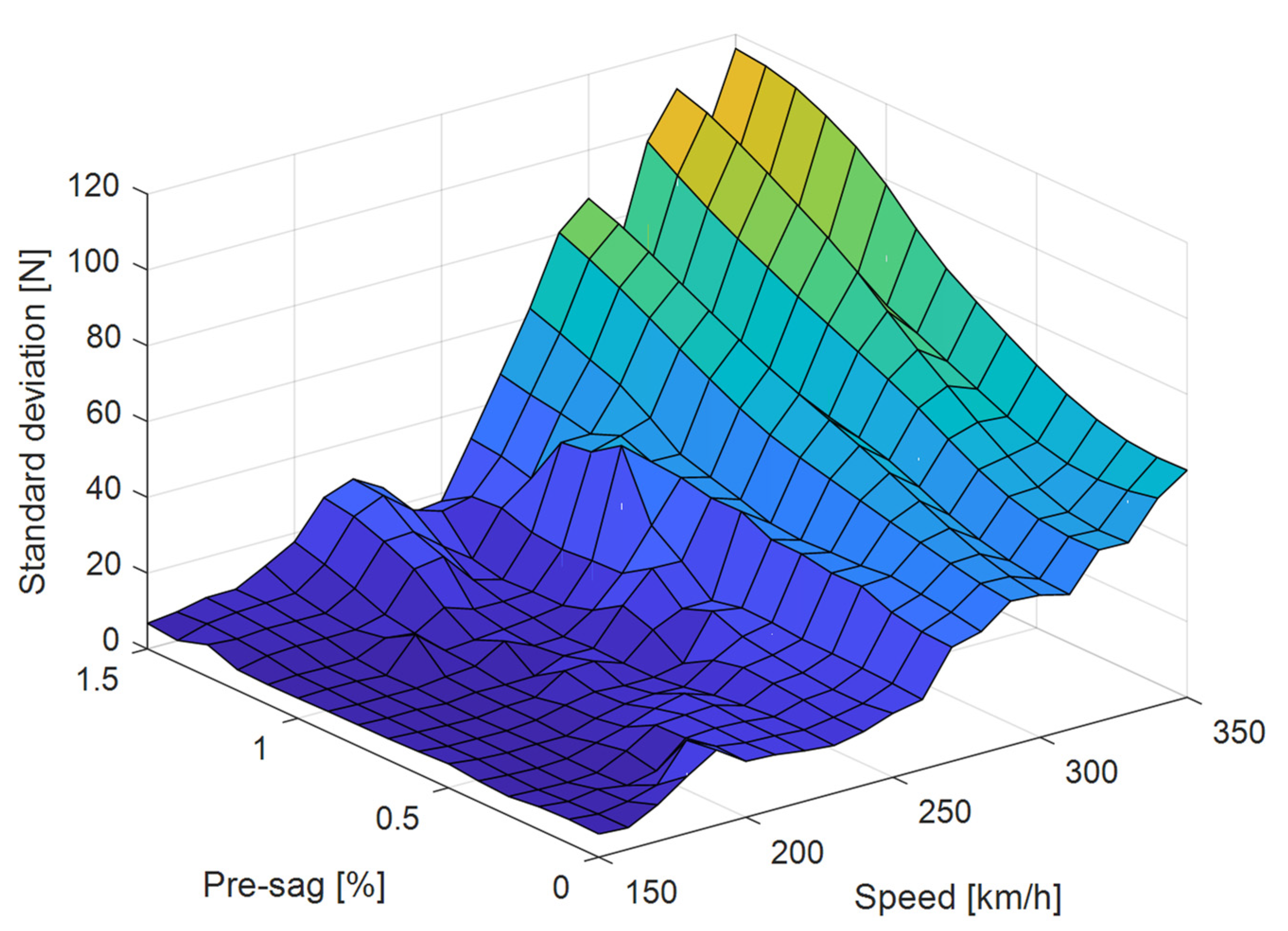
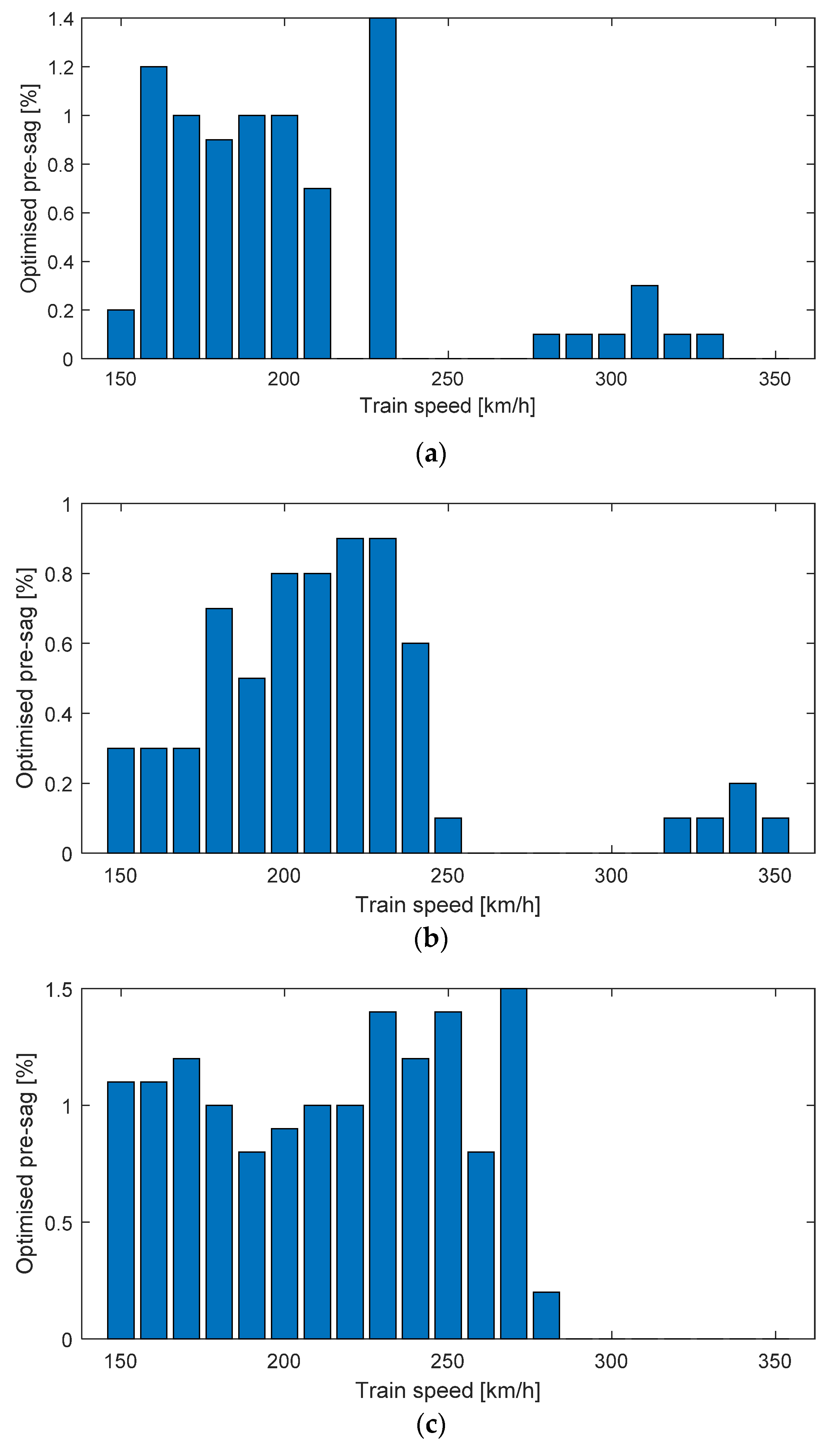
4. Optimisation of Pre-Sag
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EN 50119; Railway Applications—Fixed Installations—Electric Traction Overhead Contact Lines. European Standards (EN): Brussels, Belgium, 2015.
- Li, Y.; Jin, T.; Liu, L.; Yuan, K. Dynamic Performance Simulation and Stable Current Collection Analysis of a Pantograph Catenary System for Trolley Wire Overhead Electrically Actuated LHD. Energies 2020, 13, 1015. [Google Scholar] [CrossRef]
- Avila-Sanchez, S.; Lopez-Garcia, O.; Cuerva, A.; Meseguer, J. Assesment of the transverse galloping stability of a railway overhead located above a railway bridge. Int. J. Mech. Sci. 2017, 131–132, 649–662. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Wang, H. A response spectrum analysis of wind deflection in railway overhead contact lines using pseudo-excitation method. IEEE Trans. Veh. Technol. 2021, 70, 1169–1178. [Google Scholar] [CrossRef]
- Zhang, M.; Song, Y.; Abdelkefi, A.; Yu, H.; Wang, J. Vortex-induced vibration of a circular cylinder with nonlinear stiffness: Prediction using forced vibration data. Nonlinear Dyn. 2022, 108, 1867–1884. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Ye, Y.; Zhu, B.; Huang, P.; Peng, B. OORNet: A deep learning model for on-board condition monitoring and fault diagnosis of out-of-round wheels of high-speed trains. Meas. J. Int. Meas. Confed. 2022, 199, 111268. [Google Scholar] [CrossRef]
- Ye, Y.; Huang, P.; Sun, Y.; Shi, D. MBSNet: A deep learning model for multibody dynamics simulation and its application to a vehicle-track system. Mech. Syst. Signal Process. 2021, 157, 107716. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Xu, Z.; Lu, X. Wave propagation analysis in high-speed railway catenary system subjected to a moving pantograph. Appl. Math. Model. 2018, 59, 20–38. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F. Performance assessment of pantograph and overhead system based on a vertical coupling dynamics model of the railway system. Complex Eng. Syst. 2022, 2, 9. [Google Scholar] [CrossRef]
- Mariscotti, A.; Sandrolini, L. Detection of harmonic overvoltage and resonance in AC railways using measured pantograph electrical quantities. Energies 2021, 14, 5645. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z.; Lin, F.; Cao, J. Harmonic Loss Analysis of the Traction Transformer of High-Speed Trains Considering Pantograph-OCS Electrical Contact Properties. Energies 2013, 6, 5826–5846. [Google Scholar] [CrossRef]
- Calleja-Duro, V.; Fernández-Díaz, R.Á.; Barreiro-García, J.; Calvo-Hernández, Á. Desarrollo y ensayo de un amortiguador de masas sintonizadas para sistemas de catenaria rígida. DYNA 2017, 92, 680–687. [Google Scholar] [CrossRef]
- Gao, G.; Hao, J.; Wei, W.; Hu, H.; Zhu, G.; Wu, G. Dynamics of Pantograph-Catenary Arc during the Pantograph Lowering Process. IEEE Trans. Plasma Sci. 2016, 44, 2715–2723. [Google Scholar] [CrossRef]
- Song, Y.; Jiang, T.; Nåvik, P.; Rønnquist, A. Geometry deviation effects of railway catenaries on pantograph–catenary interaction: A case study in Norwegian Railway System. Railw. Eng. Sci. 2021, 29, 350–361. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Ronnquist, A.; Navik, P.; Liu, Z. Contact wire irregularity stochastics and effect on high-speed railway pantograph-catenary interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B. A Review of Fault Detection and Diagnosis for the Traction System in High-Speed Trains. IEEE Trans. Intell. Transp. Syst. 2020, 21, 450–465. [Google Scholar] [CrossRef]
- Gao, S. Automatic Detection and Monitoring System of Pantograph-Catenary in China’s High-Speed Railways. IEEE Trans. Instrum. Meas. 2021, 70, 3502012. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Han, Z. A high-precision detection approach for catenary geometry parameters of electrical railway. IEEE Trans. Instrum. Meas. 2017, 66, 1798–1808. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Li, Q.; Han, Z.; Nunez, A. High-Precision Detection Method for Structure Parameters of Catenary Cantilever Devices Using 3-D Point Cloud Data. IEEE Trans. Instrum. Meas. 2021, 70, 3507811. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Li, Y.; Wang, H.; Yang, C.; Wang, D.; Zhai, D. An automatic loose defect detection method for catenary bracing wire components using deep convolutional neural networks and image processing. IEEE Trans. Instrum. Meas. 2021, 70, 5016814. [Google Scholar] [CrossRef]
- Wei, X.; Jiang, S.; Li, Y.; Li, C.; Jia, L.; Li, Y. Defect detection of pantograph slide based on deep learning and image processing technology. IEEE Trans. Intell. Transp. Syst. 2020, 21, 947–958. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Wang, H.; Nunez, A.; Han, Z. Automatic defect detection of fasteners on the catenary support device using deep convolutional neural network. IEEE Trans. Instrum. Meas. 2018, 67, 257–269. [Google Scholar] [CrossRef]
- Luo, L.; Ye, W.; Wang, J. Defect detection of the puller bolt in high-speed railway catenary based on deep learning. J. Railw. Sci. Eng. 2021, 18, 605–614. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, J.; Liu, J.; Cao, Y.; Li, H.; Xu, X. Comprehensive evaluation method of catenary status based on improved multivariate statistical control chart. J. Railw. Sci. Eng. 2021, 18, 3048–3056. [Google Scholar] [CrossRef]
- Bruni, S.; Ambrosio, J.; Carnicero, A.; Cho, Y.H.; Finner, L.; Ikeda, M.; Kwon, S.Y.; Massat, J.P.; Stichel, S.; Tur, M.; et al. The results of the pantograph-catenary interaction benchmark. Veh. Syst. Dyn. 2015, 53, 412–435. [Google Scholar] [CrossRef]
- Wu, T.X.; Brennan, M.J. Dynamic stiffness of a railway overhead wire system and its effect on pantograph-catenary system dynamics. J. Sound Vib. 1999, 219, 483–502. [Google Scholar] [CrossRef]
- Poetsch, G.; Evans, J.; Meisinger, R.; Kortüm, W.; Baldauf, W.; Veitl, A.; Wallaschek, J. Pantograph/catenary dynamics and control. Veh. Syst. Dyn. 1997, 28, 159–195. [Google Scholar] [CrossRef]
- Vesali, F.; Rezvani, M.A.; Molatefi, H. Analysis of conceptual similarities and differences of wave speed and critical speed in the overhead catenary system. Measurement 2021, 176, 109164. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F.; Liu, Z. Analysis of Critical Speed for High-Speed Railway Pantograph-Catenary System. IEEE Trans. Veh. Technol. 2022, 71, 3547–3555. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Nåvik, P. Assessment of the high-frequency response in railway pantograph-catenary interaction based on numerical simulation. IEEE Trans. Veh. Technol. 2020, 69, 10596–10605. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Patel, M.D.; Tinsley, B.; Shabana, A.A. Contact force control In multibody pantograph/catenary systems. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2016, 230, 307–328. [Google Scholar] [CrossRef]
- Chu, W.; Song, Y. Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact. Vibration 2020, 3, 18–33. [Google Scholar] [CrossRef]
- Zhang, W.H.; Mei, G.M.; Wu, X.J.; Chen, L.Q. A study on dynamic behaviour of pantographs by using hybrid simulation method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 189–199. [Google Scholar] [CrossRef]
- Song, Y.; Antunes, P.; Pombo, J.; Liu, Z. A methodology to study high-speed pantograph-catenary interaction with realistic contact wire irregularities. Mech. Mach. Theory 2020, 152, 103940. [Google Scholar] [CrossRef]
- Bautista, A.; Montesinos, J.; Pintado, P. Dynamic interaction between pantograph and rigid overhead lines using a coupled FEM—Multibody procedure. Mech. Mach. Theory 2016, 97, 100–111. [Google Scholar] [CrossRef]
- Kim, J.W.; Chae, H.C.; Park, B.S.; Lee, S.Y.; Han, C.S.; Jang, J.H. State sensitivity analysis of the pantograph system for a high-speed rail vehicle considering span length and static uplift force. J. Sound Vib. 2007, 303, 405–427. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Z.; Zhang, J.; Wang, H.; Song, Y.; Duan, F. Prior-Information-Based Finite-Frequency H∞ Control for Active Double Pantograph in High-Speed Railway. IEEE Trans. Veh. Technol. 2017, 66, 8723–8733. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Z.; Song, Y.; Wang, H.; Zhang, J.; Wang, Y. Estimator-based multiobjective robust control strategy for an active pantograph in high-speed railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1064–1077. [Google Scholar] [CrossRef]
- Vera, C.; Suarez, B.; Paulin, J.; Rodríguez, P. Simulation model for the study of overhead rail current collector systems dynamics, focused on the design of a new conductor rail. Veh. Syst. Dyn. 2006, 44, 595–614. [Google Scholar] [CrossRef] [Green Version]
- EN 50367; Railway Applications—Current Collection Systems—Technical Criteria for the Interaction between Pantograph and Overhead Line. European Standards (EN): Brussels, Belgium, 2016.
- Song, Y.; Ouyang, H.; Liu, Z.; Mei, G.; Wang, H.; Lu, X. Active control of contact force for high-speed railway pantograph-catenary based on multi-body pantograph model. Mech. Mach. Theory 2017, 115, 35–59. [Google Scholar] [CrossRef]
- Zdziebko, P.; Martowicz, A.; Uhl, T. An investigation on the active control strategy for a high-speed pantograph using co-simulations. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 370–383. [Google Scholar] [CrossRef]
- Ambrósio, J.; Pombo, J.; Pereira, M. Optimization of high-speed railway pantographs for improving pantograph-catenary contact. Theor. Appl. Mech. Lett. 2013, 3, 013006. [Google Scholar] [CrossRef]
- Di Stefano, E.; Avizzano, C.A.; Bergamasco, M.; Masini, P.; Menci, M.; Russo, D. Automatic inspection of railway carbon strips based on multi-modal visual information. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 178–184. [Google Scholar] [CrossRef]
- Zhu, M.; Zhang, S.Y.; Jiang, J.Z.; Macdonald, J.; Neild, S.; Antunes, P.; Pombo, J.; Cullingford, S.; Askill, M.; Fielder, S. Enhancing pantograph-catenary dynamic performance using an inertance-integrated damping system. Veh. Syst. Dyn. 2021, 60, 1909–1932. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Lu, X.; Wang, H. Study on wind-induced vibration behavior of railway catenary in spatial stochastic wind field based on nonlinear finite element procedure. J. Vib. Acoust. Trans. ASME 2018, 140, 011010. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear analysis of wind-induced vibration of high-speed railway catenary and its influence on pantograph–catenary interaction. Veh. Syst. Dyn. 2016, 54, 723–747. [Google Scholar] [CrossRef]
- Song, Y.; Duan, F.; Gao, S.; Wu, F.; Liu, Z. Crosswind Effects on Current Collection Quality of Railway Pantograph-catenary: A Case Study in Chengdu-Chongqing Passenger Special Line. IEEE Trans. Instrum. Meas. 2021, 71, 9000713. [Google Scholar] [CrossRef]
- Stickland, M.T.; Scanlon, T.J.; Craighead, I.A.; Fernandez, J. An investigation into the mechanical damping characteristics of catenary contact wires and their. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2001, 217, 63–72. [Google Scholar] [CrossRef]
- Zhang, Y.; Yue, Y.; Zhao, S.; Sihua, W. Research on galloping response of catenary positive feeder in gale area considering surface roughness of stranded wire. J. Railw. Sci. Eng. 2021, 18, 1885–1894. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Zhang, J.; Lu, X.; Duan, F. Analysis of the galloping behaviour of an electrified railway overhead contact line using the non-linear finite element method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 2339–2352. [Google Scholar] [CrossRef]
- Zhai, W.M.; Cai, C.B. Effect of locomotive vibrations on pantograph-catenary system dynamics. Veh. Syst. Dyn. 1998, 29, 47–58. [Google Scholar] [CrossRef]
- Yao, Y.; Zhou, N.; Mei, G.; Zhang, W. Dynamic Analysis of Pantograph-Catenary System considering Ice Coating. Shock Vib. 2020, 2020, 8887609. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Lu, X. Dynamic Performance of High-Speed Railway Overhead Contact Line Interacting with Pantograph Considering Local Dropper Defect. IEEE Trans. Veh. Technol. 2020, 69, 5958–5967. [Google Scholar] [CrossRef]
- Vesali, F.; Rezvani, M.A.; Molatefi, H.; Hecht, M. Static form-finding of normal and defective catenaries based on the analytical exact solution of the tensile Euler–Bernoulli beam. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 691–700. [Google Scholar] [CrossRef]
- Van, O.V.; Massat, J.P.; Laurent, C.; Balmes, E. Introduction of variability into pantograph-catenary dynamic simulations. Veh. Syst. Dyn. 2014, 52, 1254–1269. [Google Scholar] [CrossRef]
- Cho, Y.H.; Lee, K.; Park, Y.; Kang, B.; Kim, K.N. Influence of contact wire pre-sag on the dynamics of pantographrailway catenary. Int. J. Mech. Sci. 2010, 52, 1471–1490. [Google Scholar] [CrossRef]
- Kiessling, F.; Puschmann, R.; Schmieder, A.; Schneider, E. Contact Lines for Electric Railways, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; Volume 116, ISBN 3-8957-152-5. [Google Scholar]
- Qin, R.; Zhu, B.; Qiao, K.; Wang, D.; Sun, N.; Yuan, X. Simulation study of the protective performance of composite structure carbon fiber bulletproof board. Chin. J. Eng. 2021, 43, 1346–1354. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Li, H.; Zhang, L.; Zhang, B. Warpage deformation behavior of metal laminates. Chin. J. Eng. 2021, 43, 409–421. [Google Scholar] [CrossRef]
- Shabana, A.A. Definition of ANCF Finite Elements. J. Comput. Nonlinear Dyn. 2015, 10, 054506. [Google Scholar] [CrossRef]
- Pil Jung, S.; Guk Kim, Y.; Sung Paik, J.; Won Park, T. Estimation of dynamic contact force between a pantograph and catenary using the finite element method. J. Comput. Nonlinear Dyn. 2012, 7, 041006. [Google Scholar] [CrossRef]
- Song, Y.; Rønnquist, A.; Jiang, T.; Nåvik, P. Identification of short-wavelength contact wire irregularities in electrified railway pantograph–catenary system. Mech. Mach. Theory 2021, 162, 104338. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements. Veh. Syst. Dyn. 2015, 53, 1455–1479. [Google Scholar] [CrossRef]





| Material Property | |
|---|---|
| Contact line | Line density: 1.082 kg/m; Tensile rigidity: 106 N/m; Tension: 27 kN; Cross-section: 120 mm2 |
| Messenger line | Line density: 1.068 kg/m; Tensile rigidity: 106 N/m; Tension: 20 kN; Cross-section: 120 mm2 |
| Dropper | Line density: 0.14 kg/m; Tensile rigidity: 105 N/m |
| Geometrical Property | |
| Span length: 50 m; Encumbrance: 1.6 m; Droppers interval: 10 m; Number of droppers: 5; Span number: 15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, G.; Song, Y. Effect of Overhead Contact Line Pre-Sag on the Interaction Performance with a Pantograph in Electrified Railways. Energies 2022, 15, 6875. https://doi.org/10.3390/en15196875
Mei G, Song Y. Effect of Overhead Contact Line Pre-Sag on the Interaction Performance with a Pantograph in Electrified Railways. Energies. 2022; 15(19):6875. https://doi.org/10.3390/en15196875
Chicago/Turabian StyleMei, Guiming, and Yang Song. 2022. "Effect of Overhead Contact Line Pre-Sag on the Interaction Performance with a Pantograph in Electrified Railways" Energies 15, no. 19: 6875. https://doi.org/10.3390/en15196875





