Organization and Reliability Testing of a Wind Farm Device in Its Operational Process

Abstract

This article deals with the importance of simulation studies for the reliability of wind farm (WF) equipment during the operation process. Improvements, upgrades, and the introduction of new solutions that change the reliability, quality, and conditions of use and operation of wind farm equipment present a research problem during study. Based on this research, it is possible to continuously evaluate the reliability of WF equipment. The topic of reliability testing of complex technical facilities is constantly being developed in the literature. The article assumes that the operation of wind farm equipment is described and modeled based on Markov processes. This assumption justified the use of Kolmogorov–Chapman equations to describe the developed research model. Based on these equations, an analytical model of the wind farm operation process was created and described. As a result of the simulation analysis, the reliability of the wind farm was determined in the form of a probability function (R0(t)) for the WPPs system.

1. Introduction and Analysis of the Issue

Wind farm power equipment, such as wind power plants, block transformers, etc., are technical items that are either in continuous operation or on standby. The application of a certain operating policy is necessary to maintain the technical condition of these devices at a good level for their operational characteristics. The goal of this method of equipment renewal for wind farms is to reduce the cost and time involved in the process of repairing or replacing operating characteristics. The goal is also to shorten the time required for the process of replacing these devices. It is expensive and challenging to create an acceptable policy for the process of maintaining wind farm equipment. To facilitate this process, a variety of methods are applied when renovating wind farm (WF) devices. The SERV expert program is one such remedy that has been proposed in the literature [1,2]. The SERV (Intelligent Expert System to Support the Restoration of Complex Technical Objects) system’s job is to come up with a way to improve the way a wind farm’s machines work in the environment where they will be used. To operate wind farm machinery, the SERV system, an extended expert computer program, needs diagnostic data. A WF equipment’s rejection mechanism is built in compliance with specifications set by SERV. The SERV technology significantly reduces the price and duration of wind farm equipment replacement. The main research goal that needs to be accomplished in this paper is to evaluate the equipment quality and dependability of WF when it is in use.

The issues with a simulation assessment of WF equipment’s dependability during use are discussed in the paper. A significant cognitive challenge is testing the process of exploitation of complex technical objects, such as the WF and TWG electrical subsystems (Main Power Supply Point). This issue is particularly crucial since WF users need to know how to manage organizational and technical operations that renew WFs in the technical service system. Only a well-structured WF renewal system can effectively save costs and guarantee that these facilities are run at the optimum degree of energy efficiency. The establishment of trustworthy and appropriate techniques and a WF facility utilization policy is the outcome of such research activities. The literature has not addressed the aforementioned issues in a thorough manner.

The issue of a simulation study of the quality of the exploitation process—renewal of the exploitation features that increase the dependability of the WF equipment—is presented in this paper. The following will be used to address the issues raised in the article. In the second section of this study, a methodology for evaluating WF equipment’s dependability based on the effectiveness of the process of updating operational features will be described. The third section of the study discusses the cognitive challenges as well as the organization of the exploitation process (the use and operation of the wind farm equipment). The dependability assessment of the WF equipment following the introduction of, among other things, intelligent renewal systems, will be another topic examined in this section of the study. The concerns that reduce the reliability of WF equipment will also be covered in this part of the report. The article’s primary research goal is to address this issue. In the fourth part of the essay, the results and their analysis will be given in terms of how well the exploitation process works. This will include an evaluation of how reliable the WF devices are and a review of how they work.

The paper discusses the issue of simulation tests for the operation process’ quality: the regeneration of operational attributes enhances FW equipment dependability. The following will be carried out in order to solve the issues raised in the article. In the second part of the paper, we will talk about how to test the dependability of WF devices by evaluating the process of regeneration.

The concerns surrounding the comprehension and description of the action (i.e., the use and upkeep of WF equipment) will be covered in the third section of the article. The paper’s model of the WF device operation process utilizes intelligent SERV application to plan the simulation testing. The evaluation of WF device dependability following the adoption of intelligent re-generation technology is another topic covered in this section of the article. It is crucial that these concerns that can be addressed to improve the reliability of WF devices and are thus presented in this section of the research. The study’s main focus is on this issue. Most of the research for this study is presented in the fourth section.

In the fourth section, we will discuss the results and how they relate to the research on the quality of the operation process, including the rebuilding of operational features to make FW equipment more reliable.

The performance of complicated technical objects utilized in the operating procedure degrades. Their capacity to carry out the necessary (intended) tasks is diminished. The utility problem is referred to as a functional resource in the literature [3,4,5,6,7,8,9]. The deterioration in technical facility dependability, notably that of WF equipment, is intimately related to the loss of operating capacity. Aging and the detrimental effects of external variables are the main causes of the loss in the dependability of technological structures. This makes estimating the current reliability of WF equipment and simulating the operation of complex technological components more challenging. The issue is very complicated when it comes to medical devices, wind farm equipment, and other goods that continuously perform their intended function.

With the widespread usage of contemporary solutions, such as artificial intelligence and intelligent systems, current research supporting the development of expert and advisory systems focuses on challenges connected to the improvement of methods for obtaining the specialized knowledge of a person. Previous studies [10,11] have addressed this issue. Figure 1 graphically demonstrates the difficulties of evaluating the reliability of wind farm equipment is while it is being used.

Labels in Figure 1 represent the following:

• X(e_{i, j}) represents whether the diagnostic signal is the j-th element of the i-th set;
• X_(w)(e_{i, j}) is a reference signal for X(e_i,j) signal;
• F_C is the min. or max. item use feature value;
• {M_E(e_{i, j})} is the service knowledge base;
• {M_E} is the technical facility renovation system;
• W(ε(e_{i, j}) = {3, 2, 1, 0}) is the diagnostic state evaluation logic information value for the item ”j” within the ”i” object module.

Through this diagnosis, it is possible to determine the present level of the reliability of the equipment used by WFs and other sophisticated technical facilities. It is especially helpful to make a diagnosis utilizing inference (state recognition) in multi-valued logic [12]. Today, there has been a significant advancement in the creation of specialist diagnostic tools. Previous research [13,14] has addressed these concerns. In the diagnostics of medical devices, energy technology, etc., these issues are blatantly visible. However, because they are diagnostic tools, each one is particular to the thing being assessed. There is no diagnostic tool available on the market with a broad range of useful diagnostic applications. According to research by Duer and colleagues, diagnostic tools are a frequent and dependable type of technical repair method. This modular approach’s functional components include measurement, diagnosis, and a diagnostic knowledge base. Any piece of equipment or technological process that has been diagnosed can only use information bases, measuring systems, acquisition, etc. that are related to measuring.

Minimizing the costs related to preventive measures is possible thanks to the proposed system of automatic facility performance regeneration. The expenditures related to organizing a facility maintenance system are completely minimized by this approach. When necessary, the object can be regenerated. This offers a facility-based artificial neural network-based intelligent diagnostic system; crucially, one that reliably and reliably recognizes the states of the facility for which preventive actions should be taken [15,16,17,18,19,20]. No loss and no expenses are incurred as a result of the inefficient use of the facility, which may happen during operation when the facility is not in use or only partially efficient. The costs involved in performing regeneration on facility elements that have already been regenerated or are capable of doing so are eliminated by this method. The internal (structural) components of the object that need regeneration are given incomplete conditions of 1, or over 0, by the intelligent traffic maintenance system (including the intelligent diagnostic system), which was created for the specific component.

A summary of the effective measurement system, a crucial component of the diagnostic system structure, is given in the works by Kacalak et al. and others [21,22,23]. Also given are the theoretical underpinnings for the creation of a measurement system employing a computer measurement card to build a measurement database for the diagnostic system. An example of a database monitoring data for the subject in question was used to support the investigation. The studies [24,25,26] talk about how hard it is to automate technical procedures and use human knowledge when making intelligent systems for diagnosing and testing technical parts.

Another important issue that encourages the coordination of technical duties is the technical diagnostics of technological apparatus. The diagnostic tests carried out by the apparatus are intended to assess and characterize the technical state of the structure under examination. State recognition in bivalent and trivalent logic is utilized for technical device diagnostics. When planning how to renovate a technical facility, the diagnostician’s three-valued logical diagnoses are the most important aspects to understand.

The seminal works in this field are the studies by Zurada and Duer [27,28,29,30].

In their study, the writers discussed, among other things, the fundamentals and methodologies of creating models of how complicated technical facilities operate. The writers of these papers discuss the issue of the qualitative evaluation of such a structured traffic maintenance process, which is the focus of this research. Our study provides simulation testing software to achieve this. The test program must include a description of the operational process models for the technical facilities and the selection of the test inputs—the service life of the technical facility, which is the total amount of time it takes to regenerate (repair); the use of the facilities; and the establishment of qualitative indicators for the evaluation of the regeneration of the facility during the operational process. As an example to back up the study, simulations were used examine what would happen when a technical object was regenerated in an intelligent system with an artificial neural network.

Reliability is described in the study by Dyduch and Siergiejczyk et al. In-service investigations are required [31,32,33]. Although equally crucial, the electromagnetic compatibility of the electrical and electronic equipment used is not covered in this article. However, it is impossible to ignore how electromagnetic interference affects how electronic equipment operates [34,35,36,37,38,39]. It is crucial to model the technological object itself and its operating process, just as in reliability research. The reliability of wind farm equipment is a significant research question.

The works of Sergey and colleagues [40] illustrate the issues with graphical and analytical modeling for the evaluation of the dependability of technical facilities. In the theory and practice of technological object reliability, models of the exploitation processes for technical objects based on the Markov process theory are crucial. These models assess the dependability of technical items using the Kolmogorov–Chapman equation. This article also presents this research methodology.

The application of Chapman–Kolmogorov equations to the operation of technical structures and systems is another area of reliability research. In the writings of Sergey and others, this is especially clear [41]. The dependability and operational analysis of power supply systems in PSS transport telematics systems in TTD are discussed in the article. The study presents power supply system solutions and defines PSS in TTD from the primary and backup sources. This makes it possible to identify dependencies that show the likelihood that the system continuing to function normally or resulting in a security emergency or security failure. The PSS quality analysis in TTD was completed, and the usefulness of the quality index for supply continuity was assessed. With the help of this indicator, it can be seen how the CQoPS power supply’s quality of continuity is dependent on more than just reliability. The example demonstrates how to calculate CQoPS using three observations, each of which has an impact on quality, for both main and backup power. Other public facilities can use the factors offered in the area of quality and the reliability-in-service modeling of PSS (including critical infrastructure). This is the kind of task that vital infrastructure performs.

The modeling of the technical facility operation processes is described in further works by Nakagawa et al. [42,43,44,45]. Research conducted by the author is also important. The mathematical approach used to replicate this process is described in these publications. The author evaluates both the object’s current states and any transitions (changes) that might have taken place during the exploitation process. The strategy for organizing the process of renewal displayed (or used) in the maintenance system is a crucial component of modeling the facility’s operational process. The author’s research led to the development of an innovative method called “using the object’s current state”, which is also called “operating the object according to its state”.

In papers by Badrzadeh et al. and Pogaku et al. [46,47], issues relating to the use and operation of electrical equipment in wind farms are presented. This study analyses the work that has been performed to model, run, and build electrical equipment for wind farms.

The creation of a model of the process of updating the intelligent traffic maintenance system is a crucial step in simulating the functioning of a complicated technical structure. Publications, among other places, have discussed these topics. Buchanan et al. [48,49], Duer et al. The author discusses problems with the definition of systems maintenance models in his investigations. For this reason, the form of the object matrix structure (dimension) is taken for granted. It changes into a matrix for object upkeep. The holding matrix’s elements are matched up with the object’s fundamental components. To renew a given element of the structure, certain subsets of these technical and technological operations must be carried out, as is made obvious by the elements of the structural maintenance matrix. It is a difficult effort to divide up the structure’s components into tasks for the renovation that uses the right materials and resources. The author’s publications consistently develop and enhance these concerns.

Understanding the design, functionality, and erroneous diagnosis of technical gadgets is essential. In a later study, operational issues with wind farm infrastructure are discussed.

In his works [50,51], Duer published analyses of the dependability of wind farm machinery using analytical models that take reliability dependencies into account. The results show that it is quite challenging to use this strategy in simulation research, nevertheless. The paper outlines the planning, execution, and analysis of simulations performed for the evaluation of the effectiveness of the maintenance system for wind power plant equipment. The reader will find it important that models of the operational procedures for wind farm equipment are presented. The reader can discover information about the organization of the building and the operation of sophisticated technical facilities in [52]. The simulation made use of three WF models of the equipment’s functioning procedures. Model A, a wind power operational approach, uses an artificial neural network-based intelligent traffic maintenance system. The second model, known as Model B, is an object operation process that employs bivalent logic and includes a maintenance system that is created to come up with the best preventive measures. The third is Model C, a technique for operating a maintenance system for a wind power plant with a typically constructed structure that does not include a status test during the evaluation phase. The way the building is maintained is by planning preventive measures by hand and picking the operator for its responsibility at random.

Publications do a good job of presenting issues relating to the description and testing of individual elements characterized by the operation of technical structures. However, there are no studies that completely outline the difficulties in organizing the functioning of sophisticated technical equipment for research. The purpose of the paper is to simulate the WF equipment’s operational reliability as a result. The following research issues need to be resolved for this task: The first challenge is understanding and describing issues regarding the diagnosis of WF devices. Another problem is determining and describing how to maintain and run the machinery utilized in wind farms. A big part of the study is about how important it is to understand and sketch out the structure of the technical maintenance system while the tested structure is in use.

Intelligent systems-based wind farm technical equipment reliability tests are meticulously planned. The developed WF model and analytical dependencies have been used to obtain the tested reliability values in the form of the capacity function (Kg(t)) for the described operating process.

In this article, the issue of evaluating WF dependability in light of the impact of one parameter on this value—the average time between successive failures—is discussed. This test parameters’ application to WF reliability in this manner has not yet been documented in publications. The article’s use of a LabView computer application as a research tool in is another innovative feature. The results of the simulation studies were fascinating, but they were not presented as in this study. The task of uncovering how reliable WF equipment is the main study goal discussed in this paper.

2. Methodology of Testing the Reliability of a Wind Farm Device in the Process of Exploitation

An input that characterizes the actual operation of the chosen class of the technical object and its simulation models is necessary for every test, but especially a simulation test, of a component (Figure 2). Data for simulation studies of process models is collected by studying how the structure actually operates.

The required test inputs are the following:

-

the time of use of the object T is the time the object is in a fit condition;

-

the object interoperability removal time, T_a;

-

the time of preventive repair, T_p;

-

the period of anticipated (optimal) prevention, θ*;

-

the planned prevention (servicing) period θ.

The aforementioned information can be gleaned via observing actual operational procedures and a properly designed and carried out simulation experiment. The study shows, among other things, the results of testing how well different types of technological structures really work. The simulation experiment consists of the following elements (Figure 2):

-

model of the operation process of the tested structure;

-

test program;

-

research tools—use of a computer in research;

-

analysis of the data obtained;

-

the testing of the facility operation process models was conducted using the same test criteria of the test conditions, such as:

-

functions describing the object operation process and the inputs consumed;

-

input data characterizing the operation process of complex facilities.

To find a good way to describe the quality of the facility operation process, other numbers must be examined to demonstrate how well the equipment used to run a wind farm is functioning.

Research, analytical, and evaluation activity in this area focuses on the methods for assessing the dependability of the operation process of wind farm equipment. Figure 2 is a picture of this operation that was made to help people understand the research that is being carried out to analyze how reliable the process of running wind farm equipment is. The key points of this algorithm are as follows:

Understanding and describing the process of operating (using and refurbishing) wind farm equipment.

The development of process models for the operation of wind farm equipment.

Adopting the size (function) that characterizes the reliability test of the operation process of wind farm equipment. For reliability testing, a well-known value of reliability [2,38] is proposed, which is the reliability function (R_o(t)) of the WFD:

$$\mathrm{Ro}\left(\mathrm{t}\right)= \mathrm{P}\left[\mathrm{S}\left(\mathrm{t}\right)\right]$$

(1)

where the following means: P[S(t)] is the probability that the wind farm device system WFD is in a serviceable state.

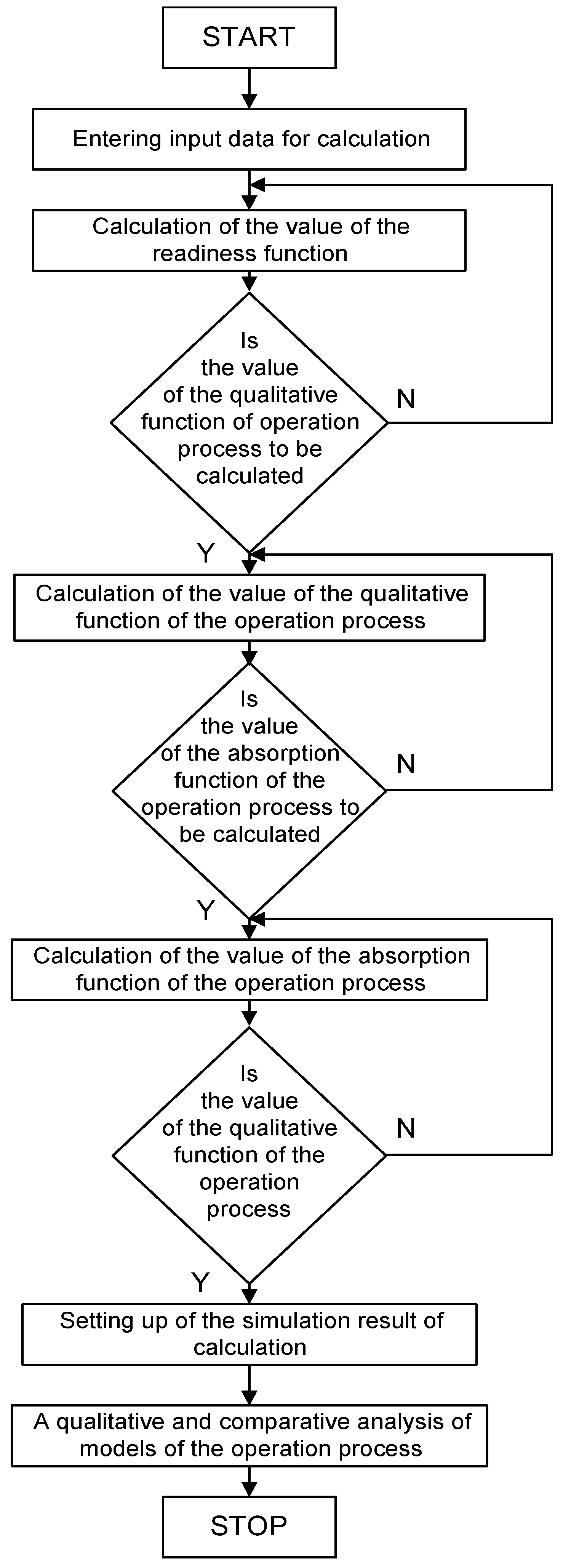
• Reliability simulation tests of the wind farm equipment operation process are carried out using the same computer program.
• The same inputs are used in wind farm reliability simulation tests.
• Results obtained from simulation studies on the reliability of the operation process of wind farm equipment are graphically presented in common graphs presenting the tested quantities.

3. Organization and Testing of the Reliability of Wind Power Plant Equipment in the Operation Process

The following assumptions have been made for the qualitative analysis of the operation process of a wind farm facility regarding the organization of its structure:

• Wind farm device system (WFD) in the state (S₁) z is in full technical fitness, this condition occurs if and only if the function of the WFD target is fulfilled and its energy efficiency is 100%. The operational model is shown in Figure 3.

2.

If damage or a malfunction occurs in the WFD, the WFD then passes with the intensity of damage (λ₁₂) to state (S₂). In state (S₂), the efficiency of the WF power system is below 100%. The WFD unit is basically efficient, its required function is realized to a limited extent (partially)—the state of partial WFD efficiency is state (S₂). In this state, WFDs are subject to repair if the transition to this state was caused by a malfunction. Then WFD with repair intensity (µ₂₁) goes to state (S₁). In the case when the transition of the WFD to the state (S₂) was forced by the necessity to perform the required technological tasks or activities from the set of activities (T₁), the current operations improving the WFD occur in this state. The execution of technological tasks (T₁) causes the WFD to move with the intensity of repairs (µ₂₁) to the state (S₁). If there is damage to the WFD in the state (S₂) it passes with the intensity of damage (λ₂₃) to the state (S₃). Performing WFD repair activities with repair intensity (µ₂₁) goes to state (S₁).

3.

The WFD system is in the state (S₃) if the event of a failure or failure of the WFD occurs, the WFD system passes with the intensity of the damage (λ₁₃) to the state (S₃). In the state (S3), the efficiency of the power system WF is far below 100%. The WFD team is partially operational, and its function is required to be implemented in a limited (partial) scope—the status of the critical suitability of the WFD is the state (S₃). In the state (S₃), WFDs are subject to repairs if the transition to this state was caused by a malfunction. Then WFD with repair intensity (µ₃₁) change to state (S₁). In the case when the transition of the WFD to the state (S₃) was forced by the necessity of performing the required technological tasks or activities from the set of activities (T₂), then, in this state, the periodic technological (improvement) activities of the WFD take place. The execution of technological tasks (T₂) causes the WFD to move with the intensity of repairs (µ₃₁) to the state (S₁). If there is damage to the WFD in the state (S₃), it passes with the intensity of damage (λ₃₄) to the state (S₄).

4.

If the event of damage or failure of the WFD occurs in state (S₃), the WFD system passes with the intensity of damage (λ₁₃) to the state (S₃). In the state (S₃ efficiency of the power system WF is far below 100%. The WFD team is partially operational its function is required to be implemented in a limited (partial) scope—the status of the critical suitability of the WFD is the state (S₃). In the state (S₃), WFDs are subject to repairs if the transition to this state was caused by a malfunction. Then WFD with repair intensity (µ₃₁) go to state (S₁). In the case when the transition of the WFD to the state (S₃) was forced by the necessity to perform the required technological tasks or activities from the set of activities (T₂), then, in this state, the periodic technological (improvement) activities of the UFW take place. The execution of technological tasks (T₂) causes the WFD to move with the intensity of repairs (µ₃₁) to the state (S₁). If there is damage to the WFD in the state (S₃), it passes with the intensity of damage (λ₃₄) to state (S₄).

5.

In case of damage or the malfunction of the WFD in the state (S₁), then the UWF system with the intensity of damage (λ₁₄) will move to the state (S₄). In the state (S₄) the assessed efficiency of the power system FW is very significantly below 100% (Figure 1). The WFD team is critically fit. In the state (S₄), the function required by the WFD is implemented in a limited scope. This is the critical fitness status of the WFD is fit being in the state (S₄). In state (S₄), WFDs are subject to repairs if the transition to this state was caused by a malfunction. Then UFW with repair intensity (µ₄₁) goes to (S₁). In a case when the transition of the UFW to the state (S₄) was forced by the necessity of performing the required technological tasks from the set of activities (T₃). In the state (S₄), the periodic technological (improvement) activities of the WFD are performed. The execution of technological tasks (T₃) causes the WFD to move with the intensity of repairs (µ₄₁) to the state (S₁). When there is damage to the WFD in the state (S₄), it moves with the intensity of damage (λ₄₅) to the state (S₅).

6.

If the (S₁) state experiences damage or a malfunction in the WFD system, the system moves with the intensity of the damage (λ₁₅) to the (S₅) state. In state (S₅), the efficiency of the WF power system is critically below 100%. In the state (S₅, the WFD team is operational in the minimum (critical) range. The function required by the WFD is performed to a limited extent, this is the pre-fault condition. In the state (S₅), WFDs are subject to essential (primary) repairs if the transition to this state was caused by a malfunction. Then WFD with repair intensity (µ₅₁) go to state (S₁). In case when the transition of the WFD to the state (S₅) was forced by the necessity to perform the required technological tasks from the set of operations (T₄). In the state (S₅), periodic main technological activities of the WFD are performed. The execution of technological tasks (T₄) causes the WFD to move with the intensity of repairs (µ₅₁) to the state (S₁). If there is damage to the WFD in the state (S₅), then the required corrective actions are performed, and after they are completed, it passes with the intensity of repairs (µ₅₁) to the state (S₁).

The markings in Figure 3 show the following system functions and transition intensities:

-

${\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)$—probability function for a WFD system in fully physically fit S₁;

-

${\mathrm{Q}}_2\left(\mathrm{t}\right)$—probability function for a WFD system in partially operational S₂;

-

${\mathrm{Q}}_3\left(\mathrm{t}\right)$—probability function for a WFD system in partially operational S₃;

-

${\mathrm{Q}}_4\left(\mathrm{t}\right)$—probability function for a WFD system in partially incapacitated S₄;

-

${\mathrm{Q}}_5\left(\mathrm{t}\right)$—probability function for a WFD system in incapacitated S₅;

-

${\mathsf{\lambda }}_{12 }$—transition intensity from full efficiency (S₁) to the state of partial fitness (S₂);

-

${\mathsf{\mu }}_{21}$—intensity of transitions from the state of partial fitness (S₂) to the state of full fitness (S₁);

-

${\mathsf{\Lambda }}_{13}$—intensity of transitions from the state of full fitness (S₁) to the state of partial fitness (S₃);

-

${\mathsf{\mu }}_{31}$—intensity of transitions from the state of partial fitness (S₃) to the state of full fitness (S₁);

-

${\mathsf{\lambda }}_{14}$—intensity of transitions from the state of full fitness (S₁) to the state of partial unfitness (S₄);

-

${\mathsf{\mu }}_{41}$—intensity of transitions from the state of partial unfitness (S₄) to the state of full fitness (S₁);

-

${\mathsf{\lambda }}_{15}$—intensity of transitions from the state of full fitness (S₁) to the state of full unfitness (S₅);

-

${\mathsf{\mu }}_{51}$—intensity of transitions from the state of full unfitness (S₅) to the state of full fitness (S₁);

-

${\mathsf{\lambda }}_{23}$—the intensity of transitions from the S₂ state to the S₃ partial-use state;

-

${\mathsf{\Lambda }}_{34}$—transition intensity from partial airworthiness (S₃), transition from partial airworthiness (S₄);

-

${\mathsf{\Lambda }}_{45}$—S₄ to the state of full unfitness (S₅).

The operating model in Figure 3 is shown in the form of Kolmogorov–Chapman equations.

$$\begin{gathered} {{\mathrm{R}}^{\prime }}_{\mathrm{o}}\left(\mathrm{t}\right)=-{\mathsf{\lambda }}_{12}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)+{\mathsf{\mu }}_{21}\mathsf{·}{\mathrm{Q}}_2\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{13}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)+{ \mathsf{\mu }}_{31}\mathsf{·}{\mathrm{Q}}_3\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{14}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right) \\ +{\mathsf{\mu }}_{41}\mathsf{·}{\mathrm{Q}}_4\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{15}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)+{\mathsf{\mu }}_{51}\mathsf{·}{\mathrm{Q}}_5\left(\mathrm{t}\right) \end{gathered}$$

(2)

$${{\mathrm{Q}}^{\prime }}_2\left(\mathrm{t}\right)={\mathsf{\lambda }}_{12}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)-{\mathsf{\mu }}_{21}\mathsf{·}{\mathrm{Q}}_2\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{23}\mathsf{·}{\mathrm{Q}}_2\left(\mathrm{t}\right)$$

(3)

$${{\mathrm{Q}}^{\prime }}_3\left(\mathrm{t}\right)={\mathsf{\lambda }}_{13}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)-{\mathsf{\mu }}_{31}\mathsf{·}{\mathrm{Q}}_3\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{34}\mathsf{·}{\mathrm{Q}}_3\left(\mathrm{t}\right)+{\mathsf{\lambda }}_{23}\mathsf{·}{\mathrm{Q}}_2\left(\mathrm{t}\right)$$

(4)

$${{\mathrm{Q}}^{\prime }}_4\left(\mathrm{t}\right)={\mathsf{\lambda }}_{14}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)-{\mathsf{\mu }}_{41}\mathsf{·}{\mathrm{Q}}_4\left(\mathrm{t}\right)-{\mathsf{\lambda }}_{45}\mathsf{·}{\mathrm{Q}}_4\left(\mathrm{t}\right)+{\mathsf{\lambda }}_{34}\mathsf{·}{\mathrm{Q}}_3\left(\mathrm{t}\right)$$

(5)

$${{\mathrm{Q}}^{\prime }}_5\left(\mathrm{t}\right)={\mathsf{\lambda }}_{15}\mathsf{·}{\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)-{\mathsf{\mu }}_{51}\mathsf{·}{\mathrm{Q}}_5\left(\mathrm{t}\right)+{\mathsf{\lambda }}_{45}\mathsf{·}{\mathrm{Q}}_4\left(\mathrm{t}\right)$$

(6)

Assuming baseline conditions:

$${\mathrm{R}}_{\mathrm{o}}\left(0\right)=1$$

(7)

$${\mathrm{Q}}_2\left(0\right)={\mathrm{Q}}_3\left(0\right)={\mathrm{Q}}_4\left(0\right)={\mathrm{Q}}_5\left(0\right)=0$$

(8)

Applying the Laplace transform, the following system of linear equations was obtained:

$$\begin{gathered} \mathrm{s}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)-1=-{\mathsf{\lambda }}_{12}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)+{\mathsf{\mu }}_{21}\mathsf{·}{\mathrm{Q}}^{*}{}_2\left(\mathrm{s}\right)-{\mathsf{\lambda }}_{13}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)+{\mathsf{\mu }}_{31}\mathsf{·}{\mathrm{Q}}^{*}{}_3\left(\mathrm{s}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\mathsf{\lambda }}_{14}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)+{\mathsf{\mu }}_{41}\mathsf{·}{\mathrm{Q}}^{*}{}_4\left(\mathrm{s}\right)-{\mathsf{\lambda }}_{15}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)+{\mathsf{\mu }}_{51}\mathsf{·}{\mathrm{Q}}^{*}{}_5\left(\mathrm{s}\right) \end{gathered}$$

(9)

$$\mathrm{s}\mathsf{·}{\mathrm{Q}}^{*}{}_2\left(\mathrm{s}\right)={\mathsf{\lambda }}_{12}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)-{\mathsf{\mu }}_{21}\mathsf{·}{\mathrm{Q}}^{*}{}_2\left(\mathrm{s}\right)-{\mathsf{\lambda }}_{23}\mathsf{·}{\mathrm{Q}}^{*}{}_2\left(\mathrm{s}\right)$$

(10)

$$\mathrm{s}\mathsf{·}{\mathrm{Q}}^{*}{}_3\left(\mathrm{s}\right)={\mathsf{\lambda }}_{13}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)-{\mathsf{\mu }}_{31}\mathsf{·}{\mathrm{Q}}^{*}{}_3\left(\mathrm{s}\right)-{\mathsf{\lambda }}_{34}\mathsf{·}{\mathrm{Q}}^{*}{}_3\left(\mathrm{s}\right)+{\mathsf{\lambda }}_{23}\mathsf{·}{\mathrm{Q}}^{*}{}_2\left(\mathrm{s}\right)$$

(11)

$$\mathrm{s}\mathsf{·}{\mathrm{Q}}^{*}{}_4\left(\mathrm{s}\right)={\mathsf{\lambda }}_{14}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)-{\mathsf{\mu }}_{41}\mathsf{·}{\mathrm{Q}}^{*}{}_4\left(\mathrm{s}\right)-{\mathsf{\lambda }}_{45}\mathsf{·}{\mathrm{Q}}^{*}{}_4\left(\mathrm{s}\right)+{\mathsf{\lambda }}_{34}\mathsf{·}{\mathrm{Q}}^{*}{}_3\left(\mathrm{s}\right)$$

(12)

$$\mathrm{s}\mathsf{·}{\mathrm{Q}}^{*}{}_5\left(\mathrm{s}\right)={\mathsf{\lambda }}_{15}\mathsf{·}{\mathrm{R}}^{*}{}_{\mathrm{o}}\left(\mathrm{s}\right)-{\mathsf{\mu }}_{51}\mathsf{·}{\mathrm{Q}}^{*}{}_5\left(\mathrm{s}\right)+{\mathsf{\lambda }}_{45}\mathsf{·}{\mathrm{Q}}^{*}{}_4\left(\mathrm{s}\right)$$

(13)

The probabilities of the operation of the monitoring system in the given operating states of the system are as follows:

$${\mathrm{R}}^{*}{}_{\mathrm{o}}(\mathrm{s})=\frac{({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot ({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})}{\begin{array}{c}({\mathsf{\lambda }}_{13}\cdot ({\mathsf{\lambda }}_{23}\cdot {\mathsf{\mu }}_{31}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+{\mathsf{\mu }}_{21}\cdot ({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot (\mathrm{s}\cdot {\mathsf{\mu }}_{41}+({\mathsf{\lambda }}_{45}+{\mathsf{\mu }}_{41})\cdot {\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot ({\mathsf{\lambda }}_{13}\cdot \\ \cdot ({\mathsf{\lambda }}_{34}\cdot {\mathsf{\lambda }}_{45}\cdot {\mathsf{\mu }}_{51}+{\mathsf{\lambda }}_{34}\cdot {\mathsf{\mu }}_{41}\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\mu }}_{31}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{14}\cdot (\mathrm{s}\cdot {\mathsf{\mu }}_{41}+({\mathsf{\lambda }}_{45}+{\mathsf{\mu }}_{41})\cdot {\mathsf{\mu }}_{51})+\\ +({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot ({\mathsf{\lambda }}_{15}\cdot {\mathsf{\mu }}_{51}-({\mathsf{\lambda }}_{12}+{\mathsf{\lambda }}_{13}+{\mathsf{\lambda }}_{14}+{\mathsf{\lambda }}_{15}+\mathrm{s})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})))))\end{array}}$$

(14)

$${\mathrm{Q}}^{*}{}_2(\mathrm{s})=\frac{({\mathsf{\lambda }}_{12}\cdot ({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51}))}{\begin{array}{c}(\mathrm{s}\cdot ({\mathsf{\lambda }}_{12}\cdot ({\mathsf{\lambda }}_{23}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot (({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot ({\mathsf{\lambda }}_{15}+\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{14}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+{\mathsf{\lambda }}_{13}\cdot (({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+{\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51})))))\end{array}}$$

(15)

$${\mathrm{Q}}^{*}{}_3(\mathrm{s})=\frac{(({\mathsf{\lambda }}_{12}\cdot {\mathsf{\lambda }}_{23}+{\mathsf{\lambda }}_{13}\cdot ({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21}))\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51}))}{\begin{array}{c}(\mathrm{s}\cdot ({\mathsf{\lambda }}_{12}\cdot ({\mathsf{\lambda }}_{23}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot (({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot ({\mathsf{\lambda }}_{15}+\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{14}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+{\mathsf{\lambda }}_{13}\cdot (({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+{\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51})))))\end{array}}$$

(16)

$${\mathrm{Q}}^{*}{}_4(\mathrm{s})=\frac{(({\mathsf{\lambda }}_{12}\cdot {\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot ({\mathsf{\lambda }}_{13}\cdot {\mathsf{\lambda }}_{34}+{\mathsf{\lambda }}_{14}\cdot ({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})))\cdot (\mathrm{s}+{\mathsf{\mu }}_{51}))}{\begin{array}{c}(\mathrm{s}\cdot ({\mathsf{\lambda }}_{12}\cdot ({\mathsf{\lambda }}_{23}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot (({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot ({\mathsf{\lambda }}_{15}+\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{14}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+{\mathsf{\mu }}_{13}\cdot (({\mathsf{\mu }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+{\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51})))))\end{array}}$$

(17)

$${\mathrm{Q}}^{*}{}_5(\mathrm{s})=\frac{({\mathsf{\lambda }}_{12}\cdot {\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot {\mathsf{\lambda }}_{45}+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot ({\mathsf{\lambda }}_{13}\cdot {\mathsf{\lambda }}_{34}\cdot {\mathsf{\lambda }}_{45}+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{14}\cdot {\mathsf{\lambda }}_{45}+{\mathsf{\lambda }}_{15}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41}))))}{\begin{array}{c}(\mathrm{s}\cdot ({\mathsf{\lambda }}_{12}\cdot ({\mathsf{\lambda }}_{23}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{23}\cdot {\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+({\mathsf{\lambda }}_{23}+\mathrm{s}+{\mathsf{\mu }}_{21})\cdot (({\mathsf{\lambda }}_{34}+\mathrm{s}+{\mathsf{\mu }}_{31})\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot ({\mathsf{\lambda }}_{15}+\mathrm{s}+{\mathsf{\mu }}_{51})+\\ +{\mathsf{\lambda }}_{14}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51}))+{\mathsf{\lambda }}_{13}\cdot (({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{41})\cdot (\mathrm{s}+{\mathsf{\mu }}_{51})+{\mathsf{\lambda }}_{34}\cdot ({\mathsf{\lambda }}_{45}+\mathrm{s}+{\mathsf{\mu }}_{51})))))\end{array}}$$

(18)

Computer simulation allowed the quick determination of the effect of changes in various reliability and operational indicators on the values of indicators describing the states of the analyzed UFW system. The intensity of the repairs and damages of the installation is assumed to be the one shown in

Table 1. System reliability parameters.

Parameter	Value [1/h]
λ12	0.00005
λ13	0.00004
λ14	0.00003
λ15	0.00000514
λ23	0.000031
λ34	0.000033
λ45	0.00000541
μ21	0.0279
μ31	0.0524
μ41	0.167
μ51	0.6

. The assumed values were calculated on the basis of [17,18,19,20].

By taking the Equations (13)–(18), using the inverse Laplace transform and the values in Table 1, we obtain the following probabilities of the test system present in the various states of work for the exponential distribution: the duration of the WFD system test—1 year (Figure 4):

t = 8760 [h]

(19)

• probability of the tested WFD system remaining in a state of full fitness (S₁) for a period of 1 year:

$${\mathrm{R}}_{\mathrm{o}}\left(\mathrm{t}\right)=0.998831$$

(20)

• probability of the tested WFD system remaining in a state of partial fitness (S₂) for a period of 1 year:

$${\mathrm{Q}}_2\left(\mathrm{t}\right)=0.0004794$$

(21)

• probability of the tested WFD system remaining in a state of partial fitness (S₃) for a period of 1 year:

$${\mathrm{Q}}_3\left(\mathrm{t}\right)=0.0004801$$

(22)

• probability of the tested WFD system remaining in a state of partial unfitness (S₄) for a period of 1 year:

$${\mathrm{Q}}_4\left(\mathrm{t}\right)=0.000199$$

(23)

• probability of the tested WFD system remaining in a state of full unfitness (S₅) for a period of 1 year:

$${\mathrm{Q}}_5\left(\mathrm{t}\right)=0.00000832$$

(24)

Assuming that the time of restoring the analyzed system to the state of full fitness (μ₅₁ = t₅₁ − 1 [h]) is confined within a limited range $({\mathrm{t}}_{51} \mathsf{ϵ} 12;178\left[\mathrm{h}\right])$. This means that within 1 to 7 days, it is probable that the analyzed WFD system will find itself in the state of full fitness, which is shown in Figure 5.

4. Discussion

The Reliability Function Simulation Test (R_o(t)) has yielded results from which the WFD system’s ability to perform the required tasks can be assessed. Obtaining these answers was the main purpose of this study. New to other such publications [50] is the acceptance of the five-state WFD model in research. In the work [51], models of the operation process have been accepted for testing in the form of two-, three- and four-state models. Based on the results obtained from this study (Figure 4 and Figure 5) it can be concluded that the five-state model of WFD most accurately represents the operation process of a wind farm. The conducted simulation test of the reliability function (R_o(t)) of the WFD was performed in two aspects:

-

The first was to examine the reliability function (R_o(t)) of the WFD in operation.

-

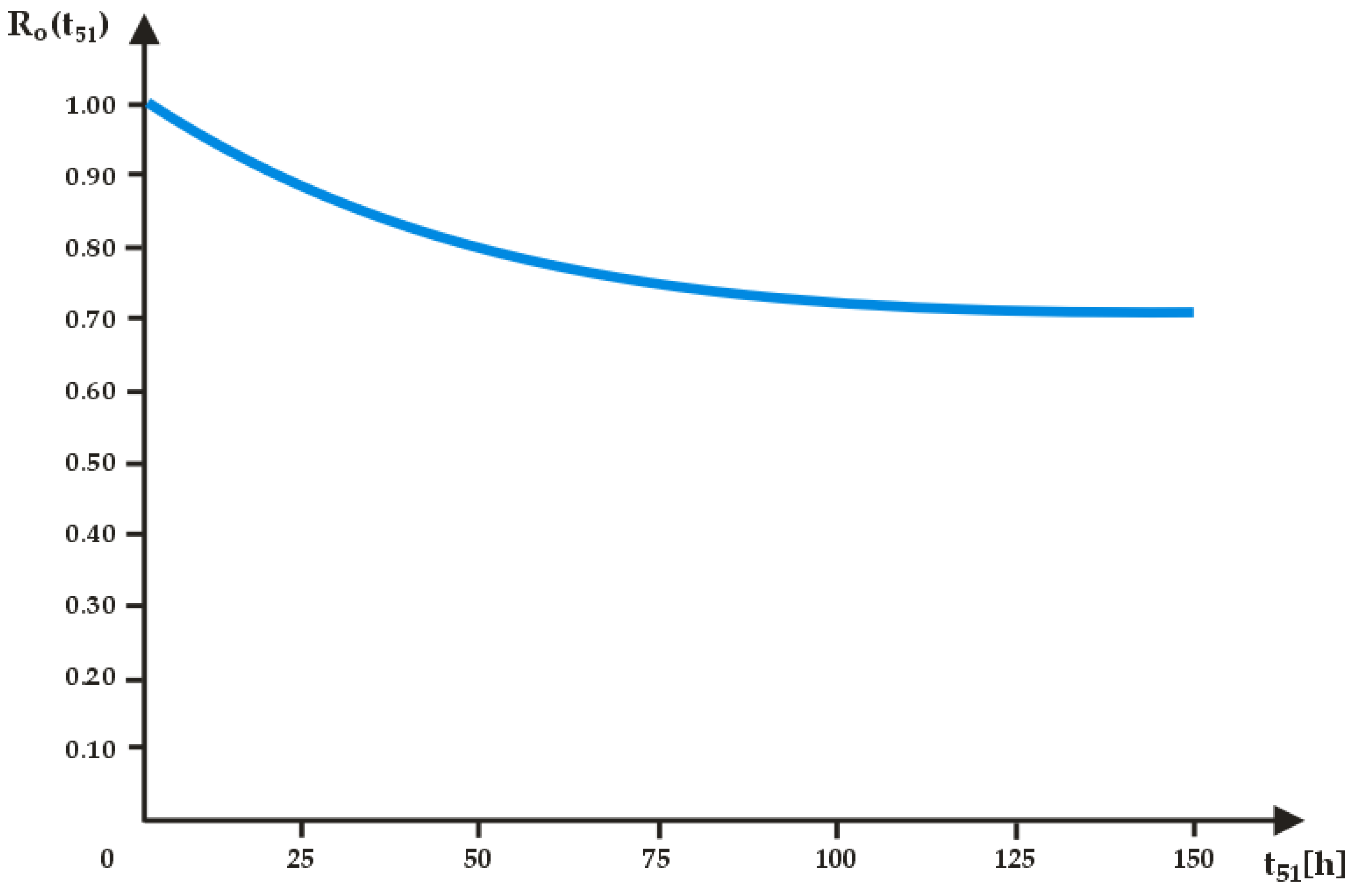
The second direction of the simulation study of the WFD was the time-flow current (t₅₁) of the residence of the WFD in the state (S₅) during the implementation of the essential technical and technological work renewing the WFD.

The basic simulation test of the WFD was the assessment of the reliability function (R_o(t)) in its operation. Results from this study are shown in Figure 4. An important assumption of simulation testing was the time (t) of the test to be performed at 1 year, corresponding to the time (t = 8760 [h]). Based on the graph of the reliability function (R_o(t)) of the WFD shown in Figure 1, it follows that for the operating life normalized at (t = 4000 [h]) the value of the reliability function is (R_o(t) = 0.84985). The value of the reliability function (R_o(t)) of the WFD is satisfactory. In practical interpretation, the value of the reliability function directly translates into the value of the required function (F_C) (Figure 1) determining the capacity of the WFD to perform its tasks, that is, to produce electricity. Thus, the value of the function required for WFD is (F_C = 0.84985 < 1). Its value is not unified, but it is satisfactory at a fairly high level.

The second major direction of the simulation study of WFD was the time-out (t₅₁) current in the presence of WFD in state (S₅) of its reliability level. In the state (S₅), WFDs are subject to the implementation of the essential periodic technical and technological works or “resurrection”, renewing WFD. This type of study is a publication novelty in comparison to other works [52]. The performed study of the effect of time changes (t₅₁) on the level of reliability function values (R_o(t₅₁)) is presented in (Figure 5). The assumed changes in the time (t₅₁) of the WFD in the state (S₅) result from the necessity to accomplish the important (main) goals of renewing the WFD. Thus, the implementation of periodic technical and technological renovations of the WFD is related to the time of their implementation. The simulation study assumes that the renovation activities performed are additionally increased by time (t = 0, 12 and 20 [h]). From the analysis, Figure 5 shows that the normalized value of the reliability function (R_o(t₅₁)) evaluated at (t = 100 [h]) is (R_o(t₅₁) = 0.8198). The completed simulation test regarding the effect of time changes (t₅₁) on the level of reliability function values (R_o(t₅₁)) is presented in Figure 4. From the analysis (Figure 4) it follows that:

• t₀ = 0 [h] value (R_o(t₅₁) = 0.7489),
• t₁ = 12 [h] value (R_o(t₅₁) = 0.6109),
• t₂ = 20 [h] value (R_o(t₅₁) = 0.4978).

This type of research results in the following practical conclusions for users of WFD:

-

the duration of the WFD in the state (S₅) should be reduced by increasing the efficiency and quality of technical and technological work, thus renewing the WFD.

-

modern technical solutions, such as smart expert systems, e.g., SERV, which significantly change the organization of technical and technological works renewing WFD in (S₅), are beneficial.

-

new strategies (policies) for the organization of technical and technological works to renew WFD should be developed to improve the technical abilities of personnel serving WFD.

5. Conclusions

The aim presented in this paper was to study the reliability properties of wind farm equipment during its operation, which is a difficult organizational and technical task. The difficulty of this result is also due to the acquisition of input data for the study. The numerical data describing the process of exploitation of the WFD were obtained through research conducted over a long period of time. It was assumed that the observation time (measurement of downtime, service life, etc.) would be sufficient for a period of one year. In turn, the reliability testing of wind farm equipment was conducted as a simulation test. This type of testing requires the knowledge and description of the actual operation process of WFD and the identification of reliable test input data. At the core of each study is a good test plan (how to test and when to test) of the WFD. The basis of the simulation research of the exploitation process of the WFD is the developed model of the exploitation process organization. Therefore, a model of the operational process of wind farm equipment was developed, which is known as the four-stage model in the literature.