Variable Incremental Controller of Permanent-Magnet Synchronous Motor for Voltage-Based Flux-Weakening Control
Abstract
:1. Introduction
2. Analysis of the Application of Voltage-Based Flux-Weakening Control According to the Controller
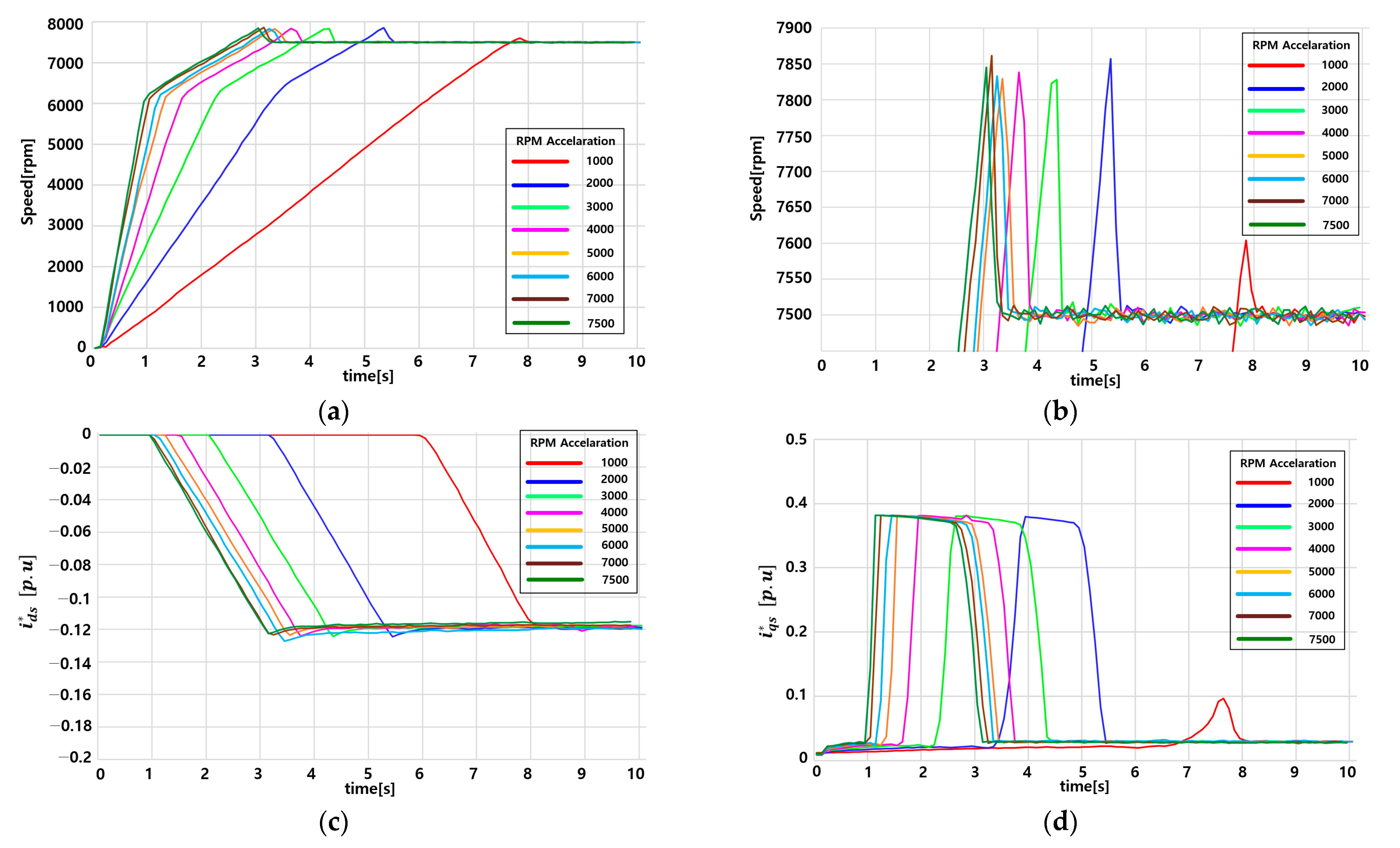
2.1. Application of Voltage-Based Flux-Weakening Control Using a PI Controller
2.2. Voltage-Based Flux-Weakening Control Using Variable Incremental Controller
3. Voltage-Based Flux-Weakening Control Applied with the Proposed Variable Incremental Controller
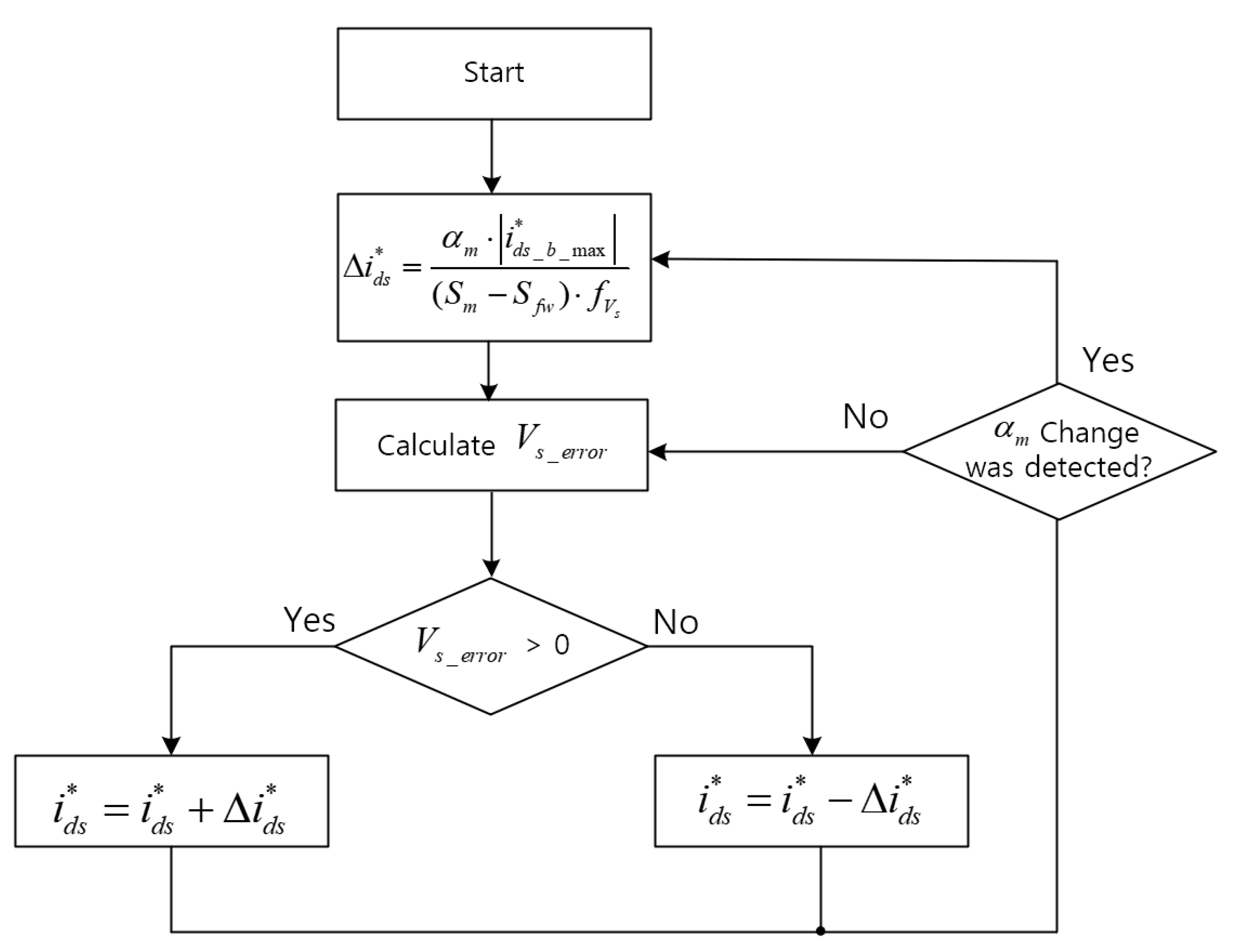
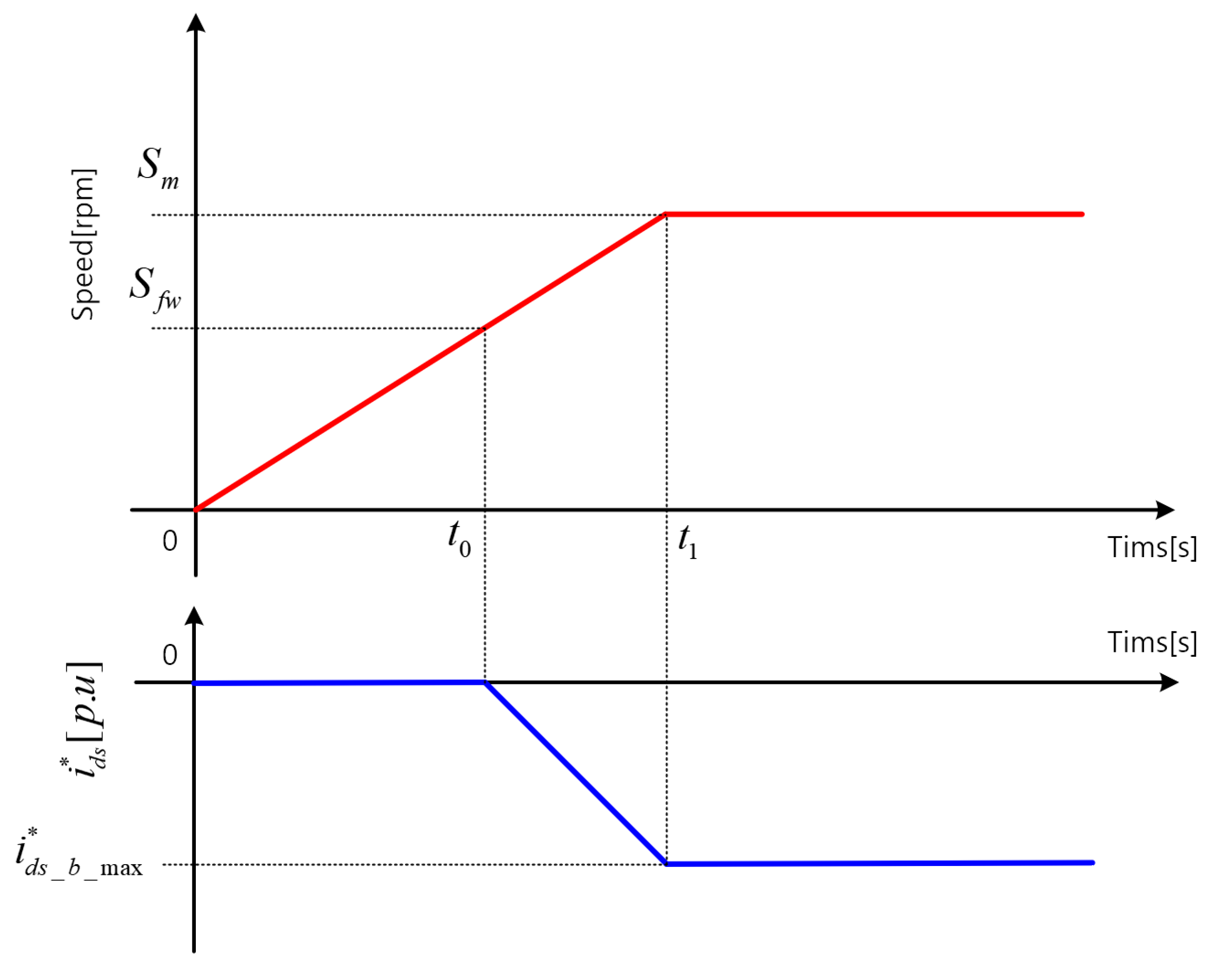
3.1. Derivation of
- (p.u.)—Normalized maximum d-axis current;
- (rpm)—Maximum motor speed;
- (rpm)—Flux-weakening start speed;
- (Hz)—Motor acceleration;
- (Hz)—Calculation period.
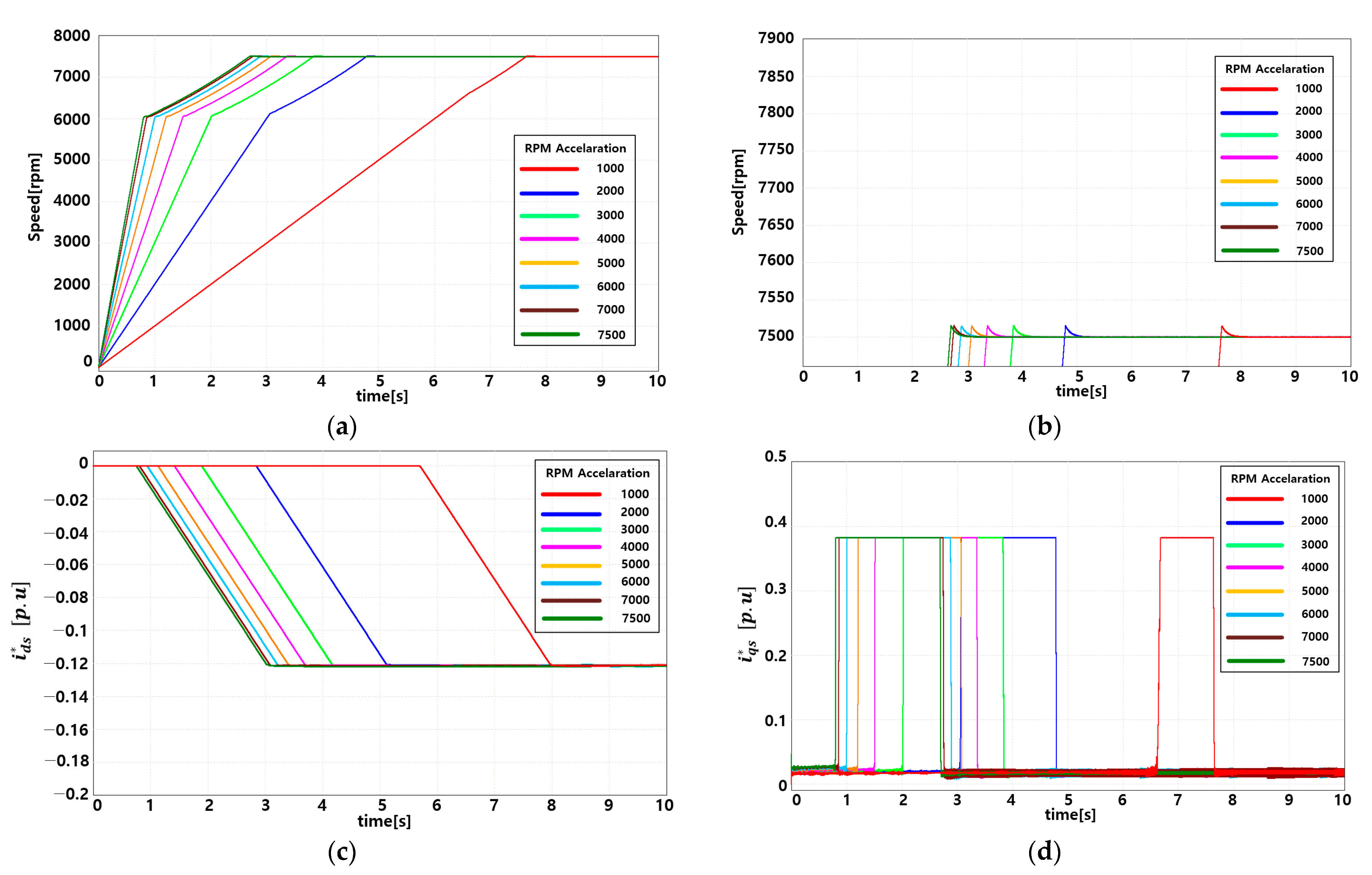
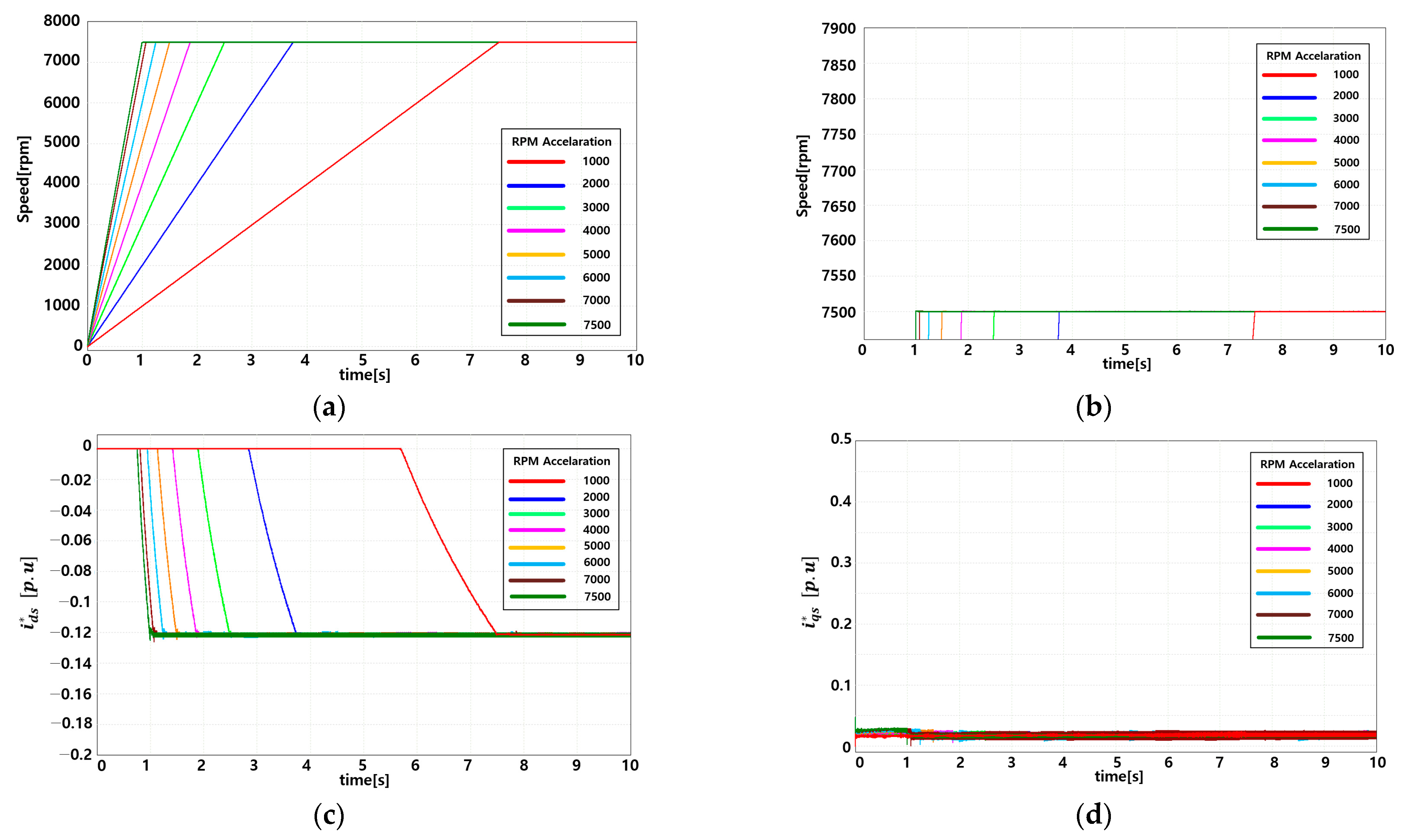
3.2. Simulation of Voltage-Feedback-Based Flux-Weakening Control Applied with the Proposed Variable Incremental Controller
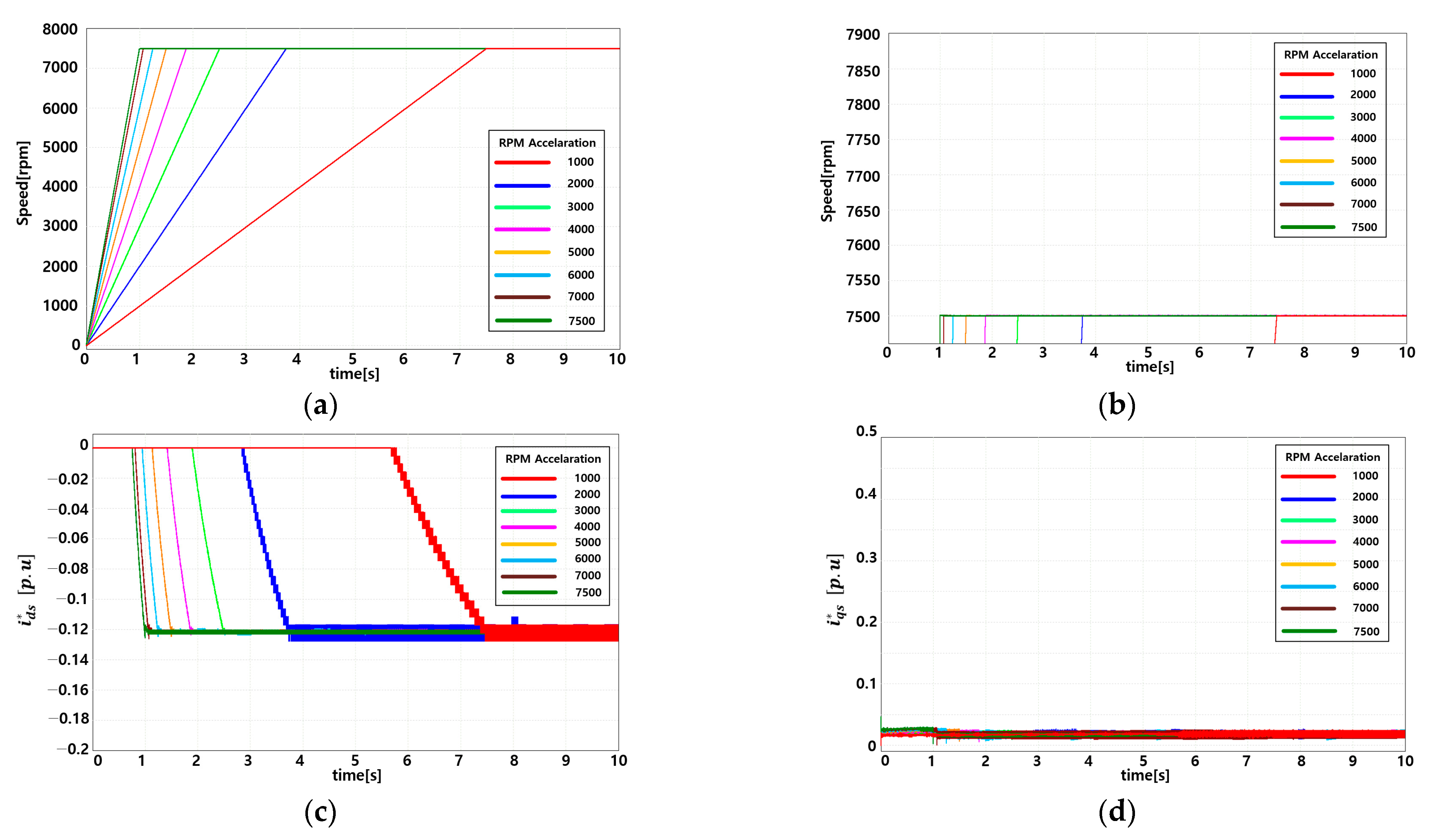
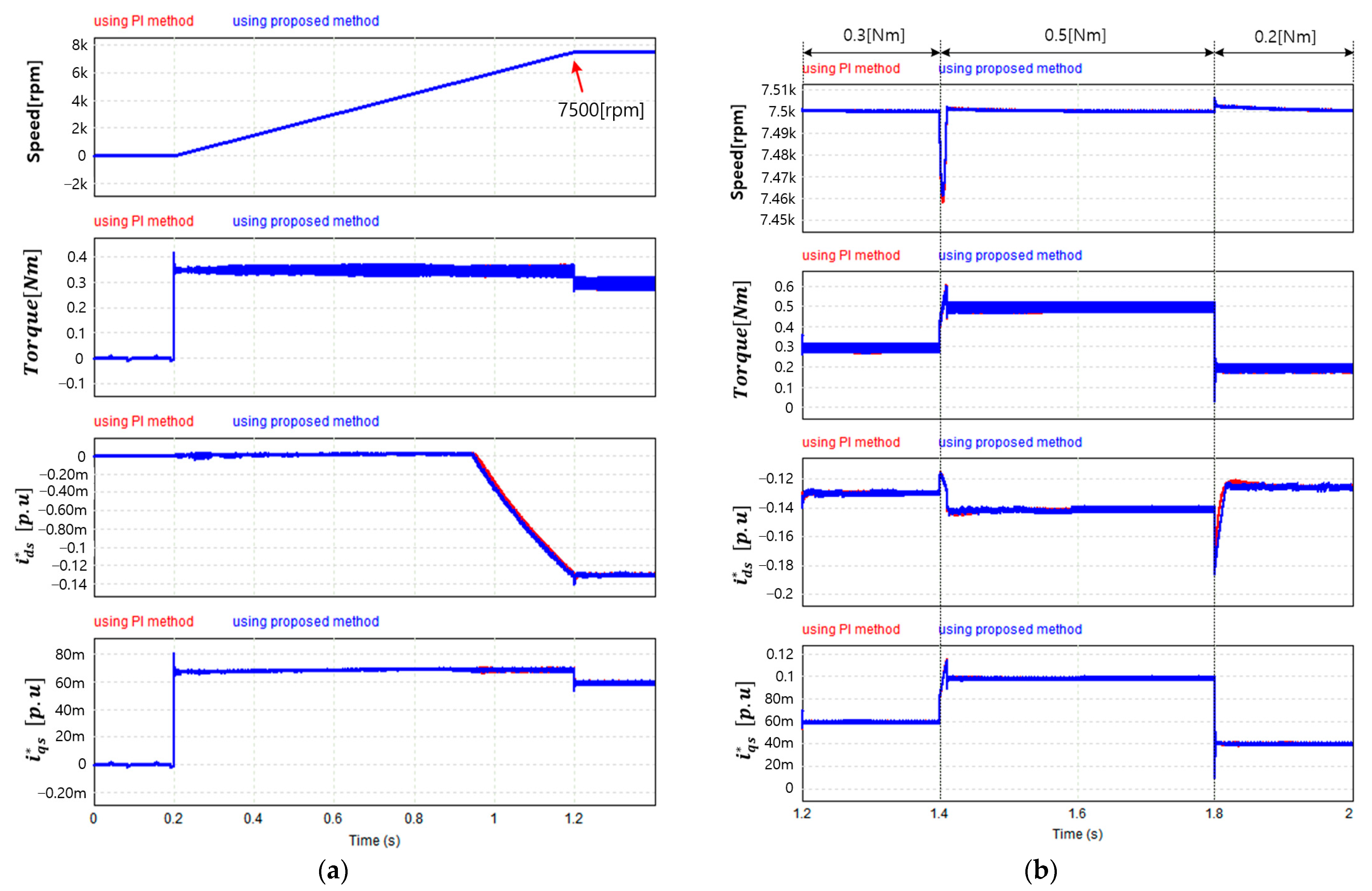
4. Experiment and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- The Government of the Republic of Korea. 2050 Carbon Neutral Strategy of the Republic of Korea towards a Sustainable and Green Society; The Government of the Republic of Korea: Seoul, Korea, 2020; pp. 16–17.
- Sustainable Development Solutions Network. America’s Zero Carbon Action Plan; Sustainable Development Solutions Network: New York, NY, USA, 2020; p. 27. [Google Scholar]
- Hasoun, M.; El Afia, A.; Chikh, K.; Khafallah, M.; Benkirane, K. A PWM Strategy for Dual Three-Phase PMSM Using 12-Sector Vector Space Decomposition for Electric Ship Propulsion. In Proceedings of the 19th IEEE MELECON, Marrakech, Morocco, 2–7 May 2018; pp. 243–248. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S.S. A Simplified Space Vector Pulse Width Modulation Implementation in Modular Multilevel Converters for Electric Ship Propulsion Systems. IEEE Trans. Trans. Elect. 2019, 5, 335–342. [Google Scholar] [CrossRef]
- Sieklucki, G. Optimization of Powertrain in EV. Energies 2021, 14, 725. [Google Scholar] [CrossRef]
- Stanescu, A.; Mocioi, N.; Dimitrescu, A. Hybrid Propulsion Train with Energy Storage in Metal Hydrides. In Proceedings of the Electric Vehicles International Conference (EV), Bucharest, Romania, 3–4 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Yao, M.; Qin, D.; Zhou, X.; Zhan, S.; Zeng, Y. Integrated optimal control of transmission ratio and power split ratio for a CVT-based plug-in hybrid electric vehicle. Mech. Mach. Theory 2019, 136, 52–71. [Google Scholar] [CrossRef]
- Pillay, P.; Knshnan, R. Modeling of Permanent Magnet Motor Drives. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef] [Green Version]
- Tong, W.; Dai, S.; Wu, S.; Tang, R. Performance Comparison Between an Amorphous Metal PMSM and a Silicon Steel PMSM. IEEE Trans. Magn. 2019, 55, 8102705. [Google Scholar] [CrossRef]
- Fang, S.; Liu, H.; Wang, H.; Yang, H.; Lin, H. High Power Density PMSM with Lightweight Structure and High-Performance Soft Magnetic Alloy Core. IEEE Trans. Appl. Supercond. 2019, 29, 0602805. [Google Scholar] [CrossRef]
- Fan, W.J.; Zhu, X.Y.; Quan, L.; Wu, W.Y.; Xu, L.; Liu, Y.F. Flux-Weakening Capability Enhancement Design and Optimization of a Controllable Leakage Flux Multilayer Barrier PM Motor. Trans. Ind. Electron. 2021, 68, 7814–7825. [Google Scholar] [CrossRef]
- Jeong, M.T.; Lee, K.B.; Pyo, H.Y.; Nam, D.W.; Kim, W.H. A Study on the Shape of the Rotor to Improve the Performance of the Spoke-Type Permanent Magnet Synchronous Motor. Energies 2021, 14, 3785. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-speed electrical machines: Technologies, trends, and developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Ahn, J.H.; Han, C.; Kim, C.W.; Choi, J.Y. Rotor design of high-speed permanent magnet synchronous motors considering rotor magnet and sleeve materials. IEEE Trans. Appl. Supercond. 2018, 28, 5201504. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Huang, X.Y.; Wang, J.; Niu, F.; Zhang, J.; Fang, Y.T.; Wu, L.J. Improved Flux-Weakening Control of IPMSMs Based on Torque Feedforward Technique. IEEE Trans. Power. Electron. 2018, 33, 10970–10978. [Google Scholar] [CrossRef]
- Deng, T.; Su, Z.H.; Li, J.Y.; Tang, P.; Chen, X.; Liu, P. Advanced Angle Field Weakening Control Strategy of Permanent Magnet Synchronous Motor. IEEE Trans. Veh. Technol. 2019, 68, 3424–3435. [Google Scholar] [CrossRef]
- Zhang, X.A.; Foo, G.H.B.; Rahman, M.F. A Robust Field-Weakening Approach for Direct Torque and Flux Controlled Reluctance Synchronous Motors with Extended Constant Power Speed Region. IEEE Trans. Ind. Electron. 2020, 67, 1813–1823. [Google Scholar] [CrossRef]
- Xu, X.; Novotny, D.W. Selecting the flux reference for induction machine drives in the field weakening region. IEEE Trans. Ind. Appl. 1992, 28, 1353–1358. [Google Scholar] [CrossRef]
- Kim, S.H.; Sul, S.K. Maximum Torque Control of an Induction Machine in the Field Weakening Region. IEEE Trans. Ind. Appl. 1995, 31, 787–794. [Google Scholar] [CrossRef]
- Ye, M.T.; Shi, T.N.; Wang, H.M.; Li, X.M.; Xia, C.L. Sensorless-MTPA Control of Permanent Magnet Synchronous Motor Based on an Adaptive Sliding Mode Observer. Energies 2019, 12, 3773. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.Z.; Sun, D.; Zheng, Z.H.; Nian, H. A Novel Lookup Table Based Direct Torque Control for OW-PMSM Drives. IEEE Trans. Ind. Electron. 2021, 68, 10316–10320. [Google Scholar] [CrossRef]
- Lee, D.Y.; Lee, J.H. Compensation of Interpolation Error for Look-Up Table-Based PMSM Control Method in Maximum Power Control. Energies 2021, 14, 5526. [Google Scholar] [CrossRef]
- Lee, D.Y.; Lee, J.H. Low Cost Simple Look-Up Table-Based PMSM Drive Considering DC-Link Voltage Variation. Energies 2020, 13, 3904. [Google Scholar] [CrossRef]
- Jacob, J.; Bottesi, O.; Calligaro, S.; Petrella, R. Design Criteria for Flux-Weakening Control Bandwidth and Voltage Margin in IPMSM Drives Considering Transient Conditions. IEEE Trans. Ind. Appl. 2021, 57, 4884–4900. [Google Scholar] [CrossRef]
- Miguel-Espinar, C.; Heredero-Peris, D.; Gross, G.; Llonch-Masachs, M.; Montesinos-Miracle, D. Maximum Torque per Voltage Flux-Weakening Strategy with Speed Limiter for PMSM Drives. IEEE Trans. Ind. Electron. 2021, 68, 9254–9264. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. MTPV Flux-Weakening Strategy for PMSM High Speed Drive. IEEE Trans. Ind. Appl. 2018, 54, 6081–6089. [Google Scholar] [CrossRef]
- Dong, Z.; Yu, Y.; Li, W.; Wang, B.; Xu, D. Flux-Weakening Control for Induction Motor in Voltage Extension Region: Torque Analysis and Dynamic Performance Improvement. IEEE Trans. Ind. Electron. 2018, 65, 3740–3751. [Google Scholar] [CrossRef]
- Lee, H.J.; Shon, J.G. Improved Voltage Flux-weakening Strategy of Permanent Magnet Synchronous Motor in High-speed Operation. Energies 2021, 14, 7464. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Jiang, H.; Jiang, D. Adaptive PI Parameter of Flux-Weakening Controller Based on Voltage Feedback for Model Predictive Control of SPMSM. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 2674–2681. [Google Scholar] [CrossRef]
- Kim, S.H.; Sul, S.K. Voltage Control Strategy for Maximum Torque Operation of an Induction Machine in the Field-Weakening Region. IEEE Trans. Ind. Electron. 1997, 44, 512–518. [Google Scholar] [CrossRef]





| Device | Parameter | Unit | Value |
|---|---|---|---|
| Inverter | DC-LINK voltage | (V) | 290 |
| Max current | (A) | 3.82 | |
| Switching frequency | (Hz) | 20,000 | |
| Motor | Back EMP(Ke) | (Vpk/krpm) | 49 |
| Number of poles | (P) | 8 | |
| Resistance | (Ω) | 2.2 | |
| Inductance | (H) | 0.0109 | |
| Inertia | (oz-in-s2) | 0.00439 |
| RPM Reference (rpm) | RPM Acceleration (rpmps) | |||
|---|---|---|---|---|
| 7500 | 1000 | |||
| 2000 | ||||
| 3000 | ||||
| 4000 | ||||
| 5000 | ||||
| 6000 | ||||
| 7000 | ||||
| 7500 |
| (Unit) | ||||
|---|---|---|---|---|
| 2.672 × 10−4 | 5.34 × 10−5 | 1.068 × 10−4 | ||
| Speed Arrival Time | (s) | 4.78 | 3.75 | 3.75 |
| Speed max. Overshoot | (rpm) | 7515 | 7500 | 7500 |
| ripple | (p.u.) | 0.000053 | 0.0106 | 0.000641 |
| (p.u.) | 0.381 | 0.0271 | 0.0243 | |
| ripple | (p.u.) | 0.00647 | 0.0165 | 0.0065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Lee, G.; Kim, G.; Shon, J. Variable Incremental Controller of Permanent-Magnet Synchronous Motor for Voltage-Based Flux-Weakening Control. Energies 2022, 15, 5733. https://doi.org/10.3390/en15155733
Lee H, Lee G, Kim G, Shon J. Variable Incremental Controller of Permanent-Magnet Synchronous Motor for Voltage-Based Flux-Weakening Control. Energies. 2022; 15(15):5733. https://doi.org/10.3390/en15155733
Chicago/Turabian StyleLee, Hyunjae, Gunbok Lee, Gildong Kim, and Jingeun Shon. 2022. "Variable Incremental Controller of Permanent-Magnet Synchronous Motor for Voltage-Based Flux-Weakening Control" Energies 15, no. 15: 5733. https://doi.org/10.3390/en15155733







