Potential Benefits for Residential Building with Photovoltaic Battery System Participation in Peer-to-Peer Energy Trading
Abstract
:1. Introduction
- A P2P energy trading model is developed; the trading framework includes a FiT scheme for the retail market and a discriminatory CDA trading mechanism for the P2P energy trading coordinator.
- A SBEMS is proposed to realize rolling optimal energy scheduling while determining energy bids. With respect to the previous works of the energy-management systems, this method integrates two strategies for enhancing participation in the P2P market.
- Simulations of the competition between prosumers on the local P2P market are examined using three strategic combinations under an imposed dynamic retail price. A discussion of the potential benefits of residential prosumers who have installed a PV battery system participating in P2P energy trading systems is evaluated using five indices.
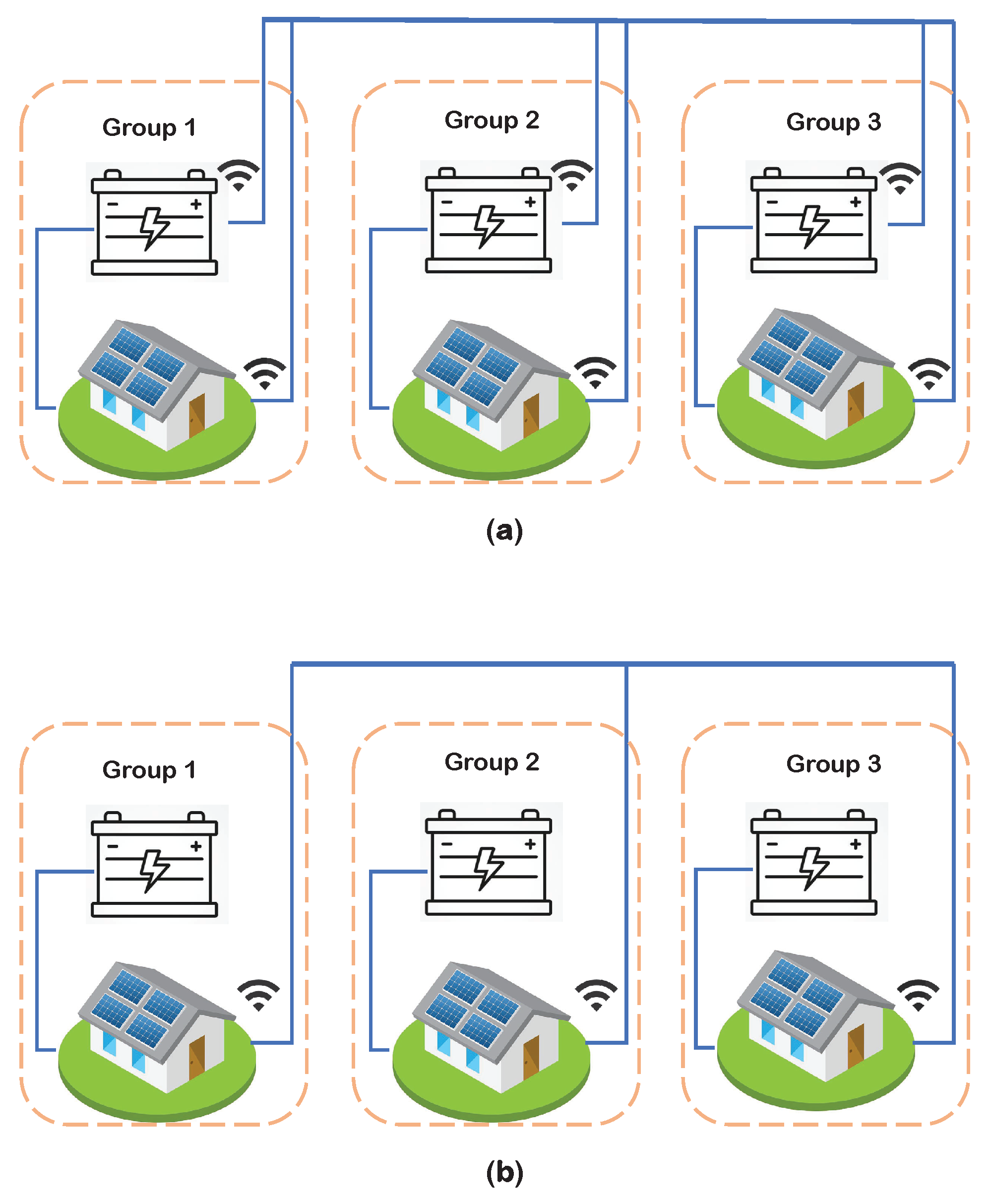
2. P2P Trading Scheme Description
2.1. P2P Trading Framework
2.2. CDA Transaction Formulation
| Algorithm 1:The transaction algorithm of t. |
Input: Output: clearing price , Transaction quantity |
|
3. Separate Bidding Energy-Management System Model
3.1. Battery Constraints
3.2. Energy Balance Constraints
3.3. Controllable Device Bidding Strategy
3.4. Uncontrollable Device Bidding Strategy
3.5. Bidding Constrains
4. Case Studies
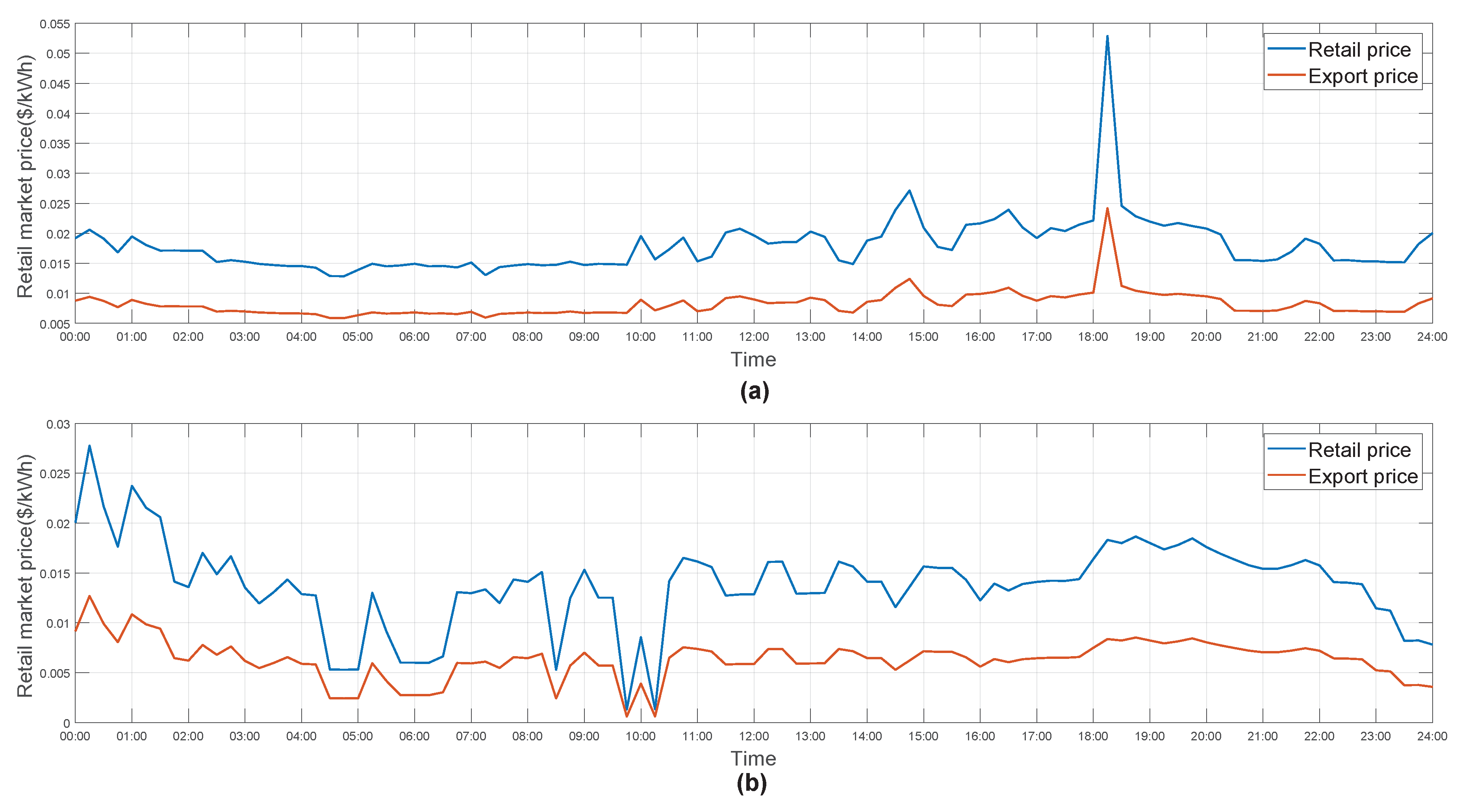
4.1. Simulation Platform and Data
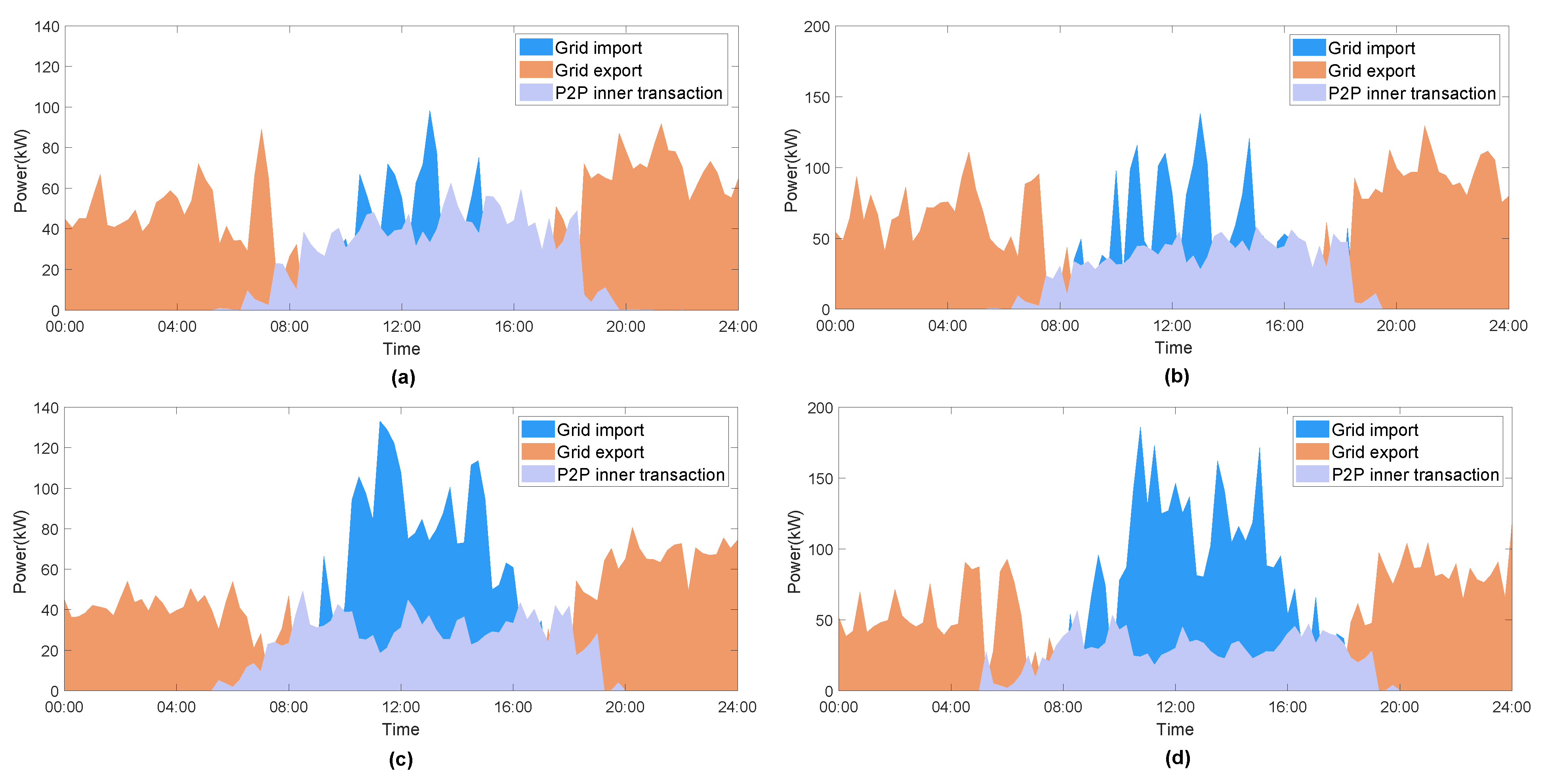
4.2. Local P2P Energy Transaction Results
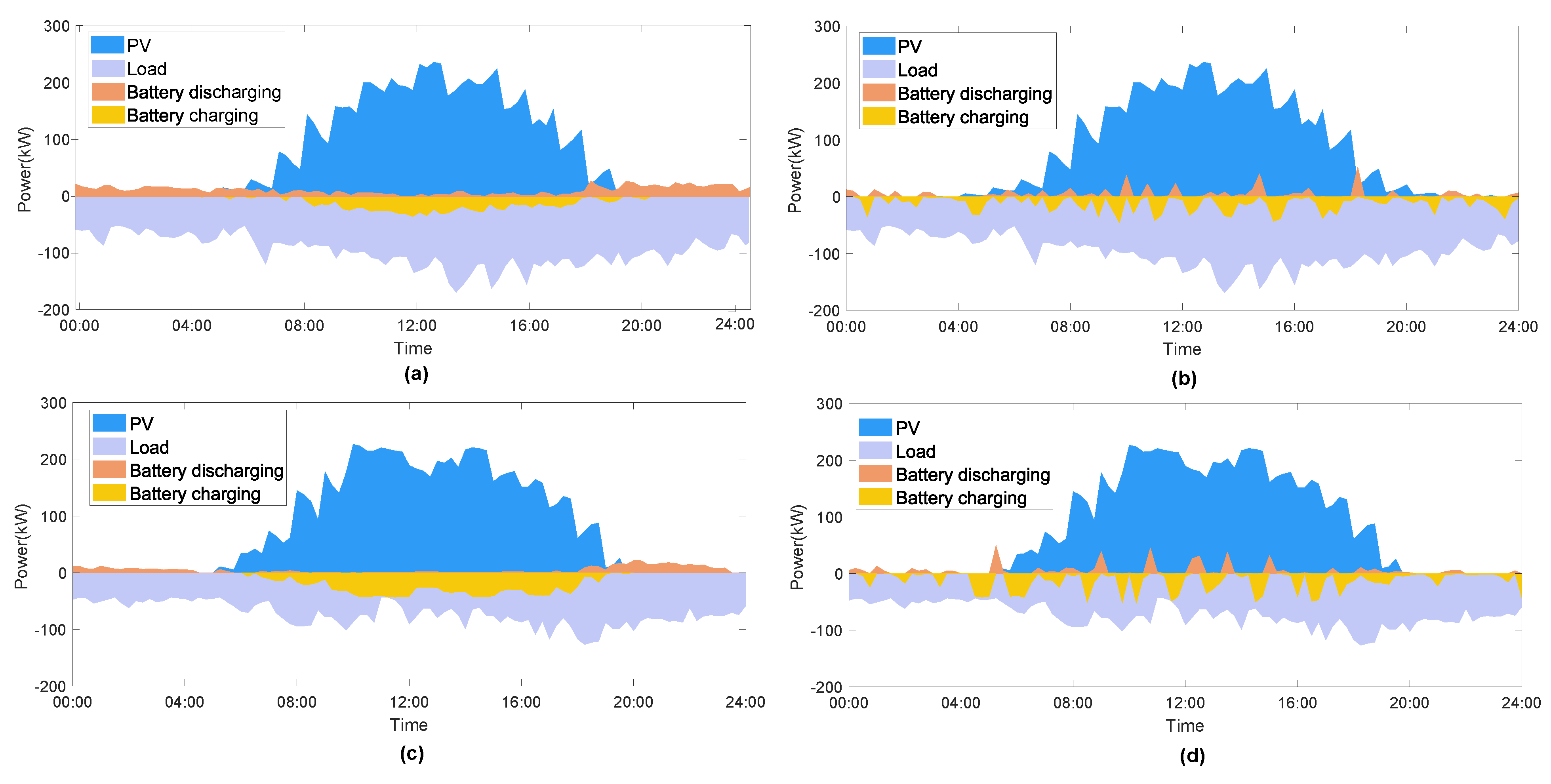
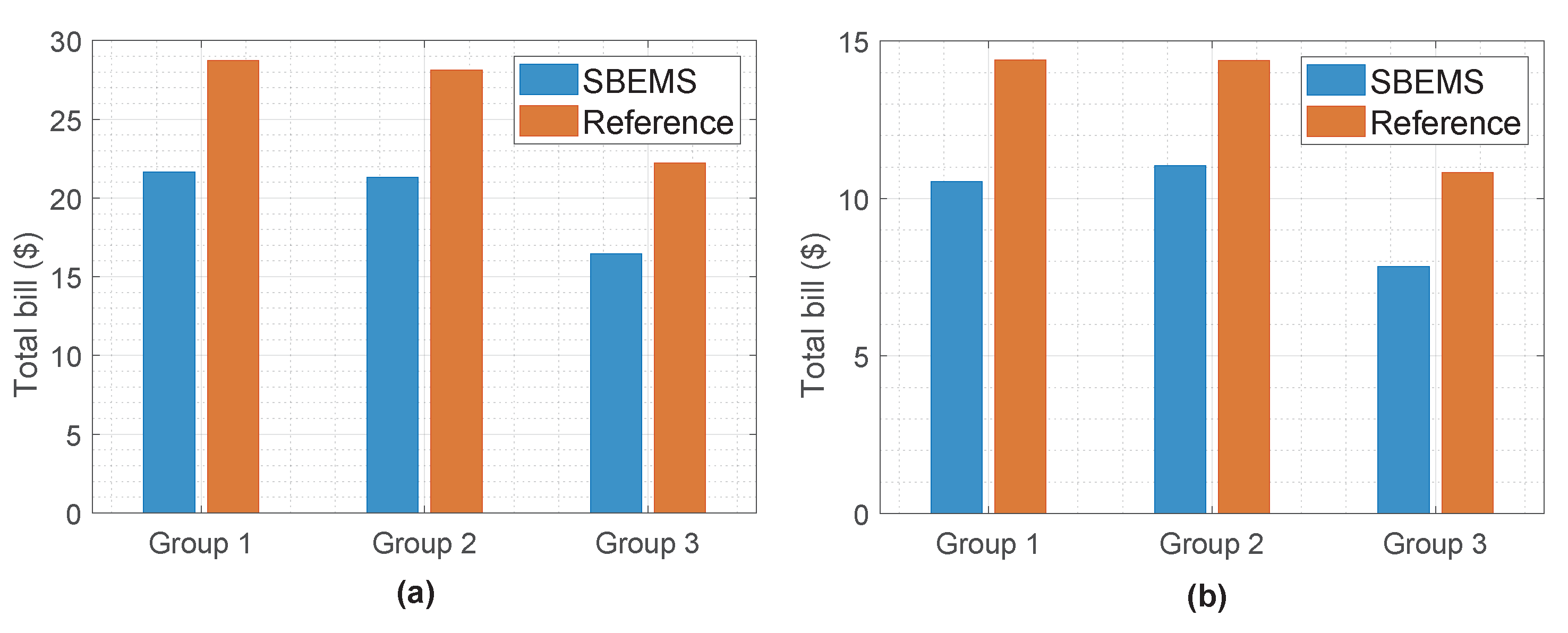
4.3. Energy Analysis
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| t | Index to refer to the tth trading time unit |
| Trading time horizon | |
| Order book buy, contains all buyers at t | |
| Order book sell, contains all sellers at t | |
| Total benefit of a prosumer at t | |
| Profit from battery discharging at t | |
| Profit from selling energy in P2P market at t | |
| Profit from PV surplus supplementing demand at t | |
| Battery charging cost at t | |
| Cost of energy purchased from P2P market at t | |
| Clearing price of buyer i order k with seller order n | |
| Order price of buyer i | |
| Order k quantity of buyer i | |
| Order price of seller j | |
| Order n quantity of seller | |
| k | Order number of buyer |
| n | Order number of seller |
| Export price | |
| Battery operating cost | |
| Battery charging from | |
| Battery charging from P2P market | |
| Retail price | |
| Battery charging from utility grid | |
| Battery bidding price for buyer | |
| Battery discharging for utility grid | |
| Battery bidding price for seller | |
| Battery discharging for market | |
| Uncontrolled energy bidding price for buyer | |
| Energy selling to P2P market | |
| Uncontrolled energy bidding price for seller | |
| Energy buying from P2P market | |
| Minimum limitation of battery discharging | |
| Maximum limitation of battery discharging | |
| Minimum limitation of battery charging | |
| Maximum limitation of battery charging | |
| State of charge of the battery at t | |
| Minimum allowable state of charge | |
| Maximum allowable state of charge | |
| Charging efficiency of battery | |
| Discharging efficiency of battery | |
| Energy sold to P2P market from PV | |
| Maximum energy produced by PV at t | |
| Demand at t | |
| Probability of success in buying | |
| Probability of success in selling | |
| Random value | |
| Weight parameter of deal i | |
| Target price | |
| Limit price for buyer | |
| Limit price for seller | |
| r | Aggressiveness degree |
| Learning parameter | |
| The normalized standard deviation value | |
| Varies parameter | |
| Current target price in AA strategy | |
| r | Current degree of aggressiveness |
| Preference value of battery bidding |
References
- Net Generation by Energy Source: Residential Sector, 2014-April 2020; U.S. Energy Information Administration: Washington, DC, USA, 2020.
- Form EIA-861M Detailed Data Net Metering; U.S. Energy Information Administration: Washington, DC, USA, 2020. Available online: https://www.eia.gov/electricity/data/eia861m/xls/net_metering2020.xlsx (accessed on 2 January 2021).
- Askeland, M.; Backe, S.; Bjarghov, S.; Lindberg, K.B.; Korpås, M. Activating the potential of decentralized flexibility and energy resources to increase the EV hosting capacity: A case study of a multi-stakeholder local electricity system in Norway. Smart Energy 2021, 3, 100034. [Google Scholar] [CrossRef]
- Toquica, D.; Agbossou, K.; Henao, N.; Malhamé, R.; Kelouwani, S.; Amara, F. Prevision and planning for residential agents in a transactive energy environment. Smart Energy 2021, 2, 100019. [Google Scholar] [CrossRef]
- Yang, J.; Dong, Z.Y.; Wen, F.; Chen, Q.; Luo, F.; Liu, W.; Zhan, J. A Penalty Scheme for Mitigating Uninstructed Deviation of Generation Outputs From Variable Renewables in a Distribution Market. IEEE Trans. Smart Grid 2020, 11, 4056–4069. [Google Scholar] [CrossRef]
- Wen, H.; Du, Y.; Chen, X.; Lim, E.; Wen, H.; Jiang, L.; Xiang, W. Deep Learning Based Multistep Solar Forecasting for PV Ramp-Rate Control Using Sky Images. IEEE Trans. Ind. Inform. 2021, 17, 1397–1406. [Google Scholar] [CrossRef]
- Javadi, M.S.; Gough, M.; Lotfi, M.; Esmaeel Nezhad, A.; Santos, S.F.; Catalão, J.P.S. Optimal self-scheduling of home energy-management system in the presence of photovoltaic power generation and batteries. Energy 2020, 210, 118568. [Google Scholar] [CrossRef]
- Morstyn, T.; Teytelboym, A.; Hepburn, C.; McCulloch, M.D. Integrating P2P Energy Trading With Probabilistic Distribution Locational Marginal Pricing. IEEE Trans. Smart Grid 2020, 11, 3095–3106. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Wen, H.; Jiang, L.; Xiao, W. Forecasting-Based Power Ramp-Rate Control Strategies for Utility-Scale PV Systems. IEEE Trans. Ind. Electron. 2019, 66, 1862–1871. [Google Scholar] [CrossRef]
- Chen, X.Y.; Du, Y.; Lim, E.; Wen, H.Q.; Yan, K.; Kirtley, J. Power ramp-rates of utility-scale PV systems under passing clouds: Module-level emulation with cloud shadow modeling. Appl. Energy 2020, 268, 114980. [Google Scholar] [CrossRef]
- Littlechild, S. Retail competition in electricity markets. Expectations, outcomes and economics. Energy Policy 2009, 37, 759–763. [Google Scholar] [CrossRef]
- Couture, T.D.; Cory, K.; Kreycik, C.; Williams, E. Policymaker’s Guide to Feed-in Tariff Policy Design; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; McCulloch, M.D.; Poor, H.V.; Wood, K.L. A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid. Appl. Energy 2019, 243, 10–20. [Google Scholar] [CrossRef]
- An, D.; Yang, Q.; Yu, W.; Yang, X.; Fu, X.; Zhao, W. SODA: Strategy-Proof Online Double Auction Scheme for Multimicrogrids Bidding. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 48, 1177–1190. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.; Poor, H.V.; Wood, K.L. Transforming Energy Networks via Peer-to-Peer Energy Trading The potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Xu, Z.Y.; Wang, N.; Lyu, X.Y.; Xu, W.S. “Peer-to-Peer Plus” Electricity Transaction within Community of Active Energy Agents Regarding Distribution Network Constraints. Energies 2020, 13, 2408. [Google Scholar] [CrossRef]
- Luth, A.; Zepter, J.M.; del Granado, P.C.; Egging, R. Local electricity market designs for peer-to-peer trading: The role of battery flexibility. Appl. Energy 2018, 229, 1233–1243. [Google Scholar] [CrossRef] [Green Version]
- Neves, D.; Scott, I.; Silva, C.A. Peer-to-peer energy trading potential: An assessment for the residential sector under different technology and tariff availabilities. Energy 2020, 205, 118023. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhou, Y.; Jenkins, N. Peer-to-peer energy sharing through a two-stage aggregated battery control in a community Microgrid. Appl. Energy 2018, 226, 261–276. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Long, C.; Zhou, Y.; Wu, J. A game theoretic approach for Peer-to-Peer energy trading. Energy Procedia 2019, 159, 454–459. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power and Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Chen, K.X.; Lin, J.; Song, Y.H. Trading strategy optimization for a prosumer in continuous double auction based peer-to-peer market: A prediction-integration model. Appl. Energy 2019, 242, 1121–1133. [Google Scholar] [CrossRef]
- Faqiry, M.N.; Das, S. Double Auction With Hidden User Information: Application to Energy Transaction in Microgrid. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2326–2339. [Google Scholar] [CrossRef]
- Lin, J.; Pipattanasomporn, M.; Rahman, S. Comparative analysis of auction mechanisms and bidding strategies for P2P solar transactive energy markets. Appl. Energy 2019, 255. [Google Scholar] [CrossRef]
- Guerrero, J.; Sok, B.; Chapman, A.C.; Verbic, G. Electrical-distance driven peer-to-peer energy trading in a low-voltage network. Appl. Energy 2021, 287. [Google Scholar] [CrossRef]
- Li, Z.; Ma, T. Peer-to-peer electricity trading in grid-connected residential communities with household distributed photovoltaic. Appl. Energy 2020, 278, 115670. [Google Scholar] [CrossRef]
- Vytelingum, P.; Cliff, D.; Jennings, N.R. Strategic bidding in continuous double auctions. Artif. Intell. 2008, 172, 1700–1729. [Google Scholar] [CrossRef] [Green Version]
- Jian, W.; Wang, Q.; Zhou, N.; Yuan, C. A Novel Electricity Transaction Mode of Microgrids Based on Blockchain and Continuous Double Auction. Energies 2017, 10, 1971. [Google Scholar]
- Han, D.; Zhang, C.Z.H.; Ping, J.; Yan, Z. Smart contract architecture for decentralized energy trading and management based on blockchains. Energy 2020, 199, 117417. [Google Scholar] [CrossRef]
- Guerrero, J.; Chapman, A.C.; Verbic, G. Decentralized P2P Energy Trading Under Network Constraints in a Low-Voltage Network. IEEE Trans. Smart Grid 2019, 10, 5163–5173. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Xia, X.H. Techno-economic and environmental optimization of a household photovoltaic-battery hybrid power system within demand side management. Renew. Energy 2017, 108, 132–143. [Google Scholar] [CrossRef] [Green Version]
- Raziei, A.; Hallinan, K.P.; Brecha, R.J. Clean energy utility for multifamily housing in a deregulated energy market. Energy Build. 2016, 127, 806–817. [Google Scholar] [CrossRef]
- Pietila, A.; Beausoleil-Morrison, I.; Newsham, G.R. Zero peak housing: Exploring the possibility of eliminating electrical draws from houses during periods of high demand on the electrical grid. Build. Environ. 2012, 58, 103–113. [Google Scholar] [CrossRef]
- Müller, D.; Monti, A.; Stinner, S.; Schlösser, T.; Schütz, T.; Matthes, P.; Wolisz, H.; Molitor, C.; Harb, H.; Streblow, R. Demand side management for city districts. Build. Environ. 2015, 91, 283–293. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V.; Yang, Z. Energy Storage Sharing in Smart Grid: A Modified Auction-Based Approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Mo, Y.; Liu, H.; Zhang, Y. Operational flexibility enhancements using mobile energy storage in day-ahead electricity market by game-theoretic approach. Energy 2021, 232, 121008. [Google Scholar] [CrossRef]
- El-Baz, W.; Tzscheutschler, P.; Wagner, U. Integration of energy markets in microgrids: A double-sided auction with device-oriented bidding strategies. Appl. Energy 2019, 241, 625–639. [Google Scholar] [CrossRef]
- Rodrigues, D.L.; Ye, X.; Xia, X.; Zhu, B. Battery energy storage sizing optimisation for different ownership structures in a peer-to-peer energy sharing community. Appl. Energy 2020, 262, 114498. [Google Scholar] [CrossRef]
- Huang, H.; Nie, S.L.; Lin, J.; Wang, Y.Y.; Dong, J. Optimization of Peer-to-Peer Power Trading in a Microgrid with Distributed PV and Battery Energy Storage Systems. Sustainability 2020, 12, 923. [Google Scholar] [CrossRef] [Green Version]
- Alabdullatif, A.M.; Gerding, E.H.; Perez-Diaz, A. Market Design and Trading Strategies for Community Energy Markets with Storage and Renewable Supply. Energies 2020, 13, 31. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.R.; St-Hilaire, M.; Kunz, T. Peer-to-peer energy trading among smart homes. Appl. Energy 2019, 238, 1434–1443. [Google Scholar] [CrossRef]
- Ilic, D.; Silva, P.G.D.; Karnouskos, S.; Griesemer, M. An energy market for trading electricity in smart grid neighbourhoods. In Proceedings of the 2012 6th IEEE International Conference on Digital Ecosystems and Technologies (DEST), Campione d’Italia, Italy, 18–20 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Vytelingum, P.; Ramchurn, S.D.; Voice, T.D.; Rogers, A.; Jennings, N.R. Trading agents for the smart electricity grid. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 10–14 May 2010. [Google Scholar]
- ENERGY MARKET and OPERATIONAL DATA. Available online: https://www.nyiso.com/energy-market-operational-data (accessed on 2 January 2021).
- Pecanstreet Dataport. 2021. Available online: https://www.pecanstreet.org/dataport/ (accessed on 2 January 2021).

| Index | SBEMS | Reference | ||||
|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 3 | Group 1 | Group 2 | Group 3 | |
| Average clearing price weekday ($/kWh) | 0.0164 | 0.0162 | 0.0153 | 0.0168 | 0.0167 | 0.0156 |
| Average clearing price weekend ($/kWh) | 0.0119 | 0.0119 | 0.0113 | 0.0126 | 0.0127 | 0.0121 |
| Success rate weekday | 0.3240 | 0.4345 | 0.6826 | 0.3608 | 0.4947 | 0.7565 |
| Success rate weekend | 0.4166 | 0.4896 | 0.7765 | 0.4276 | 0.4868 | 0.8195 |
| Index | Case 1: SBEMS | Case 2: Reference | Conventional Paradigm: FiT Scheme | |||
|---|---|---|---|---|---|---|
| Weekday | Weekend | Weekday | Weekend | Weekday | Weekend | |
| Economic benefit index | 0.248 | 0.224 | 0.109 | 0.101 | 0 | 0 |
| Participation willingness index | 0.833 | 0.880 | 0.826 | 0.805 | 0.280 | 0.280 |
| Energy balance index | 0.668 | 0.545 | 0.486 | 0.428 | 0.287 | 0.197 |
| Power flatness index | 0.717 | 0.833 | 0.759 | 0.832 | ____ | ____ |
| Self-sufficiency index | 0.557 | 0.478 | 0.477 | 0.414 | 0.321 | 0.291 |
| Average value | 0.605 | 0.592 | 0.532 | 0.516 | 0.277 | 0.192 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Du, Y.; Chen, X.; Lim, E.G.; Jiang, L.; Yan, K. Potential Benefits for Residential Building with Photovoltaic Battery System Participation in Peer-to-Peer Energy Trading. Energies 2022, 15, 3913. https://doi.org/10.3390/en15113913
Zhang B, Du Y, Chen X, Lim EG, Jiang L, Yan K. Potential Benefits for Residential Building with Photovoltaic Battery System Participation in Peer-to-Peer Energy Trading. Energies. 2022; 15(11):3913. https://doi.org/10.3390/en15113913
Chicago/Turabian StyleZhang, Bidan, Yang Du, Xiaoyang Chen, Eng Gee Lim, Lin Jiang, and Ke Yan. 2022. "Potential Benefits for Residential Building with Photovoltaic Battery System Participation in Peer-to-Peer Energy Trading" Energies 15, no. 11: 3913. https://doi.org/10.3390/en15113913






