Discrete Wavelet Transform for the Real-Time Smoothing of Wind Turbine Power Using Li-Ion Batteries
Abstract
:1. Introduction
1.1. Objectives and Novel Contributions
1.2. Organization of the Study
2. Case Study
2.1. Grid Code Requirements
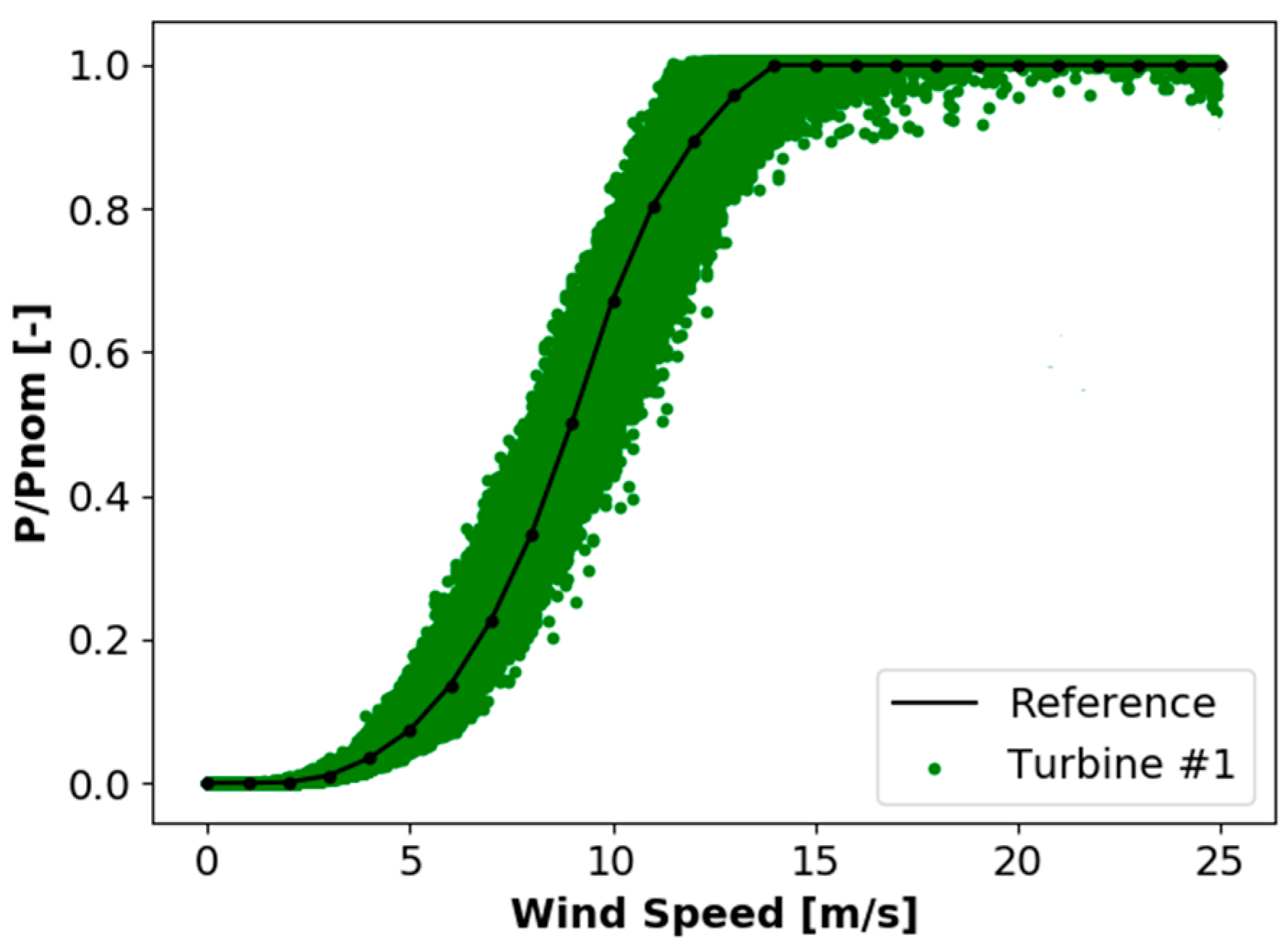
2.2. Case Study
3. Methodology
3.1. Discrete-Wavelet Based Signal Approximation
- Redundancy, since CWT is defined as a continuous integral, affecting considerably the calculation time;
- CWT is defined on an infinite number of wavelets identified by the scale and translation factors, which can assume infinite values;
- For most of the functions the wavelet transforms have no analytical solutions, and they can be calculated only numerically.
3.2. Wavelet-Based Smoothing Algorithm and ESS Model
3.2.1. DWT-Based Battery Operation Design Algorithm
3.2.2. DWT-Based Real-Time Battery Control
3.2.3. ESS Model
3.2.4. Effects of Battery Constraints on the Wavelet Smoothing Algorithm
3.3. Conventional Power-Smoothing Methods for Benchmarking
3.4. Cost Analysis
4. Results
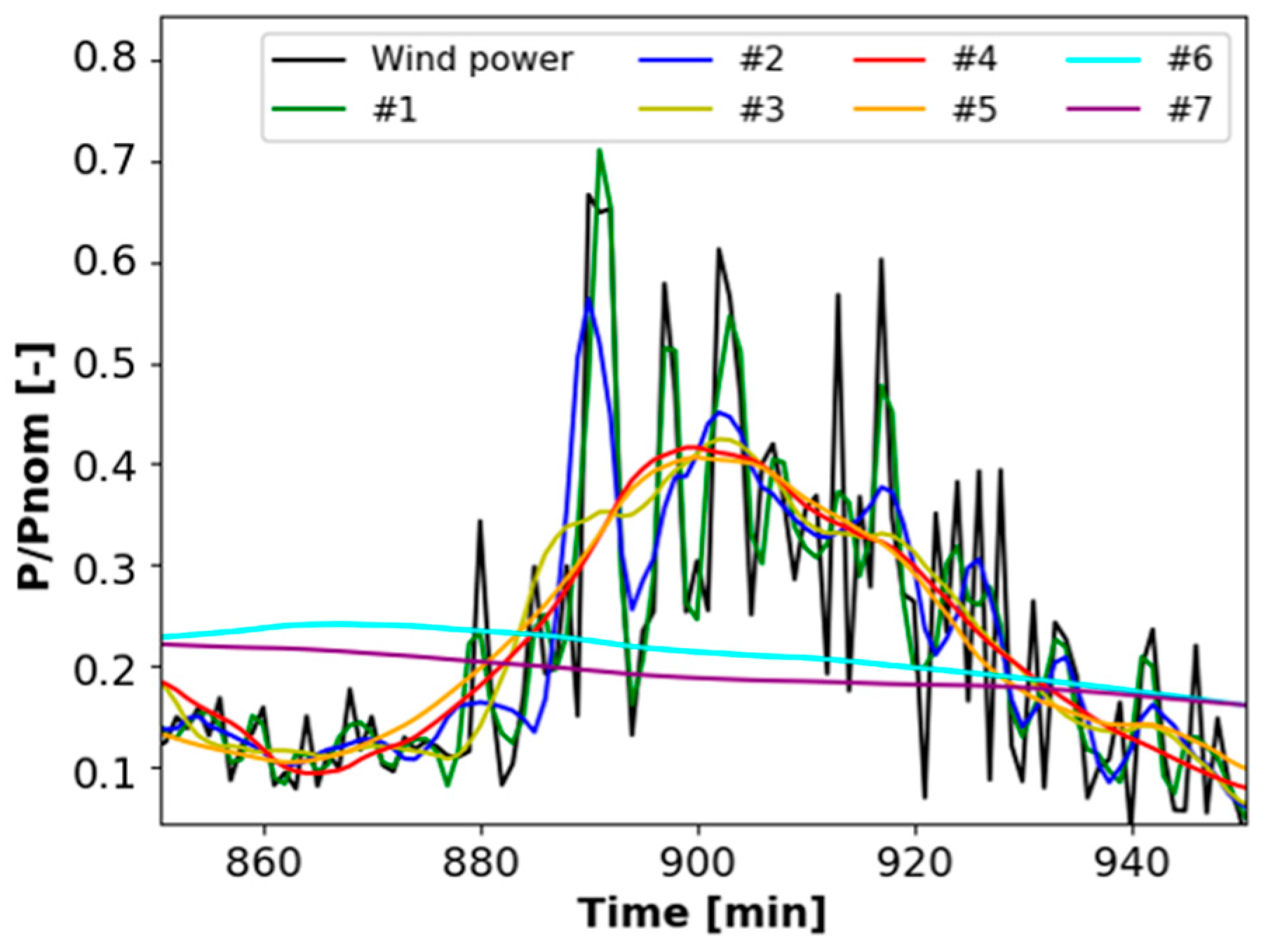
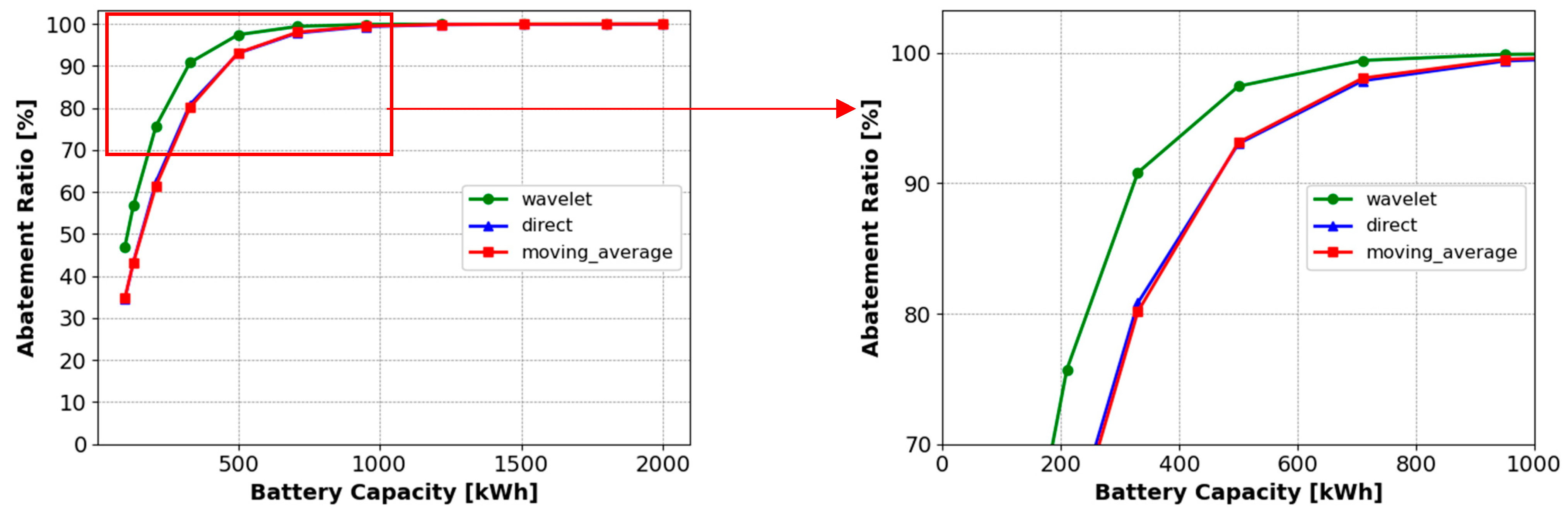
4.1. Sensitivity Analysis on the Wavelet Level Decomposition and Abatement Ratio
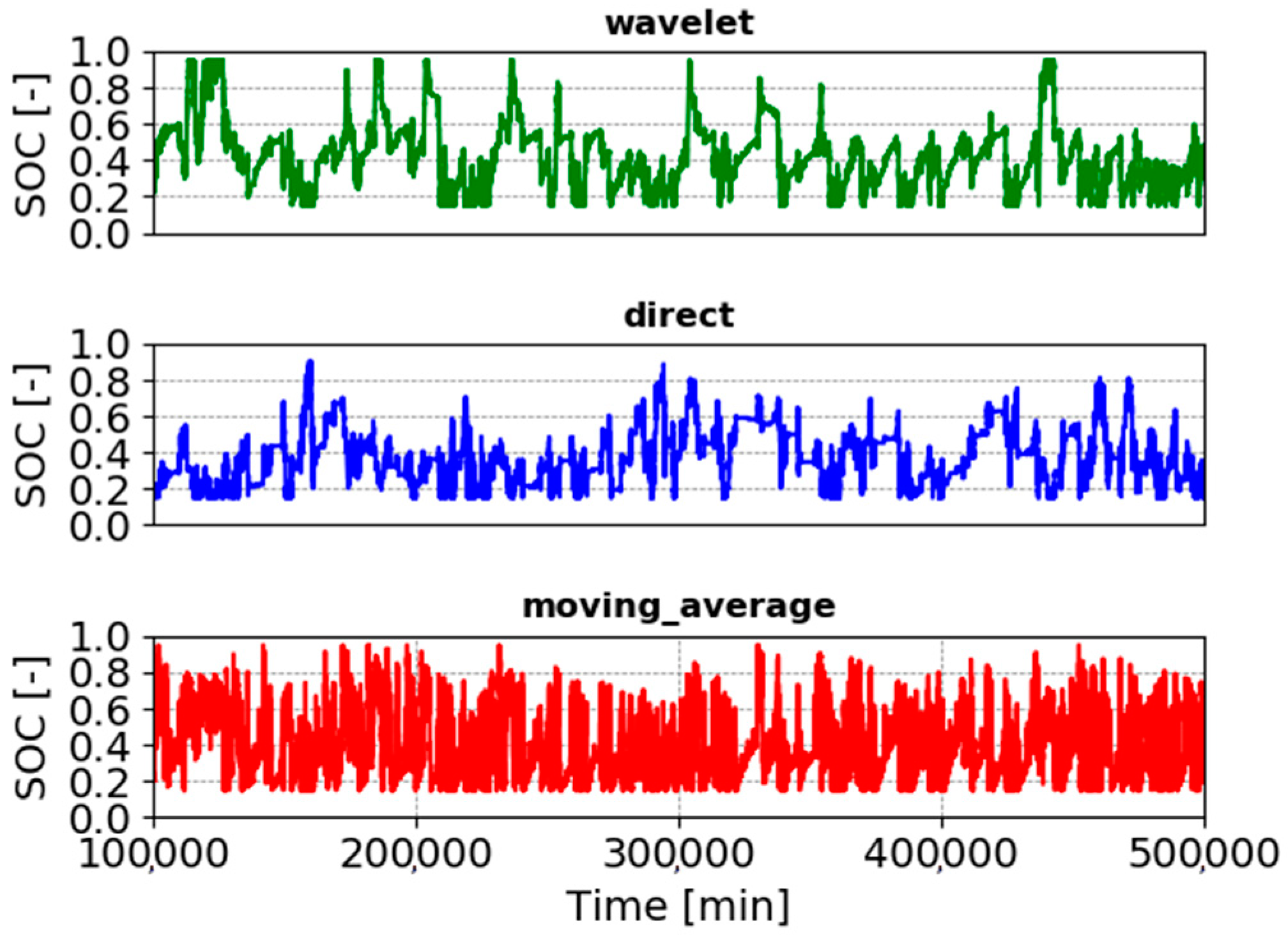
4.2. Wavelet-Based Power Smoothing Performance against Conventional Methods
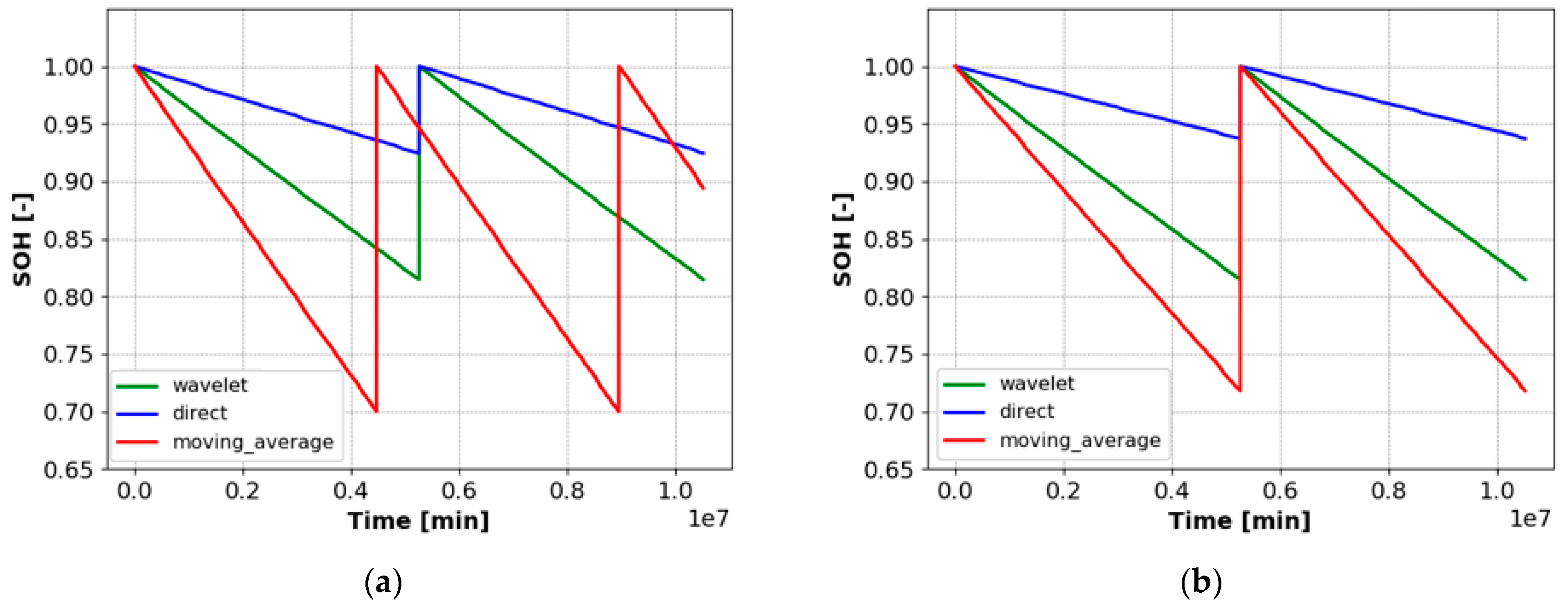
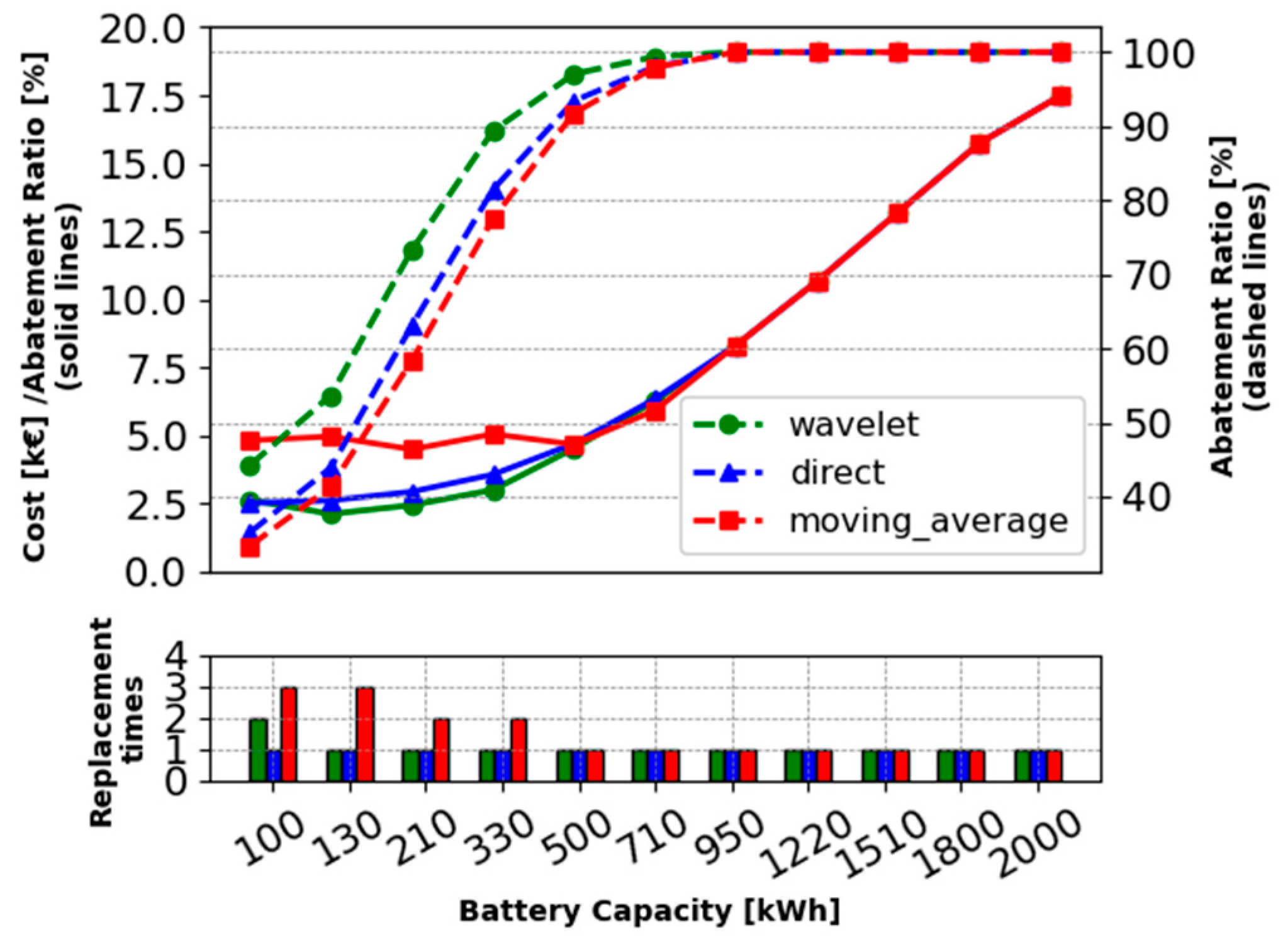
4.3. Wavelet-Based Power Smoothing Economics against Conventional Methods
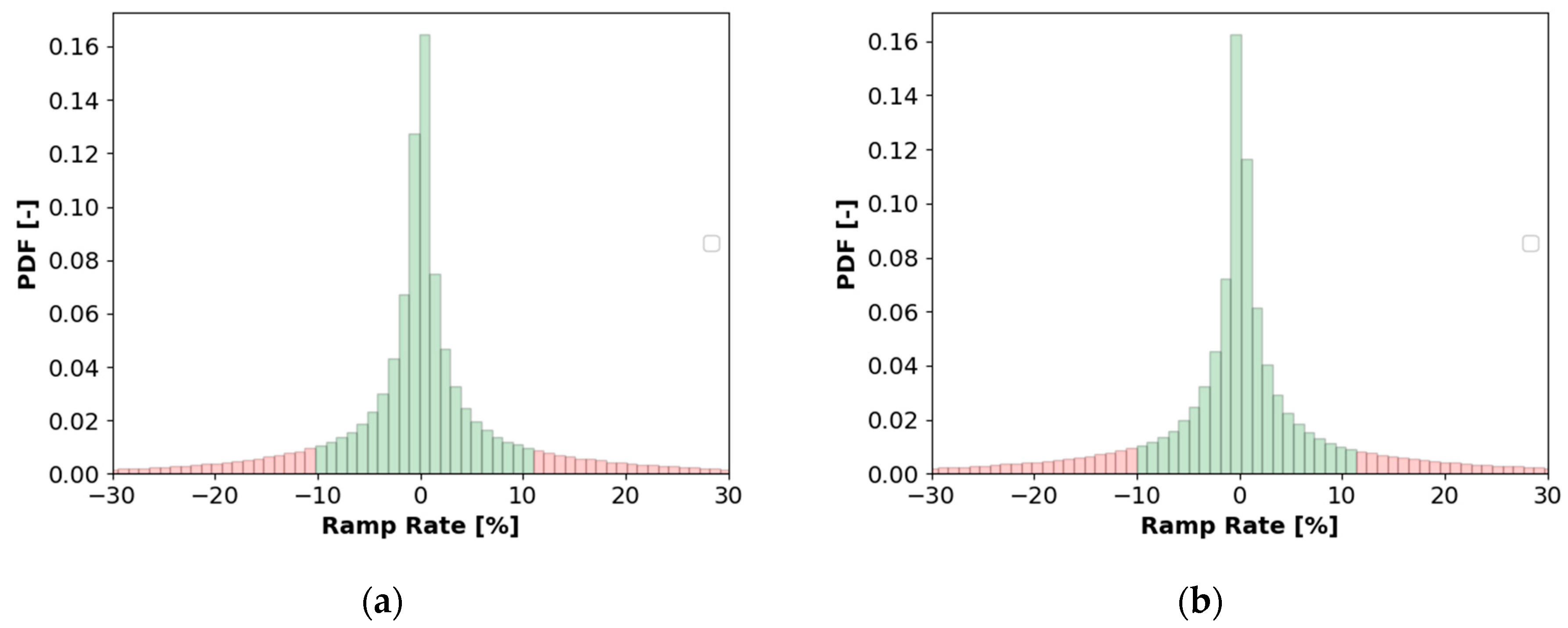
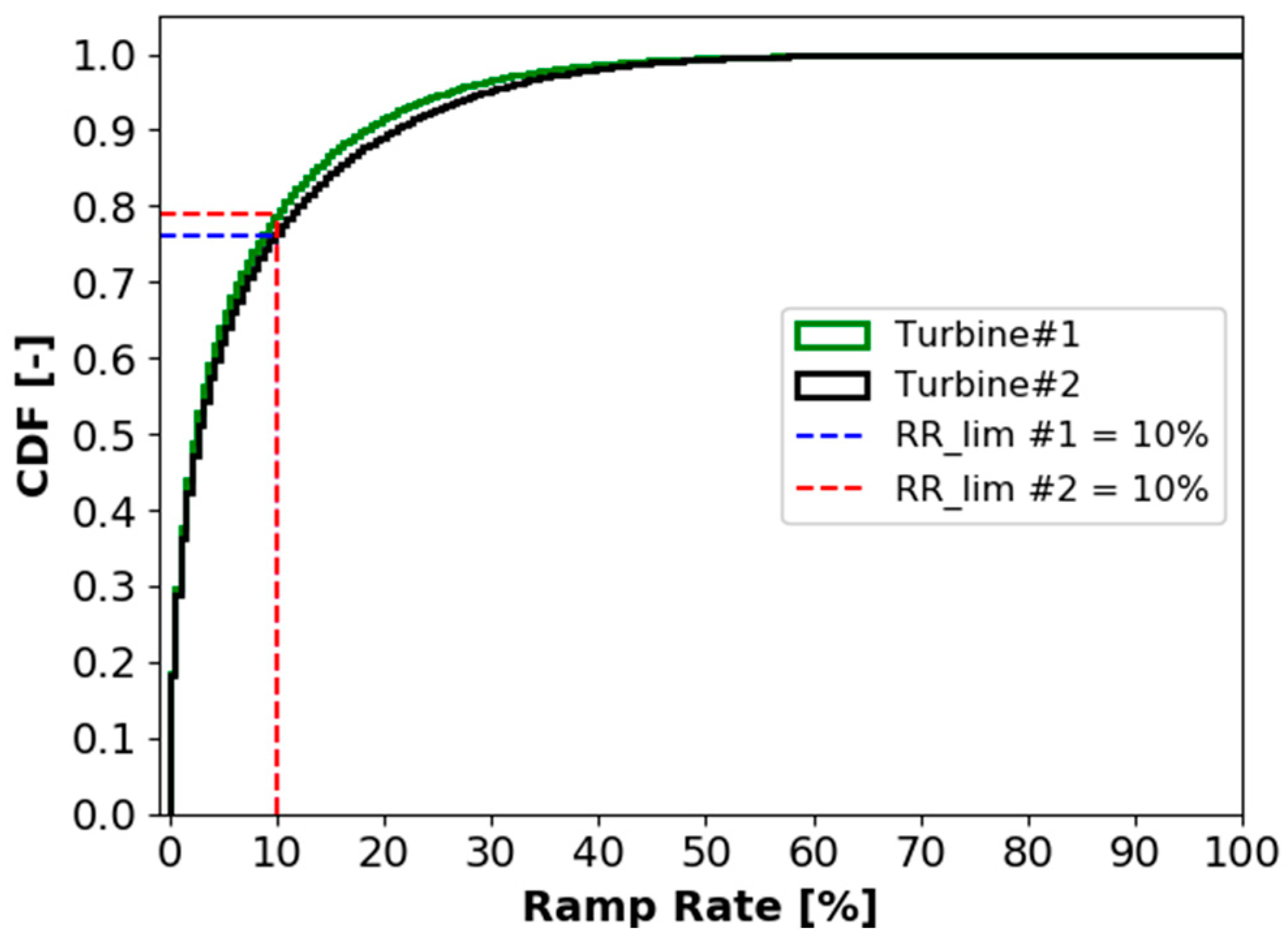
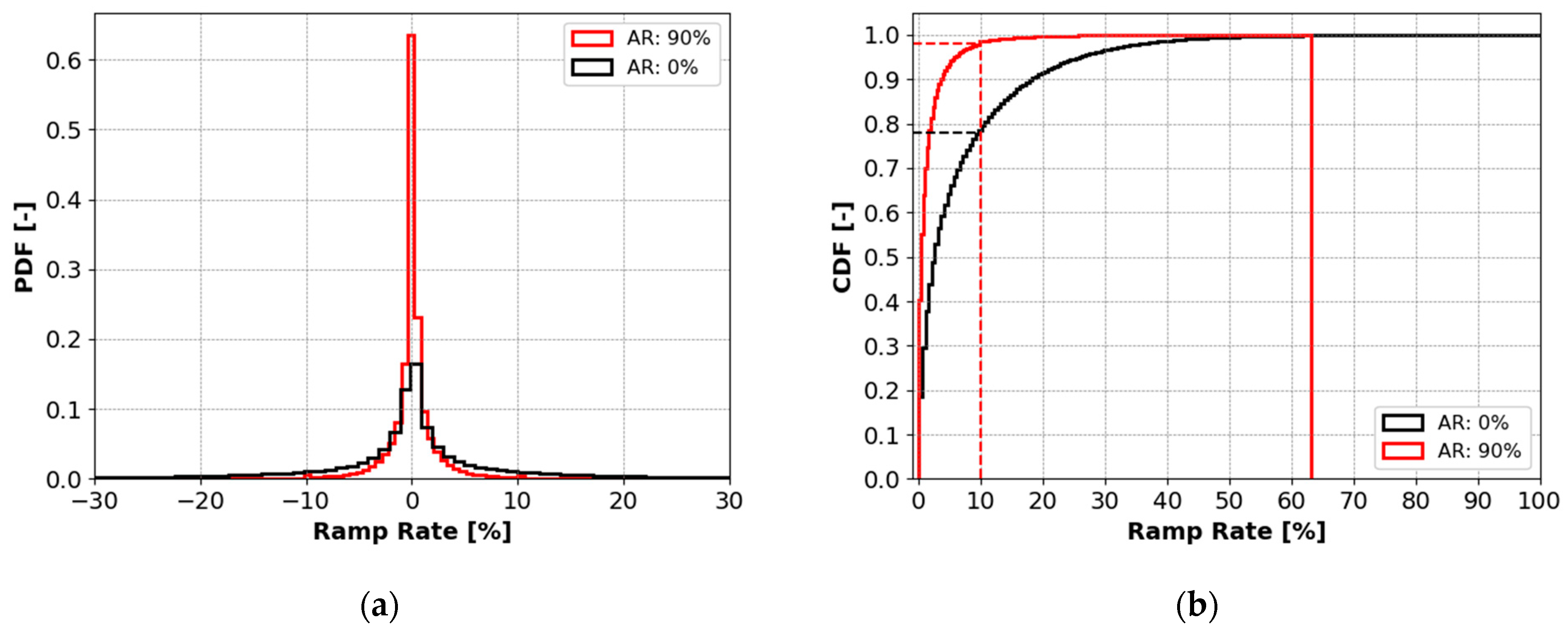
4.4. Effectiveness in Case of A Reduction of the Ramp Rate Requirements
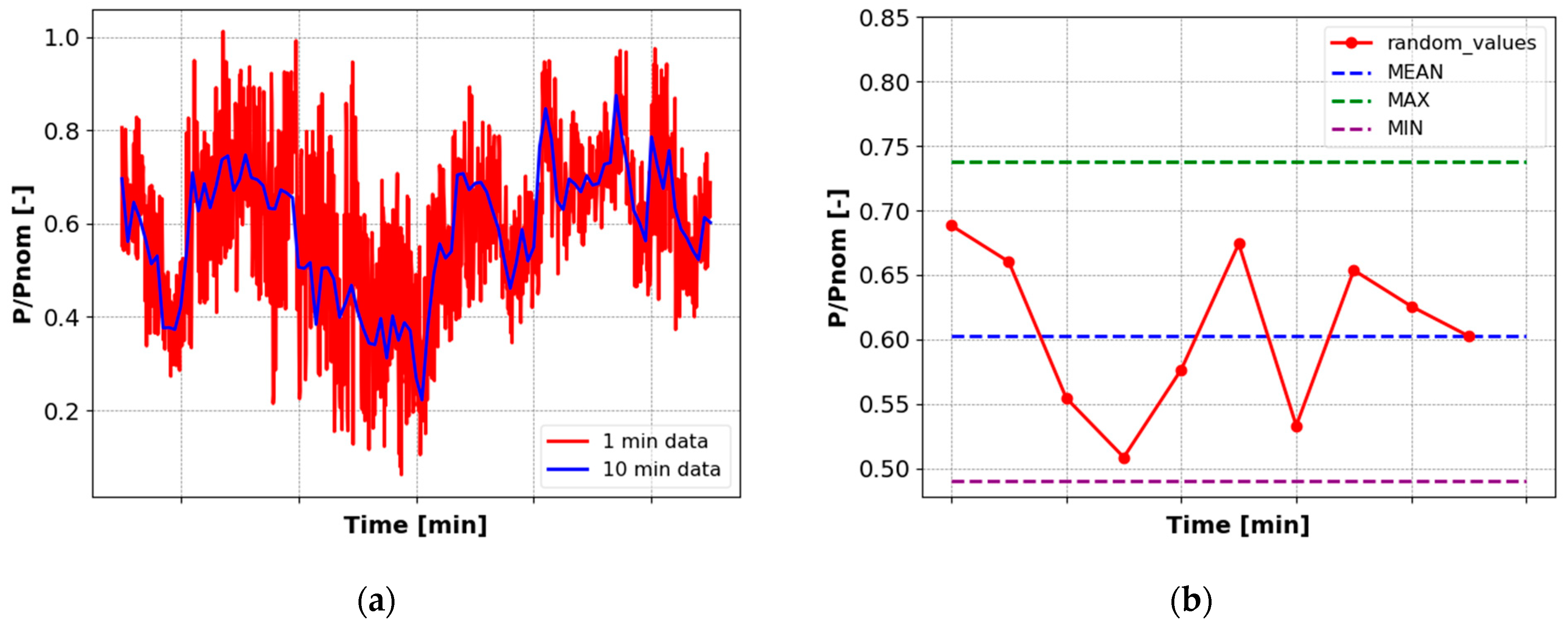
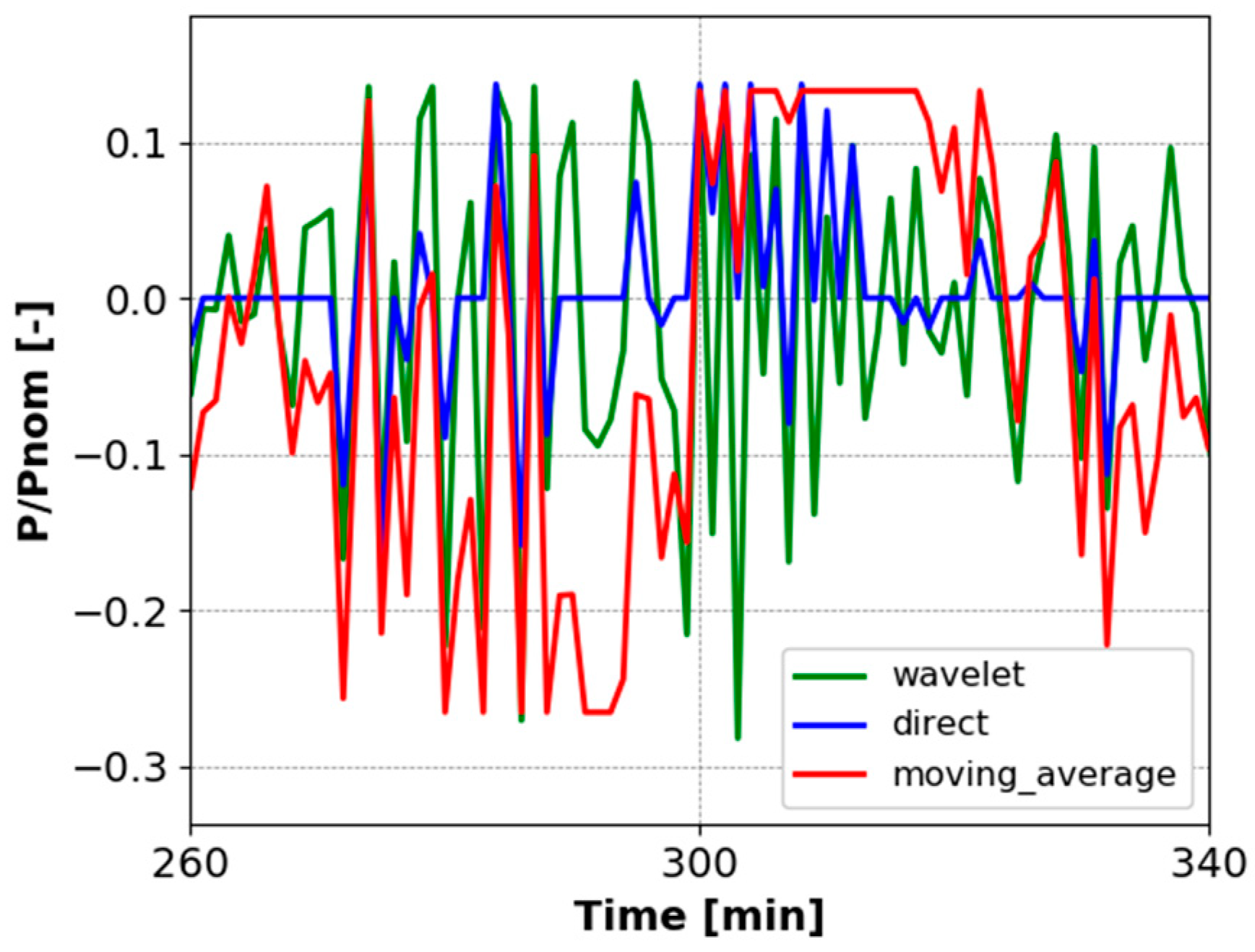
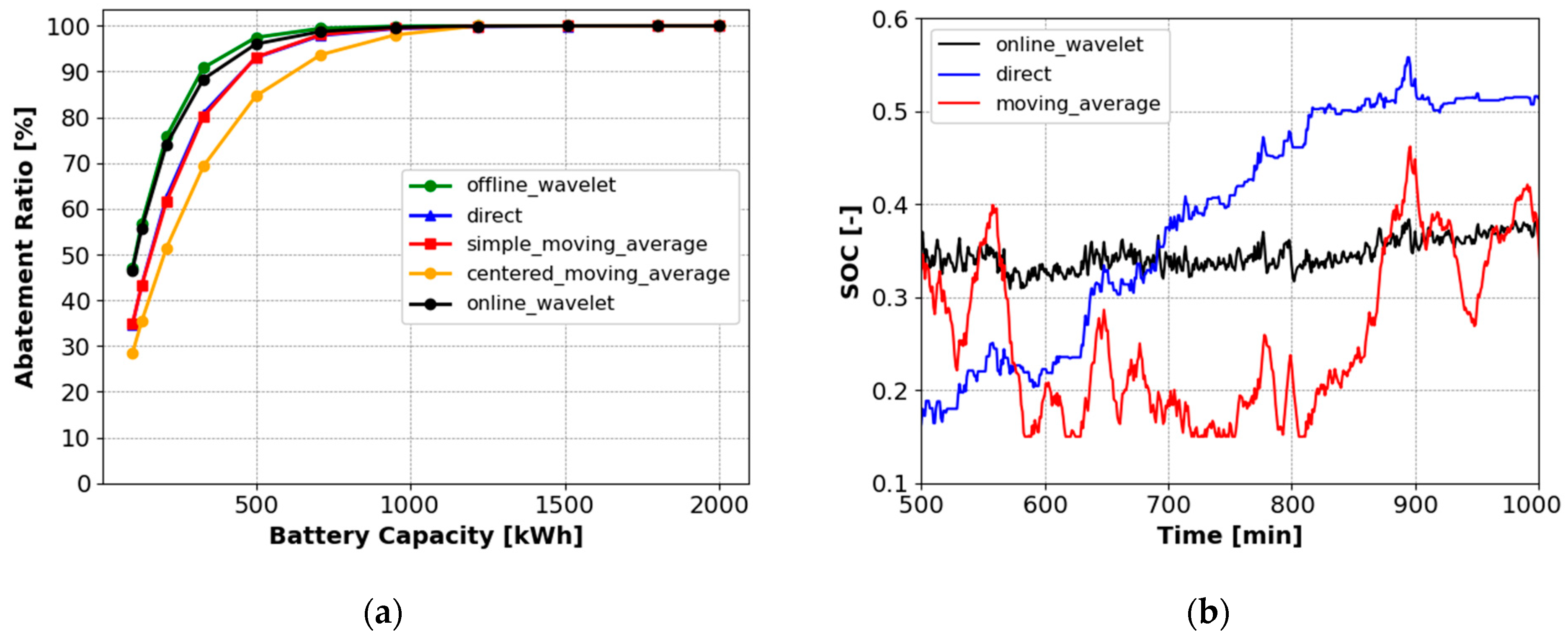
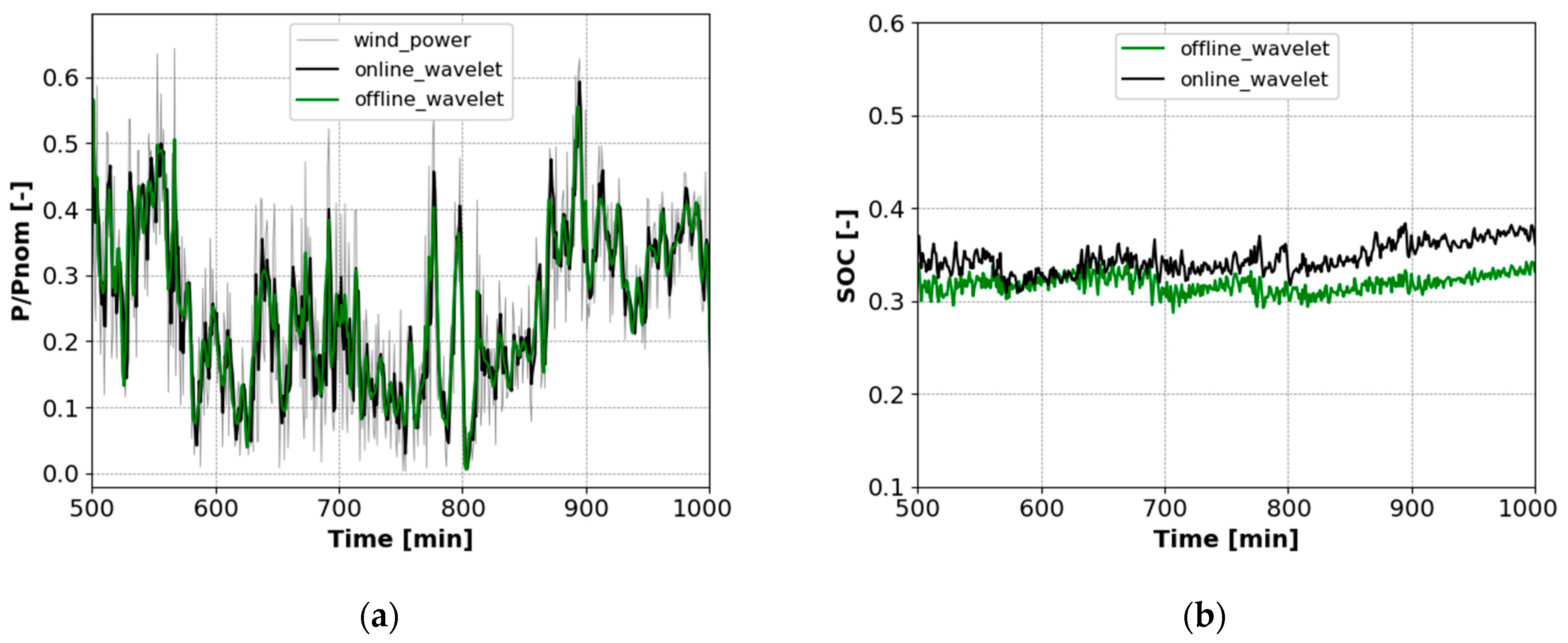
4.5. Wavelet-Based Power Smoothing Performance in Real-Time Operation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| SCADA | Supervisory Control And Data Acquisition |
| POC | Point of Connection |
| MPPT | Maximum Power Point Tracking |
| RR | Ramp Rate |
| SMA | Simple Moving Average |
| ESS | Energy Storage System |
| BESS | Battery Energy Storage System |
| FESS | Flywheel Energy Storage System |
| HESS | Hybrid Energy Storage System |
| SMES | Superconducting Magnetic Energy System |
| ECS | Energy Capacitor System |
| FC/ELZ | Fuel Cell and Electrolyzer Hybrid System |
| FT | Fourier Transform |
| STFT | Short-Time Fourier Transform |
| DFT | Discrete Fourier Transform |
| MRA | Multiresolution Analysis |
| CWT | Continuous Wavelet Transform |
| DWT | Discrete Wavelet Transform |
| SOC | State of Charge |
| SOH | State of Health |
| WT | Wind Turbine |
| AR | Abatement Ratio |
| KPI | Key Performance Indicator |
| P | Power |
| Pnom | Nominal Power |
| ls | Symmetric extension length |
| lw | Moving window length |
| i | Inflation rate |
| d | Discount rate |
References
- Yan, J.; Ouyang, T. Advanced wind power prediction based on data-driven error correction. Energy Convers. Manag. 2019, 180, 302–311. [Google Scholar] [CrossRef]
- Chen, B.; Xiong, R.; Li, H.; Sun, Q.; Yang, J. Pathways for sustainable energy transition. J. Clean. Prod. 2019, 228, 1564–1571. [Google Scholar] [CrossRef]
- Babazadehrokni, H. Power Fluctuations Smoothing and Regulations in Wind Turbine Generator Systems. Ph.D. Thesis, University of Denver, Denver, CO, USA, 2013; p. 104.
- Frate, G.F.; Cherubini, P.; Tacconelli, C.; Micangeli, A.; Ferrari, L.; Desideri, U. Ramp rate abatement for wind power plants: A techno-economic analysis. Appl. Energy 2019, 254, 113600. [Google Scholar] [CrossRef]
- Jabir, M.; Illias, H.A.; Raza, S.; Mokhlis, H. Intermittent Smoothing Approaches for Wind Power Output: A Review. Energies 2017, 10, 1572. [Google Scholar] [CrossRef] [Green Version]
- Ochoa, D.; Martinez, S. Frequency dependent strategy for mitigating wind power fluctuations of a doubly-fed induction generator wind turbine based on virtual inertia control and blade pitch angle regulation. Renew. Energy 2018, 128, 108–124. [Google Scholar] [CrossRef]
- Mejia, C.; Kajikawa, Y. Emerging topics in energy storage based on a large-scale analysis of academic articles and patents. Appl. Energy 2020, 263, 114625. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Rasmussen, C.N. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Palazoglu, A.; El-Farra, N.H.; Shah, N. Optimization and control of offshore wind systems with energy storage. Energy Convers. Manag. 2018, 173, 426–437. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, J.; Jia, B.; He, F.; Yang, Y.; Sun, N. Advance short-term wind energy quality assessment based on instantaneous standard deviation and variogram of wind speed by a hybrid method. Appl. Energy 2019, 238, 643–667. [Google Scholar] [CrossRef]
- Jauch, C. A flywheel in a wind turbine rotor for inertia control. Wind Energy 2015, 18, 1645–1656. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Bianchi, F.D. Energy management of flywheel-based energy storage device for wind power smoothing. Appl. Energy 2013, 110, 207–219. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Techno-economic analysis of grid-connected battery storage. Energy Convers. Manag. 2015, 91, 394–404. [Google Scholar] [CrossRef]
- Jannati, M. Analysis of power allocation strategies in the smoothing of wind farm power fluctuations considering lifetime extension of BESS units. J. Clean. Prod. 2020, 266, 122045. [Google Scholar] [CrossRef]
- Kasem, A.H.; El-Saadany, E.F.; El-Tamaly, H.H.; Wahab, M.A.A. Ramp rate control and voltage regulation for grid directly connected wind turbines. In 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, J.; Wang, L.; Lee, W.-J.; Cheng, X.; Zong, X. Hybrid Energy Storage System (HESS) optimization enabling very short-term wind power generation scheduling based on output feature extraction. Appl. Energy 2019, 256, 113915. [Google Scholar] [CrossRef]
- Sun, B.; Su, X.; Wang, D.; Zhang, L.; Liu, Y.; Yang, Y.; Liang, H.; Gong, M.; Zhang, W.; Jiang, J. Economic analysis of lithium-ion batteries recycled from electric vehicles for secondary use in power load peak shaving in China. J. Clean. Prod. 2020, 276, 123327. [Google Scholar] [CrossRef]
- Rallo, H.; Casals, L.C.; de la Torre, D.; Reinhardt, R.; Marchante, C.; Amante, B. Lithium-ion battery 2nd life used as a stationary energy storage system: Ageing and economic analysis in two real cases. J. Clean. Prod. 2020, 272, 122584. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Y.; Zhao, J.; Zhu, Y.; Liu, J. A dynamic wavelet-based robust wind power smoothing approach using hybrid energy storage system. Int. J. Electr. Power Energy Syst. 2020, 116, 105579. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, Y. Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms. Energy Convers. Manag. 2015, 100, 16–22. [Google Scholar] [CrossRef]
- Jiang, Q.; Hong, H. Wavelet-Based Capacity Configuration and Coordinated Control of Hybrid Energy Storage System for Smoothing Out Wind Power Fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Trung, T.T.; Ahn, S.-J.; Choi, J.-H.; Go, S.-I.; Nam, S.-R. Real-Time Wavelet-Based Coordinated Control of Hybrid Energy Storage Systems for Denoising and Flattening Wind Power Output. Energies 2014, 7, 6620–6644. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, Y.; Han, X.; Hui, D. Application of Fuzzy Wavelet Transform to Smooth Wind/PV Hybrid Power System Output with Battery Energy Storage System. Energy Procedia 2011, 12, 994–1001. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Kim, J.; Baldick, R. Ramp Rates Control of Wind Power Output Using a Storage System and Gaussian Processes; University of Texas at Austin: Austin, TX, USA, 2012; p. 22. [Google Scholar]
- Marcos, J.; Storkël, O.; Marroyo, L.; Garcia, M.; Lorenzo, E. Storage requirements for PV power ramp-rate control. Sol. Energy 2014, 99, 28–35. [Google Scholar] [CrossRef] [Green Version]
- Nordel. Nordic Grid Code. 2007. Technical Report. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/pre2015/publications/nordic/planning/070115_entsoe_nordic_NordicGridCode.pdf (accessed on 13 April 2021).
- Energinet. Technical Regulation 3.2.5 for Wind Power Plants above 11 kW. 2016. Available online: https://en.energinet.dk/Electricity/Rules-and-Regulations/Regulations-for-grid-connection (accessed on 13 April 2021).
- Collation of European Grid Codes, D2.6 Marinet Project; Technical Peport; p. 39. Available online: https://www.researchgate.net/profile/Mohan_Muniappan/post/How_much_variation_in_active_power_in_wind_turbine_generators_during_start_ups_and_shutdowns/attachment/5c62b6983843b0544e658041/AS%3A725454101159937%401549973144460/download/2013+-+Collation+of+European+Grid+Codes.pdf (accessed on 13 April 2021).
- Kiviluoma, J.; Holttinen, H.; Weir, D.; Scharff, R.; Söder, L.; Menemenlis, N.; Cutululis, N.A.; Danti Lopez, I.; Lannoye, E.; Estanqueiro, A.; et al. Variability in large-scale wind power generation. Wind Energy 2016, 19, 1649–1665. [Google Scholar] [CrossRef] [Green Version]
- Enercon. Enercon Product Overview; Enercon: Aurich, Germany, 2015. [Google Scholar]
- Popov, D.; Gapochkin, A.; Nekrasov, A. An Algorithm of Daubechies Wavelet Transform in the Final Field When Processing Speech Signals. Electronics 2018, 7, 120. [Google Scholar] [CrossRef] [Green Version]
- Rioul, O.; Duhamel, P. Fast algorithms for discrete and continuous wavelet transforms. IEEE Trans. Inf. Theory 1992, 38, 569–586. [Google Scholar] [CrossRef] [Green Version]
- Valens, C. A Really Friendly Guide to Wavelets; Springer: New York, NY, USA, 1999. [Google Scholar]
- Burrus, C.S.; Gopinath, R.A.; Guo, H. Introduction to Wavelets and Wavelet Transforms: A Primer, 1st ed.; Pearson College Div: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Wavelet Toolbox User’s Guide; MathWorks: Natick, MA, USA, 1997; p. 700.
- Osgood, B.G. Lectures on the Fourier Transform and Its Applications; Amer Mathematical Society: Providence, RI, USA, 2019. [Google Scholar]
- Rioul, O.; Vetterli, O. Wavelets and signal processing. IEEE Signal Process. Mag. 1991, 8, 14–38. [Google Scholar] [CrossRef] [Green Version]
- Merry, R.J.E. Wavelet Theory and Applications; Eindhoven University of Technology: Eindhoven, The Netherlands, 2005; p. 50. [Google Scholar]
- Alekseev, V.V.; Kaliakin, I.V. The role of sampling rate in wavelet transform decomposition. In Proceedings of the 2016 XIX IEEE International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 25–27 May 2016; pp. 392–394. [Google Scholar] [CrossRef]
- Karim, S.A.A.; Kamarudin, M.H.; Karim, B.A.; Hasan, M.K.; Sulaiman, J. Wavelet Transform and Fast Fourier Transform for signal compression: A comparative study. In Proceedings of the 2011 International Conference on Electronic Devices, Systems and Applications (ICEDSA), Kuala Lumpur, Malaysia, 25–27 April 2011; pp. 280–285. [Google Scholar] [CrossRef]
- Sharma, A. Machine Learning and Statistical Forecasting of High Resolution Load and Wind Power Data Using Wavelet Transformations. Master’s Thesis, Cornell University, Ithaca, NY, USA, 2016; p. 90. [Google Scholar]
- Qibing, J.; Khursheed, S. General theory on online wavelets denoising based on moving window. In Proceedings of the 2013 The International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 157–161. [Google Scholar] [CrossRef]
- Xia, R.; Meng, K.; Qian, F.; Wang, Z.-L. Online Wavelet Denoising via a Moving Window. Acta Autom. Sin. 2007, 33, 897–901. [Google Scholar] [CrossRef]
- Youssef, O.A.S. Online Applications of Wavelet Transforms to Power System Relaying—Part II. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Zhi, L.; Liu, W.; Liu, Q. Matrix Operation of Discrete Wavelet Transform. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; pp. 1214–1216. [Google Scholar] [CrossRef]
- Divya, K.C.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- MIT Electric Vehicle Team. A Guide to Understanding Battery Specifications; MIT: Boston, MA, USA, 2008; p. 3. [Google Scholar]
- Li, K.; Tseng, K.J. Energy efficiency of lithium-ion battery used as energy storage devices in micro-grid. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 5235–5240. [Google Scholar] [CrossRef]
- Pugi, L. Meccatronica. Elementi di Trazione Elettrica; E-book. Formato PDF; Società Editrice Esculapio: Bologna, Italy, 2019. [Google Scholar]
- Casals, L.C.; Rodríguez, M.; Corchero, C.; Carrillo, R.E. Evaluation of the End-of-Life of Electric Vehicle Batteries According to the State-of-Health. World Electr. Veh. J. 2019, 10, 63. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Xu, B.; Tan, Y.; Zhang, B. A Convex Cycle-based Degradation Model for Battery Energy Storage Planning and Operation. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4590–4596. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Xu, B.; Tan, Y.; Kirschen, D.; Zhang, B. Optimal Battery Control Under Cycle Aging Mechanisms in Pay for Performance Settings. IEEE Trans. Autom. Control. 2019, 64, 2324–2339. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yan, Z.; Li, N. A Novel State of Charge Feedback Strategy in Wind Power Smoothing Based on Short-Term Forecast and Scenario Analysis. IEEE Trans. Sustain. Energy 2017, 8, 870–879. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, Y. Coordinated Control Strategy of a Battery Energy Storage System to Support a Wind Power Plant Providing Multi-Timescale Frequency Ancillary Services. IEEE Trans. Sustain. Energy 2017, 8, 1140–1153. [Google Scholar] [CrossRef]
- Sourkounis, C.; Tourou, P. Grid Code Requirements for Wind Power Integration in Europe. Conf. Pap. Energy 2013, 2013, e437674. [Google Scholar] [CrossRef] [Green Version]
- Haque, M.E.; Khan, M.N.S.; Sheikh, M.R.I. Smoothing control of wind farm output fluctuations by proposed Low Pass Filter, and Moving Averages. In Proceedings of the 2015 International Conference on Electrical Electronic Engineering (ICEEE), Savar, Bangladesh, 4–6 November 2015; pp. 121–124. [Google Scholar] [CrossRef]
- Ferrari, L.; Bianchini, A.; Galli, G.; Ferrara, G.; Carnevale, E.A. Influence of actual component characteristics on the optimal energy mix of a photovoltaic-wind-diesel hybrid system for a remote off-grid application. J. Clean. Prod. 2018, 178, 206–219. [Google Scholar] [CrossRef]
- Cole, W.J.; Frazier, A. Cost Projections for Utility-Scale Battery Storage; NREL/TP-6A20-73222; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [Google Scholar] [CrossRef] [Green Version]
- Beltran, H.; Ayuso, P.; Pérez, E. Lifetime Expectancy of Li-Ion Batteries used for Residential Solar Storage. Energies 2020, 13, 568. [Google Scholar] [CrossRef] [Green Version]
- IRENA. Future of Wind—Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; IRENA: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]


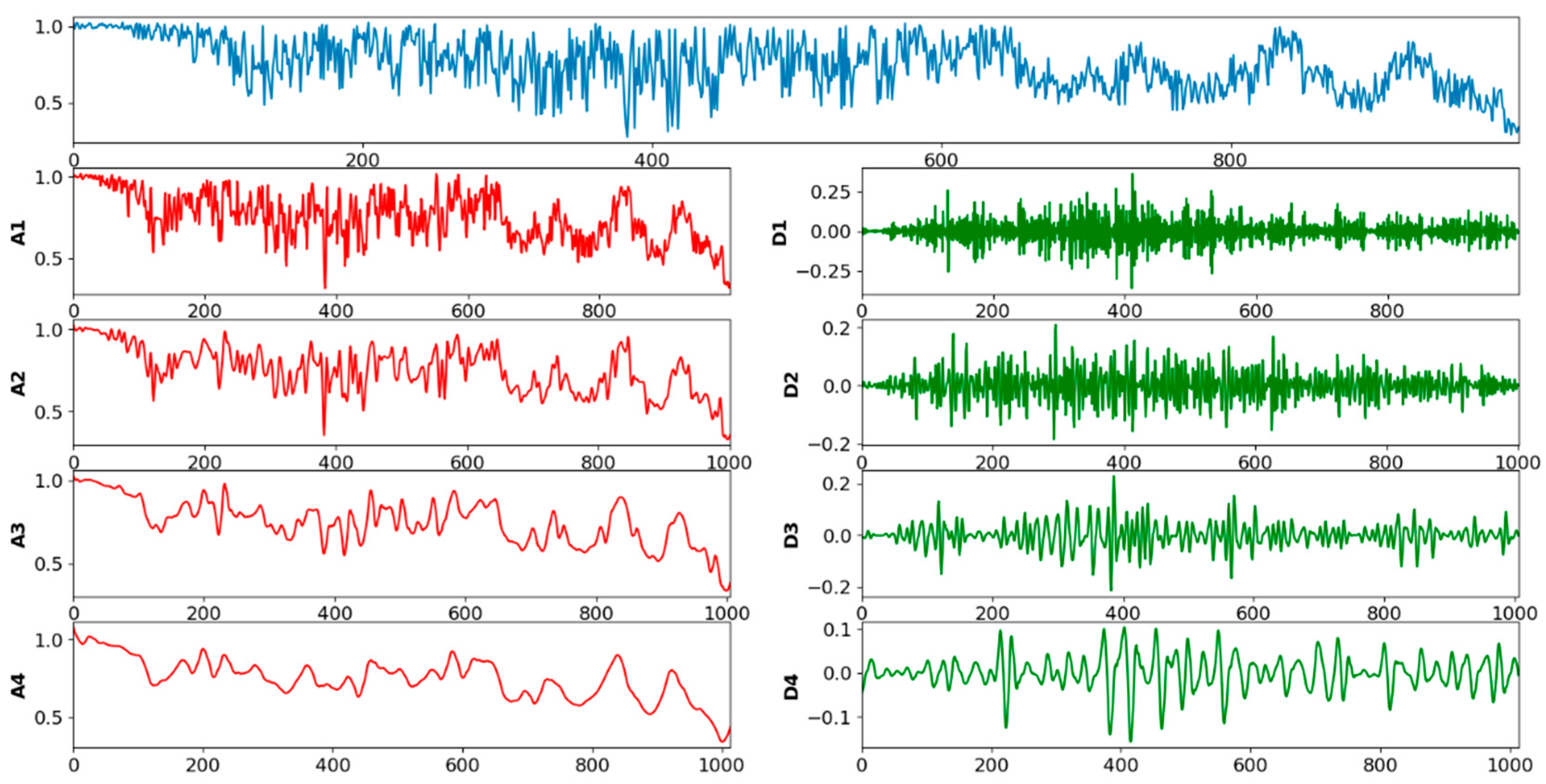
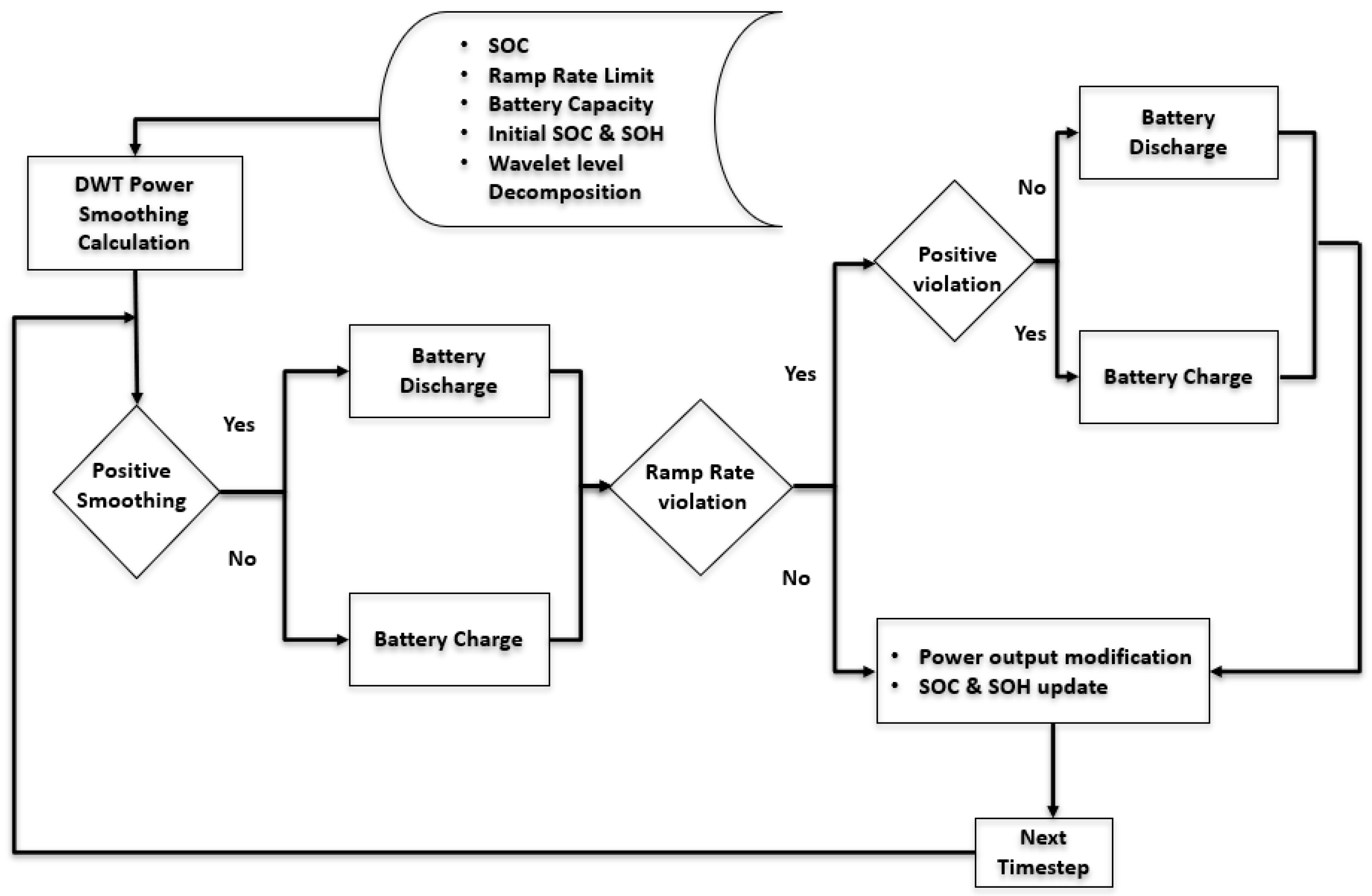

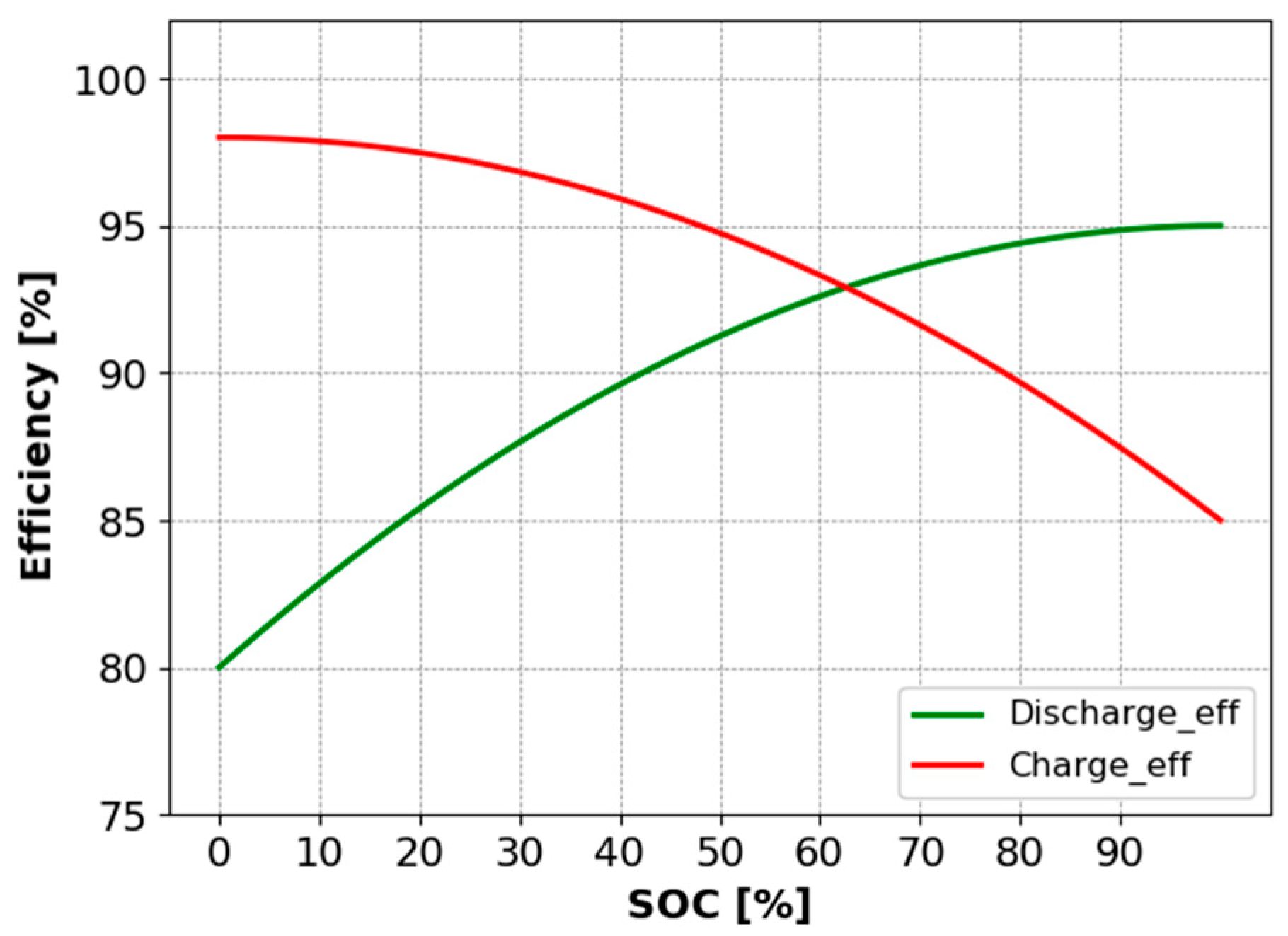
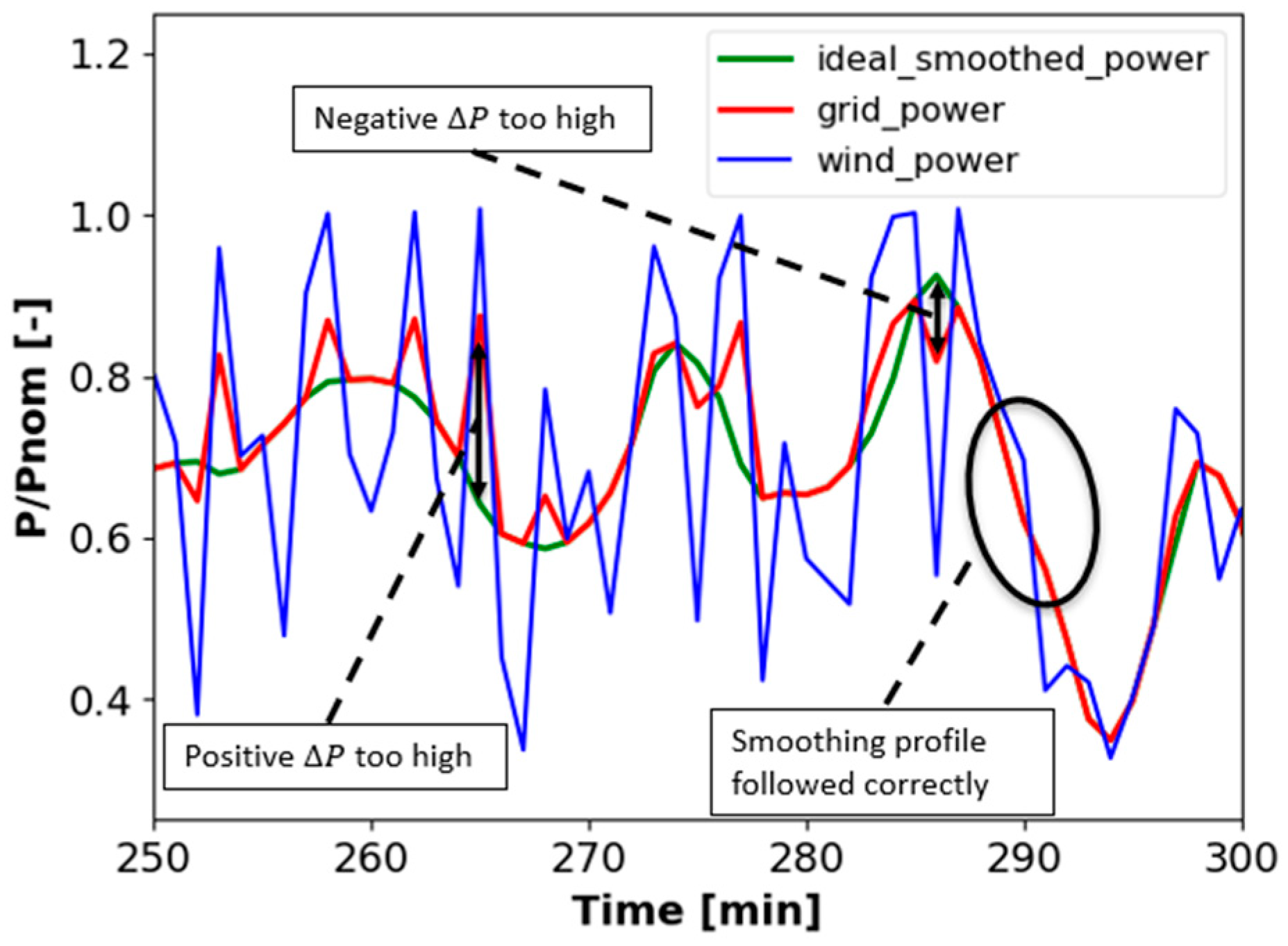






| Grid | Ramp Rate Limit (dP/dt) | Ref. |
|---|---|---|
| Germany | 10% Pnom per min | [15] |
| Norway | 10% Pnom per min | [26] |
| UK | No limit for wind farms up to 300 MW capacity, 50 MW/min for 300 < Pnom < 1000 40 MW/min for Pnom > 1000 MW | [15] |
| Denmark | 100 kW/s | [27] |
| Ireland | 8% Pnom per min & 4% Pnom per 10 min | [28] |
| USA | 10% Pnom per min | [19] |
| Puerto Rico | 10% Pnom per min | [4] |
| Canada | 10% Pnom per min | [19] |
| China | 3 MW/min for wind farms up to 30 MW capacity, 10% Pnom per min for 30 < Pnom < 150 MW 15 MW/min for Pnom >150 MW in size. | [19] |
| DWT features: |
|
| Ramp rate constraint: |
|
| Technical storage parameters: |
|
| PHEV-1/Samsung SDI 94 Ah | |
|---|---|
| Weight | 670 kg |
| Size | 800 × 850 × 2034 mm (W × L × H) |
| Energy | 62.3 kWh |
| Nominal voltage | 662 V |
| Min. voltage | 486 V |
| Max. voltage | 747 V |
| Nominal capacity @25 °C | 94 Ah |
| Max continuous discharge current @25 °C | 230 A |
| Max continuous charge current @25 °C | 100 A |
| Cell temperature operating | 0 to 55 °C |
| Cycle lifetime EOL80%/EOL70% | 3200/5200 Cycles |
| Charging Mode () |
|
| Discharging mode () |
|
| Battery unit cost | 500 €/kWh |
| Wind Turbine lifetime | 20 years |
| Li-ion battery lifetime | 10 years |
| Discount rate (d) | 5% |
| Inflation rate (i) | 2% |
| Method | Average | Standard Deviation |
|---|---|---|
| Wavelet | 0.43 | 0.18 |
| Direct | 0.29 | 0.11 |
| Moving average | 0.37 | 0.19 |
| Method | Average | Standard Deviation |
|---|---|---|
| Wavelet | 0.43 | 0.18 |
| Direct | 0.38 | 0.16 |
| Moving average | 0.40 | 0.20 |
| Layout | BESS Capacity [kWh] |
|---|---|
| Separate systems | 690 |
| Combined system | 445 |
| Increment | −35% |
| Method | BESS Capacity [kWh] | Discounted Cost [k€] |
|---|---|---|
| Wavelet | 330 (-) | 288 (-) |
| Direct | 460 (+39%) | 402 (+39%) |
| Moving average | 465 (+41%) | 406 (+41%) |
| Moving Window Length (lw) | ||||||
|---|---|---|---|---|---|---|
| 4 | 8 | 16 | 24 | 32 | ||
| Symmetric Extension Length (ls) | 4 | 85.49217 | 87.9971 | 88.2814 | 88.2782 | 88.2782 |
| 8 | / | 88.0969 | 88.3445 | 88.3482 | 88.3303 | |
| 16 | / | / | 88.3448 | 88.3446 | 88.3447 | |
| 24 | / | / | / | 88.3439 | 88.3439 | |
| 32 | / | / | / | / | 88.3439 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannelli, A.; Papi, F.; Pechlivanoglou, G.; Ferrara, G.; Bianchini, A. Discrete Wavelet Transform for the Real-Time Smoothing of Wind Turbine Power Using Li-Ion Batteries. Energies 2021, 14, 2184. https://doi.org/10.3390/en14082184
Mannelli A, Papi F, Pechlivanoglou G, Ferrara G, Bianchini A. Discrete Wavelet Transform for the Real-Time Smoothing of Wind Turbine Power Using Li-Ion Batteries. Energies. 2021; 14(8):2184. https://doi.org/10.3390/en14082184
Chicago/Turabian StyleMannelli, Andrea, Francesco Papi, George Pechlivanoglou, Giovanni Ferrara, and Alessandro Bianchini. 2021. "Discrete Wavelet Transform for the Real-Time Smoothing of Wind Turbine Power Using Li-Ion Batteries" Energies 14, no. 8: 2184. https://doi.org/10.3390/en14082184









