Finite Element Analysis of Tidal Turbine Blade Subjected to Impact Loads from Sea Animals †
Abstract
:1. Introduction
2. Geometry and Numerical Modelling
2.1. Tidal Turbine Blade
2.2. Killer Whale (Orcinus orca)
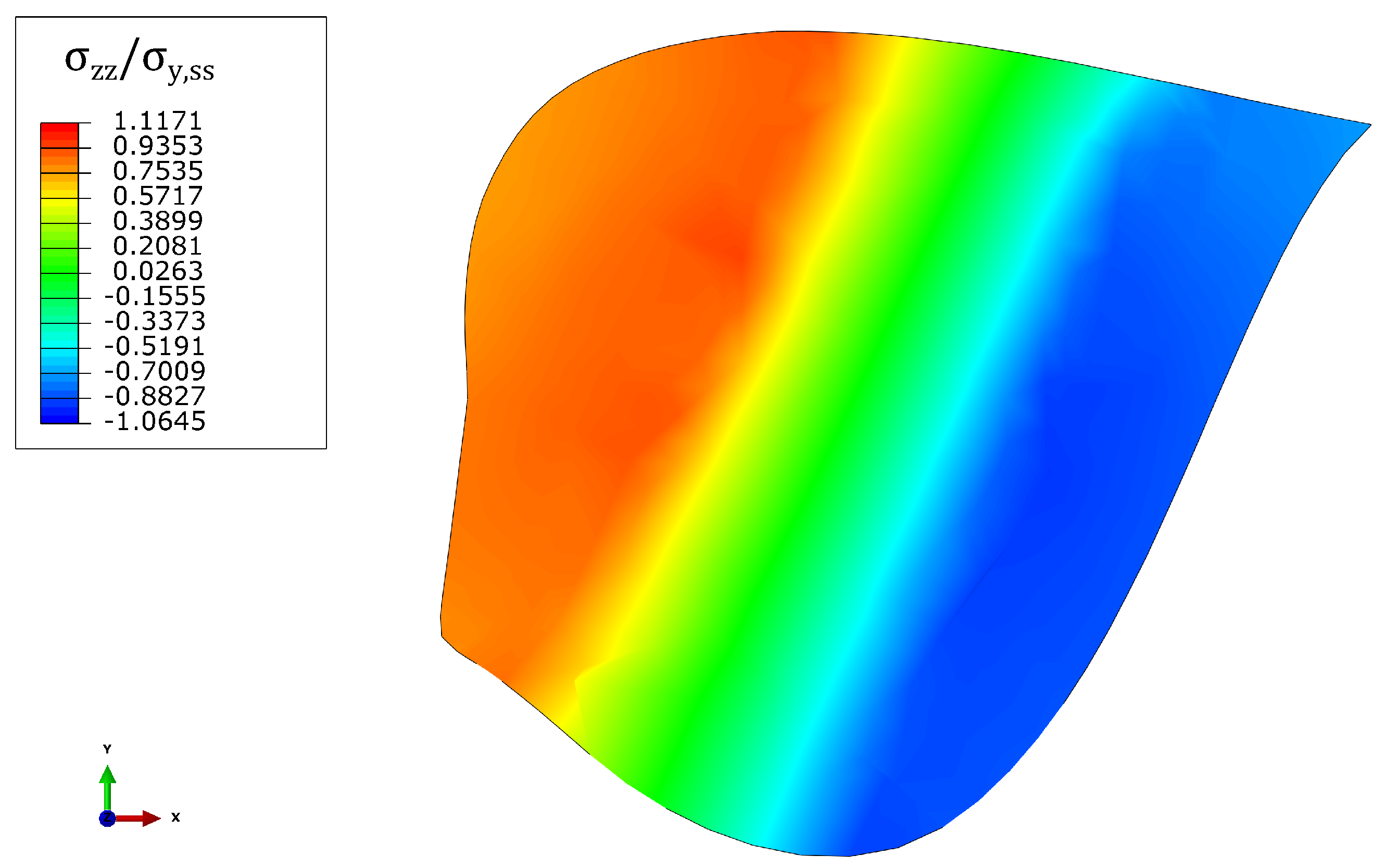
3. Numerical Results
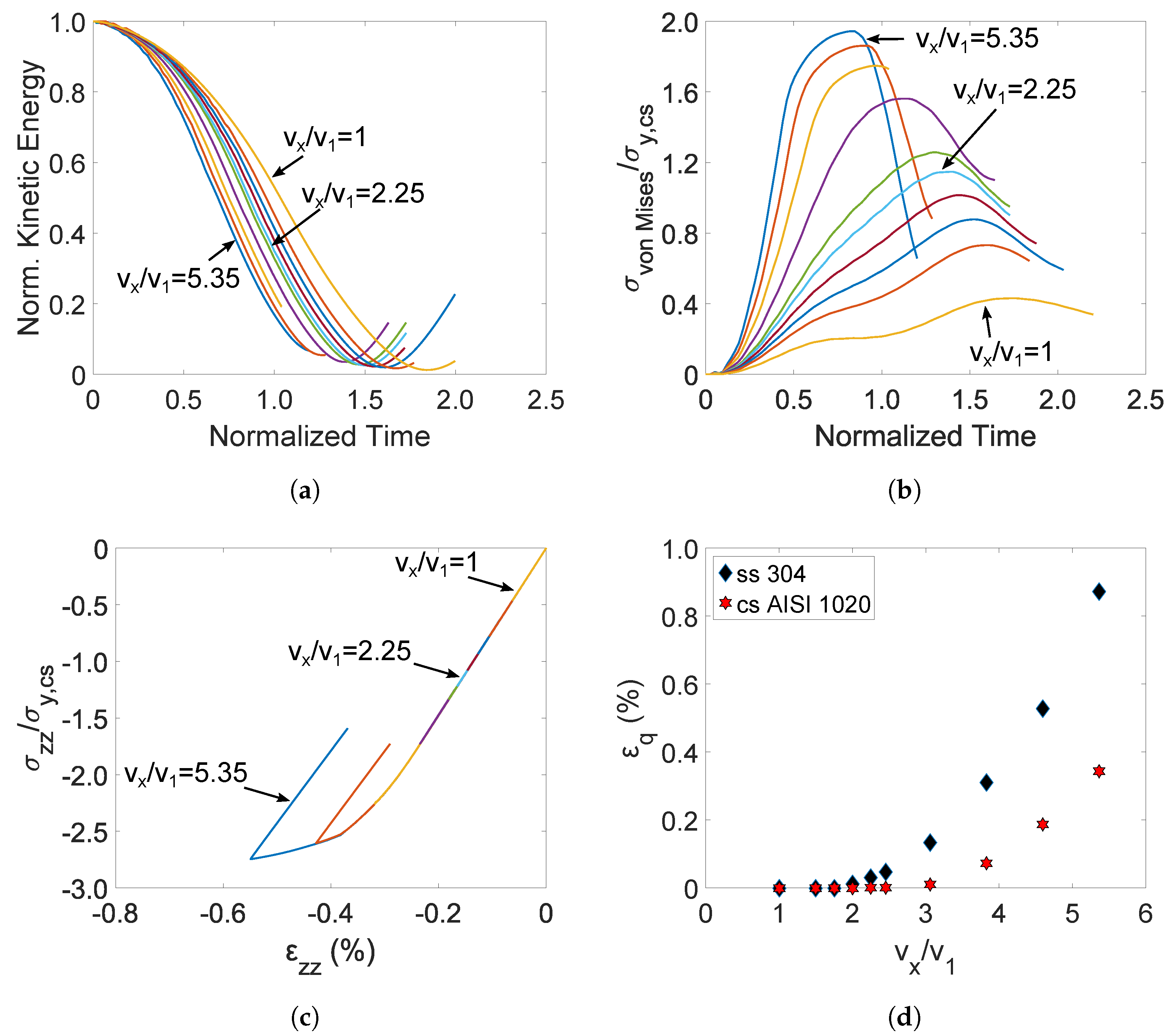
4. Parametric Studies Assuming Different Material and Loading Parameters
4.1. Carbon Steel Material of Grade AISI 1020
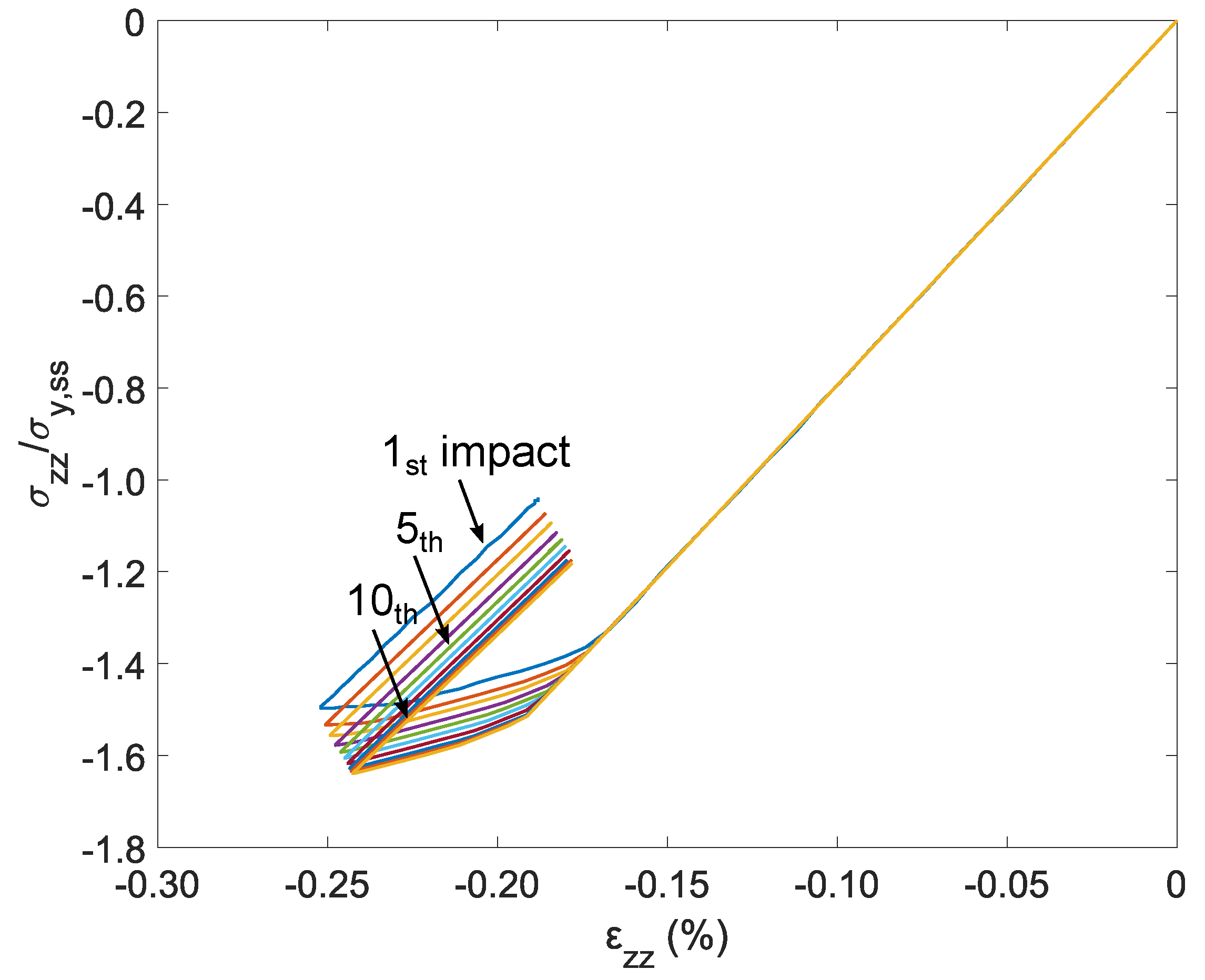
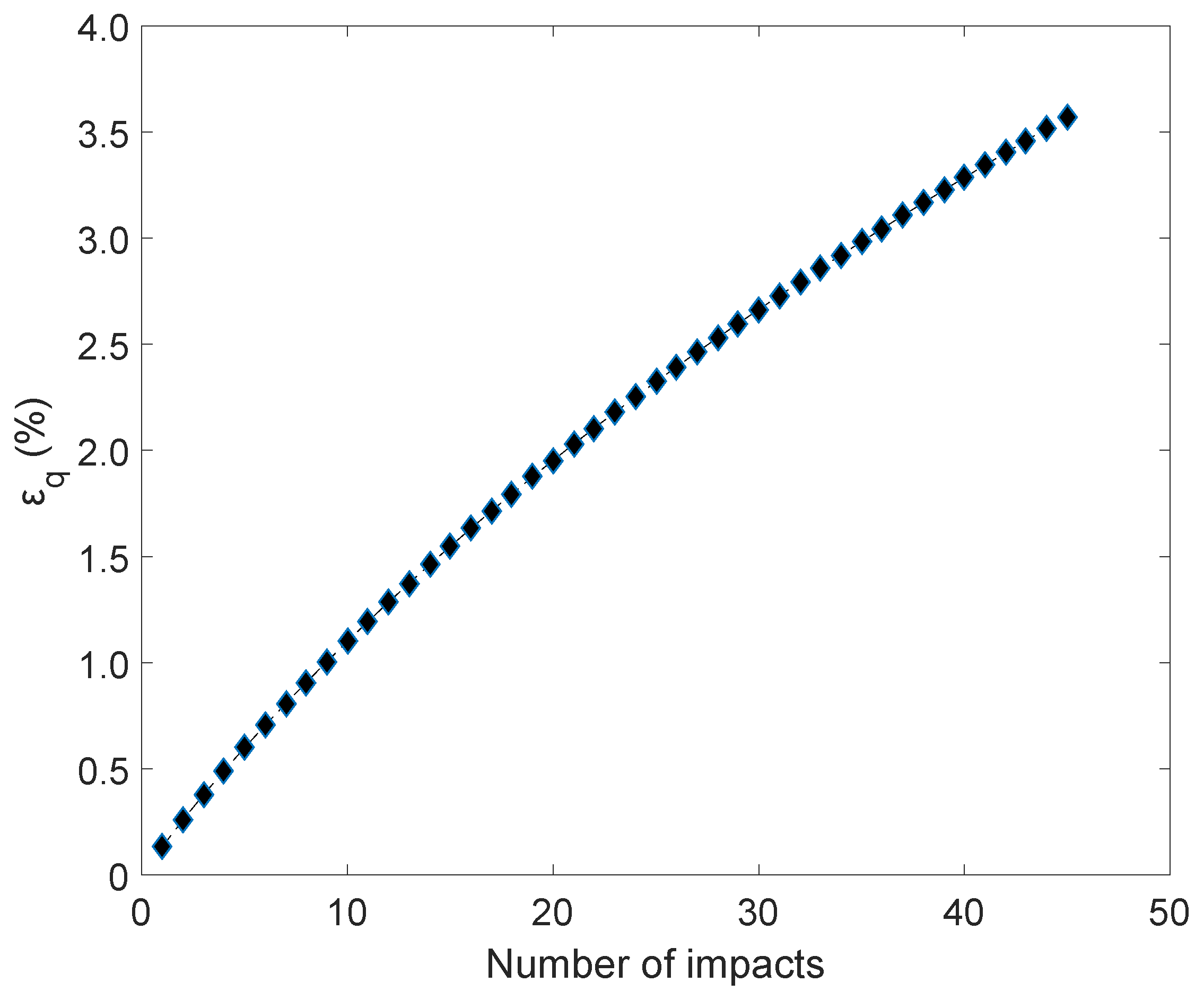
4.2. Multiple Impacts
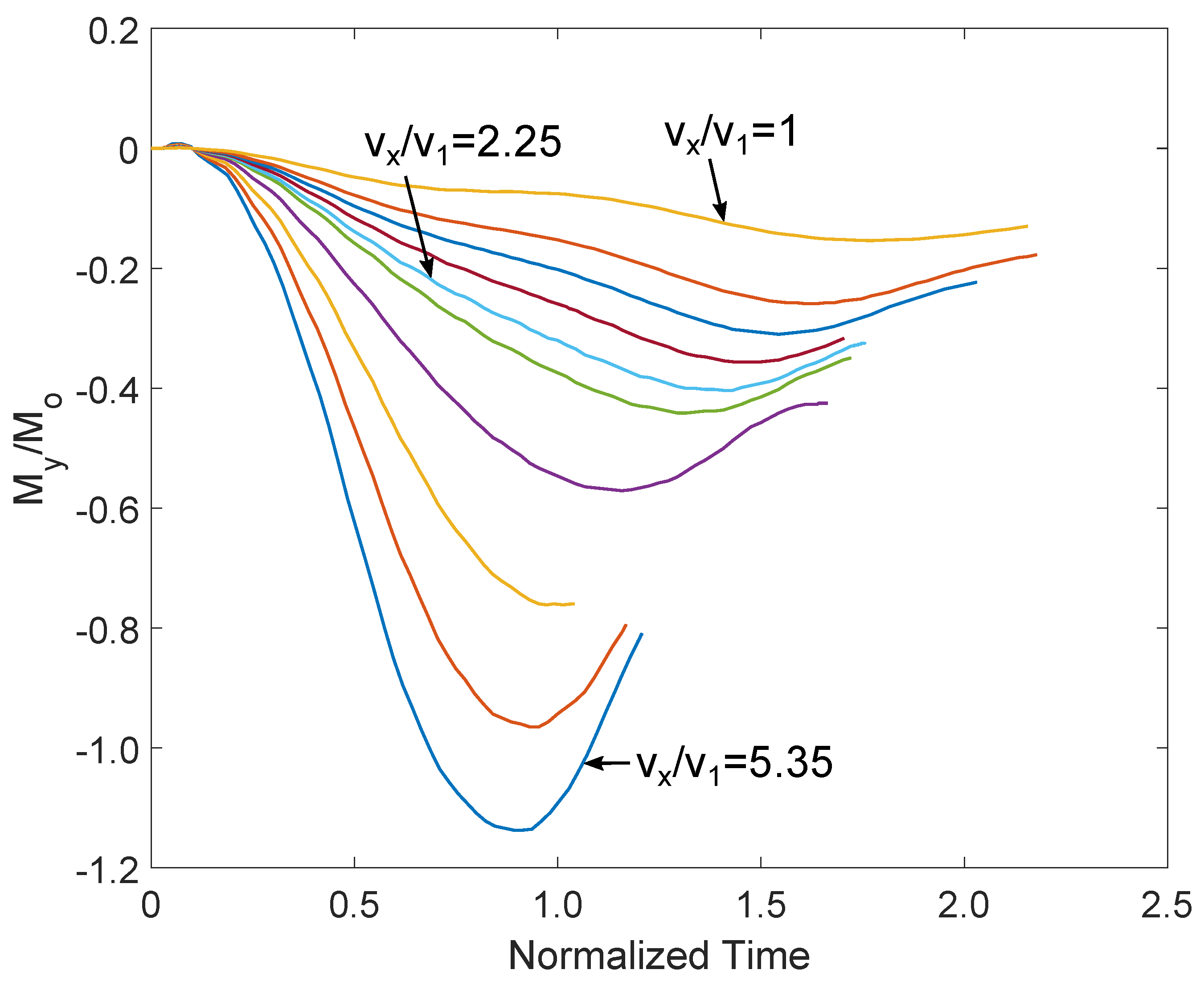
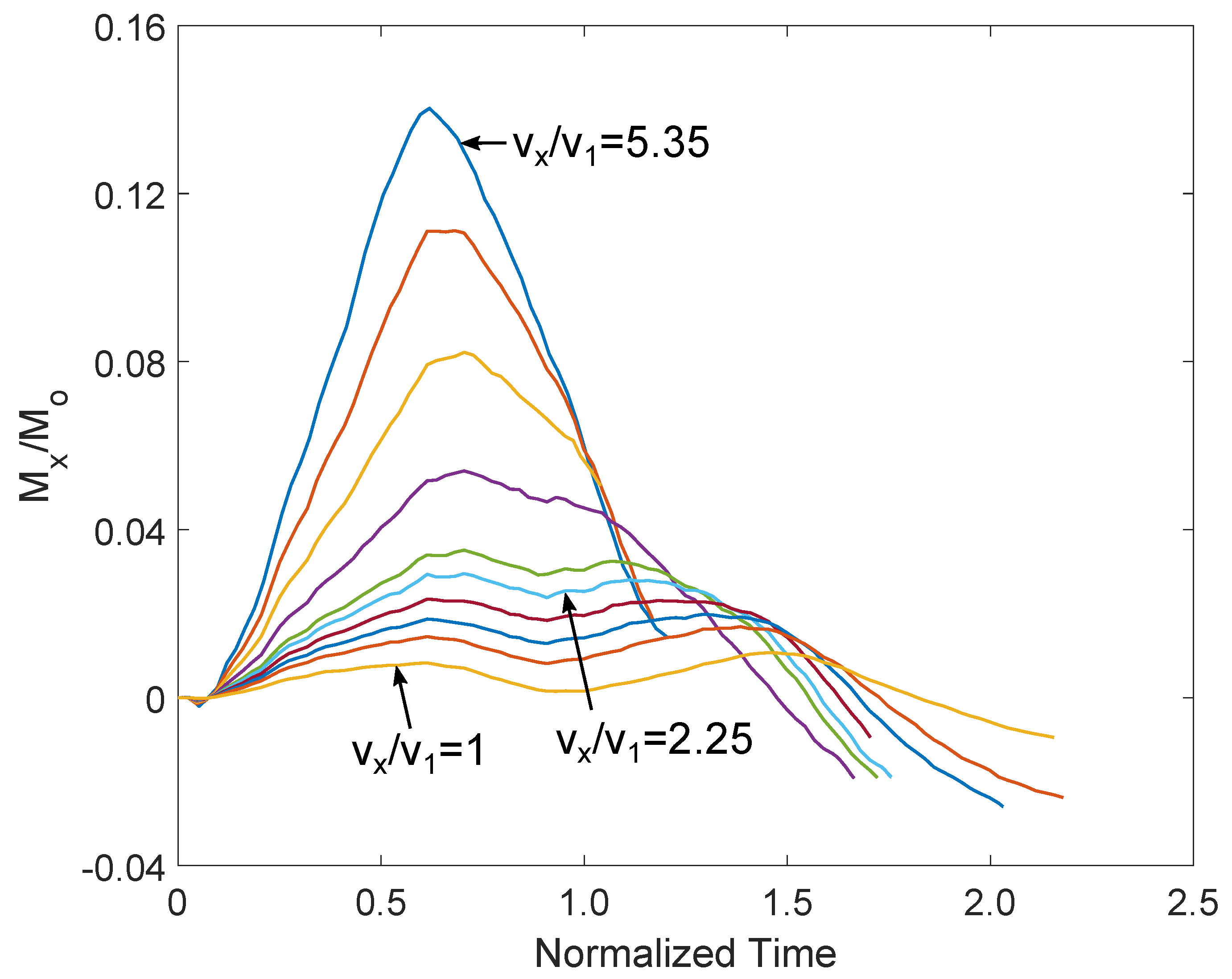
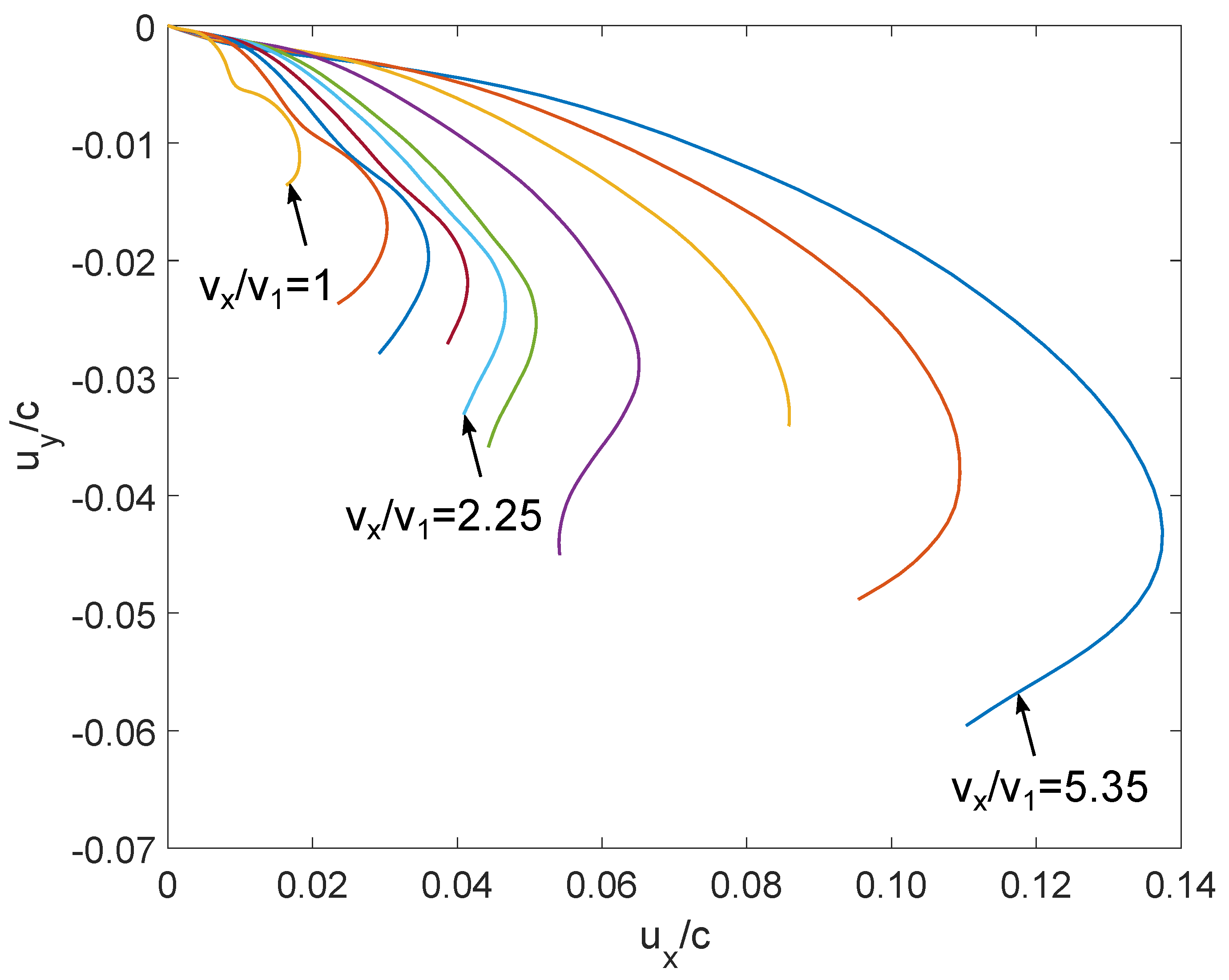
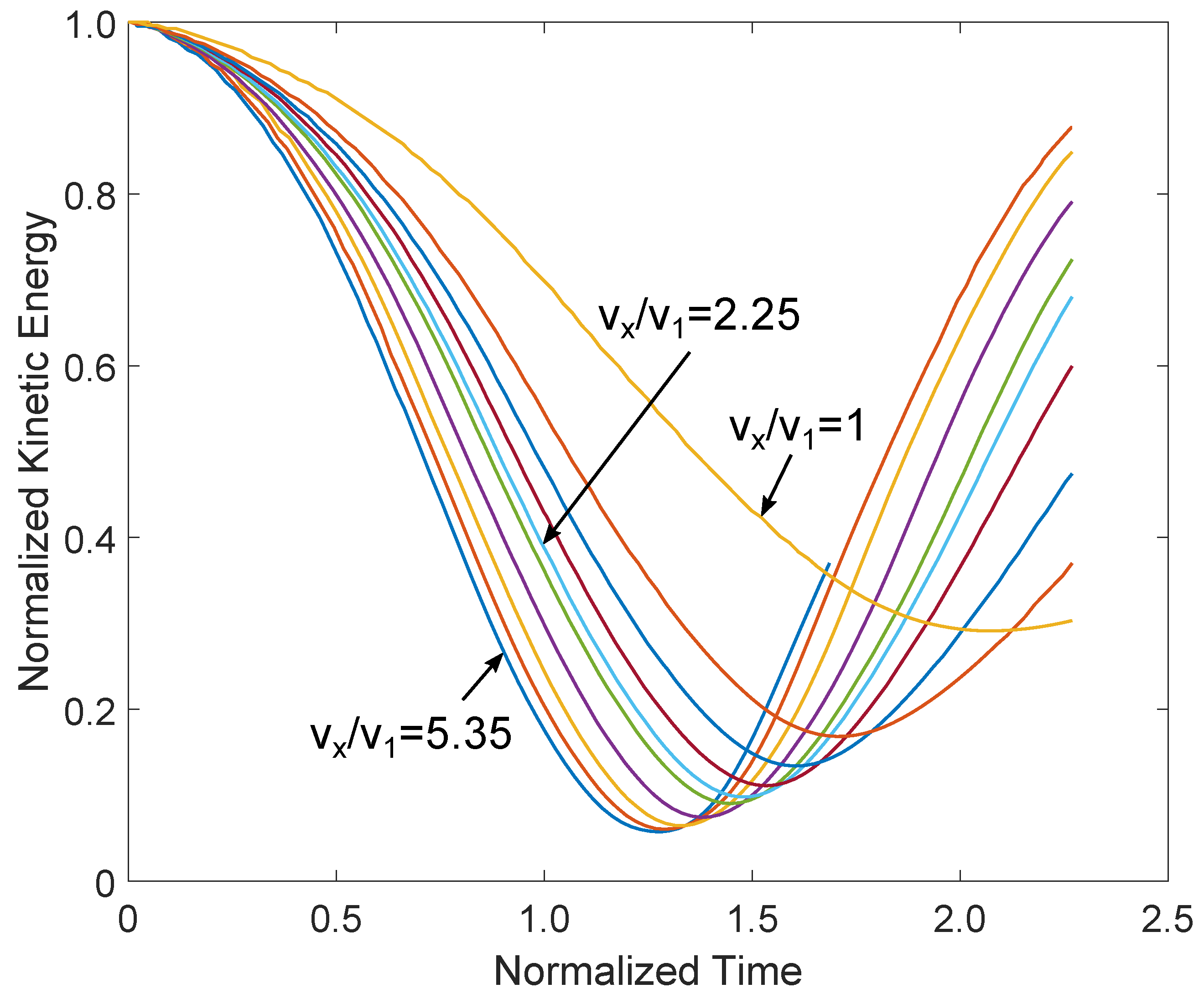
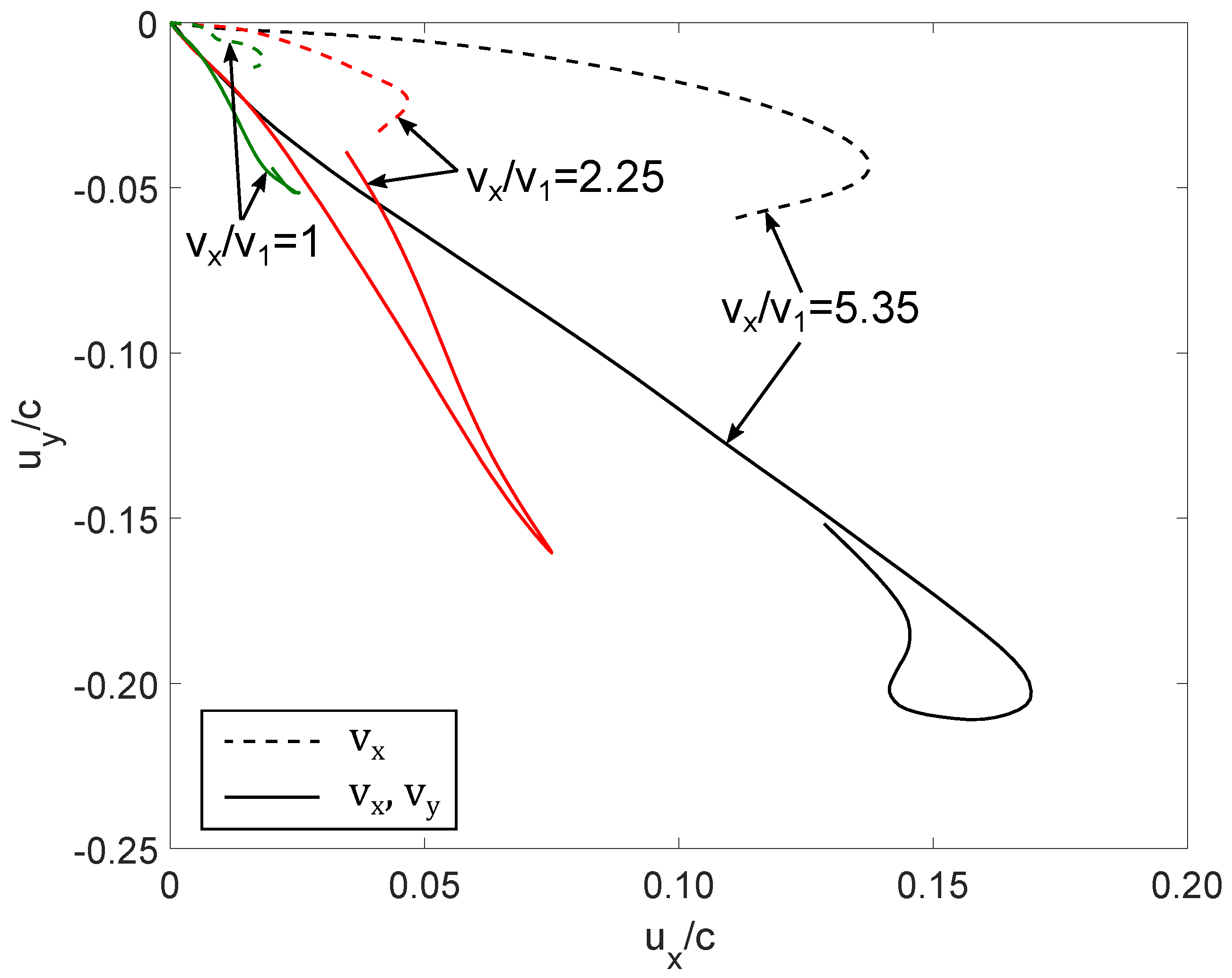
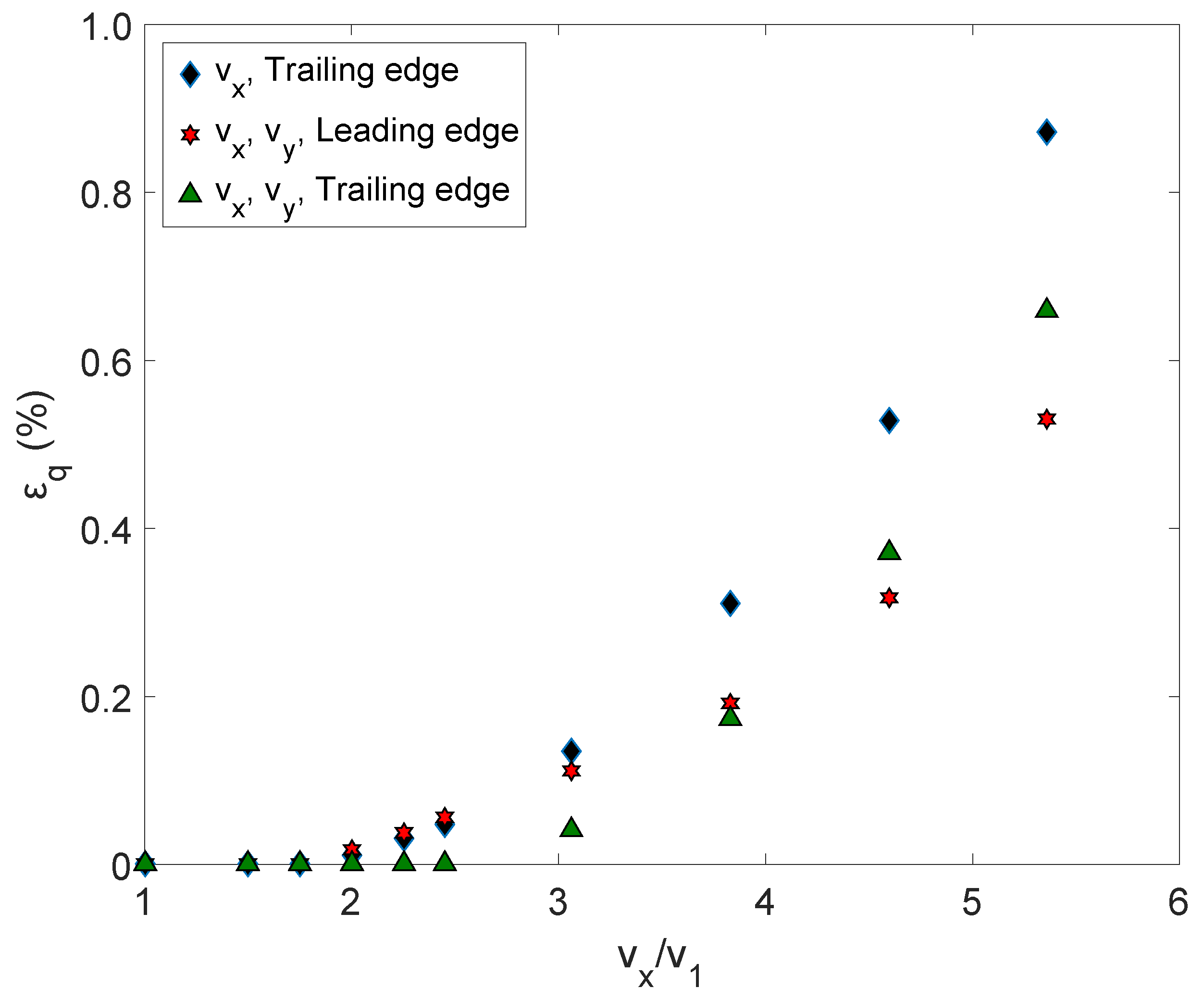
4.3. Two-Directional Velocity of the Killer Whale
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| AISI | American Iron and Steel Institute |
| BEM | Blade Element Momentum |
| CAD | Computer-Aided Design |
| CFD | Computational Fluid Dynamics |
| HACTs | Horizontal Axis Current Turbines |
| MCT | Marine Current Turbine |
| NACA | National Advisory Committee for Aeronautics |
| PVC | Polyvinyl Chloride |
| RPM | Rounds Per Minute |
| SHM | Structural Health Monitoring |
| SRKW | Southern Resident Killer Whale |
| VACTs | Vertical Axis Current Turbines |
References
- Day, A.H.; Babarit, A.; Fontaine, A.; He, Y.P.; Kraskowski, M.; Murai, M.; Penesis, I.; Salvatore, F.; Shin, H.K. Hydrodynamic modelling of marine renewable energy devices: A state of the art review. Ocean. Eng. 2015, 108, 46–69. [Google Scholar] [CrossRef] [Green Version]
- Ponta, F.L.; Jacovkis, P.M. Marine-current power generation by diffuser-augmented floating hydro-turbines. Renew. Energy 2008, 33, 665–673. [Google Scholar] [CrossRef]
- Ng, K.W.; Lam, W.H.; Ng, K.C. 2002–2012: 10 Years of Research Progress in Horizontal-Axis Marine Current Turbines. Energies 2013, 6, 1497–1526. [Google Scholar] [CrossRef] [Green Version]
- Fraenkel, P.L. Power from marine currents. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 1–14. [Google Scholar] [CrossRef]
- Commission of the European Communities, DGXII. Wave Energy Project Results: The Exploitation of Tidal Marine Currents; Report EUR16683EN; Commission of the European Communities: Brussels, Belgium, 1996. [Google Scholar]
- Bahaj, A.S.; Molland, A.F.; Chaplin, J.R.; Batten, W.M.J. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Batten, W.M.J.; McCann, G. Experimental verifications of numerical predictions for the hydrodynamic performance of horizontal axis marine current turbines. Renew. Energy 2007, 32, 2479–2490. [Google Scholar] [CrossRef]
- Batten, W.M.J.; Bahaj, A.S.; Molland, A.F.; Chaplin, J.R. Hydrodynamics of marine current turbines. Renew. Energy 2006, 31, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Barnsley, M.J.; Wellicome, J.F. Wind tunnel investigation of stall aerodynamics for a 1.0 m horizontal axis rotor. J. Wind Eng. Ind. Aerodyn. 1992, 39, 11–21. [Google Scholar] [CrossRef]
- Ellis, R.; Allmark, M.; O’Doherty, T.; Mason-Jones, A.; Ordonez-Sanchez, S.; Johannesen, K.; Johnstone, C. Design process for a scale horizontal axis tidal turbine blade. In Proceedings of the 4th Asian Wave and Tidal Energy Conference, Taipei, Taiwan, 9–13 September 2018. [Google Scholar]
- Payne, G.S.; Stallard, T.; Martinez, R. Design and manufacture of a bed supported tidal turbine model for blade and shaft load measurement in turbulent flow and waves. Renew. Energy 2017, 107, 312–326. [Google Scholar] [CrossRef]
- Hou, E.; Du, M.; Jiang, B.; Han, L.; Wu, G.; Wang, X. Study on characteristics of turbine wake and the effect of different array arrangement. In Proceedings of the Institution of Civil Engineers—Maritime Engineering; ICE: London, UK, 2021; pp. 1–12. [Google Scholar]
- Olczak, A.; Stallard, T.; Feng, T.; Stansby, P.K. Comparison of a RANS blade element model for tidal turbine arrays with laboratory scale measurements of wake velocity and rotor thrust. J. Fluids Struct. 2016, 64, 87–106. [Google Scholar] [CrossRef]
- Funke, S.W.; Farrell, P.E.; Piggott, M.D. Tidal turbine array optimisation using the adjoint approach. Renew. Energy 2014, 63, 658–673. [Google Scholar] [CrossRef]
- Pintar, M.; Kolios, A.J. Design of a Novel Experimental Facility for Testing of Tidal Arrays. Energies 2013, 6, 4117–4133. [Google Scholar] [CrossRef]
- Gillibrand, P.A.; Walters, R.A.; McIlvenny, J. Numerical Simulations of the Effects of a Tidal Turbine Array on Near-Bed Velocity and Local Bed Shear Stress. Energies 2016, 9, 852. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T.J.; Elster, J.L.; Jones, M.E.; Watson, B.E.; Copping, A.E.; Watkins, M.L.; Jepsen, R.A.; Metzinger, K. Assessment of Strike of Adult Killer Whales by an OpenHydro Tidal Turbine Blade; Technical Report; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2012. [Google Scholar]
- Payne, G.S.; Stallard, T.; Martinez, R. Experimental Investigation of Tidal Rotor Loading due to Wave, Current and Impact with Sea Animals. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–9. [Google Scholar]
- Grear, M.E.; Motley, M.R. Numerical Modeling of the Impact Response of Tidal Devices and Marine Mammals. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Copping, A.; Grear, M.; Jepsen, R.; Chartrand, C.; Gorton, A. Understanding the potential risk to marine mammals from collision with tidal turbines. Int. J. Mar. Energy 2017, 19, 110–123. [Google Scholar] [CrossRef]
- Grear, M. Characterization of Marine Mammal Biomechanics to Evaluate Tidal Turbine Collision Impact. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2018. [Google Scholar]
- Hammar, L.; Eggertsen, L.; Andersson, S.; Ehnberg, J.; Arvidsson, R.; Gullström, M.; Molander, S. A Probabilistic Model for Hydrokinetic Turbine Collision Risks: Exploring Impacts on Fish. PLoS ONE 2015, 10, e0117756. [Google Scholar] [CrossRef] [Green Version]
- Onoufriou, J.; Brownlow, A.; Moss, S.; Hastie, G.; Thompson, D. Empirical determination of severe trauma in seals from collisions with tidal turbine blades. J. Appl. Ecol. 2019, 56, 1712–1724. [Google Scholar] [CrossRef]
- Pitman, R.L.; Ensor, P. Three different forms of killer whales in Antarctic waters. J. Cetacean Res. Manag. 2003, 5, 131–139. [Google Scholar]
- Pitman, R.L.; Perryman, W.L.; LeRoi, D.; Eilers, E. A dwarf form of killer whale in Antarctica. J. Mammal. 2007, 88, 43–48. [Google Scholar] [CrossRef]
- Ford, J.K.B. Killer Whale: Orcinus orca. In Encyclopedia of Marine Mammals, 2nd ed.; Perrin, W.F., Würsig, B., Thewissen, J.G.M., Eds.; Academic Press: London, UK, 2009; pp. 650–657. [Google Scholar]
- Douglas, C.A.; Harrison, G.P.; Chick, J.P. Life cycle assessment of the Seagen marine current turbine. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2008, 222, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Shiekh Elsouk, M.N.; Santa Cruz, A.; Guillou, S. Review on the characterization and selection of the advanced materials for tidal turbine blades. In Proceedings of the 7th International Conference on Ocean Energy, Cherbourg, France, 12–14 June 2018. [Google Scholar]
- Gavriilidis, I.; Huang, Y. Dynamic response of tidal turbine blade under impact load. In Proceedings of the 2021 World Congress on Advances in Structural Engineering and Mechanics (ASEM21), GECE, Seoul, Korea, 23–26 August 2021. [Google Scholar]
- Hepperle, M. JAVAFOIL User’s Guide. Available online: https://www.mh-aerotools.de/airfoils/jf_users_manual.htm (accessed on 25 October 2021).
- Abbott, I.H.; Von Doenhoff, A.E. Theory of Wing Sections; Dover Publications: New York, NY, USA, 1959. [Google Scholar]
- Dassault Systèmes. SolidWorks. Available online: https://www.3ds.com/prod./solidworks/ (accessed on 25 October 2021).
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Hibbitt, H.; Karlsson, B.; Sorensen, P. Abaqus Analysis User’s Manual Version 2016; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2016. [Google Scholar]
- Baddoo, N.R. Stainless steel in construction: A review of research, applications, challenges and opportunities. J. Constr. Steel Res. 2008, 64, 1199–1206. [Google Scholar] [CrossRef]
- Gedge, G. Structural uses of stainless steel—Buildings and civil engineering. J. Constr. Steel Res. 2008, 64, 1194–1198. [Google Scholar] [CrossRef]
- Rossi, B. Discussion on the use of stainless steel in constructions in view of sustainability. Thin-Walled Struct. 2014, 83, 182–189. [Google Scholar] [CrossRef] [Green Version]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Lee, S.; Barthelat, F.; Hutchinson, J.W.; Espinosa, H.D. Dynamic failure of metallic pyramidal truss core materials—Experiments and modeling. Int. J. Plast. 2006, 22, 2118–2145. [Google Scholar] [CrossRef]
- Campbell-Malone, R.P. Biomechanics of North Atlantic Right Whale Bone: Mandibular Fracture as a Fatal Endpoint for Blunt Vessel-Whale Collision Modeling. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Asserin, J.; Zahouani, H.; Humbert, P.; Couturaud, V.; Mougin, D. Measurement of the friction coefficient of the human skin in vivo: Quantification of the cutaneous smoothness. Colloids Surf. B Biointerfaces 2000, 19, 1–12. [Google Scholar] [CrossRef]
- Whelan, J.I.; Stallard, T. Arguments for modifying the geometry of a scale model rotor. In Proceedings of the 9th European Wave and Tidal Energy Conference (EWTEC2011), Southampton, UK, 5–9 September 2011. [Google Scholar]
- Bashistakumar, M.; Pushkal, B. Finite element analysis of orthogonal cutting forces in machining AISI 1020 steel by using a carbide tip tool. J. Eng. Sci. 2018, 5, A1–A10. [Google Scholar] [CrossRef]
- Worden, K.; Farrar, C.R.; Manson, G.; Park, G. The fundamental axioms of structural health monitoring. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1639–1664. [Google Scholar] [CrossRef]
- Li, D.; Ho, S.C.M.; Song, G.; Ren, L.; Li, H. A review of damage detection methods for wind turbine blades. Smart Mater. Struct. 2015, 24, 033001. [Google Scholar] [CrossRef]
- Noren, D.P.; Johnson, A.H.; Rehder, D.; Larson, A. Close approaches by vessels elicit surface active behaviors by southern resident killer whales. Endanger. Species Res. 2009, 8, 179–192. [Google Scholar] [CrossRef]
- Noren, D.P. Estimated field metabolic rates and prey requirements of resident killer whales. Mar. Mammal Sci. 2011, 27, 60–77. [Google Scholar] [CrossRef] [Green Version]
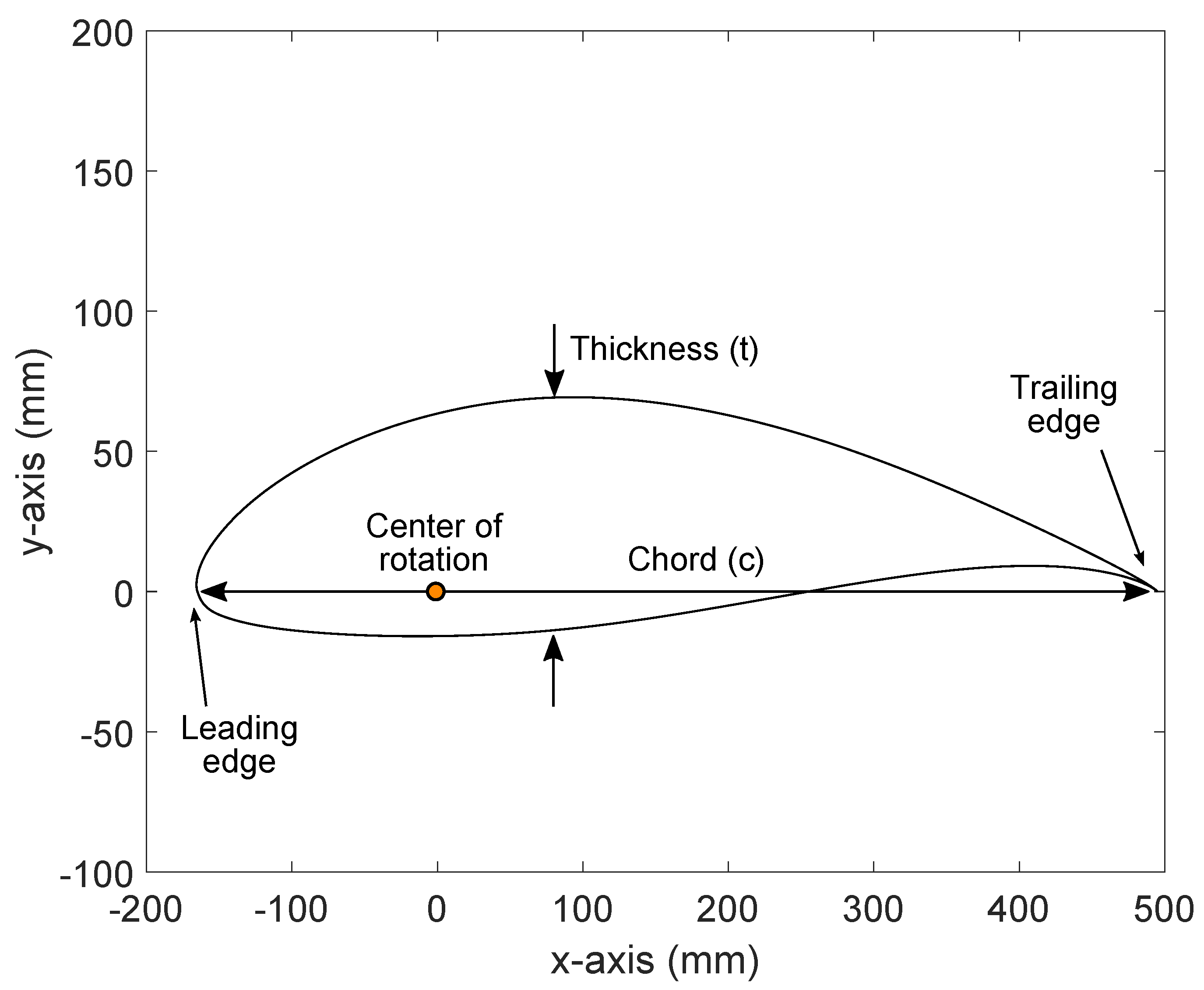
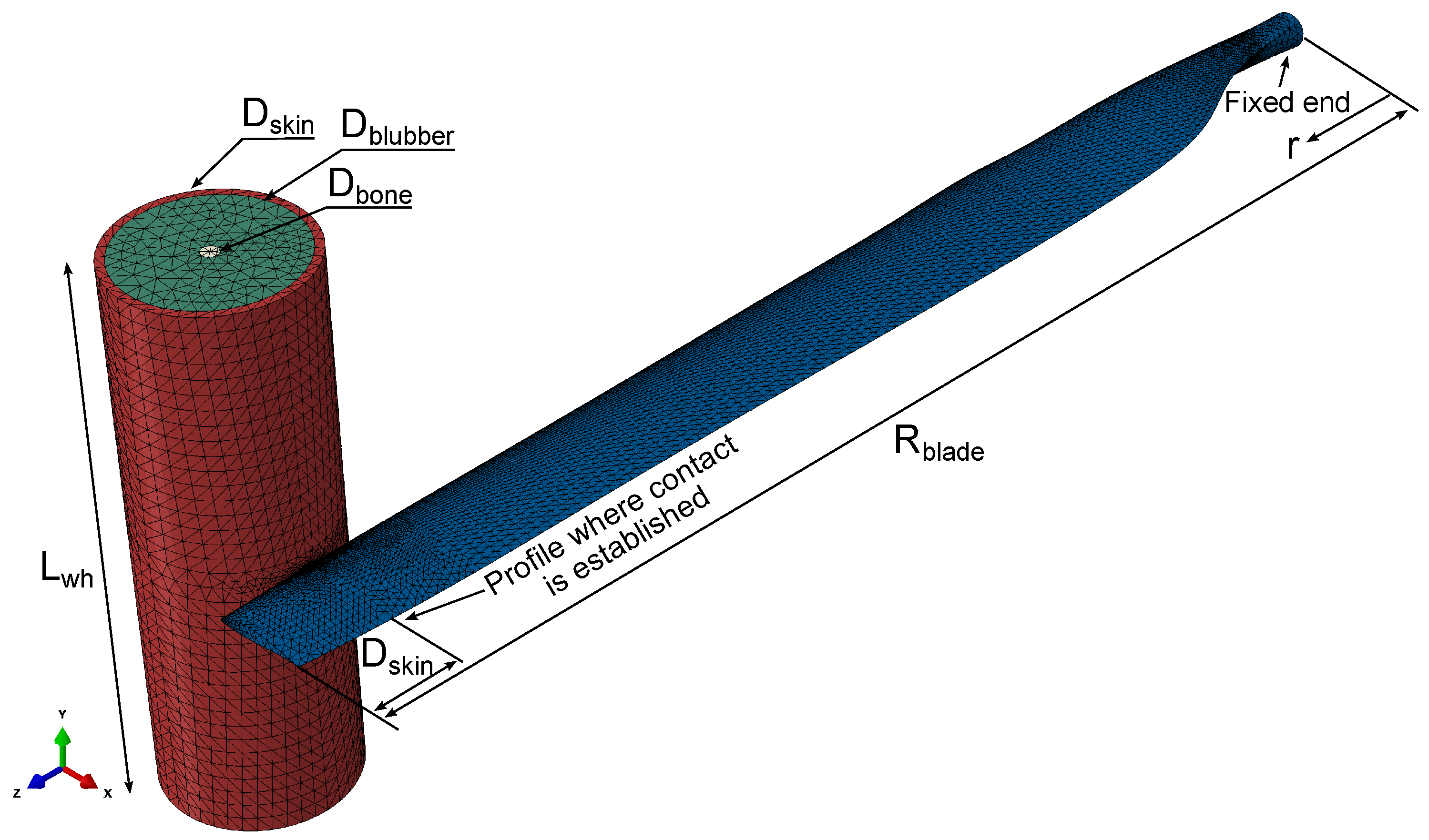
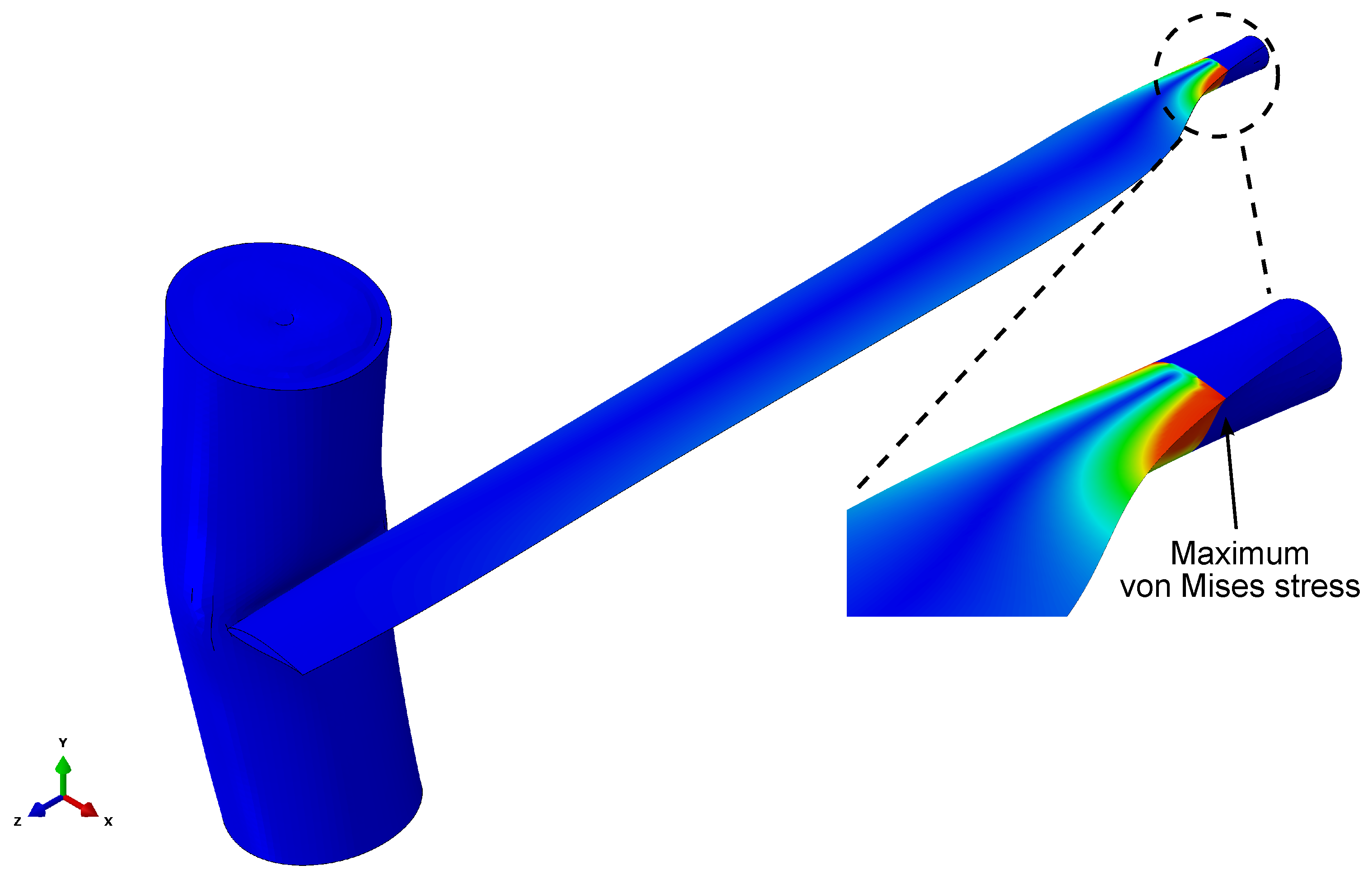

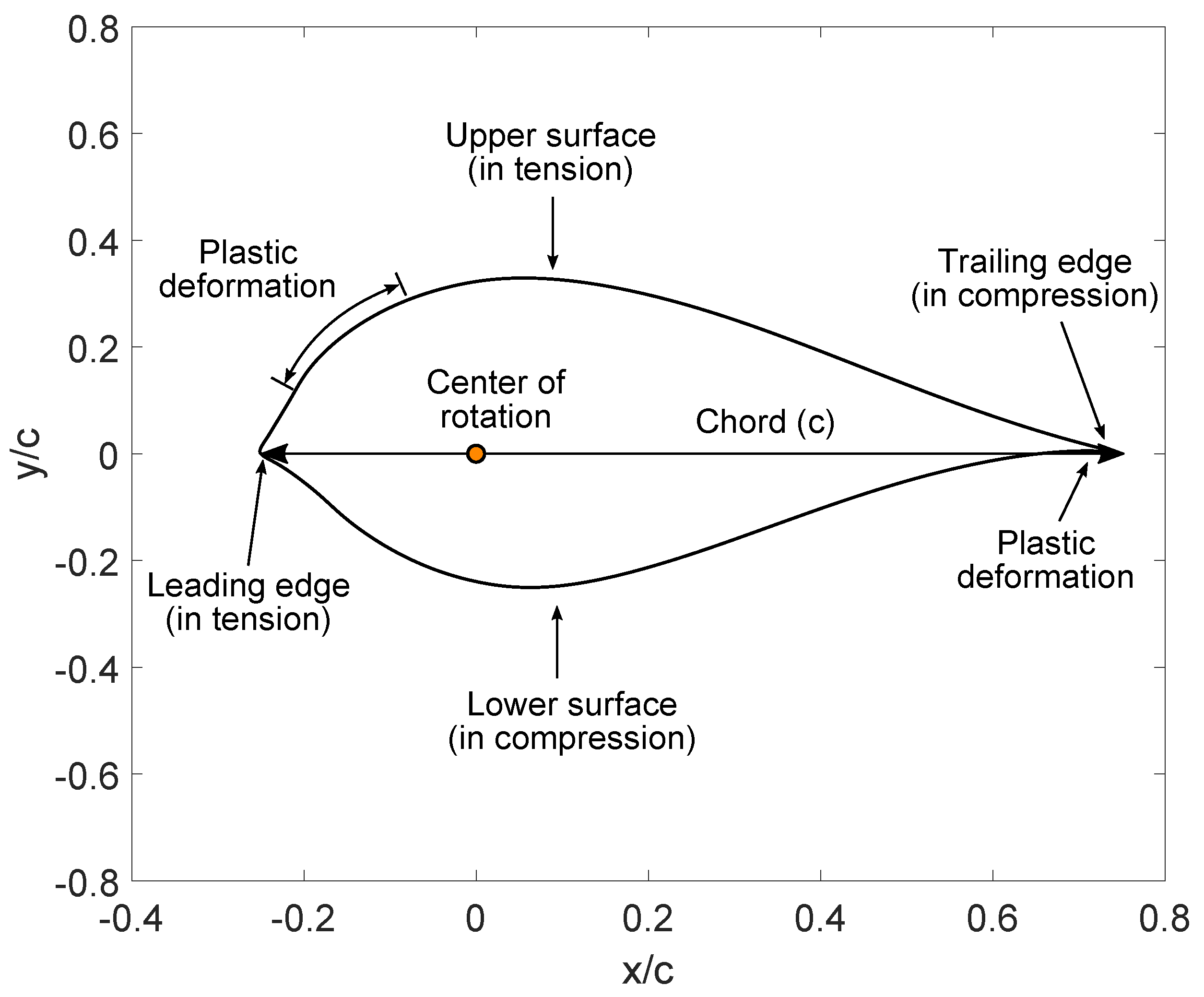
| r (mm) | c (mm) | t/c (%) | t (mm) | Twist (°) | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 28.0 | 252.3 | 100.00 | 252.30 | - |
| 0.1 | 900 | 48.3 | 453.0 | 58.00 | 252.30 | 23.00 |
| 0.2 | 1800 | 111.7 | 1005.0 | 25.00 | 251.25 | 19.00 |
| 0.3 | 2700 | 110.9 | 998.4 | 23.45 | 234.15 | 12.35 |
| 0.4 | 3600 | 104.5 | 940.8 | 21.90 | 205.95 | 9.96 |
| 0.5 | 4500 | 98.8 | 889.5 | 20.35 | 181.05 | 8.91 |
| 0.6 | 5400 | 93.2 | 838.8 | 18.80 | 157.65 | 8.00 |
| 0.7 | 6300 | 88.3 | 794.7 | 17.25 | 137.10 | 7.03 |
| 0.8 | 7200 | 85.7 | 771.6 | 15.70 | 121.20 | 6.21 |
| 0.9 | 8100 | 83.0 | 747.3 | 14.15 | 105.75 | 5.74 |
| 0.99 | 8910 | 73.3 | 660.0 | 12.60 | 83.10 | 5.50 |
| Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | (K) | (K) | |
|---|---|---|---|---|---|
| 7900 | 200 | 0.3 | 1673 | 293 | |
| ()(MPa) | B(MPa) | n | c | () | m |
| 310 | 1000 | 0.65 | 0.07 | 1 | 1.00 |
| (m) | (m) | (m) | (m) |
|---|---|---|---|
| 1.200 | 1.091 | 0.109 | 3.557 |
| Density (kg/) | Young’s Modulus (GPa) | Poisson’s Ratio | (K) | (K) | |
|---|---|---|---|---|---|
| 7870 | 200 | 0.3 | 1798 | 293 | |
| A()(MPa) | B(MPa) | n | c | (s−1) | m |
| 333 | 737 | 0.15 | 0.008 | 1 | 1.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavriilidis, I.; Huang, Y. Finite Element Analysis of Tidal Turbine Blade Subjected to Impact Loads from Sea Animals. Energies 2021, 14, 7208. https://doi.org/10.3390/en14217208
Gavriilidis I, Huang Y. Finite Element Analysis of Tidal Turbine Blade Subjected to Impact Loads from Sea Animals. Energies. 2021; 14(21):7208. https://doi.org/10.3390/en14217208
Chicago/Turabian StyleGavriilidis, Ilias, and Yuner Huang. 2021. "Finite Element Analysis of Tidal Turbine Blade Subjected to Impact Loads from Sea Animals" Energies 14, no. 21: 7208. https://doi.org/10.3390/en14217208






