Energy Saving Approach for an Electric Pump Using a Fuzzy Controller
Abstract
:1. Introduction
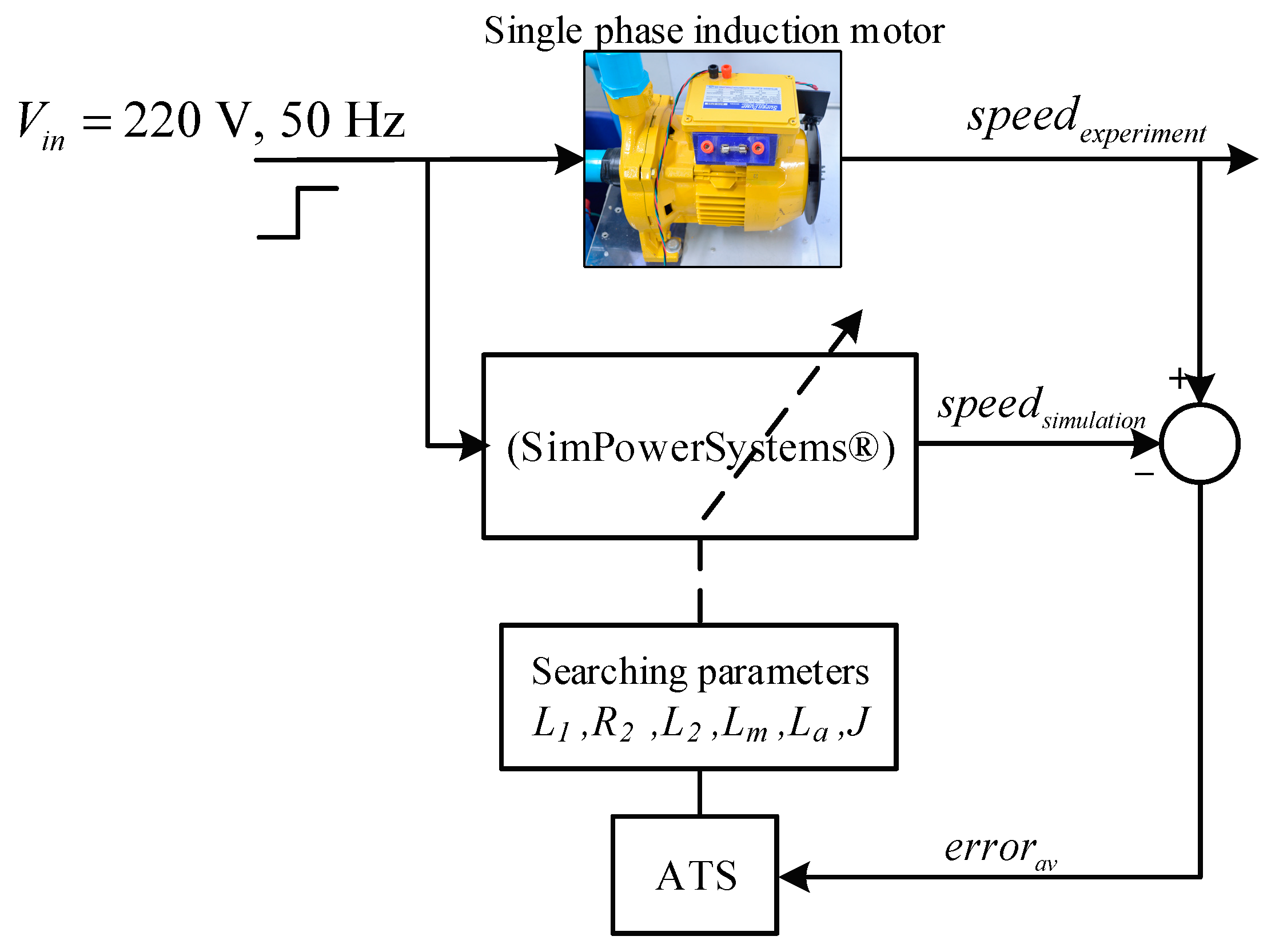
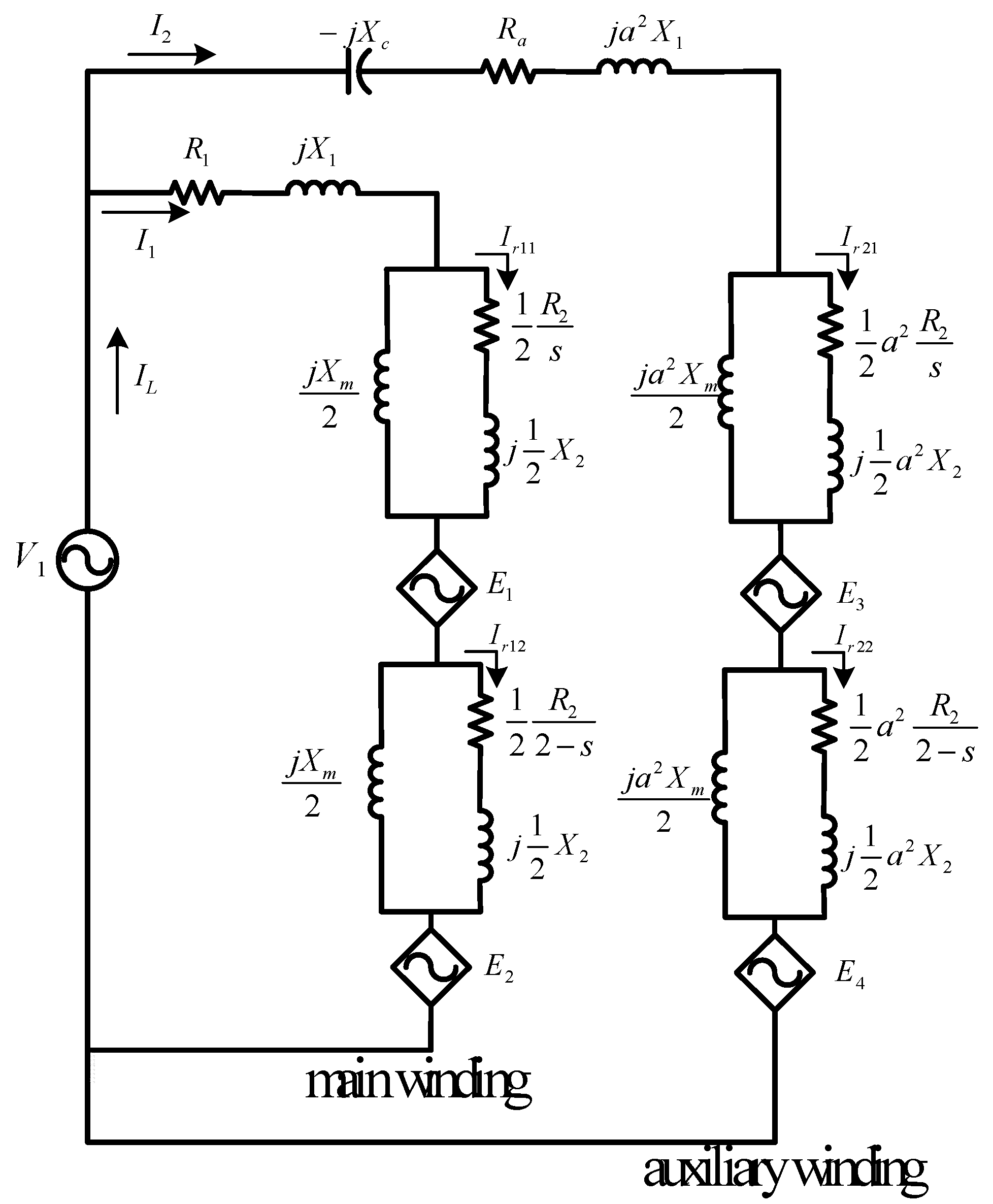
2. SPIM Parameters Identification
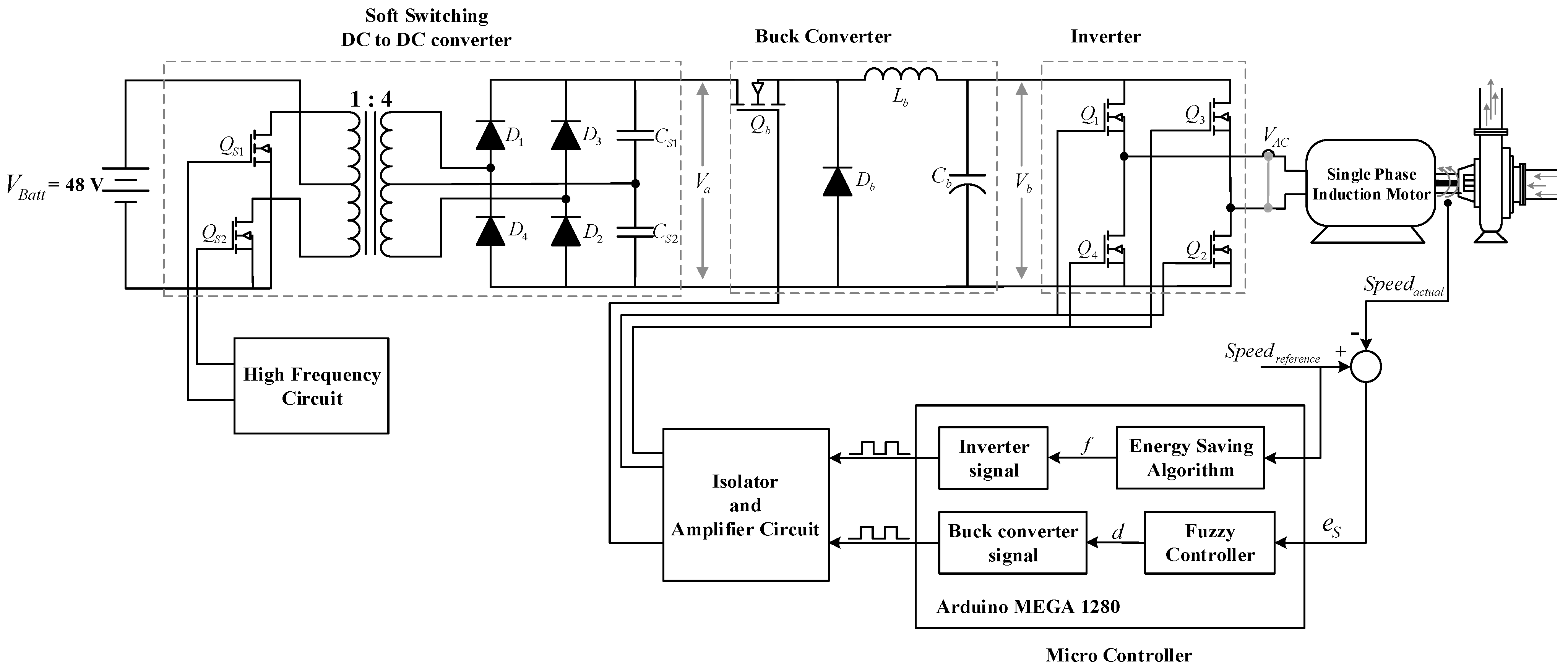
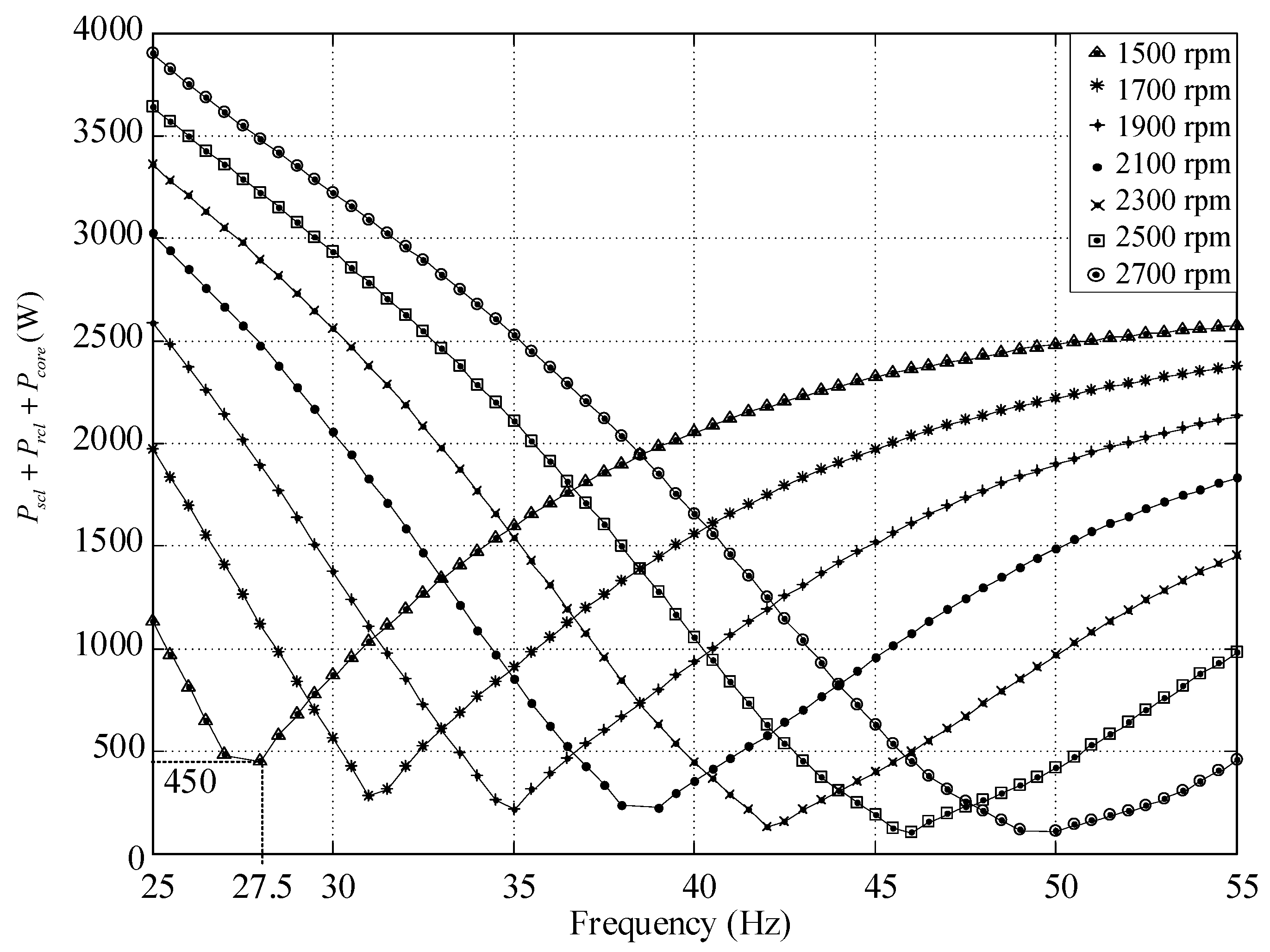
3. The Energy-Saving Algorithm
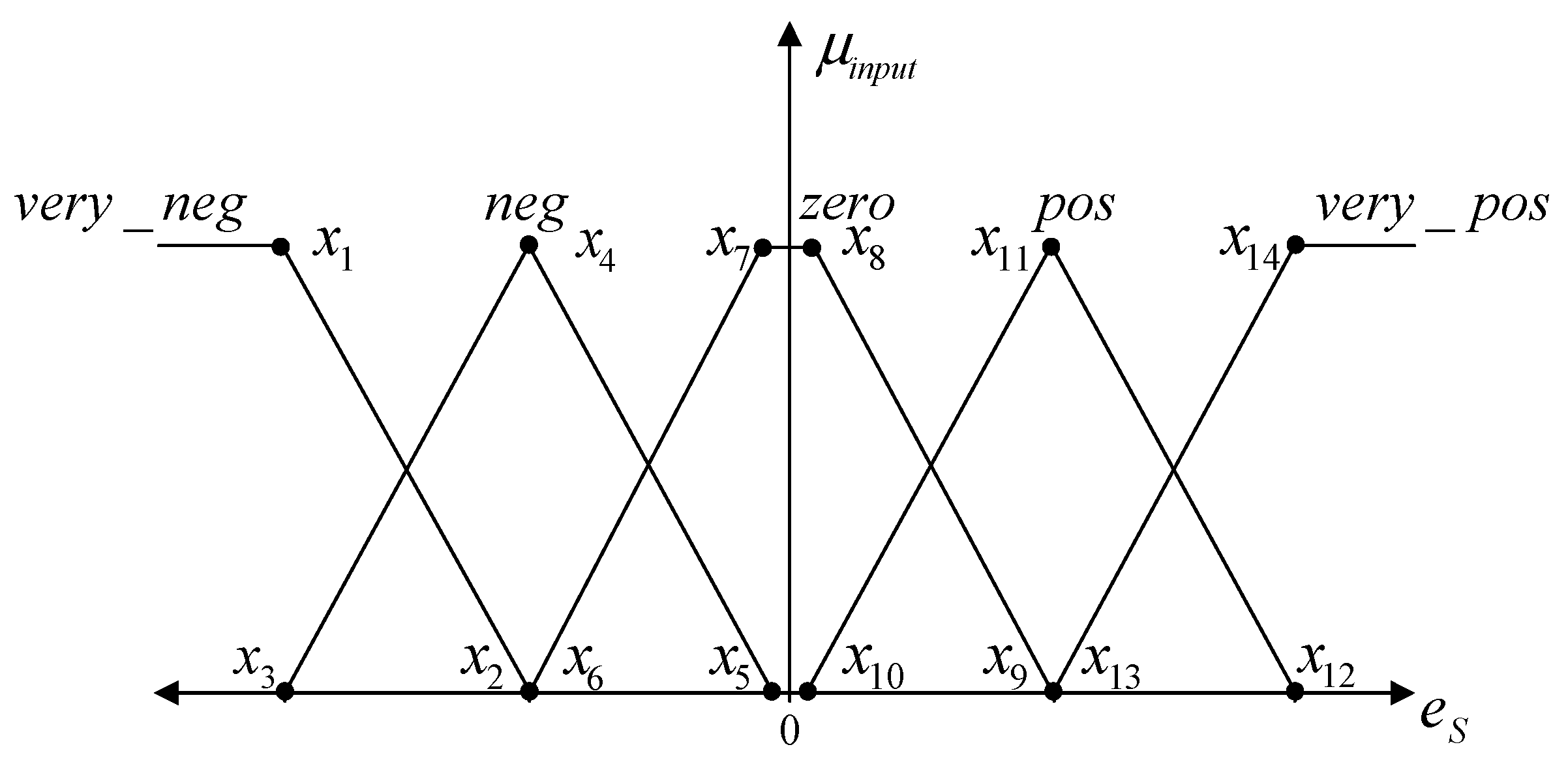
4. FUZZY Controller Design
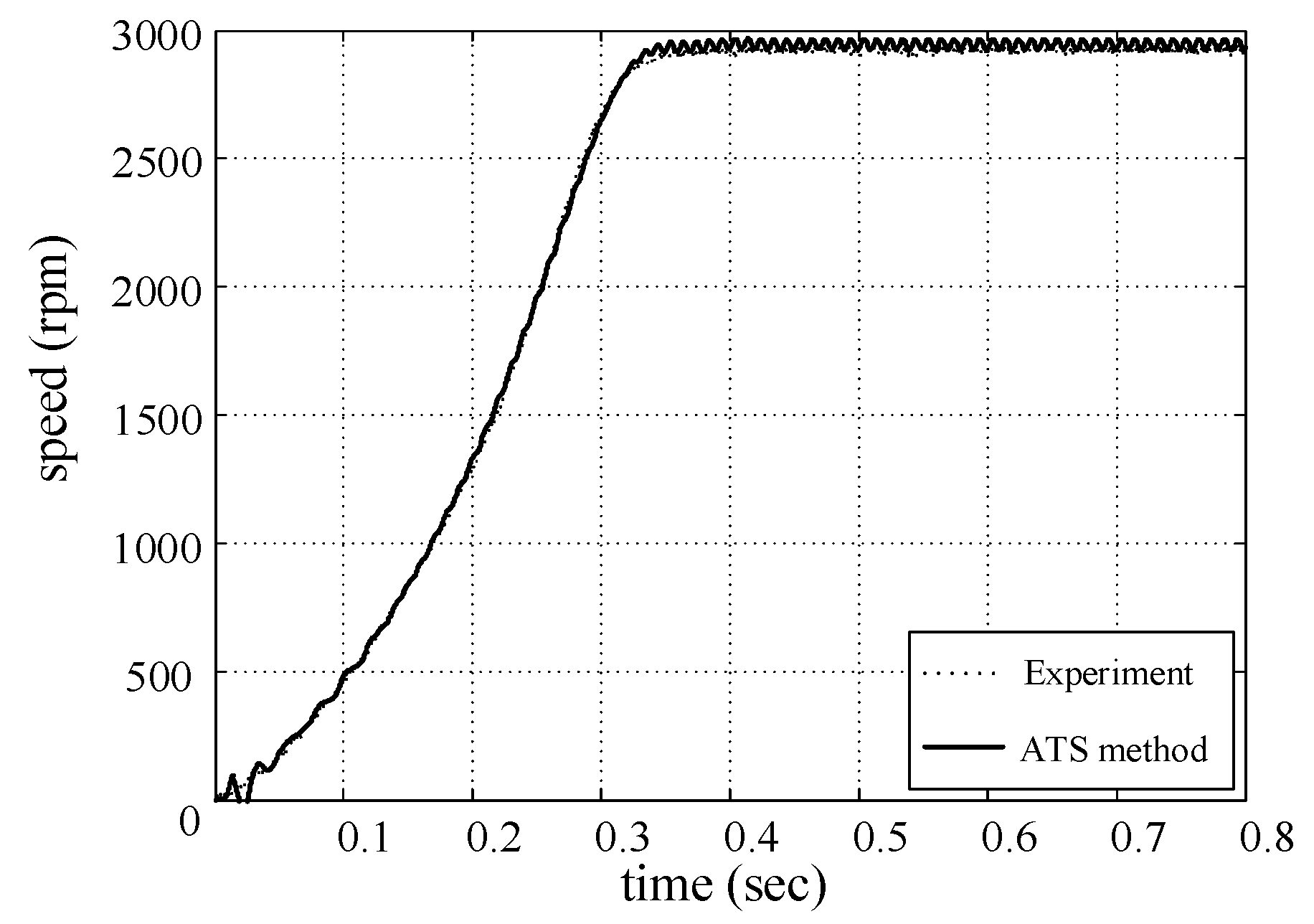
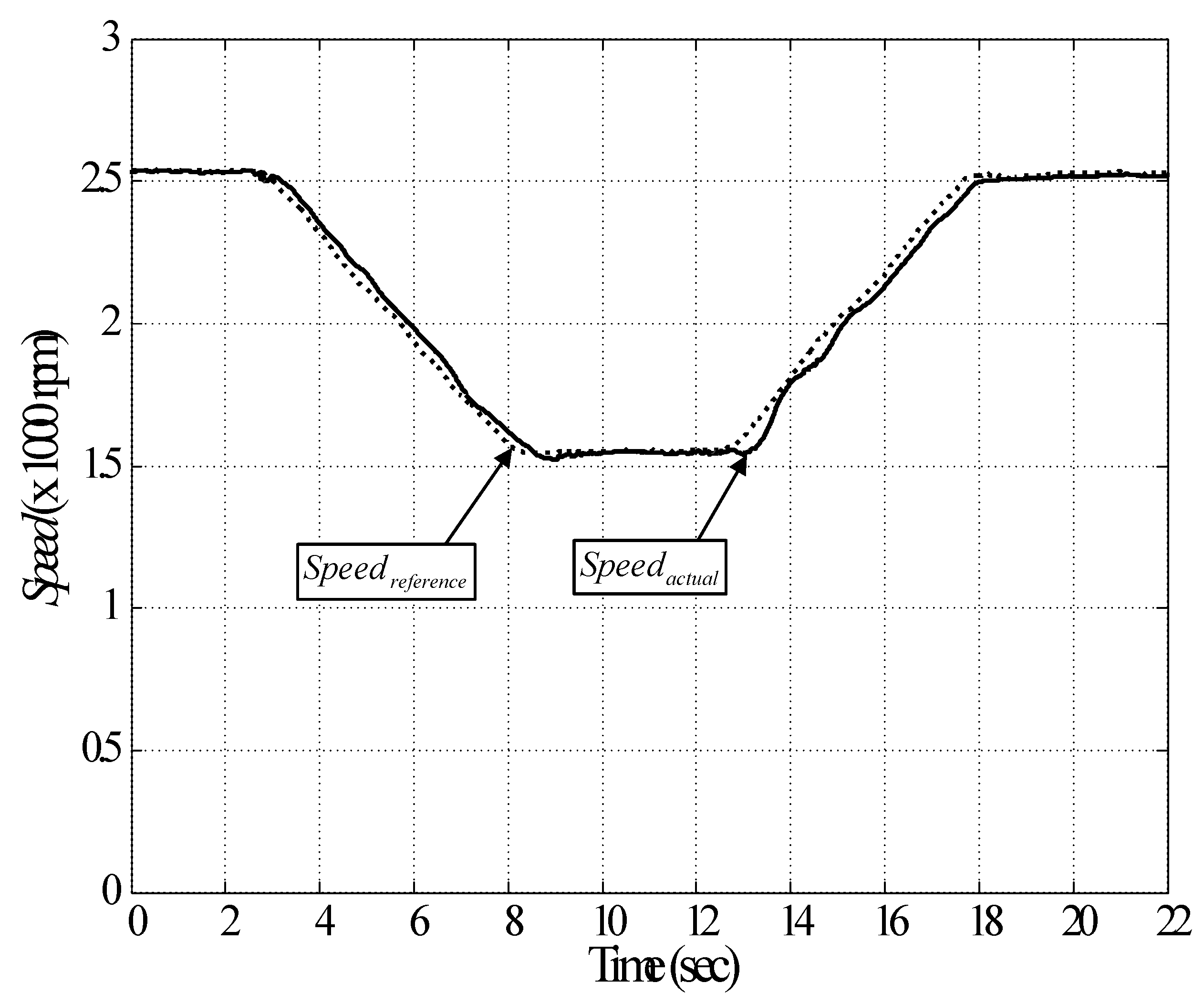
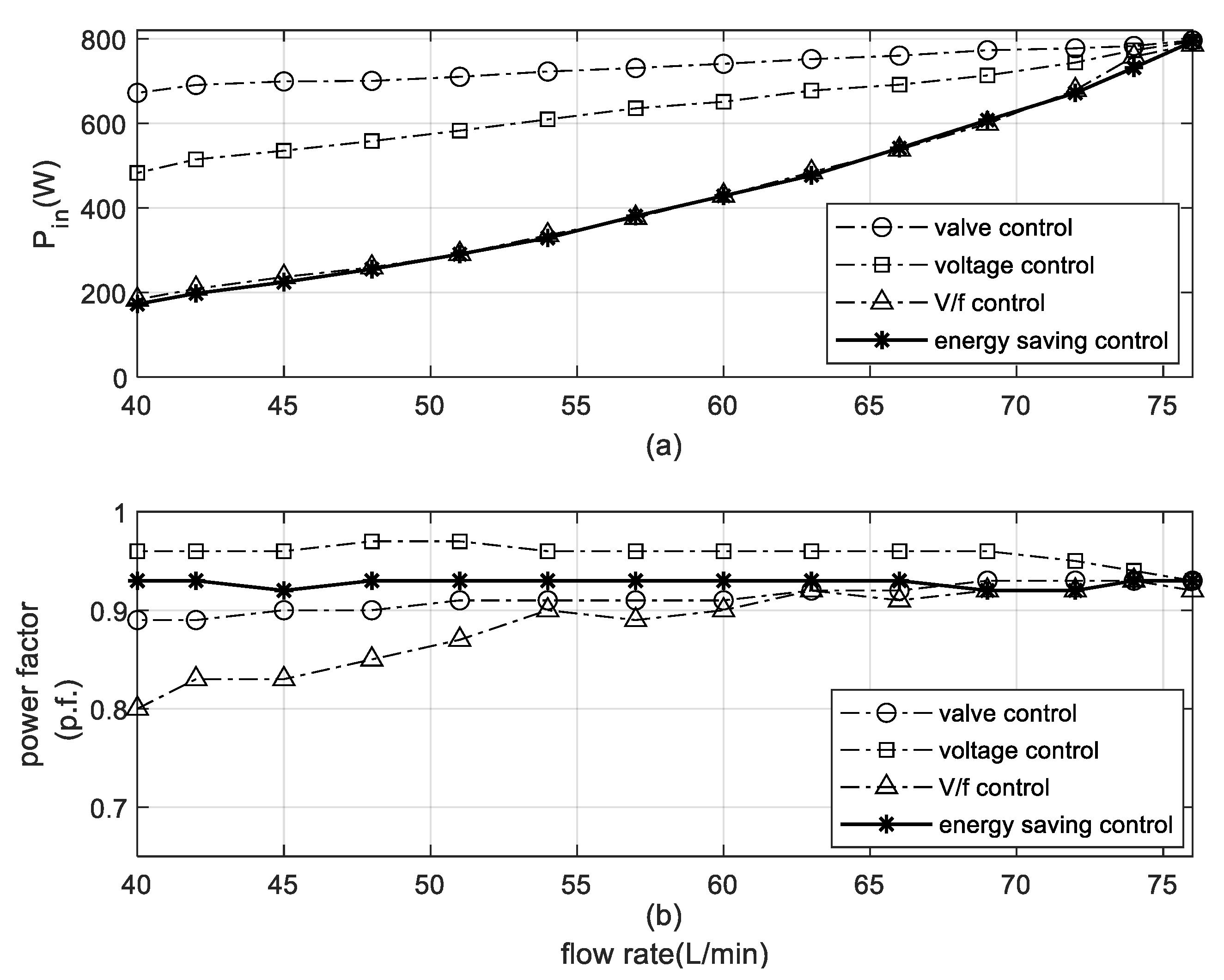
5. The Experimental Result
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| AC | alternating current |
| ATS | adaptive Tabu search |
| DC | direct current |
| V/f | voltage per frequency |
| SCR | silicon control rectifier |
| SPIM | single-phase induction motor |
| C | motor capacitance (F) |
| Cb | buck converter capacitance (F) |
| I1 | main coil current (A) |
| I2 | auxiliary coil current (A) |
| J | moment of inertia (kg·m2) |
| Lb | buck converter inductance (H) |
| Lm | mutual inductance (H) |
| Lmutual | mutual inductance (H) |
| L1 | main coil inductance (H) |
| L2 | rotor inductance (H) |
| La | auxiliary coil inductance (H) |
| NT | number of data |
| P | number of poles |
| Pcore | core copper loss (W) |
| Plosses | total power losses (W) |
| Prcl | rotor copper loss (W) |
| Pscl | stator copper loss (W) |
| Ra | auxiliary coil resistance (Ω) |
| R1 | main coil resistance (Ω) |
| R2 | rotor resistance (Ω) |
| Speedactual | actual speed (rpm) |
| Speedexperiment | experimental speed (rpm) |
| Speedreference | reference speed (rpm) |
| Speedsimulation | simulated speed (rpm) |
| VAC | input voltage of SPIM (V) |
| Va | input voltage for buck converter (V) |
| Vb | output voltage of buck converter (V) |
| Vbatt | battery voltage (V) |
| V1 | input voltage of the main and auxiliary coils (V) |
| Xm | magnetizing reactance (Ω) |
| X2 | rotor reactance (Ω) |
| Zf | forward impedance (Ω) |
| Zb | backward impedance (Ω) |
| a | turn ratio of coil |
| d | duty cycle (0–100%) |
| errorav | average errors of the motor speed (rpm) |
| es | speed error (rpm) |
| f | frequency (Hz) |
| kc | coefficient of core loss |
| S | slip of induction machine |
| x1,x2,…,x14 | input membership function of fuzzy controller |
| y1,y2,…,y5 | output membership function of fuzzy controller |
References
- Salvador, R.; Bautista-Capetillo, C.; Playán, E. Irrigation performance in private urban landscapes: A study case in Zaragoza (Spain). Landsc. Urban Plan. 2011, 100, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Farooq, M.; Hussain, M.; Ul-Allah, S.; Siddique, K.H.M. Physiological and agronomic approaches for improving water-use efficiency in crop plants. Agric. Water Manag. 2019, 219, 95–108. [Google Scholar] [CrossRef]
- Law, J.D.; Lipo, T.A. A single phase induction motor voltage controller with improved performance. In Proceedings of the 1984 IEEE Power Electronics Specialists Conference, Gaithersburg, MD, USA, 18–21 June 1984. [Google Scholar]
- Jannati, M.; Anbaran, S.A.; Asgari, S.H.; Goh, W.Y.; Monadi, A.; Aziz, M.J.A.; Idris, N.R.N. A review on Variable Speed Control techniques for efficient control of Single-Phase Induction Motors: Evolution, classification, comparison. Renew. Sustain. Energy Rev. 2017, 75, 1306–1319. [Google Scholar] [CrossRef]
- Piyarat, W.; Hothongkham, P.; Charumit, C.; Kinnares, V. Simple speed control of an asymmetrical type two-phase induction motor drive. In Proceedings of the ECTI-CON2010: The 2010 ECTI International Confernce on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Mai, Thailand, 19–21 May 2010. [Google Scholar]
- Collins, E.R. Torque and slip behavior of single-phase induction motors driven from variable-frequency supplies. IEEE Trans. Ind. Appl. 1992, 28, 710–715. [Google Scholar] [CrossRef]
- Gastli, A.; Matsui, N. Stator flux controlled V/f PWM inverter with identification of IM parameters (induction motors). IEEE Trans. Ind. Electron. 1992, 39, 334–340. [Google Scholar] [CrossRef]
- Kafle, B.; Basnet, P.; Ghimire, A.; Lamichhane, A. Speed Control of a Single Phase Induction Motor using the V/f Method. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019. [Google Scholar]
- Qudsi, O.A.; Rosalina, I.I.; Yanaratri, D.S. V/f SPWM Inverter for Single-phase Induction Motor Contrller Using Adaptive Neuro-Fuzzy Inference System. In Proceedings of the 2018 3rd International Conference on Information Technology, Information System and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 13–14 November 2018. [Google Scholar]
- Batarseh, I.; Harb, A. Soft-Switching dc-dc Converters. In Power Electronics: Circuit Analysis and Design; Batarseh, I., Harb, A., Eds.; Springer International Publishing: Cham, Germany, 2018; pp. 347–460. [Google Scholar]
- Yung-Fu, H.; Chih-Wen, L.; Yoshihiro, K. Soft-switching PWM full-bridge DC-DC converter with energy recovery transformer and auxiliary passive lossless snubbers. In Proceedings of the INTELEC 07—29th International Telecommunications Energy Conference, Rome, Italy, 30 September–4 October 2007. [Google Scholar]
- Sabate, J.A.; Vlatkovic, V.; Ridley, R.B.; Lee, F.C.; Cho, B.H. Design considerations for high-voltage high-power full-bridge zero-voltage-switched PWM converter. In Proceedings of the Fifth Annual Proceedings on Applied Power Electronics Conference and Exposition, Los Angeles, CA, USA, 1–16 March 1990. [Google Scholar]
- Ma, W.; Bai, L. Energy-Saving Principles and Technologies for Induction Motors; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Sundareswaran, K. An improved energy-saving scheme for capacitor-run induction motor. IEEE Trans. Ind. Electron. 2001, 48, 238–240. [Google Scholar] [CrossRef]
- Park, S.-K.; Lim, H.-W.; Cho, G.-b.; Baek, H.L.; Lee, S.-K.; Chang, Y.-H.; Seo, J.-Y. A study on the reduction of in-rush current for energy saving of single phase induction motor. in ICEMS’2001. In Proceedings of the Fifth International Conference on Electrical Machines and Systems (IEEE Cat. No.01EX501), Shenyang, China, 18–20 August 2001. [Google Scholar]
- Thanyaphirak, V.; Kinnares, V.; Kunakorn, A. PWM AC chopper control schemes for energy saving of single-phase induction motors. In Proceedings of the 2012 10th International Power & Energy Conference (IPEC), Ho Chi Minh City, Vietnam, 12–14 December 2012. [Google Scholar]
- Gorbunov, R.L. Power conversion quality of AC buck voltage converter in comparison with SCR voltage converter. In Proceedings of the 2017 18th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 29 June–3 July 2017. [Google Scholar]
- Famouri, P.; Cathey, J.J. Loss minimization control of an induction motor drive. IEEE Trans. Ind. Appl. 1991, 27, 32–37. [Google Scholar] [CrossRef]
- Kirschen, D.S.; Novotny, D.W.; Suwanwisoot, W. Minimizing Induction Motor Losses by Excitation Control in Variable Frequency Drives. IEEE Trans. Ind. Appl. 1984, IA-20, 1244–1250. [Google Scholar] [CrossRef]
- Kusko, A.; Galler, D. Control Means for Minimization of Losses in AC and DC Motor Drives. IEEE Trans. Ind. Appl. 1983, IA-19, 561–570. [Google Scholar] [CrossRef]
- Molina, J.J.M.; Scarpetta, J.M.R. Optimal U/f Control for Induction Motors. IFAC Proc. Vol. 2002, 35, 329–333. [Google Scholar] [CrossRef]
- Sridharan, S.; Krein, P.T. Induction motor drive design for traction application based on drive-cycle energy minimization. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014. [Google Scholar]
- Yin, S.; Meng, D.; Diao, L.; Li, Y.; Dong, K. Improved hybrid loss control with optimized flux for traction induction motor under light load. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 485–492. [Google Scholar] [CrossRef]
- Puangdownreong, D.; Areerak, K.-N.; Srikaew, A.; Sujitjorn, S.; Totarong, P. System identification via Adaptive Tabu Search. In Proceedings of the 2002 IEEE International Conference on Industrial Technology, Bankok, Thailand, 11–14 December 2002. [Google Scholar]
- Sujitjorn, S.; Kulworawanichpong, T.; Puangdownreong, D.; Areerak, K.-N. Adaptive Tabu Search and Applications in Engineering Design. In Proceedings of the Integrated Intelligent Systems for Engineering Design, Amsterdam, The Netherlands, 30 May 2006; pp. 233–257. [Google Scholar]
- Ketthanom, C.; Artameeyanant, P.; Pratumshat, V. Application of Adaptive Tabu Search to PIDA Controller Design. In Proceedings of the 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 10–13 July 2019. [Google Scholar]
- Guinee, R.A.; Lyden, C. Motor parameter identification using response surface simulation and analysis. In Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148), Arlington, VA, USA, 25–27 June 2001. [Google Scholar]
- Warachart, S.-K.; Lumyong, P. Characteristics evaluation of 3 phase induction motors based on an acceleration method with increasing moment of inertia technique. In Proceedings of the 4th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, 2003. SDEMPED 2003, Atlanta, GA, USA, 24–26 August 2003. [Google Scholar]
- Andoh, F. Moment of Inertia Identification Using the Time Average of the Product of Torque Reference Input and Motor Position. IEEE Trans. Power Electron. 2007, 22, 2534–2542. [Google Scholar] [CrossRef]
- Pakdeeto, J.; Chanpittayagit, R.; Areerak, K.-N.; Areerak, K.-L. The Optimal Controller Design of Buck-Boost Converter by using Adaptive Tabu Search Algorithm Based on State-Space Averaging Model. J. Electr. Eng. Technol. 2017, 12, 1146–1155. [Google Scholar] [CrossRef] [Green Version]
- Udomsuk, S.; Areerak, K.-L.; Areerak, K.-N.; Srikaew, A. Parameters identification of separately excited DC motor using adaptive tabu search technique. In Proceedings of the 2010 International Conference on Advances in Energy Engineering, Beijing, China, 19–20 June 2010. [Google Scholar]
- Boldea, I.; Nasar, S.A. The Induction Machines Design Handbook; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2010. [Google Scholar]
- Mannan, A.; Murata, T.; Tamura, J.; Tsuchiya, T. Efficiency optimized speed control of field oriented induction motor including core loss. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No.02TH8579), Osaka, Japan, 2–5 April 2002. [Google Scholar]
- Piazza, M.C.D.; Luna, M.; Pucci, M. Electrical Loss Minimization Technique for Wind Generators Based on a Comprehensive Dynamic Modeling of Induction Machines. IEEE Trans. Ind. Appl. 2017, 53, 3696–3706. [Google Scholar] [CrossRef]
- Bazzi, A.M.; Krein, P.T. Review of Methods for Real-Time Loss Minimization in Induction Machines. IEEE Trans. Ind. Appl. 2010, 46, 2319–2328. [Google Scholar] [CrossRef]
- Li, Y.; Adeleke, O.P.; Xu, X. Methods and applications of energy saving control of in-wheel motor drive system in electric vehicles: A comprehensive review. J. Renew. Sustain. Energy 2019, 11, 062701. [Google Scholar] [CrossRef]
- Aarniovuori, L.; Niemelä, M.; Pyrhönen, J.; Cao, W.; Agamloh, E.B. Loss Components and Performance of Modern Induction Motors. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar]
- Emadi, A.; Andreas, J.C. Energy-Efficient Electric Motors; Marcel Dekker: New York, NY, USA, 2005. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education: Harlow, UK, 2016. [Google Scholar]
- Pfingsten, G.V.; Steentjes, S.; Hameyer, K. Operating Point Resolved Loss Calculation Approach in Saturated Induction Machines. IEEE Trans. Ind. Electron. 2017, 64, 2538–2546. [Google Scholar] [CrossRef]
- Pfingsten, G.V.; Steentjes, S.; Hameyer, K. Transient approach to model operating point dependent losses in saturated induction machines. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016. [Google Scholar]
- Palanisamy, V.; Vijayanathan, S. A Novel Agent Based Depth First Search Algorithm. In Proceedings of the 2020 IEEE 5th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 30–31 October 2020. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Narongrit, T.; Areerak, K.-L.; Areerak, K.-N. Adaptive Fuzzy Control for Shunt Active Power Filters. Electr. Power Compon. Syst. 2016, 44, 646–657. [Google Scholar] [CrossRef]
- Narongrit, T.; Areerak, K.-L.; Areerak, K.-N. A New Design Approach of Fuzzy Controller for Shunt Active Power Filter. Electr. Power Compon. Syst. 2015, 43, 685–694. [Google Scholar] [CrossRef]
- Shukla, S.; Mishra, S.; Singh, B. TS fuzzy based intelligent control of a three phase shunt filter under balanced and unbalanced conditions. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, New Delhi, India, 20–23 December 2010. [Google Scholar]
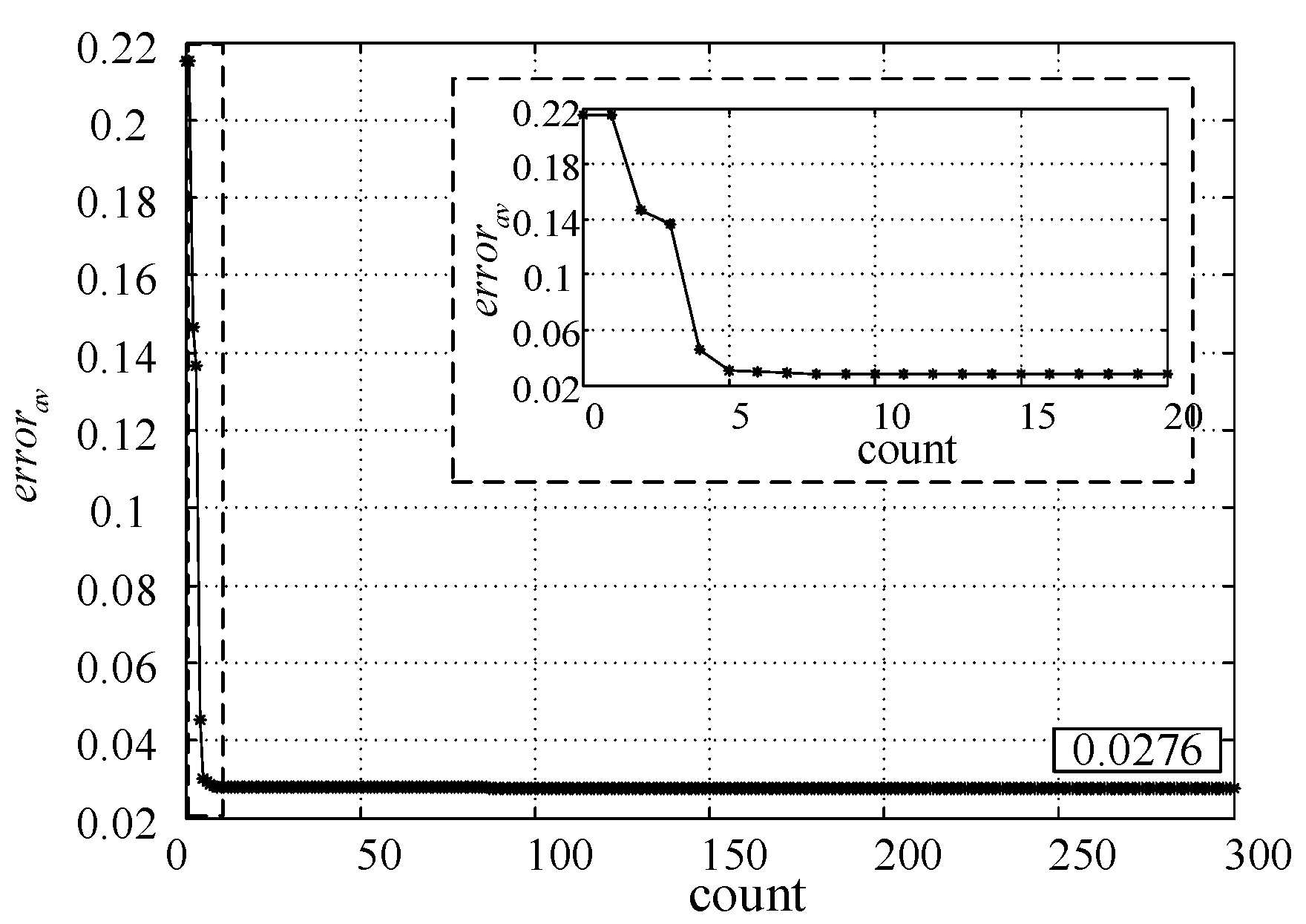


| Parameters | Searching Interval | Identified Value Using ATS |
|---|---|---|
| L1 | [0.01744 0.02131] | 19.30 × 10−3 |
| R2 | [0.01161 0.01419] | 13.26 |
| L2 | [0.01744 0.02131] | 19.50 × 10−3 |
| Lm | [0.35 0.43] | 0.40 |
| La | [0.02131 0.02604] | 24.20 × 10−3 |
| J | [0.0001 0.005] | 0.0016 |
| State | Linguistic Variables | Linguistic Values | Definition |
|---|---|---|---|
| Input | es (speed error value) | very_neg (very negative) | Speedreference << Speedactual |
| neg (negative) | Speedreference < Speedactual | ||
| zero | Speedreference = Speedactual | ||
| (positive) | Speedreference > Speedactual | ||
| (very positive) | Speedreference >> Speedactual | ||
| Output | d (duty cycle) | very decrease | |
| decrease | |||
| constant | |||
| increase | |||
| very increase |
| Input Membership Function | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −300 | −300 | −300 | −300 | −300 | −150 | −10 | 10 | 150 | 10 | 150 | 300 | 150 | 300 | ||||
| Output membership function | |||||||||||||||||
| 10 | 10 | 10 | 10 | 10 | |||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suwongsa, T.; Areerak, K.; Areerak, K.; Pakdeeto, J. Energy Saving Approach for an Electric Pump Using a Fuzzy Controller. Energies 2021, 14, 3330. https://doi.org/10.3390/en14113330
Suwongsa T, Areerak K, Areerak K, Pakdeeto J. Energy Saving Approach for an Electric Pump Using a Fuzzy Controller. Energies. 2021; 14(11):3330. https://doi.org/10.3390/en14113330
Chicago/Turabian StyleSuwongsa, Tuchapong, Kongpol Areerak, Kongpan Areerak, and Jakkrit Pakdeeto. 2021. "Energy Saving Approach for an Electric Pump Using a Fuzzy Controller" Energies 14, no. 11: 3330. https://doi.org/10.3390/en14113330






