Energy Fluctuations in the Homogenized Hyper-Elastic Particulate Composites with Stochastic Interface Defects
Abstract
:1. Introduction
2. Methods
- -
- for corner nodes:
- -
- for side nodes:
3. Results and Discussion
3.1. Deterministic Numerical Experiments
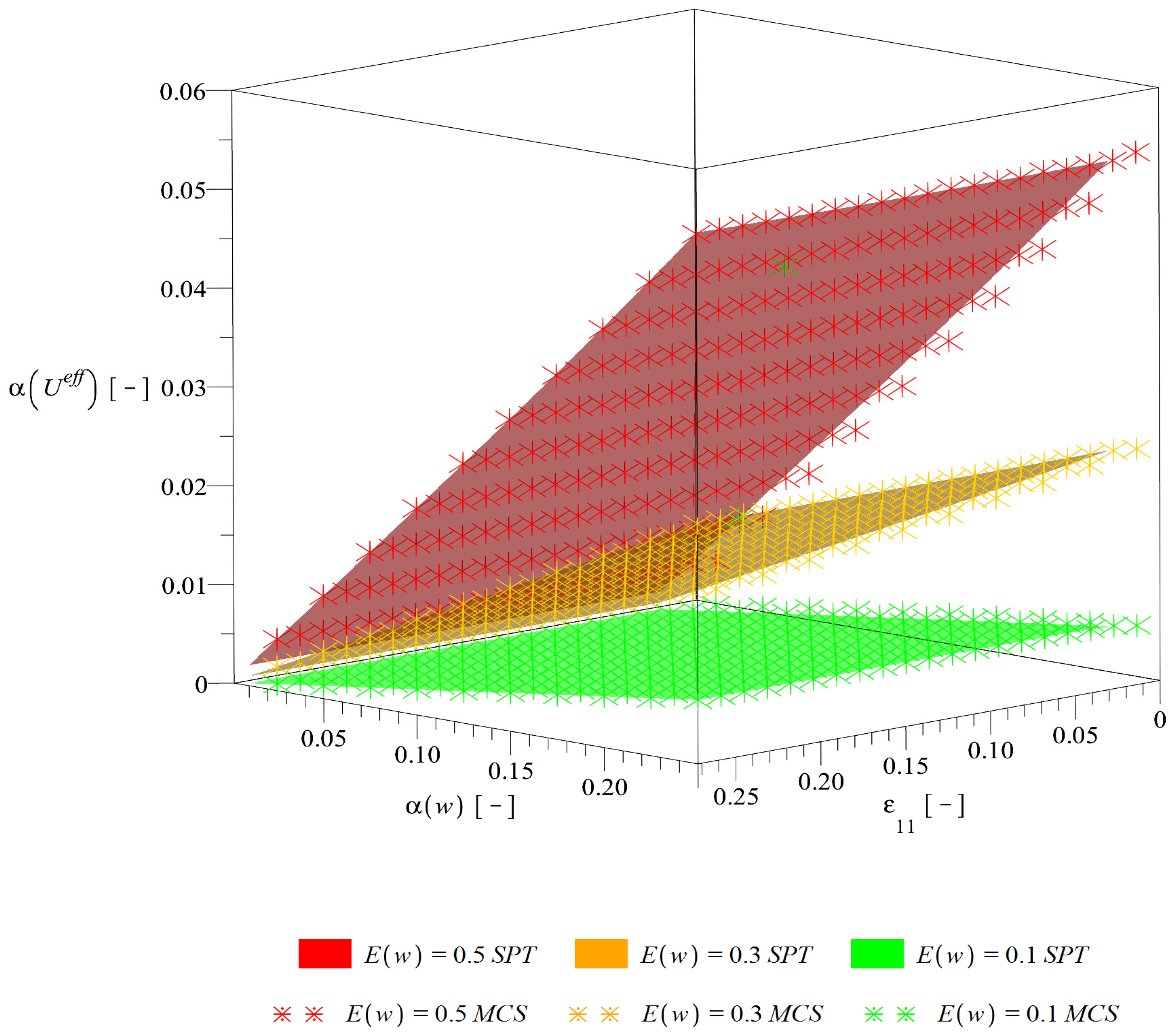
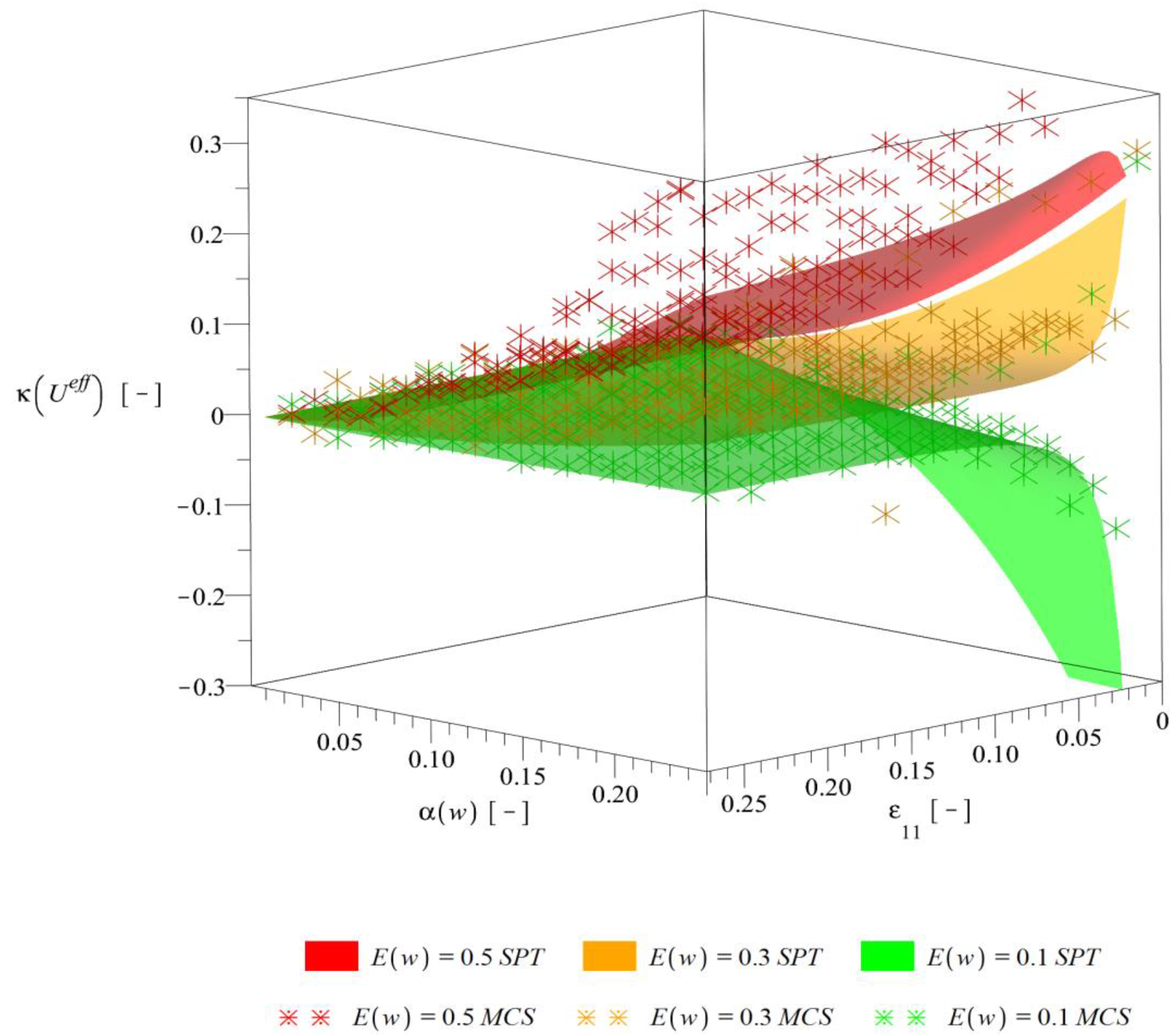
3.2. Stochastic Numerical Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bismarck, A.; Blaker, J.J.; Anthony, D.B.; Qian, H.; Maples, H.A.; Robinson, P.; Shaffer, M.S.P.; Greenhalgh, E.S. Development of novel composites through fibre and interface/interphase modification. IOP Conf. Ser. Mater. Sci. Eng. 2016, 139, 012001. [Google Scholar] [CrossRef] [Green Version]
- Whitehouse, A.F.; Clyne, T.W. Effects of reinforcement contact and shape on cavitation and failure in metal-matrix composites. Composites 1993, 24, 256–261. [Google Scholar] [CrossRef]
- Beckmann, C.; Hohe, J. Effects of material uncertainty in the structural response of metal foam core sandwich beams. Compos. Struct. 2014, 113, 382–395. [Google Scholar] [CrossRef]
- Duigou, A.L.; Davies, P.; Baley, C. Exploring durability of interfaces in flax fibre/epoxy micro-composites. Comp. Part A 2013, 48, 121–128. [Google Scholar] [CrossRef] [Green Version]
- Koutsawa, Y.; Karatrantos, A.; Yu, W.; Ruch, D. A micromechanics approach for the effective thermal conductivity of composite materials with general linear imperfect interfaces. Compos. Struct. 2018, 200, 747–756. [Google Scholar] [CrossRef]
- Kamiński, M. Multiscale homogenization of n-component composites with semi-elliptical interface defects. Int. J. Sol. Struct. 2005, 42, 3571–3590. [Google Scholar] [CrossRef]
- Hashin, Z. Thermoelastic properties of fiber composites with imperfect interface. Mech. Mat. 1990, 8, 333–348. [Google Scholar] [CrossRef]
- Theocaris, P.S. Definition of interphase in composites. In The Role of the Polymeric Matrix in the Processing and Structural Properties of Composite Materials; Seferis, J.C., Nicolais, L., Eds.; Plenum: New York, NY, USA, 1983; pp. 481–502. ISBN 978-1-4615-9293-8. [Google Scholar]
- Livanov, K.; Yang, L.; Nissenbaum, A.; Wagner, D. Interphase tuning for stronger and tougher composites. Sci. Rep. 2016, 6, 26305. [Google Scholar] [CrossRef] [Green Version]
- Hashin, Z. Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J. Mech. Phys. Solids 2002, 50, 2509–2537. [Google Scholar] [CrossRef]
- Jesson, A.D.; Watts, J.F. The Interface and Interphase in Polymer Matrix Composites: Effect on Mechanical Properties and Methods for Identification. Polym. Rev. 2012, 52, 321–354. [Google Scholar] [CrossRef]
- Ruchevskis, S.; Reichhold, J. Effective elastic constants of fiber-reinforced polymer-matrix composites with the concept of interphase. Sci. Proc. RTU Sect. Archit. Constr. Sci. 2002, 3, 148–161. [Google Scholar]
- Sokołowski, D.; Kamiński, M. Computational homogenization of carbon/polymer composites with stochastic interface defects. Compos. Struct. 2017, 183, 434–449. [Google Scholar] [CrossRef]
- Nazarenko, L.; Stolarski, H.; Altenbach, H. A statistical interphase damage model of random particulate composites. Int. J. Plast. 2019, 116, 118–142. [Google Scholar] [CrossRef]
- Barulich, N.D.; Godoy, L.A.; Dardati, P.M. A computational micromechanics approach to evaluate elastic properties of composites with fiber-matrix interface damage. Compos. Struct. 2016, 154, 309–318. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Homogenization of carbon/polymer composites with anisotropic distribution of particles and stochastic interface defects. Acta Mech. 2018, 229, 3727–3765. [Google Scholar] [CrossRef] [Green Version]
- Kamiński, M.; Sokołowski, D. Dual probabilistic homogenization of the rubber-based composite with random carbon black particle reinforcement. Comp. Struct. 2016, 140, 783–797. [Google Scholar] [CrossRef]
- Firooz, S.; Javili, A. Understanding the role of general interfaces in the overall behavior of composites and size effects. Comp. Mater. Sci. 2019, 162, 245–254. [Google Scholar] [CrossRef]
- Goudarzi, T.; Spring, D.W.; Paulino, G.H.; Lopez-Pamies, O. Filled elastomers: A theory of filler reinforcement based on hydrodynamic and interphasial effects. J. Mech. Phys. Sol. 2015, 80, 37–67. [Google Scholar] [CrossRef] [Green Version]
- Paran, S.M.R.; Saeb, M.R.; Formela, K.; Goodarzi, V.; Vijayan, P.; Puglia, D.; Khonakdar, H.A.; Thomas, S. To What Extent Can Hyperelastic Models Make Sense the Effect of Clay Surface Treatment on the Mechanical Properties of Elastomeric Nanocomposites? Macromol. Mater. Eng. 2017, 302, 1700036. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Sol. 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Springer Science & Business Media: Dordrecht, The Netherlands, 1987; ISBN 978-90-247-3256-2. [Google Scholar]
- Jahanshahi, M.; Ahmadi, H.; Khoei, A.R. A hierarchical hyperelastic-based approach for multi-scale analysis of defective nano-materials. Mech. Mat. 2020, 140, 103206. [Google Scholar] [CrossRef]
- Masud, A.; Truster, T.J. A framework for residual-based stabilization of incompressible finite elasticity: Stabilized formulations and F methods for linear triangles and tetrahedra. Comput. Method Appl. Mech. Eng. 2013, 267, 359–399. [Google Scholar] [CrossRef]
- Bisegna, P.; Luciano, R. Bounds on the overall properties of composites with debonded frictionless interfaces. Mech. Mater. 1998, 28, 23–32. [Google Scholar] [CrossRef]
- Huang, Z.P.; Wang, J. A theory of hyper-elasticity of multi-phase media with surface/interface energy effect. Acta Mech. 2006, 182, 195–210. [Google Scholar] [CrossRef]
- López Jiménez, F. Variations in the distribution of local strain energy within different realizations of a representative volume element. Compos. Part B Eng. 2019, 176, 107111. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Barbat, A.H. Monte-Carlo techniques in computational stochastic mechanics. Arch. Comput. Meth. Eng. 1998, 5, 3–30. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.N. Elasticity Theory; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Ogden, R.W. Non-Linear Elastic Deformations, 1st ed.; Dover Publications: Dover, UK, 1984. [Google Scholar]
- Ogden, R.W. On the overall moduli of non-linear elastic composite materials. J. Mech. Phys. Solids 1974, 22, 541–553. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Kamiński, M. The Stochastic Perturbation Method for Computational Mechanics, 1st ed.; Wiley: Chichester, UK, 2013; ISBN 9780470770825. [Google Scholar]
- Sokołowski, D.; Kamiński, M. Hysteretic behavior of random particulate composites by the Stochastic Finite Element Method. Materials 2019, 12, 2909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Meth. Appl. Mech. Eng. 2005, 39–41, 4135. [Google Scholar] [CrossRef] [Green Version]
- Almasi, A.; Silani, M.; Talebi, H.; Rabczuk, T. Stochastic analysis of the interphase effects on the mechanical properties of clay/epoxy nanocomposites. Comp. Struct. 2015, 133, 1302. [Google Scholar] [CrossRef]
- Zolfaghari, H.; Silani, M.; Yaghoubi, V.; Jamshidian, M.; Hanouda, A.M. Stochastic analysis of interphase effects on elastic modulus and yield strength of nylon 6/clay nanocomposites. Int. J. Mech. Mater. Des. 2019, 15, 109. [Google Scholar] [CrossRef]
- Kamiński, M. On iterative scheme in determination of the probabilistic moments of the structural response in the Stochastic perturbation-based Finite Element Method. Int. J. Num. Meth. Eng. 2015, 104, 1038. [Google Scholar] [CrossRef]
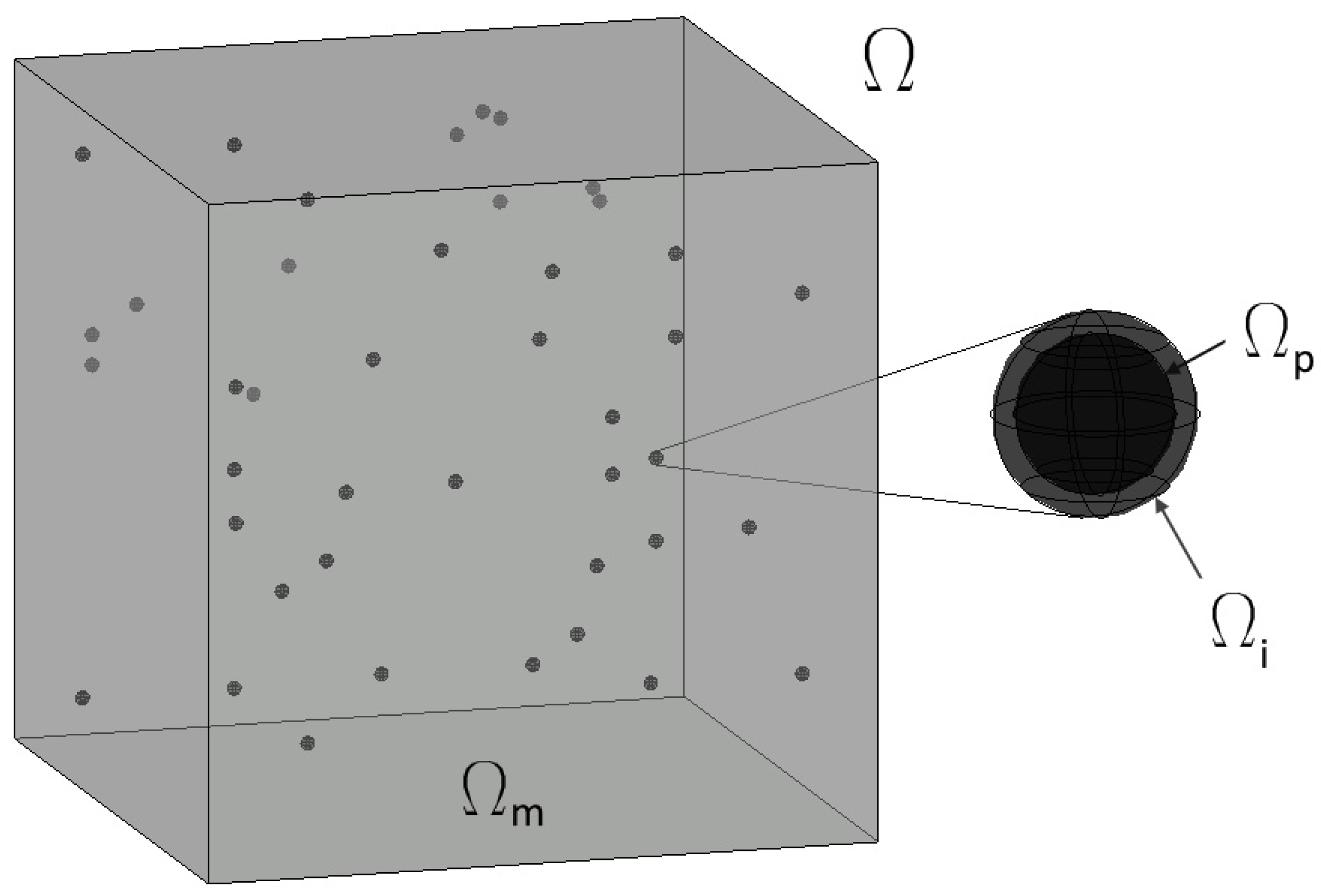
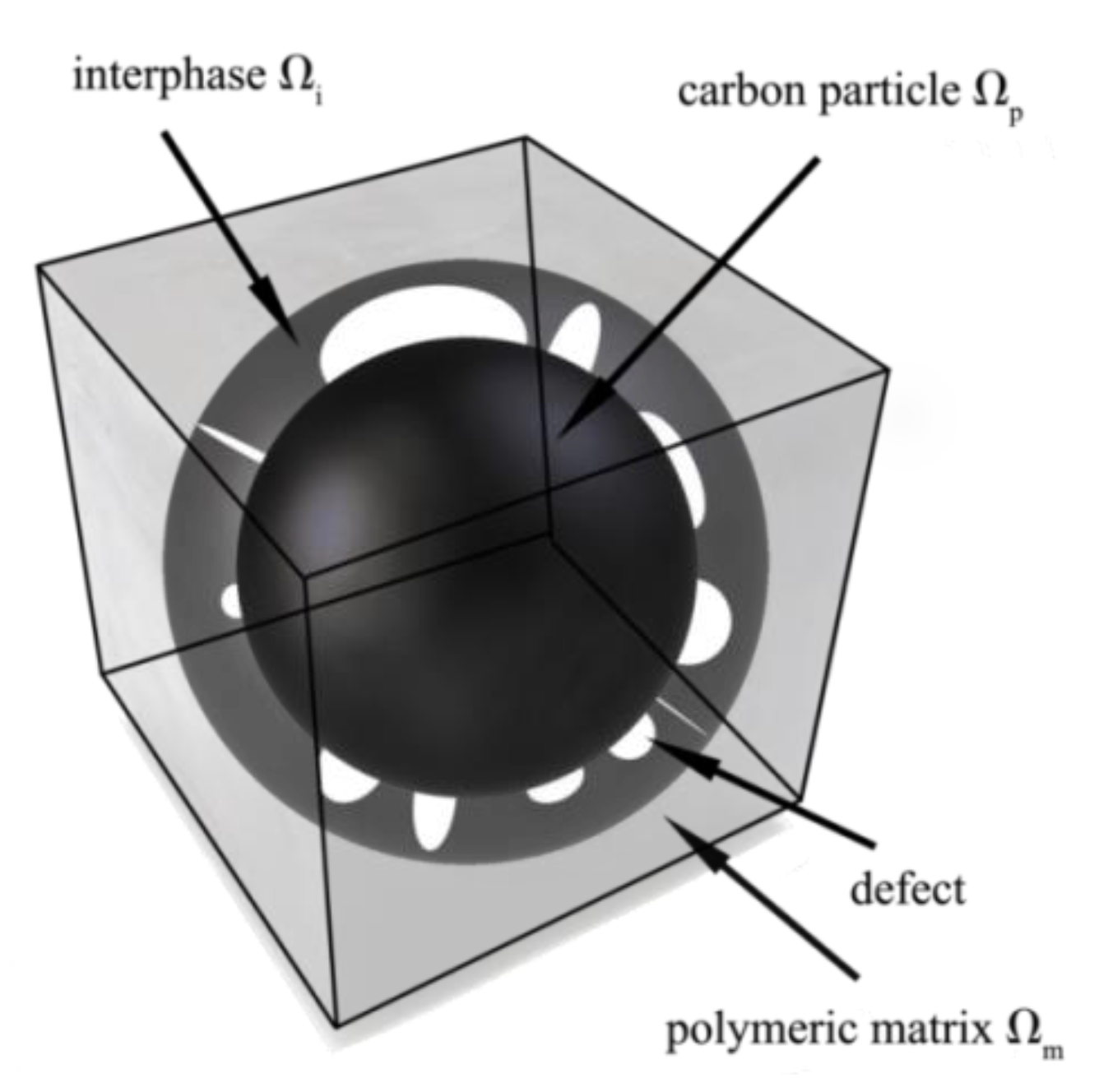


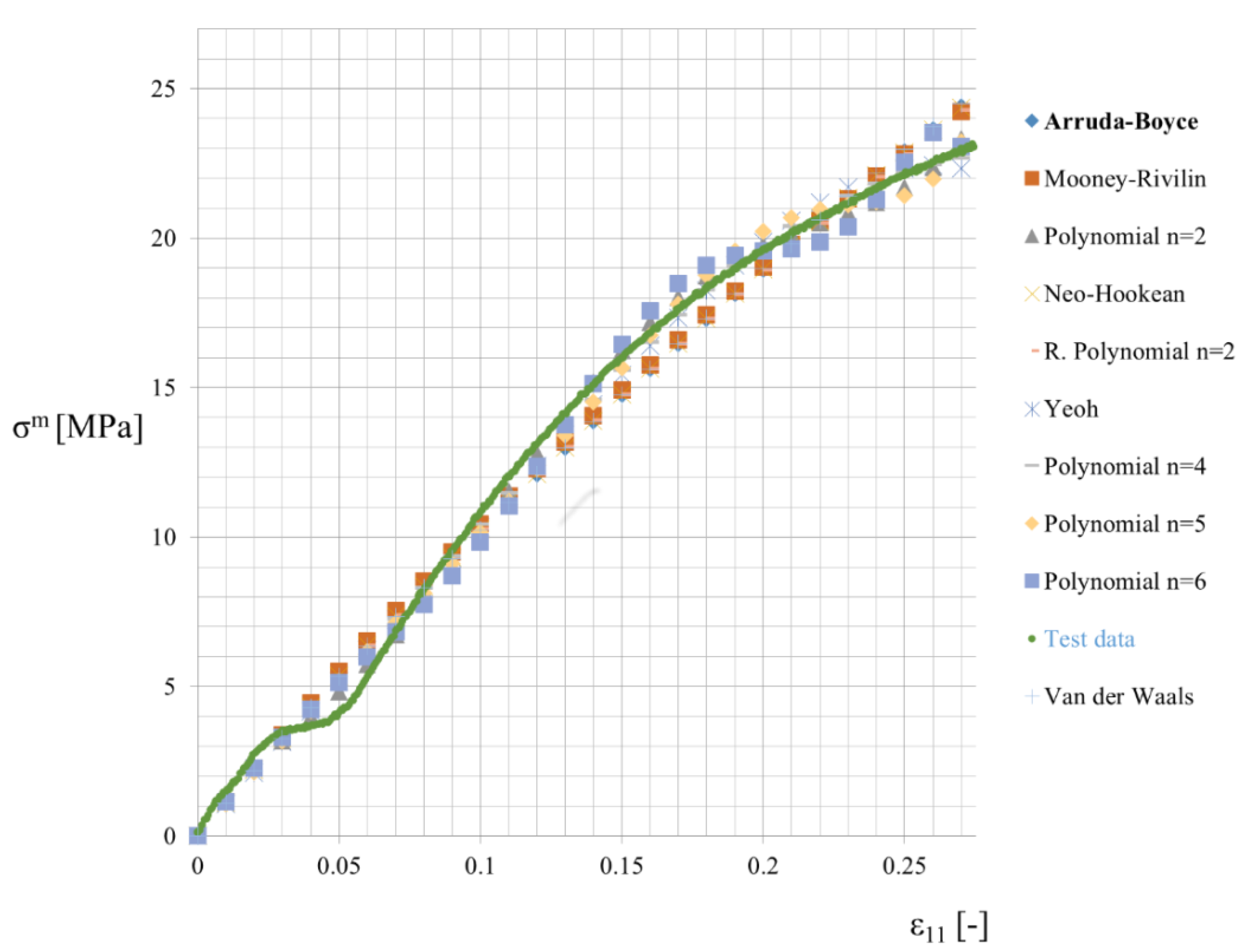
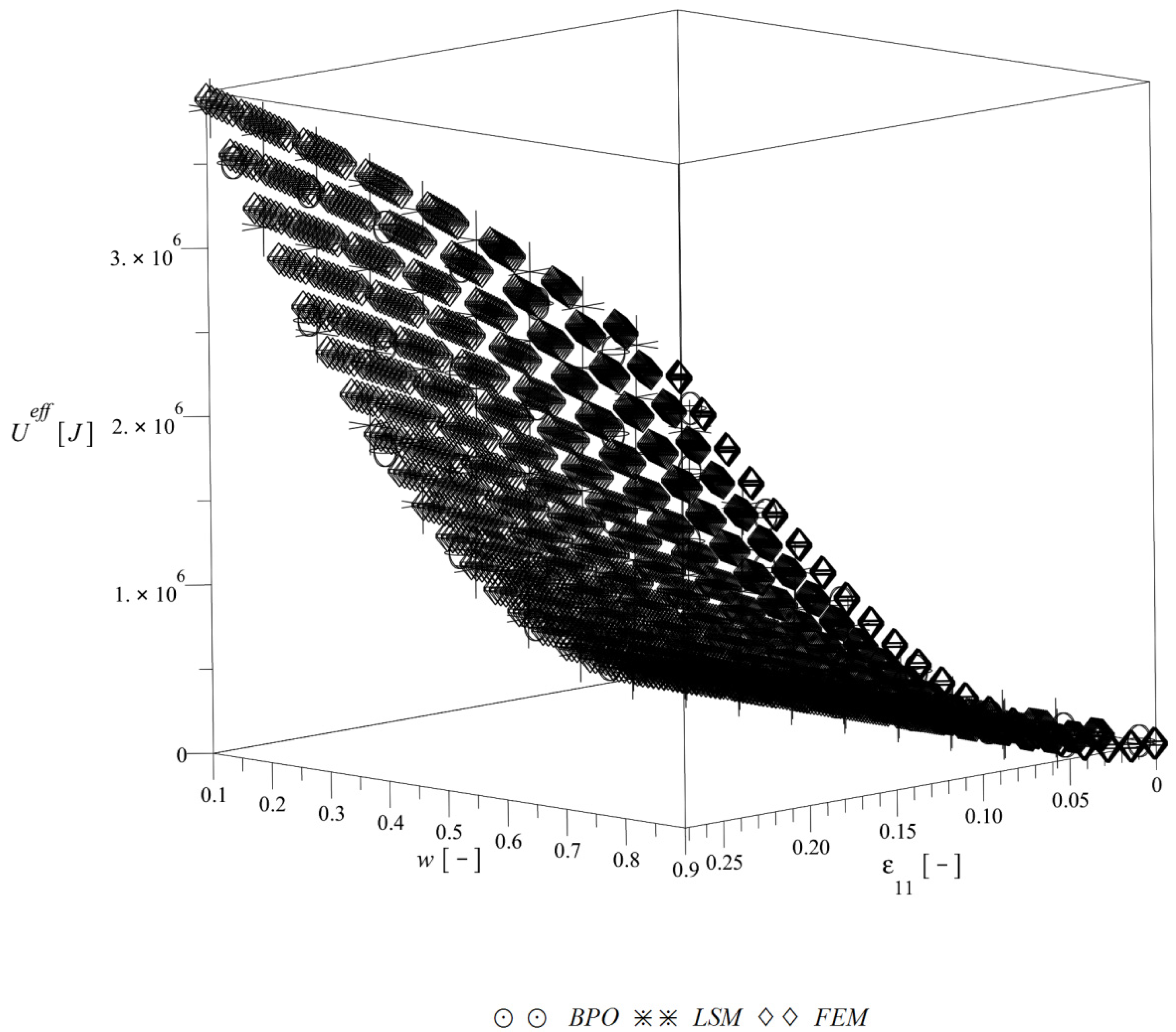



| Constitutive Theory | Elastic Potential W |
|---|---|
| Neo–Hookean | , I1—the first invariant of the strain tensor, μ—shear modulus |
| Mooney–Rivlin | —empirical material constants, —the first and the second invariants of the left Cauchy-Green deformation tensor |
| Arruda–Boyce | |
| Yeoh | , —material constants |
| Van der Waals | , β—material parameter |
| Ogden | , , , —material constants, l1l2 are principal stretches |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokołowski, D.; Kamiński, M.; Wirowski, A. Energy Fluctuations in the Homogenized Hyper-Elastic Particulate Composites with Stochastic Interface Defects. Energies 2020, 13, 2011. https://doi.org/10.3390/en13082011
Sokołowski D, Kamiński M, Wirowski A. Energy Fluctuations in the Homogenized Hyper-Elastic Particulate Composites with Stochastic Interface Defects. Energies. 2020; 13(8):2011. https://doi.org/10.3390/en13082011
Chicago/Turabian StyleSokołowski, Damian, Marcin Kamiński, and Artur Wirowski. 2020. "Energy Fluctuations in the Homogenized Hyper-Elastic Particulate Composites with Stochastic Interface Defects" Energies 13, no. 8: 2011. https://doi.org/10.3390/en13082011





