Review of Trends and Targets of Complex Systems for Power System Optimization

Abstract

Optimization systems (OSs) allow operators of electrical power systems (PS) to optimally operate PSs and to also create optimal PS development plans. The inclusion of OSs in the PS is a big trend nowadays, and the demand for PS optimization tools and PS-OSs experts is growing. The aim of this review is to define the current dynamics and trends in PS optimization research and to present several papers that clearly and comprehensively describe PS OSs with characteristics corresponding to the identified current main trends in this research area. The current dynamics and trends of the research area were defined on the basis of the results of an analysis of the database of 255 PS-OS-presenting papers published from December 2015 to July 2019. Eleven main characteristics of the current PS OSs were identified. The results of the statistical analyses give four characteristics of PS OSs which are currently the most frequently presented in research papers: OSs for minimizing the price of electricity/OSs reducing PS operation costs, OSs for optimizing the operation of renewable energy sources, OSs for regulating the power consumption during the optimization process, and OSs for regulating the energy storage systems operation during the optimization process. Finally, individual identified characteristics of the current PS OSs are briefly described. In the analysis, all PS OSs presented in the observed time period were analyzed regardless of the part of the PS for which the operation was optimized by the PS OS, the voltage level of the optimized PS part, or the optimization goal of the PS OS.

1. Introduction

Electrical power system optimization is a popular research topic. Electrical power system experts began to deal with the minimization of the active power loss in electrical power systems (PS), and minimization of the PS operation costs in the 1950s [1,2]. An important milestone in the path to modern power system optimization systems (PS OSs) was defining the Optimal Power Flow (OPF) problem [3,4]. Although the basic solution to the PS optimization problem had already been described, the low computing performance of the computers at that time did not allow for solving extensive complex optimization problems. In the coming decades, the computing performance of computers has been increased. Now, it is possible to solve challenging optimization tasks of large complex PSs, considering many operational constraints of the PS [5]. Today, PSs are under extensive changes. Conventional thermal power plants, which are easy to control and whose rated powers are in the order of hundreds of MW, are being replaced by a large number of small distributed generation units, whose operational nature is often intermittent (the units using wind or solar energy). Moreover, electrical power consumers require increased quality of the supplied power than before because they use appliances requiring very high power quality [6]. In addition to large PSs, small isolated microgrids with just a few power sources and consumers are being created today. New devices with a special operation character are being connected to PSs, e.g., battery energy storages and electric vehicles. Old analog electricity meters are substituted with new smart electricity meters enabling real-time measurement. All these current changes in PSs, and the effort to minimize operating costs and maximize power system reliability, motivate PS operators to install advanced power-flow control and communication equipment to their PSs, and to use comprehensive PS OSs for optimal control of their PSs. That is why PS researchers are nowadays engaged in creating new PS OSs and improving the abilities of the old ones. To accelerate the development of new PS OSs, these researchers often use applications and function libraries to simulate the operation of a PS in various operation states and to optimize PS parameters. Such applications and function libraries are, e.g., OpenDSS [7], GridLAB-D [8], or pandapower [9].

In this paper, we monitor current trends and dynamics of the power system research optimization. The content and form of this review paper have been chosen with respect to the goal of introducing young researchers to current trends of the PS operation optimization research area. It is important to note that the aim of this review paper is to provide a description of the current trends and dynamics of PS OSs, not a description of the current trends and dynamics of PS OSs which are based on the OPF or Unit Commitment optimization problem solution. Many PS OSs which have been analyzed for this review paper are based on these two optimization problems, but there is also many PS OSs which are based on different types of the optimization problem. Specifically, the OPF and Unit Commitment optimization problems are not solved by the PS OSs which do not observe power flows (an example of such a PS OS is an optimization system optimizing power generation of a dam hydroelectric power station, which is limited only by the maximum and minimum value of the water level, output water flow, and generator dynamics and which goal is to maximize profit [10]).

The state-of-the-art works, the challenges, and the future trends of OPF research were described in [11,12]. The Unit Commitment research was described in [13]. In addition, [14,15,16,17] also offer some interesting findings.

The paper is structured as follows. Section 2 describes the process of defining the current dynamics and trends of PS operation optimization research and presents the results of this process. Section 3 describes the characteristics of eleven basic PS-OSs research streams and presents several appropriate representatives of these research streams. Papers presented in individual subsections of Section 3 are those that best describe the solution methods of PS operation optimization problems of given research streams and which together form an overall picture of given streams of PS-OSs research.

2. Current Dynamics and Trends of Research

In order to analyze the dynamics and trends of PS OSs, 388 papers that present systems optimizing of the operation of a part of the power system, and which were published between December 2015 and July 2019, were collected. The papers for analysis were searched in the Scopus and Web of Science databases. Any paper found here which was suitable for this review was inserted into the review’s paper database. In the scope of the review’s research, any optimization system related to any part of a power system was interesting (regardless of a PS’s voltage level). As such, within the review’s paper database, there are papers presenting PS OSs optimizing of the operation of low-voltage networks systems (e.g., PS OSs optimizing of electric vehicle charging stations) and PS OSs optimizing of the operation of transmission networks systems (e.g., PS OSs optimizing the network power flows by setting the Flexible AC transmission system devices) at the same time.

Once all the PS OSs papers relevant for this review had been found and reviewed, all papers in the review’s paper database were analyzed in detail. The aim of this detailed analysis was to determine whether the paper presents a complex PS OS or not. If a paper did not present a complex PS OS, the paper was removed from the review’s database. If a detailed analysis showed that a paper deviates from the review’s research criteria in any way, the paper was also removed from the paper database. Once the detailed analysis was finished, the final paper database was obtained. The final paper database contained 255 papers that meet the review’s research criteria.

Within the detailed analysis of the final paper database, specializations and optimization goals of individual PS OSs were defined. Based on the defined PS OSs’ specializations and goals, 11 groups of PS OSs were identified. These 11 groups (subcategories) are presented in

Table 1. Topics of 11 identified electrical power system (PS) optimization systems (OSs) groups.

Group Mark	Name of the Group
A	PS OSs minimizing the price of electricity/PS OSs reducing PS operation costs
B	PS OSs optimizing the operation of renewable energy sources
C	PS OSs regulating the power consumption during the optimization process
D	PS OSs regulating the energy storage systems operation during the optimization process
E	PS OSs controlling a special PS action hardware
F	PS OSs optimizing the microgrid operation
G	PS OSs regulating the charging/discharging of electric vehicles
H	PS OSs maximizing the PS operation stability
I	PS OSs reconfiguring the network topology during the optimization process
J	PS OSs finding an optimal PS expansion plan
K	PS OSs using the market clearing during the optimization process

. A detailed definition of each of these groups is presented in Section 3.

After the PS OSs groups identification, individual papers of the paper database were assigned to 11 paper groups (individual paper groups are equivalent to PS OSs groups presented in Table 1) based on the specialization or goal of the PS OS presented in the paper. Two PS OSs papers’ assignment processes were performed. In the first assignment process, a paper was assigned to a relevant paper group based on the main characteristic of the PS OS presented in the paper. In the second assignment process, a paper was assigned to all relevant paper groups based on all identified characteristics of the PS OS presented in the paper. Since in the case of several papers, making a paper assignment decision without a doubt was impossible, the final decision to assign these papers to the most appropriate paper group was burdened with a possible error of subjective decision. However, the number of papers with this unclear assignment decision was low, so any misassignment of these papers would not have a significant impact on the results of the statistical analysis of the review’s paper database.

Figure 1 shows how many papers have been assigned to each defined paper group in the first assignment process. Figure 2 presents the same results using the relative frequency and cumulative relative frequency. Figure 1 shows that the highest number of papers has been assigned to group A (PS OSs minimizing the price of electricity/PS OSs reducing PS operation costs, 55 papers). However, it is important to note that group A is intended for the PS OSs papers which cannot be assigned to any of the other ten paper groups in the first assignment process. Since the three largest paper groups contain more than half of all papers of the review’s paper database, the characteristics of these three paper groups (groups A, B, and C) were determined as the most frequently presented in the papers published in recent years. Therefore, these three PS OSs characteristics are considered to be the mainstream of the PS OSs research.

The assigned database of papers, which was created in the first assignment process, was later analyzed for the second time, in order to obtain current trends of PS OSs research. For this reason, the frequency of individual PS-OSs characteristics described in the papers of our database was analyzed for individual years of the observed time period. Figure 3 presents the frequency of the individual PS-OSs characteristics described in the papers divided by the total number of papers in the observed year. In this figure, the color of graphs of individual PS OSs characteristics is the same as the color of the column of the PS OSs characteristic in Figure 1. This figure shows that the relative frequency of PS OSs group A is gradually increasing, while the relative frequencies of the other PS OSs groups do not change significantly (due to the small extent of the static set for individual observed years, small fluctuations observed in the graphs of individual PS OS characteristics are not considered to be significant). The growth of the relative frequency of Group A can be explained by the idea that current PS-OSs researchers try to differentiate from older papers and standard PS-OSs research streams (i.e., PS OSs research streams corresponding to paper groups B to K). Authors of recent papers try to create new PS OSs which share the main optimization idea with the older PS OSs (i.e., the minimization of the price of electricity or the reduction of the PS operation costs). However, in these recent PS OSs, unlike in the PS OSs of the standard research streams, there is an unusual secondary optimization target defined or there is an unusual PS part optimized. Regardless, for the whole observed time period, the claim that the PS OSs with usual characteristics (i.e., PS OSs characteristics corresponding to groups B to K) represent the majority of PS OSs presented in the papers of our database is still valid (In 2019, the relative frequency of group A was 35.1%, so, in the last year of the observed time period, the PS OSs with mainstream characteristics represented nearly 2/3 of all PS OSs presented in the papers of our database).

Now let’s look at the results of the second assignment process. Figure 4 shows how many papers have been assigned to each defined paper group in this assignment process. Figure 5 then presents the results of the same process using the relative frequency and cumulative relative frequency. Since the minimization of PS operation costs is the characteristic shared by the vast majority of PS OSs, group A was not considered as part of the second assignment process. Figure 4 shows that the highest number of papers has been assigned to group B (PS OSs optimizing the operation of renewable energy sources, 73 papers). Figure 5 shows that the four largest paper groups amount to more than half of all papers in our paper database (specifically, their amount is 55.6%).

3. Main Research Streams in Power System Operation Optimization

The statistical analysis of papers presented in Section 2 showed that the mainstream of PS-OSs research are PS OSs with characteristics of paper groups A, B, C, D, E, and F (according to the first assignment process, these six paper groups contain more than 80% of all papers of the database). The following six subsections of this section detail these mainstream PS OSs. The less populated paper groups (G, H, I, J, and K) are described in the last five subsections of this section. The description of these less populated paper groups is less detailed than the description of the most populated paper groups. Of the total number of PS OS papers (255) in the review’s paper database, 111 PS OSs were selected for presentation in this paper section. The papers that described the PS OS most understandably were selected.

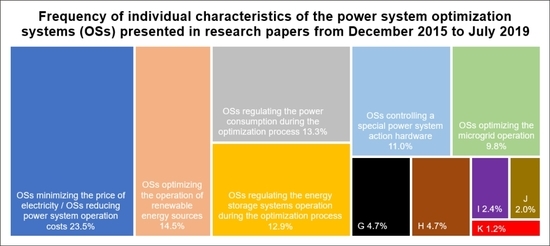
3.1. PS OSs Minimizing the Price of Electricity/PS OSs Reducing PS Operation Costs

This subsection is devoted to OSs that have the goal to minimize the PS operation costs or the electricity price. Many OSs with this goal solve the so-called economic dispatch (ED) problem. For example, OSs in [18,19,20,21] solve the real-time ED problem. In [21], a distributed OS based on a state-based potential game is proposed for the real-time ED problem in smart grids. Under the DC power flow approximation, there is the real-time ED problem with coupled operational constraints formulated as a centralized optimization problem (centralized real-time ED problem). By treating each node in the grid as an agent, centralized real-time ED problem is converted into a state-based potential game by augmenting its objective function in the designed game with a local augmented Lagrange-like function, leading to a distributed algorithm for solving this centralized ED problem. The paper’s authors reveal that the stationary-state Nash equilibrium of the state-based potential game exactly identifies the global optimum of the constrained centralized real-time ED problem. The proposed algorithm is capable of handling both equality and inequality constraints in complicated forms. During optimal solution searching, the OS considers constraints described by the network lines’ capacity limits and the capacity bounds of local generation units and local loads. The paper’s authors tested the OS performance by simulations on the IEEE 9-, 39-, and 118-bus test systems. The results of these tests indicate that the OS can quickly converge to the global optimum even under unreliable communication and plug-and-play operations. The OSs in [22,23] solve the look-ahead ED problem. An OS in [24] solves the multiple-timescale ED problem using a special stochastic system. In [25], an OS based on a comprehensive two-stage robust security-constrained unit commitment approach is presented. The OS minimizes the operation cost of the base case while guaranteeing that the robust solution can be adaptively and securely adjusted in response to continuous load and wind uncertainty intervals, as well as discrete N–K generation and transmission contingency security criteria. The OS is equipped with rigorously formulated corrective capabilities of both non-quick-start and quick-start units. Specifically, unit commitment of quick-start units is adaptively adjusted in the recourse stage for satisfying security constraints under various uncertainties, which introduces mixed-integer recourse to the proposed two-stage robust security-constrained unit commitment model. The proposed model is solved by the combination of the modified Benders decomposition method and the column-and-constraint generation algorithm, which decompose the original problem into a master unit commitment problem for the base case and security-checking subproblems for uncertainties. During optimal solution searching, the OS considers constraints described by the nodal power balance, the maximal active power supplied via the reference bus, the network lines’ capacity limits, the capacity limits of local thermal units, the generation limits of local wind farms, other power generation units’ limits (minimum on/off time limits, startup/shutdown cost limit, and ramping up/down limit), and many security constraints for handling various uncertainties. The paper’s authors tested the OS performance by simulation on the modified IEEE 118-bus system. The results of this test indicate that the OS’s optimization approach is effective. The paper’s authors also performed robustness performance tests. The results of these tests indicate that a reasonable threshold on the violation of security checking subproblems would guarantee good enough solutions from an engineering point of view, although the modified Benders decomposition does not provide the tightest lower bound and may not guarantee the global optimality. An OS in [26] minimizes the distribution system (DS) operation costs while coping with high-dimensional uncertainty in a DS with high penetration of RESs. The basic method of PS operation cost reduction is a minimization of active power losses. For example, OSs in [27,28] minimize the power losses through the network reconfiguration. To minimize power losses, an OS in [29] installs distributed power sources of various types across the DS. An OS in [30] minimizes the operation costs consisting of several parts. This OS optimally dispatches the active and reactive power of distributed photovoltaic generation (PVG), the switched capacitors, and the voltage regulators in large multi-phase unbalanced DSs to minimize the energy loss, the PVG’s active power curtailment, and the operations of capacitors and voltage regulators, in addition to the elimination of the voltage violations and the reverse power flow.

3.2. PS OSs Optimizing the Operation of Renewable Energy Sources

In order to reduce greenhouse gas emissions from power generation, the use of renewable energy sources (RES) is supported world-wide. The price of RES power plants’ technologies has dropped significantly, so the capacity of installed RES power plants is increasing globally. Since the generation of solar and wind power plants is defined by variable weather and not by the PS operator’s needs, the OSs need to be used to achieve the efficient use of RES power plants and their power generation.

If the electrical energy produced by a RES power plant cannot be consumed or accumulated nearby the RES power plant site at the time of generation, and this energy cannot be transmitted due to the limited PS transmission capacity, a PS operator curtails the instantaneous power output of the RES power plant. This way, the RES power plant’s total power generation is smaller than it could be, and the RES power plant’s owners are shorter in income. OSs presented in [31,32,33,34,35] help minimize RES power plants curtailment and maximize their total power generation, namely the OSs in [32,33,34] optimize the photovoltaic power plant operation and the OS in [35] optimizes the wind power operation. All these OSs are parts of a power management system or an economic dispatch system. The OS in [35] is based on an unusual approach to implementing a decentralized multi-area dynamic ED problem of a large-scale power system. Usual approaches are based on Lagrangian relaxation, but this OS’s solution method is based on a generalized Benders decomposition framework, a decomposition technique for solving nonlinear programming. Since the OS’s algorithm does not use the dual relaxation, primal feasible solutions can be obtained after only a few iterations. The generalized Benders decomposition algorithm applied there is modified by introducing a locally optimal cost of each area, which significantly expedites convergence. This approach is applicable for online dispatch of multi-area systems with a hierarchical control structure containing a coordinator (i.e., where each area has a local control center, and these local control centers are coordinated via an upper control center). The OS’s decentralized solution method aims to preserve the decision independence of each area while conducting multi-area dynamic ED but does not aim to compete with the centralized solution methods in computational efficiency. Since the decentralized method presented in this paper is developed for multi-period multi-area dynamic economic dispatch, it can be applied to day-ahead hourly power dispatch or intra-hour look-ahead power dispatch of a multi-area system. During optimal solution searching, the OS considers constraints described by the feasibility-cuts limit, the optimality-cuts limit, and the locally optimal cost of each area subproblem. The paper’s authors tested the OS performance by simulations on a real large-scale power system in China, which is a four-area regional power system with a total wind-power-plant installation capacity of 18 GW.

While the electrical energy produced by the first generation of RES power plants was supplied to the PS at a constant subsidized price, in some countries with favorable conditions for the RES power plants operation, there are currently RES power plants under construction which will produce energy to be sold at local energy markets [36]. To maximize RES power plants owners’ profits on the markets, some OSs use offering strategies. Such OSs are presented in [37,38,39]. In [37,38], optimal day-ahead offering strategies for wind farms equipped with energy storage systems are presented. The optimization method used in [38] describes and evaluates an integrated strategy for the day-ahead offering while accounting for the optimal operation of an energy storage system at the balancing stage, where the real-time operation policy for the storage is modeled with linear decision rules. Optimal decision rules and day-ahead offers are obtained jointly. The optimization problem is translated into a stochastic optimization problem where a trade-off is made between the expected profit maximization and the risk-aversion. Subsequently, discretization and linearization methods are employed to eventually obtain the solution of such stochastic optimization problems. This OS neglects the degradation costs of the energy storage system. It uses an assumption of being a price-taker in some European electricity markets. The OS also quantifies the value of the residual energy of the energy storage system. Furthermore, a sensitivity analysis is carried out to analyze the influence of price uncertainty and temporal correlation of wind power generation on profits. During optimal solution searching, the OS considers constraints described by the limit of the residual energy of individual ESSs at each interval, the ESS charging and discharging power limits, the wind power generation curtailment limit, and the limit of wind-farm integration capacity. The paper’s authors tested the OS performance by two case studies which were based on realistic data from the Nord Pool market and wind farms in Denmark. In these case studies, the paper’s authors used 100 scenarios. The results of these case studies indicate that the OS’s strategy is more effective than other existing strategies.

An offering strategy in [39] aggregates a few wind power plants to one virtual power plant. Operation coordination of a RES power plant with a fully-controlled power source is an appropriate way to increase the operational capability of the RES power plant. OSs in [40,41,42] also use such operation coordination. The OS in [40] coordinates the operation of hydropower plants with thermal power plants and the OS in [41] coordinates operation of wind farms and pumped-hydro storage. To maximize the total energy production of a RES power plant, it is also necessary to reduce the power losses of the power plant. To minimize wind farm’s power losses, OSs in [43,44,45] optimize the design of their internal cable networks.

3.3. PS OSs Regulating the Power Consumption During the Optimization Process

Another PS’s part which can be involved in the optimization process is the loads. Individual loads’ power consumption has an intermittent character, similar to the intermittent character of solar or wind power plants’ power generation. However, a load’s power input is primarily defined by the current needs of the consumer, not by current weather conditions. For some types of electrical appliances, the user may need to run an appliance for a certain time period (e.g., 2 h a day), but the part of the day the appliance is running does not affect the appliance’s utility. Then, PS operators can shift appliances of such types to various parts of day to achieve a power balance throughout the day and minimize the magnitude of the PS’s consumption peak. Power consumers receive financial compensation or pay a lower electricity price for allowing the PS operator to set the operation time of their appliances.

To set the operation time of each shiftable load optimally, the load shifts are controlled by OSs. OSs in [46,47] schedule the operation time of loads to reduce PS’s peak power consumption and to flatten the load profile. The OS in [47] optimally schedules the group of household appliances connected to a microgrid. To achieve optimal scheduling, the OS categorizes the appliances into flexible and non-flexible deferrable loads, according to their electrical components. The OS uses a dynamic scheduling algorithm where users can systematically manage the operation of their electric appliances. The OS algorithm solves two multi-objective optimization problems. The first one targets the activation schedule of non-flexible deferrable loads and the second one deals with the power profiles of flexible deferrable loads. These multi-objective optimization problems are solved by using a fast and elitist multi-objective genetic algorithm (specifically Non-dominated Sorting Genetic Algorithm II). During optimal solution searching, the OS considers constraints described by the limited flexibility of local shiftable loads (individual loads are limited by the total energy demand to complete their task). The paper’s authors tested the OS performance by the simulation of the collaborative system that consists of 40 microgrids registered in the program of the load curve flattening. In this simulation, every registered microgrid includes one flexible deferrable load (e.g., water heater) and a non-flexible deferrable load (e.g., dishwasher). The results of this test indicate that the OS‘s scheduling approach can reach a very flat load curve.

OSs in [48,49,50,51] optimize PS’s power flows using the residential demand-response service. Specifically, the OS in [48] controls the power consumption of domestic heat pumps in response to a PS frequency, and the OS in [49] controls a group of heating, ventilation, and air-conditioning loads. The OS in [51] combines the centralized and decentralized approach. The OS solves a centralized optimization problem for the independent system operator to minimize the social cost, i.e., the consumers’ discomfort cost and suppliers’ generation cost, subject to the power network operating constraints. The OS’s decentralized energy trading algorithm solves a decentralized optimization problem to maintain the privacy of the consumers and suppliers in the demand response program. This decentralized algorithm searches for the control signals that the independent system operator sends to the local entities. In response, the consumers and suppliers obtain their optimal load and generation levels, respectively. The paper’s authors show that, under some specific control signals from the independent system operator, the decentralized algorithm converges to the unique solution of the OS’s centralized problem. During optimal solution searching, the OS considers constraints described by the limited flexibility of local shiftable loads (individual loads are limited by their demand variation in individual time sloths, and their total energy demand to complete their task) and the minimal and maximal value of active power generated by individual local generators. The paper’s authors tested the OS performance by the simulation on the IEEE 40-bus power system. The results of this test indicate that the OS can decrease both the consumers’ and the generators’ costs and the OS’s algorithm is faster than algorithms based on a centralized approach.

Some papers propose an optimum load control and schedule system which controls many loads of various types located in various locations as one large aggregate load. Such systems are presented, for example, in [52,53,54]. When optimizing PS operation using the load control, technically, the easiest load-control method is to control large compact loads, because this type of control allows changing PS’s total power consumption by hundreds of MW, even when controlling only a small number of loads. This type of load control is used, for example, in OSs [55], [56] which control the power demand of large industrial consumers. The OS in [56] enables cement plants to provide the power regulation or the load following with the support of an onsite energy storage system. OSs in [57,58] then focus on the demand flattening, i.e., minimizing the difference between the maximum and minimum PS’s total power consumption in each time period.

3.4. PS OSs Regulating the Energy Storage Systems Operation During the Optimization Process

Many OSs use various types of energy storage systems (ESS) to regulate power flows in PS. Thanks to its energy capacity, an ESS can act as a PS power source or as a PS power consumer. By extending an OS with the ability to control the operation of an ESS, the OS gains a valuable tool which can quickly and easily change PS power flows to achieve optimal state of the PS. The pumped hydroelectric energy storage (PHES) is the most commonly used type of ESS in PSs. From an economic point of view, the PHES is particularly suitable for storing large amounts of energy from several units for up to tens of hours. If we want to store a large amount of energy for a longer time, the most economical type of ESS is the compressed air energy storage (CAES) or hydrogen production and storage. On the contrary, if we want to store a small amount of energy and only for a short time, the most economical type of ESS is the battery energy storage and the flywheels [59].

The basic method of using ESS in modern PSs is to store energy at one point in time when power generation exceeds power consumption and to release energy later, at another point in time, when power generation is lower than current power consumption. Many OSs are based on this ESS-using process, which is particularly suited to maximize RES power plants’ energy production, as mentioned in the previous subsection. OSs in [60,61] also minimize RES power plants curtailment using ESSs. The OS in [61] is based on a planning framework that finds the minimum storage sizes (power and energy) of ESS units installed at multiple locations in distribution networks to reduce curtailment from renewable distributed generation, specifically wind farms, while managing congestion and voltages. A two-stage iterative process is adopted in this framework. The first stage uses a multi-period AC OPF across the studied horizon to obtain initial ESS units sizes considering hourly wind and load profiles. The second stage adopts a high granularity minute-by-minute control driven by a mono-period bi-level AC OPF to tune the first-stage storage sizes according to the actual curtailment. Congestion and voltages are managed through the optimal control of ESS units (active and reactive power), on-load tap changers, distributed generation units’ power factor, and distributed generation unit curtailment as a last resort. During optimal solution searching, the OS considers constraints described by the power balance in the network, the node-voltage values limits, the active power losses limits, maximal branch currents, the minimal and maximal value of active power generated by individual local generators, and generators’ apparent power limits. The paper’s authors tested the OS performance by the OS application in a real 33-kV network from the North West of England for one week. The results of these tests indicate that the OS is effective in the ESS units sizing.

Some OSs using the control of an instantaneous power input/output of an ESS or of a group of ESSs help regulate power flows in a PS, thus reducing PS’s power losses, improving PS’s voltage profile, reducing frequency fluctuations in the PS, etc. OSs in [62,63,64] optimize the ESSs’ regulatory capabilities for the primary regulation service, and OSs in [65,66,67] optimize the ESS’s regulatory capabilities for the secondary regulation service. These OSs determine the optimal ESS location in a PS and determine the optimal ESS sizing. Some OSs use ESSs to improve the dynamic capabilities of power plants of various types. An OS in [68] optimally controls ESSs to meet the hybrid wind-power ramp limit.

OSs in [69,70,71,72,73,74,75,76] maximize PS operators’ profit and minimize PS operation costs by means of ESS. The OSs in [69,70] solve the security-constrained unit commitment problem using ESSs’ regulation energy. OSs in [72,73,74] optimize the supply and demand market bids and optimally schedule the ESS operation so that the ESS owner can buy cheap energy on the market, temporarily store it in the ESS, and resell it.

3.5. PS OSs Controlling a Special PS Action Hardware

Once the OS has determined what changes need to be applied to the PS to optimize it, PS’s dispatching system begins to implement these changes—this means that the dispatching system begins to send new-setting orders to individual pieces of PS’s control hardware and this process leads to physical optimization of the PS. Single PSs are equipped with many pieces of control hardware of various types of various capabilities, and the cast of the PS’s control hardware set is reflected in the form and capabilities of the PS’s OS. In other words, the PS’s OS re-sets only the pieces of control hardware which can really be found in the PS. Many OSs use shunt capacitor switching to modify PS’s reactive power flows and so the OSs optimize the PS. Such OSs are presented in [77,78,79,80,81,82]. OS in [83,84] optimize reactive power flows in a PS by changing the taps of on-load tap changers in transformers. The OS in [83] optimally sets the tap position of voltage regulation transformers installed in a distribution system. The OS’s optimization problem is described as a rank-constrained semidefinite program problem, in which the transformer tap ratios are captured by (1) introducing a secondary-side “virtual” bus per transformer, and (2) constraining the values that these virtual bus voltages can take according to the limits on the tap positions. The solved optimization problem is transformed into a convex semidefinite program problem by relaxing the non-convex rank-1 constraint in the rank-constrained semidefinite program formulation. The tap positions are determined as the ratio between the primary-side bus voltage and the secondary-side virtual bus voltage that results from the optimal solution of the relaxed semidefinite program, and then rounded to the nearest discrete tap values. To efficiently solve the relaxed semidefinite program, the OS uses a distributed algorithm based on the alternating direction method of multipliers. During optimal solution searching, the OS considers constraints described by the node-voltage values limits and transformer taps boundaries. The paper’s authors tested the OS performance by simulations of several case studies with single- and three-phase distribution systems. The results of these tests indicate that the OS’s distributed alternating-direction-method-of-multipliers based algorithm is effective in transformers’ best-tap-position finding.

OSs in [85,86] then use both the shunt capacitor switching and changing of the taps of on-load tap changers in transformers. The goal of all these OSs is to optimize a PS’s voltage profile, minimize power losses in a PS, and reduce a contingency of the PS. An OS in [87] optimizes the DS operation using the combination of the transformer tap changing, the shunt capacitors switching, and controlling the programmable thermostats of air conditioners in residential buildings. The OS’s algorithm utilizes a neural network model of controllable loads. Flexible AC transmission system (FACTS) devices are modern power flow control equipment used in transmission systems (TS). OSs in [88,89,90,91,92] maximize the transmission capacity of TS’s power lines by changing the FACTS settings. An OS in [93] determines the locations in the TS where it would be optimal to install FACTS to optimize the TS power flows while there are many wind turbines connected to the TS. For the active and reactive power flows regulation over a wide power range, phase shifting transformers (PST) are used in TSs. An OS in [94] maximizes TS’s transmission capacity using the PST and the high-voltage direct-current lines. The OS in [95] optimizes the PS operation using the energy router. The energy router is a power-electronic device installed to an electrical network transferring the power through the central DC part. The goal of this OS is to minimize the cost of power generation, the pollutant treatment cost, and the active power loss.

3.6. PS OSs Optimizing the Microgrid Operation

Here, there are many big differences between the stable control of a large PS and the stable control of a microgrid (MG). Usually, a large PS is equipped with much more pieces of the control hardware than a MG. Usually, in a large PS, there are both more types and the higher total amount of loads and power sources connected to it than in a MG. In general, any random event on the power-input side or on the power-output side has a greater impact on the operational stability of a MG than on the operational stability of a large PS. Therefore, optimizing the operation of a MG is a more difficult process than optimizing the operation of a large PS. MGs’ OSs have a smaller palette with optimization interventions to the physical infrastructure, so they have to carefully determine which optimization tool should be used and when to use it. Therefore, MGs’ OSs use methods to predict the future dynamics of the MG’s state quantities. OSs in [96,97,98,99,100,101,102] minimize the frequency and voltage deviations in a MG. An OS in [103] solves the distributed generation planning problem, allocating distributed generation units including microturbines and wind turbines in MGs, with the aim of maximizing the total profit over a long-term planning horizon. OSs in [104,105,106] optimally control the charging/discharging (C/D) of a group of ESSs to stabilize the MG operation. The OS in [105] uses a distributed algorithm that coordinates multiple battery ESSs under wind uncertainties and maximizes the total welfare of battery ESSs while respecting the supply–demand balance. By considering the energy efficiency and time-of-use pricing, the algorithm’s objective function is formulated to maximize the total welfare of multiple battery ESSs that can encourage battery ESSs to participate in grid regulation. Furthermore, the OS uses a coordination scheme of battery ESSs under wind power generation uncertainties to maintain active power balance. To make the OS’s algorithm more compatible with the requirement of the power grid, the OS’s authors developed a multi-agent system framework. By regarding each battery ESS as an agent, the agents only need to exchange information with its neighboring agents through a local communication network. Thus, the proposed strategy can work in a distributed way so that computational and communication burdens are reduced comparing with centralized methods. Besides, the information sharing of the cost function may result in the privacy concerns of the participants in the microgrid. To this end, the OS solves the formulated problem privately which is achieved by introducing a mismatch estimator to update the local power output and removing the requirement of gradient information sharing. During optimal solution searching, the OS considers constraints described by the local boundary of the output power for individual battery ESSs. The paper’s authors tested the OS effectiveness and scalability by simulations on the IEEE 14-bus system and a 30-battery ESS system with various operation conditions.

The OS in [106] collaboratively schedules the ESS C/D and the direct load control. OSs in [107,108] schedule the direct load control to minimize the MG operation costs. An energy management system in [109] is a very complex OS: It regulates several power generation and consumption units, ESSs, and electric vehicles to minimize the MG operation costs. An OS in [110] optimally aggregates spatially distributed flexible power sources connected to a MG to several strategic nodes of the MG. The OS’s algorithm seeks such an aggregation plan which accelerates the real-time PS management process to the maximum and maximizes the utilization of the power produced by local distributed sources at the local electricity market.

3.7. PS OSs Regulating the Charging/Discharging of Electric Vehicles

Section 3.3 has been dedicated to OSs which optimize PS operation through control of some power loads. One type of load is so specific that one separate OSs group was created for it (the group G). These specific loads are electric vehicles (EVs) connected to the PS through charging stations. A specific feature of these loads is that, unlike other loads, they change their location, and for the PS operator, they are controllable only occasionally, specifically when the EV is connected to the controllable charging station. To ensure that the EV charging does not jeopardize the stability of PS operation and has a minimal impact on the quality of the power supplied to customers, PS operators will have to use OSs to coordinate local EV chargers’ operation with other facilities connected to the PS. An example of such OS is presented in [111]. The OS in [111] optimally schedules charging of EVs, assuming that the future charging demand is not known a priori, but its statistical information can be estimated. In particular, OS’s authors defined the cost of EV charging as a general strictly convex increasing function of the instantaneous load demand. Minimizing such a cost leads to flattened load demand. The online EV charging scheduling problem is formulated as a finite-horizon dynamic programming problem with continuous state space and action space. To avoid the prohibitively high complexity of solving such a dynamic programming problem, the OS uses a model predictive control approach to obtain a near-optimal solution. Instead of adopting the generic convex optimization algorithms to solve the problem, OS uses an algorithm with computational complexity O(T³) by exploring the load flattening feature of the solution, where T is the total number of time stages. During optimal solution searching, the OS considers the constraint described by the charging deadline, i.e., the time when the charging of individual EV must be finished. The paper’s authors tested the OS performance by extensive simulations. The results of these tests show that the OS’s algorithm performs very closely to the optimal solution. The performance gap between the solution found by the OS and the problem’s optimal solution is smaller than 0.4% in most cases. As such, the OS is very appealing for practical implementation due to its scalable computational complexity and close to optimal performance.

An OS in [112] schedules the EV charging to minimize the EV charging cost and optimize the PS load profile. The OS has two modes: The day-ahead optimization mode and real-time optimization mode. The OS’s algorithm defines optimization actions using historical PS operation data and statistical models. The EVs of a future generation should be equipped with a system controlling both the power flow from the charger to the EV battery and the power flow from the EV battery to the charger. If PS operators connect their dispatcher systems with this EV-control system, they can use all EVs connected to the PS as a large space-dispersed battery. Thus, they can optimize PS operation in a similar way as the OSs presented in Section 3.4 of this paper. Many OSs controlling EV C/D have already been developed, e.g., OSs in the [113,114,115] control EV C/D to stabilize a PS operation. The OS in [113] uses EVs’ energy accumulation capacity for both primary and secondary frequency regulation and for the support of an inflexible power plants operation. The OS in [114] creates a day-ahead vehicle-to-grid (V2G) scheduling profile which considers the daily-mobility energy requirement of an EV fleet. An OS in [116] is similar to the last mentioned, but this OS specializes in the MG operation optimization. An OS in [117] maximizes the profit of owners of EVs which are joined to the V2G system. The OS forecasts energy supply and demand in the PS and watches market prices. The OS’s algorithm is based on a special bidding strategy which includes the EV battery degradation cost to its economic analysis. The EV battery degradation cost is considered also by the algorithm of an OS in [118]. The OS optimally control the EV charging and the V2G system to minimize the total costs of the local EVs operation, and to flatten the PS load profile.

3.8. PS OSs Maximizing the PS Operation Stability

The OSs group H is dedicated to OSs which maximize PS operation stability. An OS in [119] enhances the resilience of the PS. When the PS operating state is normal, this OS reduces the probability of the occurrence of a PS emergency state (limited operational capability state), and when the PS operating state is emergency, it decreases the extent of the PS operational capability limitation. In the normal PS state, the OS dispatches generators and changes the PS topology, while in the emergency PS state, the OS dispatches generators, changes the PS topology, and shades the PS loads. OSs in [120,121,122] enhance the stability of PSs powered by many wind power plants. The OS in [121] extends standard N-1 security criteria to multiple simultaneous PS contingencies and creates a stability enhancement plan for the worst-case scenarios. The OS solves the transmission line hardening planning problem in the context of probabilistic power flows injected by the high penetration of renewable energy. The OS’s authors assumed that the probabilistic information of renewable energy is incomplete and ambiguous, hence they used in the OS a data-driven approach to approximate the renewable uncertainty sets. The OS uses a two-stage data-driven stochastic model which is based on the joint worst-case wind output distribution and transmission line contingencies. The OS solves the proposed model by the Column-and-Constraints generation method. During optimal solution searching, the OS considers following constraints: The power flow constraint in terms of phase angles, the transmission line flow capacity limit, the bus power balance constraint, the thermal generation capacity limits and the phase angle limit. The paper’s authors tested the OS performance by simulations on the 24-bus and 118-bus test systems. The results of these tests indicate that the OS’s data-driven approach can effectively address the uncertainty ambiguity and produce effective hardening plans that improve the system resilience.

The OS in [122] is dedicated to increasing the stability of PSs powered by many wind power plants equipped with the doubly fed induction generators. An OS in [123] maximizes the operation stability of the DS powered by the distributed generation units. The OS’s algorithm is based on a distributed locational marginal pricing. The algorithm contains two parts: (1) A game theory-based loss reduction allocation to individual distributed generation units, and (2) a load feedback control with price elasticity. This OS maximizes both the profit benefits for distributed generation owners and the operation stability of the DS.

3.9. PS OSs Reconfiguring the Network Topology During the Optimization Process

The OSs group I is dedicated to OSs which achieve optimal PS operation status by changing the network topology (it is the process of opening some PS lines and closing others). An OS in [124] seeks the optimal topology of the unbalanced DS with distributed generation. The OS reconfigures the DS feeders every hour based on the status of time-varying loads, output power from distributed generation units, and faults on the network. An OS in [125] seeks the optimal topology of the PS in which some lines are fixed (uncontrollable) and the remaining ones are controllable via on/off switches. An OS in [126] changes the PS topology using the substation reconfiguration model which provides a more practical and realistic picture of switching actions and has higher flexibility in switching actions than the standard bus-branch reconfiguration model. An OS in [127] reduces the active power loss by combining the PS topology reconfiguration and the optimal control of prosumers’ reactive power generation. The prosumer is the subject connected to the PS which can both draw the electrical power from the PS and consume it, and generate the power and send it to the PS. This OS finds the optimal network topology at first and then it determines the optimal reactive power generation in the prosumer buses. The OS solves both optimization problems using a genetic algorithm. The optimization algorithm considers constraints of the maximum and minimum allowable voltages in the distribution network and the maximum and minimum available reactive powers provided by local reactive power generation. The paper’s authors tested the OS performance by simulations on the IEEE 33-bus test system. The results of these tests indicate that the OS can reach higher active power losses reduction than OSs that only finds optimal network topology or only optimally control the reactive power generation in the prosumer buses.

3.10. PS OSs Finding an Optimal PS Expansion Plan

The OSs group J is dedicated to OSs which create the optimal PS expansion plan; that is, these OSs are seeking the optimal routing of newly constructed lines and the optimal location of newly constructed power sources. An OS in [128] determines the optimal routing of medium voltage DS in sparse rural areas. The OS’s objective is evaluated by minimizing the net present cost of the network over a selected time period. The OS solves the optimization problem using a specific genetic algorithm. The OS finds the optimal network routing and the optimal network topology in a geographically constrained region. The OS simultaneously considers nonfixed candidate lines to overcome search space restrictions through a variable-length encoding structure and the use of Steiner points, and the shortest path algorithm to traverse between point-to-point connections in the constrained region. Geographical restrictions on network routing are considered through the formation of a rasterized map. The OS models the network at the branch level and considers both greenfield and expansion planning to highlight the effects of accessibility restrictions. In addition to the geographic constraints, the optimal solution found by the OS is also constrained by the radial topology, node-voltage values limits, and the reliability constraint (specifically, the optimum topology found by the OS must lead to at least as reliable operation as the topology of the existing network). The reliability constraint is described by the limit values of the approximated reliability cost. The paper’s authors tested the OS performance by its application in a real rural distribution network in the South-West of Western Australia. The results of these tests indicate that the OS can find alternative network topologies that provide significant improvements in the network operation parameters, and the OS is more effective in minimization of the operation costs of sparse rural distribution networks than are traditional reconfiguration methods.

3.11. PS OSs Using the Market Clearing During the Optimization Process

The OSs group K is dedicated to OSs which involve various entities influencing PS power flows into the internal power market and, through market price regulation, achieve the behavior of these entities which is optimal from the perspective of the PS operator. An OS in [129] uses a special cooperative trading mode for a community-level PS which consists of the energy hub and PVG prosumers with the automatic demand-response capability. The concept of energy hub was proposed to facilitate the synergies among different forms of energy carriers. This OS tries to reach a win-win situation for prosumers and the energy hub manager at the community level without bringing an extra burden to the utility PS. The OS is based on a special cooperative trading framework that uses a real-time rolling horizon energy management model based on cooperative game theory considering the stochastic characteristics of PVG prosumers and the conditional value at risk. The authors who designed this OS analyzed the validity of this energy management model through the optimality proof of the grand coalition. The OS also uses a contribution-based profit distribution scheme. In order to make the optimization problem easily solvable, the OS transforms the problem into a mixed-integer linear programming (MILP) problem by adding auxiliary variables. The searching for the problem’s optimal solution is constrained by the node-voltage values limits and the operation time of individual local appliances. The paper’s authors tested the OS performance by the case study. In the case study, the power system with the community was used. The community consisted of two office buildings and four residential buildings. They were treated as prosumers with roof-top PVG. The proportion of shiftable loads’ energy consumption was close to 30%. The results of these tests indicate that the OS can promote local consumption of PVG energy, increase hub manager’s profits, and reduce prosumers’ costs.

4. Discussion and Conclusions

The performed statistical analysis showed that PS OSs groups A (PS OSs minimizing the price of electricity/PS OSs reducing PS operation costs), B (PS OSs optimizing the operation of renewable energy sources) and C (PS OSs regulating the power consumption during the optimization process) are the mainstream of the current PS OS research. The comparison of the results of the first and second paper assignment processes shows that the PS OS groups B and D (PS OSs regulating the energy storage systems operation during the optimization process) dominate the other PS OS groups much more in the second assignment process than in the first assignment process. These results thus indicate that the optimization of the RES units and the control of the ESS units are very common secondary characteristics of current PS OSs.

The detailed analysis of PS optimization papers showed that an OS presented in a paper effectively controls only the PS for which the OS was designed. Even today, the most frequently considered goal of PS OSs remains the minimization of the amount of power lost in network elements during power transmission. With the growing number of electrical power generation units using renewable energy resources, the increasingly considered goal is to maximize the share of electrical energy produced by these units in total electrical energy consumption. To achieve this goal, many present day PS OSs utilize the ability of BESs and EVs to extract electrical power from the PS, accumulate it at a time when the power generation is higher than the consumption, and return the power to the grid at a time when the power generation is lower than the consumption. The most frequently considered constraints of the optimization process are power lines’ transmission capacity limit and minimal and maximal value of voltages at the network nodes.

Analysis of PS OSs trends has shown that the occurrence of PS OSs, which deviates from the standard research streams of power system optimization research (i.e., PS OSs research streams corresponding to paper groups B to K) in some way, increases. The increase in the relative frequency of PS OSs group A shown by Figure 3 can be explained by current PS-OSs researchers trying to differentiate from older papers and standard research streams, and try to create new PS OSs which share the main optimization idea with the older PS OSs (i.e., the minimization of the price of electricity or the reduction of the PS operation costs). However, in these new PS OSs, unlike in the PS OSs of the standard research streams, an unusual secondary optimization target is defined or there is an unusual PS part optimized. Taking a closer look at the individual PS OSs presented in the papers of our database, we see a growing interest in the impact of uncertainties on the solution to the optimization problem. The impact of uncertainties on the solution of the optimization problem is investigated mainly in PS OSs working with renewable energy sources (especially PS OSs working with wind power plants deal with uncertainties very often [37,38,40,42]).

In the future, it would be interesting to analyze new trends in PS OSs’ optimization algorithms. Some recent papers presented new optimization algorithms based on biologically inspired optimization strategies (e.g., optimization algorithms based on the Sine Cosine Algorithm [130], Particle Swarm Optimization [131], or Flower Pollination Algorithm [132]).