Carrier-Phase-Shifted Rotation Pulse-Width-Modulation Scheme for Dynamic Active Power Balance of Modules in Cascaded H-Bridge STATCOMs
Abstract
:1. Introduction
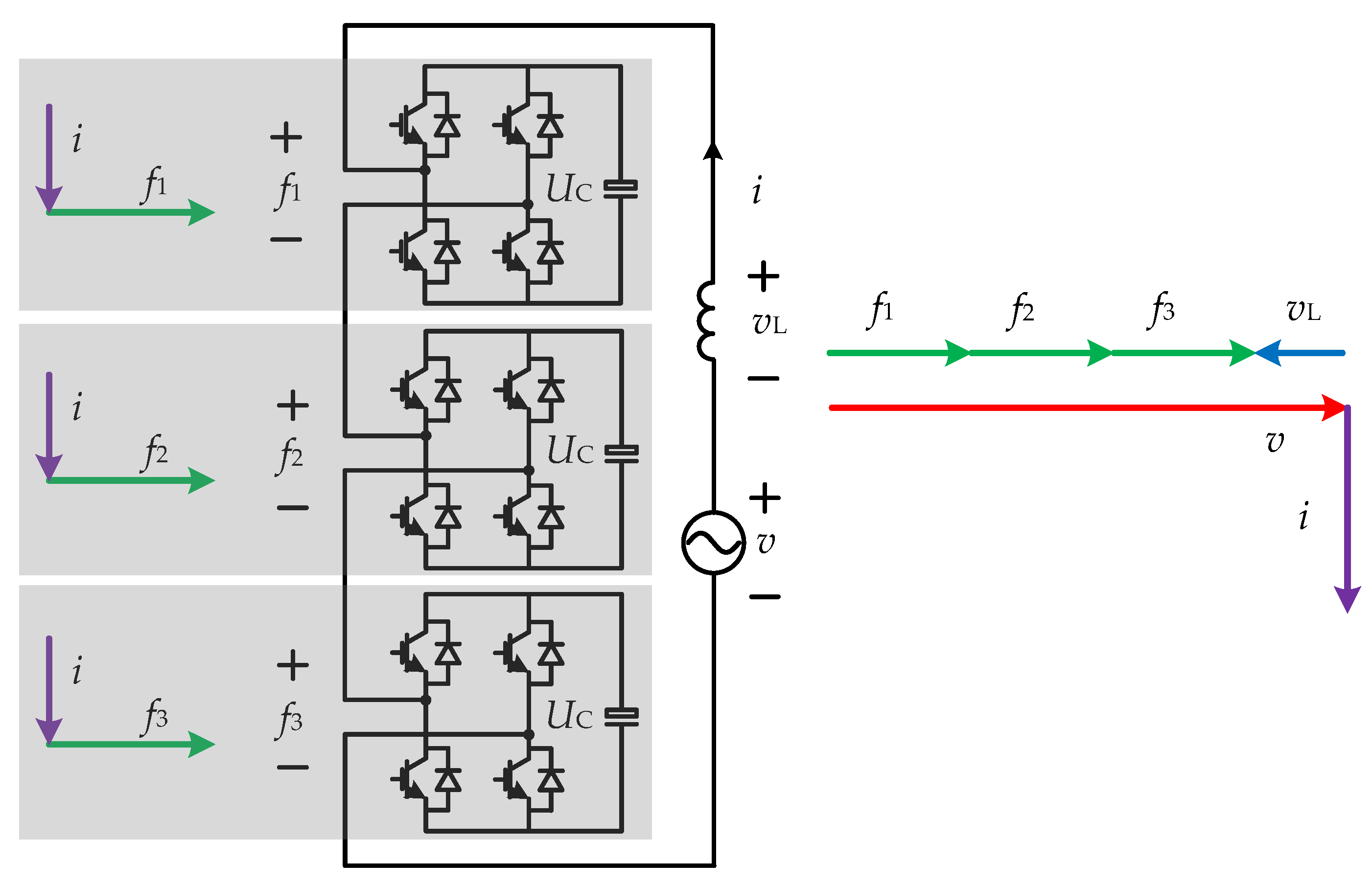
2. Basic Control Method for CHB-STATCOM
3. CPS-PWM Method and Carrier Phase Difference Influence on Module Active Power Balance
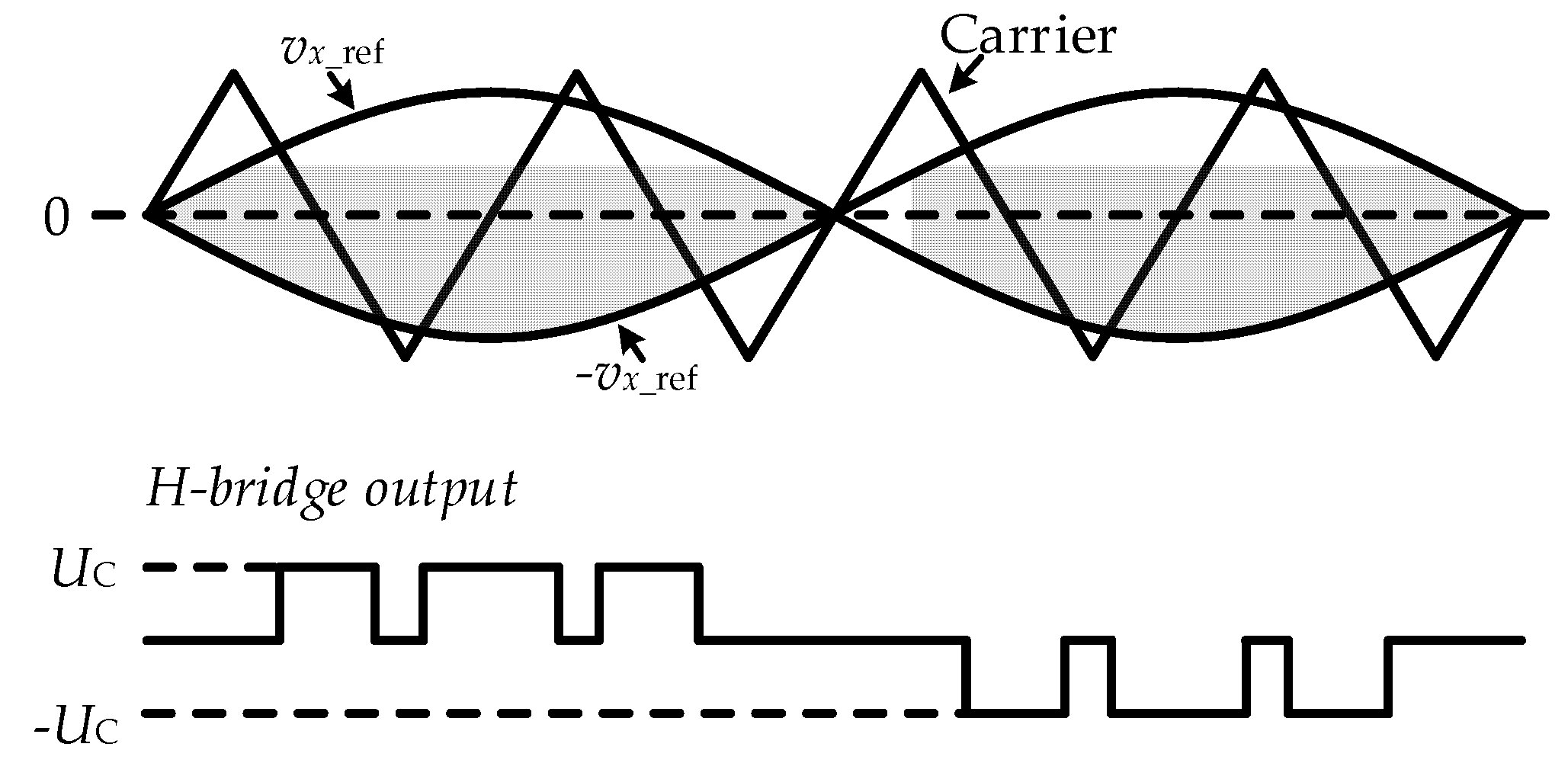
3.1. Conventional CPS-PWM Method
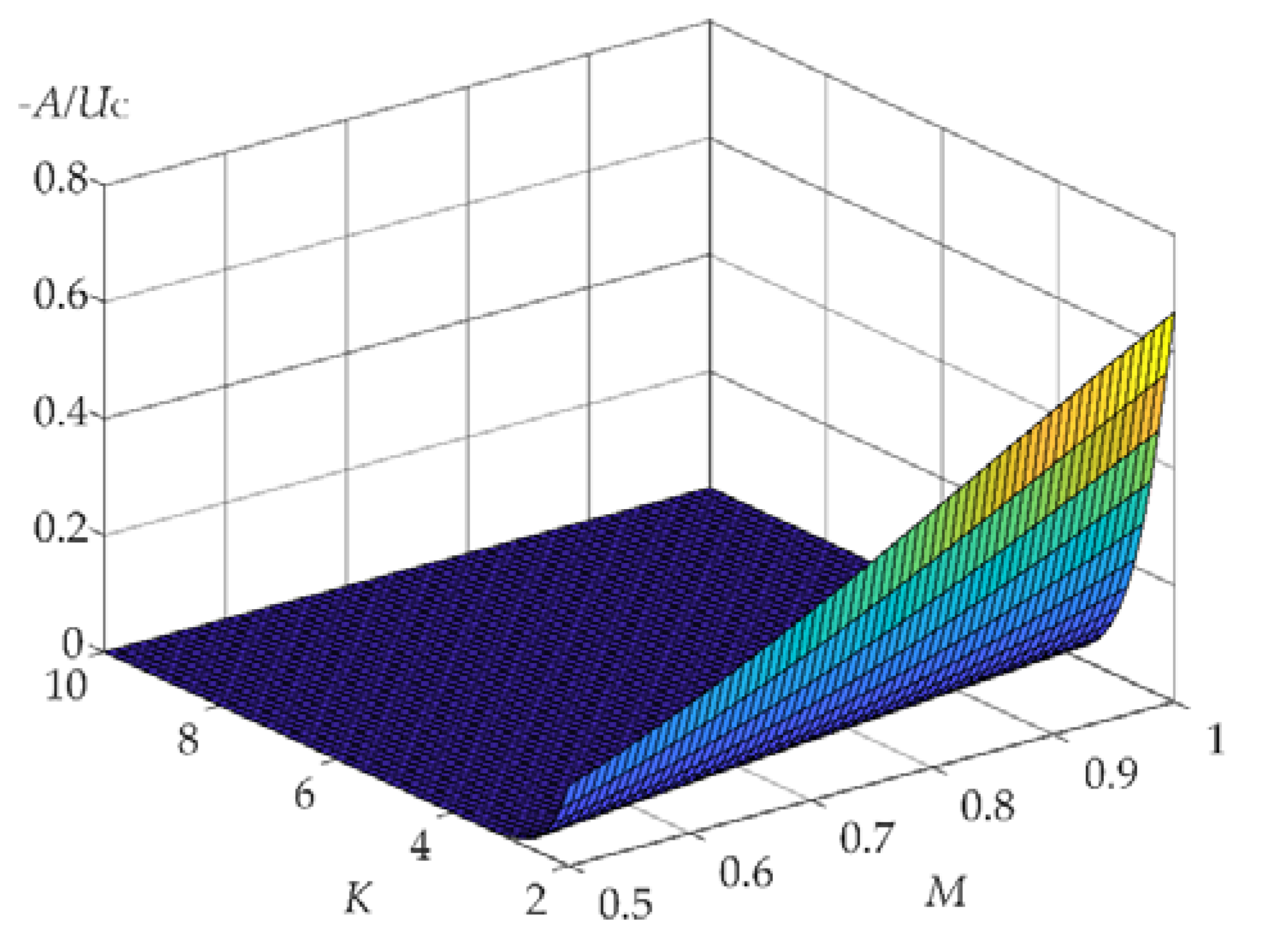
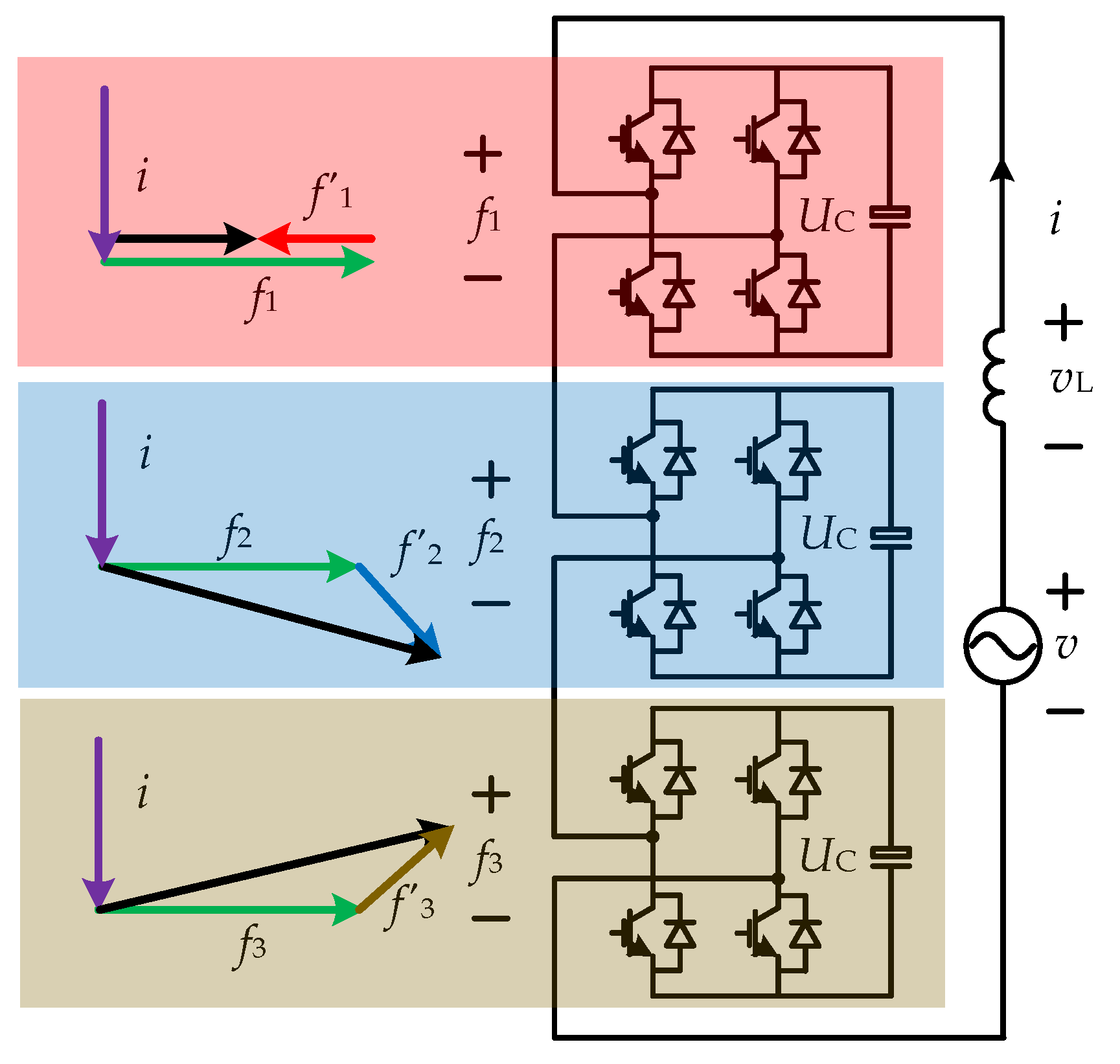
3.2. Carrier Phase Difference Influence on Module Active Power Balance
4. Proposed CPSR-PWM Scheme
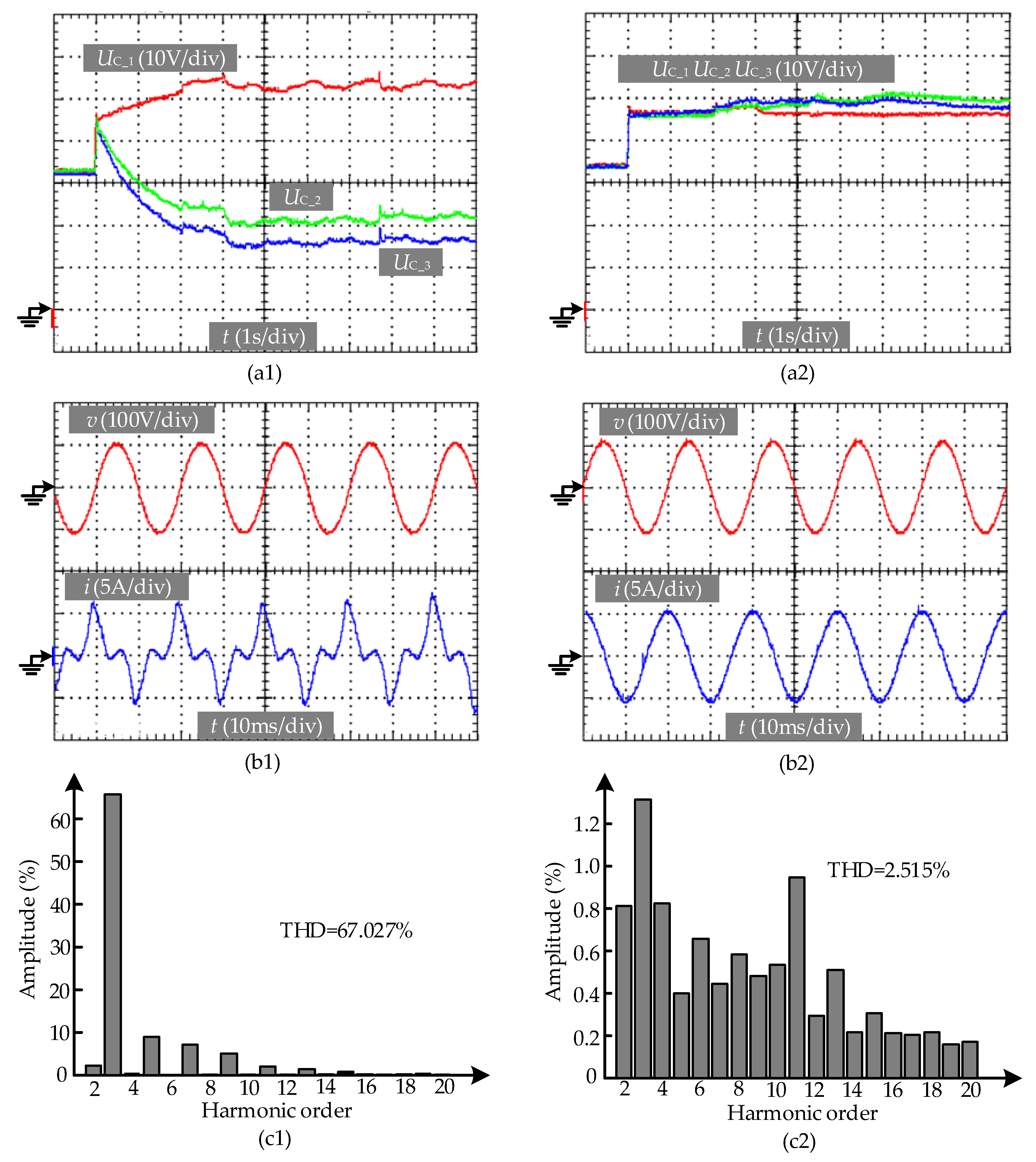
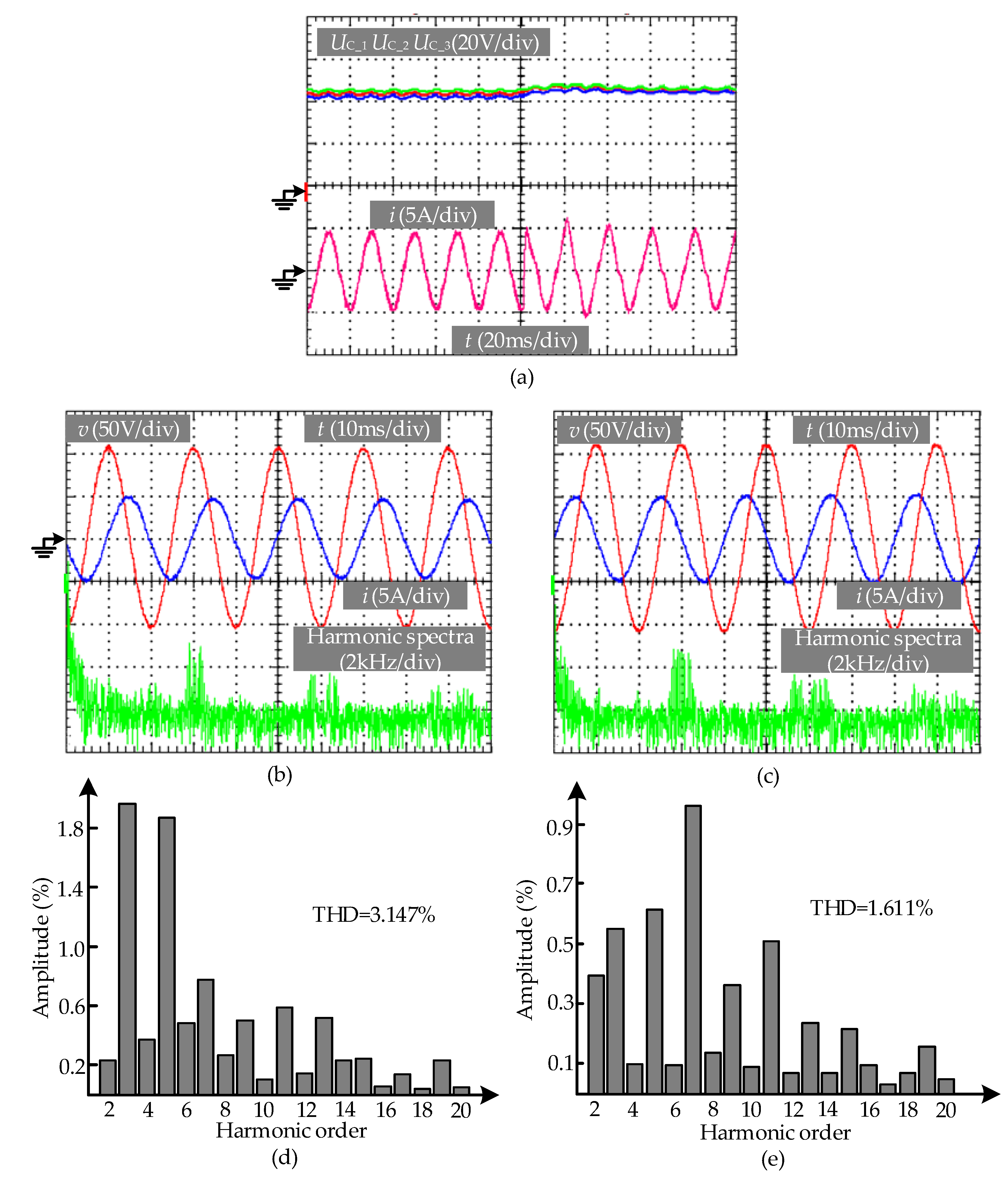
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, C.I.; Chen, Y.C.; Chin, Y.C.; Chen, C.H. Integrated power-quality monitoring mechanism for microgrid. IEEE Trans. Smart Grid 2018, 9, 6877–6885. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Issa, W.; Hossain, M.J. Overview of AC microgrid controls with inverter-interfaced generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Joksimovic, G. Transformer reactive power compensation–fixed capacitor bank calculation. IEEE Trans. Power Deliv. 2015, 30, 1629–6130. [Google Scholar] [CrossRef]
- Gyugyi, L.; Otto, R.A.; Putman, T.H. Principles and applications of static, thyristor-controlled, shunt compensator. IEEE Trans. Power Appar. Syst. 1978, 5, 1935–1945. [Google Scholar]
- Gyugyi, L. Application characteristics of converter-based FACTS controllers. In Proceedings of the International Conference on Power System Technology, Perth, WA, Australia, 4–7 December 2000; pp. 391–396. [Google Scholar]
- Wang, Y.H.; Li, Y.; Cao, Y.J.; Tan, Y.; He, L.; Han, J.Y. Hybrid AC/DC microgrid architecture with comprehensive control strategy for energy management of smart building. Int. J. Electr. Power Energy Syst. 2018, 101, 151–161. [Google Scholar] [CrossRef]
- Xu, C.; Dai, K.; Chen, X.W.; Kang, Y. Voltage droop control at point of common coupling with arm current and capacitor voltage analysis for distribution static synchronous compensator based on modular multilevel converter. IET Power Electron. 2016, 9, 1643–1653. [Google Scholar] [CrossRef]
- Kotsampopoulos, P.; Georgilakis, P.; Lagos, D.T.; Kleftakis, V.; Hatziargyriou, N. FACTS providing grid services: Applications and testing. Energies 2019, 12, 2554. [Google Scholar] [CrossRef] [Green Version]
- Han, B.M.; Baek, S.T.; Ko, J.S. New configuration of 36-pulse voltage source converter for STATCOM. In Proceedings of the 31st Annual Conference of the IEEE-Industrial-Electronics-Society, Raleigh, NC, USA, 6–10 November 2005; pp. 865–870. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A new neutral-point clamped PWM inverter. IEEE Trans. Ind. Appl. 1981, 17, 518–523. [Google Scholar] [CrossRef]
- Choi, N.S.; Cho, J.G.; Cho, G.H. A general circuit topology of multilevel inverter. In Proceedings of the 22nd Annual IEEE Power Electronics Specialists Conference, Cambridge, MA, USA, 24–27 June 1991; pp. 96–103. [Google Scholar]
- Meynard, T.A.; Foch, H. Multi-level conversion: High voltage choppers and voltage-source inverters. In Proceedings of the 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 397–403. [Google Scholar]
- Meynard, T.A.; Foch, H.; Thomas, P.; Courault, J.; Jakob, R.; Nahrstaedt, M. Multicell converters: Basic concepts and industry applications. IEEE Trans. Ind. Electron. 2002, 49, 955–964. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S.; McKeever, J.W.; VanCoevering, J. A multilevel voltage-source inverter with separate DC sources for static var generation. IEEE Trans. Ind. Appl. 1996, 32, 1130–1138. [Google Scholar] [CrossRef] [Green Version]
- Peng, F.Z.; Wang, J. A universal STATCOM with delta-connected cascade multilevel inverter. In Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 3529–3533. [Google Scholar]
- Pandey, R.; Tripathi, R.N.; Hanamoto, T. Comprehensive analysis of LCL filter interfaced cascaded H-bridge multilevel inverter-based DSTATCOM. Energies 2017, 10, 346. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Lin, L.; Yin, T.X.; Hu, J.B. An improved phase-shifted-carrier technique for hybrid modular multilevel converter with boosted modulation index. IEEE Trans. Power Electron. 2020, 35, 1340–1352. [Google Scholar] [CrossRef]
- Paris, J.M.D.; Osório, C.R.D.; Pinheiro, H.; Carnielutti, F.D.M. Phase disposition modulation with sorting algorithm for symmetrical cascaded multilevel converters. IEEE Trans. Ind. Appl. 2019, 55, 7527–7536. [Google Scholar] [CrossRef]
- Ilves, K.; Harnefors, L.; Norrga, S.; Nee, H.P. Analysis and operation of modular multilevel converters with phase-shifted carrier PWM. IEEE Trans. Power Electron. 2015, 30, 268–283. [Google Scholar] [CrossRef]
- Zha, X.M.; Yang, Z.Z.; Gong, J.W.; Li, S.S.; Liu, F.; Huang, M. Asymmetrical carrier phase-shifted pulse-width modulation for partly regenerative converter. IET Power Electron. 2017, 10, 442–450. [Google Scholar] [CrossRef]
- Solomon, L.A.; Permuy, A.; Benavides, N.D.; Opila, D.F.; Lee, C.J.; Reed, G.F. A transformerless PCB-based medium-voltage multilevel power converter with a DC capacitor balancing circuit. IEEE Trans. Power Electron. 2016, 31, 3052–3067. [Google Scholar] [CrossRef]
- Luo, L.; Zhang, Y.; Jia, L.; Yang, N.; Yang, L.; Zhang, H. Capacitor static voltage balance based on auxiliary-power supply pulse width control for MMC. IET Power Electron. 2018, 11, 1796–1803. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, B.; Duan, S.; Kang, Y. A novel DC capacitor voltage balance control method for cascade multilevel STATCOM. IEEE Trans. Power Electron. 2012, 27, 14–27. [Google Scholar] [CrossRef]
- He, Y.; Duan, W.; Fu, Y. Research on DC voltage balancing control method of star connection cascaded H-bridge static var generator. IET Power Electron. 2016, 9, 1505–1512. [Google Scholar] [CrossRef]
- Yang, D.; Yin, L.; Xu, S.; Wu, S. Power and voltage control for single-phase cascaded H-bridge multilevel converters under unbalanced loads. Energies 2018, 11, 2435. [Google Scholar] [CrossRef] [Green Version]
- Xie, C.; Zhao, X.; Li, K.; Zou, J.; Guerrero, J.M. Multirate resonant controllers for grid-connected inverters with harmonic compensation function. IEEE Trans. Ind. Electron. 2019, 66, 8981–8991. [Google Scholar] [CrossRef]
- Bahrani, B.; Karimi, A.; Rey, B.; Rufer, A. Decoupled dq-current control of grid-tied voltage source converters using nonparametric models. IEEE Trans. Ind. Electron. 2013, 60, 1356–1366. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, X.; Liu, S.; Tse, C.K. Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics. IEEE Trans. Power Electron. 2010, 25, 3119–3127. [Google Scholar] [CrossRef]
- Adam, G. Current control of voltage source inverter with unipolar double frequency PWM. In Proceedings of the 2017 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 25–30 June 2017. [Google Scholar]
- Holmes, G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principle and Practice; IEEE Press: Piscataway, NJ, USA, 2003. [Google Scholar]
- Waston, G.N. The Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Zhang, Y.; Dai, K.; Xu, C.; Kang, Y.; Dai, Z. Multiple sampling PSC-PWM with hierarchical control architecture for MMC-DSTATCOM. IET Electr. Power Appl. 2019, 13, 1431–1440. [Google Scholar] [CrossRef]
- IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Standard: Piscataway, NJ, USA, 2014; pp. 1–29.

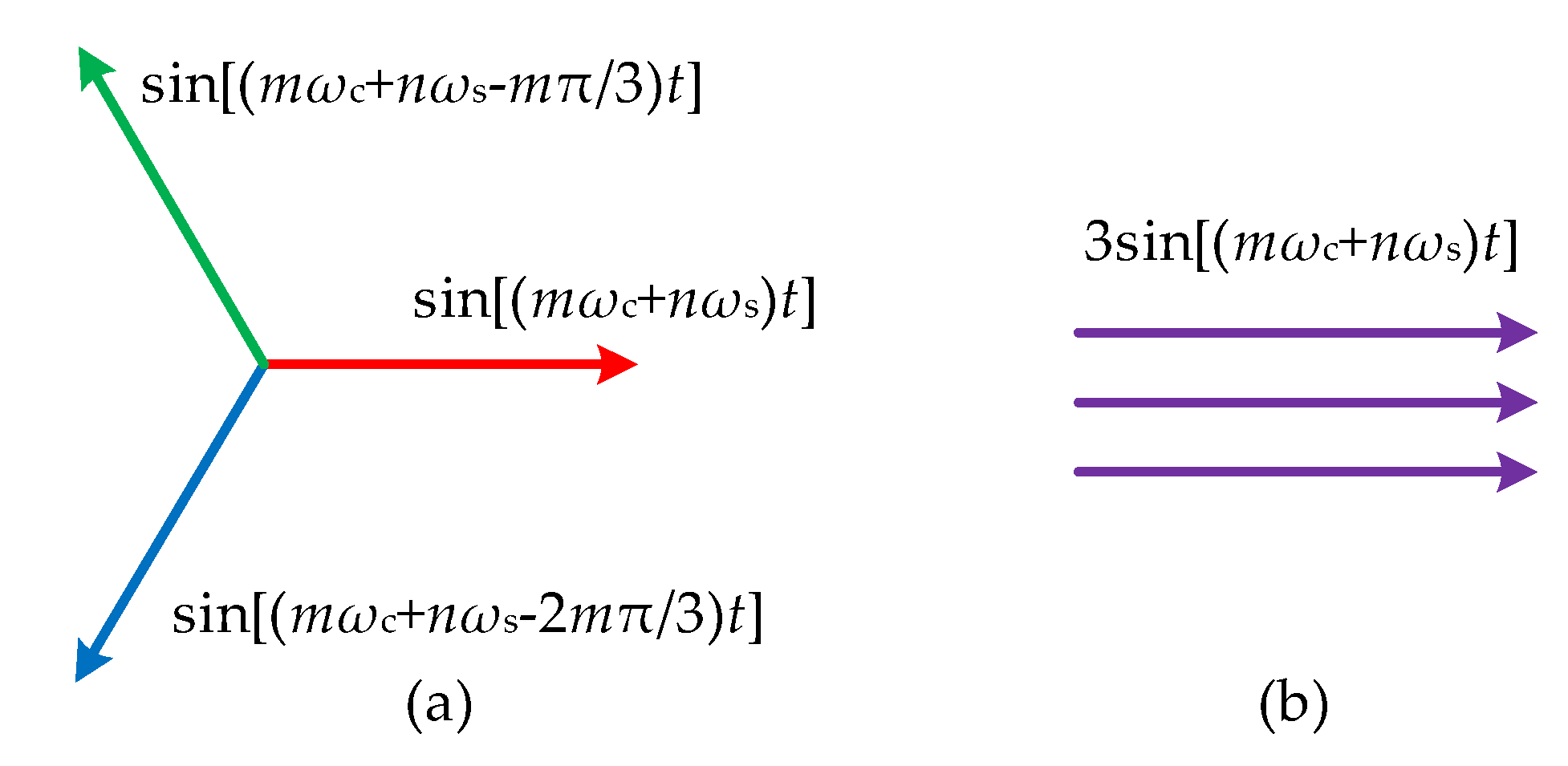
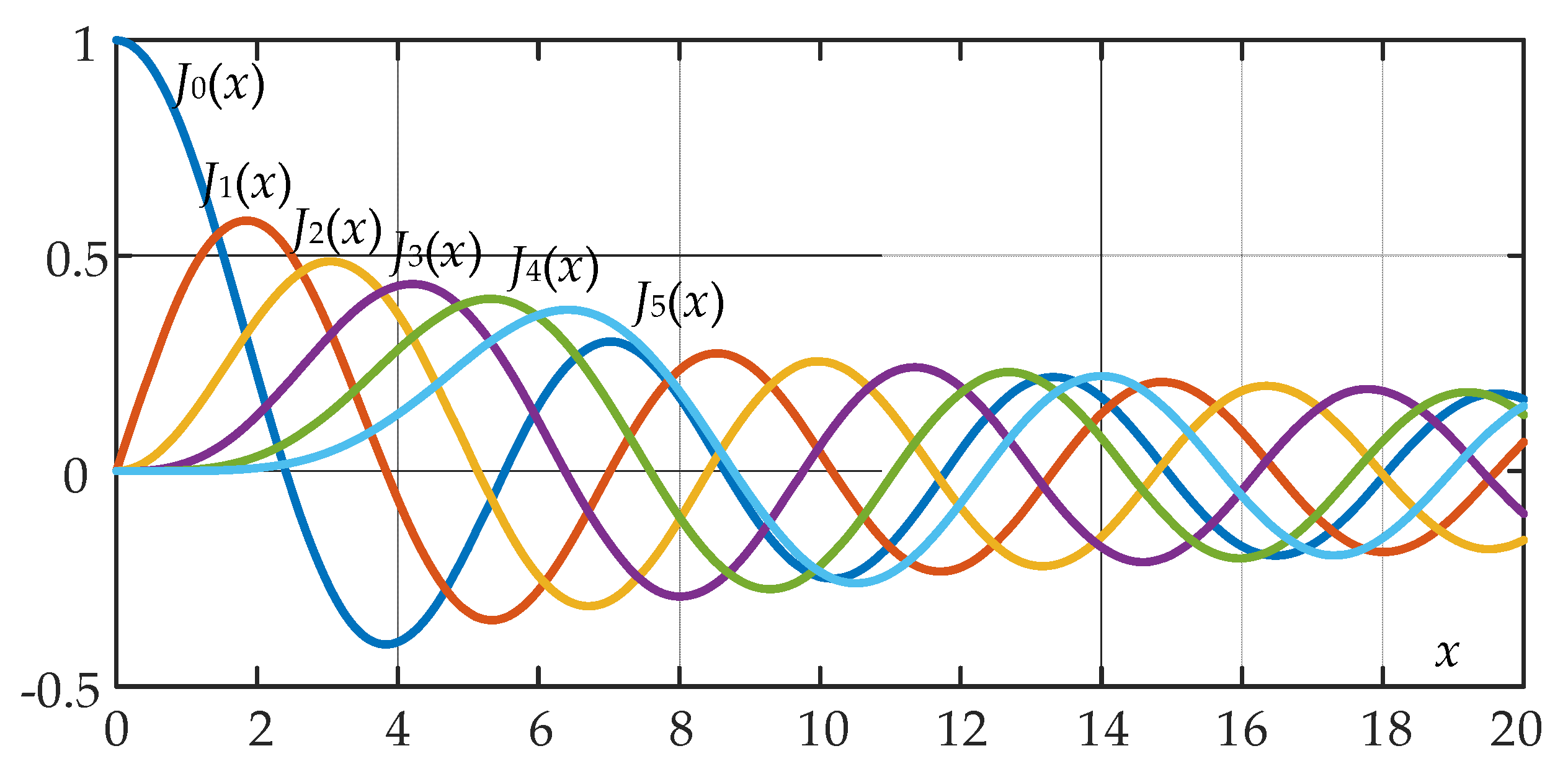


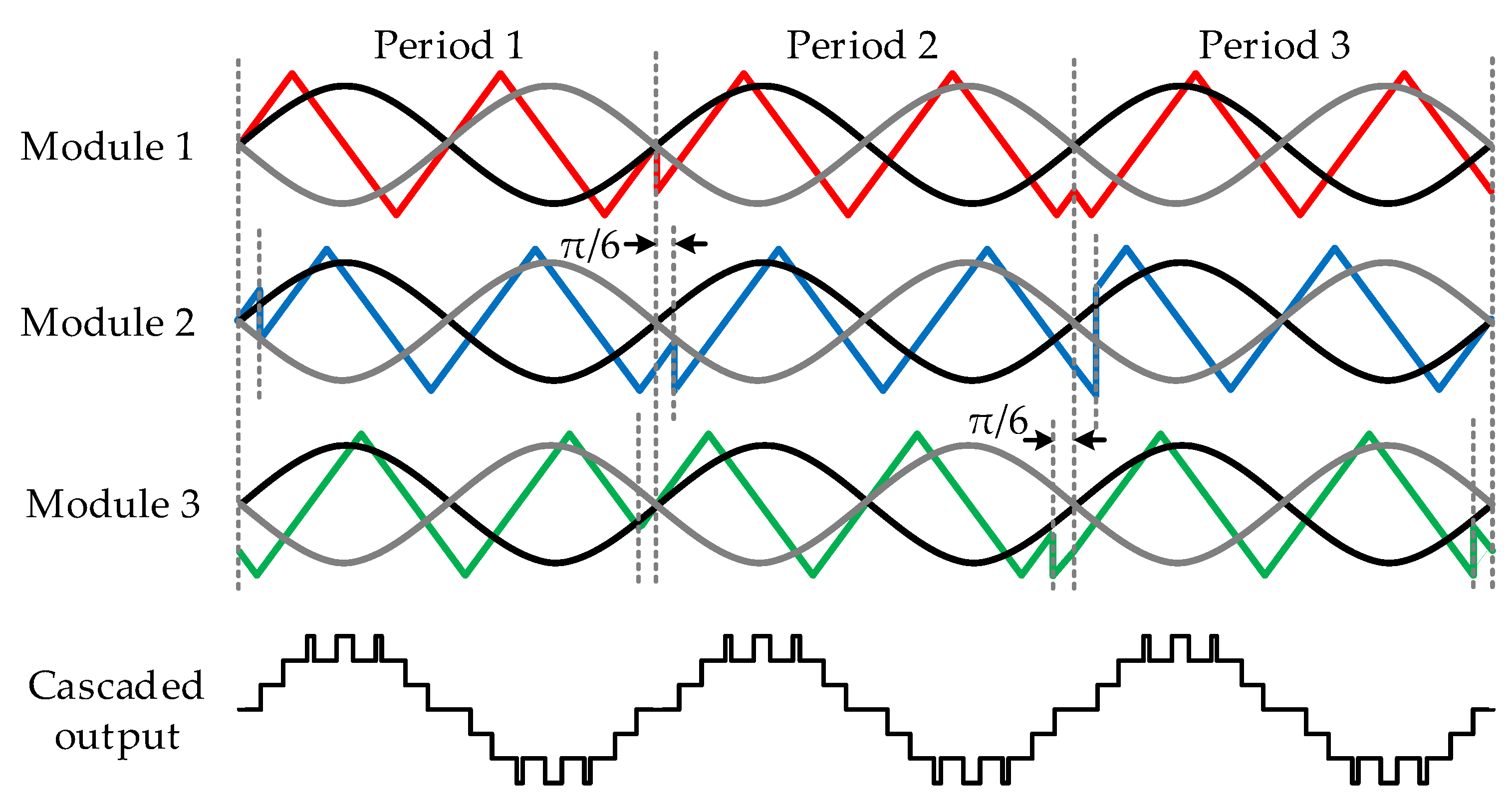
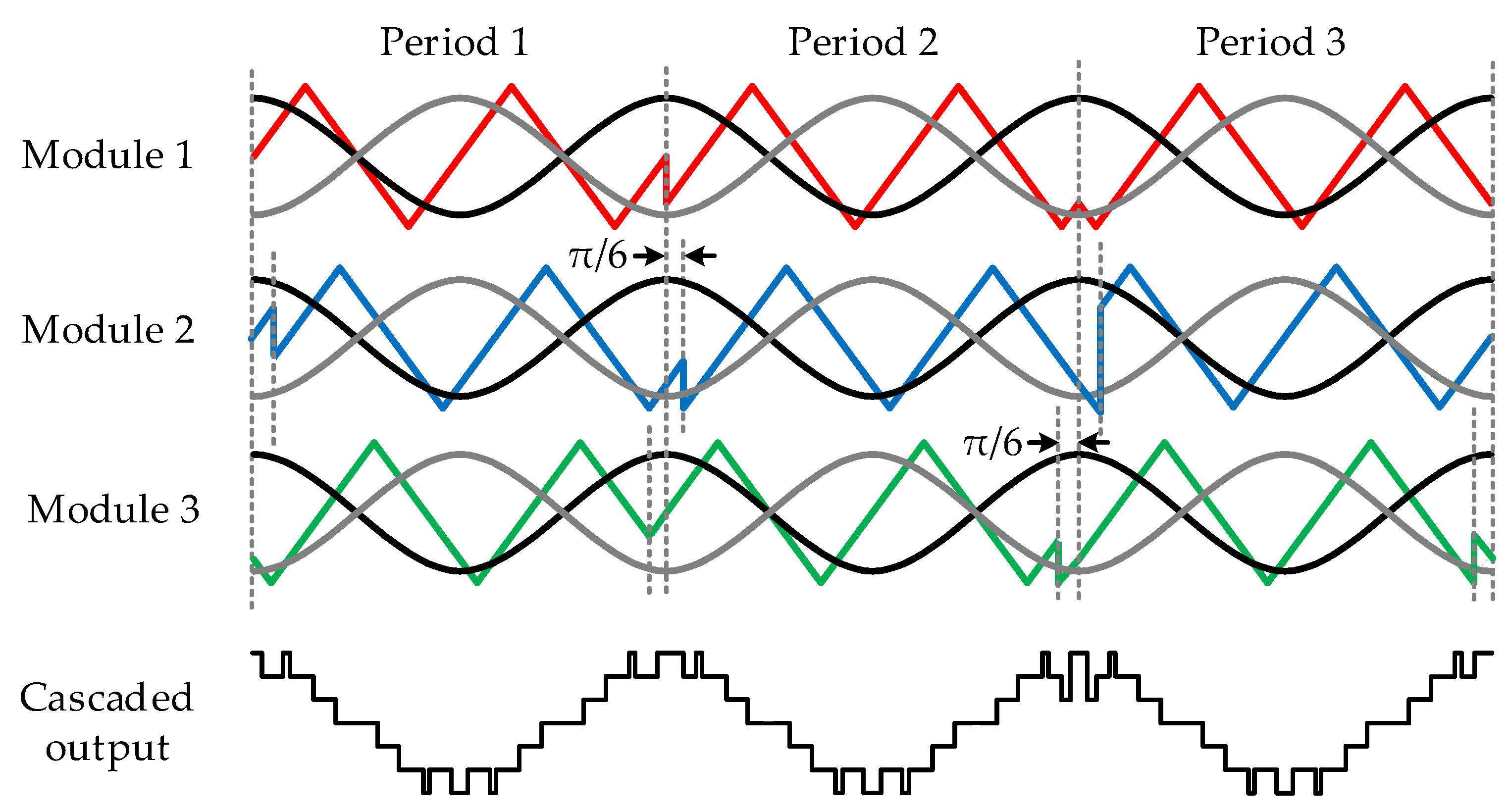
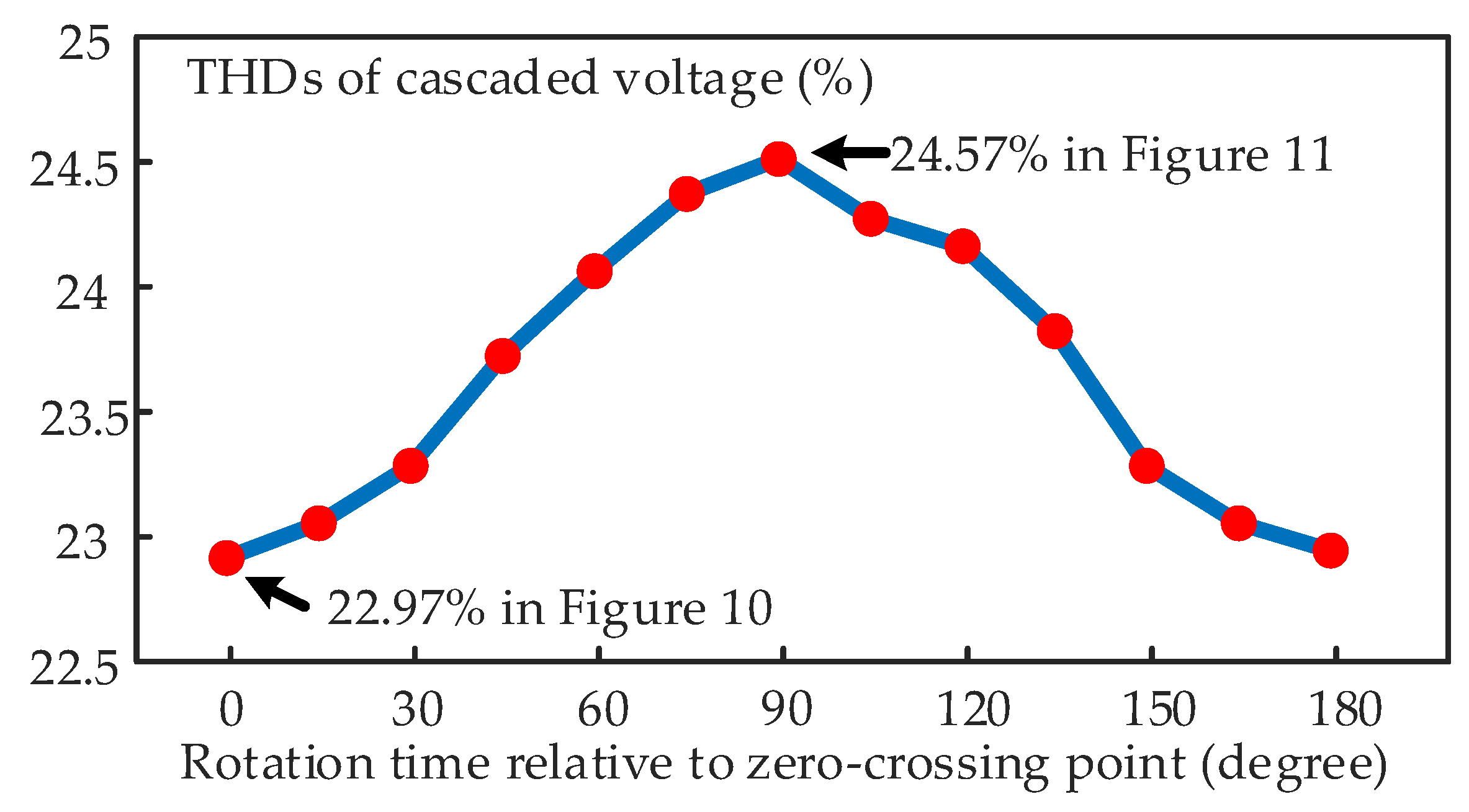
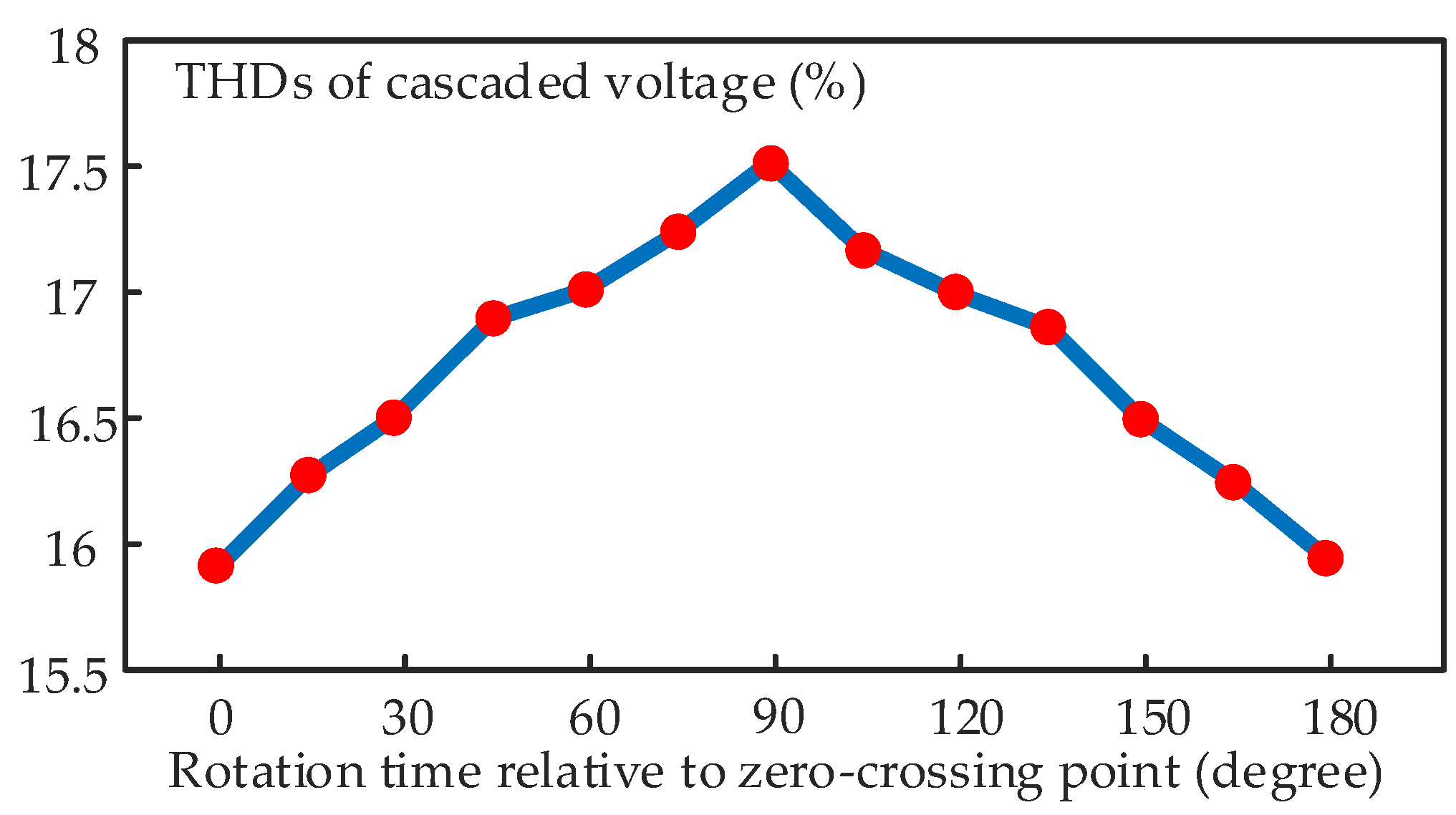

| Period 1 | Period 2 | Period 3 | Period 1~3 | |
|---|---|---|---|---|
| Zero-crossing | 24.81% | 24.63% | 24.62% | 22.97% |
| Maximum point | 24.97% | 29.43% | 29.42% | 24.57% |
| Parameters | Symbols | Values |
|---|---|---|
| Cascaded module number | N | 3 |
| Root-mean-square value of grid voltage | v | 82 V |
| Module capacitance | C | 4.7 μF |
| Compensating current reference | Iq_ref | 5 A |
| Rated capacitor voltage | UC_ref | 48 V |
| Buffer inductance | L | 8 mH |
| Fundamental/reference frequency | f | 50 Hz |
| Carrier frequency | fc | 1k Hz |
| Equivalent switching frequency | fE | 6k Hz |
| Sampling frequency | fs | 6k Hz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Chen, J.; Dai, K. Carrier-Phase-Shifted Rotation Pulse-Width-Modulation Scheme for Dynamic Active Power Balance of Modules in Cascaded H-Bridge STATCOMs. Energies 2020, 13, 1052. https://doi.org/10.3390/en13051052
Xu C, Chen J, Dai K. Carrier-Phase-Shifted Rotation Pulse-Width-Modulation Scheme for Dynamic Active Power Balance of Modules in Cascaded H-Bridge STATCOMs. Energies. 2020; 13(5):1052. https://doi.org/10.3390/en13051052
Chicago/Turabian StyleXu, Chen, Jingjing Chen, and Ke Dai. 2020. "Carrier-Phase-Shifted Rotation Pulse-Width-Modulation Scheme for Dynamic Active Power Balance of Modules in Cascaded H-Bridge STATCOMs" Energies 13, no. 5: 1052. https://doi.org/10.3390/en13051052





