Magnetic Field Characteristics and Stator Core Losses of High-Speed Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
2. Establishment of High-Speed Permanent Magnet Synchronous Motor Model
2.1. Motor Parameters and Physical Model
2.2. Solving Equations and Boundary Conditions
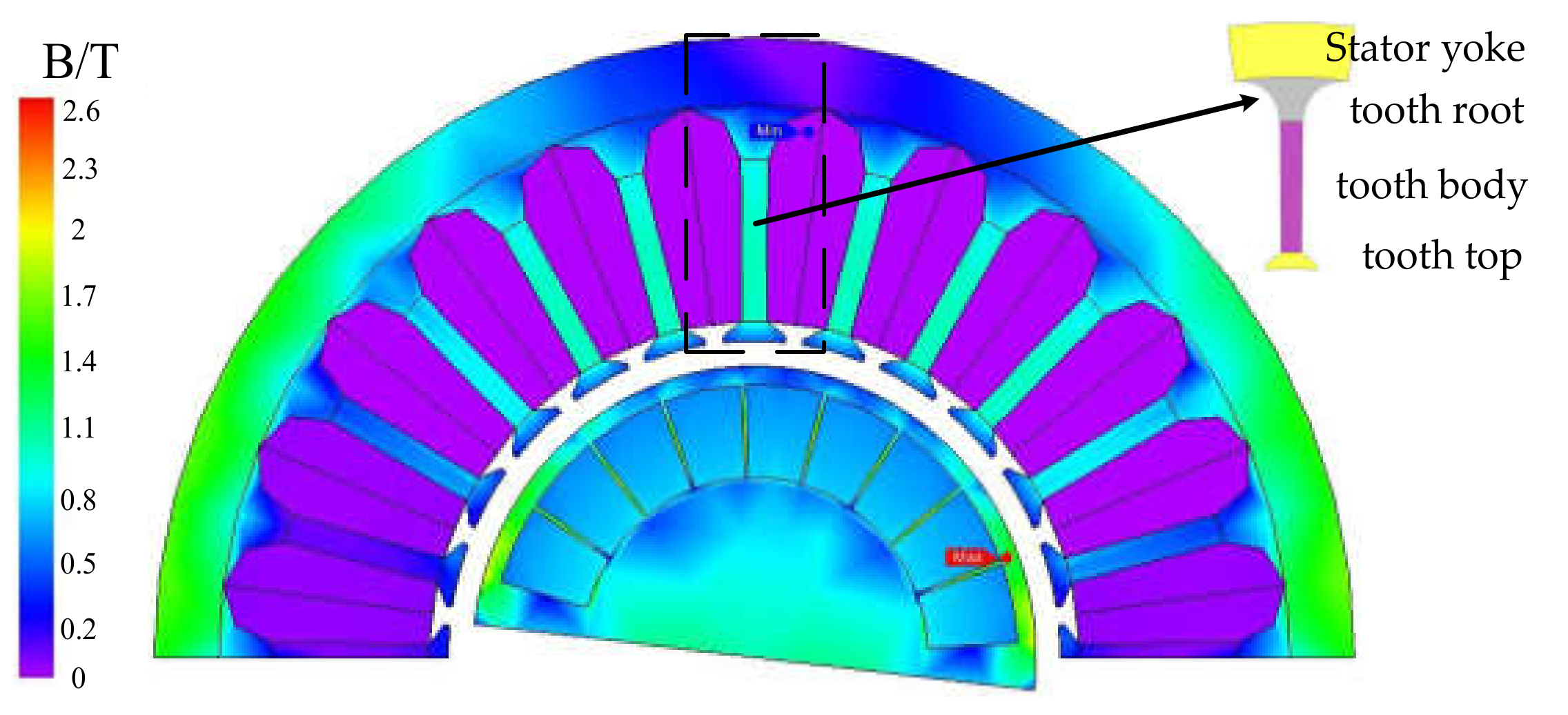
2.3. Determination of Stator Core Loss Area
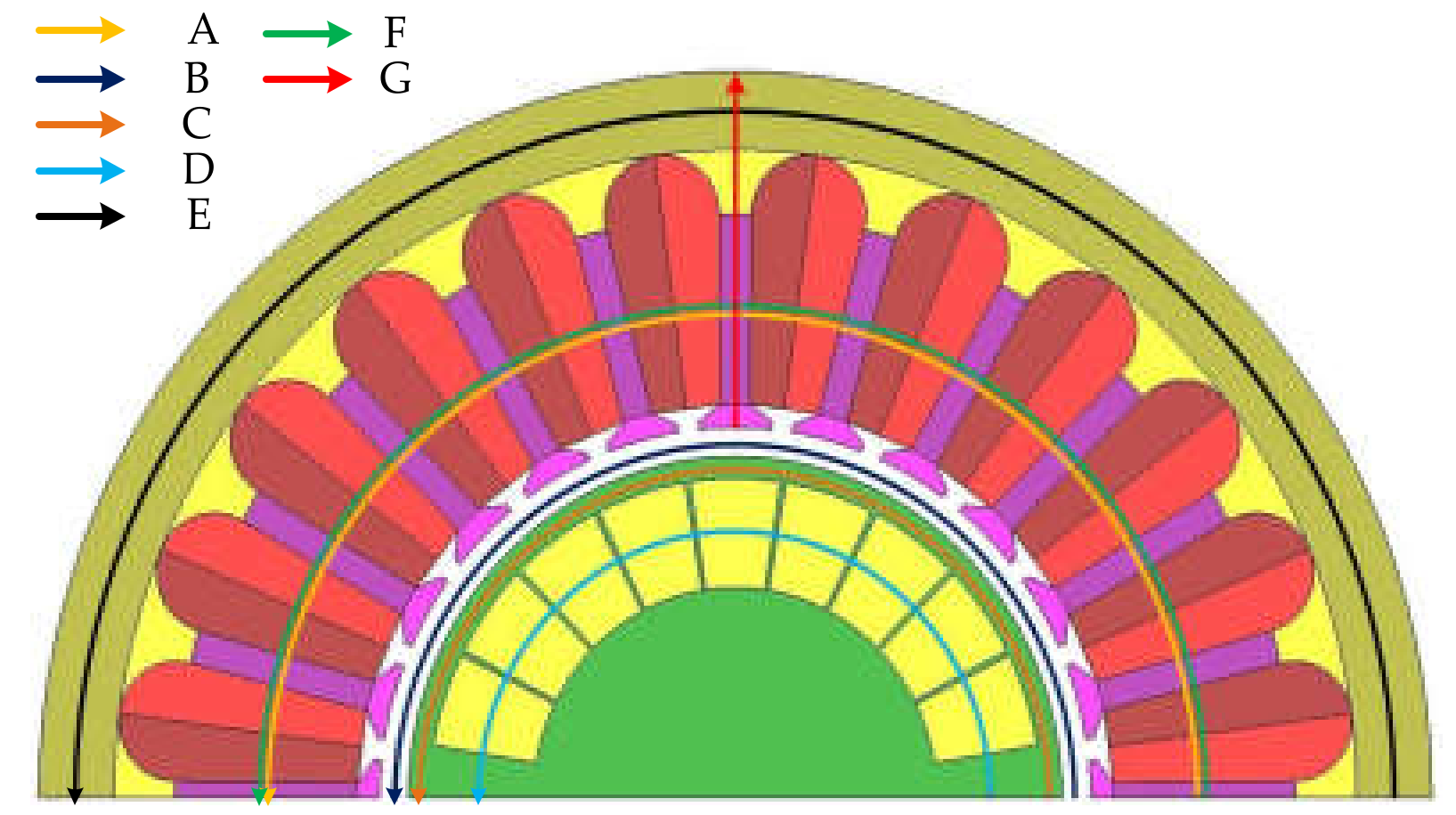
2.4. Determination of Study Location
2.5. Numerical Calculation of Core Loss
3. Magnetic Field Characteristics and Loss Analysis under Multiple Operating Conditions
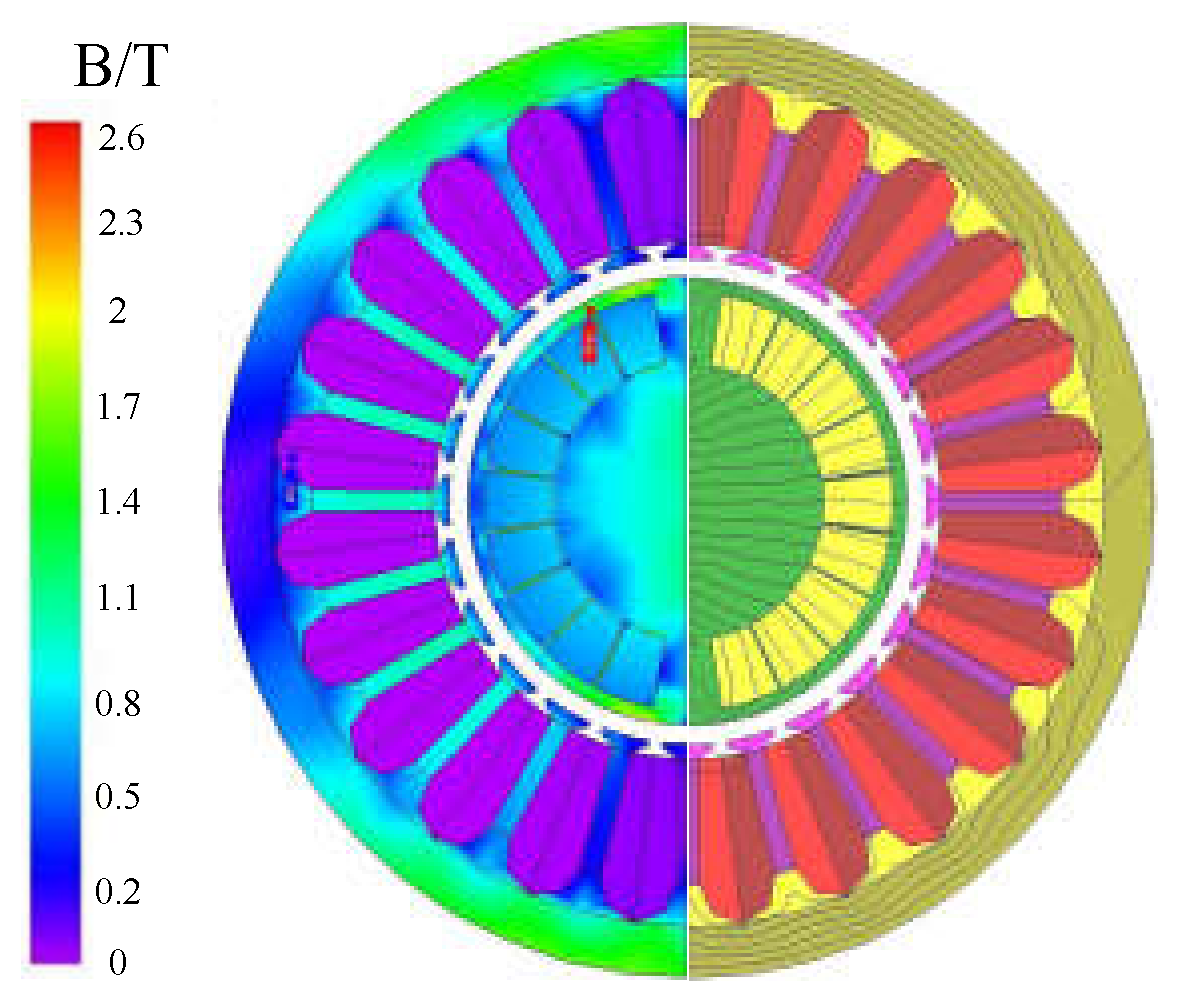
3.1. Motor Electromagnetic Field Characteristics at No-Load
- (1)
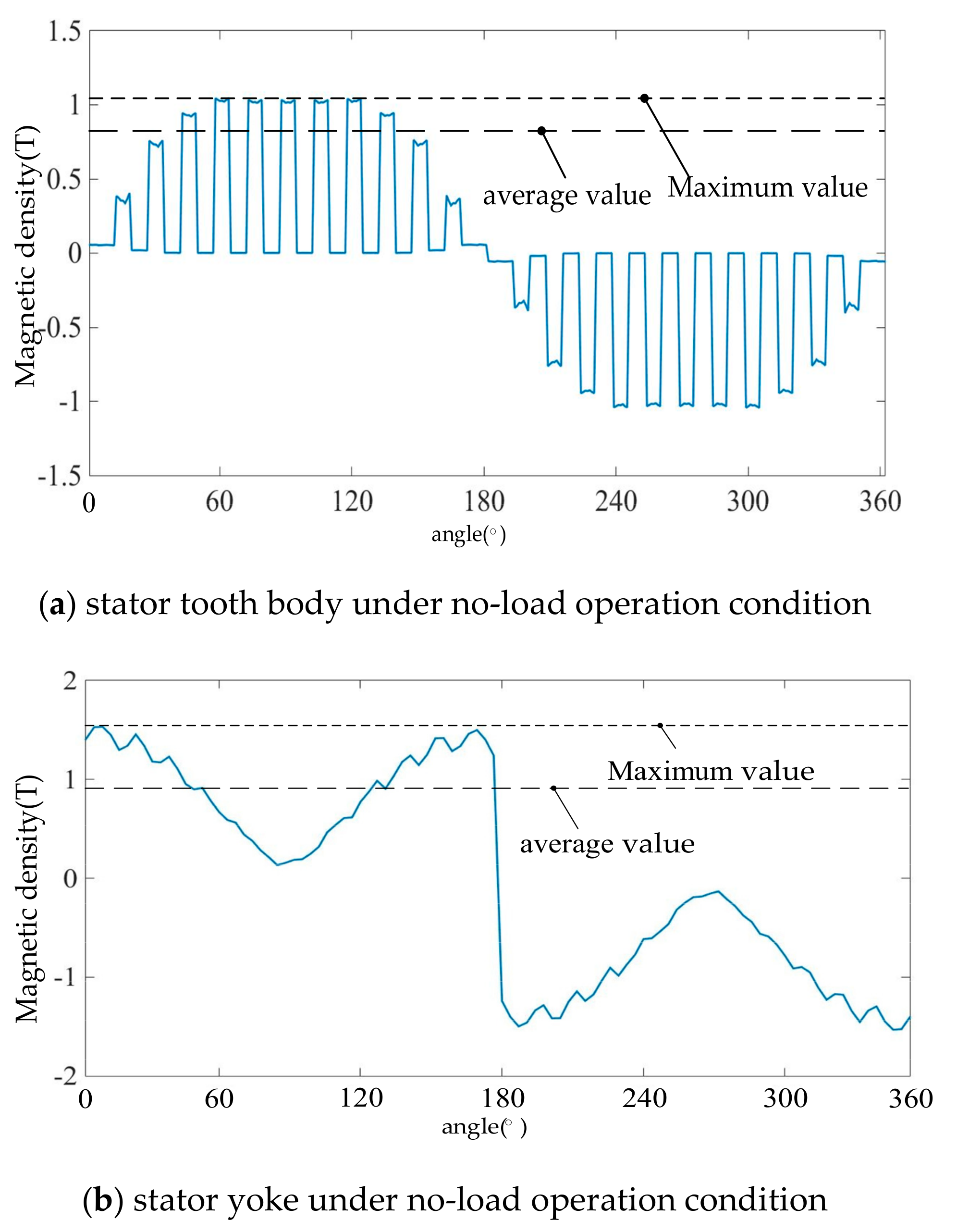
- The part of the stator teeth 1/3 teeth is just in the tooth body area. Due to the cogging effect, under no-load operating conditions, the magnetic field waveform distortion of 1/3 of the stator teeth and 1/2 of the magnetic isolation bridge is more serious than in the air gap position, and it is also more serious than in the area between the permanent magnet and the rotor edge. In comparison, the magnetic density waveform of the air gap position is closer to a sine wave.
- (2)
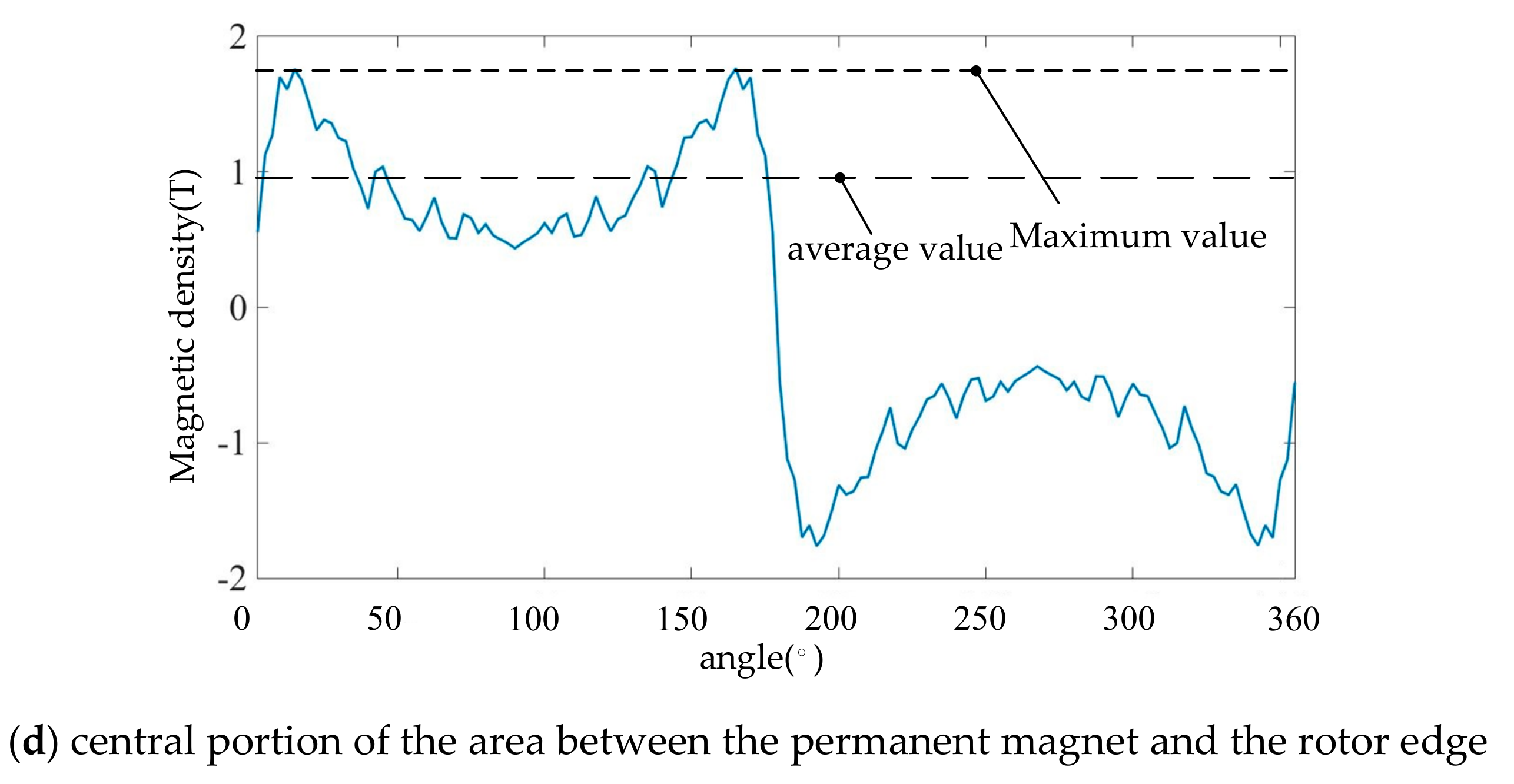
- Under no-load operating conditions, the average magnetic flux density of the air gap is about 0.3 T, and the maximum value is close to 0.4 T. The average magnetic density value of 1/3 of the stator teeth is about 0.8 T, and the maximum value is just over 1 T. The average value of the magnetic flux density when the maximum magnetic flux density of the rotor magnetic isolation bridge is approximately 1.5 T and has not yet exceeded 2 T. The average magnetic density of the central part of the area between the permanent magnet and the rotor edge is approximately 1 T, and the maximum value is close to 1.8 T.
3.2. Motor Iron Loss Distribution at No-Load
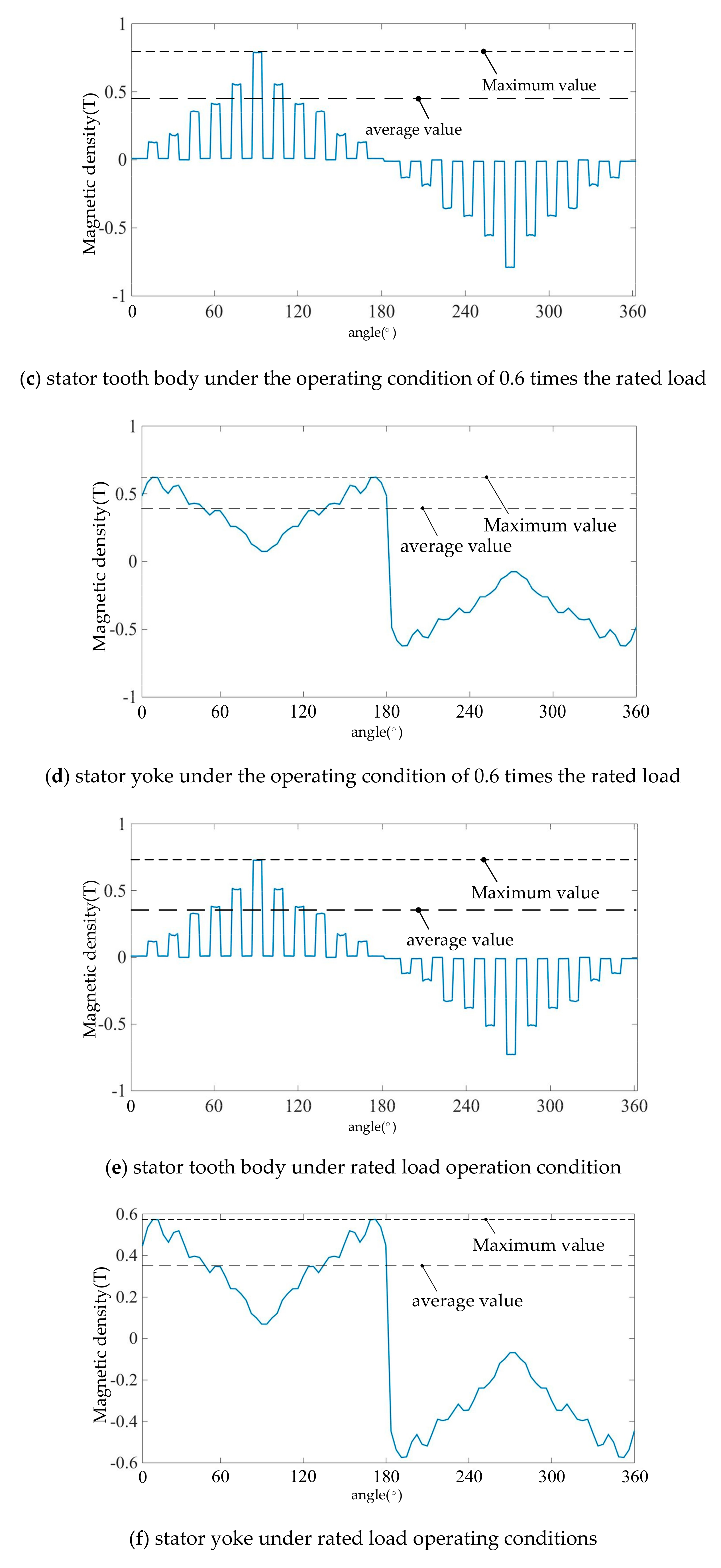
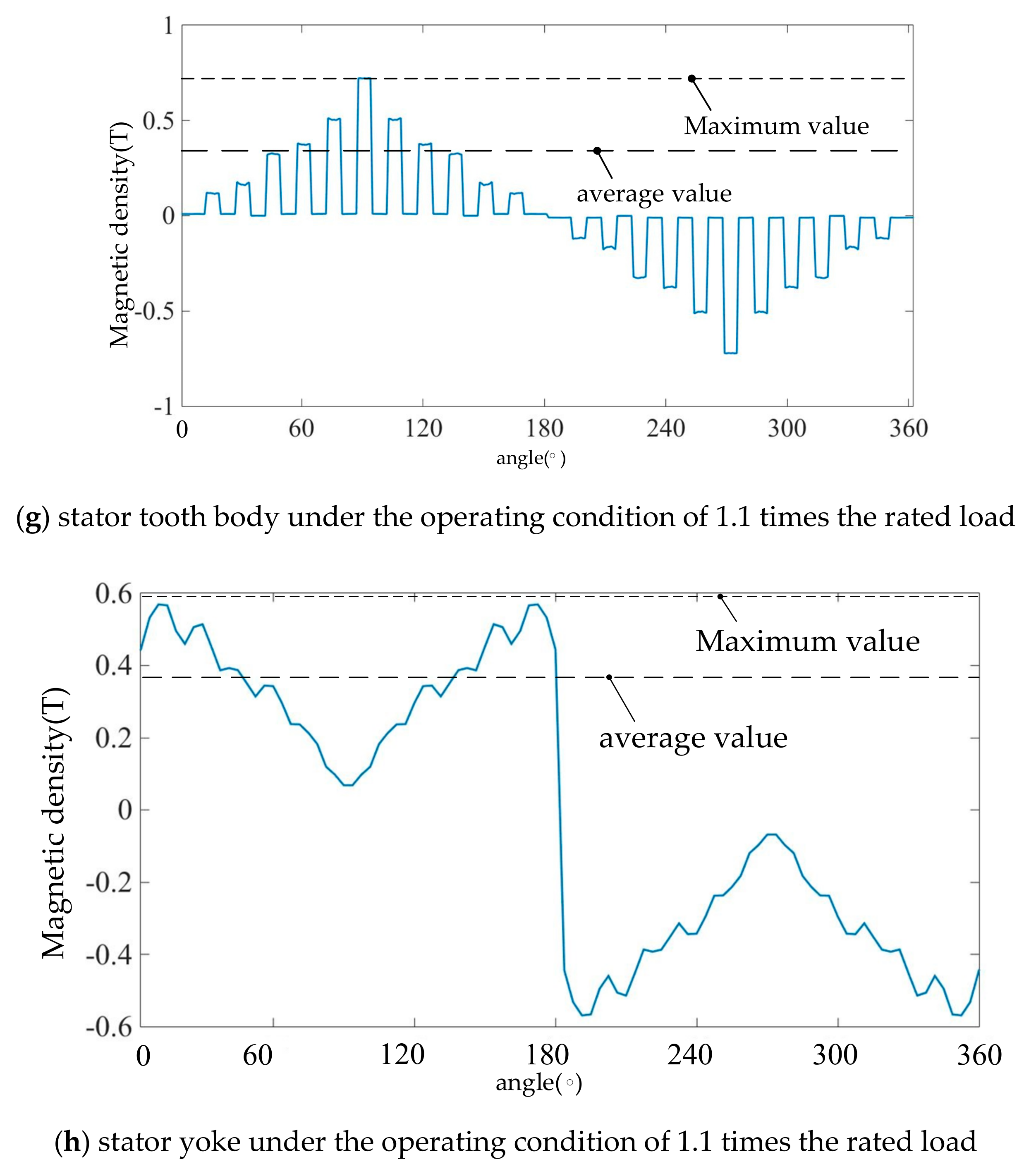
3.3. Analysis of the Internal Magnetic Field Distribution of a Motor under Multiple Load Conditions
- (1)
- Due to the influence of the cogging effect, the magnetic field waveform distortion of the stator tooth body position is more serious than the stator yoke position under any operating conditions.
- (2)
- Because the power supply contains a large number of higher harmonic components, the internal magnetic flux density waveform of the motor is severely distorted, and due to the skin effect, the high-frequency harmonics have the greatest influence on the magnetic density of the stator tooth body position.
- (3)
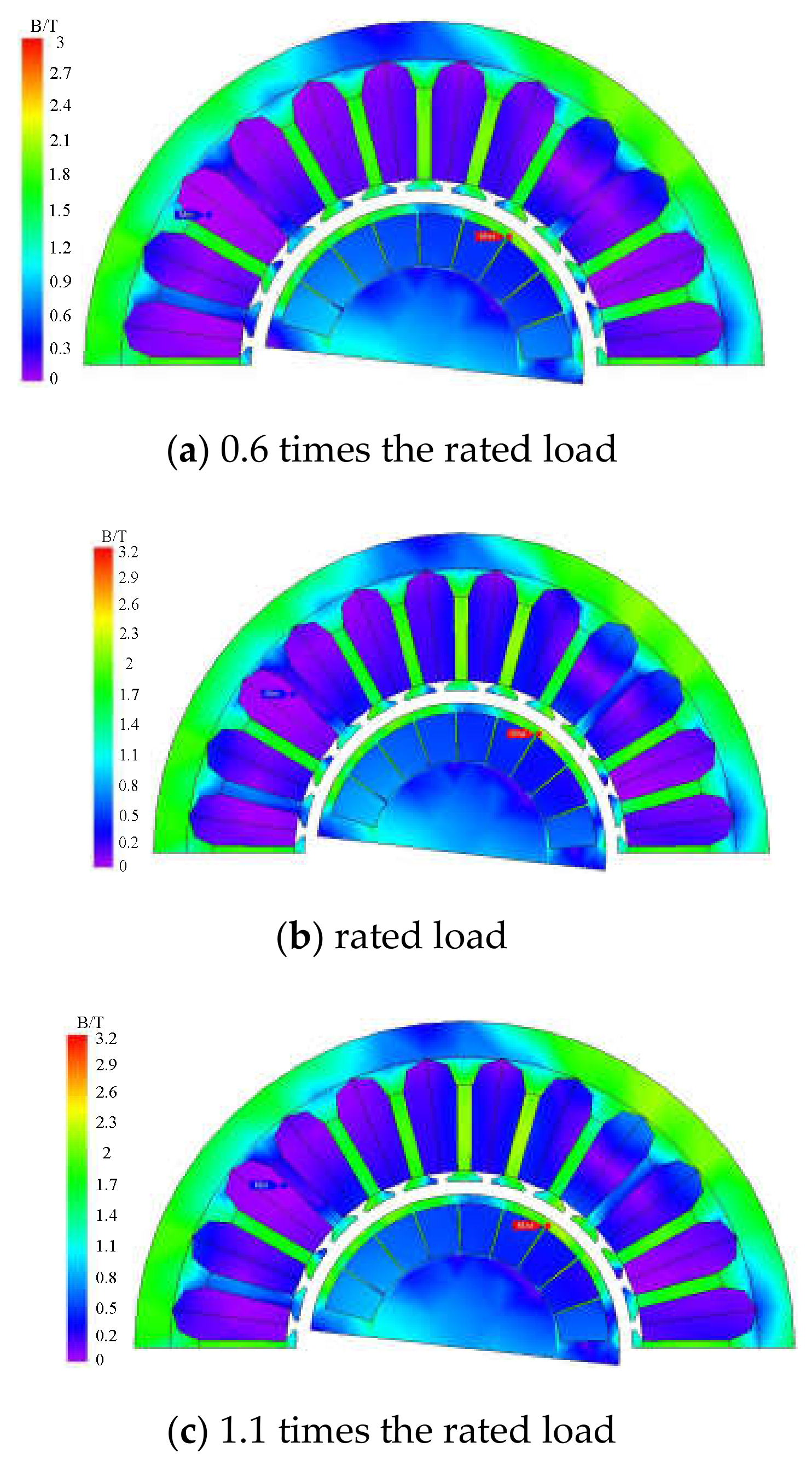
- When the load changes, the magnetic density of the tooth body area changes compared with the yoke area in a shorter and more dramatic period. Because the harmonic component of the tooth body area is larger under no-load operating conditions, the average magnetic densities of the stator tooth body and stator yoke areas are the largest. During this time, the maximum values of the magnetic density are approximately 1 T and 1.5 T, and the average values are approximately 0.8 T and 0.9 T, respectively. At 1.1 times rated load, the average magnetic densities of the stator tooth body and stator yoke areas are the smallest. During this time, the maximum magnetic density is approximately 0.7 T and 0.6 T, and the average values are approximately 0.35 T and 0.4 T, respectively.
- (4)
- At 1.1 times the rated load, the magnetic densities of the stator tooth body and stator yoke are approximately equal to the densities at the rated load. Thus, it is clear that the magnetic density has reached saturation when running at rated load.
3.4. Research on the Relationship between Load Condition and Stator Core Loss
4. Conclusions
- (1)
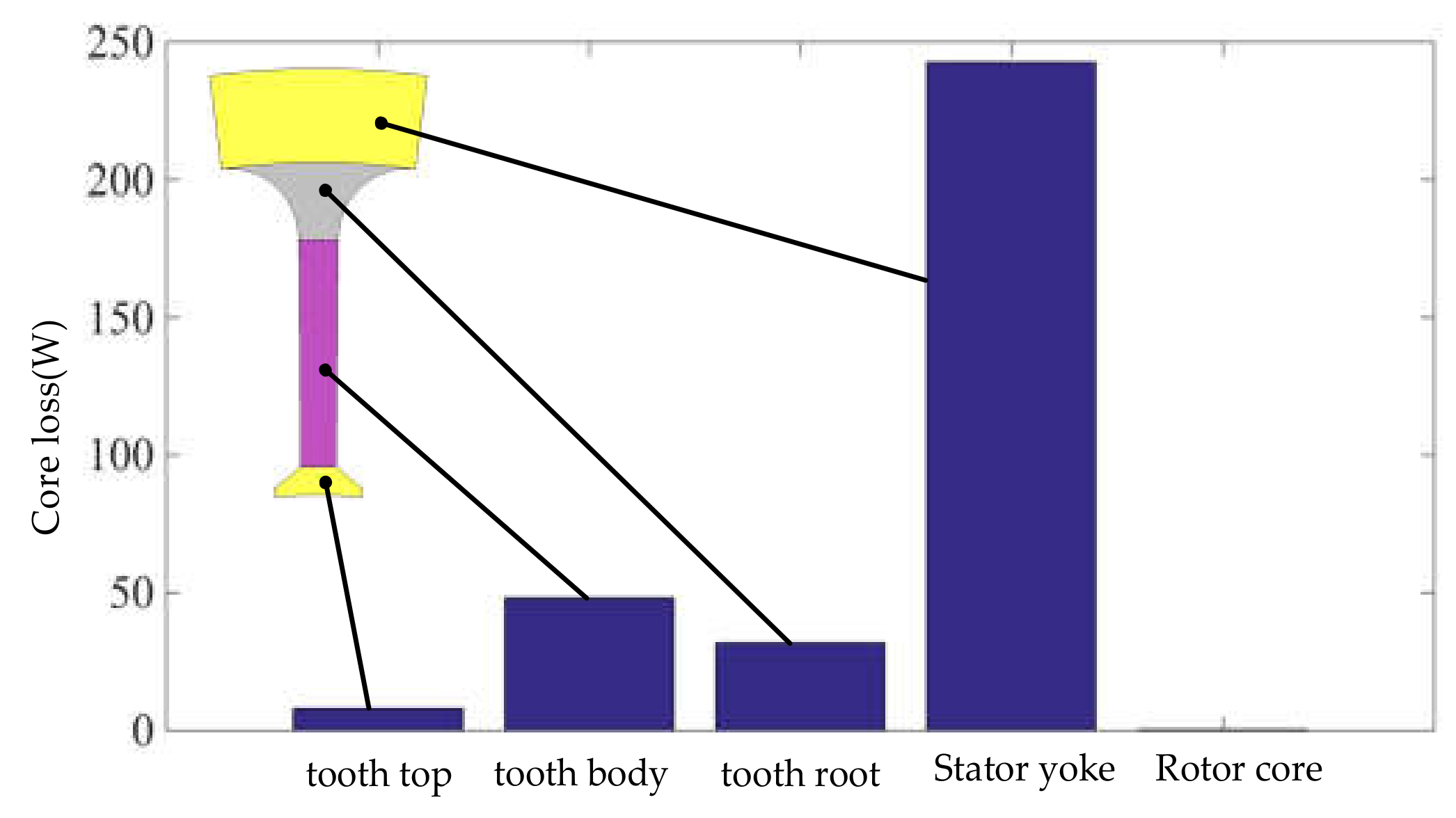
- The distribution principle of the stator core loss is that the stator yoke accounts for the largest proportion of the stator core loss, followed by the stator tooth body and stator tooth root, and the stator tooth top accounts for the smallest proportion.
- (2)
- The stator core loss under the no-load operating condition is the least, and the stator core loss under the 1.1 times rated load operating condition is the most, which is particularly evident in the stator yoke. The core loss of the stator tooth has the smallest change; however, as the load increases, the growth rate of the core loss of the stator tooth top is the largest, and the growth rate of the core loss of the stator yoke is the smallest. Under the operating conditions of rated load and 1.1 times rated load, the difference between their stator core losses is not large, particularly the difference at the top of the stator teeth, which is the smallest.
- (3)
- Comparing the average values of the magnetic flux density in the four areas on the stator, the magnetic flux density of the tooth body is larger under the no-load operating condition, and the maximum value is close to 1 T. Comparing the rated load operating conditions with 1.1 times the rated load operating conditions, the average value of the magnetic flux density at the center position of each area on the stator side under the rated load operating conditions is relatively close and the saturation of magnetic flux density is greater.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Geng, W.; Lu, J. Research status and development of stator coreless permanent magnet motor technology. Proc. CSEE 2018, 38, 582–600. [Google Scholar]
- Zhang, F.; Du, G.; Wang, T.; Liu, G. Review of Development and Design of High -Speed Motors. Trans. China Electrotech. Soc. 2016, 31, 1–18. [Google Scholar]
- Dong, J.; Huang, Y.; Jin, L.; Lin, H.; Yang, H. Review of design and analysis techniques for high-speed permanent magnet motors. Proc. CSEE 2014, 34, 4640–4653. [Google Scholar]
- Zhu, B.; Bai, B.; He, H. Effect of Inverter Parameters on the Eddy Current Losses in iNduction Motor Fed by PWM Inverter. In Proceedings of the International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 4240–4243. [Google Scholar]
- Hu, Y.; Gu, W. Adaptive robust triple-step control for compensating cogging torque and model uncertainty in a dc motor. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2396–2405. [Google Scholar] [CrossRef]
- Yamazaki, K.; Abe, A. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents. IEEE Trans. Magn. 2009, 41, 659–665. [Google Scholar] [CrossRef]
- Fouladgar, J.; Chauveau, E. The influence of the harmonics on the temperature of electrical machines. IEEE Trans. Magn. 2005, 41, 1644–1647. [Google Scholar] [CrossRef]
- Han, J. Study on the Influence of PWM Inverter Power Supply on Core Loss of Asynchronous Motor; Beijing Jiaotong University: Beijing, China, 2011. [Google Scholar]
- Yu, J.; Li, L.; Du, P.; Zhang, J. Ripple-current suppression method for high-speed permanent magnet synchronous motor based on harmonic injection PWM. J. Electr. Eng. 2017, 12, 1–10. [Google Scholar]
- Sun, M.; Tang, R.; Han, X.; Tong, W. Analysis and Modeling for Open Circuit Air Gap Magnetic Field Prediction in Axial Flux Permanent Magnet Machine. Proc. CSEE 2018, 38, 1525–1533. [Google Scholar]
- Kong, X.; Wang, F.; Xing, J. Losses calculation and temperature field analysis of high speed permanent magnet machines. Trans. China Electrotech. Soc. 2012, 27, 166–173. [Google Scholar]
- Zou, J.; Li, J.; Xu, Y.; Wei, Y. Influences of drive strategies on the loss of permanent magnet brushless direct current motor. Trans. China Electrotech. Soc. 2011, 26, 43–47. [Google Scholar]
- Han, L.; Xie, L.; Zhang, G. Influence of converter parameters on stator losses of permanent magnet synchronous generator. Electr. Mach. Control 2010, 14, 75–81. [Google Scholar]
- Huang, P.; Hu, Q.; Cui, Y.; Huang, Y. Analytical calculation of the iron losses of electric machine fed by PWM inverter. Proc. CSEE 2007, 27, 19–23. [Google Scholar]
- Zhao, H.; Luo, Y.; Liu, X.; Wang, R.H.; Chen, W. Analysis on no-load iron losses distribution of asynchronous motors with time-stepping finite element method. Proc. CSEE 2010, 30, 99–106. [Google Scholar]
- Han, S.; Cui, S.; Wang, T.; Chan, C.; Zhang, X. Application of fractional-slot concentrated winding permanent magnet machines in modular cascade machine System. Trans. China Electrotech. Soc. 2013, 28, 9–16. [Google Scholar]
- Yamazaki, K.; Suzuki, A.; Ohto, M.; Takakura, T. Harmonic Loss and Torque Analysis of High-Speed Induction Motors. IEEE Trans. Ind. Appl 2012, 48, 933–941. [Google Scholar] [CrossRef]
- Denis, N.; Inoue, M.; Fujisaki, K.; Itabashi, H.; Yano, T. Iron Loss Reduction in Permanent Magnet Synchronous Motor by Using Stator Core Made of Nanocrystalline Magnetic Material. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Okamoto, S.; Denis, N.; Kato, Y.; Ieki, M.; Fujisaki, K. Core Loss Reduction of an Interior Permanent-Magnet Synchronous Motor Using Amorphous Stator Core. IEEE Trans. Ind. Appl. 2016, 52, 2261–2268. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Lu, H.; Li, Y.; Jin, J. Core Loss Computation in a Permanent Magnet Transverse Flux Motor with Rotating Fluxes. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Li, G.; Feng, H.; Li, Y.; Deng, Y. Numerical calculation of loss under load variation for driving asynchronous motor. Electr. Mach. Control 2013, 17, 36–41. [Google Scholar]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power/kW | 120 | Air gap length/mm | 4 |
| Rated voltage/V | 380 | Iron core length/mm | 112 |
| Rated frequency/hz | 400 | Number of poles | 2 |
| Stator outer diameter/mm | 200 | Number of stator slots | 24 |
| Rotor outer diameter/mm | 94 | Connection method | Y connection |
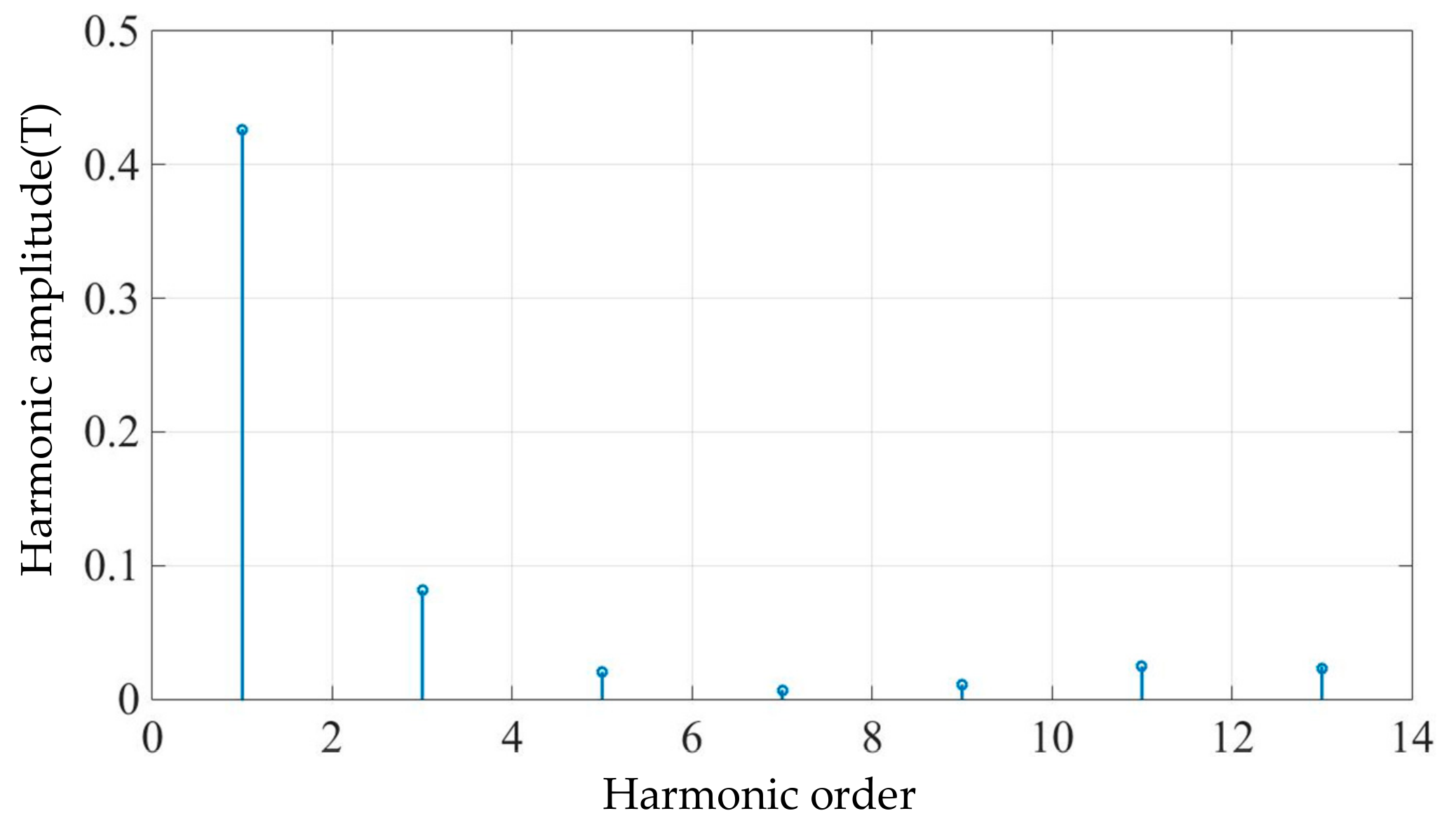
| Harmonic Order | Harmonic Amplitude/T | Proportion/% |
|---|---|---|
| One | 0.4265 | 100 |
| Three | 0.0813 | 19.06 |
| Fives | 0.0204 | 4.78 |
| Seven | 0.0068 | 1.59 |
| Nine | 0.0109 | 2.56 |
| Eleven | 0.0246 | 5.76 |
| Thirteen | 0.0233 | 5.46 |
| Divide Area | Iron Loss/W | Proportion/% |
|---|---|---|
| Stator tooth top | 8.02 | 2.42 |
| Stator tooth body | 48.21 | 14.56 |
| Stator tooth root | 31.71 | 9.58 |
| Stator yoke | 243.08 | 73.43 |
| Rotor core | 1 | 0.3 |
| Operating Conditions | Tooth Top/T | Tooth Body/T | Tooth Root/T | Yoke/T |
|---|---|---|---|---|
| no-load | 0.7618 | 0.965 | 0.5376 | 0.1808 |
| 0.6 times load | 0.5446 | 0.7385 | 0.4277 | 0.1747 |
| rated load | 0.5023 | 0.6811 | 0.3944 | 0.1611 |
| 1.1 times the rated load | 0.4974 | 0.6745 | 0.3906 | 0.1596 |
| Operating Conditions | Tooth Top/W | Tooth Body/W | Tooth Root/W | Yoke/W |
|---|---|---|---|---|
| no-load | 8.02 | 48.21 | 31.71 | 243.08 |
| 0.6 times load | 38.79 | 235.56 | 108.32 | 443.14 |
| rated load | 48.98 | 278.838 | 133.49 | 529.77 |
| 1.1 times the rated load | 51.27 | 286.62 | 138.34 | 547.83 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, D.; Zhou, K.L.; Lv, F.; Dou, Q.; Wu, J.; Sun, Y.; Zou, J. Magnetic Field Characteristics and Stator Core Losses of High-Speed Permanent Magnet Synchronous Motors. Energies 2020, 13, 535. https://doi.org/10.3390/en13030535
Tao D, Zhou KL, Lv F, Dou Q, Wu J, Sun Y, Zou J. Magnetic Field Characteristics and Stator Core Losses of High-Speed Permanent Magnet Synchronous Motors. Energies. 2020; 13(3):535. https://doi.org/10.3390/en13030535
Chicago/Turabian StyleTao, Dajun, Kai Liang Zhou, Fei Lv, Qingpeng Dou, Jianxiao Wu, Yutian Sun, and Jibin Zou. 2020. "Magnetic Field Characteristics and Stator Core Losses of High-Speed Permanent Magnet Synchronous Motors" Energies 13, no. 3: 535. https://doi.org/10.3390/en13030535




