Influence of Active Power Output and Control Parameters of Full-Converter Wind Farms on Sub-Synchronous Oscillation Characteristics in Weak Grids
Abstract
:1. Introduction
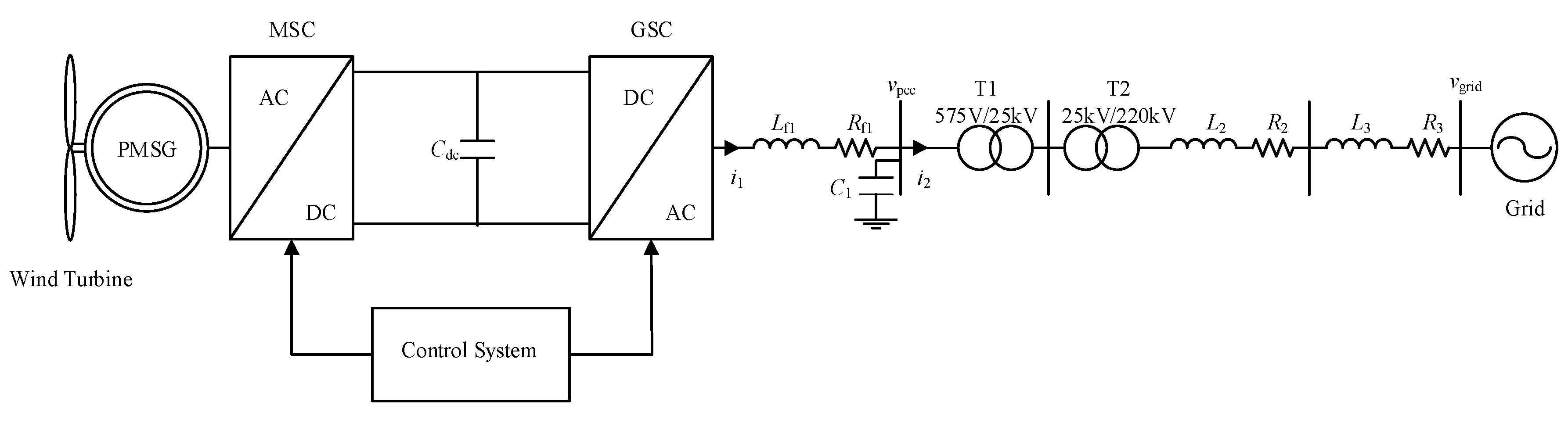
2. System Modeling
2.1. Modeling of DC-Link
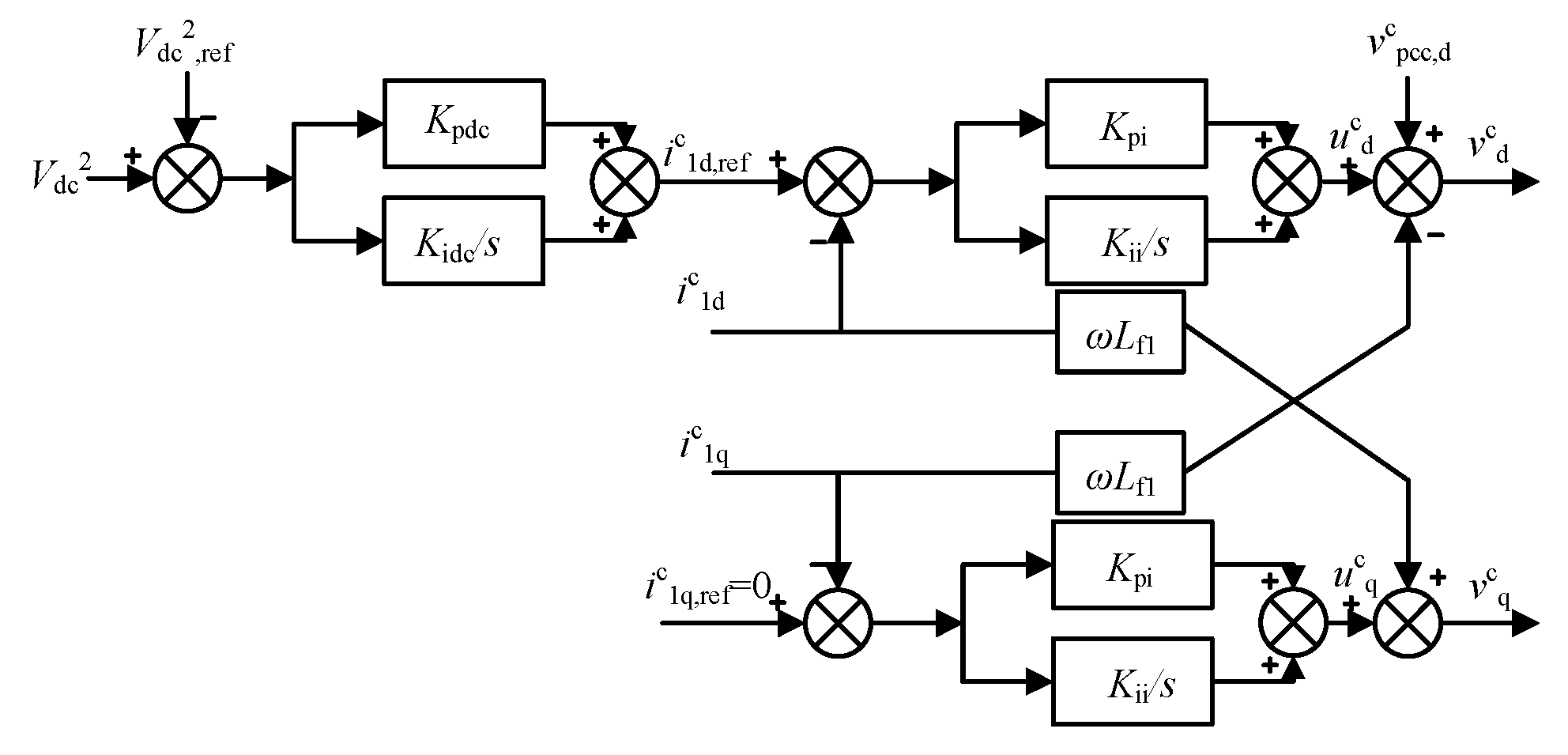
2.2. Outer and Inner Control Loop of GSC
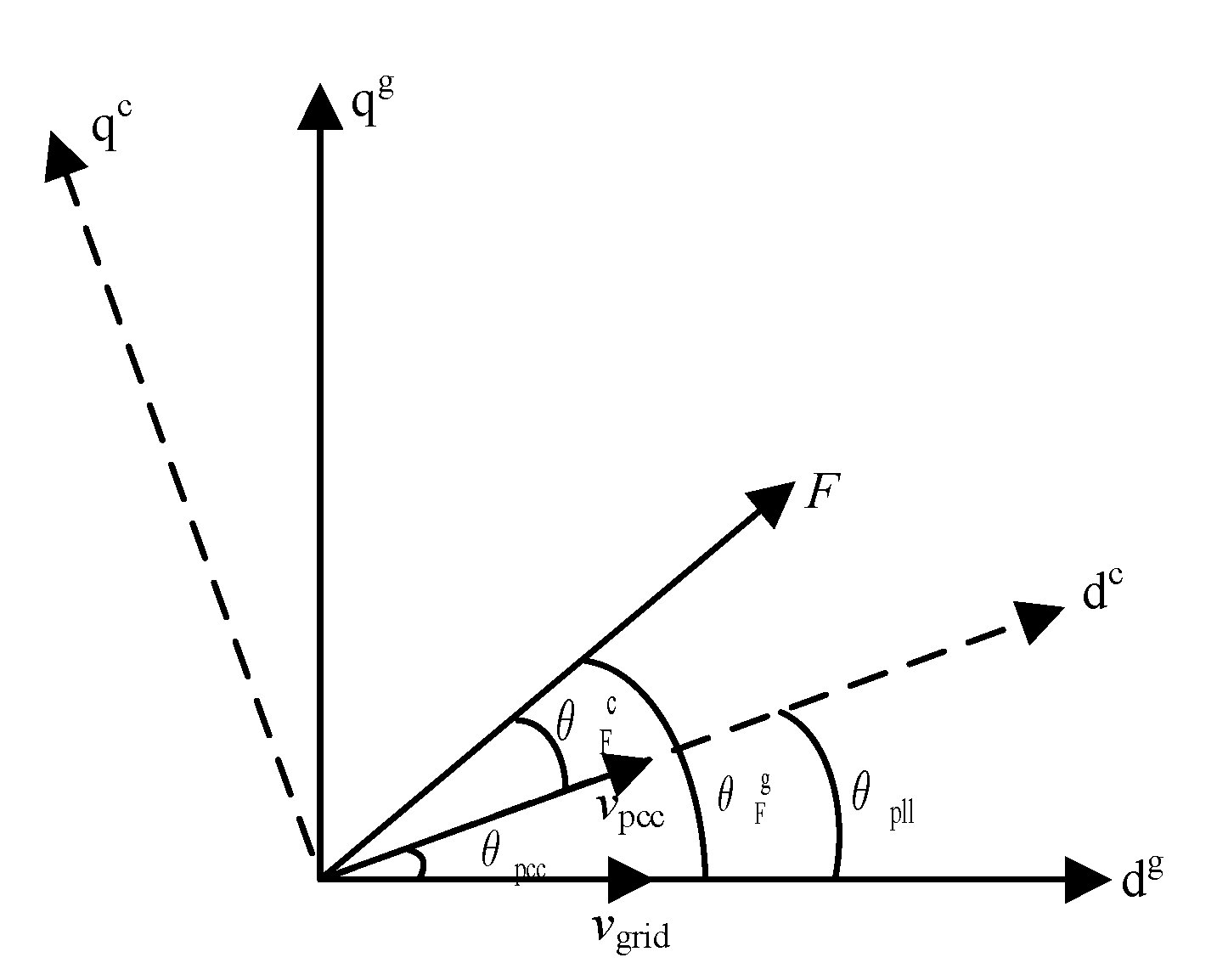
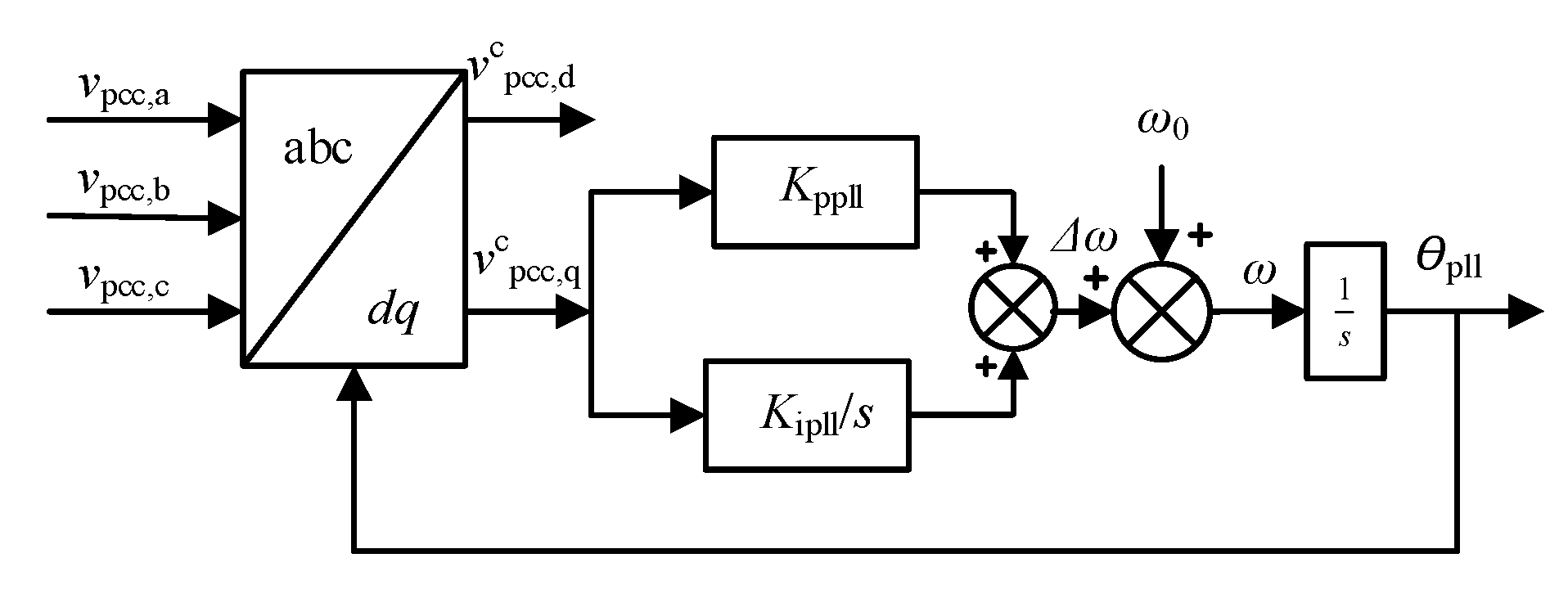
2.3. Phase-Locked Loop Model
2.4. Grid Dynamics
3. Eigenvalue Analysis
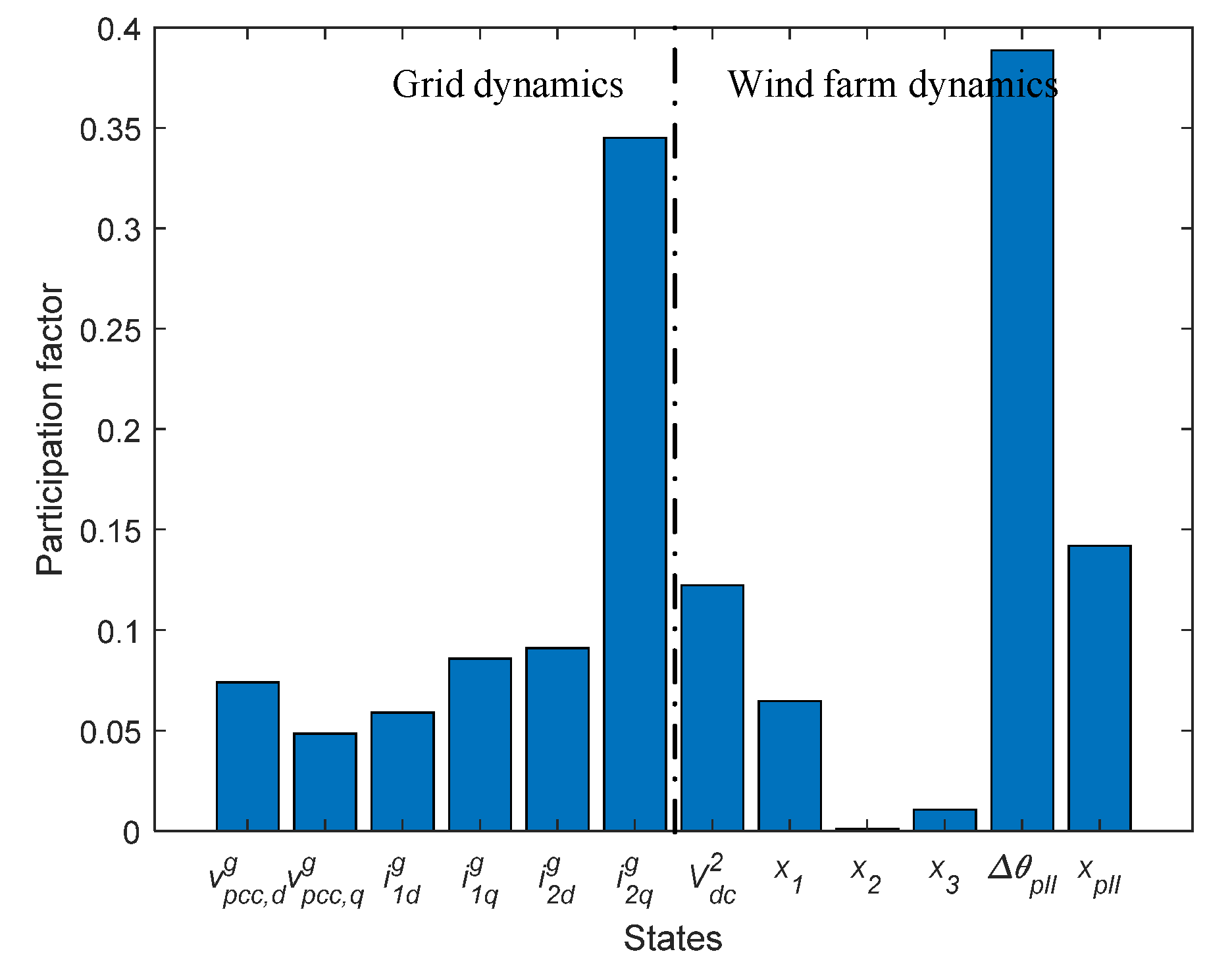
3.1. Analysis of the Dominant Oscillation Mode
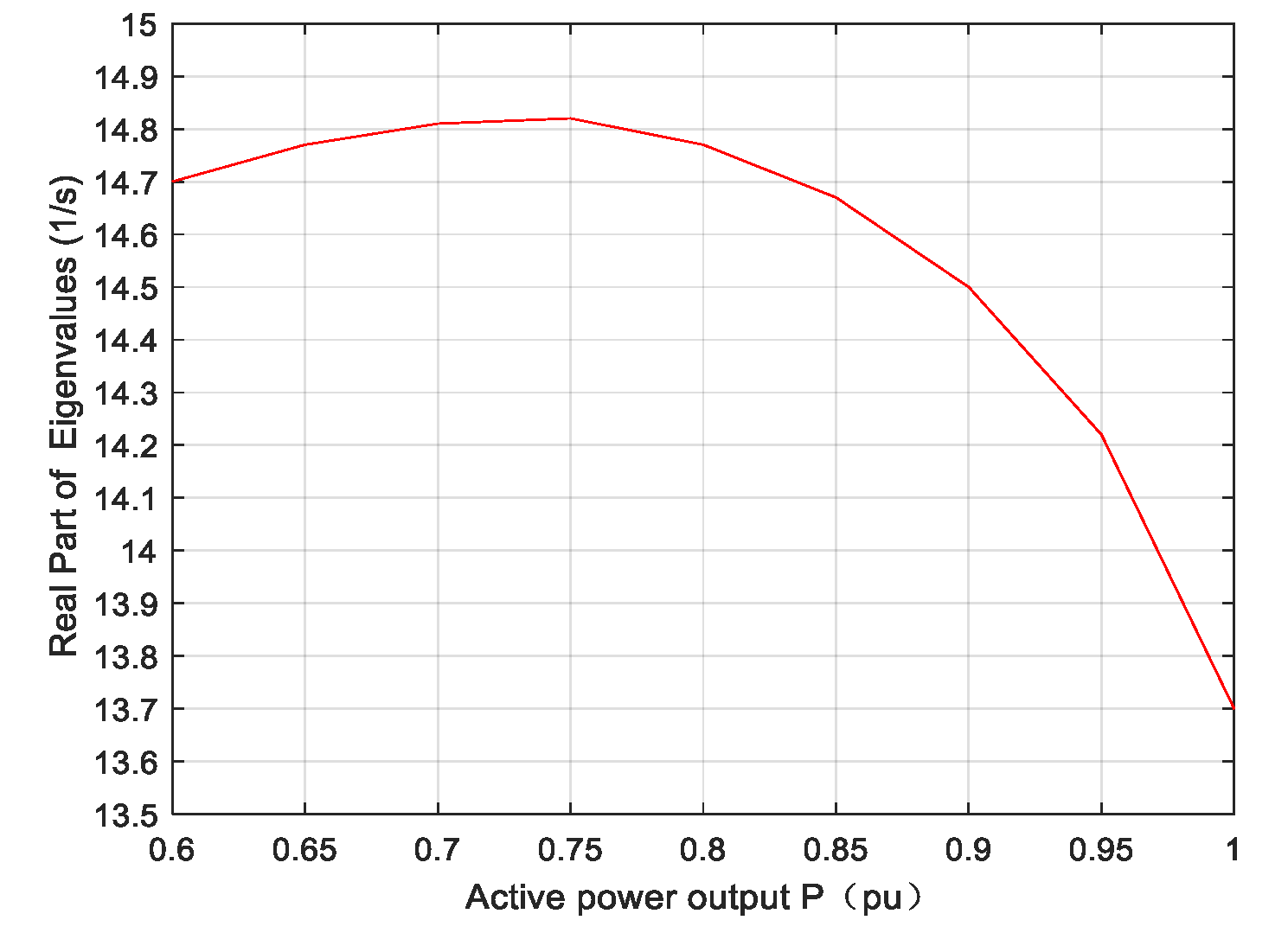
3.2. Impacts of the Active Power Outputs of the Wind Farm on Subsynchronous Oscillation Characteristics with Different Control Parameters
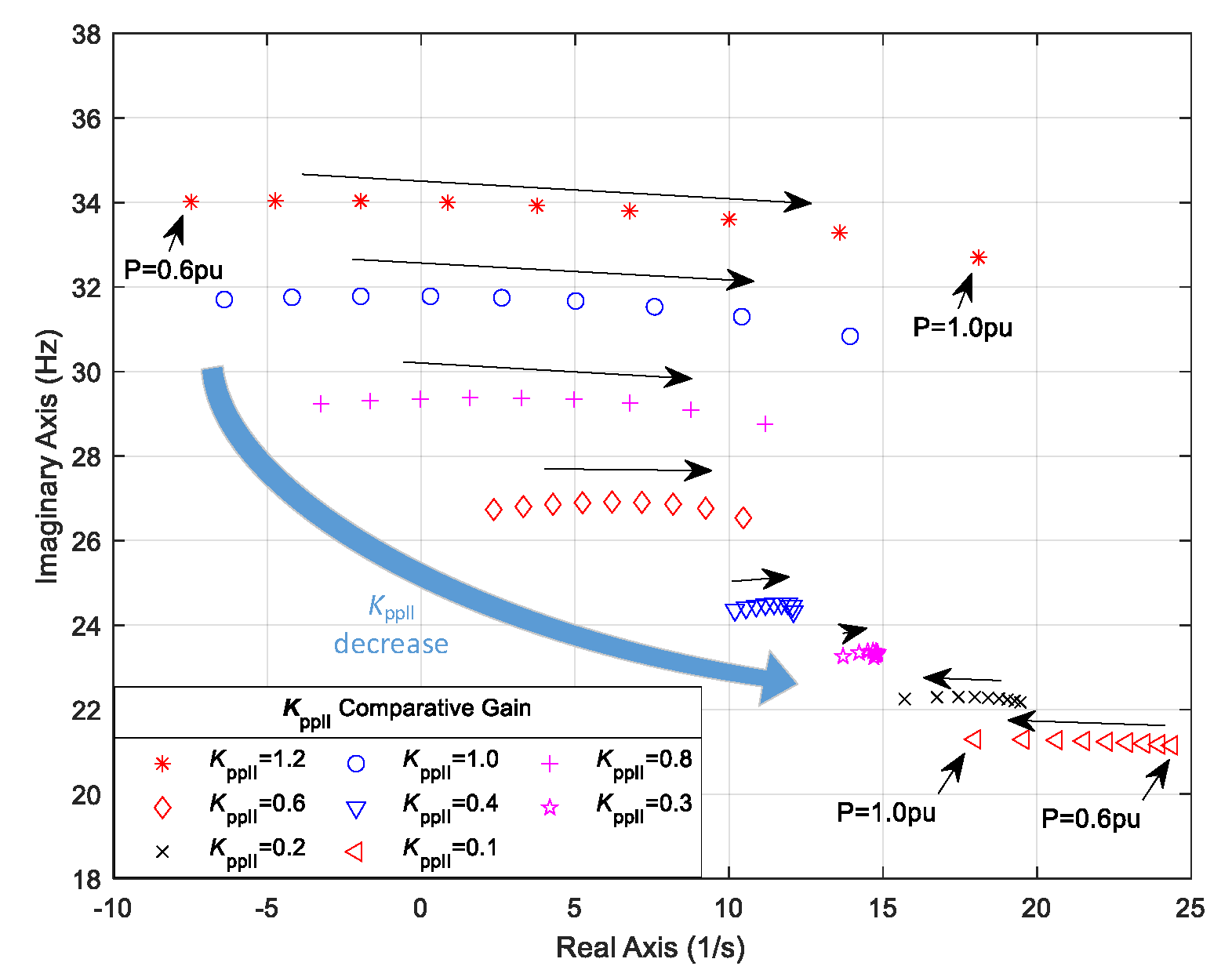
3.2.1. Impacts of Active Power Outputs with Different PLL Proportional Gains
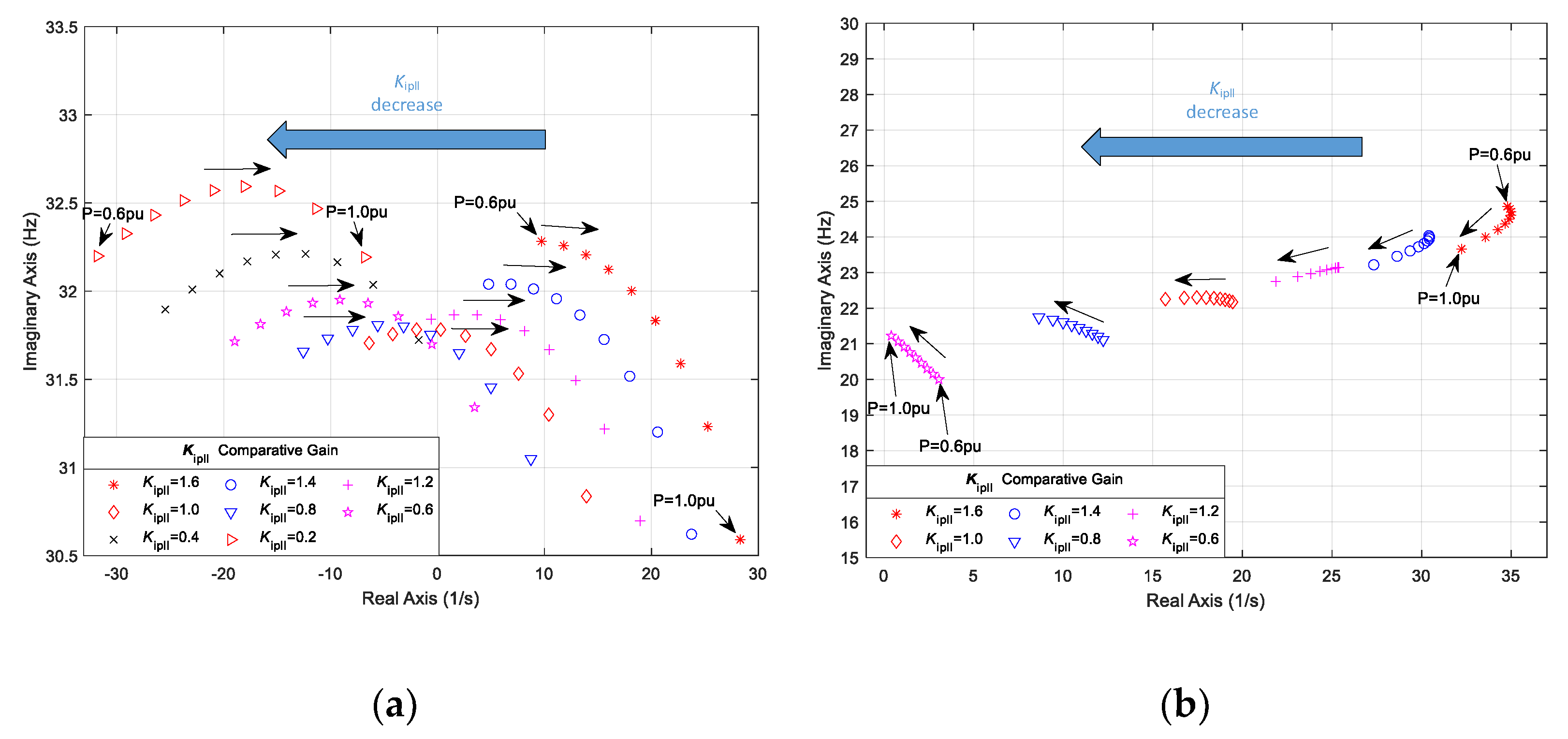
3.2.2. Impacts of Active Power Outputs with Different PLL Integral Gain
3.2.3. Impacts of the Active Power Outputs with Different DVC Proportional Gain.
4. Case Study and Simulation Verifications
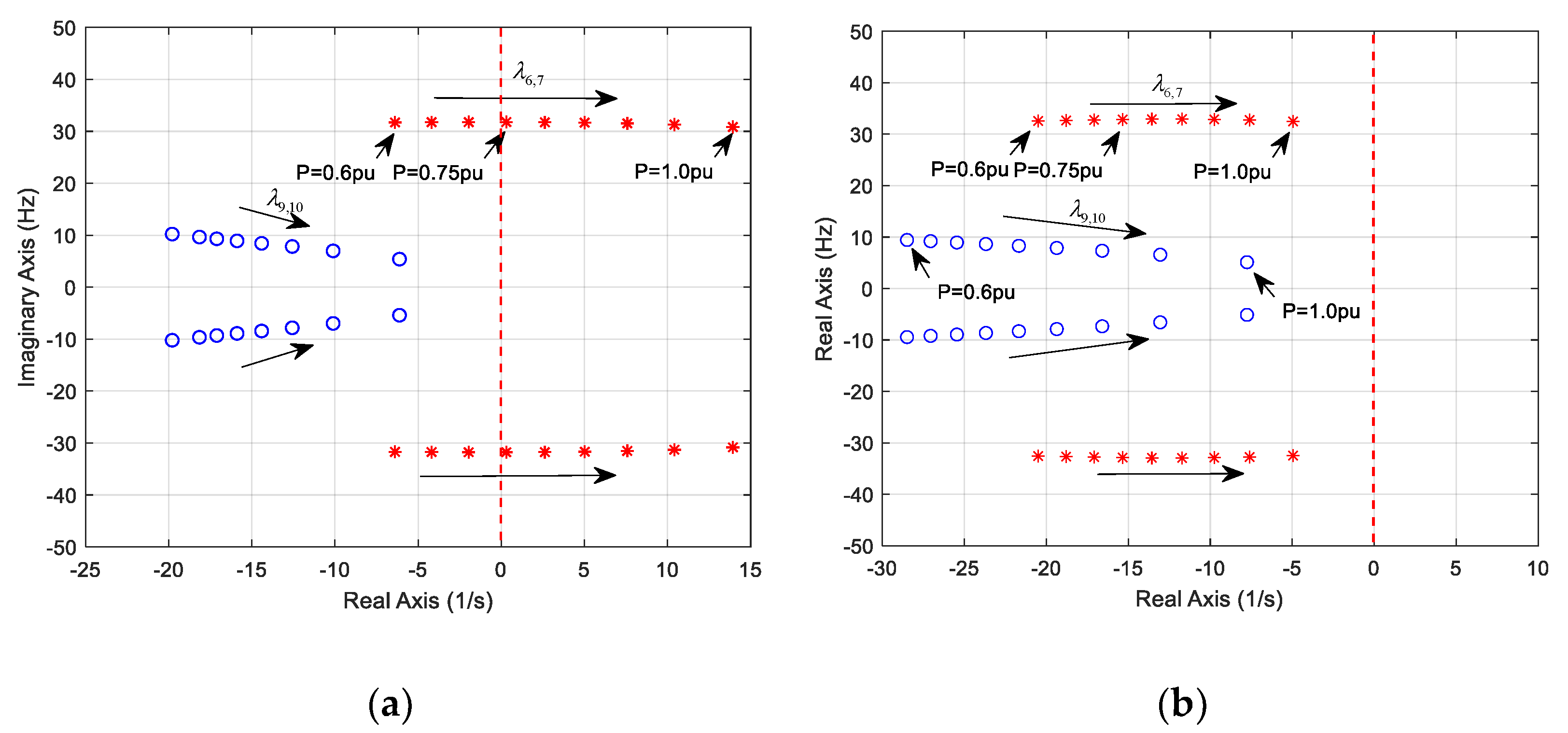
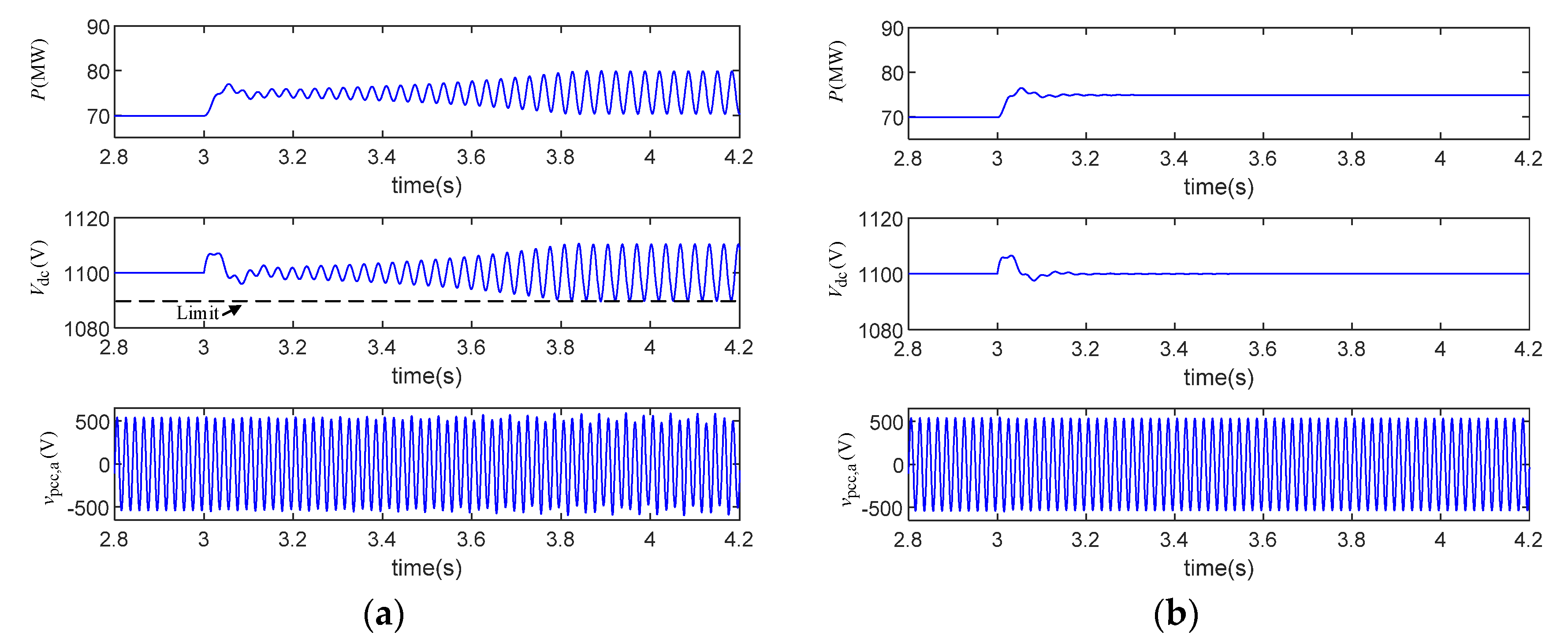
4.1. Verification of the Negative Correlation when the PLL Proportional Gain is Large
4.2. Verification of the Positive Correlation when the PLL Proportional Gain Is Small
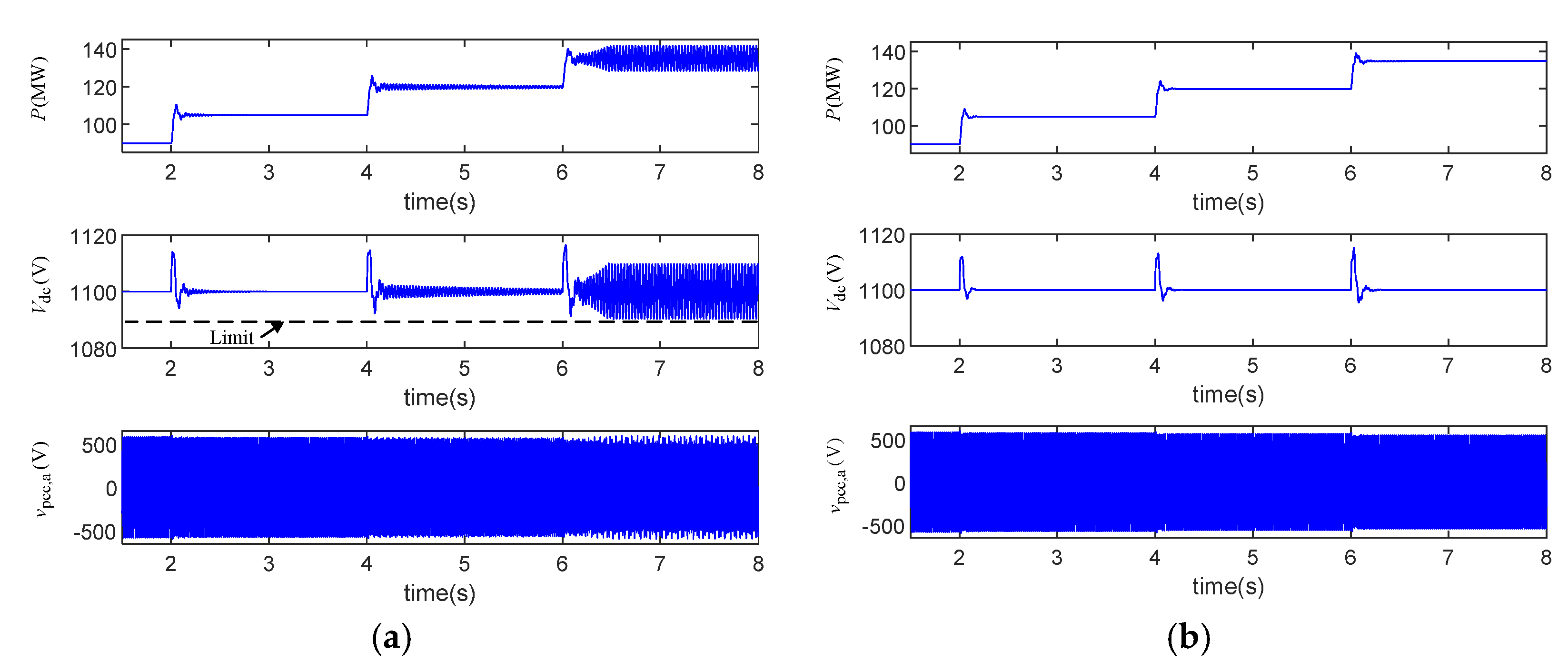
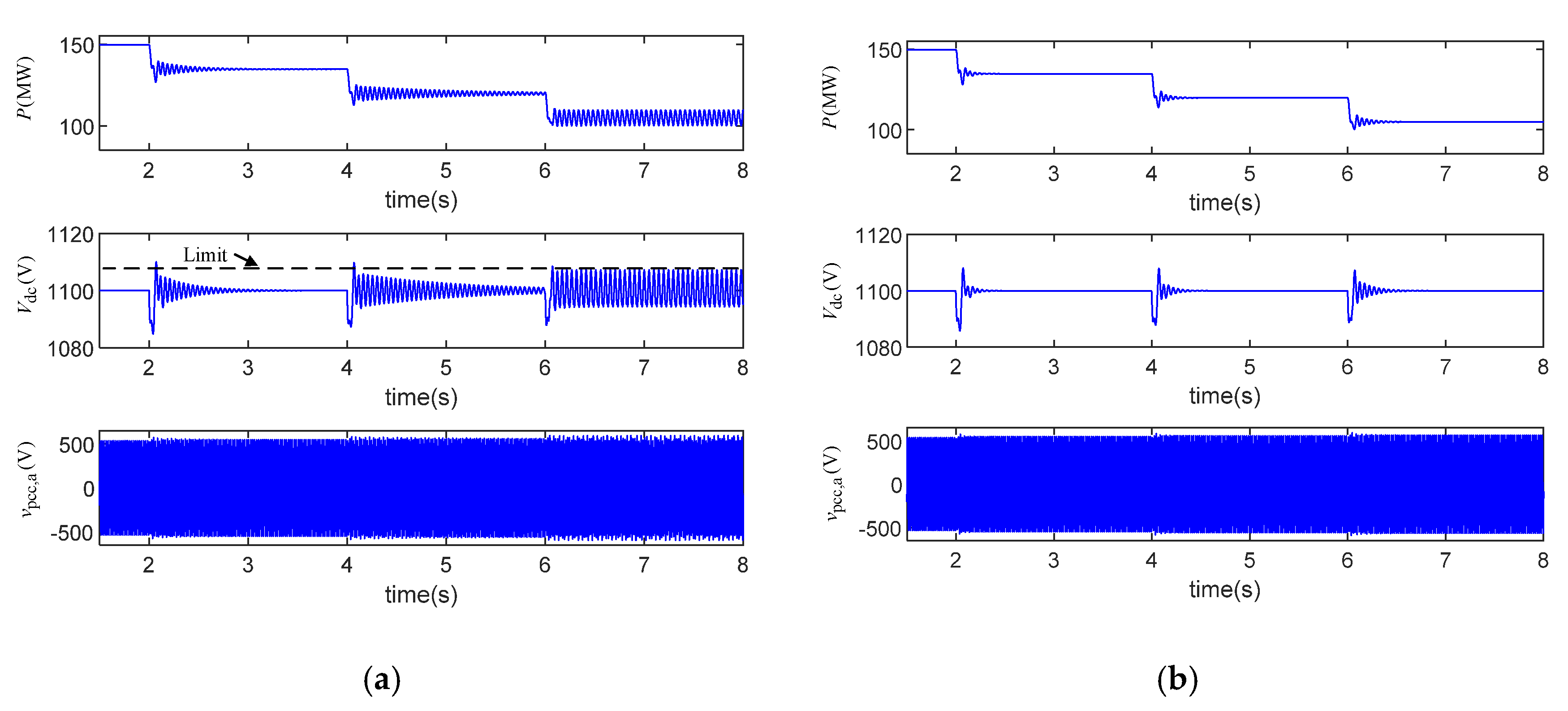
4.3. Simulation Verification for a Complex System
5. Conclusions
- When the PLL proportional gain is large, the active power output is negatively correlated with the damping of the SSO mode. When the PLL proportional gain is small, the active power output is positively correlated with the damping of the SSO mode. This clarifies the confusions in the understanding of the correlation between active power output and SSO damping.
- The PLL integral gain and the DC voltage control proportional gain have little influence on the correlation between the active power output and SSO damping. However, the system stability can be improved by appropriately retuning the PLL integral gain and the DC voltage control proportional gain.
- There is a critical range for the PLL proportional gain, in which SSO damping is near consistent irrespective to the change of active power variation. The influence of active power output on the stability can be minimized by selecting proper the PLL proportional gain first when the damping variation is at the critical range. Then adjustment of other parameters will improve the stability. This is valuable for engineering applications in designing PLL parameters.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Global Wind Energy Council. Global Wind Report 2019; Global Wind Energy Council: Brussels, Belgium, 2019. [Google Scholar]
- Leon, A.E.; Solsona, J.A. Sub-synchronous interaction damping control for DFIG wind turbines. IEEE Trans. Power Syst. 2015, 30, 419–428. [Google Scholar] [CrossRef]
- Ren, W.; Larsen, E. A refined frequency scan approach to subsynchronous control interaction (SSCI) study of wind farms. IEEE Trans. Power Syst. 2016, 31, 3904–3912. [Google Scholar] [CrossRef]
- Adams, J.; Pappu, V.A.; Dixit, A. ERCOT experience screening for sub-synchronous control interaction in the vicinity of series capacitor banks. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar]
- Strachan, N.P.; Jovcic, D. Stability of a variable-speed permanent magnet wind generator with weak ac grids. IEEE Trans. Power Del. 2010, 25, 2779–2788. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; He, J.; Xu, T.; Yu, Z.; Wang, C.; Zhang, C. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks. IEEE Trans. Power Syst. 2017, 32, 4708–4720. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Zhang, C.; Li, Y.; Liu, H.; Hu, Y. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model. IEEE Trans. Power Syst. 2017, 32, 474–483. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in practical DFIG-based wind farms connected to a series compensated power system. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-based WTs for small signal stability analysis in DVC timescale in power electronized power systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Wind in weak grids: Low-frequency oscillations, subsynchronous oscillations, and torsional interactions. IEEE Trans. Power Syst. 2020, 35, 109–118. [Google Scholar] [CrossRef]
- Wang, D.; Liang, L.; Shi, L.; Hu, J.; Hou, Y. Analysis of modal resonance between PLL and DC-Link voltage control in weak-grid tied VSCs. IEEE Trans. Power Syst. 2019, 34, 1127–1138. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, D. Effect of control-loops interactions on power stability limits of VSC integrated to AC system. IEEE Trans. Power Del. 2018, 33, 301–310. [Google Scholar] [CrossRef]
- Li, X.; Liang, J.; Li, G.; Joseph, T. Modeling and stability analysis of the sub-synchronous interactions in weak AC grids with wind power integration. In Proceedings of the 2018 International Universities Power Engineering Conference (UPEC), Glassgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- TAO, G.; Wang, Y.; WU, Y.; CHEN, Y. Subsynchronous interaction analysis of PMSG based wind farm with AC networks. In Proceedings of the 2019 International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Alawasa, K.M.; Mohamed, Y.A.-R.I.; Xu, W. Modeling, analysis, and suppression of the impact of full-scale wind-power converters on subsynchronous damping. IEEE Syst. J. 2013, 7, 700–712. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Fan, L. Modeling type-4 wind in weak grids. IEEE Trans. Sustain. Energy 2019, 10, 853–864. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P. Modeling of VSC connected to weak grid for stability analysis of DC-Link voltage control. IEEE J. Emerg. Sel. Topics Power Electron. 2015, 3, 1193–1204. [Google Scholar] [CrossRef]
- Papangelis, L.; Debry, M.-S.; Prevost, T.; Panciatici, P.; Van Cutsem, T. Stability of a voltage source converter subject to decrease of short-circuit capacity: A case study. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Huang, B.; Sun, H.; Liu, Y.; Wang, L.; Chen, Y. Study on subsynchronous oscillation in D-PMSGs-based wind farm integrated to power system. IET Renew. Power Gener. 2019, 13, 16–26. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Molinas, M. Optimal design of controller parameters for improving the stability of MMC-HVDC for wind farm integration. IEEE J. Emerg. Sel. Topics Power Electron. 2018, 6, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Jing, L.; Xu, C. Impact of controller parameters on stability of MMC-based HVDC systems for offshore wind farms. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; pp. 1–6. [Google Scholar]
- Pipelzadeh, Y.; Chaudhuri, N.R.; Chaudhuri, B.; Green, T.C. Coordinated Control of Offshore Wind Farm and Onshore HVDC Converter for Effective Power Oscillation Damping. IEEE Trans. Power Syst. 2017, 32, 1860–1872. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed Between Wind Farms and HVdc Systems. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 378–392. [Google Scholar] [CrossRef] [Green Version]
- Amin, M.; Rygg, A.; Molinas, M. Self-Synchronization of Wind Farm in an MMC-Based HVDC System: A Stability Investigation. IEEE Trans. Energy Convers. 2017, 32, 458–470. [Google Scholar] [CrossRef]
- Fan, L. Control and Dynamics in Power Systems and Microgrids; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Institute of Electrical and Electronics Engineers. IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities; IEEE Standard 1204-1997; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1997. [Google Scholar]
- Joseph, T.; Ugalde-Loo, C.E.; Balasubramaniam, S.; Liang, J. Real-Time Estimation and Damping of SSR in a VSC-HVDC Connected Series-Compensated System. IEEE Trans. Power Syst. 2018, 33, 7052–7063. [Google Scholar] [CrossRef]



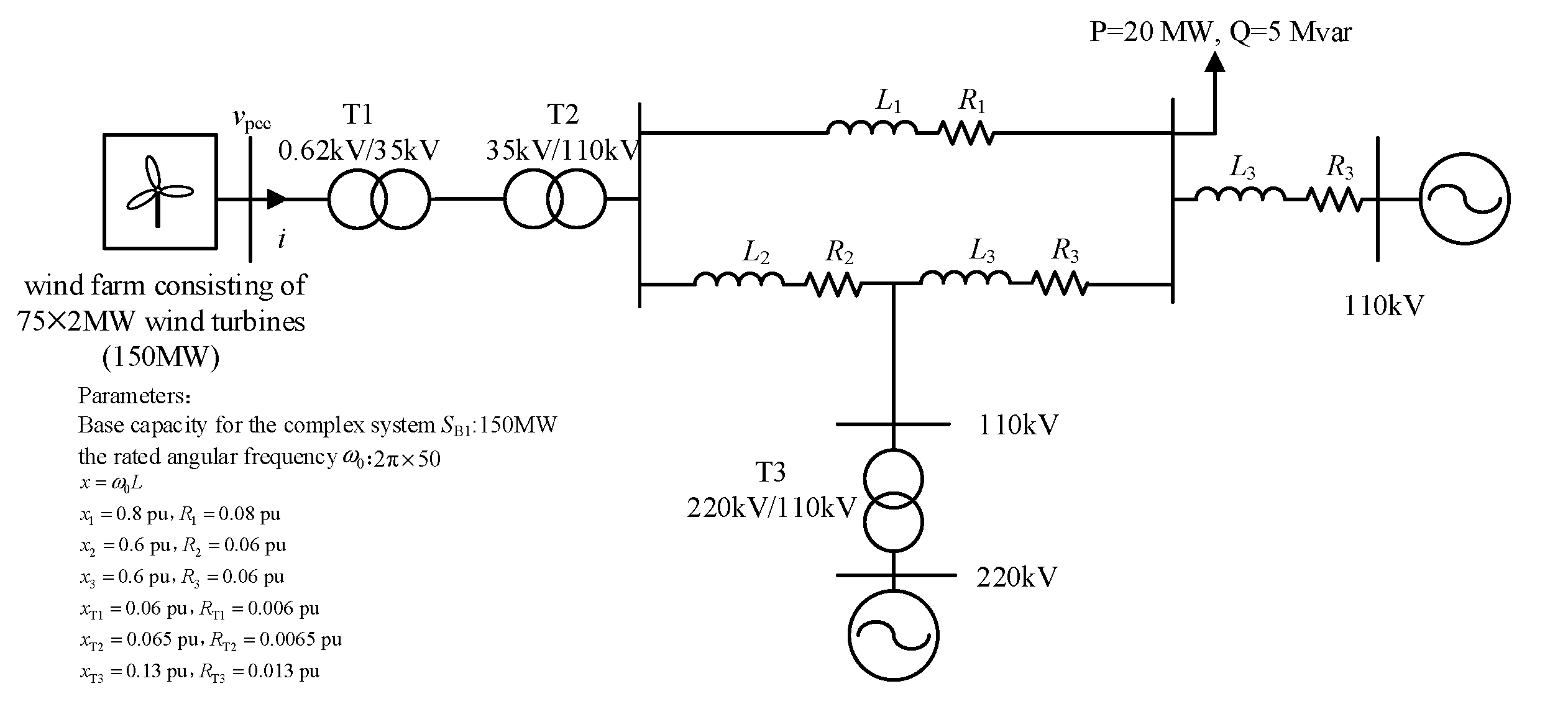
| Parameter | Value (pu, SB = 100 MVA) |
|---|---|
| Transformer T1(575 V/25 kV) | XT1 = 0.06, RT1 = 0.006 |
| Transformer T2(25 kV/220 kV) | XT2 = 0.065, RT2 = 0.0065 |
| Long-distance transmission line | X2 = 0.525, R2 = 0.0525 |
| Short-distance transmission line | X3 = 0.01, R3 = 0.001 |
| Parameter | Value (pu, SB = 2 MVA) |
|---|---|
| Rated power | 2 MW |
| Rated frequency | 50 Hz |
| GSC filter | Xf1 = 0.15, Rf1 = 0.003, yc1 = 0.25 |
| DC capacitor | 0.09 F |
| Rated DC voltage | 1100 V |
| DVC | Kpdc = 1.1, Kidc = 137.5 |
| Current control | Kpi = 0.4758, Kii = 3.28 |
| PLL | Kppll = 314, Kipll = 24,700 |
| Mode | Eigenvalue |
|---|---|
| λ1,2 | −569.33 ± j1764.69 |
| λ3,4 | −87.53 ± j836.15 |
| λ5 | −976.21 |
| λ6,7 | 2.62 ± j199.47 |
| λ8 | −91.51 |
| λ9,10 | −15.89 ± j55.99 |
| λ11 | −6.90 |
| λ12 | −6.89 |
| Kppll | Kipll | |
|---|---|---|
| Case 1 | 314 (the pre-set value) | 24,700 (the pre-set value) |
| Case 2 | 314 | 24,700 × 0.8 |
| Case 3 | 314 × 0.2 | 24,700 |
| Case 4 | 314 × 0.2 | 24,700 × 0.8 |
| Parameters | Based-Case | Group 1 | Group 2 | Group 3 | |
|---|---|---|---|---|---|
| PLL | Kppll | 314 | 314 | 314 × 0.2 | 314 × 0.2 |
| Kipll | 24,700 | 24,700 × 0.8 | 24,700 × 0.8 | 24,700 × 0.7 | |
| DVC | Kpdc | 1.1 | 1.1 × 1.6 | 1.1 × 1.6 | 1.1 × 2 |
| Kidc | 137.5 | 137.5 | 137.5 | 137.5 | |
| Inner current control loop | Kpi = 0.4758 | Kii = 3.28 | |||
| Parameters | Group 4 | Group 5 | Group 6 | Group 7 | |
|---|---|---|---|---|---|
| PLL | Kppll | 314 | 314 | 314 × 0.2 | 314 × 0.2 |
| Kipll | 24,700 | 24,700 × 0.8 | 24,700 × 0.8 | 24,700 × 0.7 | |
| DVC | Kpdc | 1.1 × 1.2 | 1.1 × 1.8 | 1.1×1.8 | 1.1 × 2.0 |
| Kidc | 137.5 | 137.5 | 137.5 | 137.5 | |
| Inner current control loop | Kpi = 0.4758 | Kii = 3.28 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Liang, J.; Wang, K.; Wu, G.; Joseph, T.; Sun, R. Influence of Active Power Output and Control Parameters of Full-Converter Wind Farms on Sub-Synchronous Oscillation Characteristics in Weak Grids. Energies 2020, 13, 5225. https://doi.org/10.3390/en13195225
Hao Y, Liang J, Wang K, Wu G, Joseph T, Sun R. Influence of Active Power Output and Control Parameters of Full-Converter Wind Farms on Sub-Synchronous Oscillation Characteristics in Weak Grids. Energies. 2020; 13(19):5225. https://doi.org/10.3390/en13195225
Chicago/Turabian StyleHao, Yafeng, Jun Liang, Kewen Wang, Guanglu Wu, Tibin Joseph, and Ruijuan Sun. 2020. "Influence of Active Power Output and Control Parameters of Full-Converter Wind Farms on Sub-Synchronous Oscillation Characteristics in Weak Grids" Energies 13, no. 19: 5225. https://doi.org/10.3390/en13195225
APA StyleHao, Y., Liang, J., Wang, K., Wu, G., Joseph, T., & Sun, R. (2020). Influence of Active Power Output and Control Parameters of Full-Converter Wind Farms on Sub-Synchronous Oscillation Characteristics in Weak Grids. Energies, 13(19), 5225. https://doi.org/10.3390/en13195225





