Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method
Abstract
:1. Introduction
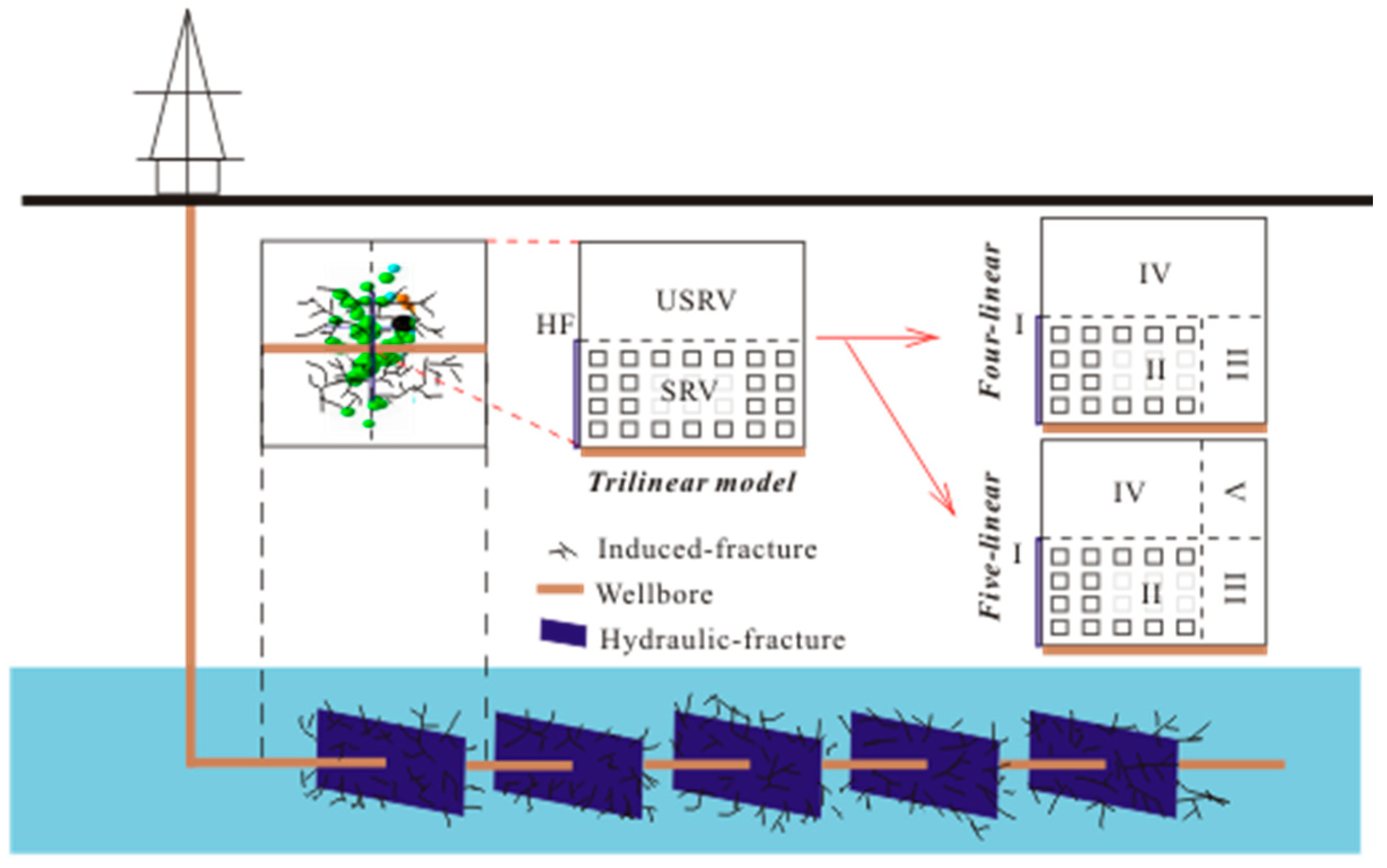
2. Fractal Semianalytic Model for Mfhws in Unconventional Gas Reservoirs
2.1. Fractal Fracture Network Permeability and Porosity in SRV
2.2. Transient Diffusivity Equations in SRV And USRV
2.2.1. Diffusivity Equations of FTMM in SRV (Region II)
2.2.2. Diffusivity Equations of FTMM in USRV (Region III, Region IV and Region V)
2.2.3. Diffusivity Equations of FTMM in HF (Region I)
3. Model Verification and Discussion
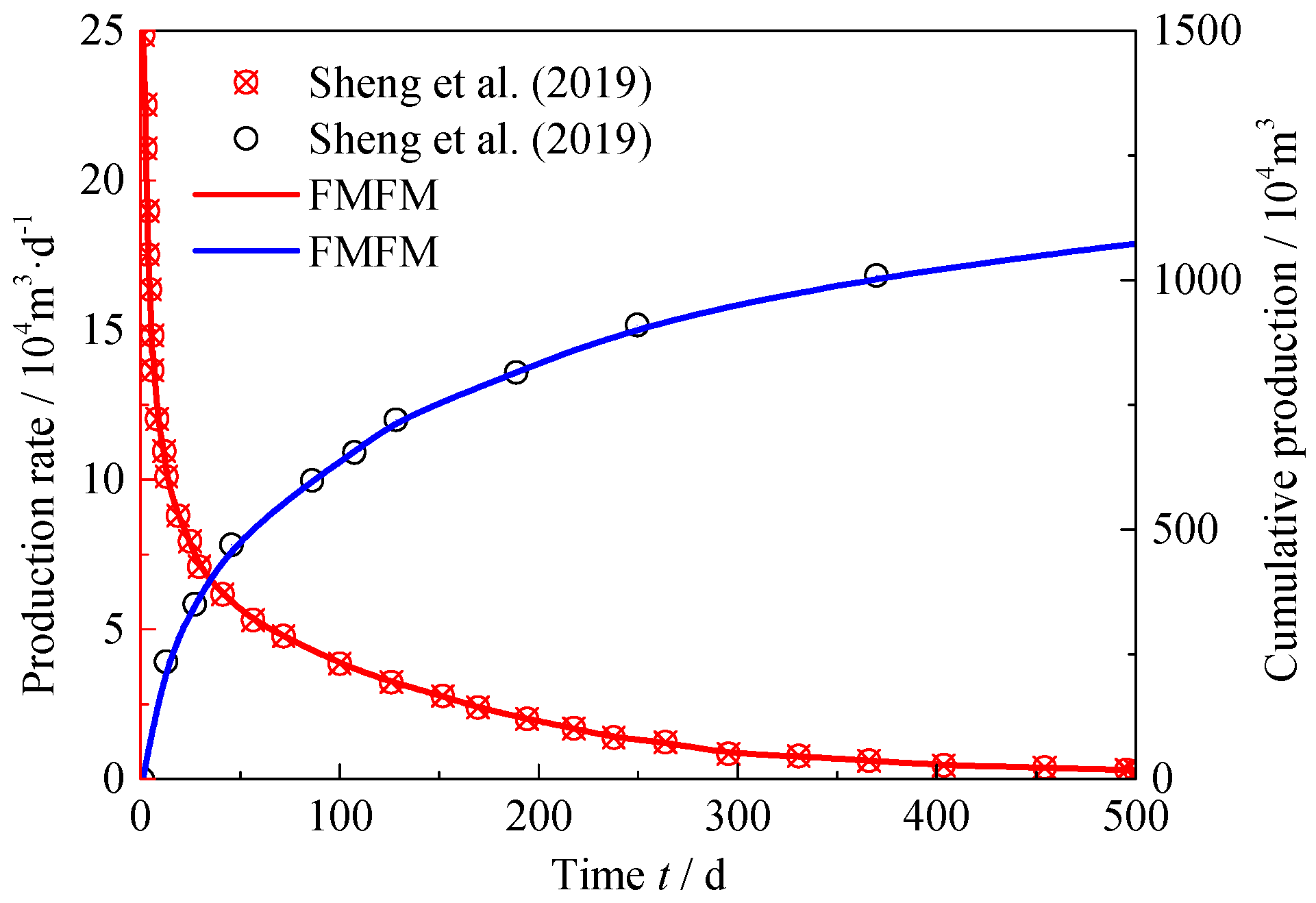
3.1. Model Verification
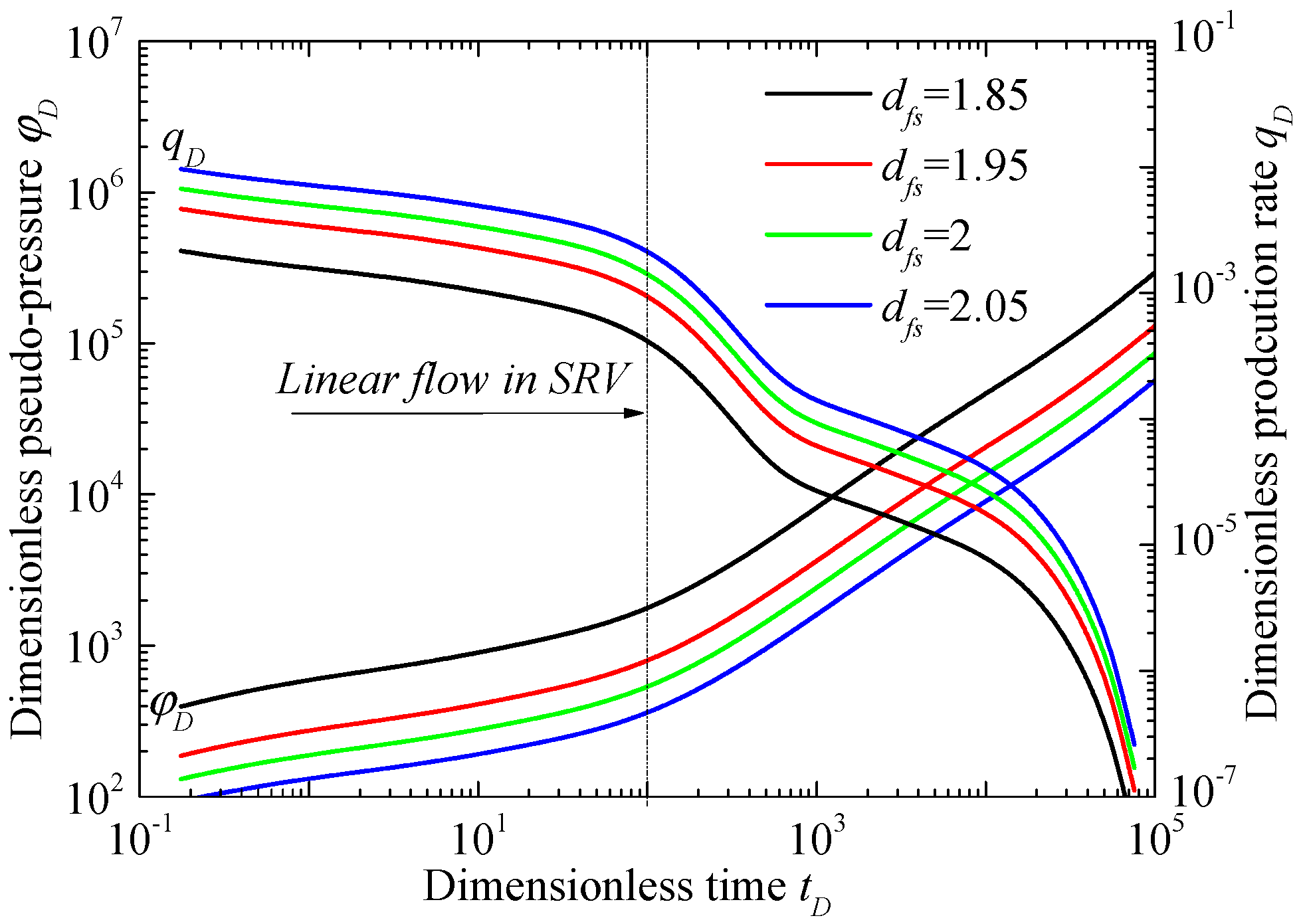
3.2. Sensitivity Analysis of Properties of SRV
4. Application of FMFM with ES-MDA Method
4.1. ES-MDA Method
- (1)
- Estimate the number of data assimilations Na, and the coefficients (), for .
- (2)
- For
- Run the ensemble from time zero for obtaining the vector of predicted datawhere is the nonlinear forward model, is assignment the model parameters to vector at time zero.
- For each ensemble member, perturb the observation vector bywhere .
- Update the ensemblewhere ; ; ; and represent the average values of model parameters and prediction parameter ensembles respectively.
4.2. Synthetic Case
4.3. Field Case
5. Conclusions
- (1)
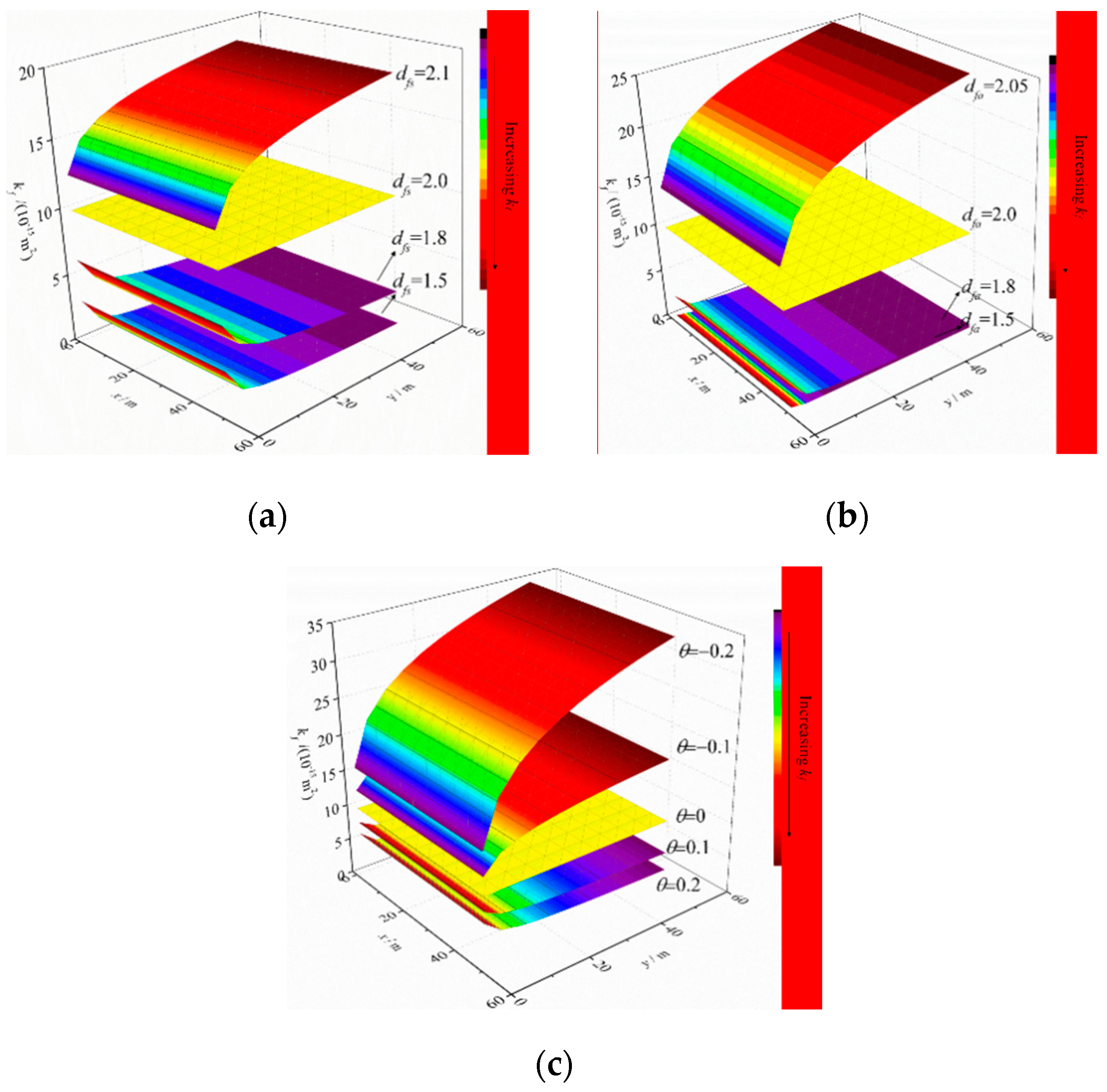
- The permeability and porosity of the induced-fracture system are affected by the heterogeneous distribution of induced-fractures spacing and aperture. When the fractal dimensions of induced-fracture spacing (dfs) and aperture (dfa) are smaller than 2.0, the permeability of the induced-fracture system decreases with the increase of the distance from HFs in SRV region, which will become increase if dfs > 2.0 or dfa > 2.0. When the tortuosity index of the induced-fracture system θ is larger than 0, the permeability of induced-fracture system also decreases with the increase of the distance from HFs in SRV region.
- (2)
- The FMFM divides the formation into three types of porous media in shale reservoirs (porous kerogen, inorganic matter, and fracture system). Triple-porosity media and dual-porosity media are used to describe the fractal SRV region and USRV region, respectively. Multiple gas transport mechanisms such as viscous flow with slippage, Knudsen diffusion, and surface diffusion are considered, and gas flow behaviors in different regions are coupled by pseudo-steady cross-flow among various media. The FMFM is verified by other presented model and the results show that the large dfs or small θ causes the small average permeability of the induced-fracture system, which results in large dimensionless pseudo-pressure and small dimensionless production rate.
- (3)
- Combining the FMFM with ES-MDA history-matching method, the synthetic case for the tight gas reservoir and field case for the shale gas reservoir are discussed. Various main parameters inversions of HFs and NFs are conducted in SRV region. Thus, the presented method can be applied for gas production predicting and history-matching in unconventional gas reservoirs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Fractal Permeability and Porosity of Induced-Fracture
Appendix B. Solution for the FMFM Model
| Parameters | Expression |
|---|---|
| Pseudo-pressure for gas phase | |
| Dimensionless pseudo-pressure | |
| Dimensionless time | |
| Dimensionless length | , , , , , |
| Total compressibility coefficient of porous kerogen | |
| Transfer coefficient from porous kerogen to inorganic matter | |
| Transfer coefficient from inorganic matter to induced-fracture | |
| Storage coefficient of porous kerogen | |
| Storage coefficient of inorganic matter | |
| Storage coefficient of HFs |
- (1)
- Dimensionless forms and solutions for USRV.According to Equations (9) and (10), the dimensionless diffusivity equations in Laplace domain for region III and V can be given bySolving Equation (A10a,b) with boundary conditions, we can obtainwhere .According to Equation (3), the dimensionless diffusivity equations in Laplace domain for region IV can be given bySolving Equation (A12) with boundary conditions, we can obtainwhere .
- (2)
- Dimensionless forms and solutions for SRV.According to Equations (3), (5), and (6), the dimensionless diffusivity equations in Laplace domain for region SRV can be given bySolving Equation (A14) with boundary conditions, we can obtainwhere , , , , , .
- (3)
- Dimensionless forms and solutions for HFs.According to Equation (14), the dimensionless diffusivity equations in Laplace domain for HFs can be given bySolving Equation (A16) with boundary conditions, we can obtain the pseudo-pressure in well bottom-hole in Laplace domain as Equation (16).
References
- Yuan, B.; Su, Y.; Moghanloo, R.G.; Rui, Z.; Wang, W.; Shang, Y. A new analytical multi-linear solution for gas flow toward fractured horizontal wells with different fracture intensity. J. Nat. Gas Sci. Eng. 2015, 23, 227–238. [Google Scholar] [CrossRef]
- Sheng, G.; Zhao, H.; Su, Y.; Javadpour, F.; Wang, C.; Zhou, Y.; Liu, J.; Wang, H. An analytical model to couple gas storage and transport capacity in organic matter with noncircular pores. Fuel 2020, 268, 117288. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Zhao, H.; Liu, J. A unified apparent porosity/permeability model of organic porous media: Coupling complex pore structure and multi-migration mechanism. Adv. Geo-Energy Res. 2020, 4, 115–125. [Google Scholar] [CrossRef]
- Arevalo-Villagran, J.A.; Wattenbarger, R.A.; Samaniego-Verduzco, F.; Pham, T.T. Production analysis of long-term linear flow in tight gas reservoirs: Case histories. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, New Orleans, LA, USA, 30 September–3 October 2001. [Google Scholar]
- Al Ahmadi, H.A.; Almarzooq, A.M.; Wattenbarger, R.A. Application of linear flow analysis to shale gas wells-field cases. In Proceedings of the SPE Unconventional Gas Conference, Society of Petroleum Engineers, Pittsburgh, PA, USA, 23–25 February 2010. [Google Scholar]
- Yu, W. Developments in Modeling and Optimization of Production in Unconventional Oil and Gas Reservoirs. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Yao, S.; Wang, X.; Zeng, F.; Li, M.; Ju, N. A composite model for multi-stage fractured horizontal wells in heterogeneous reservoirs. In Proceedings of the SPE Russian Petroleum Technology Conference and Exhibition, Society of Petroleum Engineers, Moscow, Russia, 24–26 October 2016. [Google Scholar]
- Ozkan, E.; Brown, M.L.; Raghavan, R.S.; Kazemi, H. Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs. In Proceedings of the SPE Western Regional Meeting, Society of Petroleum Engineers, San Jose, CA, USA, 24–26 March 2009. [Google Scholar]
- Brown, M.; Ozkan, E.; Raghavan, R.; Kazemi, H. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 663–676. [Google Scholar] [CrossRef]
- Stalgorova, K.; Mattar, L. Analytical model for unconventional multifractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, D.; Sheng, G.; Zhang, Q.; Su, Y. A review of stimulated reservoir volume characterization for multiple fractured horizontal well in unconventional reservoirs. Adv. Geo-Energy Res. 2017, 1, 54–63. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Tang, C.; Zhou, Y.; Ning, B.; Cai, J. A new semi-analytical method for calculating well productivity near discrete fractures. J. Nat. Gas Sci. Eng. 2018, 57, 216–223. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B. Prediction of maximum pore size of porous media based on fractal geometry. Fractals 2010, 18, 417–423. [Google Scholar] [CrossRef]
- Yang, F.; Ning, Z.; Liu, H. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China. Fuel 2014, 115, 378–384. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W.; Javadpour, F.; Tang, M. Application of fractal geometry in evaluation of effective stimulated reservoir volume in shale gas reservoirs. Fractals 2017, 25, 1740007. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.; Yortsos, Y.C. Pressure Transient Analysis of Fractal Reservoirs. SPE Form. Eval. 1990, 5, 31–38. [Google Scholar] [CrossRef]
- Cossio, M.; Moridis, G.; Blasingame, T.A. A semianalytic aolution for flow in finite-conductivity vertical fractures by use of fractal theory. SPE J. 2013, 18, 83–96. [Google Scholar] [CrossRef]
- Acuna, J.A.; Ershaghi, I.; Yortsos, Y.C. Practical application of fractal pressure transient analysis of naturally fractured reservoirs. SPE Form. Eval. 1995, 10, 173–179. [Google Scholar] [CrossRef]
- Wang, W.; Shahvali, M.; Su, Y. A Semi-Analytical Fractal Model for Production from Tight Oil Reservoirs with Hydraulically Fractured Horizontal Wells. Fuel 2015, 158, 612–618. [Google Scholar] [CrossRef]
- Sheng, G.; Xu, T.; Gou, F.; Su, Y.; Wang, W.; Lu, M.; Zhan, S. Performance analysis of multi-fractured horizontal wells with complex fracture networks in shale gas reservoirs. J. Porous Media 2019, 22, 299–320. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W. A new fractal approach for describing induced-fracture porosity/permeability/compressibility in stimulated unconventional reservoirs. J. Pet. Sci. Eng. 2019, 179, 855–866. [Google Scholar] [CrossRef]
- Samandarli, O.; Al Ahmadi, H.A.; Wattenbarger, R.A. A semi-analytic method for history matching fractured shale gas reservoirs. In Proceedings of the SPE Western North American Region Meeting, Society of Petroleum Engineers, Anchorage, AK, USA, 7–11 May 2011. [Google Scholar]
- Hategan, F.; Hawkes, V.R. Well production performance analysis for unconventional shale gas reservoirs: A conventional approach. In Proceedings of the SPE Canadian Unconventional Resources Conference, Society of Petroleum Engineers, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]
- Cho, Y.; Ozkan, E.; Apaydin, O.G. Pressure-dependent natural-fracture permeability in shale and its effect on shale-gas well production. SPE Reserv. Eval. Eng. 2013, 16, 216–228. [Google Scholar] [CrossRef]
- Ogunyomi, B.A.; Patzek, T.W.; Lake, L.W.; Kabir, C.S. History matching and rate forecasting in unconventional oil reservoirs using an approximate analytical solution to the double porosity model. In Proceedings of the SPE Eastern Regional Meeting, Society of Petroleum Engineers, Charleston, WV, USA, 21–23 October 2014. [Google Scholar]
- Clarkson, C.R.; Williams-Kovacs, J.D.; Qanbari, F.; Behmanesh, H.; Sureshjani, M.H. History-matching and forecasting tight/shale gas condensate wells using combined analytical, semi-analytical, and empirical methods. J. Nat. Gas Sci. Eng. 2015, 26, 1620–1647. [Google Scholar] [CrossRef]
- Nobakht, M.; Mattar, L. Analyzing production data from unconventional gas reservoirs with linear flow and apparent skin. J. Can. Pet. Technol. 2012, 51, 52–59. [Google Scholar] [CrossRef]
- Chen, Z.M.; Liao, X.W.; Zhao, X.L.; Liu, H.M.; Tian, J.; Zhu, L.T.; Wang, L.; Zhao, H.J. A comprehensive model for performance forecast of multiple fractured horizontal well in unconventional reservoirs: A case study. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Society of Petroleum Engineers, Port of Spain, Trinidad and Tobago, 13–15 June 2016. [Google Scholar]
- Warren, J.R.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Bour, O.; Davy, P. On the connectivity of three-dimensional fault networks. Water Resour. Res. 1998, 34, 2611–2622. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, Y.; Zhao, H.; Wang, W.; Zhang, K.; Lu, M. Analytic evaluation method of fractal effective stimulated reservoir volume for fractured wells in unconventional gas reservoirs. Fractals 2018, 26, 1850097. [Google Scholar] [CrossRef]
- Fan, D.; Ettehadtavakkol, A. Semi-Analytical Modeling of Shale Gas Flow through Fractal Induced Fracture Networks with Microseismic Data. Fuel 2017, 193, 444–459. [Google Scholar] [CrossRef]
- Mukherjee, H.; Economides, M.J. A parametric comparison of horizontal and vertical well performance. SPE Form. Eval. 1990, 6, 209–216. [Google Scholar] [CrossRef]
- Van Everdingen, A.F.; Hurst, W. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. Investigation of the sampling performance of ensemble-based methods with a simple reservoir model. Comput. Geosci. 2013, 17, 325–350. [Google Scholar] [CrossRef]
- Xu, J.; Guo, C.; Wei, M. Production performance analysis for composite shale gas reservoir considering multiple transport mechanisms. J. Nat. Gas Sci. Eng. 2015, 26, 382–395. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Analytical solutions for diffusion on fractal objects. Phys. Rev. Lett. 1985, 54, 455–458. [Google Scholar] [CrossRef]
- Bai, M.; Elsworth, D. Modeling of subsidence and stress-dependent hydraulic conductivity for intact and fractured porous media. Rock Mech. Rock Eng. 1994, 27, 209–234. [Google Scholar] [CrossRef]





| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Fractal dimension of induced-fracture spacing, dfs | 1.95 | Pore size in porous kerogen, rk (m) | 10 × 10−9 |
| Fractal dimension of induced-fracture aperture, dfa | 2.0 | Portion of kerogen volume, εks | 0.5 |
| Tortuosity index of induced-fracture, θ | −0.05 | Porous kerogen porosity, ϕk | 0.1 |
| Porosity of induced-fracture, | 10−4 | Porous kerogen tortuosity, τk | 5 |
| HF half-spacing, ye (m) | 100 | Langmuir pressure, pL (MPa) | 13.78 |
| HF half-length, xf (m) | 50 | Gas viscosity, μg (mPa·s) | 0.0184 |
| HF permeability, kF (m2) | 103 × 10−15 | Gas compressibility, Cg (MPa−1) | 5 × 10−2 |
| HF half-width, yw (m) | 0.01 | Surface diffusion coefficient, Ds (m2/s) | 1 × 10−5 |
| HF porosity, ϕF | 10−3 | Molecular mass of shale gas, M (kg/mol) | 0.016 |
| Total compressibility of the inorganic matter, Ctm (MPa−1) | 7.5 × 10−3 | Langmuir volume on kerogen surface, cμs (mol/m3) | 700 |
| Total compressibility of induced-fracture, Ctf (MPa−1) | 4 × 10−3 | Fraction of molecules striking pore wall which are diffusely reflected, f | 0.8 |
| Inorganic matter porosity, ϕm | 0.1 | Total compressibility of the porous kerogen, Ctk (MPa−1) | 7.5 × 10−3 |
| Inorganic matter tortuosity, τm | 5 | Reservoir thickness, h (m) | 19 |
| Induced-fracture permeability at yw, kw (m2) | 2 × 10−15 | Initial pressure, pi (MPa) | 17 |
| Pore size in inorganic matter, rm (m) | 20 × 10−9 | Well bottom pressure, pwf (MPa) | 12 |
| Formation temperature, T (K) | 338 | Reservoir half-width, xe (m) | 200 |
| Parameters | Eclipse | FMFM | Parameters | Eclipse | FMFM |
|---|---|---|---|---|---|
| Total compressibility coefficient, MPa−1 | 5.5 × 10−3 | 5.2714 × 10−3 | USRV matrix permeability, m2 | 1 × 10−19 | 0.887 × 10−18 |
| HF permeability, m2 | 15 × 10−13 | 7.82 × 10−13 | Induced-fracture permeability, m2 | 1 × 10−16 | 1.33 × 10−16 |
| SRV matrix permeability, m2 | 1 × 10−18 | 0.77 × 10−18 | Other parameters | Equal values | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Jiang, S.; Wu, X.; Wang, Y.; Meng, Q. Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method. Energies 2020, 13, 3718. https://doi.org/10.3390/en13143718
Zhang Q, Jiang S, Wu X, Wang Y, Meng Q. Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method. Energies. 2020; 13(14):3718. https://doi.org/10.3390/en13143718
Chicago/Turabian StyleZhang, Qi, Shu Jiang, Xinyue Wu, Yan Wang, and Qingbang Meng. 2020. "Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method" Energies 13, no. 14: 3718. https://doi.org/10.3390/en13143718
APA StyleZhang, Q., Jiang, S., Wu, X., Wang, Y., & Meng, Q. (2020). Development and Calibration of a Semianalytic Model for Shale Wells with Nonuniform Distribution of Induced Fractures Based on ES-MDA Method. Energies, 13(14), 3718. https://doi.org/10.3390/en13143718





