A Novel Design of Static Electrostatic Generator for High Voltage Low Power Applications Based on Electric Field Manipulation by Area Geometric Difference
Abstract
:1. Introduction
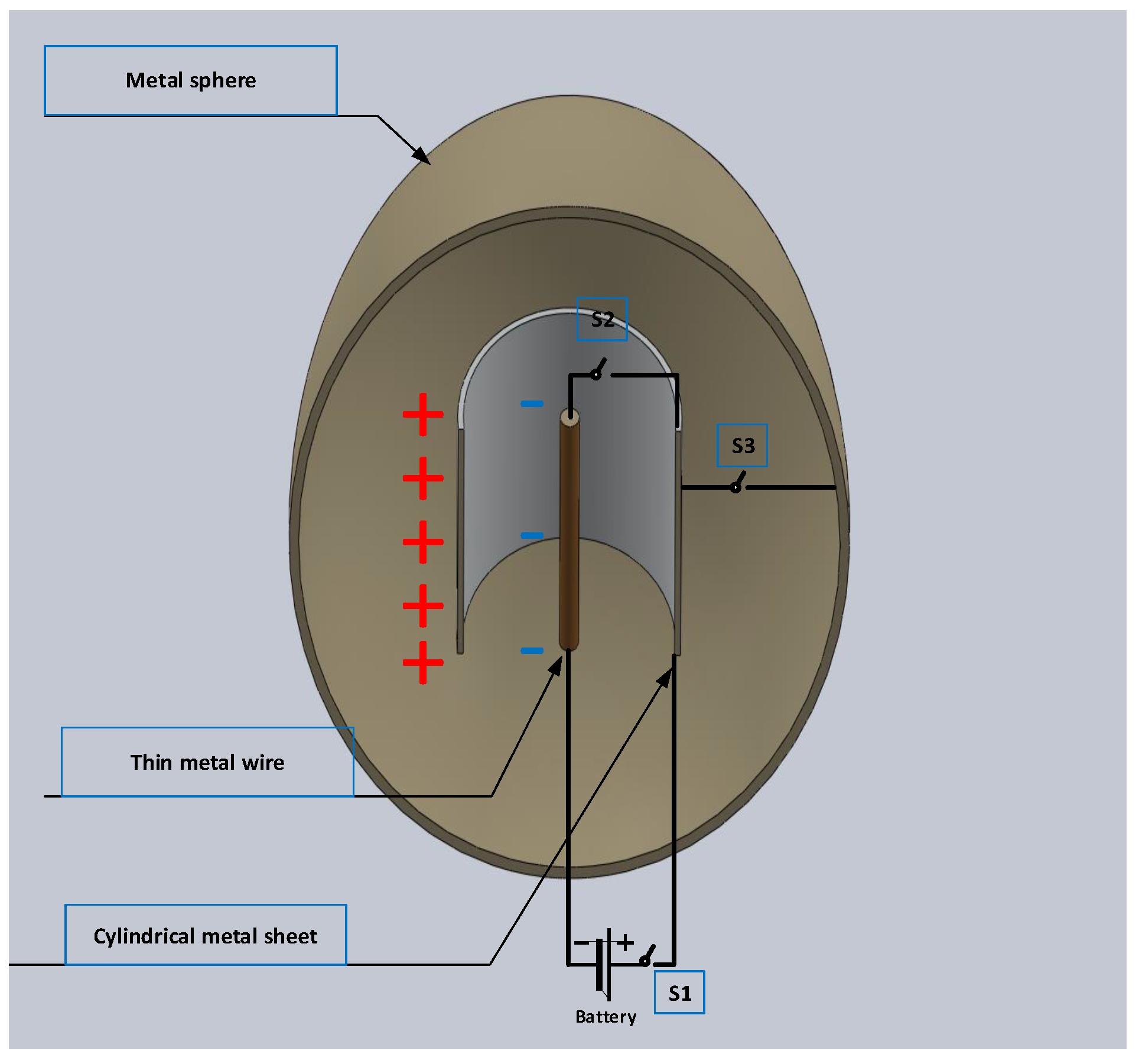
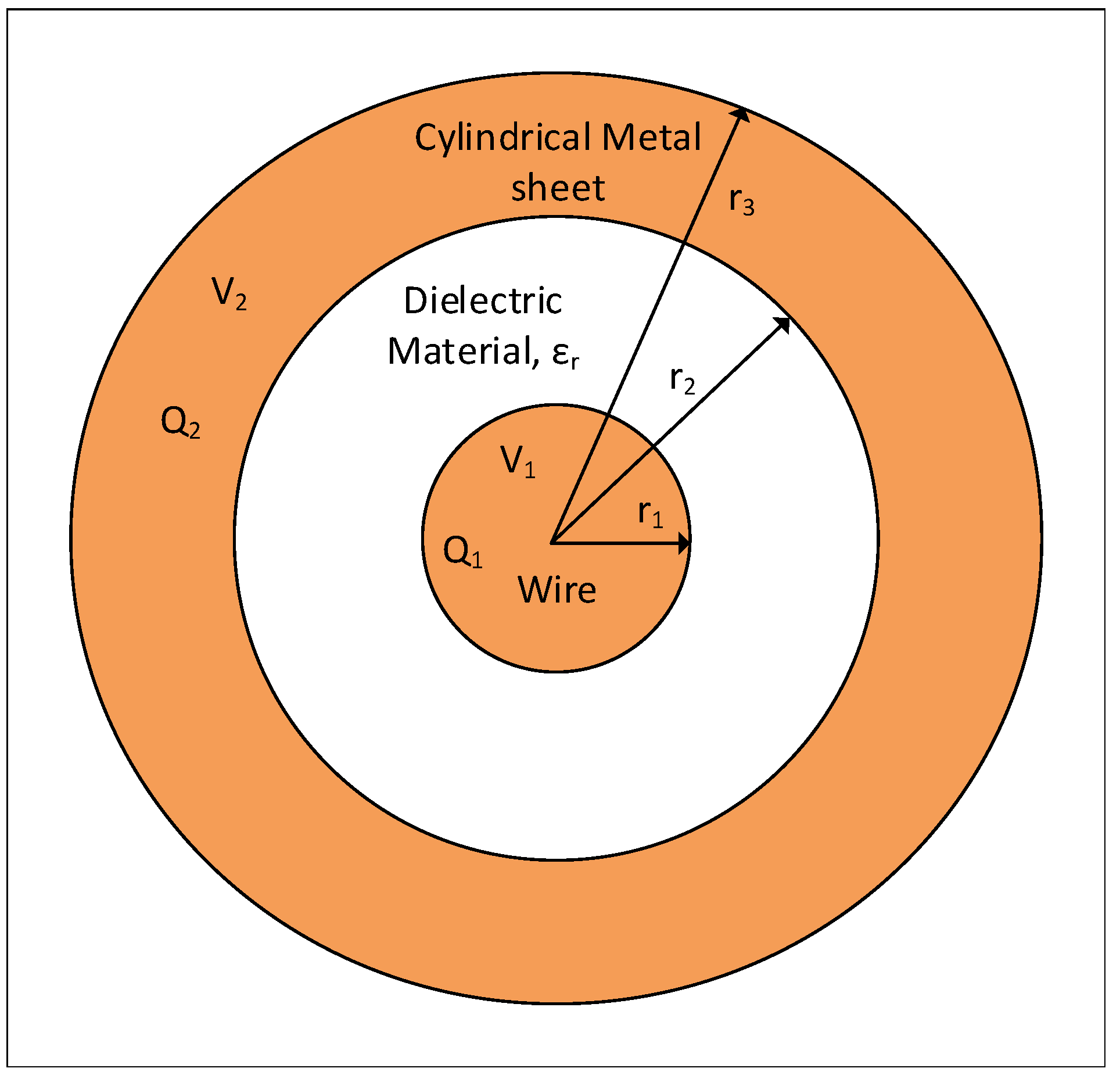
2. Proposed Device Working Principle
3. Finite Difference Method
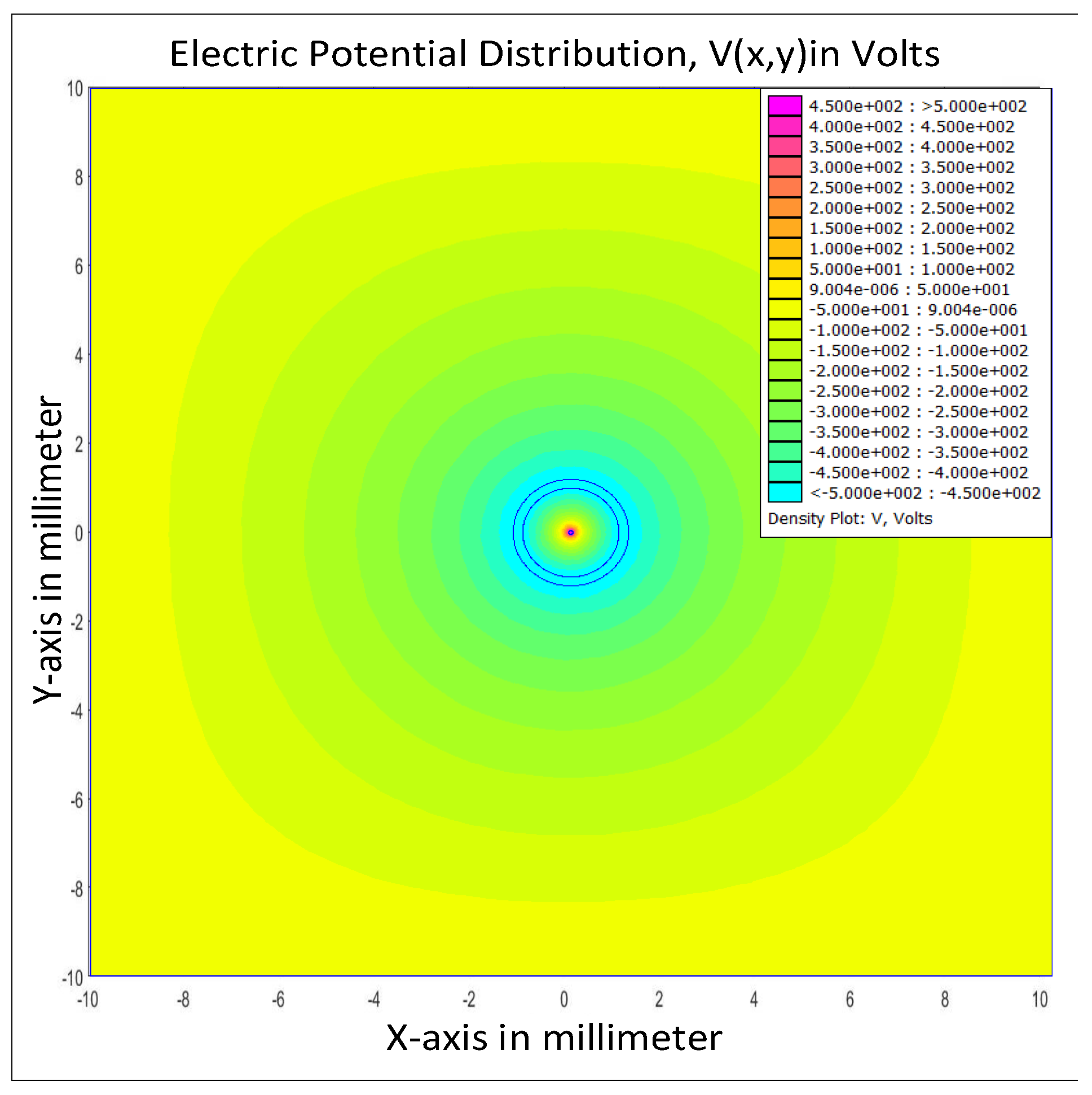
3.1. Laplace’s Equation
3.2. Poisson’s Equation
3.3. Electric Field
4. Simulation Results
4.1. CASE I: Effects of the Dielectric Material
4.2. CASE II: Effects of the Applied Voltage
4.3. CASE III: Effects of the Thin Wire Diameter
4.4. CASE IV: Effects of the Thin Metal Sheet Diameter
4.5. CASE V: Effects of the Thin Metal Sheet Thickness
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| W | Energy [J] |
| w | Energy density [] |
| D | Electric filed density [] |
| E | Electric filed [] |
| Relative permittivity | |
| Permittivity of Vacuum [] | |
| V | Voltage [V] |
| Charge density [] | |
| e | electron charge [C] |
| Q | Total charge [C] |
| Volume of cubic cell [] | |
| Direct current | |
| Alternating current | |
| Static electrostatic generator | |
| Electrostatic wind converter | |
| Maximum power point | |
| Maximum power point tracking | |
| Solar photovoltaic | |
| DC to DC converter | |
| Linear quadratic regulator | |
| Zero-voltage switches | |
| Zero-current switches | |
| electric vehicles | |
| Switches | |
| Total energy stored | |
| Energy lost | |
| Finite difference method | |
| Finite element method | |
| Efficiency |
References
- Fortescue, R.L.; Hall, P.D. The High-Voltage Electrostatic Generator at the Atomic Energy Research Establishment. Proc. IEE—Part I Gen. 1949, 96, 77–85. [Google Scholar] [CrossRef]
- van de Graaff, R.J.; Compton, K.T.; van Atta, L.C. The Electrostatic Production of High Voltage for Nuclear Investigations. Phys. Rev. 1933, 43, 149–157. [Google Scholar] [CrossRef]
- Matthew, R.E. The use of electrets in electrostatic generators for space. Electr. Eng. 1962, 81, 850–854. [Google Scholar] [CrossRef]
- O’Donnell, R.; Schofield, N.; Smith, A.C.; Cullen, J. Design Concepts for High-Voltage Variable-Capacitance DC Generators. IEEE Trans. Ind. Appl. 2009, 45, 1778–1784. [Google Scholar] [CrossRef]
- Djairam, D.; Morshuis, P.H.F.; Smit, J.J. A novel method of wind energy generation-the electrostatic wind energy converter. IEEE Electr. Insul. Mag. 2014, 30, 8–20. [Google Scholar] [CrossRef]
- Xie, Y.; Bos, D.; de Vreede, L.J.; de Boer, H.L.; van der Meulen, M.J.; Versluis, M.; Sprenkels, A.J.; van den Berg, A.; Eijkel, J.C.T. High-efficiency ballistic electrostatic generator using microdroplets. Nat. Commun. 2014, 5, 3575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Queiroz, A.C.M.; Domingues, M. The Doubler of Electricity Used as Battery Charger. IEEE Trans. Transp. Electrif. 2011, 58, 797–801. [Google Scholar] [CrossRef]
- Shih, R.M.; Contreras, D.S.; Massey, T.L.; Greenspun, J.T.; Pister, K.S.J. Characterization of electrostatic gap-closing actuator arrays in aqueous conditions. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 596–599. [Google Scholar] [CrossRef]
- Preetham, B.S.; Lake, M.A.; Hoelzle, D.J. A curved electrode electrostatic actuator designed for large displacement and force in an underwater environment. J. Micromech. Microeng. 2017, 27, 095009. [Google Scholar] [CrossRef]
- Burugupally, S.P.; Mangels, J.A. Performance evaluation of a curved electrode actuator fabricated without gold/chromium conductive layers. Microsyst. Technol. 2018, 24, 3479–3485. [Google Scholar] [CrossRef]
- Wang, L.; Yan, Y.; Hu, Y.; Qian, X. Rotational Speed Measurement Through Electrostatic Sensing and Correlation Signal Processing. IEEE Trans. Instrum. Meas. 2014, 63, 1190–1199. [Google Scholar] [CrossRef]
- Walker, G.R.; Sernia, P.C. Cascaded DC-DC converter connection of photovoltaic modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
- Marodkar, M.; Adhau, S.; Sabley, M.; Adhau, P. Design and simulation of DC-DC converters for Photovoltaic system based on MATLAB. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 1478–1483. [Google Scholar] [CrossRef]
- Savakhande, V.B.; Bhattar, C.L.; Bhattar, P.L. Voltage-lift DC-DC converters for photovoltaic application-a review. In Proceedings of the 2017 International Conference on Data Management, Analytics and Innovation (ICDMAI), Pune, India, 24–26 February 2017; pp. 172–176. [Google Scholar] [CrossRef]
- Soriano, L.A.; Ponce, P.; Molina, A. Analysis of DC-DC converters for photovoltaic applications based on conventional MPPT algorithms. In Proceedings of the 2017 14th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 20–22 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Deihimi, A.; Mahmoodieh, M.E.S. Analysis and control of battery-integrated dc/dc converters for renewable energy applications. IET Power Electron. 2017, 10, 1819–1831. [Google Scholar] [CrossRef]
- Das, M.; Agarwal, V. Design and Analysis of a High-Efficiency DC DC Converter With Soft Switching Capability for Renewable Energy Applications Requiring High Voltage Gain. IEEE Trans. Ind. Electron. 2016, 63, 2936–2944. [Google Scholar] [CrossRef]
- Freitas, A.A.A.; Tofoli, F.L.; Júnior, E.M.S.; Daher, S.; Antunes, F.L.M. High-voltage gain DC–DC boost converter with coupled inductors for photovoltaic systems. IET Power Electron. 2015, 8, 1885–1892. [Google Scholar] [CrossRef]
- Prabhala, V.A.K.; Fajri, P.; Gouribhatla, V.S.P.; Baddipadiga, B.P.; Ferdowsi, M. A DC DC Converter With High Voltage Gain and Two Input Boost Stages. IEEE Trans. Power Electron. 2016, 31, 4206–4215. [Google Scholar] [CrossRef]
- Lin, B.R.; Dong, J.Y. New zero-voltage switching DC-DC converter for renewable energy conversion systems. IET Power Electron. 2012, 5, 393–400. [Google Scholar] [CrossRef]
- Liang, Z.; Guo, R.; Li, J.; Huang, A.Q. A High-Efficiency PV Module-Integrated DC/DC Converter for PV Energy Harvest in FREEDM Systems. IEEE Trans. Power Electron. 2011, 26, 897–909. [Google Scholar] [CrossRef]
- Chen, S.M.; Lao, M.L.; Hsieh, Y.H.; Liang, T.J.; Chen, K.H. A Novel Switched-Coupled-Inductor DC DC Step-Up Converter and Its Derivatives. IEEE Trans. Ind. Appl. 2015, 51, 309–314. [Google Scholar] [CrossRef]
- Ardi, H.; Ajami, A.; Sabahi, M. A Novel High Step-Up DC–DC Converter With Continuous Input Current Integrating Coupled Inductor for Renewable Energy Applications. IEEE Trans. Ind. Electron. 2018, 65, 1306–1315. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Ji, Y.; Li, F. A Novel Reversal Coupled Inductor High-Conversion-Ratio Bidirectional DC DC Converter. IEEE Trans. Power Electron. 2018, 33, 4968–4979. [Google Scholar] [CrossRef]
- Chen, Y.T.; Lu, Z.X.; Liang, R.H.; Hung, C.W. Analysis and implementation of a novel high step-up DC DC converter with low switch voltage stress and reduced diode voltage stress. IET Power Electron. 2016, 9, 2003–2012. [Google Scholar] [CrossRef]
- Ishigaki, M.; Shin, J.; Dede, E.M. A Novel Soft Switching Bidirectional DC DC Converter Using Magnetic and Capacitive Hybrid Power Transfer. IEEE Trans. Power Electron. 2017, 32, 6961–6970. [Google Scholar] [CrossRef]
- Chen, Y.T.; Lu, Z.X.; Liang, R.H. Analysis and Design of a Novel High-Step-Up DC DC Converter With Coupled Inductors. IEEE Trans. Power Electron. 2018, 33, 425–436. [Google Scholar] [CrossRef]
- Du, S.; Wu, B.; Tian, K.; Xu, D.; Zargari, N.R. A Novel Medium-Voltage Modular Multilevel DC DC Converter. IEEE Trans. Ind. Electron. 2016, 63, 7939–7949. [Google Scholar] [CrossRef]
- Ahrabi, R.R.; Ardi, H.; Elmi, M.; Ajami, A. A Novel Step-Up Multiinput DC DC Converter for Hybrid Electric Vehicles Application. IEEE Trans. Power Electron. 2017, 32, 3549–3561. [Google Scholar] [CrossRef]
- Jou, H.L.; Huang, J.J.; Wu, J.C.; Wu, K.D. Novel Isolated Multilevel DC DC Power Converter. IEEE Trans. Power Electron. 2016, 31, 2690–2694. [Google Scholar] [CrossRef]
- Prasanna, U.R.; Singh, A.K.; Rajashekara, K. Novel Bidirectional Single-phase Single-Stage Isolated AC DC Converter With PFC for Charging of Electric Vehicles. IEEE Trans. Transp. Electrif. 2017, 3, 536–544. [Google Scholar] [CrossRef]
- Meeker, D.C. Finite Element Method Magnetics, Version 4.2. Finite Element Method Magnetics. Available online: http://www.femm.info/wiki/HomePage (accessed on 27 February 2019).
- Sadiku, M.N. Numerical Techniques in Electromagnetics with MATLAB; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Kraus, J.D. Electromagnetics; McGraw-Hill Companies: New York, NY, USA, 1992. [Google Scholar]
- Nagel, J.R. Numerical Solutions to Poisson Equations Using the Finite-Difference Method [Education Column]. IEEE Antennas Propag. Mag. 2014, 56, 209–224. [Google Scholar] [CrossRef]

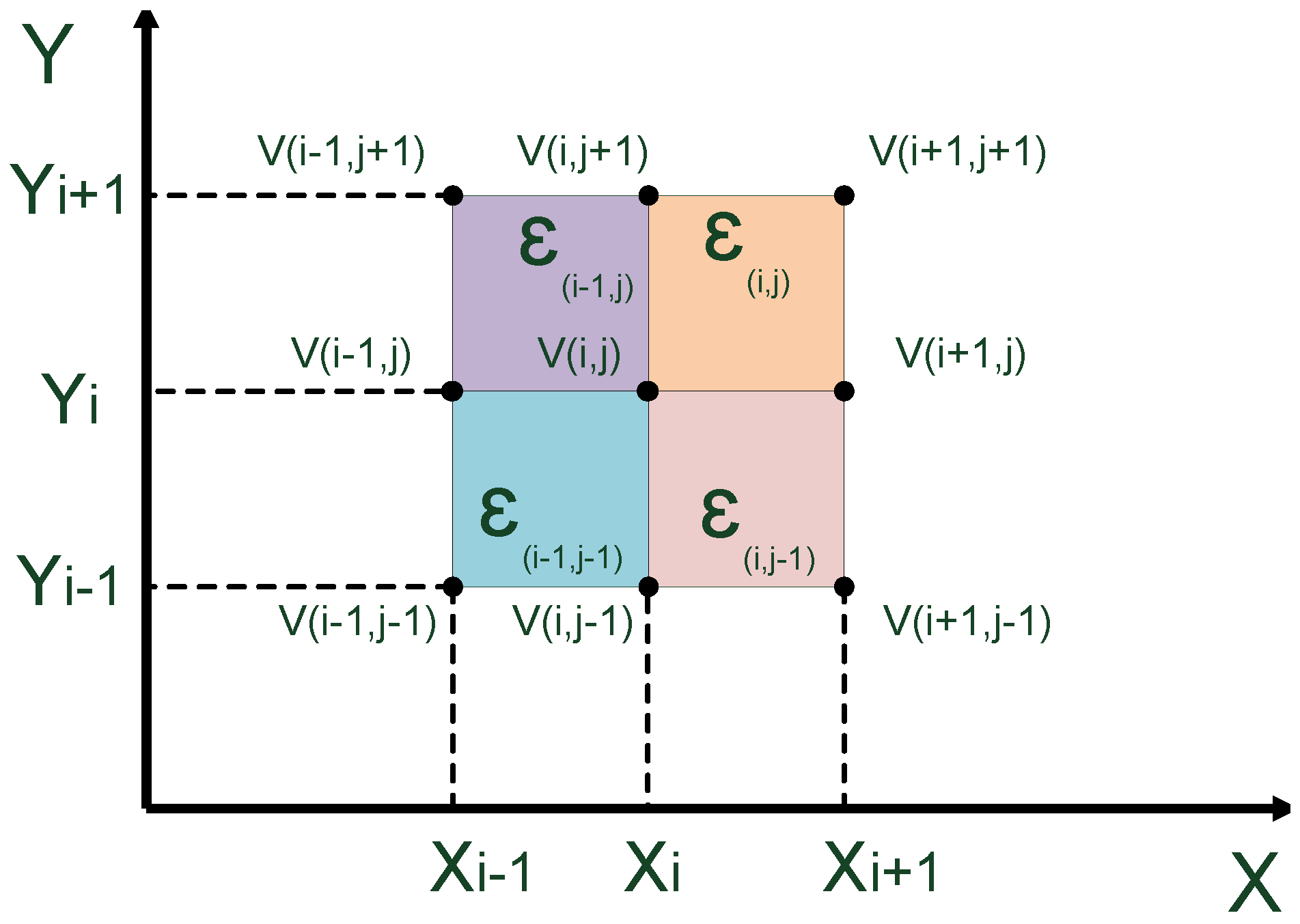
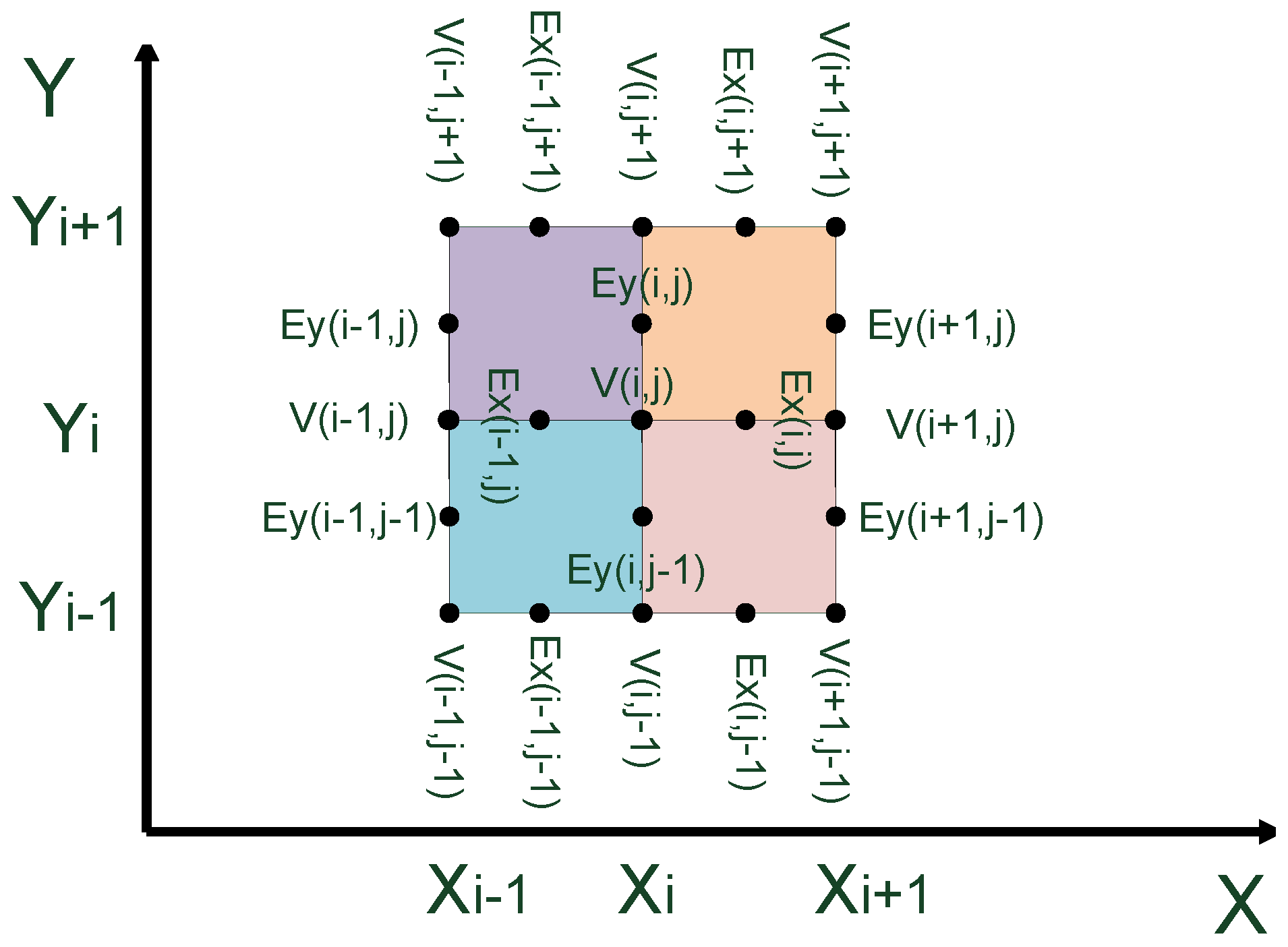
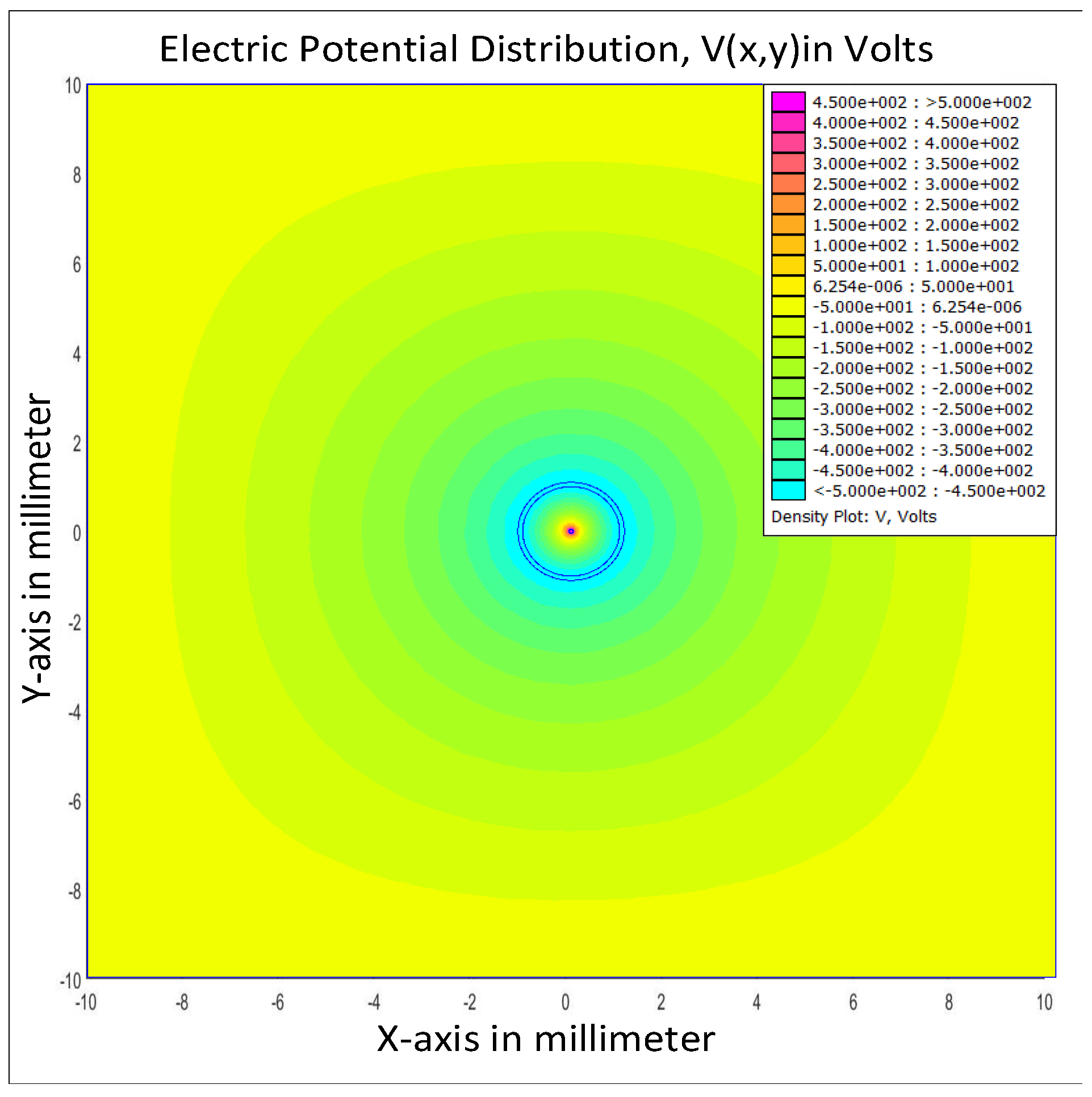
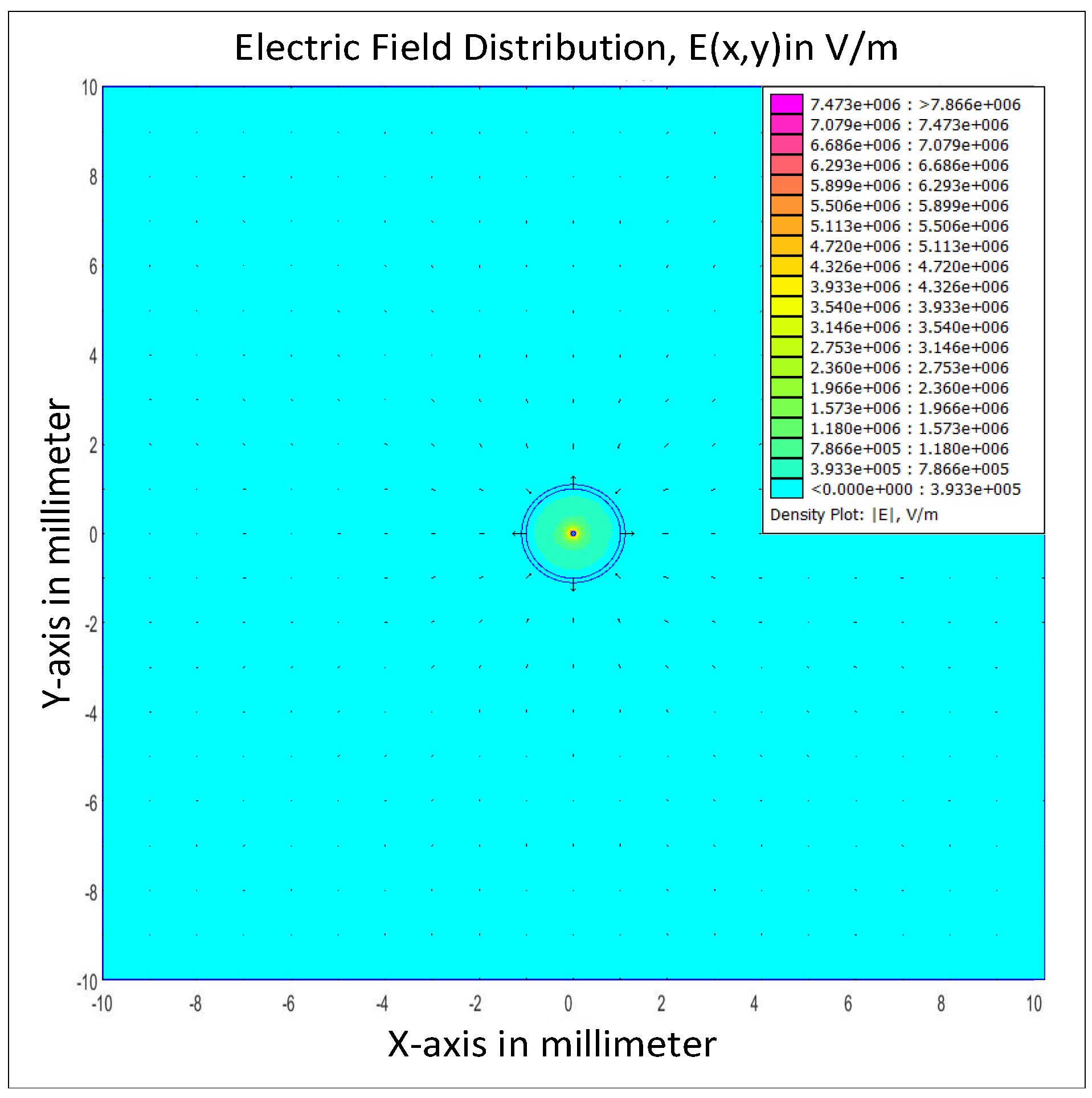
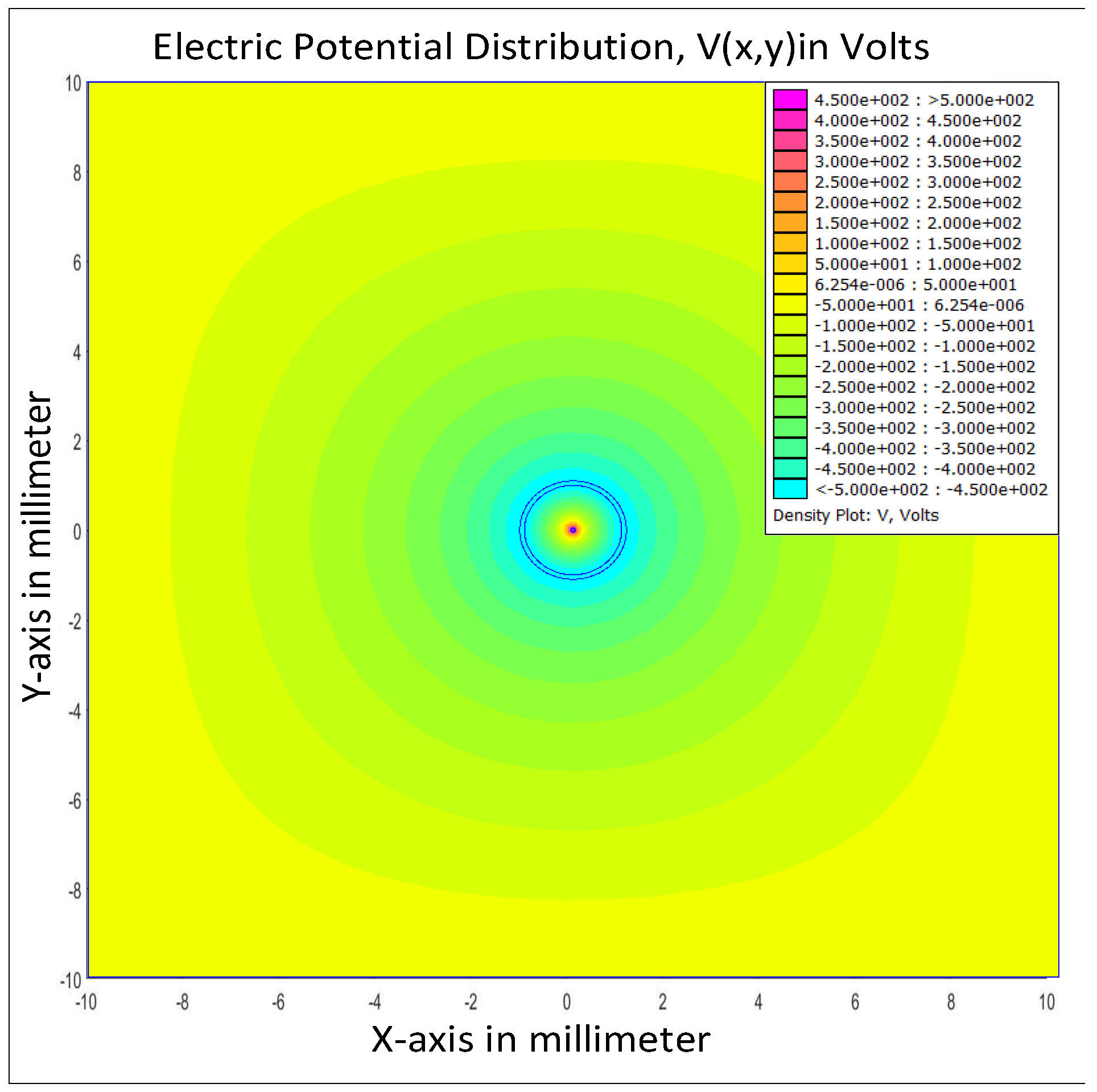

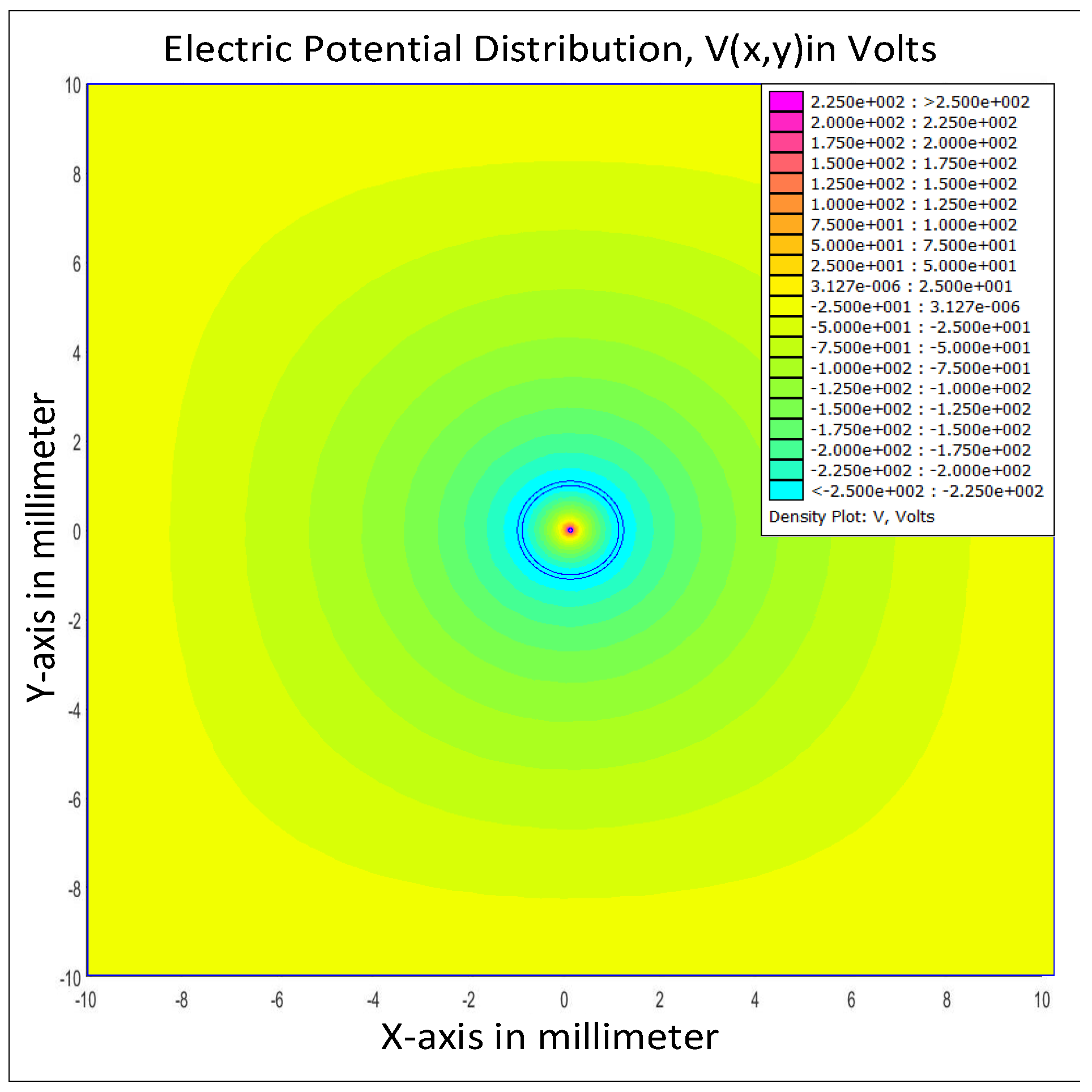
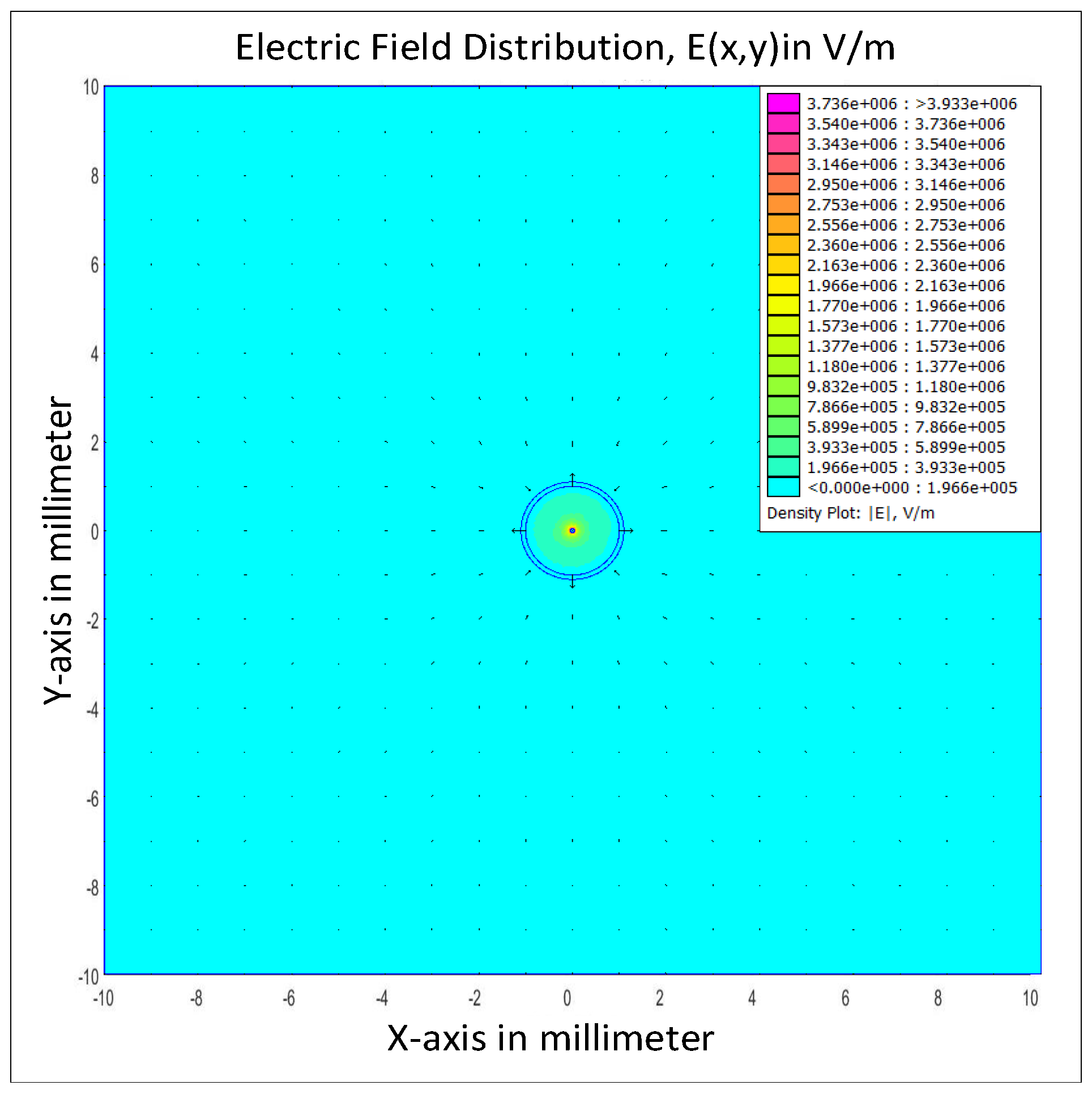
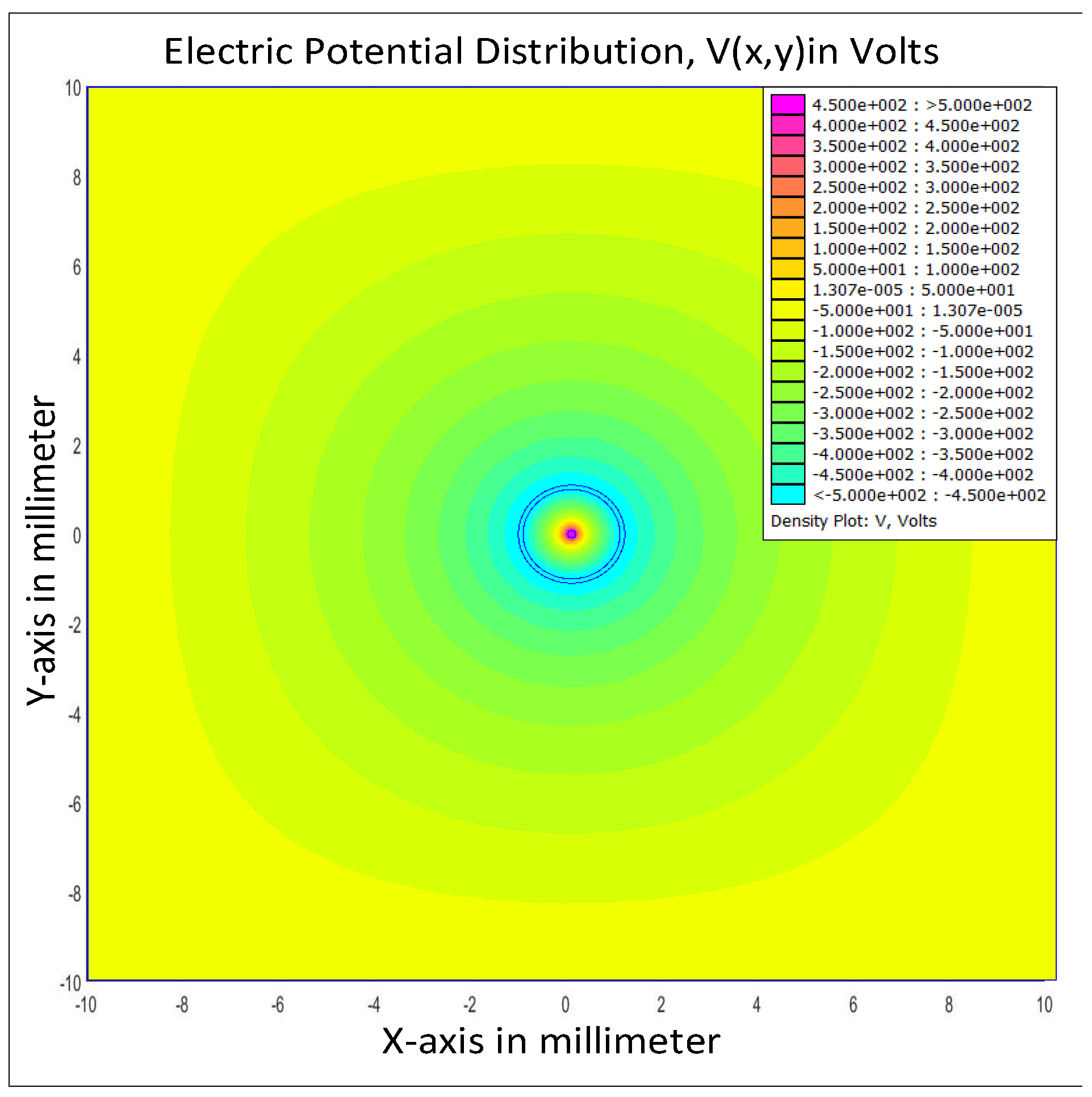

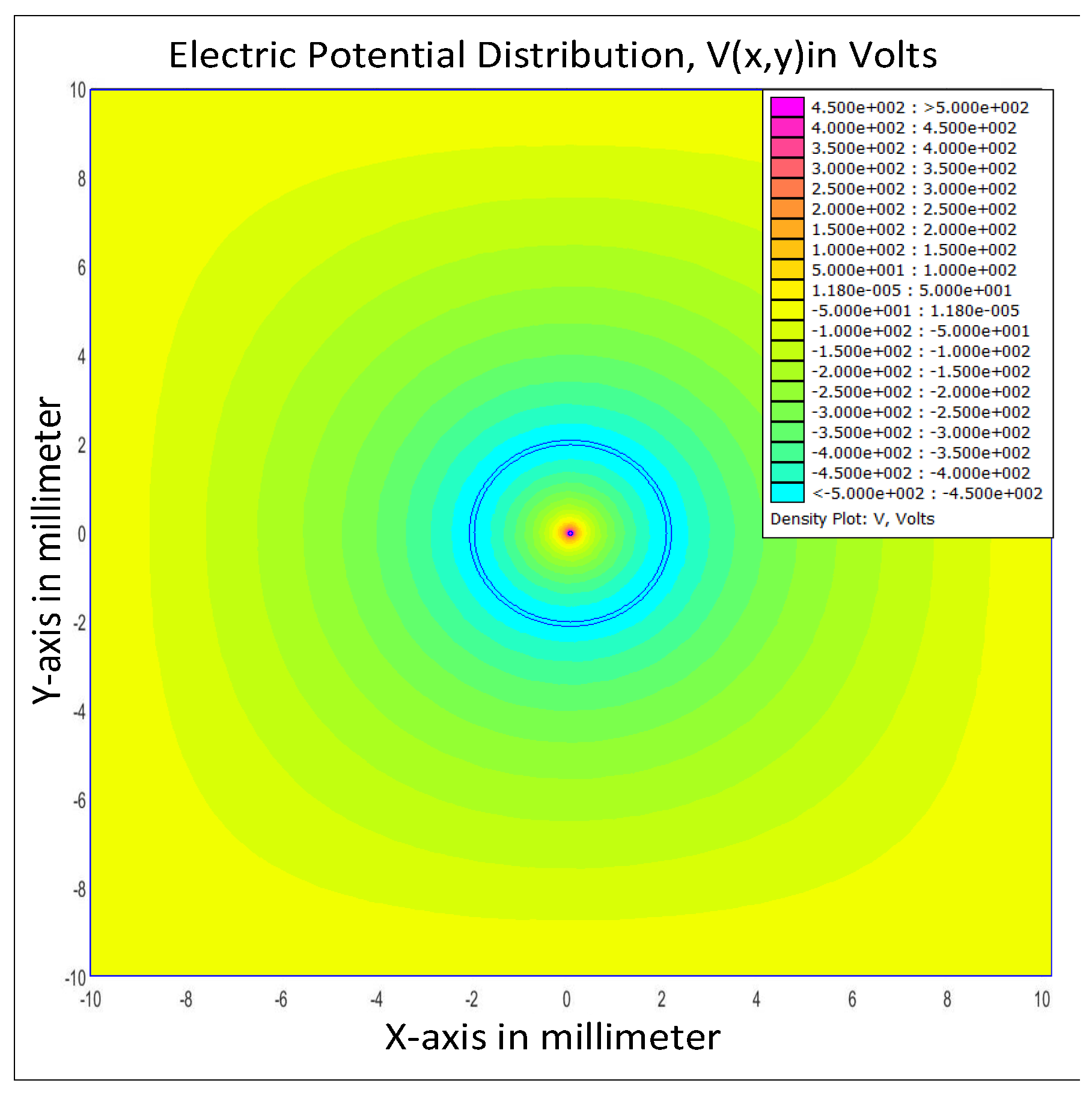
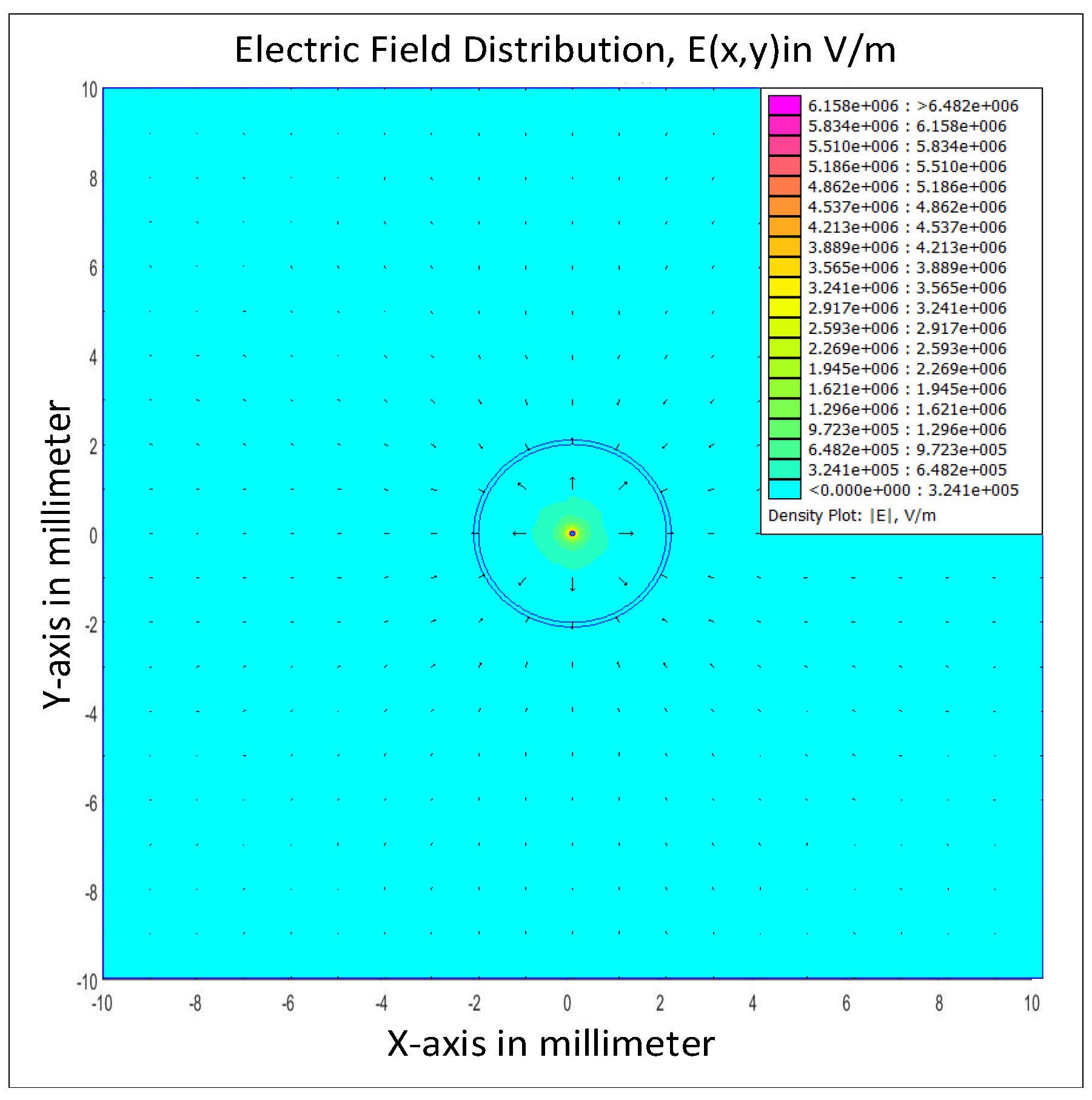

| Dimension of the Simulated Volume | ||||
| X (mm) | Y (mm) | Z (mm) | ||
| 20 | 20 | 100 | ||
| Device Parameters | ||||
| (mm) | (mm) | (mm) | (Volt) | |
| 0.04 | 1 | 1.1 | 1 | 1000 |
| Case 0 | Case I | Case II | Case III | Case IV | Case V | |
|---|---|---|---|---|---|---|
| (Volt) | 500 | 500 | 250 | 500 | 500 | 500 |
| (Volt) | −500 | −500 | −250 | −500 | −500 | −500 |
| 1 | 10 | 1 | 1 | 1 | 1 | |
| (μm) | 40 | 40 | 40 | 80 | 40 | 40 |
| (mm) | 1 | 1 | 1 | 1 | 2 | 1 |
| (mm) | 1.1 | 1.1 | 1.1 | 1.1 | 2.1 | 1.2 |
| (Coulombs) | 1.74644 × | 1.73631 × | 8.7322 × | 2.19035 × | 1.3409 × | 1.77257 × |
| (Coulombs) | −3.22398 × | −1.88247 × | −1.61199 × | −3.66845 × | −3.4159 × | −3.13439 × |
| (Coulombs) | −1.47754 × | −1.4616 × | −7.3877 × | −1.4781 × | −2.075 × | −1.36182 × |
| Energy Stored (J) | 1.17827 × | 9.03654 × | 2.94569 × | 1.41549 × | 1.14532 × | 1.19127 × |
| When = − | ||||||
| Energy Stored (J) | 6.25078 × | 8.63198 × | 2.18325 × | 1.0802 × | 6.2438 × | 8.98687× |
| Efficiency | 46.950% | 4.48% | 25.88% | 23.69% | 45.48% | 24.56% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, H.; Khalid, M.; Abido, M. A Novel Design of Static Electrostatic Generator for High Voltage Low Power Applications Based on Electric Field Manipulation by Area Geometric Difference. Energies 2019, 12, 802. https://doi.org/10.3390/en12050802
Alharbi H, Khalid M, Abido M. A Novel Design of Static Electrostatic Generator for High Voltage Low Power Applications Based on Electric Field Manipulation by Area Geometric Difference. Energies. 2019; 12(5):802. https://doi.org/10.3390/en12050802
Chicago/Turabian StyleAlharbi, Hosam, Muhammad Khalid, and Mohammad Abido. 2019. "A Novel Design of Static Electrostatic Generator for High Voltage Low Power Applications Based on Electric Field Manipulation by Area Geometric Difference" Energies 12, no. 5: 802. https://doi.org/10.3390/en12050802





