Discrete and Continuous Model of Three-Phase Linear Induction Motors “LIMs” Considering Attraction Force
Abstract
:1. Introduction
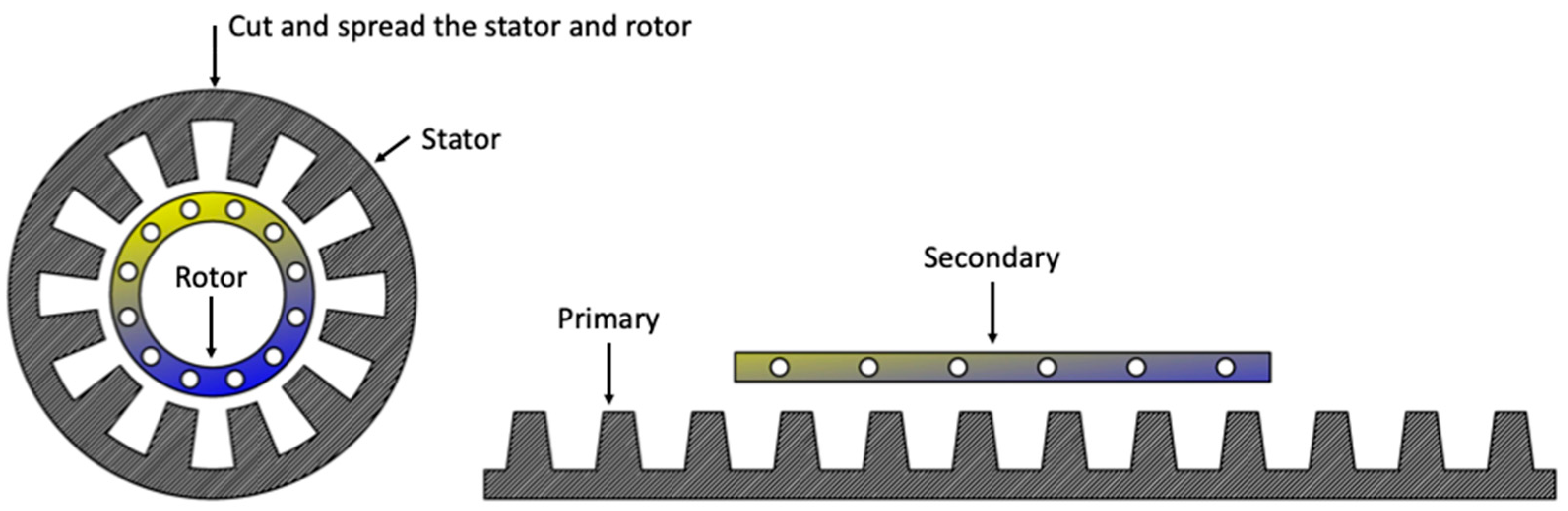
2. Construction Aspects of Linear Induction Motors (LIMs)
3. LIM Model Without End Effects and Considering Attraction Force
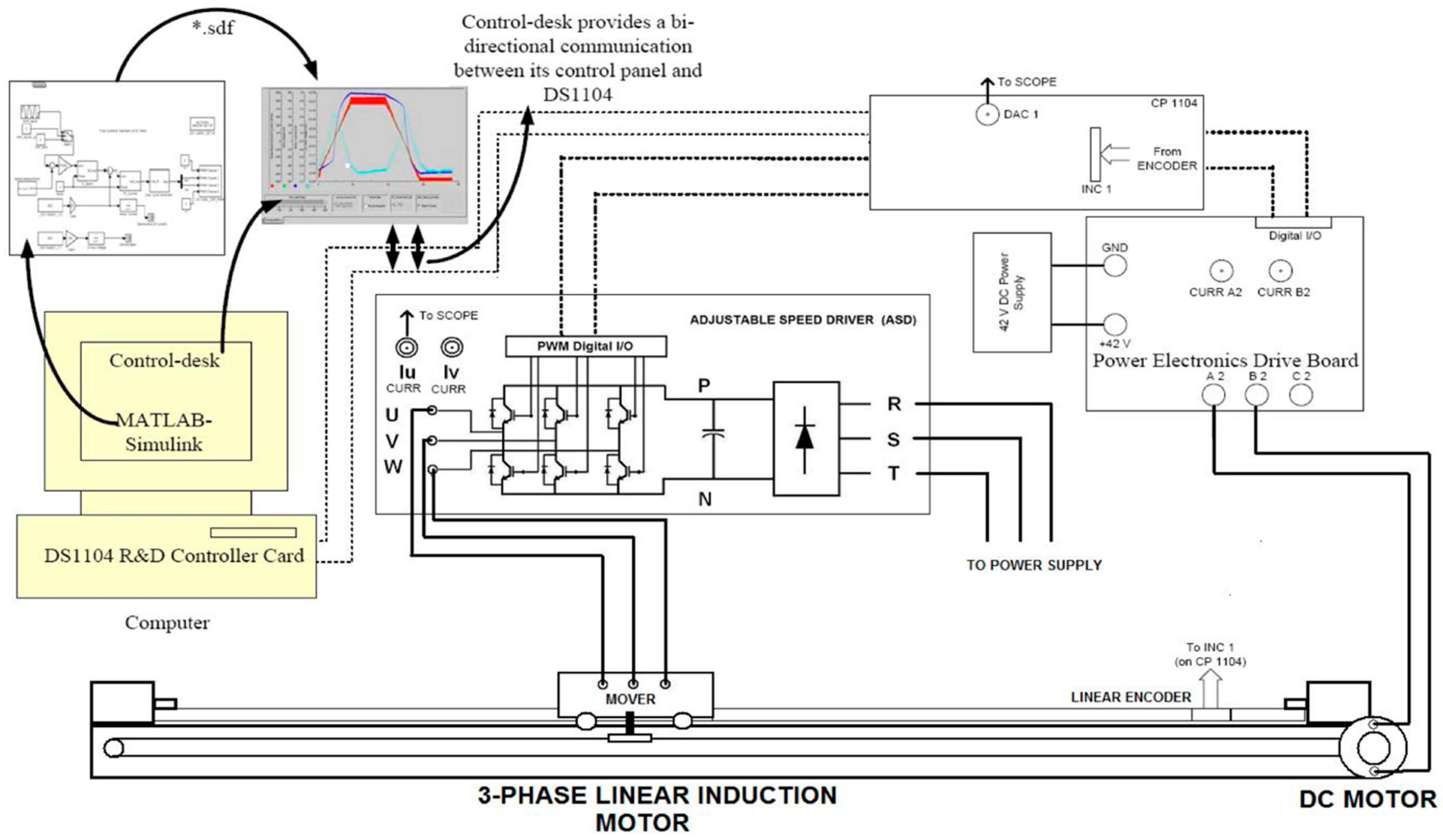
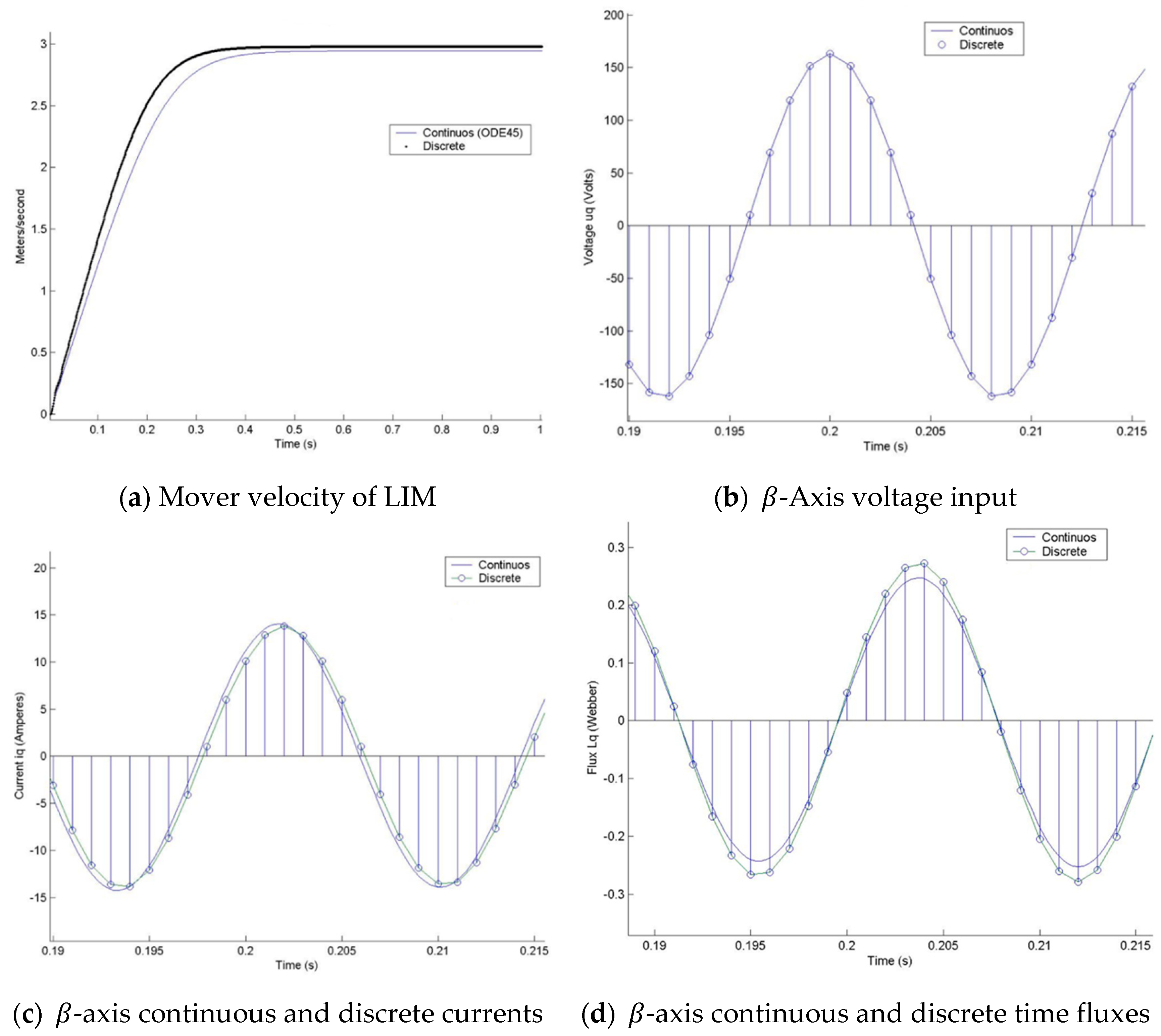
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boldea, I.; Nasar, S.A. Linear Motion Electromagnetic Devices; Taylor & Francis: New York, NY, USA, 5 November 2001. [Google Scholar]
- Boldea, I.; Nasar, S.A. Linear electric actuators and generators. IEEE Trans. Energy Convers. 1999, 14, 712–717. [Google Scholar] [CrossRef]
- Nasar, S.A.; Boldea, I. Linear Electric Motors: Theory, Design and Practical Applications; Prentice Hall Trade: Englewood Cliffs, NJ, USA, February 1987. [Google Scholar]
- Nasar, S.A.; Boldea, I. Linear Motion Electric Machines; John Wiley & Sons Inc.: New York, NY, USA, August 1976. [Google Scholar]
- Boldea, I.; Nasar, S.A. Linear Electric Actuators and Generators; Cambridge University Press: New York, NY, USA, 26 September 2005. [Google Scholar]
- Kang, G.; Nam, K. Field-oriented control scheme for linear induction motor with the end effect. IEE Proc. Electr. Power Appl. 2005, 152, 1565–1572. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K.; Shi, L. On-line parameter identification of linear induction motor based on adaptive observer. In Proceedings of the 2007 International Conference on Electrical Machines and Systems (ICEMS), Seoul, Korea, 8–11 October 2007; pp. 1606–1609. [Google Scholar]
- Xu, W.; Zhu, J.; Guo, Y.; Wang, Y. Equivalent circuits for single-sided linear induction motors. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 1288–1295. [Google Scholar]
- Du, Y.; Jin, N. Research on characteristics of single-sided linear induction motors for urban transit. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009; pp. 1–4. [Google Scholar]
- Faiz, J.; Jagari, H. Accurate modeling of single-sided linear induction motor considers end effect and equivalent thickness. IEEE Trans. Magn. 2000, 36, 3785–3790. [Google Scholar] [CrossRef]
- Blaschke, F. The principle of field orientation applied to the new transvector closed-loop control system for rotating field machines. Siemens Rev. 1971, 39, 217–220. [Google Scholar]
- Marino, R.; Tomei, P. Nonlinear Control Design; Prentice Hall: New York, NY, USA, 1995. [Google Scholar]
- Tan, H.; Chang, J. Adaptive backstepping control of induction motor with uncertainties. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999. [Google Scholar]
- Loukianov, G.A.; Cañedo, J.M.; Serrano, O.; Utkin, I.V.; Celikovsky, S. Adaptive Sliding Mode Block Control of Induction Motors; Mc Graw Hill: New York, NY, USA, 1999. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J. Sliding Mode Control in Electromechanical Systems; Taylor and Francis: London, UK; Philadelphia, PA, USA, 1999. [Google Scholar]
- Dodds, S.J.; Utkin, V.A.; Vittek, J. Self Oscillating, Synchronous Motor Drive Control System with Prescribed Closed-Loop Speed Dynamics. In Proceedings of the 2nd EPE Chapter Symposium on ‘Electric Drive Design and Applications’, Nancy, France, 4–6 June 1996; pp. 23–28. [Google Scholar]
- Wai, R.J.; Liu, W.K. Nonlinear decoupled control for linear induction motor servo-drive using the sliding-mode technique. IEEE Proc. Control Theory Appl. 2001, 148, 217–231. [Google Scholar] [CrossRef]
- Wai, R.J.; Liu, W.K. Non linear control for linear induction motor servo drive. IEEE Trans. Ind. Electron. 2013, 50, 920–935. [Google Scholar]
- Liu, J.; Lin, F.; Yang, Z.; Zheng, T.Q. Field oriented control of linear induction motor considering attraction force and end-effects. In Proceedings of the International Power Electronics and Motion Control Conference IPEMC 2006, Shanghai, China, 14–16 August 2006. [Google Scholar]
- Ortega, R.; Taoutaou, D. A globally stable discrete-time controller for current-fed induction motors. Syst. Control Lett. 1996, 28, 123–128. [Google Scholar] [CrossRef]
- Loukianov, A.G.; Rivera, J.; Cañedo, J.M. Discrete-time sliding mode control of an induction motor. In Proceedings of the 15th World Congress of IFAC, Barcelona, Spain, 21–26 July 2002; Volume 1, pp. 106–111. [Google Scholar]
- Fernandes, E.; dos Santos, C.C.; Lima, J.W. Field oriented control of linear induction motor taking into account end-effects. In Proceedings of the AMC 2004, Kawasaki, Japan, 25 March 2004; pp. 689–694. [Google Scholar]
- Fernandes, E.; dos Santos, E.B.; Machado, P.C.M.; de Oliveira, M.A.A. Dynamic model for linear induction motors. In Proceedings of the ICIT 2003, Maribor, Slovenia, 10–12 December 2003; pp. 478–482. [Google Scholar]
- Benitez, V.H.; Loukianov, A.G.; Sanchez, E.N. Identification and control of a linear induction motor using an α − β model. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Toro, N.; Garcés, Y.A.; Hoyos, F.E.; Sanchez, E.N. Parameter Estimation of Linear Induction Motor LabVolt 8228-02. In Proceedings of the Congreso Anual Asociación de Mexico de Control Automático, Saltillo, Mexican, 5–7 December 2011. [Google Scholar]
- Morfin, O.A.; Castañeda, C.E.; Valderrabano-Gonzalez, A.; Hernandez-Gonzalez, M.; Valenzuela, F.A. A Real-Time SOSM Super-Twisting Technique for a Compound DC Motor Velocity Controller. Energies 2017, 10, 1286. [Google Scholar] [CrossRef]
- Hoyos Velasco, F.E.; Candelo-Becerra, J.E.; Rincón Santamaría, A. Dynamic Analysis of a Permanent Magnet DC Motor Using a Buck Converter Controlled by ZAD-FPIC. Energies 2018, 11, 3388. [Google Scholar] [CrossRef]
- Hernández-Márquez, E.; Avila-Rea, C.A.; García-Sánchez, J.R.; Silva-Ortigoza, R.; Silva-Ortigoza, G.; Taud, H.; Marcelino-Aranda, M. Robust Tracking Controller for a DC/DC Buck-Boost Converter–Inverter–DC Motor System. Energies 2018, 11, 2500. [Google Scholar] [CrossRef]
- Lipo, T.A.; Nondahl, T.A. Pole-by-pole d-q model of a linear induction machine. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 629–642. [Google Scholar] [CrossRef]
- Boldea, I.; Nasar, S.A. The Induction Machine Handbook; Electric Power Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Benitez, V.H.; Sanchez, E.N.; Loukianov, A.G. Neural identification and control for linear induction motors. J. Intell. Fuzzy Syst. 2005, 16, 33–55. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toro-García, N.; Garcés-Gómez, Y.A.; Hoyos, F.E. Discrete and Continuous Model of Three-Phase Linear Induction Motors “LIMs” Considering Attraction Force. Energies 2019, 12, 655. https://doi.org/10.3390/en12040655
Toro-García N, Garcés-Gómez YA, Hoyos FE. Discrete and Continuous Model of Three-Phase Linear Induction Motors “LIMs” Considering Attraction Force. Energies. 2019; 12(4):655. https://doi.org/10.3390/en12040655
Chicago/Turabian StyleToro-García, Nicolás, Yeison A. Garcés-Gómez, and Fredy E. Hoyos. 2019. "Discrete and Continuous Model of Three-Phase Linear Induction Motors “LIMs” Considering Attraction Force" Energies 12, no. 4: 655. https://doi.org/10.3390/en12040655





