Preliminary Design for Wave Run-Up in Offshore Wind Farms: Comparison between Theoretical Models and Physical Model Tests

Abstract

Estimation of wave run-up has been of increasing concern for offshore wind structures and a critical aspect for designers. The highly nonlinear phenomenon makes the study difficult. That is the reason for the very few design rules and experimental data available to estimate it. Actual wave run-up is greater than commonly predicted. The goal of this research is to benchmark the theoretical formulations with the results of the physical model tests performed by Deltares in the field of crest elevation, run-up, forces and pressures. The laboratory reproduced in a wave tank (75 m length; 8.7 m width; 1 m depth; and a 1:60 scale, with Froude similarity) an offshore power converter platform located at intermediate water depths (25–43.80 m) in the Southern North Sea, designed by the Norwegian company Aibel. The purpose of this research is to offer a preliminary design guide for wave run–up using theoretical expressions both for cylinders and gravity based structures (GBS), leaning on the cited laboratory tests to validate the results obtained by such theoretical models.

1. Introduction

Offshore wind energy production has risen at a dramatic rate in the last decades. Nowadays, it supplies 1.5% (43 TWh) of the energy consumed in the European Union per year [1]. A huge progress has been made in the size of the turbines and water depths in which they are being constructed. There are already wind turbines with a capacity of 8 MW available for offshore use and great efforts in research and development are being made to reach a real capacity in the range of 10 to 12 MW [1].

Only in 2017 more than 3000 MW were installed worldwide, whereas in 2001 the total installed power was 75 MW [2,3,4]. Those figures show the undeniable present and promising future of this field. The offshore wind turbine sector will for sure continue to grow.

The barrier of 25,000 TWh of world electricity production was exceeded for the first time in 2017 [5]. Europe reached 15,780 MW at the end of 2017.

To make this huge progress, foundations have had a starring role. Although the last decade reflects a marked tendency towards mono-piled structures (with 82% of the 4555 existing foundations in 2017), there are also other typologies that have to be considered, like the gravity based structures (GBS), which reach a share of 6% [1]. Others, like tripods, jackets, tri-piles and so forth, are also important in deeper waters. These direct foundations can be observed in Figure 1. Furthermore, there are also indirect foundations, like floating systems, semi submerged moored structures or neutral buoyancy ones. They are more common in very deep waters.

Monopiles are probably the solution that will be applied in the future in deep water conditions and sand seabed, combined with indirect systems as the aforementioned ones. But since they present real problems associated with different order scour effects (mainly first order one but also second and zero order scour [6]) and they are very expensive and also not many countries have the facilities to build, transport and install them, GBS seem to be a very interesting solution for providing green energy in flat soils located at intermediate water depths. These GBS foundations do not suffer really much from scouring but they do from run-up, wave slamming and wave impacts.

Therefore, the purpose of the research here presented is to propose the application of well-known traditional formulations in order to give a preliminary design for the crown elevation level of such structures. For such purpose, this paper presents a clear and easy guide to predict wave run up on wind farms foundations. The designers should apply the different formulations offered here in order to have a first pre-dimensioning. Once in further stages of the design, more complex models and calculations have to be added to the process, as well as international rules and recommendations have also to be taken into consideration [7,8,9,10]. But, in the very beginning of such design process, the formulations provided here can be very useful for a preliminary design [11,12], in order to avoid problems like the ones showed in Figure 2.

Run-up is clearly a nonlinear effect. The crest elevation increases with the steepness of the approaching waves. Depending on the shape and size of the foundation, the maximum level of such run-up varies from the values offered using the linear diffraction theory of MacCamy and Fuchs [13], to 1.60 (or even 2.50) times (for a monochromatic wave [14,15]). Using the potential flow theory this value would be even bigger, up to 2.60 [14,16] or even six times the far field amplitude of freak waves [14,17]. These coefficients show the great magnitude of the phenomenon.

To describe the crest elevation and the run–up level reached after a violent wave impact against a structure, different formulations have been used here. This is the case of Hiroi (1919) [18], Sainflou (1928) [19], Goda (1974 and 1985) [20,21] or Suh et al. [22]. Hiroi recommended taking 0.90 times the water depth as design wave height. This formula was apparently intended for calculating the pressure caused by breaking waves. A pressure formula for standing waves was introduced by Sainflou in 1928, commonly used for non-breaking waves. The main problem with these two expressions was the ambiguity of which wave height should be used (either H_s or H_b). Goda explained the complexity of the sea states and the use of H_1/3, H_1/10 or H_max for the different wave pressures formulations. He assumed the existence of a trapezoidal pressure distribution along the vertical wall where the waves are breaking or non-breaking ones. Other theoretical models have also been used, such Hallermeier (1976), Niedzwecki and Dugal (1992), Mase et al. (2001) or De Vos et al. (2007) [23]. All these theoretical formulations have been divided into two groups: the ones commonly used for cylinders and those for gravity structures (see Section 3.2). This separation has been accomplished here since a structure not slender enough to be clearly considered as a monopile can respond to a behaviour more commonly associated to a GBS [24,25].

Once the theoretical formulations are explained, as well as the particular application of each one of them, the results obtained using them is compared with the ones given by Deltares [26], in order to calibrate the goodness and approximation of each of them to the real effect of run-up. For this comparison, the cited difficulties when defining the wave height have been taken into account, as well as the differences between the calculation methods and also the consideration of the elevation in which the wave pressure is exerted, as well as the pressure and forces occurring in front of the structure. The Ring Pontoon tested by Deltares has been used throughout the manuscript to obtain the values of run-up, as a practical example of the application of each formula, making it easier to understand them.

Such physical model tests try to resolve the wave impact loads and slamming pressures at the Ring Pontoon Platform (900 MW), an offshore power converter structure developed by Aibel for water depths in the range of 20 to 40 m in the Southern North Sea. All model tests were performed in the Atlantic Basin by Deltares, The Netherlands. The objective of such model tests was to obtain the crest elevation of the water impacting the structures and the forces and pressures acting in the different columns.

Considering all the aforementioned, the main aim of this work is to help the designers to choose which should be the optimum level to install the topside of the structure at preliminary stages of the design process. This can help to avoid undesired hydrodynamic effects during the useful life of the facility, such slamming effects, violent run-up or flooding of the decks, like the ones occurring for example in Horns Rev.

2. Methodology

To develop the investigation herein presented, the theoretical formulations introduced before have been studied. The result obtained using each one of them is presented in this manuscript. The outliers have been detected and discussed the consideration (or not) of them. The site used to obtain the climate conditions and hydrodynamic behaviour is the Ring Pontoon [26]. This way, the data obtained by Deltares can be used to calibrate the figures given by such theoretical formulations.

After using all the expressions considered here, their goodness is studied and discussed. Finally, some conclusions and recommendations are showed in this paper.

The following particular steps have been taken:

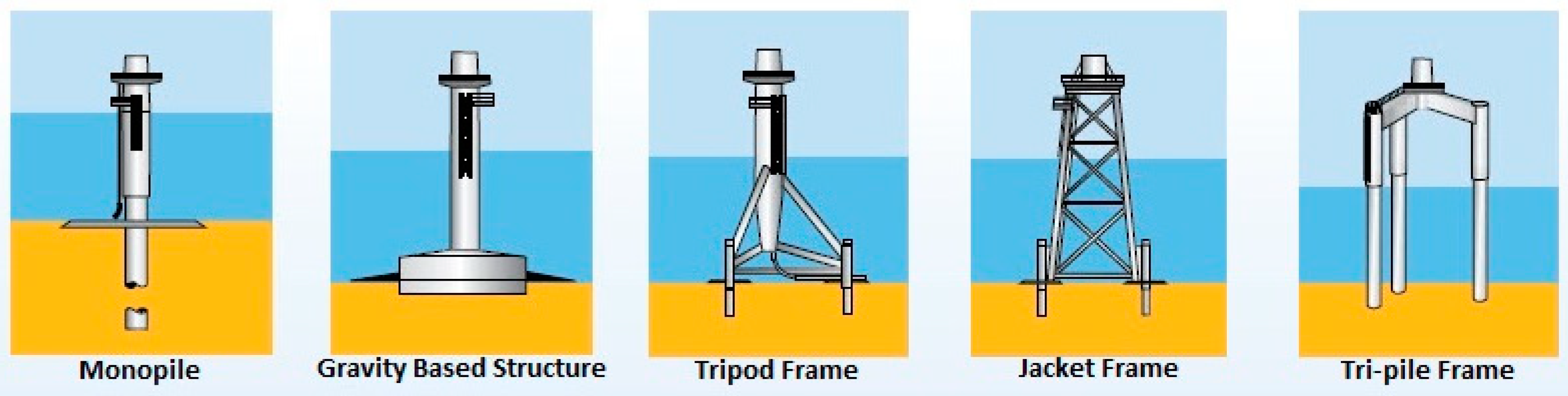
• Climate and hydrodynamic characterization at the location that will hold the platform.
• Identification of the theoretical and empirical formulations describing wave run-up in cylinders. For instance, Hallermeier (for regular waves), Niedzwecki and Huston (for regular and random waves), Mase et al.; and the experimental results for monopile and cone foundations, described by De Vos et al. [23].
• Identification of the theoretical and empirical formulations describing wave run-up for gravity based structures: Hiroi [18], Goda [20], Sainflou [19], Suh et al. [22] and Goda’s overtopping nomograms [21].
• Review and description of the physical model tests concerning wave-structure interaction under regular and irregular waves and for different wave directions.
• Analysis of the results obtained by the physical model tests.
• Comparison and discussion of the results provided by the theoretical formulations versus the water levels measured on the different 3-D tests of the Ring Pontoon Platform; and finally, the conclusions of the comparison are showed.

These aforementioned steps will be developed in the following sections of this manuscript.

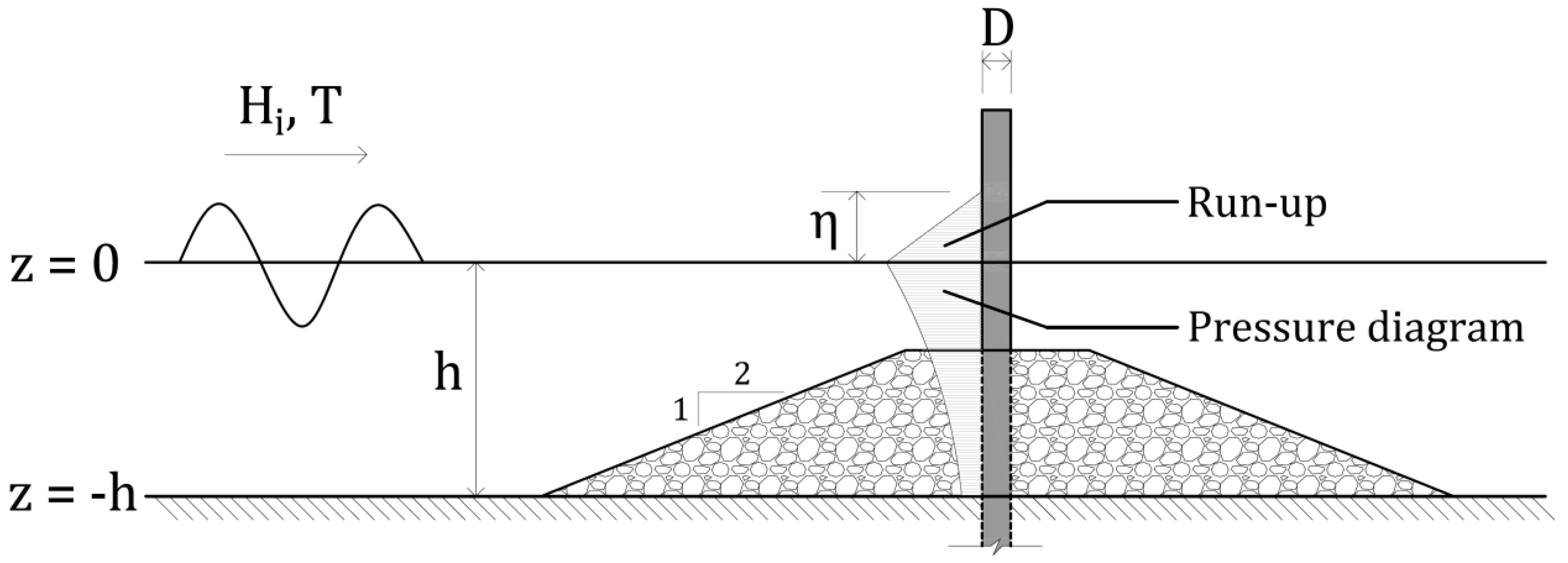
3. Theoretical and Physical Model Tests

3.1. Wave Climate and Hydrodynamic Characterization

In order to characterize the wave climate, the North Sea records from an instrumental network have been used. For the extreme condition of a 100-year return period considered in the model tests, the probability of failure results around 0.20 (for a minimum life span of 20 years) [27,28,29]. This can be seen in Equation (1):

$$T_r=\frac{-n}{\ln (1-P_f)}\to 100 years=\frac{-20 years}{\ln (1-P_f)} ; P_f\simeq 0.2$$

(1)

Directional return periods could be considered [30] but they are not used here because climatic data are not available.

Input data were collected following the undulatory mechanics criteria, proposing the conditions exposed in

Table 1. Southern North Sea study area characterization for a design return period of 100 years. Source: Own elaboration, from [26].

Relative Depth	h (m)	Hs (m)	Tp (s)	L0 (m)	L (m)	h/L (-)	Tr (yr)	Wave Regime
1/25 < h/L < 1/2	25.00	8.80	11.5	206.48	157.20	0.16	100	Intermediate
1/25 < h/L < 1/2	43.80	10.80	12.0	224.64	198.40	0.22	100	Intermediate

:

When the maximum wave height (H_max) has been measured, such value is the one that should be used when required. However, sometimes H_max is unknown. In these cases, it may be expressed as a function of the significant wave height (H_s) and the number of active waves in a storm (N), according to Longuet-Higgins [29]:

$$H_{max, N}=\frac{H_s}{\sqrt{2}}\left(\sqrt{\ln N}+\frac{0.2886}{\sqrt{\ln N}}\right)$$

(2)

When the number of active waves is unknown, it is usual to approximate the aforementioned value of H_max by H_1/250, as proposed by Goda [20], being H_1/250 = 1.80·H_1/3. This simplification can predict values for H_max under the ones really occurring but it is very useful when data is not available. Note that H_s<>H_1/3.

It seems to be feasible the breaking of the maximum wave heights either by bottom effects (when H/h>0.78) or by a high steepness value (when H/L > 1/7). However, in this research, only non-breaking waves are studied. This is because waves present low steepness values (see Table 1). This is also because the platform is intended to be located in intermediate water depths, where although waves can be affected by bottom effects, they do not usually break due to such effects, since they present low values for the H/h relation (see Table 1). Therefore, H_max is the one considered, not H_b. However, extreme and freak waves do commonly break in these site conditions (and even in deeper waters), when both their potential and kinematic energy components reach high values. But in this research, following the common practice, run-up has been calculated using a deterministic approach of the real phenomenon. This is why only non-breaking waves have been studied here. Measured maximum wave heights considered at depths of 25.0 and 43.8 m have taken values, respectively, of 20.7 and 24.9 m [26]. However, we use here Goda criterion for H_max, since we are making a theoretical approach of the problem, as stated above (limitations of it are discussed later on).

Regarding the hydrodynamics at the location, considering that wind waves are classified as gravity waves (with an undulatory period between 1 and 30 s, the wind as generating force and gravity as restorer one) [31,32], comparing prototype and model, g_p = g_m. Therefore, Fr_p = Fr_m, presenting the following expression for the Froude number [24,25]:

$$Fr=\frac{v}{\sqrt{gD}}$$

(3)

$$F{r}_p=F{r}_m\to \frac{v_p}{\sqrt{g{D}_p}}=\frac{v_m}{\sqrt{g{D}_m}}$$

(4)

The Keulegan-Carpenter number [33] express the relation between the maximum kinematic velocity and the undulatory period, divided by the nominal diameter of the structure considered, as follows:

$$KC=\frac{u·T}{D}$$

(5)

This parameter governs the hydrodynamic domain in which the structure is working. It is also important regarding the scouring effects in front of such structure, allowing having a brief estimation on how deep and wide the scouring holes will be once the facility is under operation.

3.2. Theoretical Models

3.2.1. Theoretical Models for Cylinders

The approximate results of maximum wave run up on a single cylinder according to linear diffraction theory were proposed by MacCamy and Fuchs [13]. The expression is as follows:

$$\frac{R}{{\mathsf{\eta }}_{max}}={\left[1+4{(kD)}^2\right]}^{1/2}$$

(6)

This linear diffraction method underestimates the run-up level. Kriebel [14] proposed a second order expression, which is not used here since it is not good enough either for steep waves.

Some authors have proposed formulations based on the fact that the run-up is given as a sum of potential and kinetic energy. Each author considers different importance to both energy components.

Hallermeier suggests an estimate for run-up by considering the head and the wave crest in front of the cylinder. According to this, the run-up is predicted to be:

$$R_u={\mathsf{\eta }}_{max}+\frac{u^2}{2g}$$

(7)

Niedzwecki and Dugal found, using linear wave theory, that run-up reached values under the ones predicted by Halllermeier. They corrected such effect by considering the potential component “ƞ_max” as “0.5·H” and by multiplying the kinetic component by a coefficient “m.” Later on, Niedzwecki and Huston updated the former Niedzwecki and Dugal formula, by calibrating the value of “m” to 6.52 and increasing the potential coefficient from 0.5 to 0.56. It gives good results for a single cylinder. This last formula is the one proposed to be used here, since remains in the side of safety, compared to the results given by Hallermeier or by Niedzwecki and Dugal.

Mase et al. investigated run-up height on random waves against small cylinder circular piles. They arrived to the following formula for the 2% run-up (R_u2%):

$$\frac{R_{u2\%}}{d}=\left(0.24-\frac{0.004}{tan\beta }\right)+\left(11.43-\frac{0.20}{tan\beta }\right)$$

$$exp\left[-\left(1.55-0.77exp\left\{-69.46\left(\frac{H_0}{L_0}\right)\right\}\right)·\left(1.02-\frac{0.015}{tan\beta }\right)·\left(\frac{d}{H_0}\right)\right]$$

(8)

Since the bottom slope at an offshore location for a windfarm is often very flat (especially for a foundation such a GBS), the authors have not used the Mase et al. experimental study. Actually, this formula is recommended for the following conditions:

$$\frac{1}{40}\le tan\beta \le \frac{1}{10} \& 0.004<\frac{H_0}{L_0} \& \frac{d}{H_0}<6$$

(9)

De Vos et al. [23] recommended using the Mase et al. formulation only within the specified range.

De Vos et al. proposed an estimate for R_u2% on a monopile by using the former Hallermeier formulation, modified by multiplying the kinematic component of it by 2.71. For the specific case of a cone foundation, this value will increase from 2.71 to 4.45.

For this aforementioned De Vos formulation, H_2% and T_p are the variables that have to be used to calculate the wave kinematics. The value of H_2% can be obtained from H_s as follows:

$$H_{2\%}=1.40H_s$$

(10)

None of the De Vos formulations are used, since the Niedzwecki and Huston formula remains on the side of safety compared to them (as said before).

Apart from the aforementioned expressions, Zang et al. [34] concentrated their efforts in the study of the hydrodynamic loads in vertical cylinders. They developed several tests in a shallow waters tank in DHI (Horsholm, Denmark), with large series of incident groups of waves, studying breaking waves, the structural response for horizontal loads and the variations suffered in the way waves are breaking against the pile.

So, applying the MacCamy and Fuchs formulation [13] with the data extracted from the climate characterization epigraph (with a diameter of the piles of 17 m), the following result is obtained for the 25 m water depth:

$$\frac{R_u}{{\mathsf{\eta }}_{max}}=1.687$$

(11)

And for the 43.80 m water depth:

$$\frac{R_u}{{\mathsf{\eta }}_{max}}=1.469$$

(12)

Note that as ƞ has been calculated using linear wave theory, its maximum value responds to [31,32]:

$$\mathsf{\eta }=\frac{H}{2}cos\theta \to {\mathsf{\eta }}_{max}=\frac{H_{max}}{2}$$

(13)

Applying Niedzwecki and Huston formulation and considering the design conditions of H_s = 8.80 m, T_p = 11.5 s, H_max = H_1/250 =15.84 m and h = 25 m, the following value for the run-up is obtained:

$$L_0=\frac{g{T}^2}{2\pi }=206.48m$$

(14)

$$L=\frac{g{T}^2}{2\pi }th\left(\frac{2\pi h}{L}\right)=157.20m$$

(15)

$$u=\frac{\pi H}{T}·\frac{1}{th\left(\frac{2\pi h}{L}\right)}=5.68 m/s$$

(16)

$$R_u=0.56·15.84+6.52·\left(\frac{{5.68}^2}{2g}\right)=+19.59 m$$

(17)

Considering the design conditions related to a 43.8 m water depth, such value turns into 21.94 m.

Pressures and run-up schemes against a slender cylinder can be observed in Figure 3.

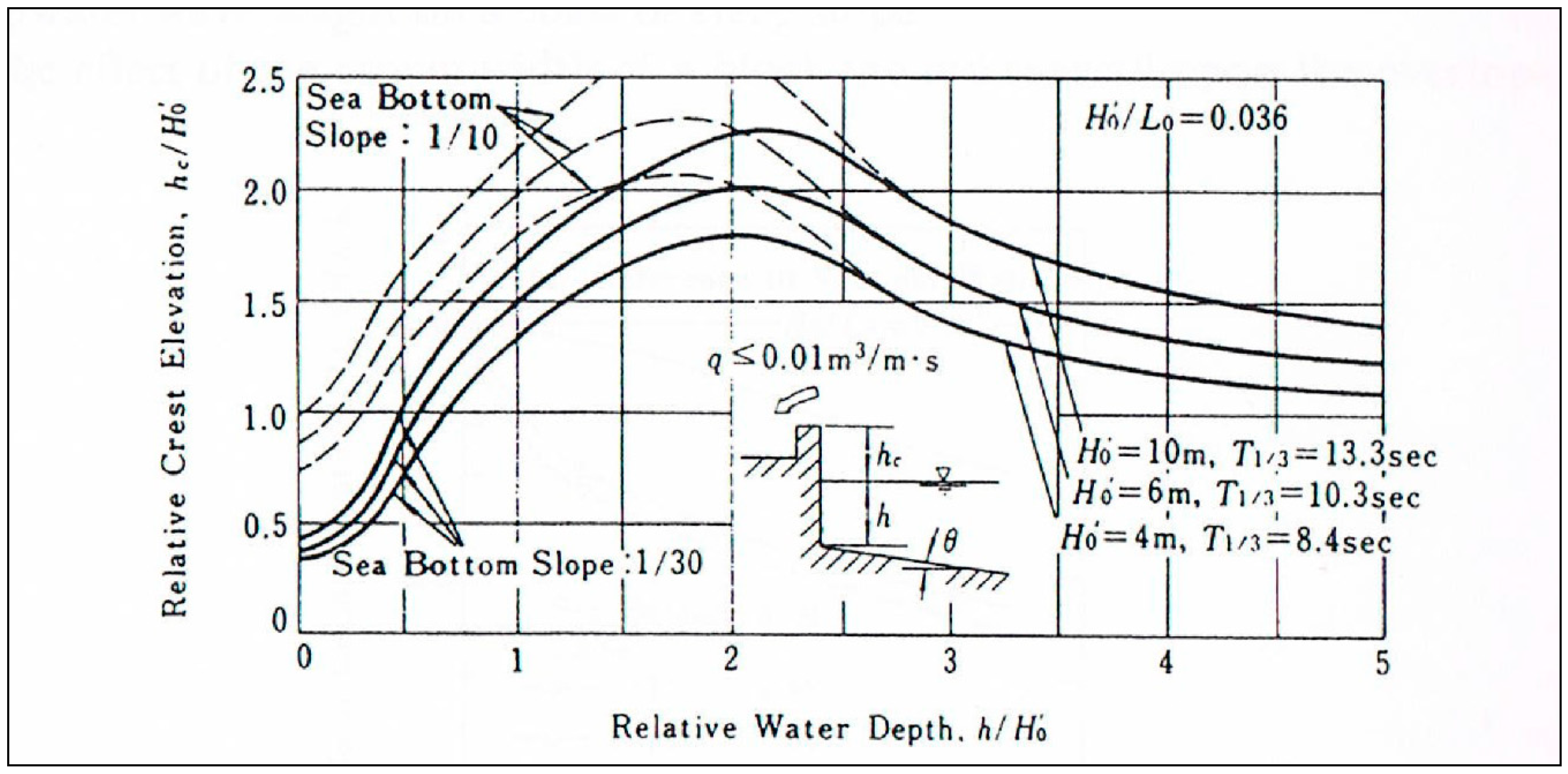
3.2.2. Theoretical models for gravity structures

Hiroi (1919), Goda (1974), Sainflou (1928), Suh et al. (2007) or Goda (2000) are theoretical models which are used here to show numerical results regarding wave run-up acting against a gravity structure.

Applying Hiroi’s theory [18], the following variables can be obtained:

$$H_{max}=H_{\frac{1}{250}}=1.80·H_{\frac{1}{3}}=\{\begin{array}{c}1.80·8.80=15.84 m\\ 1.80·10.80=19.44 m\end{array}$$

(18)

$$\mathsf{\eta }=1.25·H_{max}=\{\begin{array}{c}+19.80 m\\ + 24.30 m\end{array}$$

(19)

According to Goda’s criterion [20],

$$\mathsf{\eta }=0.75·(1+cos\theta )·H_D;\{\begin{array}{c} 0^{°} \{ \begin{array}{c}{\mathsf{\eta }}_0=0.75·(1+1)·1.8·8.8=+23.76 m\\ {\mathsf{\eta }}_0=0.75·(1+1)·1.8·10.8=+29.16 m\end{array}\\ {45}^{°}\{\begin{array}{c}{\mathsf{\eta }}_{45}=0.75·(1+\sqrt{2}/2)·1.8·8.8=+20.28 m\\ {\mathsf{\eta }}_{45}=0.75·(1+\sqrt{2}/2)·1.8·10.8=+24.88 m\end{array}\end{array}$$

(20)

To remain in the safe side, only 0° wave attack angle is considered, discarding 45°.

According to Sainflou’s equation [19] and assuming that the wind farm is located in intermediate water depths (1/25 < h/L < 1/2) [31,32], as shown in Table 1, the following value is obtained for the run-up:

$$L=157.20~198.40 m$$

(21)

$$h_0=\frac{\pi H^2}{L}coth\frac{2\pi h}{L}=6.587~6.781 m$$

(22)

$$\mathsf{\eta }\stackrel{\mathrm{def}}{=}H+h_0= \{\begin{array}{c}1.8·8.80+6.587=+22.427 m\\ 1.8·10.80+6.781=+26.221 m\end{array}$$

(23)

Although the average wave period should be the one considered for calculating the above variables, the peak period has been actually used, since the available data refers only to peak period. The relationship between average and peak period is a local characteristic, not a global correlation able to be used in all locations [35,36,37].

Hiroi, Sainflou and Goda’s pressure diagrams can be observed in Figure 4.

Suh et al. Equation [22] may also be applied,

$$k=\frac{2\pi }{L}=\frac{2\pi }{157.20~198.40}=0.032~0.040 m^{-1}$$

(24)

By entering into the kh-R_u/H graphs, the R_u/H ratio can be obtained. It is usual to maximize it to be on the safe side and, therefore, a value of 1 is to be considered, that is,

$$\frac{R_u}{H}\approx 1\to R_u=H\stackrel{\mathrm{def}}{=}{H}_{max}=15.84~19.44 m$$

(25)

Goda proposes an overtopping rate graphical method to obtain crest elevation of waves impacting against a vertical revetment [21]. This method could not be applicable in this particular case, since it is a structure made of piles (not a vertical revetment) and overtopping rate has not been measured in the Ring Pontoon. However, it can be interesting to use it here to have a first estimation, assuming the cited limitations. The results obtained need to be discussed in every case it is used. When unknown, Goda proposes a tolerable overtopping rate of q = 0.01 m³/m·s [21]. Knowing the relative water depth, relative crest elevation can be obtained using Figure 5.

$$\frac{h}{H_0{}^{\prime }}=\frac{25.00~43.80}{15.84~19.44}=1.58~2.25\to higher value:2.20$$

(26)

$$\frac{h_c}{H_0{}^{\prime }}=2.20\to h_c=2.20·[15.84~19.44]=34.85~42.77 m$$

(27)

$$\frac{h}{H_0{}^{\prime }}=\frac{25.00~43.80}{8.80~10.80}=2.84~4.05\to higher value:2.00$$

(28)

$$\frac{h_c}{H_0{}^{\prime }}=2.00\to h_c=2.00·[8.80~10.80]=17.60~21.60 m$$

(29)

The results obtained from the aforesaid calculations are shown in

Table 2. Results obtained using the different proposed criteria. Source: Own elaboration [38].

Theory	HIROI	GODA	SAINFLOU	SUH ET AL	GODA NOMOGRAM
Run-up	19.80 ̴ 24.30 m	23.76 ̴ 29.16 m	22.43 ̴ 26.22 m	15.84 ̴ 19.44 m	34.85 ̴ 42.77 m 17.60 ̴ 21.60 m

. In such table, input data from Table 1 has been used.

3.3. Physical Model Tests Description

The Ring Pontoon is designed as a gravity structure with a pontoon slab 85 m long, 85 m wide, 6.5 m thick and a total height of 60 m. It is composed of 4 columns, which have a footprint of about 17 × 17 m. The deck elevation is 20.5 m over mean sea level [26].

As said before, for intermediate water depths, the Norwegian company considered 25 m of water depth (with H_s = 8.8 m; T_p = 11.5 s, Southern North Sea). For the deep water site, the water depth was 43.8 m (H_s = 10.8 m, T_p = 12.0 s). In both cases, a 100 years return period is considered. Also in both cases, the hydrodynamic regime is far from Morison criteria (D/L < 0.05) [24,25]. Morison domain should not be applicable for the aforementioned cases, since:

$$D=17 m;h=25 m; T_p=11.5 s\to L=157.20 m\to \frac{D}{L}=\frac{17}{157.20}=0.10\gg 0.05$$

(30)

$$D=17 m;h=43.8 m; T_p=12.0 s\to L=198.40 m\to \frac{D}{L}=\frac{17}{198.40}=0.085\gg 0.05$$

(31)

Depending on the relation between the diameter of the structure and the undulatory wave length at the toe, one hydrodynamic domain or other should be considered for calculation [24,25]. According to its very reduced slenderness and the lack of pile driving into the seabed, the structure studied in this investigation responds to the GBS type, so the inertia forces domain over any other kind of forces, Reynolds and Weber effects [39,40], which are considered negligible in this case (note that for KC < 5 [33] viscous effects are typically neglected.). However, if the structure tends to the slenderness, it could be considered as a cylinder.

The Ring Pontoon designed by Aibel was tested in Deltares’ Atlantic Basin. As mentioned above, the basin dimensions are 75 m length and 8.7 m width, with a water depth of 1 m. The undistorted scale is 1:60, Froude similarity is adopted, spectral shape is JONSWAP [41] with a clear dominance of waves over currents. These tests were developed to measure water level, forces and impact pressures under regular and irregular wave attack [26].

The tests main characteristics are:

• Wave directions considered are 0° and 45°, since the structure has a square shape, so as to simplify the model. For the Goda theoretical model, only 0° wave attack angle is considered (in further steps, more wave attack angles should be also considered)
• The structure has been attacked by both regular and irregular waves.
• 4 different types of tests have been performed regarding regular wave attack, using 10 different values for wave height (which makes 40 variants in total).
• 10 different types of tests have been performed regarding irregular wave attack, with a number of waves of 1000 in each.

Wave heights were H_s = 8.8 m and H_max = 20.7 m in 25.00 m water depth and H_s = 10.8 m and H_max = 24.90 m in 43.8 m water depth (intermediate water depths).

Peak periods in prototype ranged between 11.5 and 12.0 s. However, in model tests, equivalent periods in prototype were 11.5, 12.0, 12.9 and 13.2 s. The number of active waves in the model storm exceeded 10,000, therefore the values of H_max were larger than as described by H_1/250 as suggested by Goda (15.84 m and 19.44 m, as shown before).

Figure 6 shows the conceptual design of the real platform and the 1:60 scale model to be tested.

3.4. Physical Model Tests Results and Comparison with Theoretical Models

Forces and impacts on the upstream and downstream columns of the model have been analysed for the different sea states tested, as well as the water levels reached.

Extreme water levels well exceeded +20.00 m, hitting the lowest part of the crown deck (installed at an elevation of +20.50 m). This effect can be due to resonances and interactions between the incoming and the diffracted waves. It was recorded using a high frequency camera and can be observed in Figure 7.

In Figure 8, a clear peak is observed when the diffracted wave slams into the downstream column (red line). The impact pressure on the upstream column (blue line) is lower due to the absence of slamming. The results show that the diffracted waves below the deck (grey line) are larger than the undisturbed wave heights (blue and red lines).

Under regular waves clear patterns of reflection and diffraction were observed. Under the low wave height tests. Only limited run-up occurred and no slamming impacts were observed.

Slamming on the upstream column occurred less frequently but when it happened it led to significant run-up along the upstream column.

As the topside is set at +20.50 m, the water level results under regular waves demonstrated values under twenty meters (upside part of Figure 8); the same phenomenon is observed in under irregular wave attack (see central part of Figure 8). In the downside part of Figure 8 the significant run-up along the upstream column (>20.50 m) can be observed. Such results present a very good correlation with the ones established in Table 2.

The results for the run-up can be observed in

Table 3. Comparison between the results obtained using theoretical models and those obtained by hydraulic model tests. Source: Own elaboration.

MODEL USED	h = 25 m		h = 43.80 m
	Ru/Hs	Ru/Hmax	Ru/Hs	Ru/Hmax
Potential flow theory	2.60	1.44	2.60	1.44
MacCamy and Fuchs	0.84	0.84	0.73	0.73
Niedzwecki and Huston	2.23	1.24	2.03	1.13
Hiroi	2.25	1.25	2.25	1.25
Goda	2.70	1.50	2.70	1.50
Sainflou	2.55	1.42	2.43	1.35
Suh et al.	1.80	1.00	1.80	1.00
Goda nomogram	2.00	2.20	2.00	2.20
Hydraulic model tests	2.32	1.28	1.90	1.05

, both for the theoretical models proposed in this research and for the hydraulic model tests used to adjust the goodness of each one of them. Note that such results have been expressed for a 25 m water depth (corresponding H_s = 8.80 m and H_max = 15.84 m) and for a 43.80 m water depth (corresponding H_s = 10.80 m and H_max = 19.44 m). For intermediate values of water depth between these ones, run-up can be interpolated at pre-dimensioning stages.

These results will be discussed in the following epigraph.

4. Discussion

After developing the comparison between the theoretical models proposed in this research and the hydraulic tests performed by Deltares, the results give a good enough correlation between both methods. However, some issues have to be addressed regarding such comparison.

First of all, not all the theoretical models studied here have been applied. This is the case of Hallermeier or De Vos et al., which have been discarded because they remain out of the side of safety. Others, like Mase et al., have not been considered either, due to the close range of appliance of them (which the Ring Pontoon platform is not coincident with).

The values obtained by the theoretical models show a conservative approach when using them. In fact, only the average R_u/H_s for a 25 m water depth (see Table 3) shows a value under the one predicted by the hydraulic model (actually, only 8.62% lower). For the rest of the cases, the theoretical approach gives average values, respectively, 6.25%, 8.42% and 25.71% higher than the ones given by the hydraulic model. This goodness of the adjustment could be even increased by considering some models neglected here, such the aforementioned Hallermeier or De Vos et al. but it is preferable to remain on the side of safety at the expense of assuming a less good correlation.

Goda’s models show values considerably higher than other authors. This fact can be softened by considering the use of H_s instead of H_max. Actually, for the practical application, some formulations, such as Hiroi or Sainflou recommend using the maximum wave height (Hiroi, H ≈ 0.9·h; Sainflou, standing waves), whereas other formulations such as graphic model of Goda propose using the significant wave height. This assertion is in good agreement with the experimental results obtained here. Others, like the potential flow theory or MacCamy and Fuchs, also present outlier figures. This last one, apart from being outlier, is also out of the side of safety.

H_max has had to be considered in some formulations. According to theoretical criteria, H_max is related to H_s following Longuett-Higgins expression. But to apply this formula the number of active waves has to be known. When this parameter is unknown, H_max can be approximated by H_1/250 (1.80·H_s), regarding Goda’s criterion. The problem is that for the most common storms, the H_max/H_s relation increases, reaching values between 2.00 (N = 1500) and 2.20 (N = 10,000), fact that has to be taken into account when applying these formulas (actually, in the maritime engineering field, structural damage is stabilized at around 7000 active waves [42,43]). In the Ring Pontoon, H_max/H_s reaches values of 1.86 to 1.89, which shows that Goda’s criterion is accurate in this case.

Other fact that has to be considered is the choice between breaking and non-breaking waves. Breaking waves (by bottom effect) do not appear for depths such as the ones considered here (25 m and 43.80 m). Breaking waves (by steepness effect) appear in shallower conditions. This is why in this research only non-breaking waves are considered. However, in further stages of the design process, both breaking and non-breaking ones should be considered, since there are very extreme waves that could break even in deep waters.

The last point that is discussed here is the return period choice. The hydraulic model tests took a 100 year return period. For a useful life of 20 years, the probability of failure is around 0.20 (20%), value that results very high. Reducing the probability of failure to 10% and considering a 25 years useful life (for instance, Vindeby wind farm was in operation from 1991 to 2017), the return period will be 237 years, considerably larger than 100 years. And being more restrictive, reducing P_f to 5% and increasing n to 30 years, the return period would ascend to 584 years. Therefore, it is recommended using return periods well in excess of 100 years for climate actions, in agreement with current international guidance [44,45,46].

Regarding all the aforementioned, the authors propose a preliminary estimation of 2.50 < R_u/H_si < 3.00, that will remain in the side of safety compared to the hydraulic model tests (it is among the highest coefficients, see Table 3) but will adjust very well to the real effect of run-up (since H_max/H_s >> 1.80 and T_r >> 100 years, as stated before). This relation will give good results for GBS and large diameter cylinders. It presents some limitations, due to the preliminary character it has. According to wave mechanics, it can be applied at intermediate water depths, where 1/25 < h/L < 1/2 (or considering the wave number, π/10 < kh < π). Only non-breaking waves are considered but H_b should be definitely taken into account in further stages of the design process. Regarding wave statistics, it can be applied when H_si is known (being possible to simplify H_si as H_1/3), with an associated undulatory wave period of T_s. According to the nature of the seabed, it can be applied for smooth bottom seabed. Although such limitations, it will give a good rough estimation of the run-up effect against these structures.

5. Conclusions

The main conclusion points obtained after this research work are the ones cited below:

• Run-up effects have demonstrated in the past few years that the values traditionally predicted are clearly under the ones actually happening. Decks and platforms at offshore locations are suffering from flooding and wave attack due to such unpredicted phenomena.
• The final aim of this investigation is to determine which would be the proper level to install the deck (protected from run-up effects). Theoretical models have been addressed for intermediate water depths and flat bottom, since for much deeper waters other types of structures are the ones used and for shallow waters, turbulence effects do not allow the use of such simplified theoretical models.
• Two groups of theoretical formulations may be used: those for cylinders and those for GBS. There is not a clear boundary between both types of structures. Theoretical formulations give accurate results. The designer should choose between the different expressions here presented or apply them all studying the goodness of approach of each one of them.
• The models herein presented should be used only for preliminary design. They are very simplified. In further stages of the design, more complex criteria need to be considered (breaking waves, different return periods, accurate correlation between H_max and H_s, different hydrodynamic domains…)
• Return periods should be increased from the current 100 years to higher values, up to 500 or even 1000 years. Consequently, the number of active waves in the design storms will increase, up to 10,000 or even more.
• The authors propose a preliminary estimation of 2.50 < R_u/H_si < 3.00, applicable for GBS and large diameter cylinders, for a site condition of intermediate water depths and flat bottom seabed.