1. Introduction
Interior permanent magnet synchronous motors (IPMSMs) have been widely used in the electric vehicle (EV) drives due to their simple structure, wide speed range, high power, and torque density. IPMSMs often run above the rated speed in some applications, such as EVs, which is the maximum speed that the motor can obtain in the constant torque region. The flux-weakening control is usually adopted in an IPMSM system for acquiring higher speed and meeting the application demand. A negative d-axis current is injected to the stator windings in the flux-weakening control strategy. The air gap magnetic field of an IPMSM is reduced under the direct axis armature reaction caused by negative d-axis current. Then, the motor speed increases as the magnetic field reduction. The copper and iron losses of IPMSMs increase with an increase in speed, which results in the temperature rising. The parameters of IPMSMs, such as stator resistance and inductance, vary nonlinearity with the temperature rising. The control performance of the IPMSM system is degraded under uncertain parameter variation. Meanwhile, the torque fluctuation caused by switching between the constant torque region and the flux-weakening region bring adverse effects to the smoothness of IPMSMs.
An improved feedforward control strategy is proposed to reduce the impacts from parameter variation caused by flux-weakening control in [
1,
2,
3,
4]. The reference values of d-axis and q-axis currents are given by a lookup table. The parameter identification is adopted in flux-weakening control to enhance the systemic robustness in [
5,
6]. The parameters of the motor can be identified online using this method. The influence of magnetic saturation and stator resistance are considered in [
7], and an optimal control strategy is proposed. However, the flux observation is limited by the rotor position in this strategy. A linearized and constrained model predictive control is put forward to the flux-weakening control in [
8]. However, this method involves a large amount of calculation and is extremely sensitive to parameter variation. In order to suppress the influence of parameter variation on the system, a voltage feedback control strategy is applied in the flux-weakening region. A flux-weakening current output by a proportional integral (PI) controller is added to the d-axis current reference. The input of the PI controller is the difference between the output voltage amplitude and the maximum available voltage amplitude of inverter. This method is simple, independent of motor parameters, and has good robustness, but the dynamic performance needs to be improved. The conventional voltage feedback method is improved in [
9]. The difference between DC link voltage and output voltage of current controller is used to calculate the phase angle of reference current space vector by an adaptive algorithm. However, the global stability of the IPMSM system cannot be guaranteed. A single current regulator is proposed to improve the voltage utilization of the DC bus in [
10]. This method eliminates the poor effect caused by the coupling of the d and q axis current, but the decrease of efficiency and stability is still not to be ignored. A line modulation-based flux-weakening control was proposed to maximize the DC bus voltage utilization in [
11].
The difference between the output voltage amplitude and the maximum voltage amplitude of the inverter is regarded as the judgment of whether to enter the flux-weakening region to reduce the switching fluctuation caused by different control algorithms in constant torque region and flux-weakening region in [
2,
8,
12,
13]. A variable coefficient is used to adjust the stator flux linkage which contributes to generating the maximum and most suitable torque and to achieve smooth switching [
3]. The d-axis current reference is modified by comparing the switching period and summation of active switching times for inverter pulse width modulation control in the flux-weakening region, thus extending the hexagon of the space vector modulation in [
14]. The smooth switching between the constant torque region and the flux-weakening region is realized by using the amplitude of inverter output voltage and d-axis current as input of set-reset flip-flop in [
15].
Recently, an uncertainty and disturbance estimator (UDE)-based control has attracted much attention and has been applied to unknown time delay systems, nonlinear systems, and power converters [
16,
17,
18,
19,
20,
21,
22]. The algorithm assumes that an unknown continuous signal can be estimated by an appropriate filter and compensated to the control system. It is helpful for solving the problem that the control performance deteriorates due to the parameter variations in flux-weakening control and has strong robustness. The UDE-based method is applied to the inverter for improving the output voltage quality of the inverter and reducing the total harmonic distortion in [
16,
17], and this method improves the stability of the system in nonaffine and nonlinear systems [
18]. The UDE-based control is applied to surface permanent magnet synchronous motor and proposes a simple parameter tuning algorithm in [
19], but does not analyze the operating condition in flux-weakening regions. The influence of different filters on the system has been discussed in detail [
20]. The asymptotic tracking and disturbance suppression are realized under different types of reference values.
In this paper, an improved UDE-based flux-weakening control strategy for an IPMSM system is proposed to solve the poor robustness caused by parameter variation in the flux-weakening region, and the torque fluctuation when the operation point switches between the constant torque region and flux-weakening region. The motor model and flux-weakening control strategy are presented in
Section 2. The UDE-based control is introduced and the parameter tuning method is improved in
Section 3. The flux-weakening adjusting factor and its lookup table method are proposed in
Section 4. The analysis of parameter mismatches is carried out in
Section 5. The experimental validation of proposed method is carried out in
Section 6. Finally,
Section 7 comprises the summary.
2. Mode and Flux-Weakening Control Strategy
The model of an IPMSM in the synchronous rotating coordinate system is expressed as
where
Rs,
Ld, and
Lq are the stator resistance, d-axis, and q-axis inductance, respectively;
ψf is permanent magnet flux linkage;
p is pole pairs;
id and
iq are d-axis and q-axis currents;
ωe is the electric angular of rotor; and
Te is the electromagnetic torque.
The maximum torque per ampere (MTPA) control strategy is often used in IPMSMs to achieve the optimal configuration of the given current when the IPMSM runs in the constant torque region. This strategy makes full use of the reluctance torque due to the difference between
Ld and
Lq. It can minimize the stator current at the same electromagnetic torque. In the MTPA, the d-axis current
id*.
MTPA is shown as
where
iq* stands for the q-axis current reference which is obtained by the output of the speed controller.
A valid operating point of the IPMSM is limited by the voltage and current constraints. Considering the influence of the stator resistance, the voltage and current constraints are shown as follows:
where
Usmax and
Ismax represent the maximum voltage and maximum current, and they are limited by the inverter and motor.
The reference voltage output obtained by the current controller can reach or exceed the maximum value of the inverter with the increase of motor speed. Thus, the MTPA control strategy cannot further improve the speed of the IPMSM. The flux-weakening control is usually adopted to solve this problem. The negative d-axis current is further increased in flux-weakening region. According to the Equations (5) and (6), the d-axis current
i*d.FW in flux-weakening control is expressed as follows:
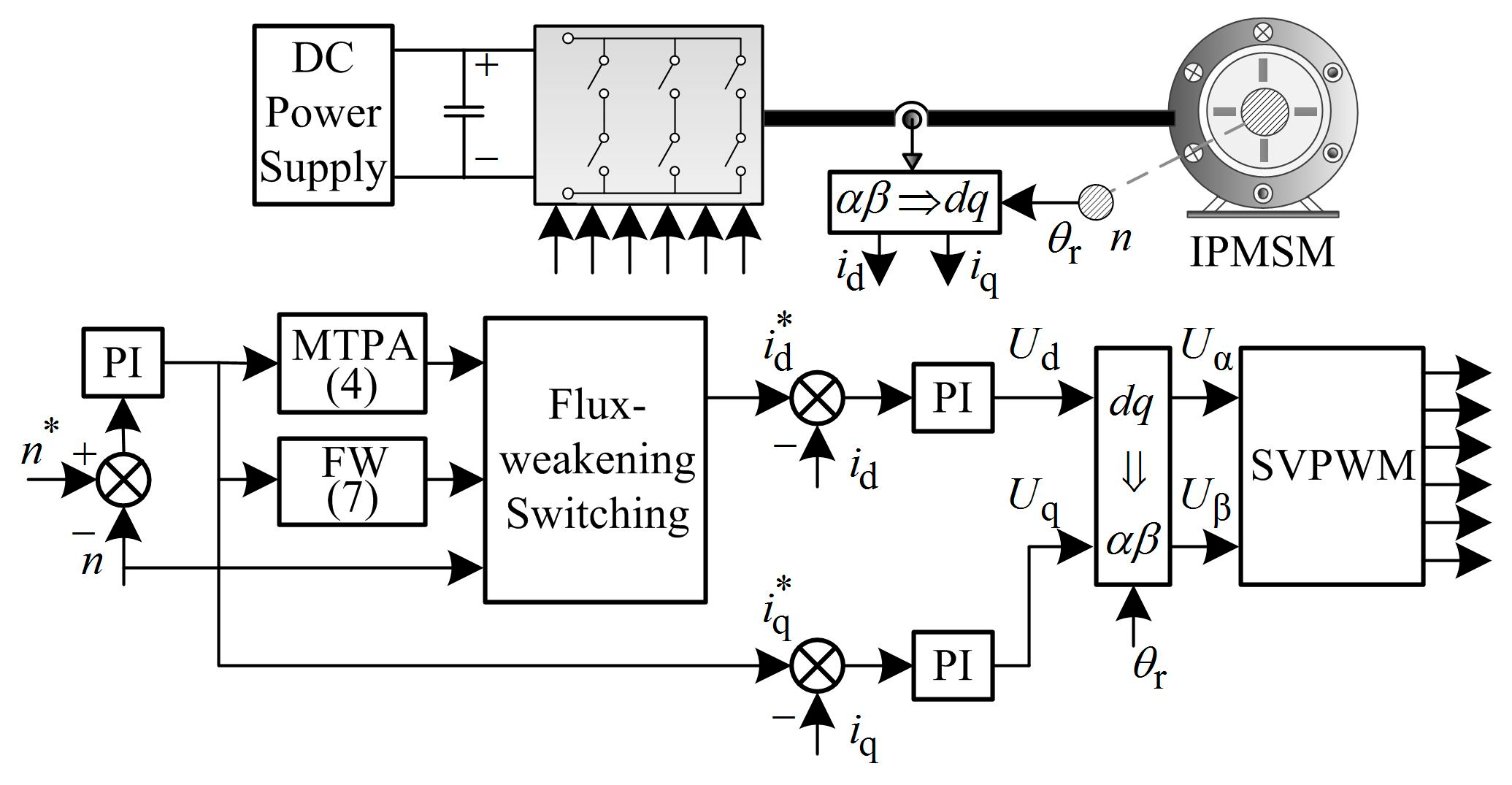
The MTPA control strategy is adopted when the motor is running in the constant torque region, and the motor is switched to flux-weakening control when the motor speed is higher than the maximum speed of the constant torque region. The traditional control strategy based on PI controller is shown in
Figure 1.
It can be seen from
Figure 1 that the d-axis current is calculated by formulas. The parameters of PI controller cannot match well with the variable motor parameter caused by flux weakening. This leads to the performance decline of the IPMSM system. In addition, the fluctuation caused by the switching between the constant torque region and flux-weakening region at a fixed speed is necessary to be solved.
3. The Design of UDE-Based Control
The uncertainty and disturbance are regarded as unknown signal in a UDE-based control system. A stable reference model is used to satisfy the desired tracking performance of the closed-loop system. Uncertainties and disturbances are compensated to the controller by using an appropriate filter. Thus, the control law of UDE-based control is obtained.
The motor parameter variations and systemic random disturbances are regarded as an unknown signal in the IPMSM control system. The current-loop model of UDE-based control under the synchronous rotating coordinate system is obtained as
where
Dd and
Dq are the d-axis and q-axis systemic random disturbances;
fd and
fq are the d-axis and q-axis uncertainties caused by the variations of motor resistance, inductances, and flux linkage. The
fd and
fq are expressed as the average current ripple vector in sample period (0,
Ts] and (
Ts, 2
Ts] are defined as follows:
Equations (8) and (9) can be rewritten in matrix from as
where
x(
t) = [
id iq]
T,
u(
t) = [
ud uq]
T,
f(
t) = [
fd fq]
T,
D(
t) = [
Dd Dq]
T,
3.1. The Reference Model
A stable reference model is used to achieve asymptotic tracking of the motor reference current in UDE-based control. The selection of reference model is related to control object. According to the structure of the IPMSM control system, the following linear reference model is adopted.
where
xm = [
idm iqm]
T is the d-axis and q-axis current reference state vector,
c = [
id* iq*]
T is the d-axis and q-axis current reference command vector.
xm(
t) and
c(
t) are the second-order matrices selected in the reference model for achieving the desired tracking performance of the control system. Due to the difference between the d-axis and q-axis inductances in IPMSMs, the coefficient matrix of reference model is given as
where
α and
β are two independent positive real numbers.
Based on the above reference model, the currents can asymptotically track the reference state vector of the d-axis and q-axis current by controlling the input voltage
u(
t) of the control system. The tracking error and dynamic error are expressed as
where
K is an error feedback gain matrix of the reference model which is used to guarantee the system stability.
When
K is a zero matrix, the current state vector can be expressed as follows by combining Equations (12), (14) and (15).
since matrix
B and
Bm are invertible as they are both diagonal matrices. By substituting (16) into (11), the input
u(
t) can be expressed as
If (17) is used as the input of the control system, by substituting (17) into (15), the error dynamics of current is obtained:
The eigenvalues −α and −β of the matrix Am are negative, so the dynamic tracking error of current is asymptotically stable according to Lyapunov stability theory. The error feedback gain matrix K should be selected as a zero matrix. From Equation (17), the control input u(t) can maintain stability of the reference model tracking the current. However, u(t) cannot be directly used in the control system because of the parameter uncertainties and systemic random disturbances.
3.2. The UDE-Based Control Law
In [
22], the uncertainty and disturbance are estimated and compensated in the linear time invariant system by a filter with desired bandwidth, and this method improves the robustness of the system. The parameter uncertainties and systemic random disturbances of motor can be defined as
According to the current state Equation (11), Equation (19) is further written as
From Equation (20), it can be seen that the motor parameter uncertainties and the systemic random disturbances can be represented by the known state variable
x(
t) and the control variable
u(
t). The filter
gf(t) is designed with unity gain and zero phase shifts for estimating the parameters uncertainties and the systematic random disturbances. The estimating value can be expressed as
where “*” is the convolution operator.
The design of the filter is mainly related to the suppression ability of the parameter uncertainties and systemic random disturbances. A detailed discussion is made for the step and sinusoidal disturbances in [
20], and the corresponding filter is designed to achieve asymptotic tracking. Considering that the disturbance of IPMSM control system is mainly step signals, it is sufficient to choose a first-order low-pass filter to meet the actual working conditions. The frequency domain transfer function of filter is
where
γ = 1/
T and
γ is the bandwidth for the selected first-order low-pass filter.
Therefore, the frequency domain form of the parameter uncertainties and systematic random disturbances can be expressed as
The UDE-based control law can be obtained by substituting (23) into the frequency domain form of (17).
By simplification, Equation (24) can be rewritten as follows:
where
From the Equation (25), the traditional UDE-based control without parameter tuning is shown in
Figure 2. This structure is mainly divided into three parts, including differential feedforward, PI regulator, and model inversion.
The eigenvalues −
α and −
β of the matrix
Am are influenced by the system itself, so the adjustable range of
Am is small and
γ plays an important role in asymptotic reference tracking. A simple dual-loop parameter tuning algorithm for PMSMs is adjusted by the current reference tracking performance in [
19]. This method avoids the trial-and-error procedure, but is not suitable for IPMSMs.
3.3. Parameter Tuning Method
The rapidity of system response depends on
KP, while the following performance depends on
KI. The
KP and
KI can be adjusted by tuning
α,
β, and
γ in order to achieve the asymptotic following of the current reference in UDE-based control. The tracking performance is not only related to known disturbances, but also influenced by unknown external disturbances. Therefore, the following performance can be further improved by tuning
KI online when
KP is determined. The
KI is represented by intrinsic components
Md and
Mq and variable components
Nd and
Nq in this paper. The new integral gain
is shown in (26).
The intrinsic components
Md and
Mq can be determined by previous analysis. The variable components
Nd and
Nq can be obtained by the out of proportional component whose inputs are the d-axis and q-axis current tracking errors. Thus, the online tuning of
KI can be achieved. The d-axis current is negative, and the q-axis current is positive in the control process. Therefore, the d-axis current tracking error is obtained by subtracting the given value from the feedback value. On the contrary, the q-axis current tracking error is obtained by subtracting the feedback value from the given value. This method can guarantee the positive output of proportional component during the bigger current errors. The coefficients
KId and
KIq are used to represent variation of
Nd and
Nq. Equation (26) is rewritten as follows:
Therefore, the structure of the improved UDE-based control with parameter tuning is shown in
Figure 3.
4. The Flux-Weakening Switching Control
4.1. Analysis of Switching Point
The two different d-axis current calculation methods need to be switched when the motor is switched between the constant torque region and the flux-weakening region. Considering the motor parameter variations, Equations (4) and (7) can be expressed as
where “~” represents a variable scalar.
It can be seen from (28) and (29) that the d-axis current of the smooth switching point fluctuates due to the motor parameter variations. The currents at the selected switching points are usually smaller than that of the ideal switching points for ensuring the stability. The voltage and current constraints are represented in the plane of d-q axis current, as shown in
Figure 4.
The maximum speed of the MTPA control strategy can reach point A in the constant torque region, that is, the theoretical switching point, and the corresponding d-axis current is A′. The optimal switching point is the point which does not lead any fluctuation during the switching. The optimal switching point may deviate from A to B or C, which leads to corresponding current deviation from A′ to B′ or C′ because of the motor parameter variations. Thus, the deviation of flux-weakening current may result in fluctuations during switching. The d-axis current can be adjusted with the size of voltage limit ellipse in a small range.
4.2. Flux-Weakening Adjusting Factor
From the above analysis, it is known that the d-axis current can be regulated by changing the size of voltage limit ellipse in a small range so that the flux-weakening current can reach the optimal switching point.
The d-axis current is calculated by the (7) in flux-weakening region. The voltage-drop on the stator resistance
RsIsmax is very small, so the
RsIsmax/
ωe can be ignored with the increase of motor speed. A flux-weakening adjusting factor
k is introduced before the speed in (7) and the d-axis current in flux-weakening region
can be written as
It can be seen from (30) that the size of voltage limit ellipse can be regulated by adjusting the factor k, so that the d-axis current reaches the optimal switching point.
4.3. Online Control Method
The error between the d-axis current reference under MTPA control and the d-axis current reference under flux-weakening control is defined as the reference error of d-axis current.
The d-axis current under different methods can be reflected by the reference error of d-axis current considering the motor parameter variations, and the load torque can be regarded as the function of q-axis current reference. The flux-weakening adjusting factor k can be determined by the reference error of d-axis current i*d.error and the q-axis current reference iq*. Therefore, the i*d.error and iq* can reflect the switching situation in real time.
Due to the transience of switching period, it is significant to obtain the factor
k in a current control cycle. The lookup table method is effective for getting the
k value as quickly as possible.
Figure 5 shows a 3D table of the factor
k varies with
i*d.error and
iq*. The DC bus voltage range is from 270 to 320 V, with an interval of 5 V, and the given speed ramp range is from 0 to 1.1, with an interval of 0.1 in the table. The given speed ramp is defined as reached speed per unit time, where 1 represents the speed, that reaches 3000 r/min per second. The base value of
i*d.error and
iq* is 62.5 A.
From the above analysis, the improved UDE-based control strategy for IPMSMs is shown in
Figure 6.
5. Analysis of Parameter Mismatches
The d-axis inductance, q-axis inductance, and flux linkage vary with the increase in speed, which results in parameter mismatches. The parameter mismatches between the controller and the motor reduce the systemic control performance. The mismatch of flux linkage is usually ignored in flux-weakening control. The robust analysis of parameter mismatches is implemented by combining with Bode plots of the transfer function in the traditional PI controller, the traditional UDE-based control without parameter tuning, and the improved UDE-based control with parameter tuning. The nominal parameters of an IPMSM in simulation are listed in
Table 1, which are the same as for the experimental motor.
The variation of d-axis and q-axis inductance with 20% nominal value is utilized to analyze the robustness of parameter mismatches in the flux-weakening region. The speed of the motor is 6000 r/min, the angular velocity is 2513 rad/s, the q-axis current is 84 A, and the d-axis current is obtained using Formula (7).
Figure 7 are the Bode plots of parameter mismatches in the traditional control strategy-based PI controller, the traditional UDE-based control without parameter tuning, and the improved UDE-based control with parameter tuning. The parameters in controller are nominal
Ld and
Lq. The actual motor parameters are
Ld′ and
Lq′.
It can be seen that the Bode plot of the traditional control strategy-based PI controller masks the Bode plot of the traditional UDE-based control without parameter tuning, which illustrates that the essence of traditional UDE-based control is same as the traditional control strategy. The improved UDE-based control optimizes the phase margin in the operation area compared with the traditional PI controller and traditional UDE-based control. The Bode plots of nominal parameters is shown by a black line in
Figure 7, and the Bode plots considering the parameter mismatches are shown by green and red lines. The phase margin is reduced when the controller parameters are larger than the motor parameters, which is not conducive to the stability of the system. The phase margin is improved when the parameters of the controller are less than those of the motor, which is beneficial to the stability of the system.