Study on the Optimum Design of a Ground Heat Pump System Using Optimization Algorithms
Abstract
:1. Introduction
1.1. Research Background
1.2. Research Method
2. Materials and Methods
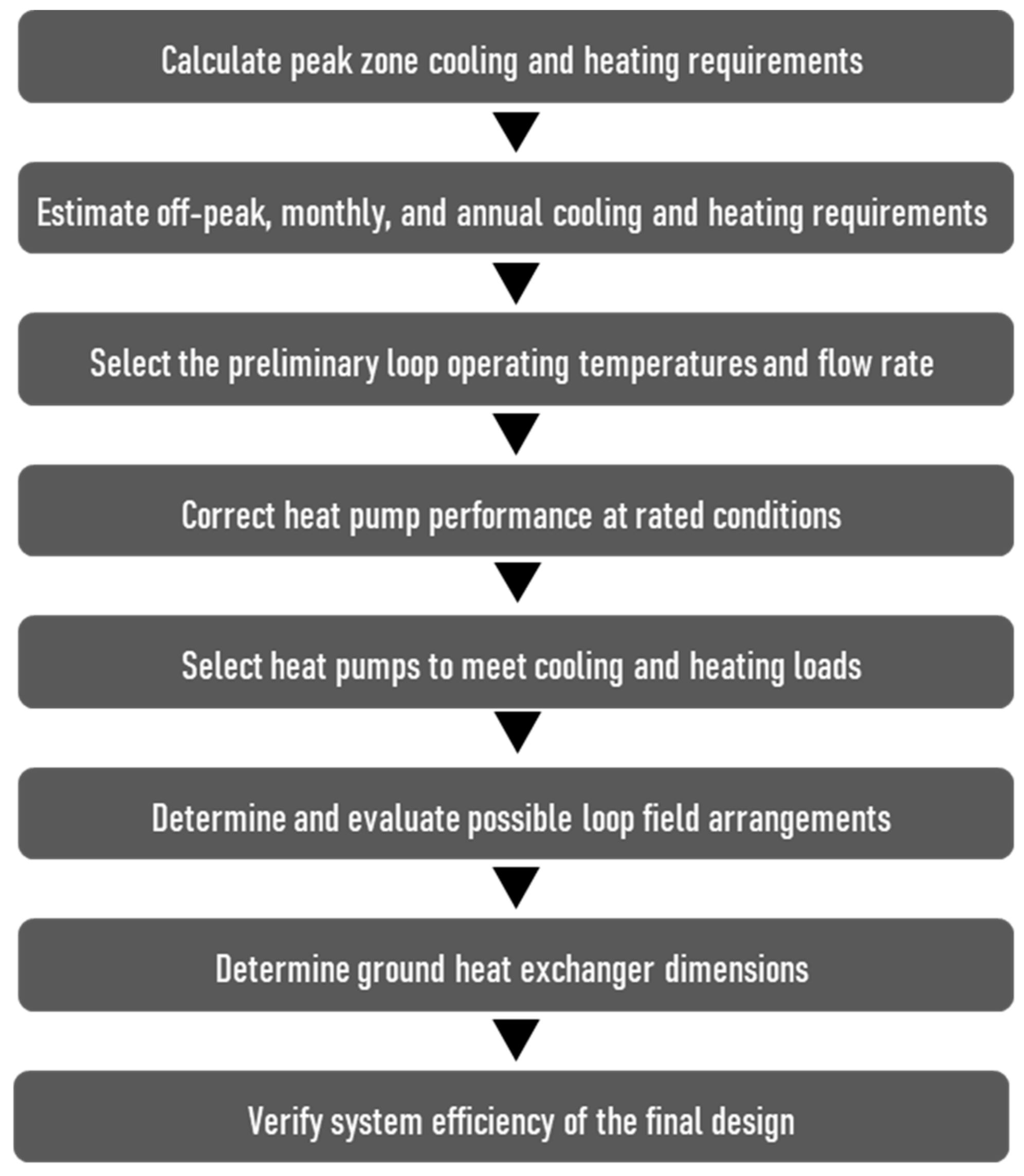
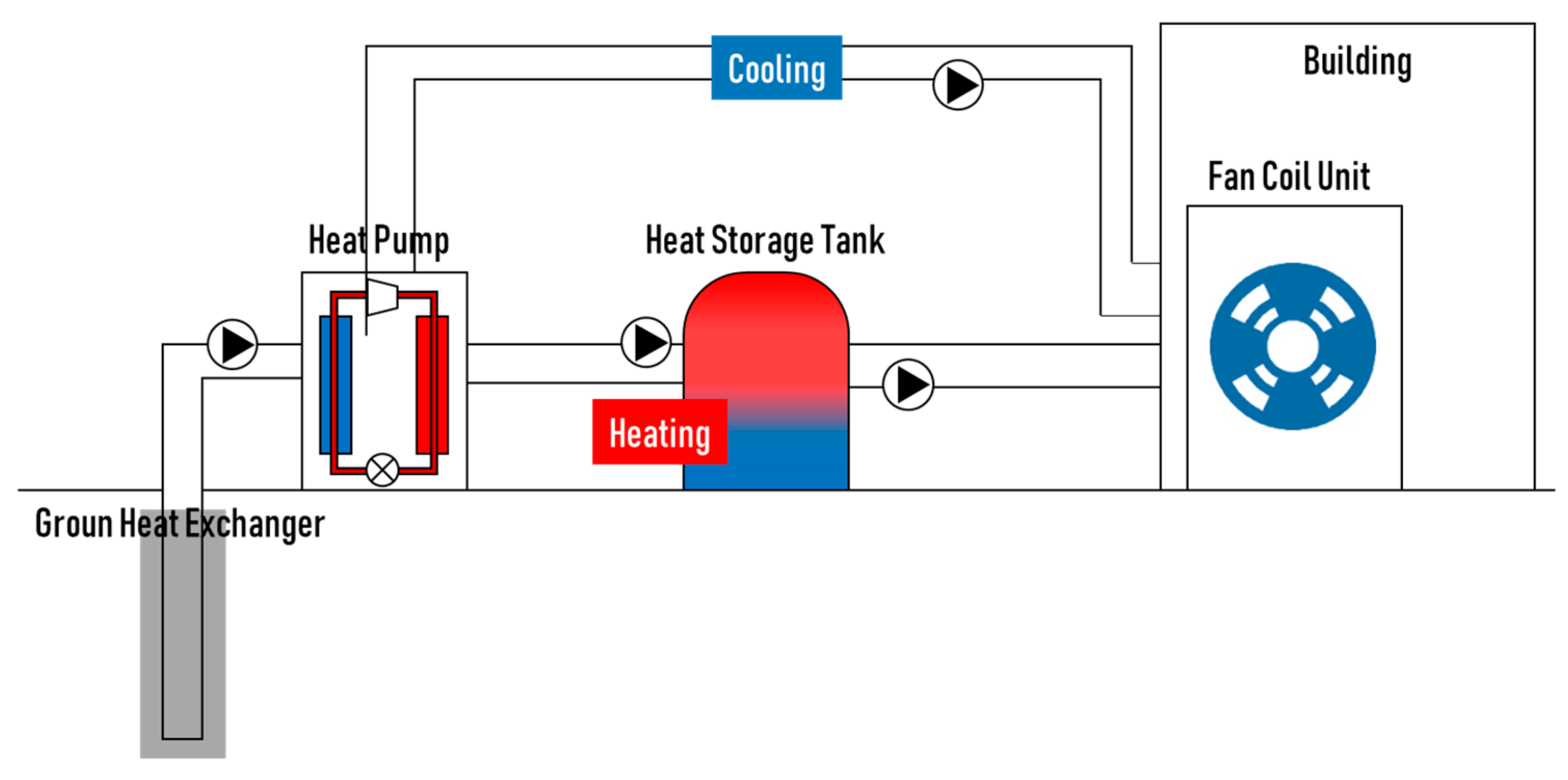
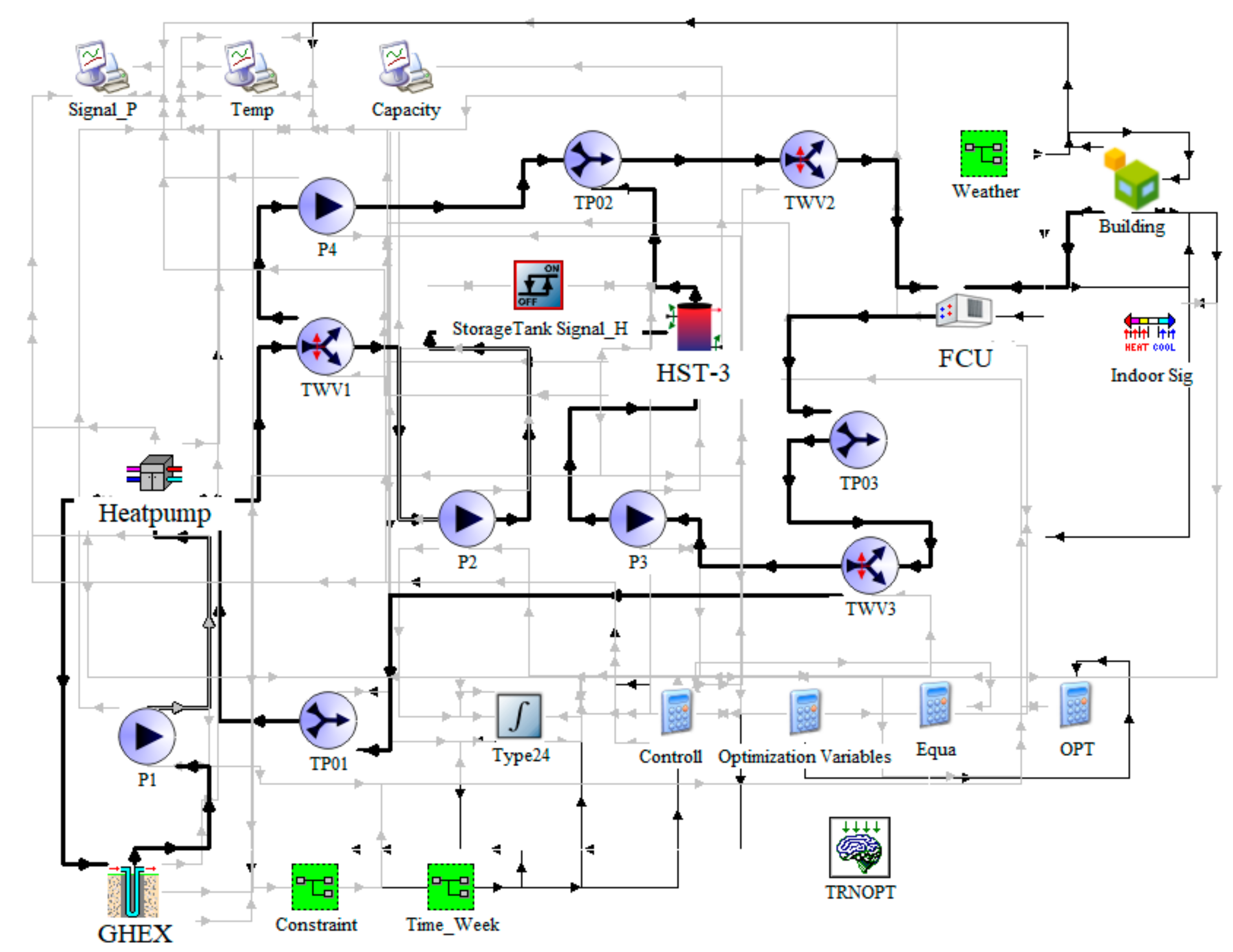
2.1. GSHP System Design
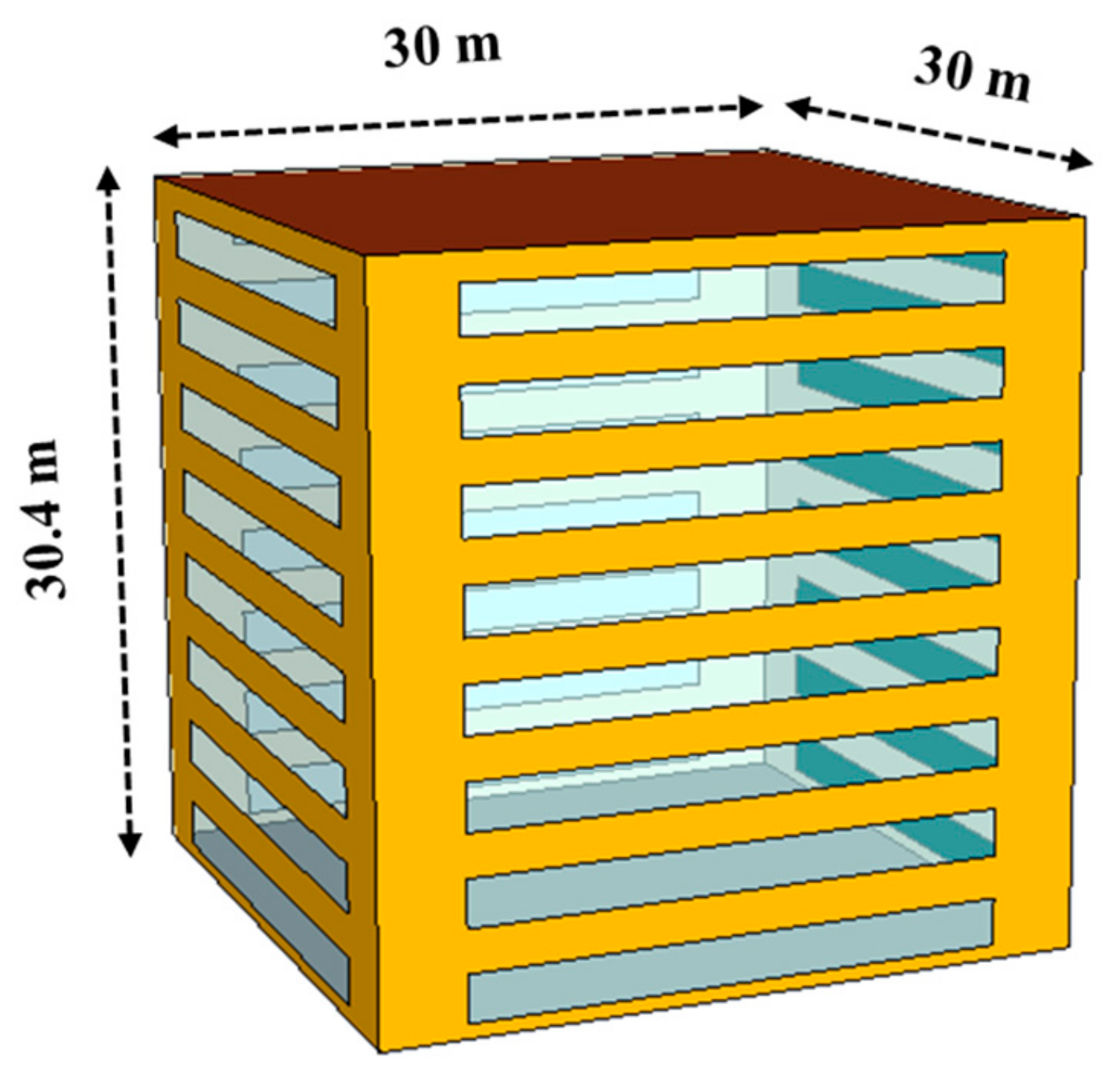
2.1.1. Target Building Modeling
2.1.2. Initial Design Values for the GSHP System
2.2. Optimization Algorithms
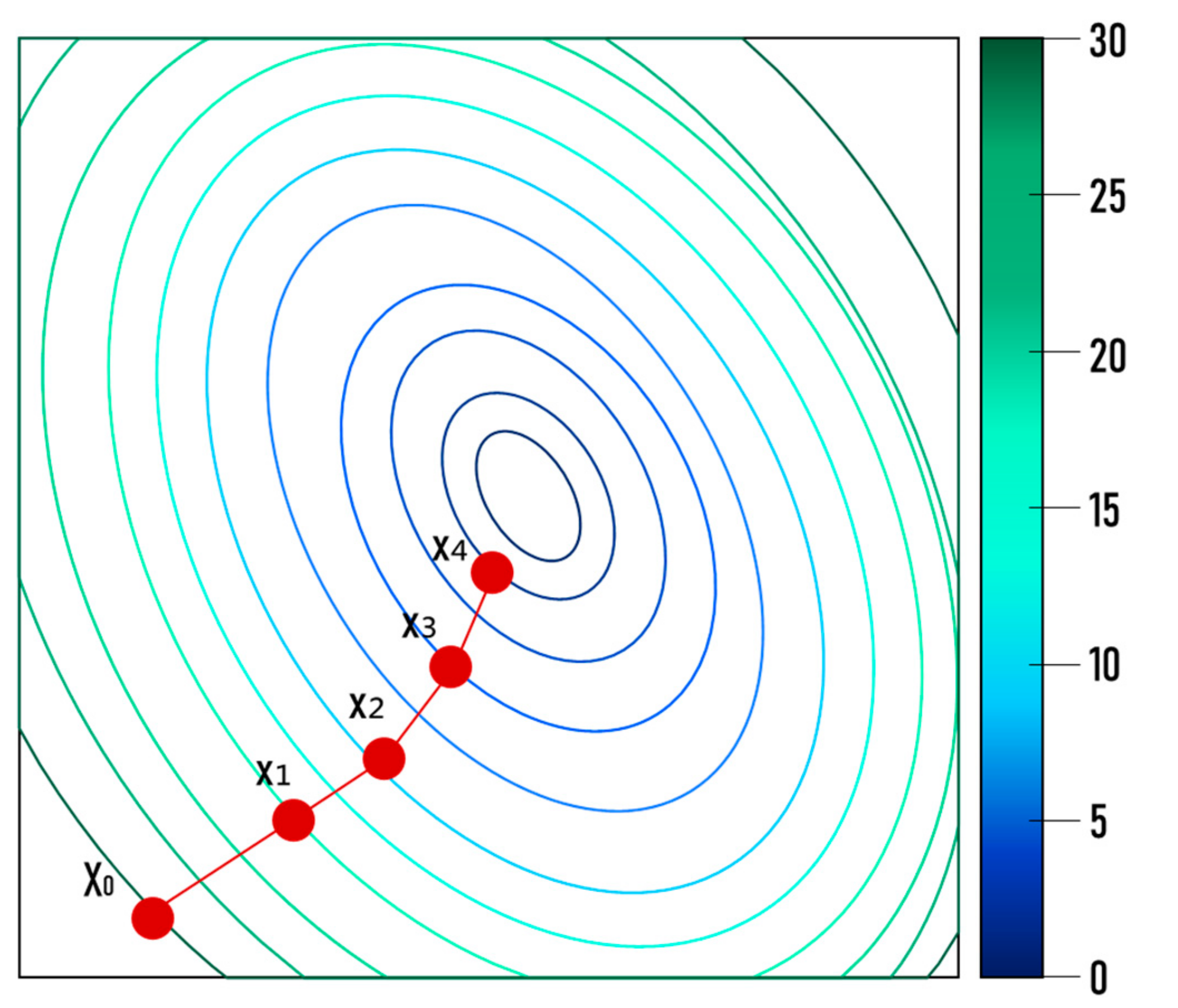
2.2.1. Discrete Armijo Gradient
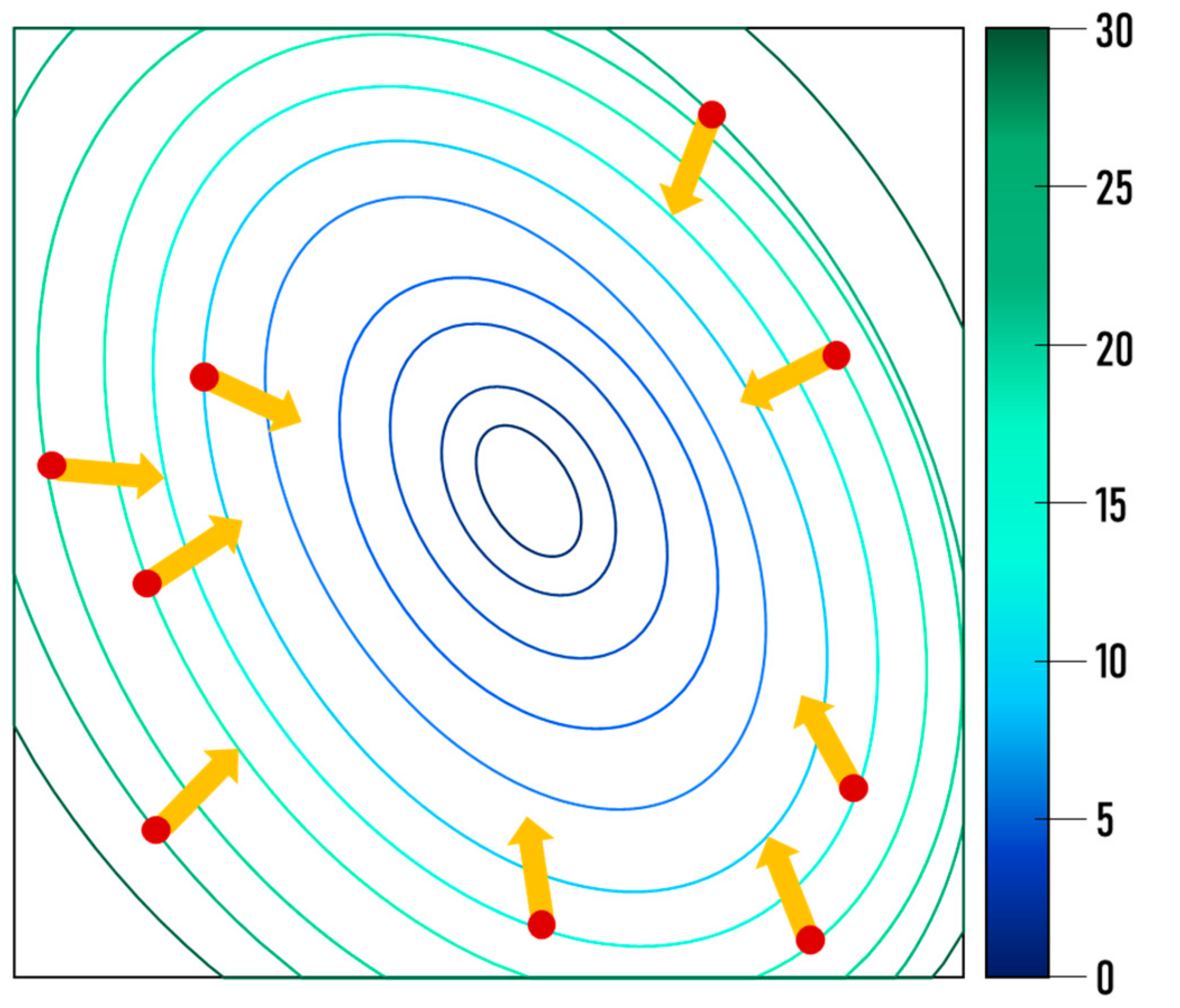
2.2.2. Particle Swarm Optimization Algorithm (PSO algorithm)
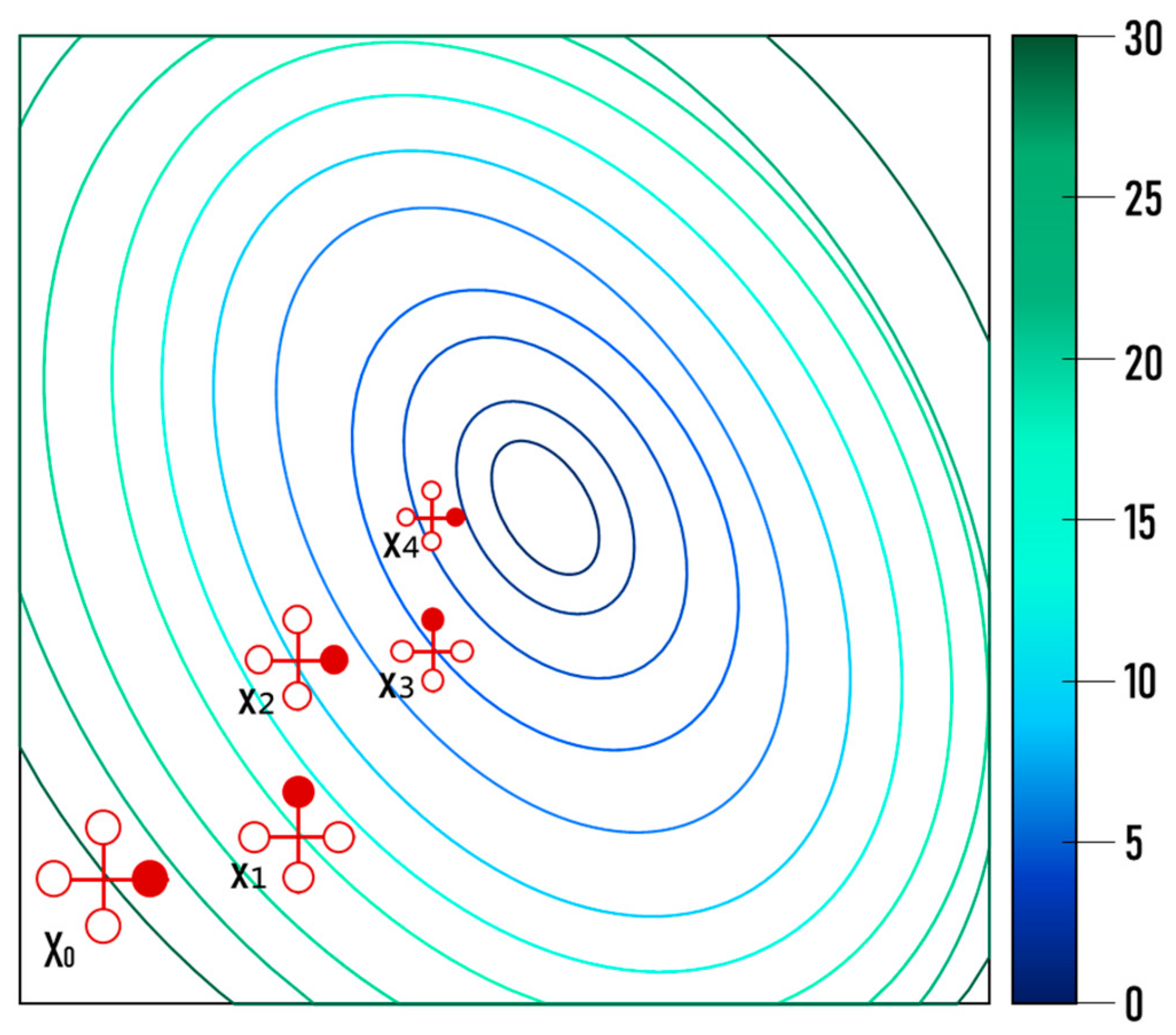
2.2.3. Coordinate Search Method
2.3. Classification of the Properties of Optimization
3. Simulation Results
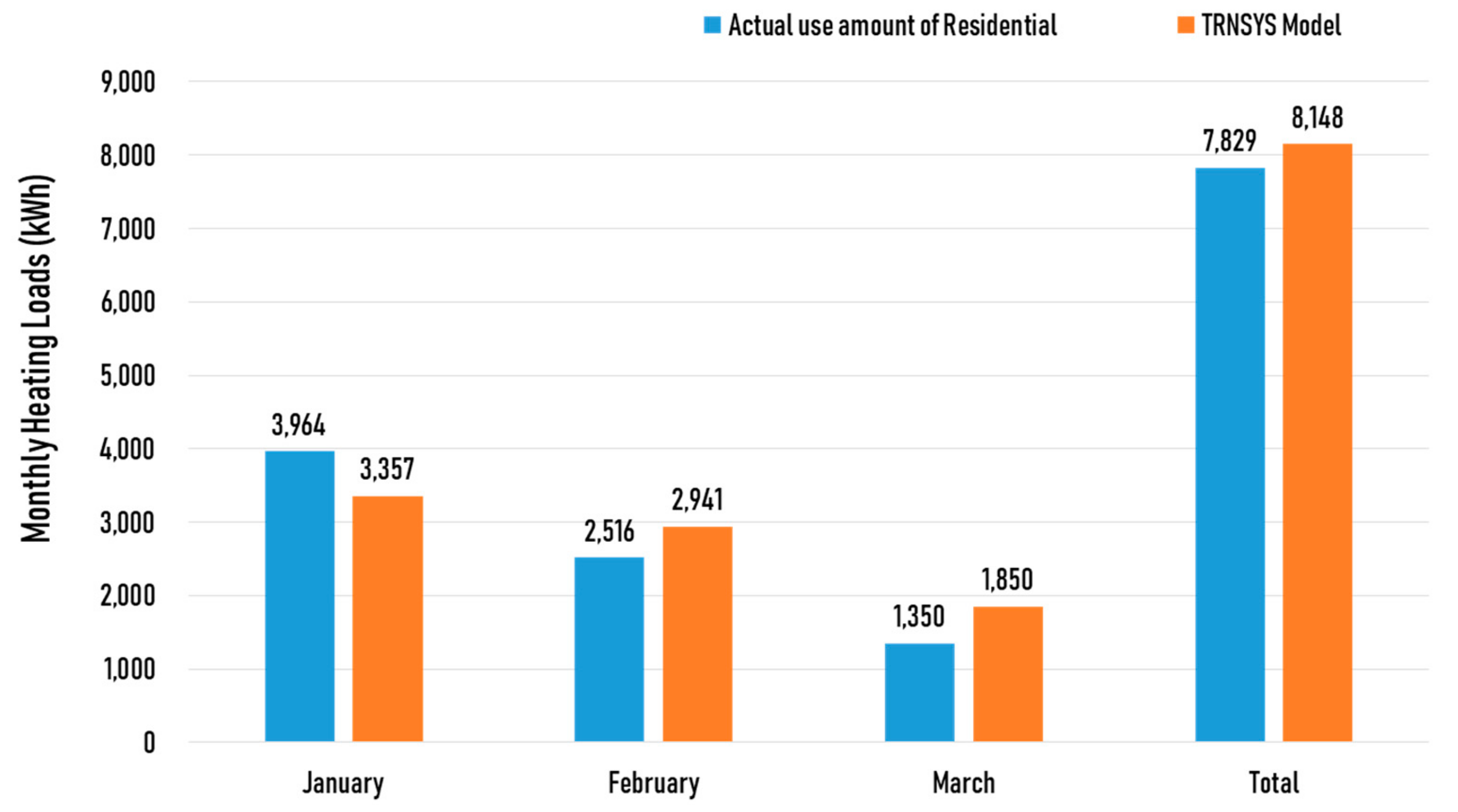
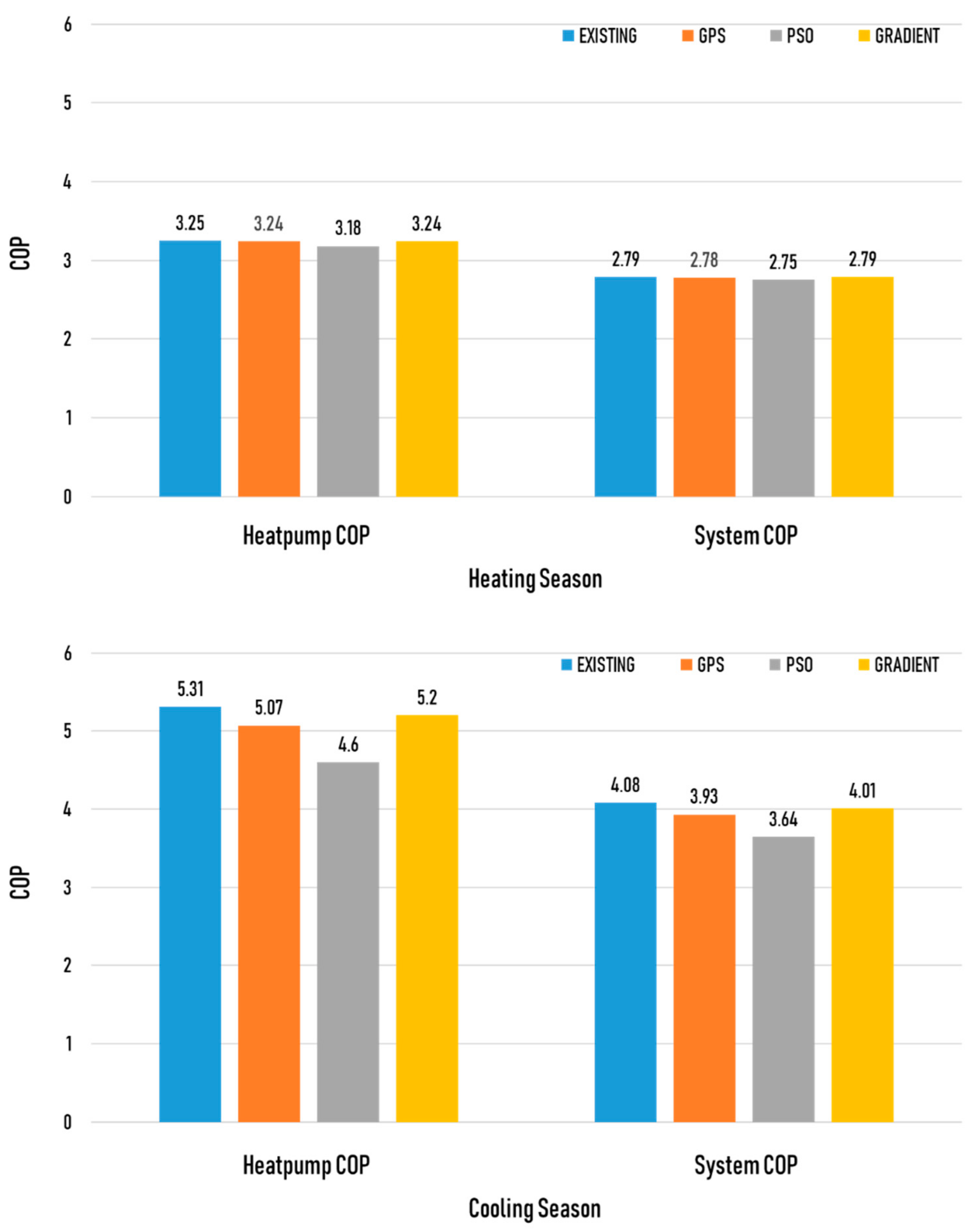
3.1. Heat Source Temperature and COP
3.2. Optimization Results
4. Conclusions
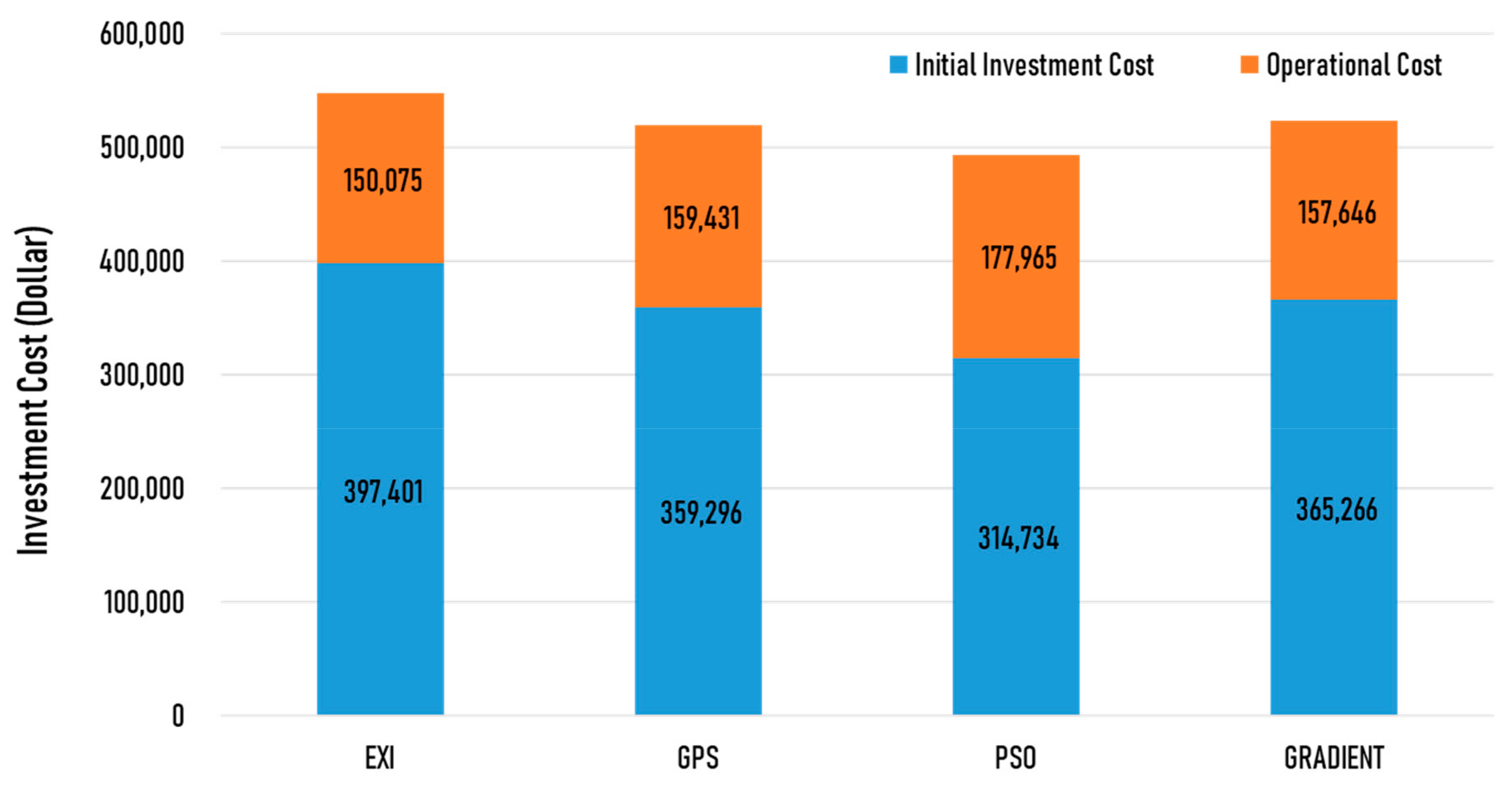
- All of the optimization algorithms used in this study reduced the cost of the GSHP system compared to the existing design.
- In this study, the PSO algorithm was best algorithm for GSHP optimization, with minimal investment costs. The time to complete the optimization was short; the PSO algorithm took the least time, followed by the coordinate search method, and finally the discrete Armijo gradient algorithm.
- For the operating period of 20 years, compared to the existing design, the investment cost was reduced by approximately 4.5% for the discrete Armijo gradient algorithm, 10.0% for the PSO algorithm, and 5.3% for the coordinate search method algorithm.
- For the operating period of 10 years, compared to the existing design, the investment cost was reduced by approximately 4.9% for the discrete Armijo gradient algorithm, 21.3% for the PSO algorithm, and 23.2% for the coordinate search method algorithm.
- Regarding the coordinate search method, the life-cycle cost was effectively reduced, but local optimization was a possibility, which may be different from the real optimal value.
- Compared to the existing design, the heat pump COP and the system COP of the PSO algorithm, which exhibited the lowest investment cost, were reduced by approximately 13% and 11%, respectively.
- In the future, the optimal operation method for GSHP systems should be developed while considering the characteristics of the building load and energy efficiency. Furthermore, the optimization of hybrid systems with other heat source systems should be considered for real building applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UNFCCC. Updated Synthesis Report on the Intended Nationally Determined Contributions; UNFCCC: Rio de Janeiro, Brazil; New York, NY, USA, 2016. [Google Scholar]
- Korea Energy Economics Institute. A Comparative Analysis of Post 2020 GHG Reduction Targets in Major Countries; Korea Energy Economics Institute: Ulsan, Korea, 2016. [Google Scholar]
- South Korean Government. 2030 Roadmap. Available online: http://www.me.go.kr/home/file/readDownloadFile.do?field=158551&fileSeq=1 (accessed on 27 June 2018.).
- Ministry of Trade, Industry and Energy. Renewable Energy 3020 Plan. 2017.12. pp. 2–3. Available online: http://www.lse.ac.uk/GranthamInstitute/wp-content/uploads/2018/02/Implementation-plans-for-renewable-20-by-2030.pdf (accessed on 23 December 2007).
- Renewable Energy Center, Korea Energy Agency. Available online: http://www.energy.or.kr/web/kem_home_new/new_energy/RPS_01.asp (accessed on 1 February 2012).
- Korea Energy Agency. Zero-Energy Building. Available online: https://zeb.energy.or.kr/introduceZero/introduce.aspx (accessed on 23 October 2017).
- Kavanaugh, S.; Rafferty, K. Geothermal Heating and Cooling Design of Ground-Source Heat Pump Systems; ASHRAE: Atlanta, GA, USA, 2014; pp. 91–92. [Google Scholar]
- Roger, W.H.; Michale, E.M. HVAC System Design Handbook, 5th ed.; Mc Graw Hill: New York, NY, USA, 2010; pp. 28–30. [Google Scholar]
- Ryu, H.; Chung, M.; Lee, B.; Choi, H.; Choi, H. A Study on Selection of Pipe Materials Considering EWT. Korea Soc. Geotherm. Energy Eng. 2014, 10, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Min, K.C.; Choi, J.H. Effect of the Design Parameters of Geothermal Heat Exchanger Design Length. Korea Soc. Geotherm. Energy Eng. 2011, 7, 10–15. [Google Scholar]
- Park, S.; Lee, H.; Jang, Y.; Kim, E. Sizing of Vertical Borehole Heat Exchangers using TRNOPT. Korean J. Air-Cond. Refrig. Eng. 2016, 28, 402–407. [Google Scholar] [CrossRef]
- Bonamente, E.; Aquino, A. Life-Cycle Assessment of an Innovative Ground-Source Heat Pump System with Upstream Thermal Storage. Energies 2017, 10, 1854. [Google Scholar] [CrossRef]
- Kim, J.; Hong, T.; Chae, M.; Koo, C.; Jeong, J. An Environmental and Economic Assessment for Selecting the Optimal Ground Heat Exchanger by Considering the Entering Water Temperature. Energies 2015, 8, 7752–7776. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Chen, W.; Jin, X.; Zhou, X.; Shi, X. Performance Assessment of Algorithms for Building Energy Optimization Problems with Different Properties. Sustainability 2018, 11, 18. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Tang, P.; Shi, X. Performance indices and evaluation of algorithms in building energy efficient design optimization. Energy 2016, 114, 100–112. [Google Scholar] [CrossRef]
- Choi, M.; Ko, M.; Kim, Y.; Park, J.; Rhee, U. Investigation and Analysis on the present state of Geothermal Source Heat Pump System Applied in Korea. Korean J. Air-Cond. Refrig. Eng. 2009, 21, 267–272. [Google Scholar]
- Lim, H. Ground source heat pump. Korean J. Air-Cond. Refrig. Eng. Korea 2010, 39, 22–32. [Google Scholar]
- Kim, D.; Lee, D.; Heo, J.; Kim, M. Empirical Results and Operational Cost Analysis of Geothermal Heat Pump System using Thermal Energy Storage in Cooling Season. Korean J. Air-Cond. Refrig. Eng. 2018, 30, 167–174. [Google Scholar]
- Yu, M.G.; Nam, Y.; Lee, K.H. Design method of heat storage type ground source heat pump system considering energy load pattern of greenhouse. Korea Inst. Ecol. Archit. Environ. 2015, 15, 57–63. [Google Scholar] [Green Version]
- Lee, H. Performance-based Energy Standard of the Total Annual Energy Use in Office and Apartment Buildings. J. Korean Living Environ. Syst. 2008, 15, 596–602. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. Energy Saving Design Standard of Building. September 2018. Available online: http://www.law.go.kr/ (accessed on 1 September 2018).
- ASHRAE Standard 90.1-2013. Energy Standard for Buildings Except Low-Rise Residential Buildings; (I-P Edition); ASHRAE: Atlanta, GA, USA, 2013. [Google Scholar]
- ASHRAE Standard 62.1-2013. Ventilation for Acceptable Indoor Air Quality; ASHRAE: Atlanta, GA, USA, 2013. [Google Scholar]
- ASHRAE. ASHRAE Handbook-Fundamentals; SI Edition Supported by ASHRAE Research; ASHRAE: Atlanta, GA, USA, 2005. [Google Scholar]
- Design Guide for Ground Source Heat Pump System. Korean Inst. Archit. Sustain. Environ. Build. Syst. 2015, 3, 6.
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks IV, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. Direct search solution of numerical and statistical problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Dolan, E.D.; Lewis, R.M.; Torczon, V.J. On the local convergence of pattern search. SIAM J. Optim. 2003, 14, 567–583. [Google Scholar] [CrossRef]
- Frandi, E.; Papini, A. Coordinate Search Algorithms in Multilevel Optimization. Optim. Methods Softw. 2014, 29, 1020–1041. [Google Scholar] [CrossRef]
- Wetter, M. GenOpt® Generic Optimization Program User Manual Version 3.1.0; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2011. Available online: http://simulationresearch.lbl.gov/GO/download/manual-3-1-0.pdf (accessed on 8 August 2018).
- Korean On-Line E-Procurement System. Available online: http://shopping.g2b.go.kr (accessed on 23 October 2016).
- Korea Energy Agency. New & Renewable Energy Center. Available online: http://www.knrec.or.kr (accessed on 23 October 2010).
- Korean Electric Power Corporation (KEPCO). Available online: http://cyber.kepco.co.kr (accessed on 1 July 2019).
- ASHRAE Standard 90.1—2004. Energy Standard for Buildings Except Low-Rise Residential Buildings; (I-P Edition) Appendix G3.1.2.2; ASHRAE: Atlanta, GA, USA, 2004; p. 176. [Google Scholar]
- Korea Energy Agency, New & Renewable Energy Center. Geothermal Review Check List; Korea Energy Agency, New & Renewable Energy Center: Ulsan, Korea. Available online: http://kempia.kemco.or.kr/KemcoMain/RegeRR/%E2%91%A0%EC%B2%B4%ED%81%AC%EB%A6%AC%EC%8A%A4%ED%8A%B8.hwp (accessed on 23 September 2011).




| Year | 2012 | 2016 | 2020 | 2025 | 2030 |
|---|---|---|---|---|---|
| Renewable energy proportion | 3.2% | 4.8% | 6.5% | 10.3% | 14.3% |
| Building Construction | Heat Transfer Coefficient | |
|---|---|---|
| External Wall | 0.32 | |
| Internal Wall | 0.43 | |
| Ground Floor | 0.25 | |
| Roof | 0.18 | |
| Window | 1.70 |
| Value | Units | ||
|---|---|---|---|
| Floor area | 0.32 | ||
| Floor height | 3.8 | ||
| Window area ratio | 0.4 | ||
| Gains | People Load | 130 | W/person |
| Lighting Load | 12 | ||
| Equipment Load | 20 | ||
| Ventilation | 0.4 | ACH (Air changes per hour) | |
| Infiltration | 0.35 | ACH (Air changes per hour) | |
| Set Point Temperature (Cooling/Heating) | 26/22 | ℃ | |
| Operating Period | Cooling | May–September | Month |
| Heating | January–March, November, and December | Month | |
| Ground Heat Exchanger | Heat Pump | Heat Storage Tank | |
|---|---|---|---|
| Value | 150 m (Number of boreholes: 63) | 484.17 | 5 tons |
| Design Variable | Minimum Value | Initial Value | Maximum Value | Step Size |
|---|---|---|---|---|
| Ground Heat Exchanger | 50 m | 150 m | 250 m | 10 m |
| Heat Pump | 408 | 484.17 | 581 | 0.3 |
| Heat Storage Tank | 1 ton | 5 tons | 10 tons | 0.1 ton |
| Optimization Algorithm | Ground Heat Exchanger | Heat Pump | Heat Storage Tank | Objective Function |
|---|---|---|---|---|
| Existing Design | 150 m (9450 m) | 484.17 | 5 tons | 463,189 dollars |
| Coordinate Search Method | 105 m (6615 m) | 482.89 | 4.25 tons | 389,422 dollars |
| Particle Swarm Optimization | 106.18 m (6689.34 m) | 493.27 | 6.14 tons | 397,338 dollars |
| Discrete Armijo Gradient | 140.39 m (8844.59 m) | 484.00. | 5 tons | 447,265 dollars |
| Optimization Algorithm | Ground Heat Exchanger | Heat Pump | Heat Storage Tank | Objective Function |
|---|---|---|---|---|
| Existing Design | 150 m (9450 m) | 484.17 | 5 tons | 547,477 dollars |
| Coordinate Search Method | 131.25 m (8268.75 m) | 484.69 | 4.73 tons | 518,727 dollars |
| Particle Swarm Optimization | 106.85 m (6731.55 m) | 497.02 | 6.10 tons | 492,699 dollars |
| Discrete Armijo Gradient | 133.99 m (8441.37 m) | 484.38 | 5.01 tons | 522,912 dollars |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, H.; Kim, H.; Nam, Y. Study on the Optimum Design of a Ground Heat Pump System Using Optimization Algorithms. Energies 2019, 12, 4033. https://doi.org/10.3390/en12214033
Moon H, Kim H, Nam Y. Study on the Optimum Design of a Ground Heat Pump System Using Optimization Algorithms. Energies. 2019; 12(21):4033. https://doi.org/10.3390/en12214033
Chicago/Turabian StyleMoon, Hyeongjin, Hongkyo Kim, and Yujin Nam. 2019. "Study on the Optimum Design of a Ground Heat Pump System Using Optimization Algorithms" Energies 12, no. 21: 4033. https://doi.org/10.3390/en12214033





