Performance Analysis of Synchronous Reluctance Motor with Limited Amount of Permanent Magnet
Abstract
:1. Introduction
2. Mathematical Model and Configuration of Investigated Motors
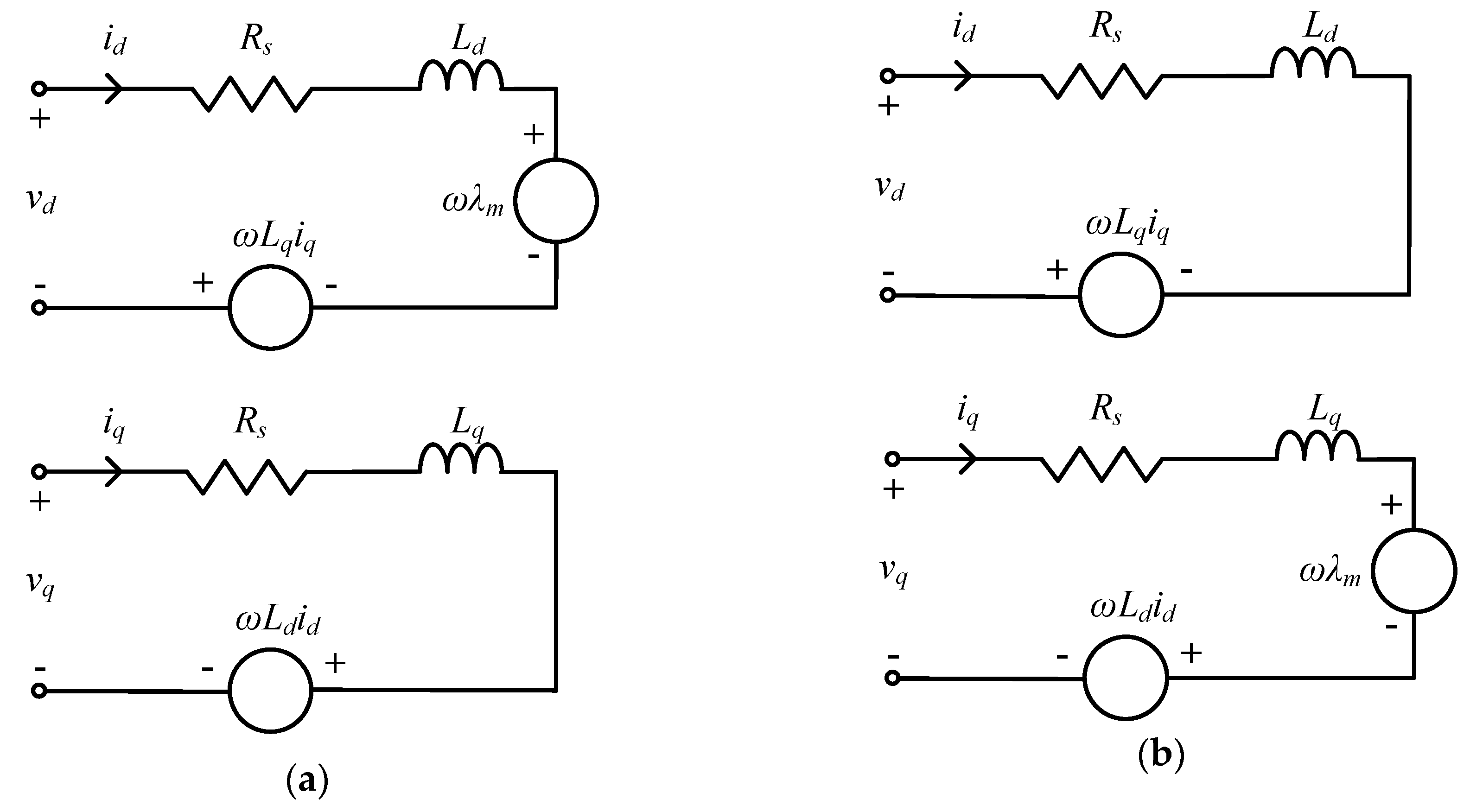
2.1. Mathematical Modeling of Investigated Motors
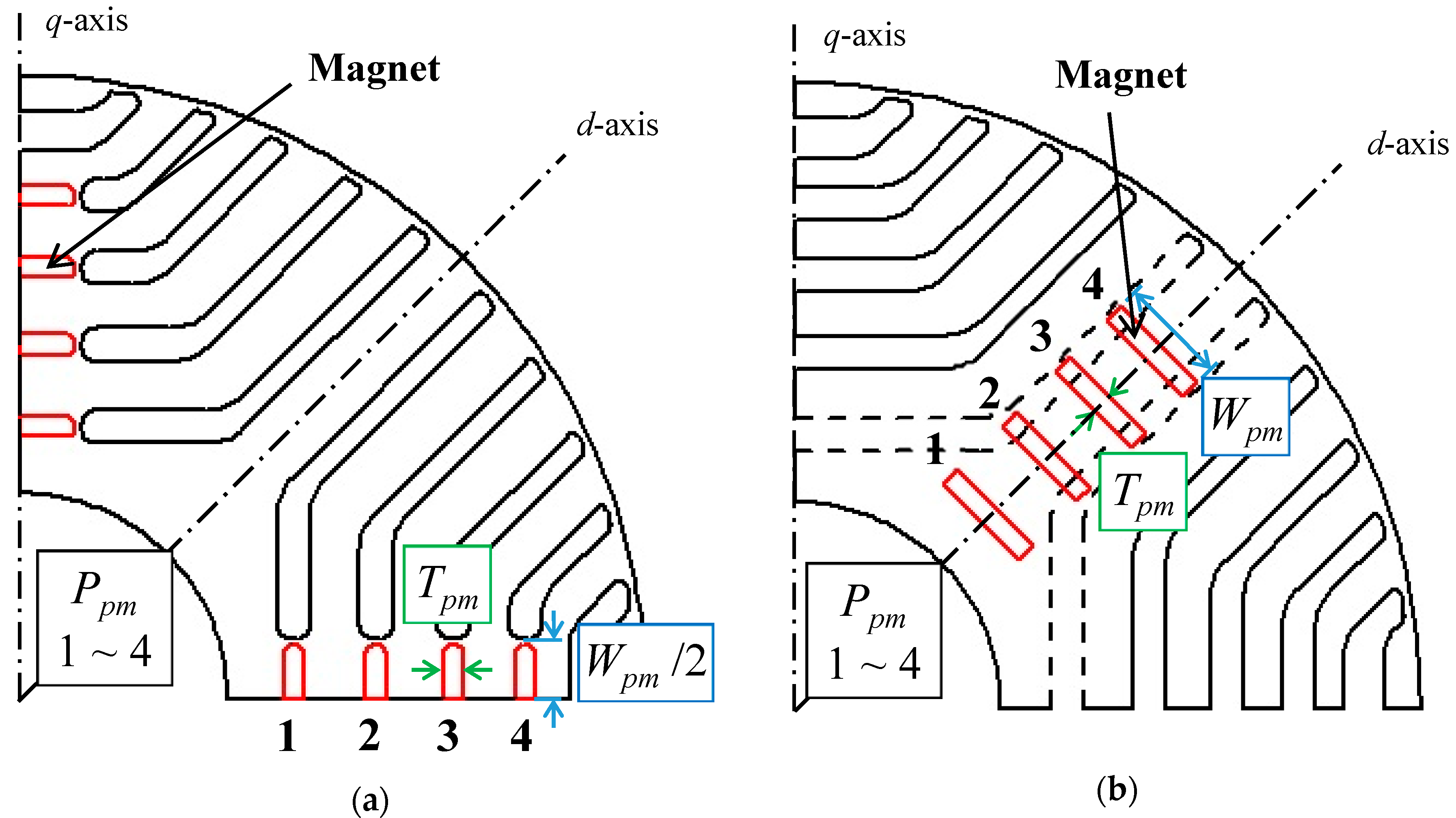
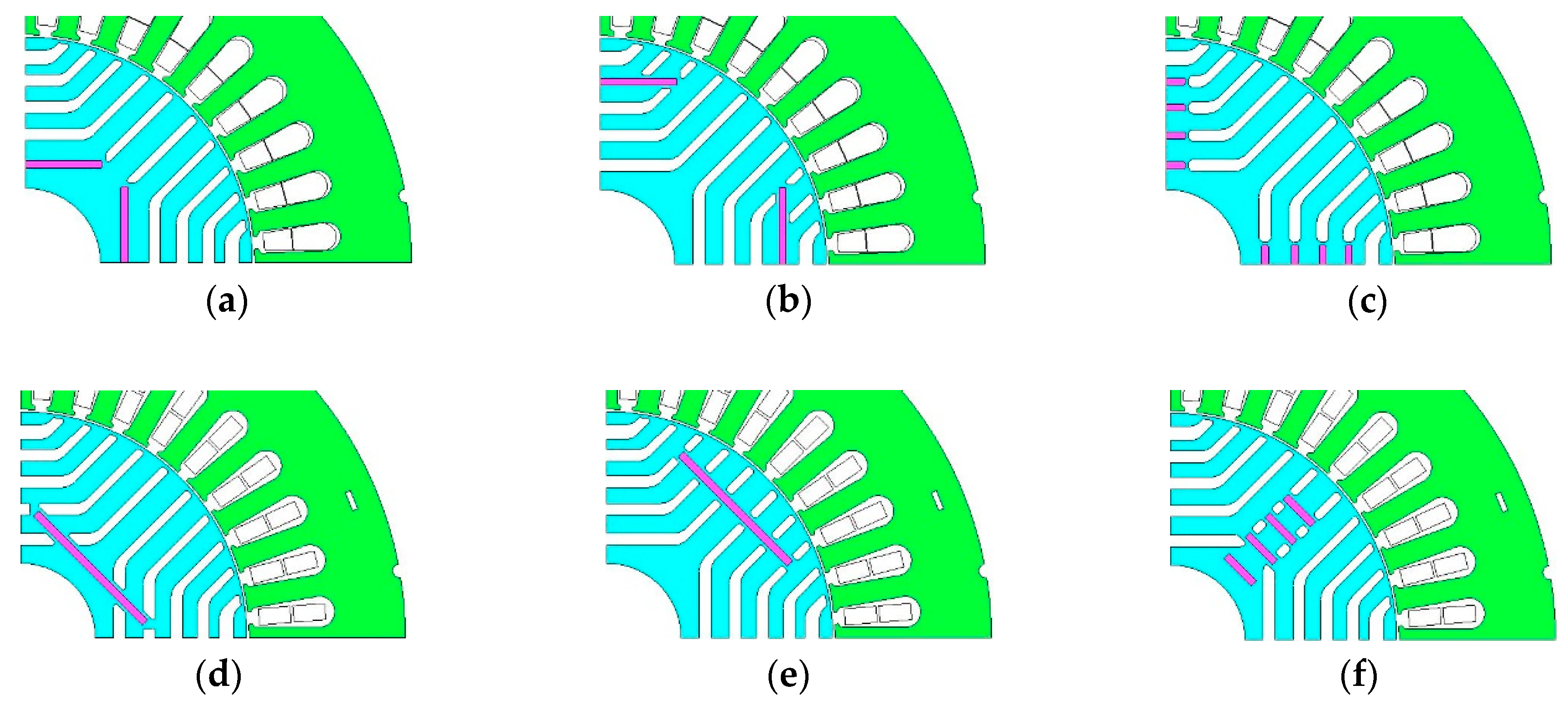
2.2. Configuration of Investigated Motors
3. Comparative Analysis of Influence of PM Position
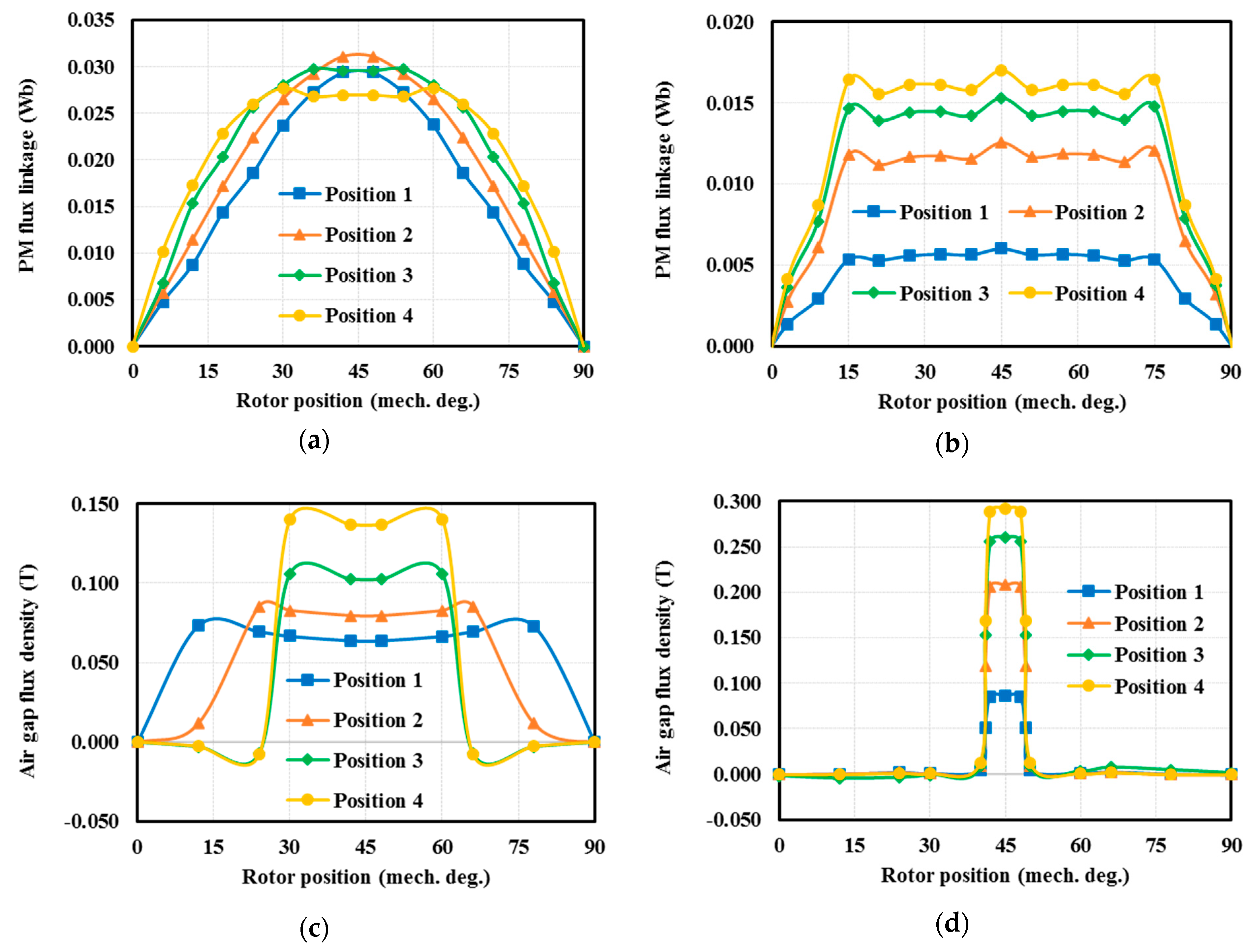
3.1. No-Load Operation Comparison
3.2. On-Load Operation Comparison and Flux Balance Index
4. Comparative Analysis of Motor Characteristics
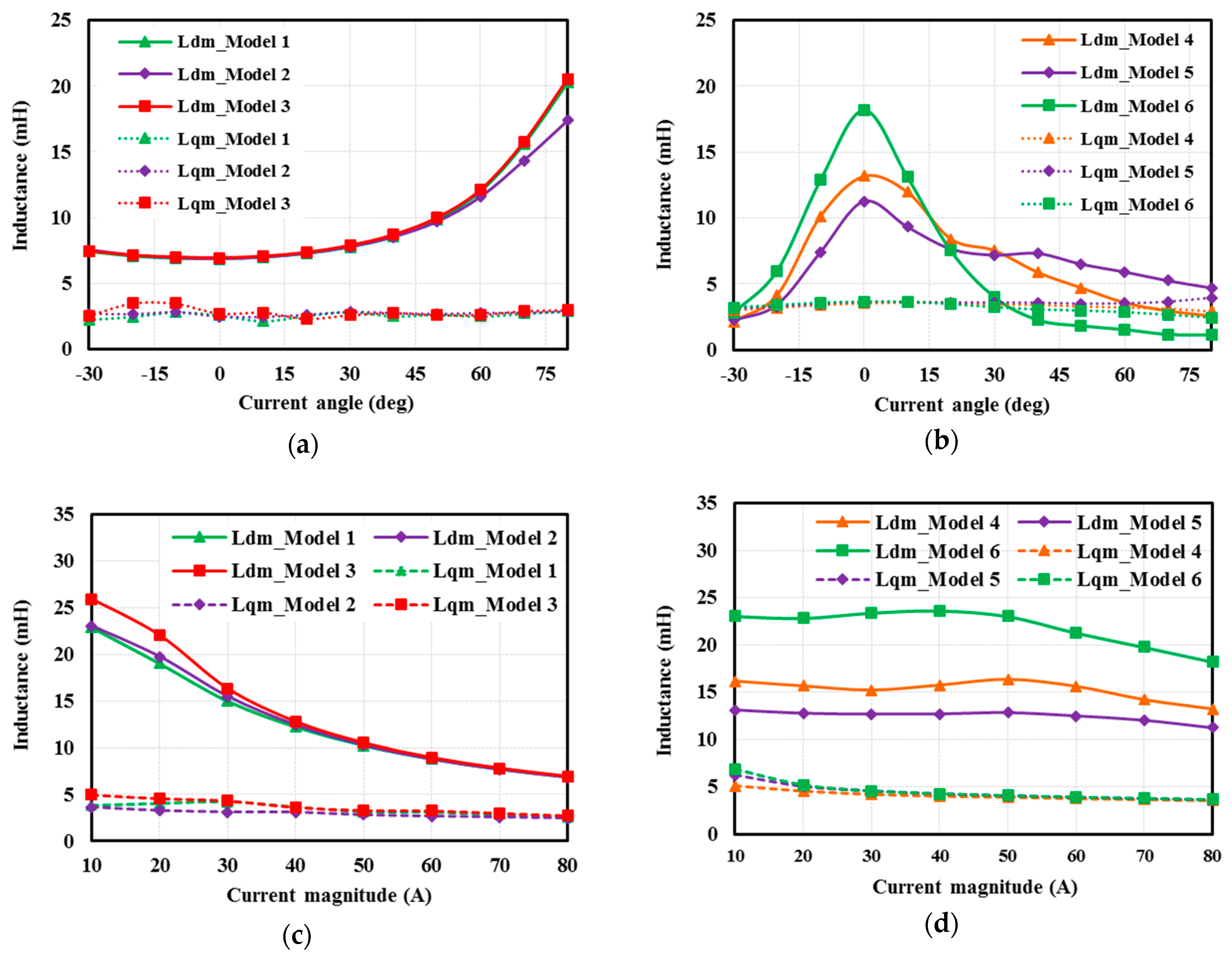
4.1. Motor Inductances
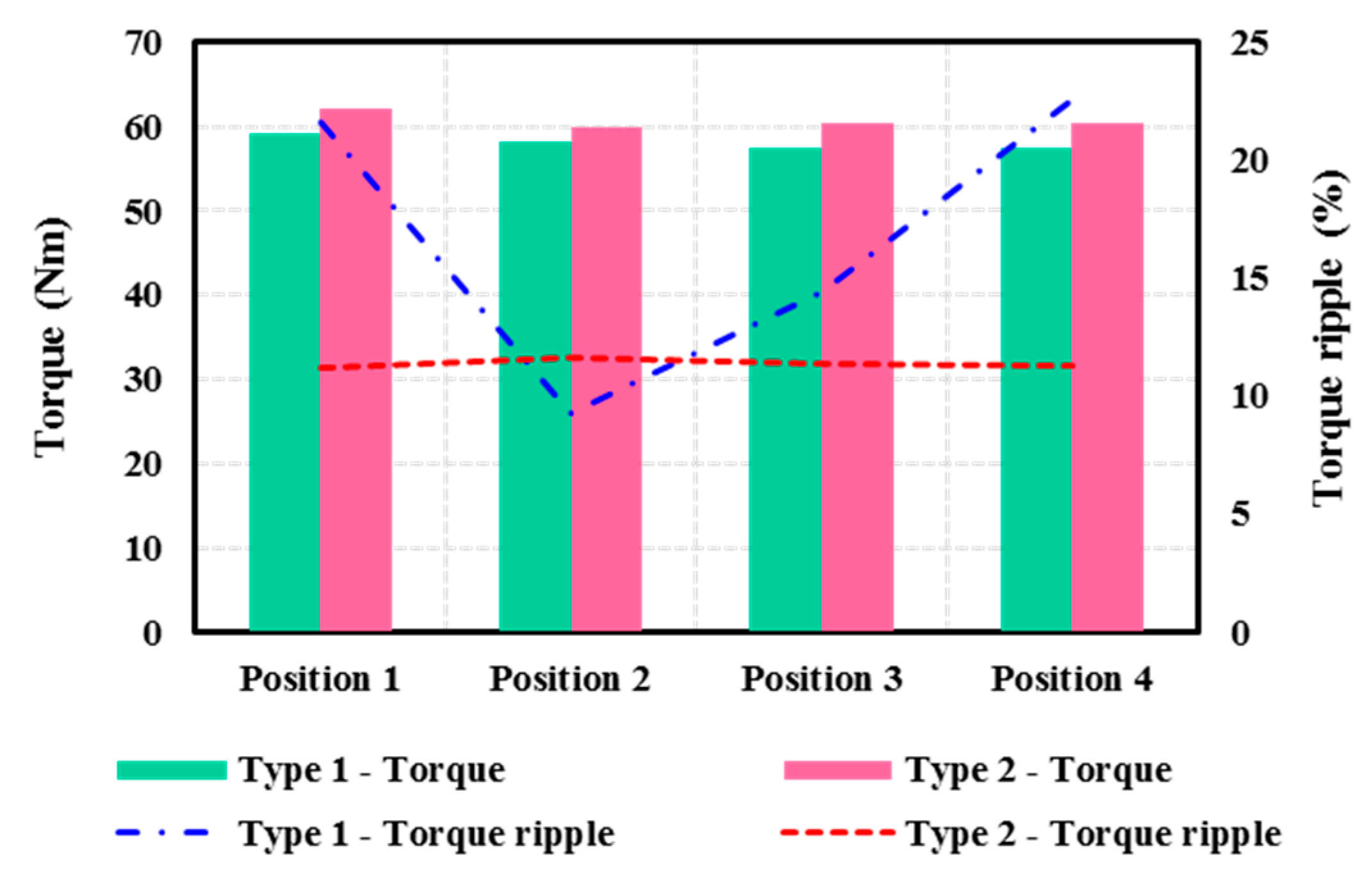
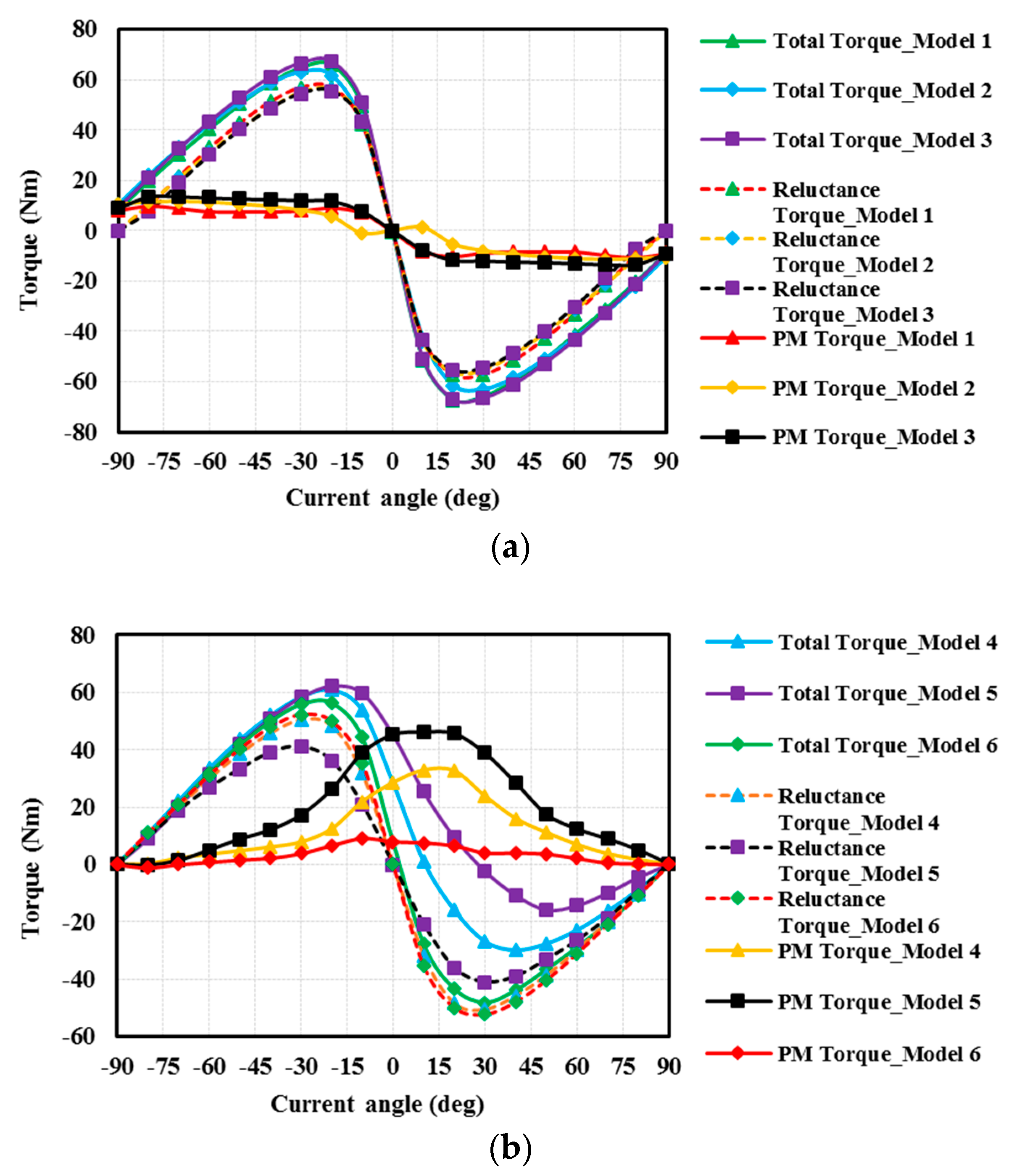
4.2. Torque Production
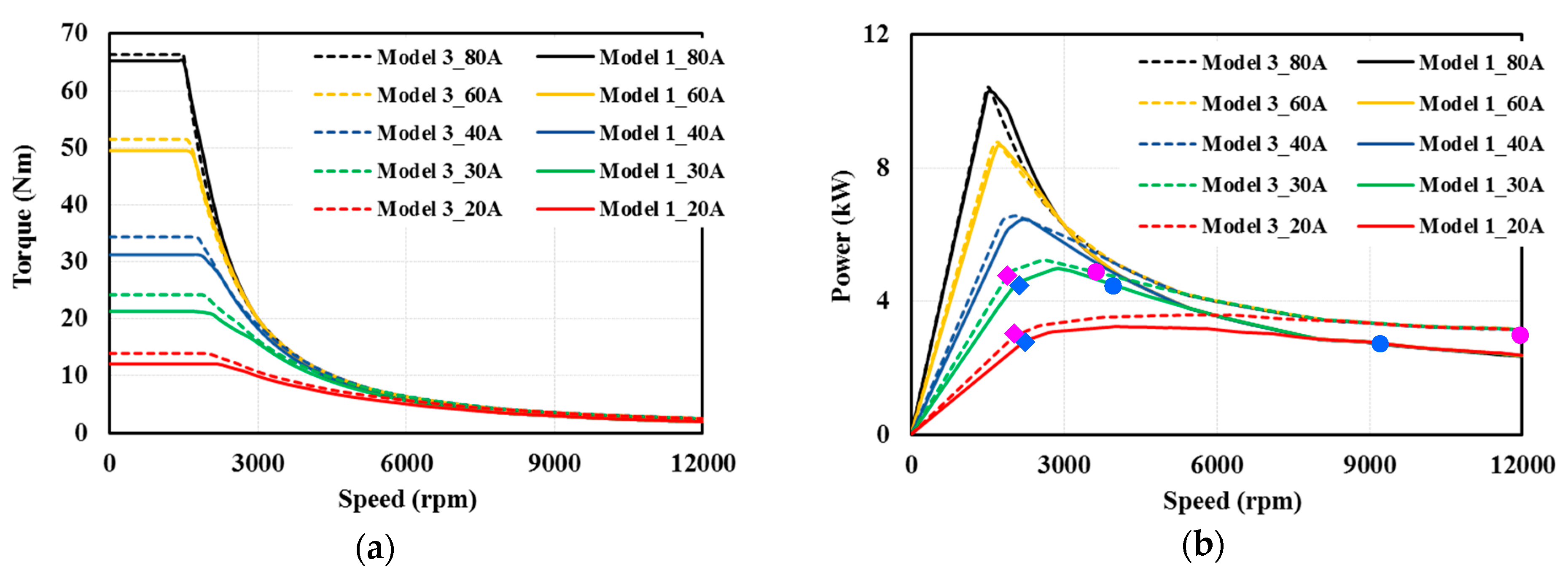
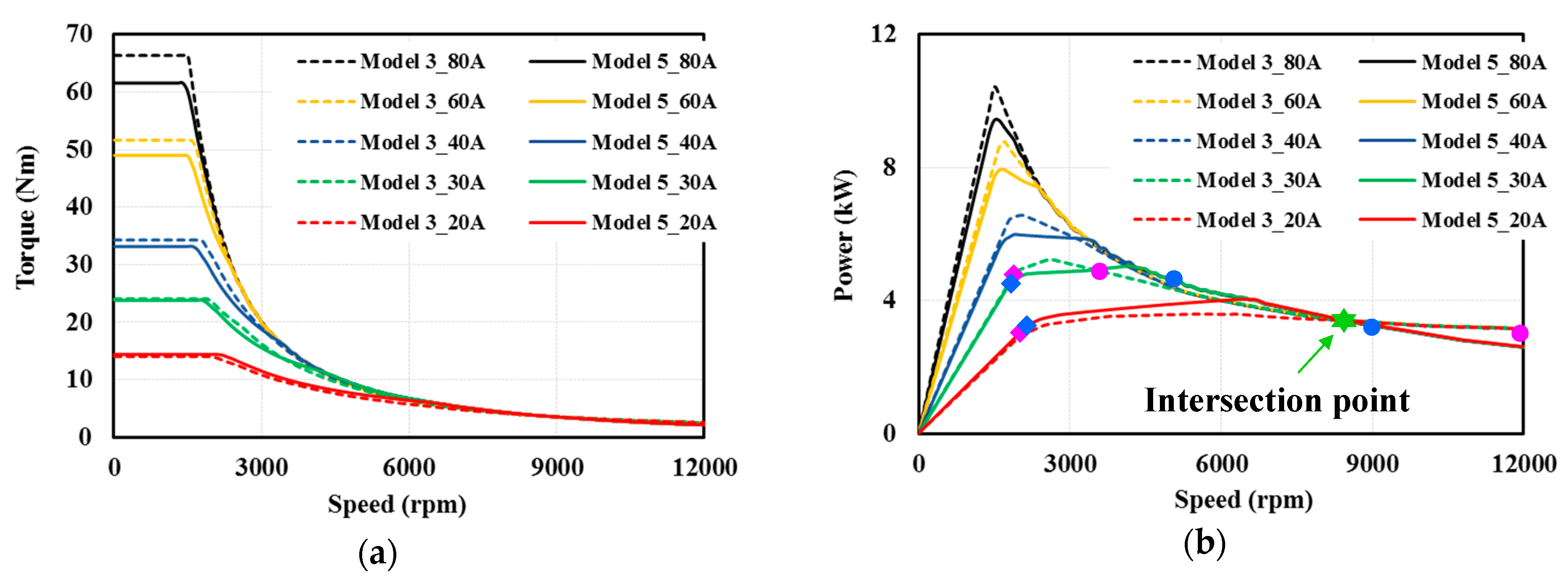
4.3. Torque and Power-Speed Curves
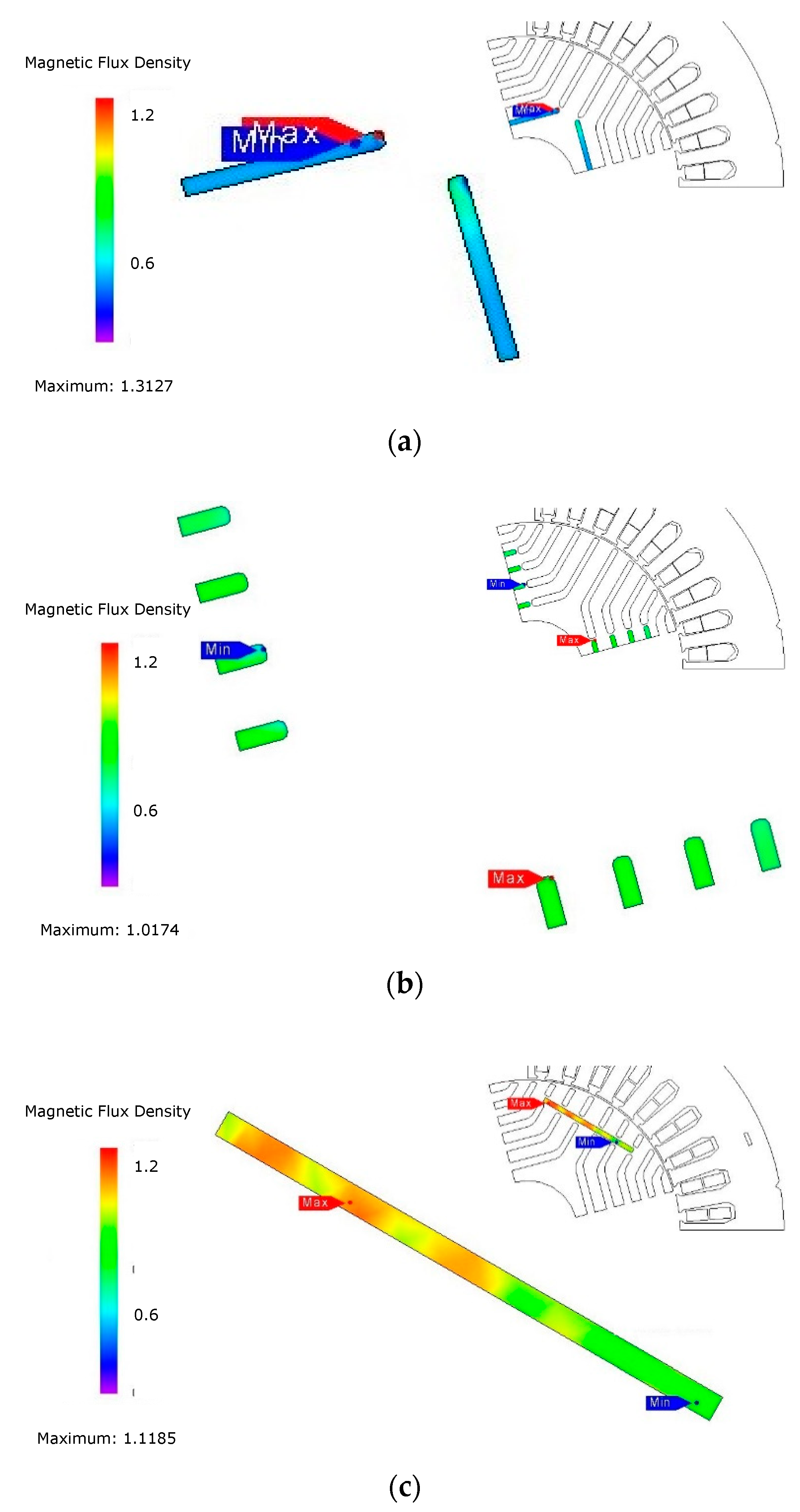
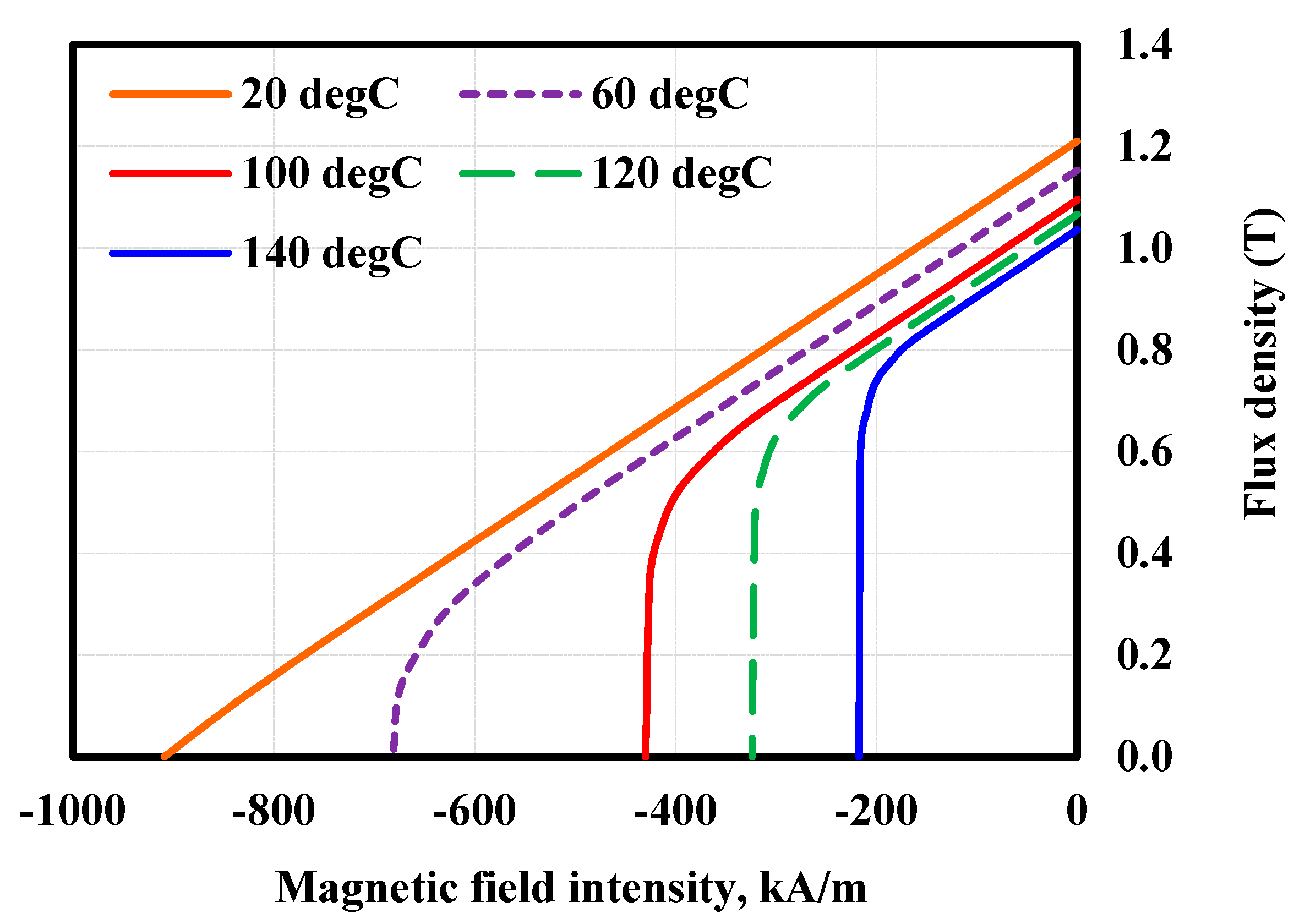
4.4. Demagnetization Analysis
5. Discussion
- For the effect of the PM position, the outward PMs generally produce greater air-gap flux density but torque production does not exactly have the same trend.
- The PM position and its arrangement in the d- or q-axis have a great impact on flux distribution in the rotor where the d-axis PM arrangement possesses a higher flux balance index.
- The PM position has a greater impact on motor inductance of the Type 2 motor than the Type 1 one and the effect is approximately linear.
- Model 3 (conventional multiple-layer PMa-SynRM) has the highest torque production while Model 5 (FI-PMa-SynRM) has the most utilization of PM.
- Model 5 (FI-PMa-SynRM) is the best choice for demagnetization resistance while Model 1 is the worst one.
- For SynRM with a limited PM amount, the reduction of armature current Is leads to an increase of CPSR but a trade-off with torque reduction should be considered.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lipo, T. Synchronous reluctance machines—A viable alternative for AC drives. Electr. Mach. Power Syst. 1991, 19, 659–671. [Google Scholar] [CrossRef]
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous reluctance motor vs. induction motor at low-power industrial applications: Design and comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Sergeant, P.; Rashad, E.M. Synchronous reluctance motor performance based on different electrical steel grades. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Reddy, P.B.; El-Refaie, A.M.; Galioto, S.; Alexander, J.P. Design of synchronous reluctance motor utilizing dual-phase material for traction applications. IEEE Trans. Ind. Appl. 2017, 53, 1948–1957. [Google Scholar] [CrossRef]
- Cai, S.; Jin, M.-J.; Hao, H.; Shen, J.-X. Comparative study on synchronous reluctance and PM machines. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 607–623. [Google Scholar] [CrossRef]
- Guan, Y.; Zhu, Z.Q.; Afinowi, I.A.A.; Mipo, J.C.; Farah, P. Design of synchronous reluctance and permanent magnet synchronous reluctance machines for electric vehicle application. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 586–606. [Google Scholar] [CrossRef]
- Carraro, E.; Degano, M.; Morandi, M.; Bianchi, N. PM synchronous machine comparison for light electric vehicles. In Proceedings of the IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–8. [Google Scholar]
- Ibrahim, M.N.F.; Rashad, E.; Sergeant, P. Performance comparison of conventional synchronous reluctance machines and PM-assisted types with combined star-delta winding. Energies 2017, 10, 1500. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E.; Soong, W. Selection of PM flux linkage for maximum low-speed torque rating in a PM-assisted synchronous reluctance machine. IEEE Trans. Ind. Appl. 2015, 51, 3600–3608. [Google Scholar] [CrossRef]
- Guglielmi, P.; Boazzo, B.; Armando, E.; Pellegrino, G.; Vagati, A. Permanent magnet minimization in PM-assisted synchronous reluctance motors for wide speed range. IEEE Trans. Ind. Appl. 2013, 49, 31–41. [Google Scholar] [CrossRef]
- Bianchi, N.; Mahmoud, H.; Bolognani, S. Fast synthesis of permanent magnet assisted synchronous reluctance motors. IET Electr. Power App. 2016, 10, 312–318. [Google Scholar] [CrossRef]
- Niazi, P.; Toliyat, H.A.; Cheong, D.-H.; Kim, J.-C. A low-cost and efficient permanent-magnet-assisted synchronous reluctance motor drive. IEEE Trans. Ind. Appl. 2007, 43, 542–550. [Google Scholar] [CrossRef]
- Lee, J.H.; Jang, Y.J.; Hong, J.P. Characteristic analysis of permanent magnet-assisted synchronous reluctance motor for high power application. J. Appl. Phys. 2005, 97, 10Q503. [Google Scholar] [CrossRef]
- Huynh, T.A.; Hsieh, M.F. Performance analysis of permanent magnet motors for electric vehicles (EV) traction considering driving cycles. Energies 2018, 11, 1385. [Google Scholar] [CrossRef]
- Cai, H.; Guan, B.; Xu, L. Low-Cost ferrite PM-Assisted synchronous reluctance machine for electric vehicles. IEEE Trans. Ind. Electron. 2014, 61, 5741–5748. [Google Scholar] [CrossRef]
- Huynh, T.A.; Hsieh, M.-F. Comparative study of PM-assisted SynRM and IPMSM on constant power speed range for EV applications. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Vagati, A. Synchronous Reluctance Electrical Motor Having a Low Torque-Ripple Design. U.S. Patent 5,818,140, 6 October 1998. [Google Scholar]
- Ferrari, M.; Bianchi, N.; Fornasiero, E. Rotor saturation impact in synchronous reluctance and PM assisted reluctance motors. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2014; pp. 1235–1242. [Google Scholar]
- Binns, K.J.; Lawrenson, P.J.; Trowbridge, C.W. The Analytical and Numerical Solution of Electric and Magnetic Fields; Wiley: Chichester, UK, 1992. [Google Scholar]
- Moghaddam, R.R. Synchronous Reluctance Machine (SYNRM) in Variable Speed Drives (VSD) Applications. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Morimoto, S.; Sanada, M.; Takeda, Y. Performance of PM-Assisted synchronous reluctance motor for high-efficiency and wide constant-power operation. IEEE Trans. Ind. Appl. 2001, 37, 1234–1240. [Google Scholar] [CrossRef]
- Imamura, K.; Sanada, M.; Morimoto, S.; Inoue, Y. Improvement of characteristics by flux barrier shape and magnet thickness of IPMSM with Dy-free rare-earth magnet. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Huynh, T.A.; Hsieh, M.-F.; Shih, K.-J.; Kuo, H.-F. An investigation into the effect of PM arrangements on PMa-SynRM performance. IEEE Trans. Ind. Appl. 2018, 54, 5856–5868. [Google Scholar] [CrossRef]
- Pellegrino, G.; Vagati, A.; Guglielmi, P. Design tradeoffs between constant power speed range, uncontrolled generator operation, and rated current of IPM motor drives. IEEE Trans. Ind. Appl. 2011, 47, 1995–2003. [Google Scholar] [CrossRef]
- Prins, M.H.A.; Kamper, M.J. Design optimisation of field-intensified permanent magnet machine. In Proceedings of the IEEE International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 117–123. [Google Scholar]
- Ngo, D.-K.; Hsieh, M.-F.; Huynh, T.A. Torque enhancement for a novel flux intensifying PMa-SynRM using surface-inset permanent magnet. IEEE Trans. Magn. 2019, 55, 8106108. [Google Scholar] [CrossRef]
- Pillay, P.; Krishnan, R. Modeling of permanent magnet motor drives. IEEE Trans. Ind. Electron. 1988, 35, 537–541. [Google Scholar] [CrossRef]
- Morimoto, S.; Takeda, Y.; Hatanaka, K.; Tong, Y.; Hirasa, T. Designand control system of inverter-driven permanent magnet synchronous motors for high torque operation. IEEE Trans. Indus. Appl. 1993, 29, 1150–1155. [Google Scholar] [CrossRef]
- Baek, J.; Bonthu, S.S.R.; Choi, S. Design of five-phase permanent magnet assisted synchronous reluctance motor for low output torque ripple applications. IET Electr. Power App. 2016, 10, 339–346. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.C.; Hyun, D.S. Effect analysis of magnet on Ld and Lq inductance of permanent magnet assisted synchronous reluctance motor using finite element method. IEEE Trans. Magn. 1999, 35, 1199–1202. [Google Scholar] [CrossRef]
- Ngo, D.-K.; Hsieh, M.-F. Analysis of flux intensifying effect on synchronous motors applied to electric scooter. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (IEEE-VPPC), Hanoi, Vietnam, 14–17 October 2019. [Google Scholar]
- Jahns, T.M. Flux-weakening regime operation of an interior permanent-magnet synchronous motor drive. IEEE Trans. Ind. Appl. 1987, 23, 681–689. [Google Scholar] [CrossRef]
- Soong, W.L.; Miller, T.H.E. Field-weakening performance of brushless synchronous AC motor drives. IEE Proc. Electr. Power Appl. 1994, 141, 331–340. [Google Scholar] [CrossRef]
- Jahns, T.M.; Kliman, G.B.; Neumann, T.W. Interior permanent-magnet synchronous motors for adjustable-speed drives. IEEE Trans. Ind. Appl. 1986, 22, 738–747. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Permanent-magnet optimization in permanent-magnet-assisted synchronous reluctance motor for a wide constant-power speed range. IEEE Trans. Ind. Electron. 2012, 59, 2495–2502. [Google Scholar] [CrossRef]
- Kim, W.-H.; Kim, K.-S.; Kim, S.-J.; Kang, D.-W.; Go, S.-C.; Chun, Y.-D.; Lee, J. Optimal PM design of PMA-SynRM for wide constant-power operation and torque ripple reduction. IEEE Trans. Magn. 2009, 45, 4660–4663. [Google Scholar] [CrossRef]
- Ferrari, M.; Bianchi, N.; Doria, A.; Fornasiero, E. Design of synchronous reluctance motor for hybrid electric vehicles. IEEE Trans. Ind. Appl. 2015, 51, 3030–3040. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, S.; Du, Y.; Xiang, Z.; Xu, L. Electromagnetic performance analysis and verification of a new flux-intensifying permanent magnet brushless motor with two-layer segmented permanent magnets. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- N35H—Arnold Magnetic Technologies. Available online: https://www.arnoldmagnetics.com/wp-content/uploads/2017/11/N35H-151021.pdf (accessed on 23 July 2019).
- Zhu, X.; Wu, W.; Yang, S.; Xiang, Z.; Quan, L. Comparative design and analysis of new type of flux-intensifying interior permanent magnet motors with different q-axis rotor flux barriers. IEEE Trans. Energy Convers. 2018, 33, 2260–2269. [Google Scholar] [CrossRef]
- Limsuwan, N.; Shibukawa, Y.; Reigosa, D.D.; Lorenz, R.D. Novel design of flux-intensifying interior permanent magnet synchronous machine suitable for self-sensing control at very low speed and power conversion. IEEE Trans. Ind. Appl. 2011, 47, 2004–2012. [Google Scholar] [CrossRef]






| Reference Motor Source | [10] | [11] | [21] | [22] | [23] |
|---|---|---|---|---|---|
| Stator diameter (mm) | 150 | 200 | 125 | 112 | 160 |
| Stack length (mm) | 105 | 40 | 27 | 40 | 120 |
| Motor volume (L) | 1.856 | 1.257 | 0.331 | 0.394 | 2.413 |
| PM volume (L) | 0.066 | 0.077 | 0.013 | 0.009 | 0.023 |
| PM-to-Motor volume ratio (%) | 3.58 | 6.13 | 3.93 | 2.28 | 0.95 |
| PM material type | Rare earth | Ferrite | Ferrite | Rare earth | Rare earth |
| Number of poles | 4 | 4 | 4 | 4 | 4 |
| Number of flux barriers for each pole | 4 | 3 | 2 | 1 | 5 |
| Number of PM layers | 4 | 3 | 2 | 1 | 4 |
| PM size between layers | Unequal | Unequal | Unequal | - | Equal |
| Torque (Nm) | 17.9 | 12.47 | 1.27 | 4.54 | 67.8 |
| Torque density (Nm/L) | 9.7 | 9.9 | 3.8 | 11.5 | 28.1 |
| Parameter/ Specification | Unit | Value | Parameter/ Specification | Unit | Value |
|---|---|---|---|---|---|
| Desired peak power | kW | 10 | Stator diameter | mm | 160 |
| Number of phases | - | 3 | Rotor diameter | mm | 94 |
| Number of poles | - | 4 | Air-gap | mm | 0.5 |
| Number of slots | - | 36 | Stack length | mm | 120 |
| DC voltage | V | 220 | PM meterial | - | N35H |
| Maximum current | A | 80 | PM volume | mm3 | 23040 |
| Number of turns | turns | 6 | PM/Motor volume ratio | % | 0.95 |
| PM Position | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Air-gap flux density for Type 1 (T) | 0.056 | 0.060 | 0.067 | 0.075 |
| Air-gap flux density for Type 2 (T) | 0.025 | 0.059 | 0.074 | 0.083 |
| PM Position | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Lowest flux density for Type 1 (T) | 0.262 | 0.302 | 0.355 | 0.372 |
| Average flux density in rotor core for Type 1 (T) | 1.104 | 1.111 | 1.103 | 1.120 |
| Flux balance index, Ku for Type 1 (%) | 23.74 | 27.19 | 32.18 | 33.23 |
| Lowest flux density for Type 2 (T) | 0.663 | 0.640 | 0.645 | 0.641 |
| Average flux density in rotor core for Type 2 (T) | 1.190 | 1.171 | 1.172 | 1.169 |
| Flux balance index, Ku for Type 2 (%) | 55.73 | 54.67 | 55.05 | 54.82 |
| Items | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
|---|---|---|---|---|---|---|
| PM position | 1 | 4 | 1, 2, 3,4 | 1 | 4 | 1, 2, 3, 4 |
| PM dimenssion | 1.5 × 32 mm | 1.5 × 32 mm | 1.5 × 8 mm | 1.5 × 32 mm | 1.5 × 32 mm | 1.5 × 8 mm |
| Items | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
|---|---|---|---|---|---|---|
| Maximum torque (Nm) | 66.3 | 63.7 | 67.8 | 60.9 | 62.4 | 57.3 |
| PM torque at maximum torque (Nm) | 8.6 | 7.4 | 11.9 | 11.6 | 28.5 | 5.5 |
| PM torque ratio (%) | 13.0 | 11.6 | 17.6 | 19.0 | 45.7 | 9.6 |
| Is (A) | 80 | 60 | 40 | 30 | 20 |
|---|---|---|---|---|---|
| Ich (A) (Model 1) | 18.9 | 17.1 | 13.7 | 10.2 | 9.4 |
| Is/Ich (Model 1) | 4.23 | 3.52 | 2.93 | 2.95 | 2.13 |
| Ich (A) (Model 3) | 12.0 | 10.7 | 9.3 | 8.6 | 7.5 |
| Is/Ich (Model 3) | 6.67 | 5.59 | 4.28 | 3.50 | 2.68 |
| Ich (A) (Model 5) | 19.7 | 17.2 | 15.1 | 14.2 | 13.7 |
| Is/Ich (Model 5) | 4.06 | 3.49 | 2.65 | 2.12 | 1.46 |
| Temperature | 20 °C | 90 °C | 105 °C | 120 °C | 130 °C | 155 °C |
|---|---|---|---|---|---|---|
| Model 1 | 0.403 T | 0.354 T | 0.342 T | 0.327 T | 0.273 T | 0.133 T |
| Model 3 | 0.711 T | 0.614 T | 0.595 T | 0.577 T | 0.563 T | 0.508 T |
| Model 5 | 0.912 T | 0.869 T | 0.860 T | 0.852 T | 0.845 T | 0.828 T |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngo, D.-K.; Hsieh, M.-F. Performance Analysis of Synchronous Reluctance Motor with Limited Amount of Permanent Magnet. Energies 2019, 12, 3504. https://doi.org/10.3390/en12183504
Ngo D-K, Hsieh M-F. Performance Analysis of Synchronous Reluctance Motor with Limited Amount of Permanent Magnet. Energies. 2019; 12(18):3504. https://doi.org/10.3390/en12183504
Chicago/Turabian StyleNgo, Duc-Kien, and Min-Fu Hsieh. 2019. "Performance Analysis of Synchronous Reluctance Motor with Limited Amount of Permanent Magnet" Energies 12, no. 18: 3504. https://doi.org/10.3390/en12183504
APA StyleNgo, D.-K., & Hsieh, M.-F. (2019). Performance Analysis of Synchronous Reluctance Motor with Limited Amount of Permanent Magnet. Energies, 12(18), 3504. https://doi.org/10.3390/en12183504






