An Intelligent Battery Energy Storage-Based Controller for Power Quality Improvement in Microgrids
Abstract
:1. Introduction
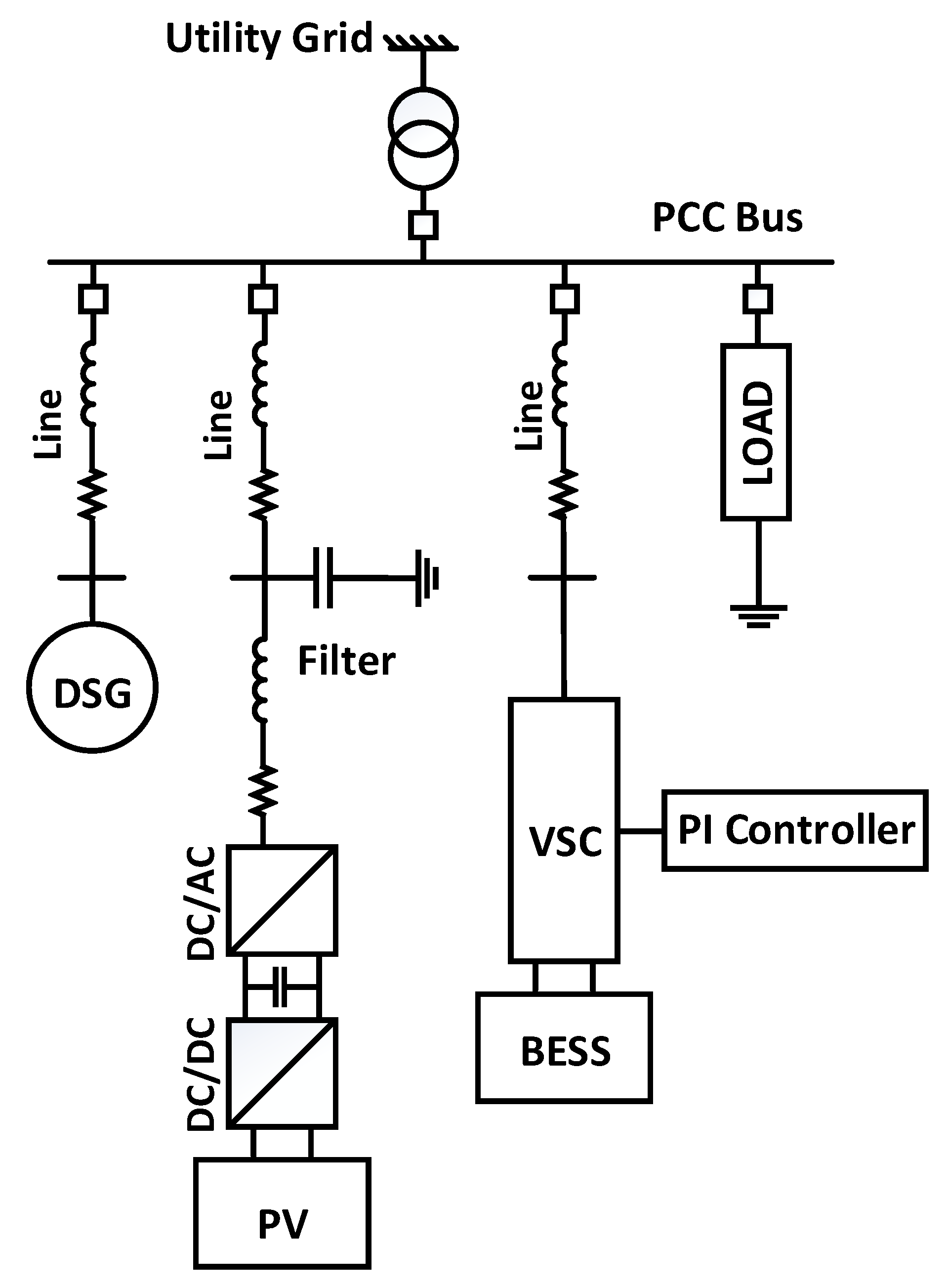
2. Problem Description
3. Mathematical System Modelling
3.1. Diesel Synchronous Generator
- : output electrical power
- : input mechanical power
- : inertia constant
- : reference angular speed.
- : d-axis synchronous reactance
- : d-axis transient reactance
- : exciter time constant
- : exciter gain
- : open circuit field constant
- : reference field voltage
- : DSG reference terminal voltage.
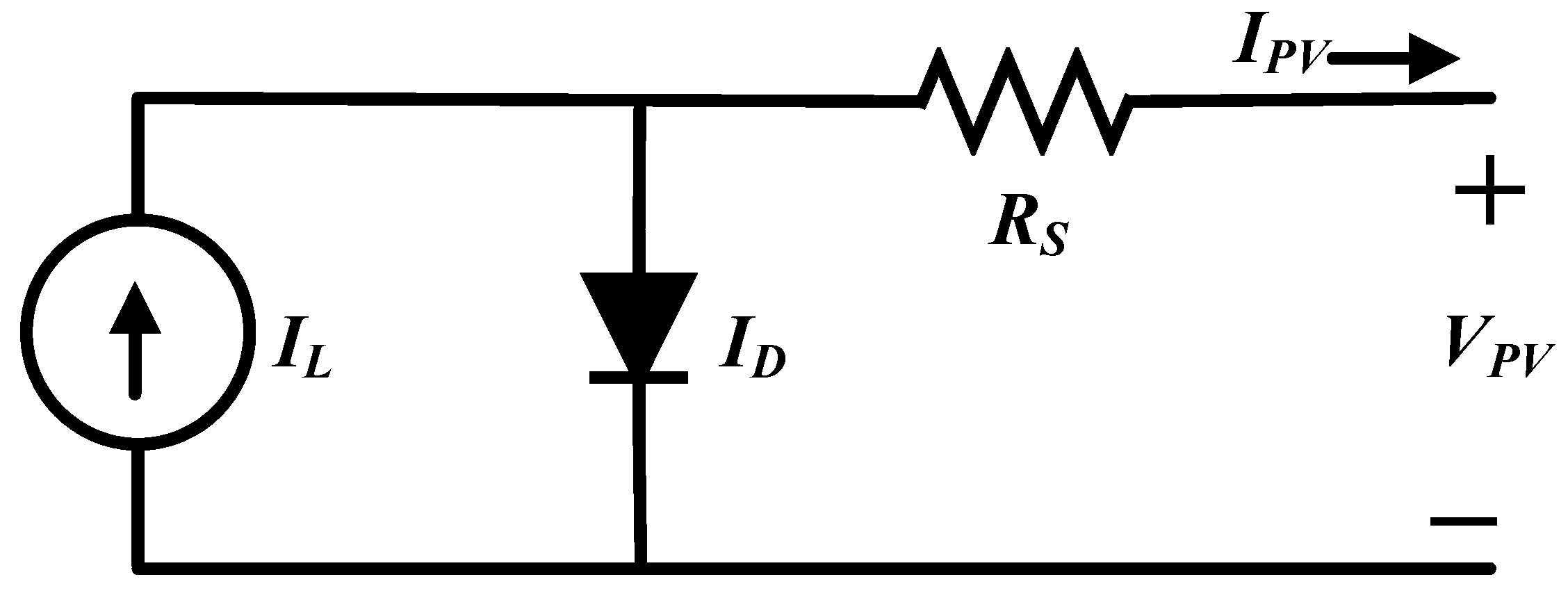
3.2. Photovoltaic System
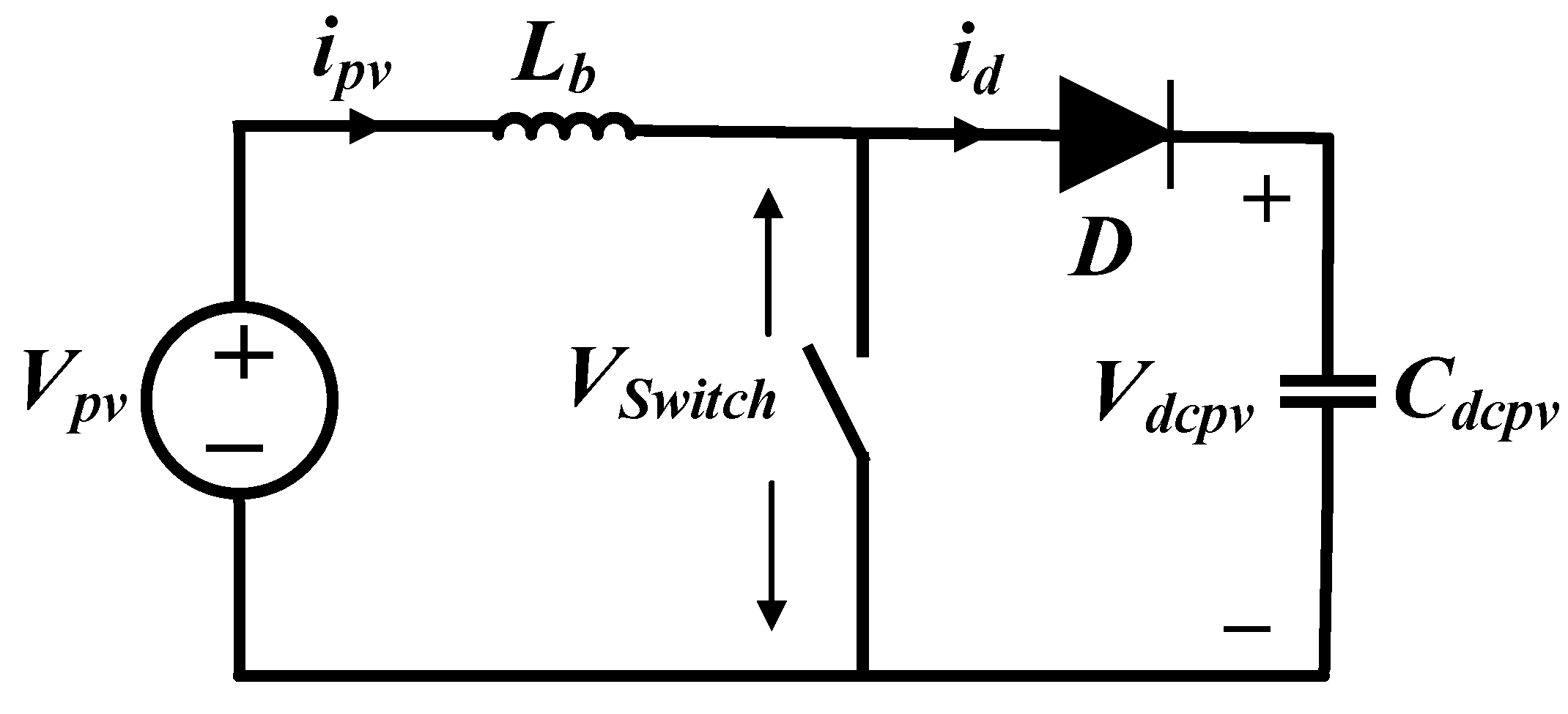
3.2.1. DC/DC Converter and DC Link
- : boost converter inductor
- : DC link capacitor
- : DC/DC converter duty ratio.
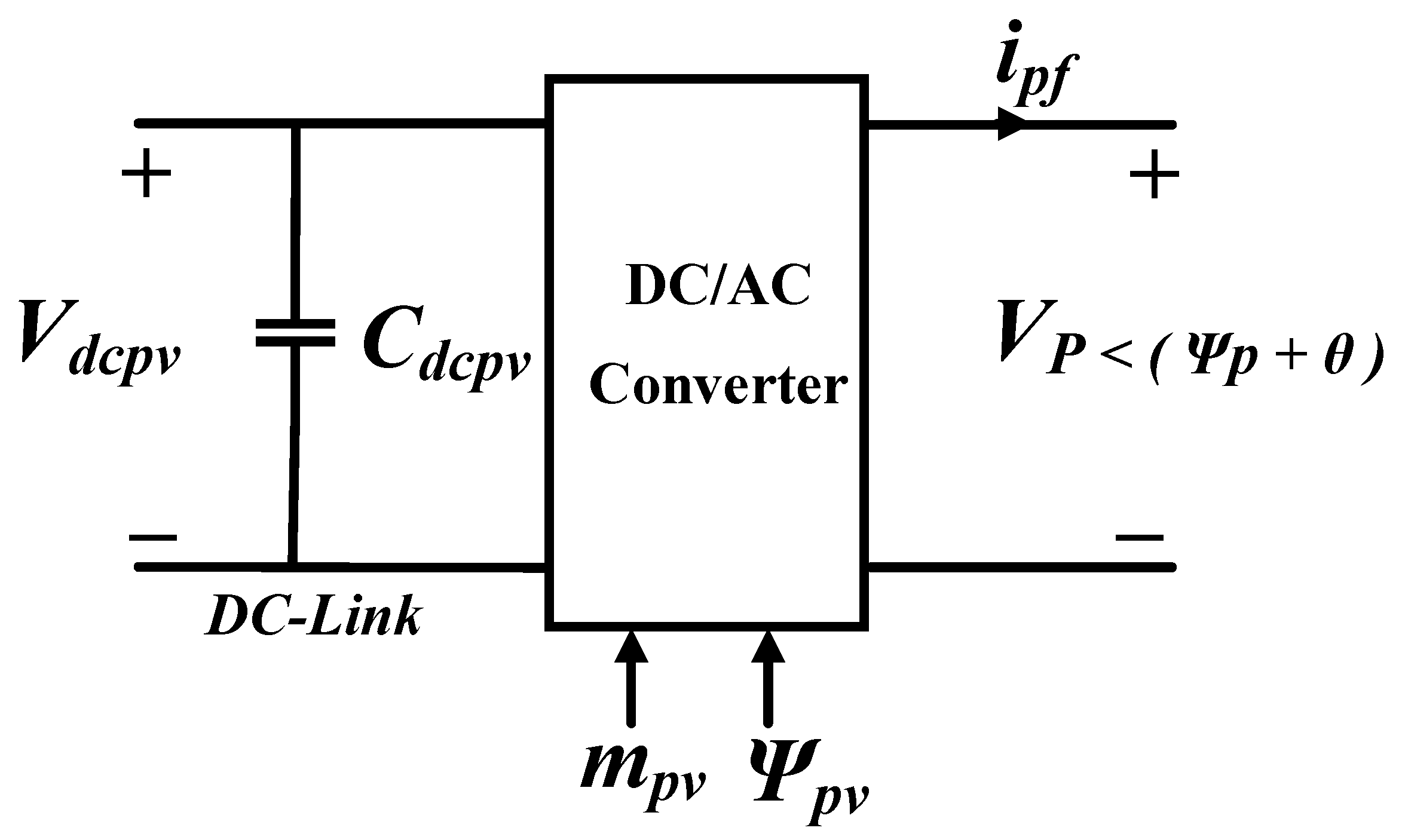
3.2.2. DC/AC Voltage Source Inverter
- : inverter modulation index
- : inverter phase angle.
3.2.3. LC Filter and Coupling Transmission Line
- : filter resistance
- : coupling line resistance
- : filter inductance
- : coupling line inductance
- : filter capacitor
- : damping resistor.
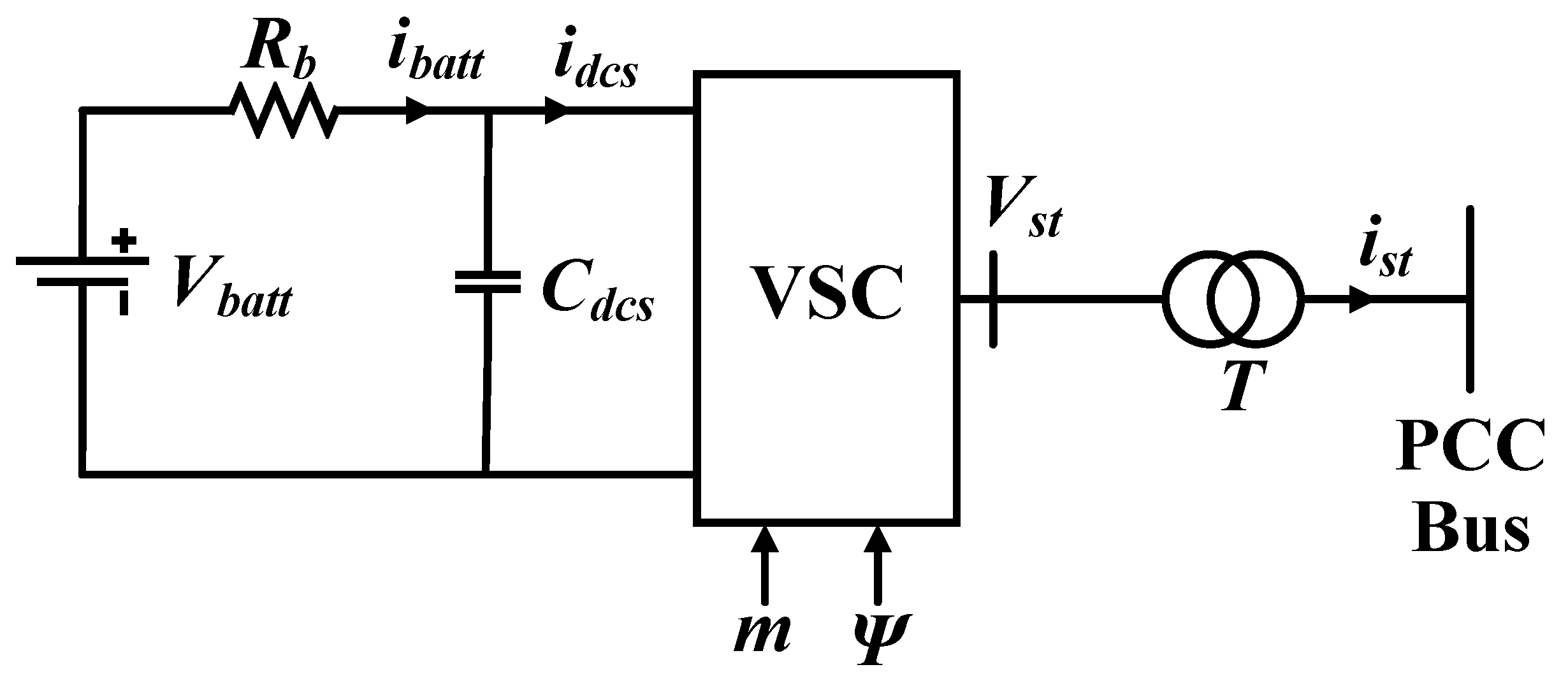
3.3. Battery Energy Storage System
- : VSC resistance
- : VSC inductance
- : converter modulation index
- : converter phase angle
- : DC-link capacitance
- : battery resistance.
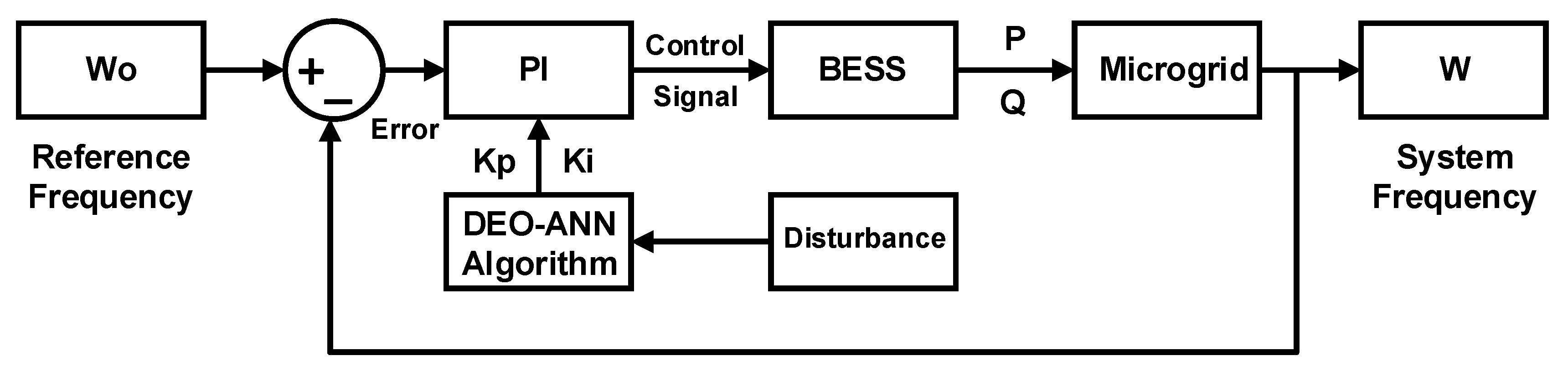
4. Problem Formulation
- : reference frequency
- : system frequency.
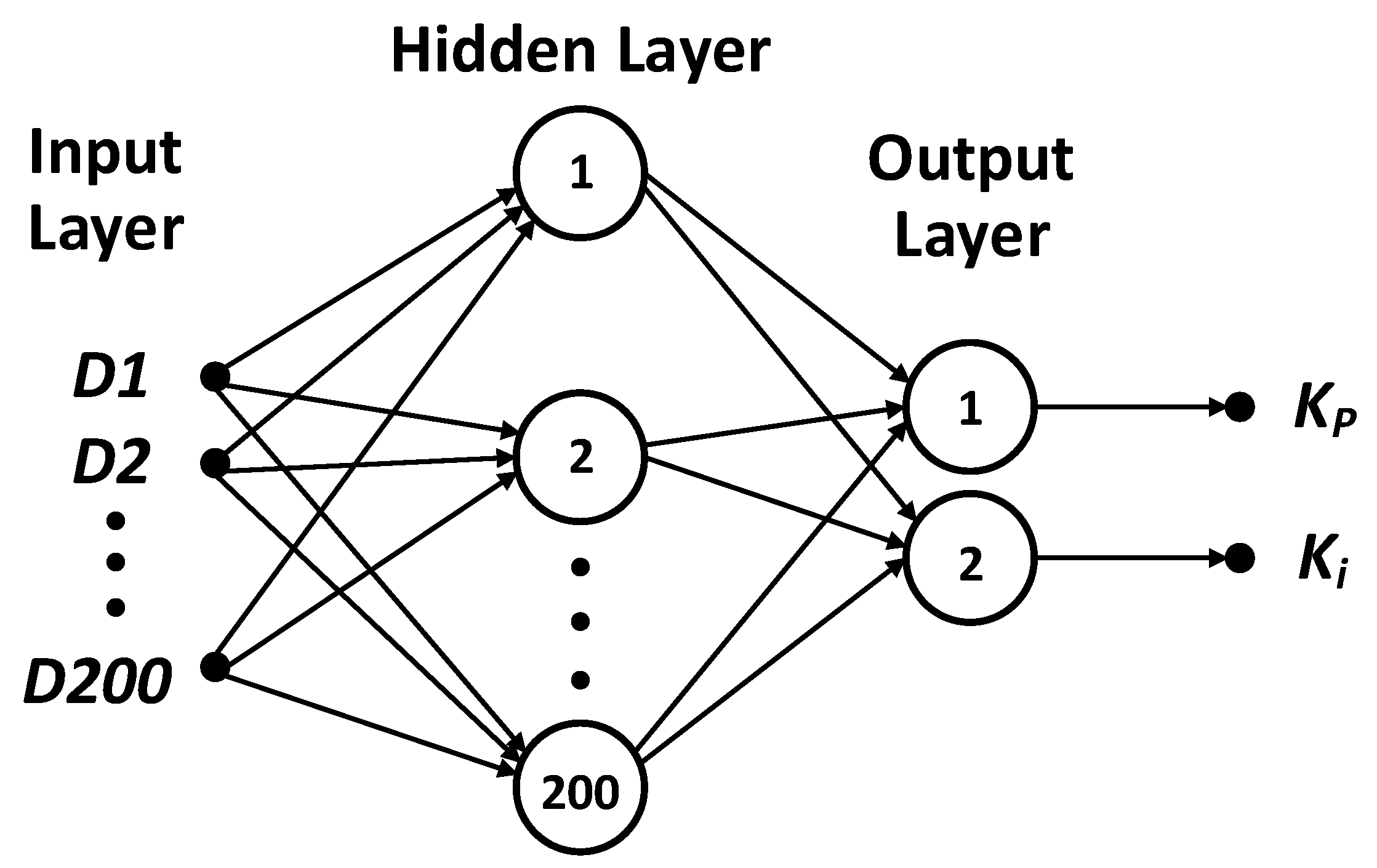
5. The Proposed Methodology
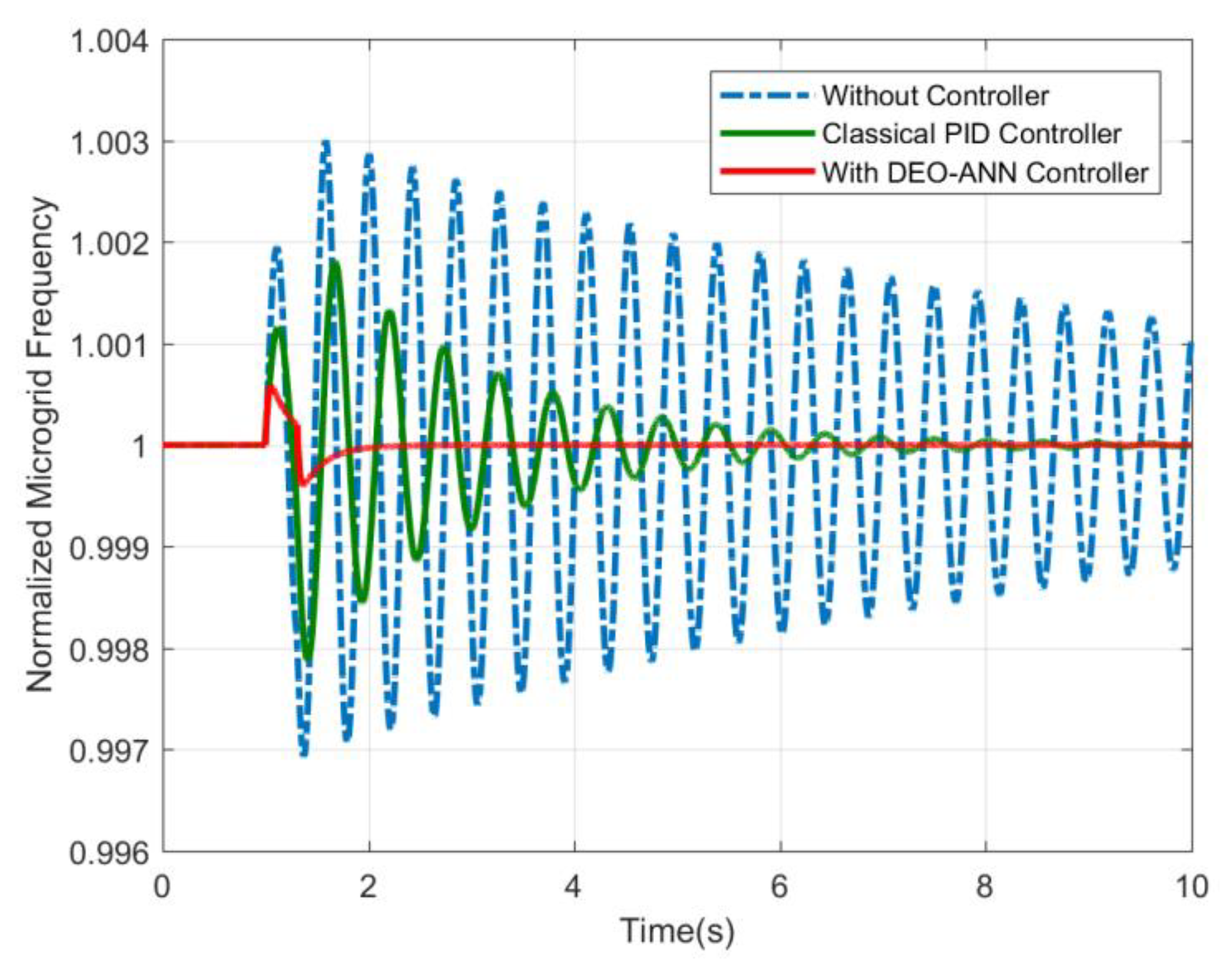
6. Results and Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ANN | Artificial neural networks |
| BESS | Battery energy storage system |
| DEO | Differential evolution optimization |
| DER | Distrusted energy resources |
| DG | Distrusted generation |
| DSG | Diesel synchronous generator |
| EA | Evolutionary algorithms |
| EP | Evolutionary programming |
| ES | Evolution strategy |
| ESD | Energy storage devices |
| ESS | Energy storage system |
| FC | Fuel cells |
| FESS | Flywheel energy storage system |
| FL | Fuzzy logic |
| FR | Frequency restoration |
| GA | Genetic algorithm |
| GP | Genetic programming |
| GT | Gas turbines |
| HIL | Hardware-in-loop |
| HT | Hydro turbines |
| ICE | Internal combustion engines |
| IGBT | Insulated-gate bipolar transistor |
| ISE | Integral squared-error |
| LC | Inductance-capacitance |
| MG | Microgrid |
| PCC | Point of common coupling |
| PI | Proportional-integral |
| PID | Proportional-integral-derivative |
| PSO | Particle swarm optimization |
| PV | Photovoltaic system |
| PWM | Pulse-width modulation |
| RES | Renewable energy sources |
| RPS | Reactive power-sharing |
| SCESS | Super-capacitor energy storage system |
| SMES | Superconducting magnetic energy storage |
| VSC | Voltage source converter |
| VSI | Voltage source inverter |
References
- Ustun, T.S.; Ozansoy, C.; Zayegh, A. Recent developments in microgrids and example cases around the world—A review. Renew. Sustain. Energy Rev. 2011, 15, 4030–4041. [Google Scholar] [CrossRef]
- Kaviri, S.M.; Pahlevani, M.; Jain, P.; Bakhshai, A. A review of ac microgrid control methods. In Proceedings of the 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianópolis, Brazil, 17–20 April 2017; pp. 1–8. [Google Scholar]
- Khalid, M.; Akram, U.; Shafiq, S. Optimal planning of multiple distributed generating units and storage in active distribution networks. IEEE Access 2018, 6, 55234–55244. [Google Scholar] [CrossRef]
- Jiayi, H.; Chuanwen, J.; Rong, X. A review on distributed energy resources and microgrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Hussain, S.A.; Abido, M.A. Modeling and control of microgrid: An overview. J. Frankl. Inst. 2014, 351, 2822–2859. [Google Scholar] [CrossRef]
- Basak, P.; Chowdhury, S.; nee Dey, S.H.; Chowdhury, S. A literature review on integration of distributed energy resources in the perspective of control, protection and stability of microgrid. Renew. Sustain. Energy Rev. 2012, 16, 5545–5556. [Google Scholar] [CrossRef]
- Lidula, N.; Rajapakse, A. Microgrids research: A review of experimental microgrids and test systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef] [Green Version]
- Vechiu, I.; Curea, O.; Llaria, A.; Camblong, H. Control of power converters for microgrids. COMPEL 2011, 30, 300–309. [Google Scholar] [CrossRef]
- Marwali, M.N.; Jung, J.-W.; Keyhani, A. Control of distributed generation systems-part ii: Load sharing control. IEEE Trans. Power Electron. 2004, 19, 1551–1561. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; PortilloGuisado, R.C.; Prats, M.M.; León, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Micro-grid autonomous operation during and subsequent to islanding process. IEEE Trans. Power Deliv. 2005, 20, 248–257. [Google Scholar] [CrossRef]
- Tsikalakis, A.G.; Hatziargyriou, N.D. Centralized control for optimizing microgrids operation. In Proceedings of the Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Zamora, R.; Srivastava, A. Controls for microgrids with storage: Review, challenges, and research needs. Renew. Sustain. Energy Rev. 2010, 14, 2009–2018. [Google Scholar] [CrossRef]
- Ribeiro, P.F.; Johnson, B.K.; Crow, M.L.; Arsoy, A.; Liu, Y. Energy storage systems for advanced power applications. Proc. IEEE 2001, 89, 1744–1756. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M. A coordinated frequency regulation framework based on hybrid battery-ultracapacitor energy storage technologies. IEEE Access 2018, 6, 7310–7320. [Google Scholar] [CrossRef]
- Valverde, L.; Rosa, F.; Bordons, C. Design, planning and management of a hydrogen-based microgrid. IEEE Trans. Ind. Inform. 2013, 9, 1398–1404. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Zhao, D.; Lei, H.; Cui, B.; Li, S. Incorporating energy storage and user experience in isolated microgrid dispatch using a multi-objective model. IET Renew. Power Gener. 2019, 13, 973–981. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, J.; Zhang, L.; Zhang, X.; Qin, R.; Lin, X. Three representative island microgrids in the east china sea: Key technologies and experiences. Renew. Sustain. Energy Rev. 2018, 96, 262–274. [Google Scholar] [CrossRef]
- López-González, A.; Domenech, B.; Ferrer-Martí, L. Sustainability and design assessment of rural hybrid microgrids in venezuela. Energy 2018, 159, 229–242. [Google Scholar] [CrossRef]
- Bellido, M.H.; Rosa, L.P.; Pereira, A.O.; Falcão, D.M.; Ribeiro, S.K. Barriers, challenges and opportunities for microgrid implementation: The case of federal university of rio de janeiro. J. Clean. Prod. 2018, 188, 203–216. [Google Scholar] [CrossRef]
- Feng, W.; Jin, M.; Liu, X.; Bao, Y.; Marnay, C.; Yao, C.; Yu, J. A review of microgrid development in the united states–a decade of progress on policies, demonstrations, controls, and software tools. Appl. Energy 2018, 228, 1656–1668. [Google Scholar] [CrossRef]
- Green, T.; Prodanović, M. Control of inverter-based micro-grids. Electr. Power Syst. Res. 2007, 77, 1204–1213. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Tyagi, B. A state of art review of microgrid control and integration aspects. In Proceedings of the 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; pp. 1–6. [Google Scholar]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Bevrani, H.; Habibi, F.; Babahajyani, P.; Watanabe, M.; Mitani, Y. Intelligent frequency control in an ac microgrid: Online pso-based fuzzy tuning approach. IEEE Trans. Smart Grid 2012, 3, 1935–1944. [Google Scholar] [CrossRef]
- Rajesh, K.; Dash, S.; Rajagopal, R.; Sridhar, R. A review on control of ac microgrid. Renew. Sustain. Energy Rev. 2017, 71, 814–819. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B.; Luo, W. A decentralized control method for frequency restoration and accurate reactive power sharing in islanded microgrids. J. Frankl. Inst. 2018, 355, 8874–8890. [Google Scholar] [CrossRef]
- Yang, P.; Xia, Y.; Yu, M.; Wei, W.; Peng, Y. A decentralized coordination control method for parallel bidirectional power converters in a hybrid ac–dc microgrid. IEEE Trans. Ind. Electron. 2018, 65, 6217–6228. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.; Ker, P.J.; Hussain, A.; Mansur, M.; Blaabjerg, F. Review of energy storage system technologies in microgrid applications: Issues and challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M.; Shafiq, S. An innovative hybrid wind-solar and battery-supercapacitor microgrid system—Development and optimization. IEEE Access 2017, 5, 25897–25912. [Google Scholar] [CrossRef]
- Parise, G.; Martirano, L.; Kermani, M.; Kermani, M. Designing a power control strategy in a microgrid using pid/fuzzy controller based on battery energy storage. In Proceedings of the International Conference on Environment and Electrical Engineering and Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Kermani, M. Transient voltage and frequency stability of an isolated microgrid based on energy storage systems. In Proceedings of the 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–5. [Google Scholar]
- Li, H.; Wang, X.; Xiao, J. Differential evolution-based load frequency robust control for micro-grids with energy storage systems. Energies 2018, 11, 1686. [Google Scholar] [CrossRef]
- Ali, M.A. Control of a Microgrid through Energy Storage Devices using Evolutionary and Neuro-Fuzzy Methods. Master’s Thesis, King Fahd University of Petroleum and Minerals Dhahran, Dhahran, Saudi Arabia, 2013. [Google Scholar]
- Fu, C.; Tan, W. Decentralised load frequency control for power systems with communication delays via active disturbance rejection. IET Gener. Transm. Distrib. 2017, 12, 1397–1403. [Google Scholar] [CrossRef]
- Ma, M.; Zhang, C.; Liu, X.; Chen, H. Distributed model predictive load frequency control of the multi-area power system after deregulation. IEEE Trans. Ind. Electron. 2017, 64, 5129–5139. [Google Scholar] [CrossRef]
- Shankar, R.; Chatterjee, K.; Bhushan, R. Impact of energy storage system on load frequency control for diverse sources of interconnected power system in deregulated power environment. Int. J. Electr. Power Energy Syst. 2016, 79, 11–26. [Google Scholar] [CrossRef]
- Mu, C.; Tang, Y.; He, H. Improved sliding mode design for load frequency control of power system integrated an adaptive learning strategy. IEEE Trans. Ind. Electron. 2017, 64, 6742–6751. [Google Scholar] [CrossRef]
- Rinaldi, G.; Cucuzzella, M.; Ferrara, A. Third order sliding mode observer-based approach for distributed optimal load frequency control. IEEE Control Syst. Lett. 2017, 1, 215–220. [Google Scholar] [CrossRef]
- Dasgupta, D.; Michalewicz, Z. Evolutionary Algorithms in Engineering Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the Biennial Conference of the North American Fuzzy Information Processing Society (NAFIPS), Berkeley, CA, USA, 19–22 June 1996. [Google Scholar]
- Åström, K.J.; Hägglund, T. Revisiting the ziegler–nichols step response method for pid control. J. Process Control 2004, 14, 635–650. [Google Scholar] [CrossRef]





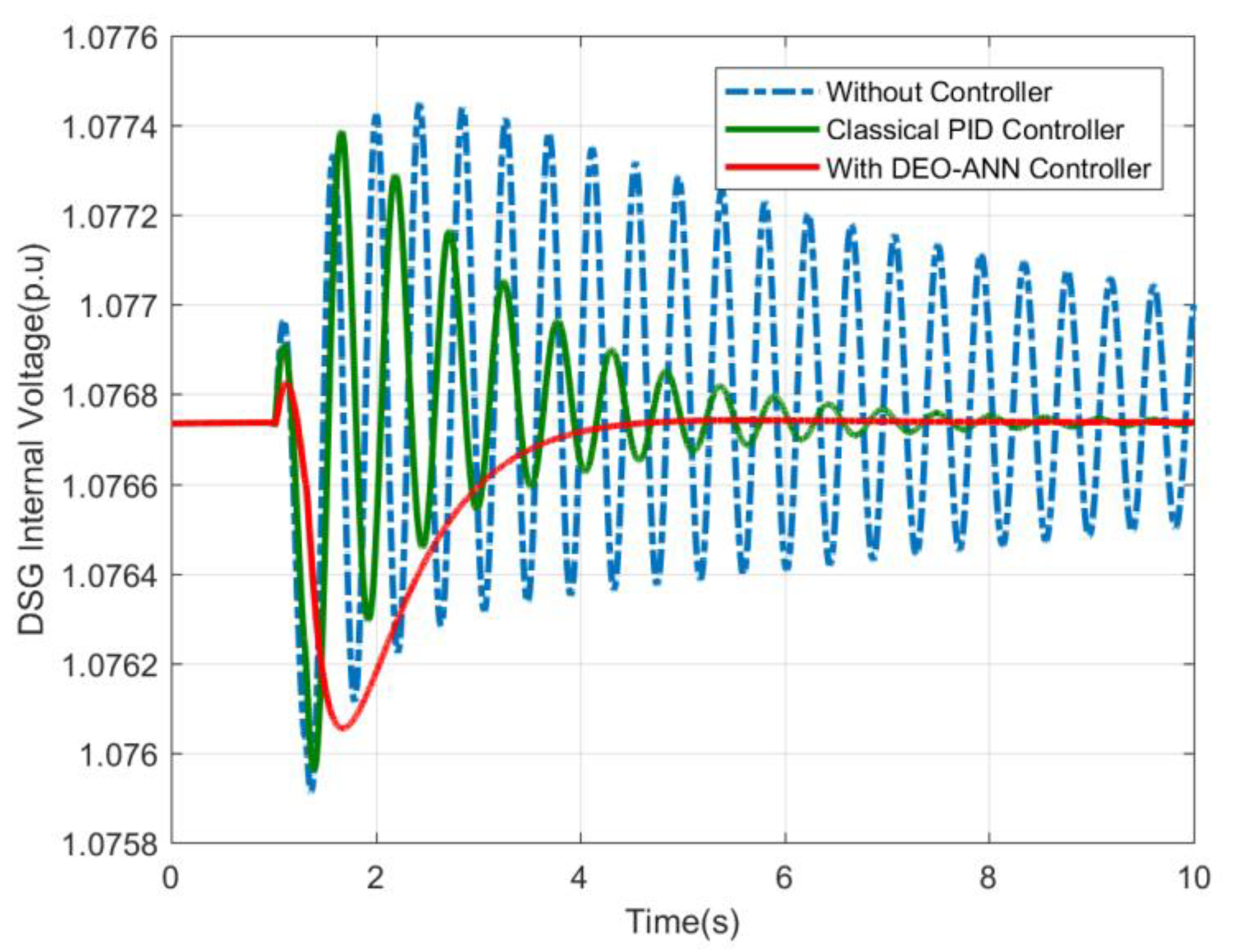
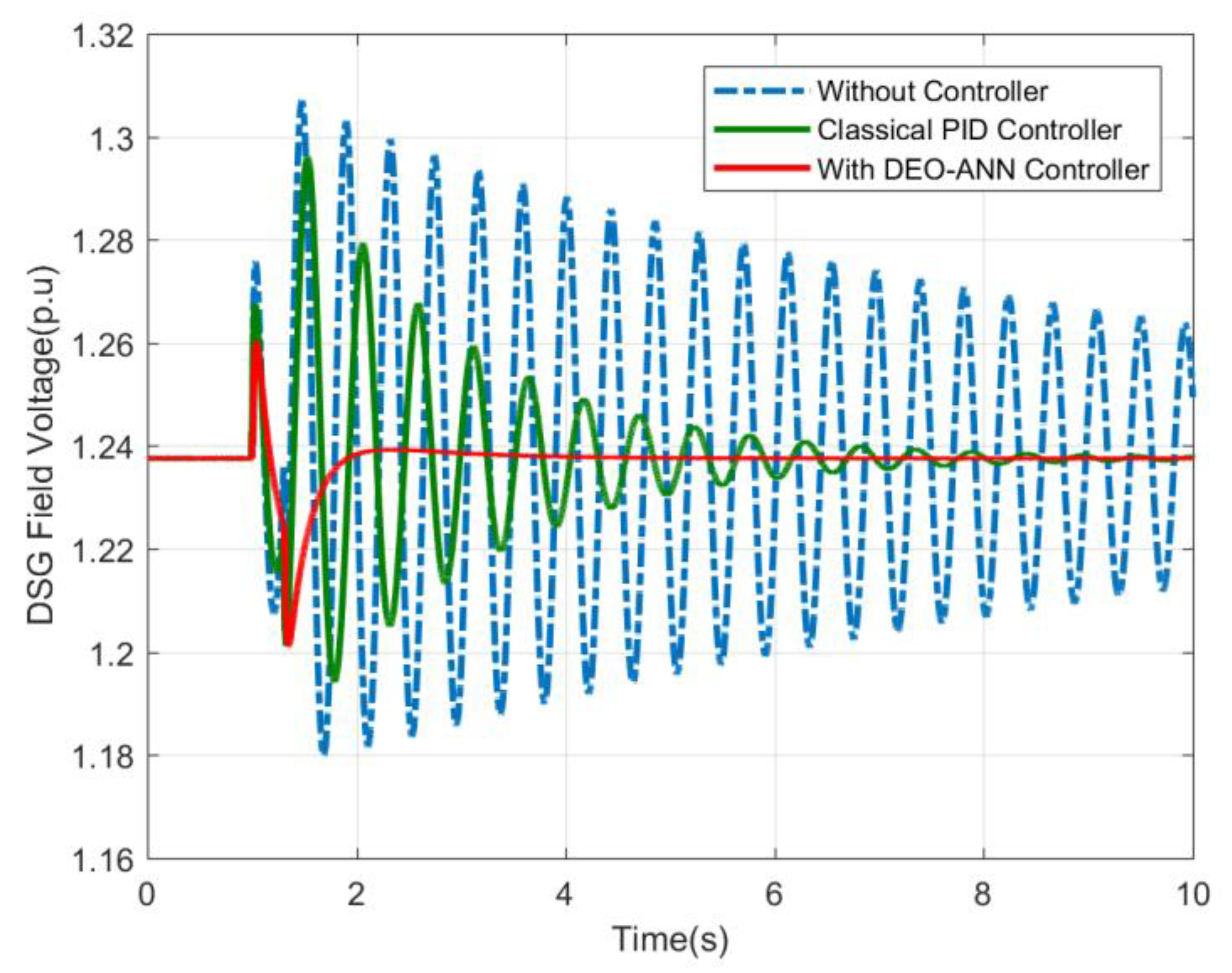
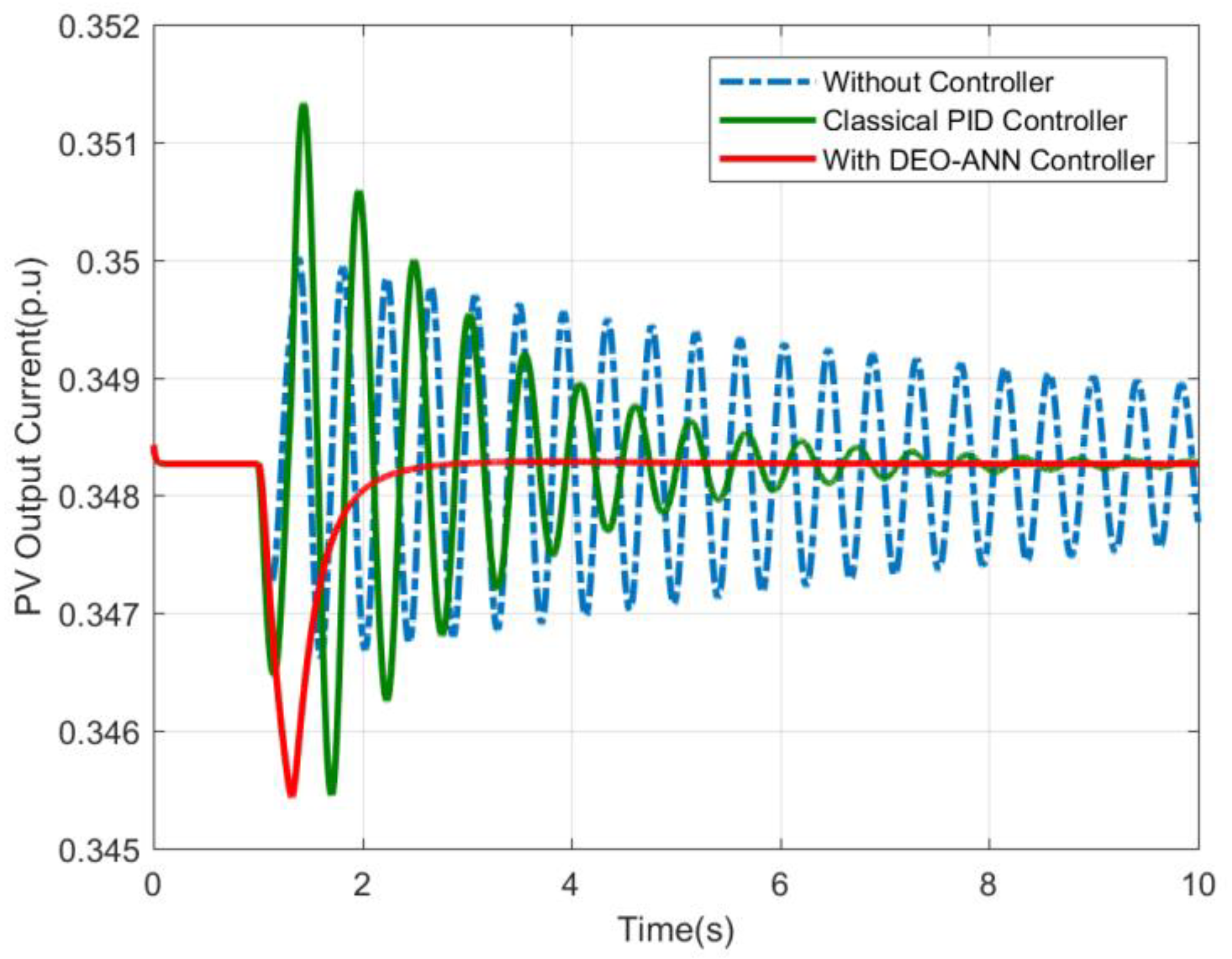

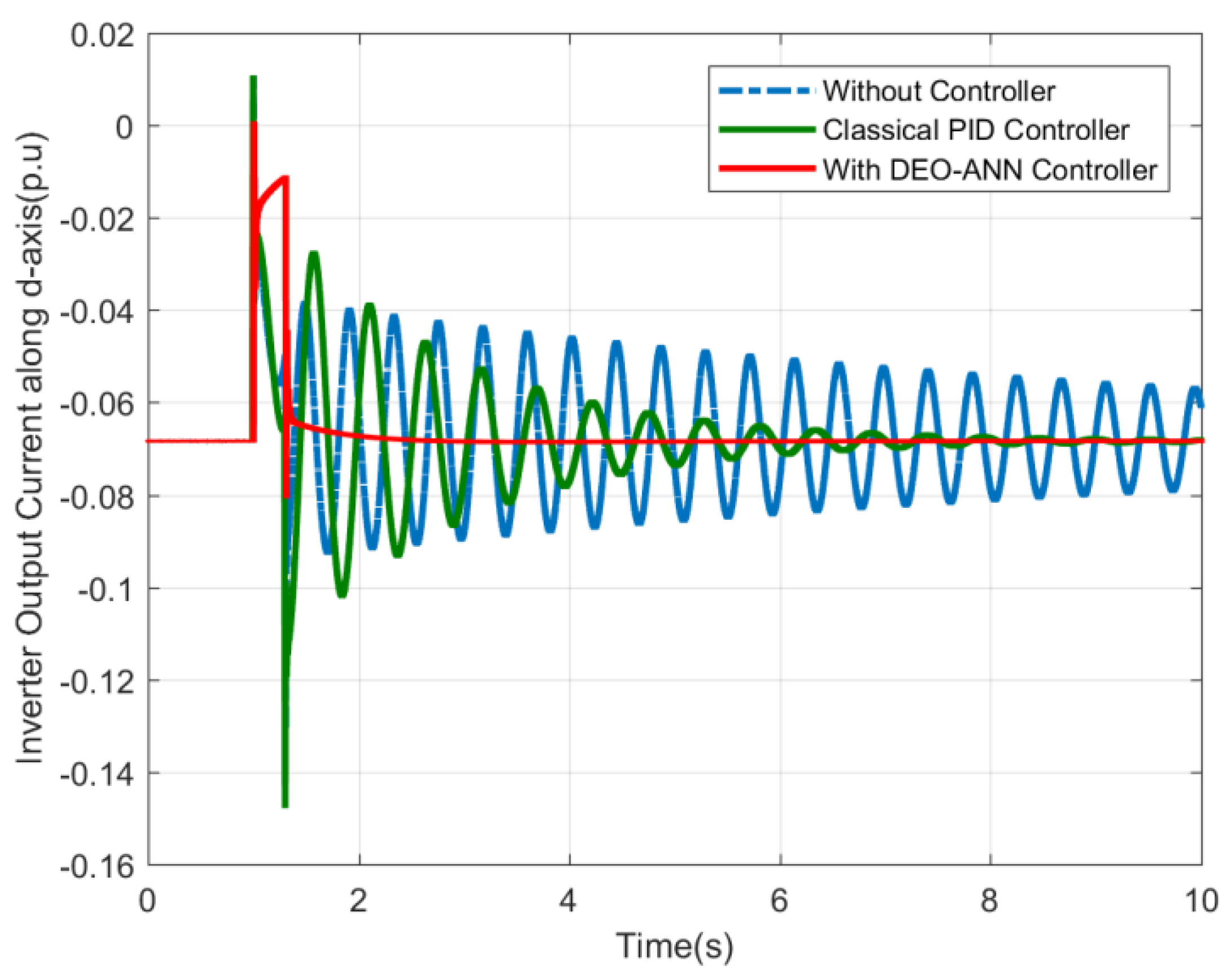

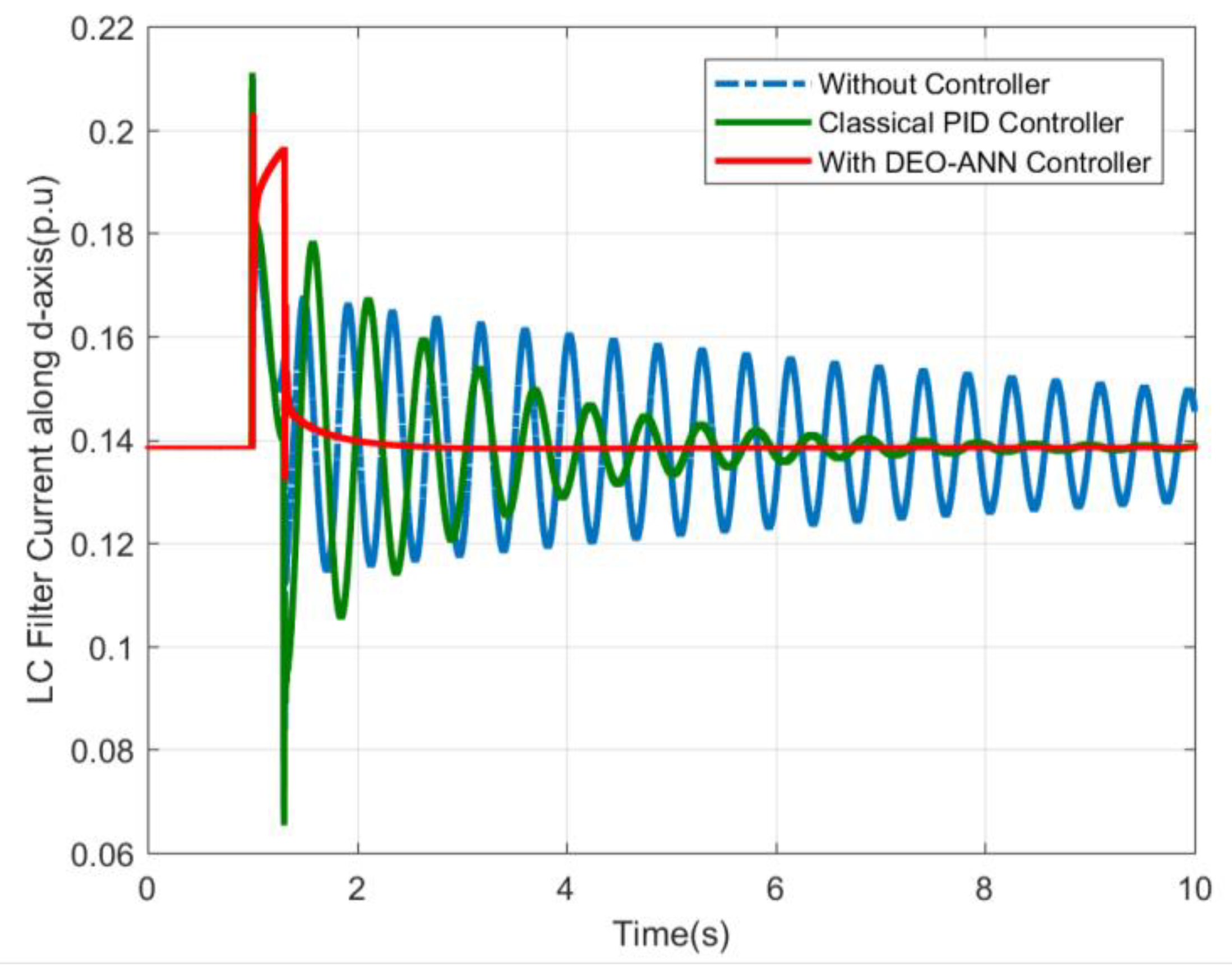


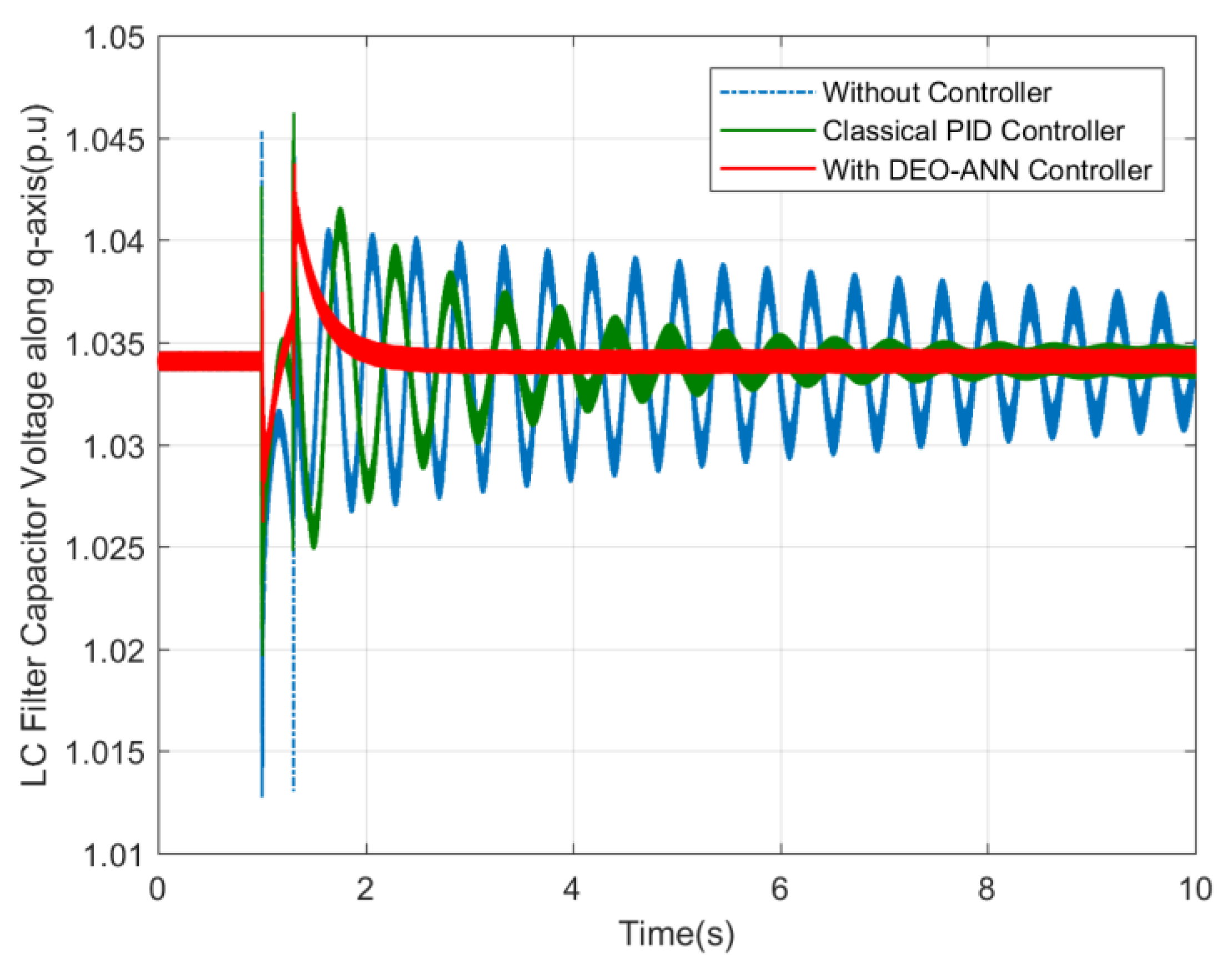

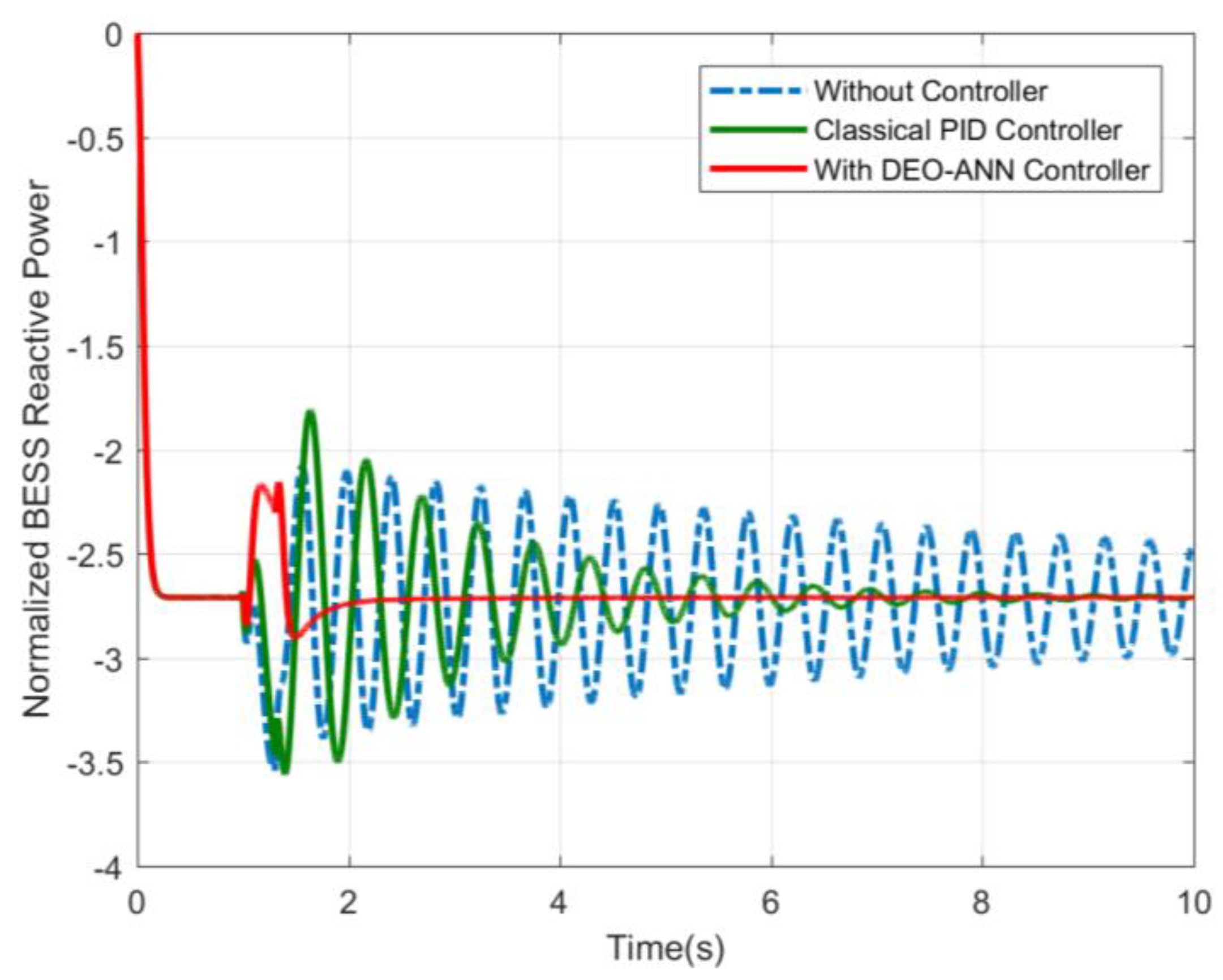
| Quantity | Minimum Value (p.u) | Maximum Value (p.u) |
|---|---|---|
| Frequency | 0.999 | 1.001 |
| Voltage | 0.95 | 1.05 |
| Parameter Description | Value |
|---|---|
| Generation number | 50 |
| Population size | 20 |
| Crossover factor | 0.5 |
| Mutation factor | 0.5 |
| Controller Parameter | Value |
|---|---|
| Kp | 128.22 |
| Ki | 161.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, J.; Khalid, M.; Alzahrani, A. An Intelligent Battery Energy Storage-Based Controller for Power Quality Improvement in Microgrids. Energies 2019, 12, 2112. https://doi.org/10.3390/en12112112
Alshehri J, Khalid M, Alzahrani A. An Intelligent Battery Energy Storage-Based Controller for Power Quality Improvement in Microgrids. Energies. 2019; 12(11):2112. https://doi.org/10.3390/en12112112
Chicago/Turabian StyleAlshehri, Jaber, Muhammad Khalid, and Ahmed Alzahrani. 2019. "An Intelligent Battery Energy Storage-Based Controller for Power Quality Improvement in Microgrids" Energies 12, no. 11: 2112. https://doi.org/10.3390/en12112112





