A Fractional Order Power System Stabilizer Applied on a Small-Scale Generation System
Abstract
:1. Introduction
- ▪
- Novel methodology to design PSS based on fractional-order network compensator, emphasizing the novel form to choose α parameter.
- ▪
- Experimental assessment of PSS based on fractional-order applied on generates a system in small scale.
2. Fractional Order System
2.1. Background of Fractional Order System in the Frequency Domain
2.2. Phase and Gain Contributions Due to Fractional Order Lead-Lag System
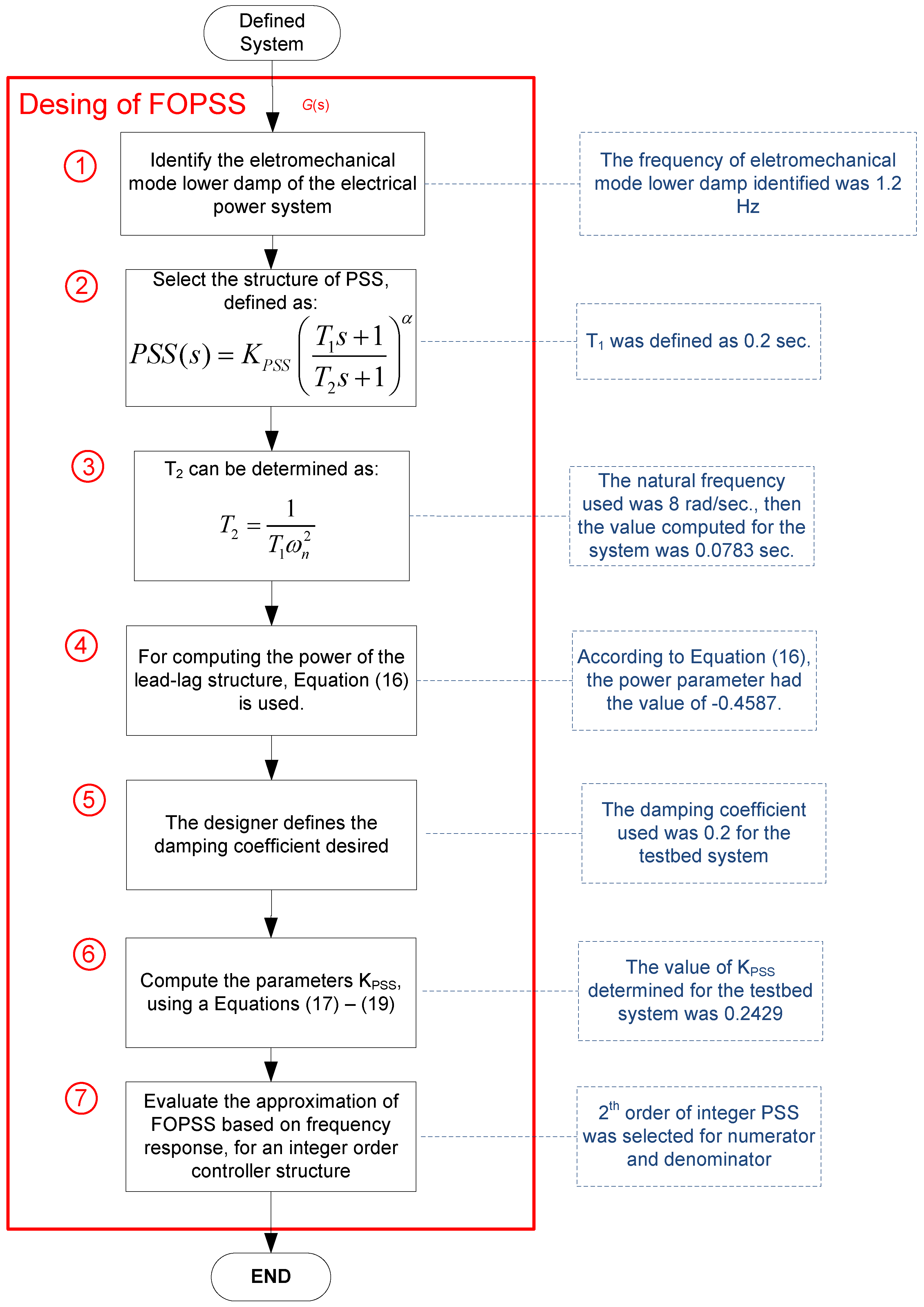
3. Tuning Method for Fractional Order Power System Stabilizer
3.1. Classical Tuning Method for Power System Stabilizer
3.2. Fractional Order Compensator Tuning Method
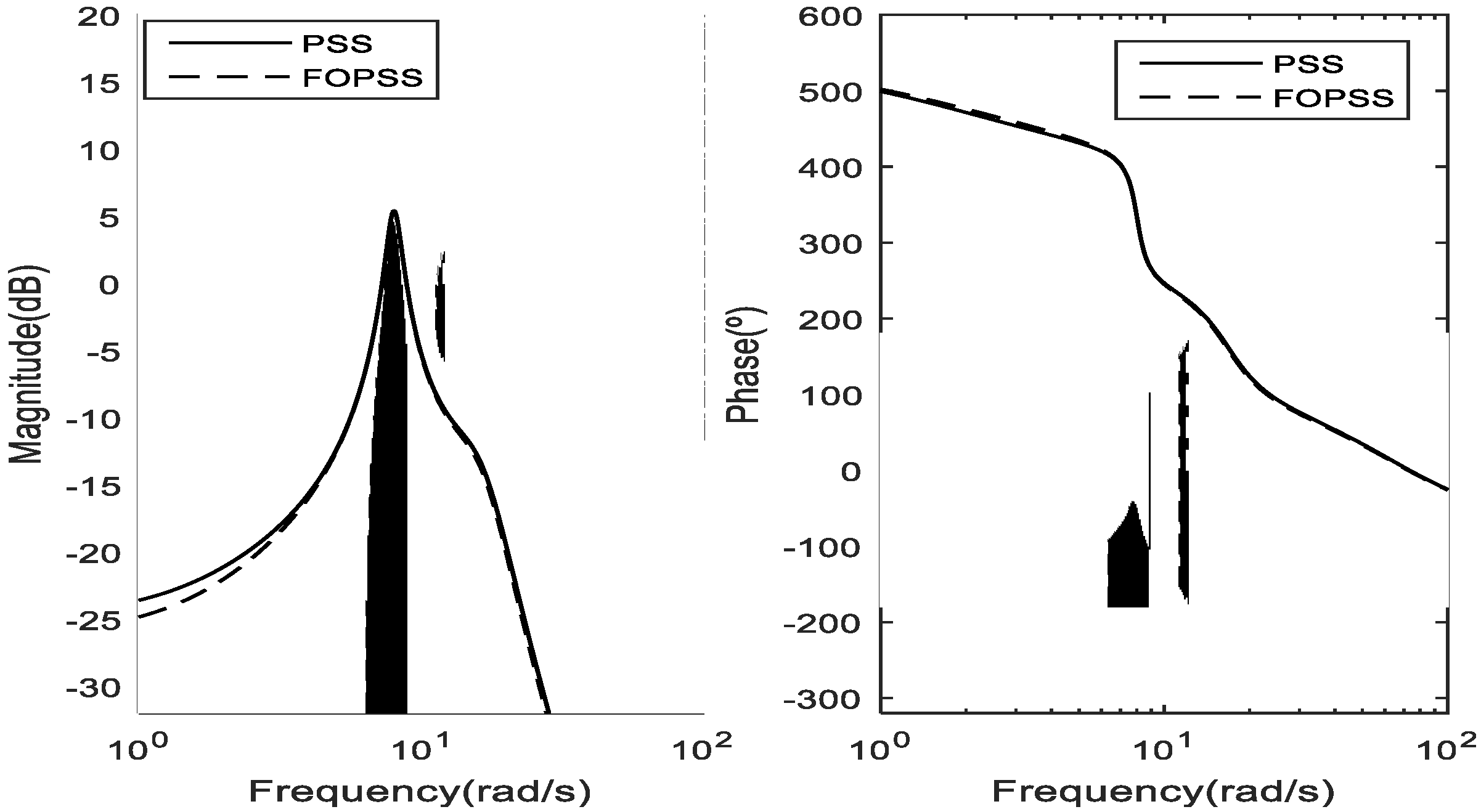
3.3. Fractional Order Approximation
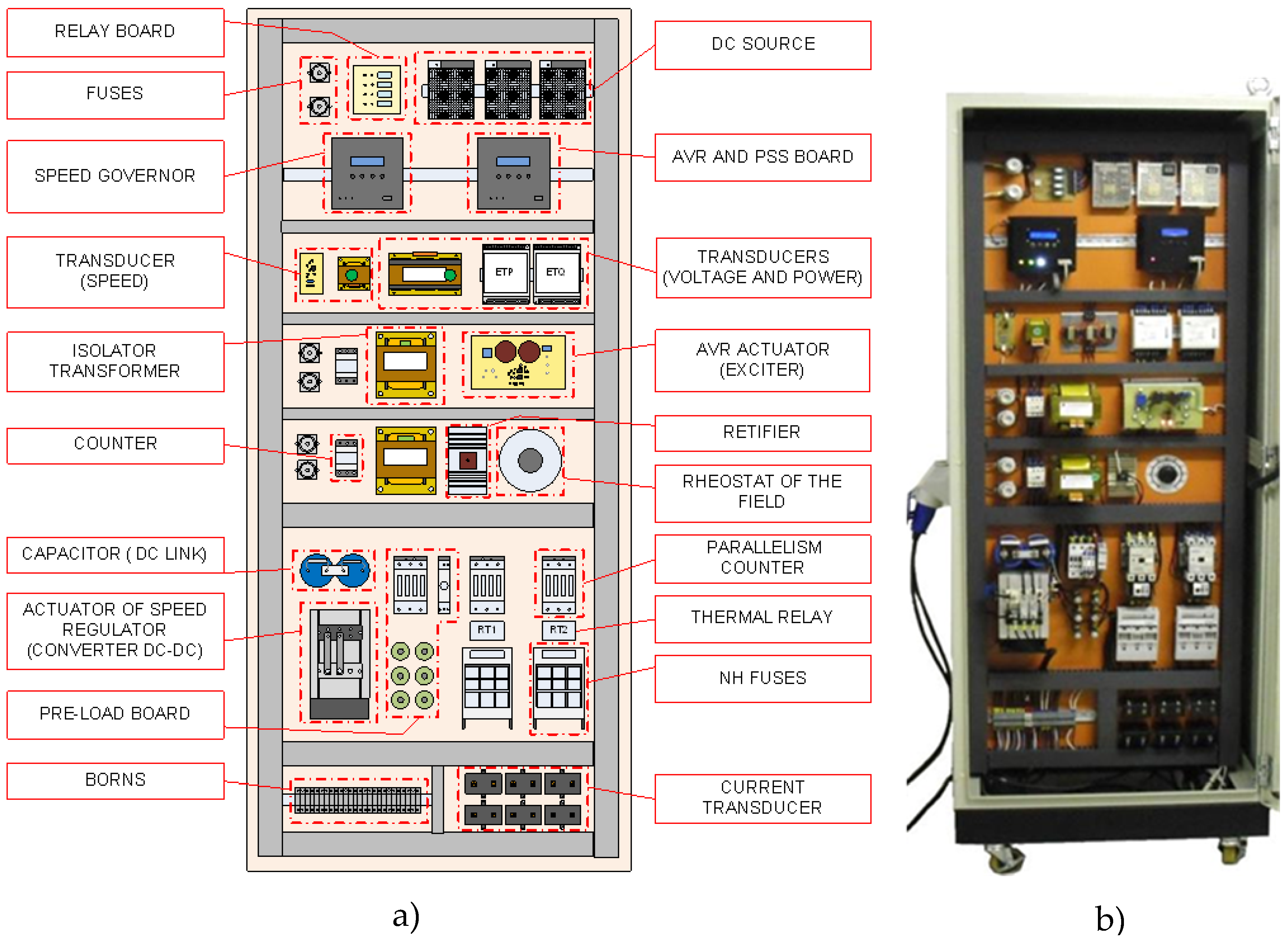
4. Laboratory Power System and Identification Tests
4.1. Small-Scale 10 kVA Power System
4.2. Experimental Environment
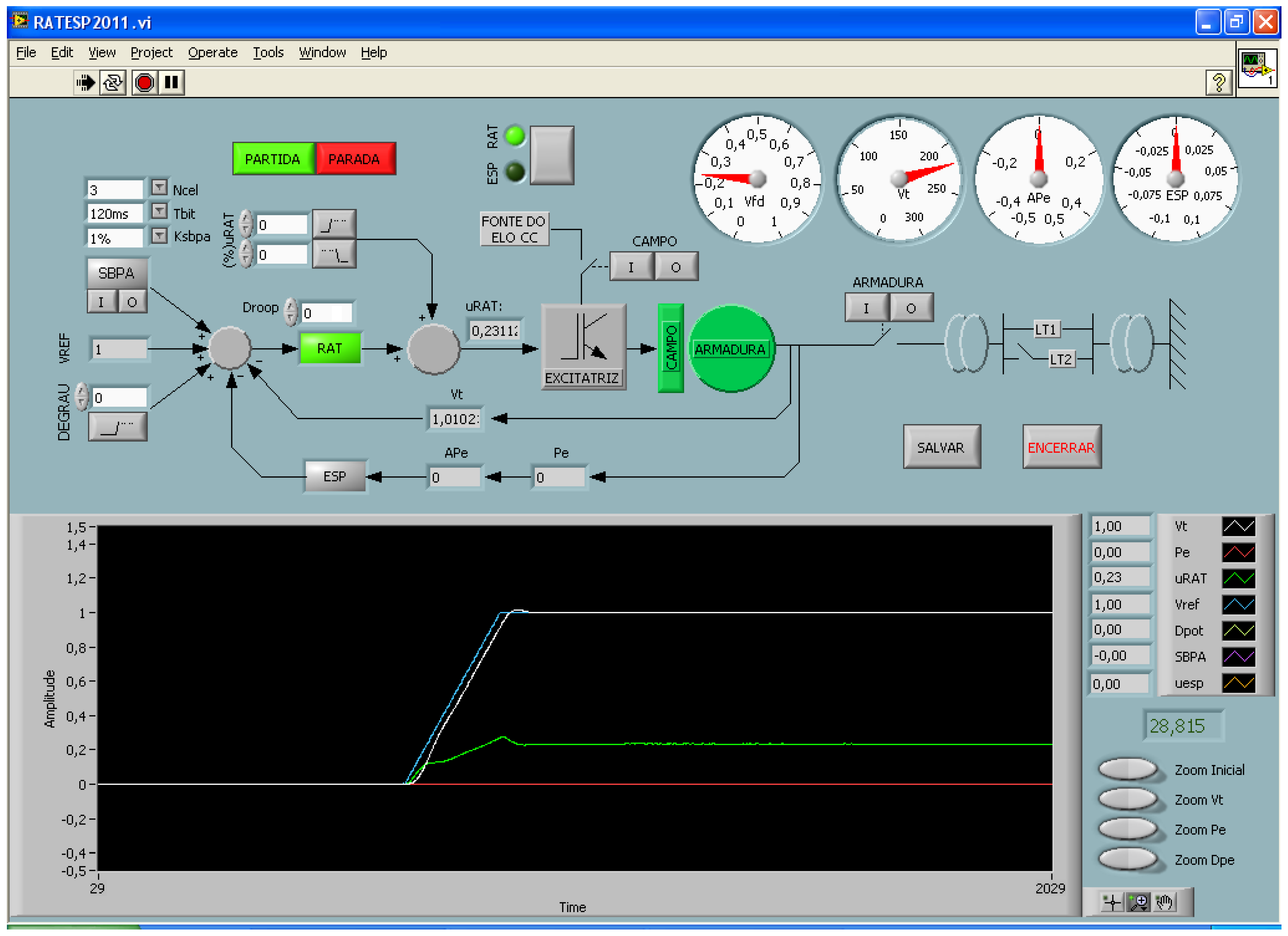
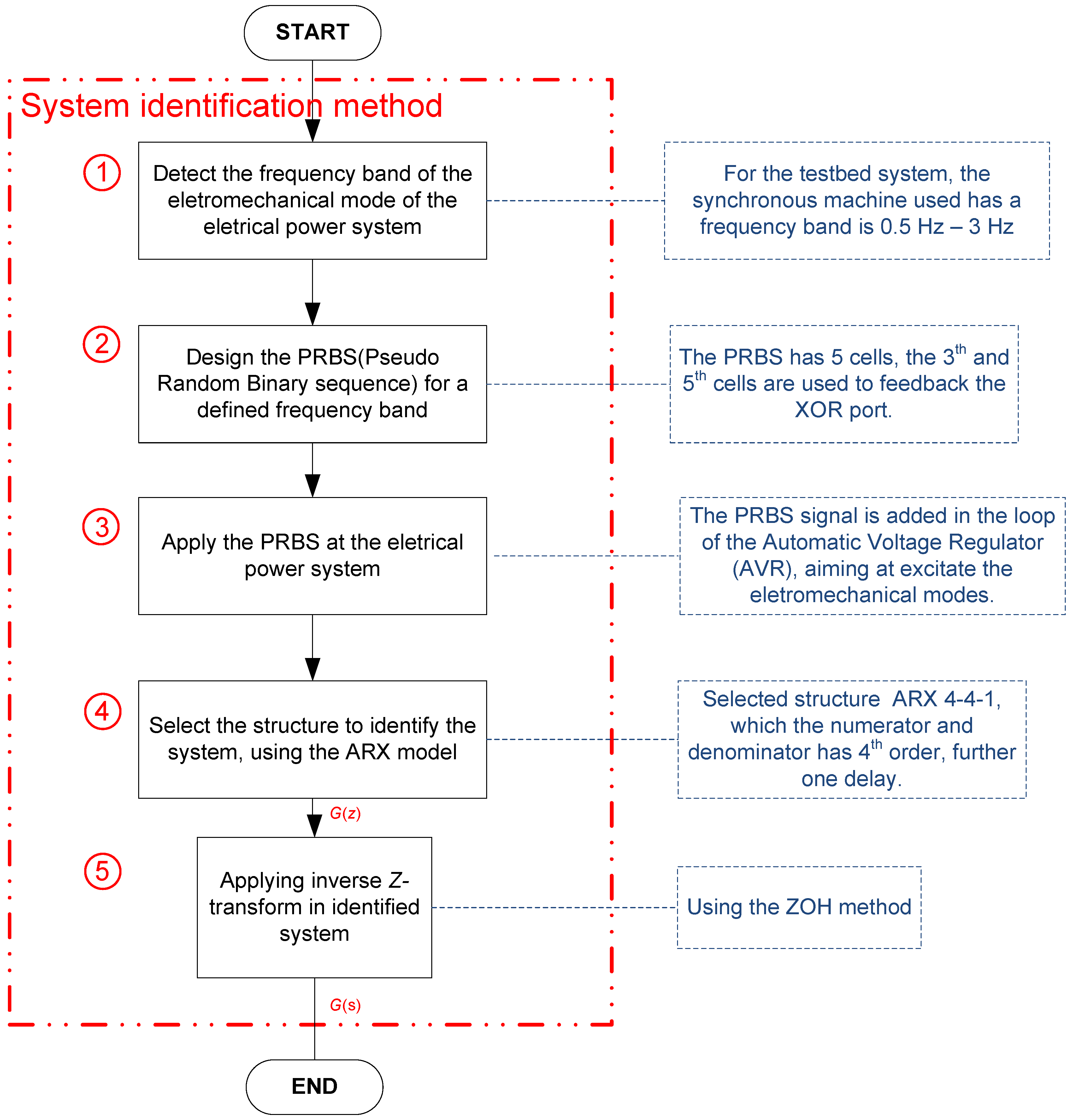
4.3. System Identification Tests
5. Design of the Fractional Order PSS and Tests in the 10 kVA Laboratory Power System
6. Robust Performance Assessments for the Designed Fractional Order Power System Stabilizer
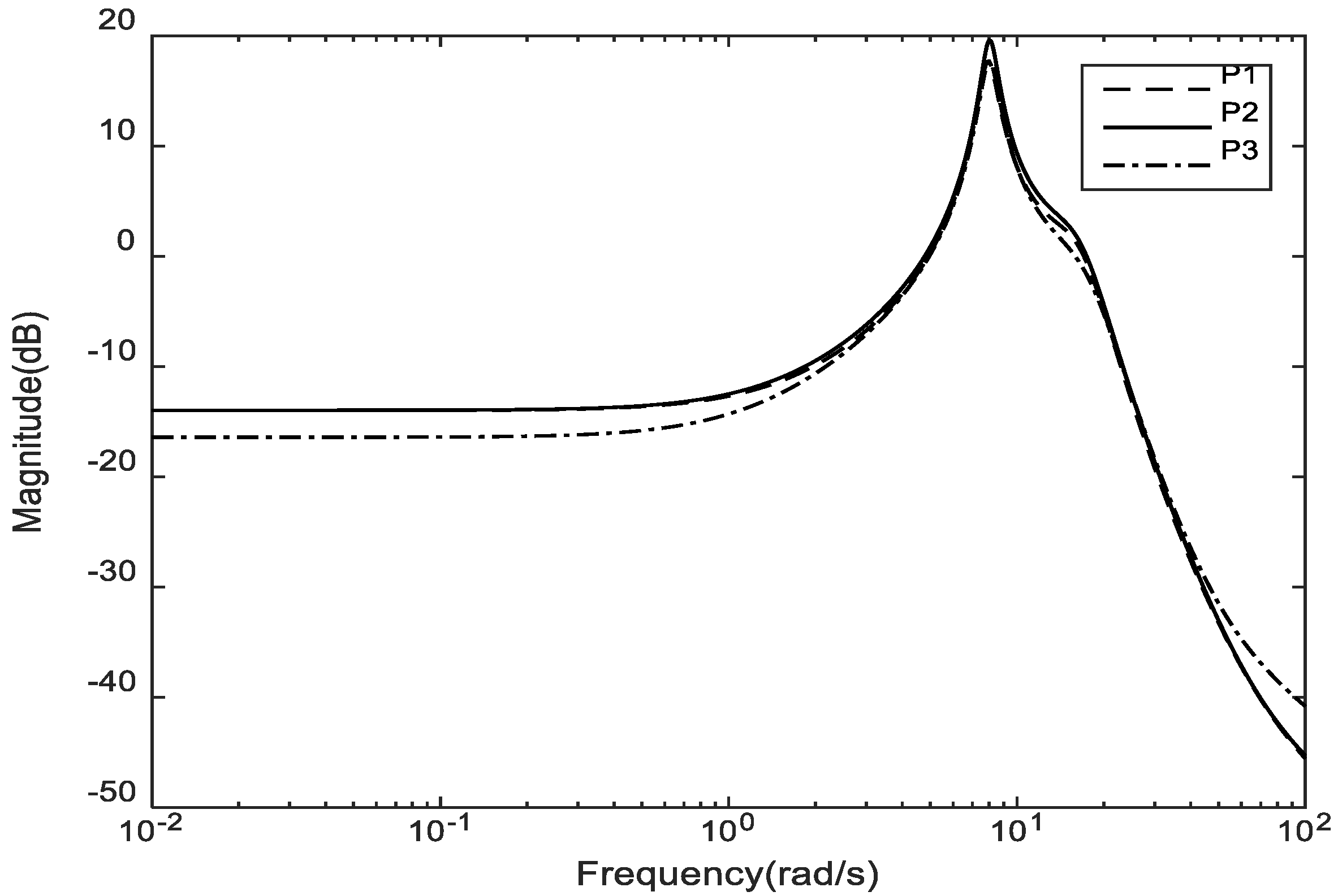
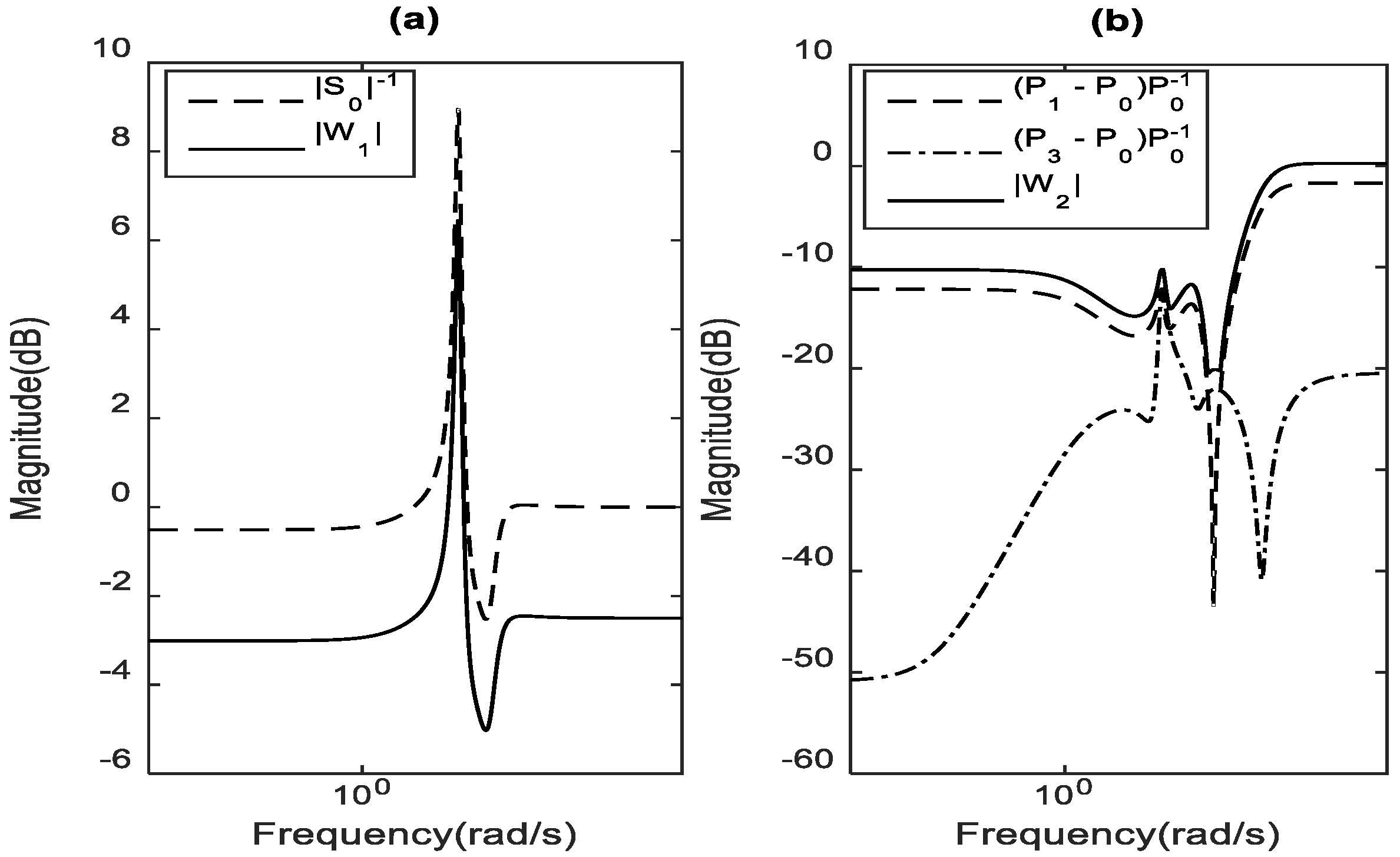
6.1. Robust Performance Boundaries Computation
6.1.1. Selecting the Nominal Plant Model P0(jω)
6.1.2. Selecting the Performance Weighting Function
6.1.3. Selecting the Performance Weighting Function
6.2. FOPSS Robust Performance Assessment
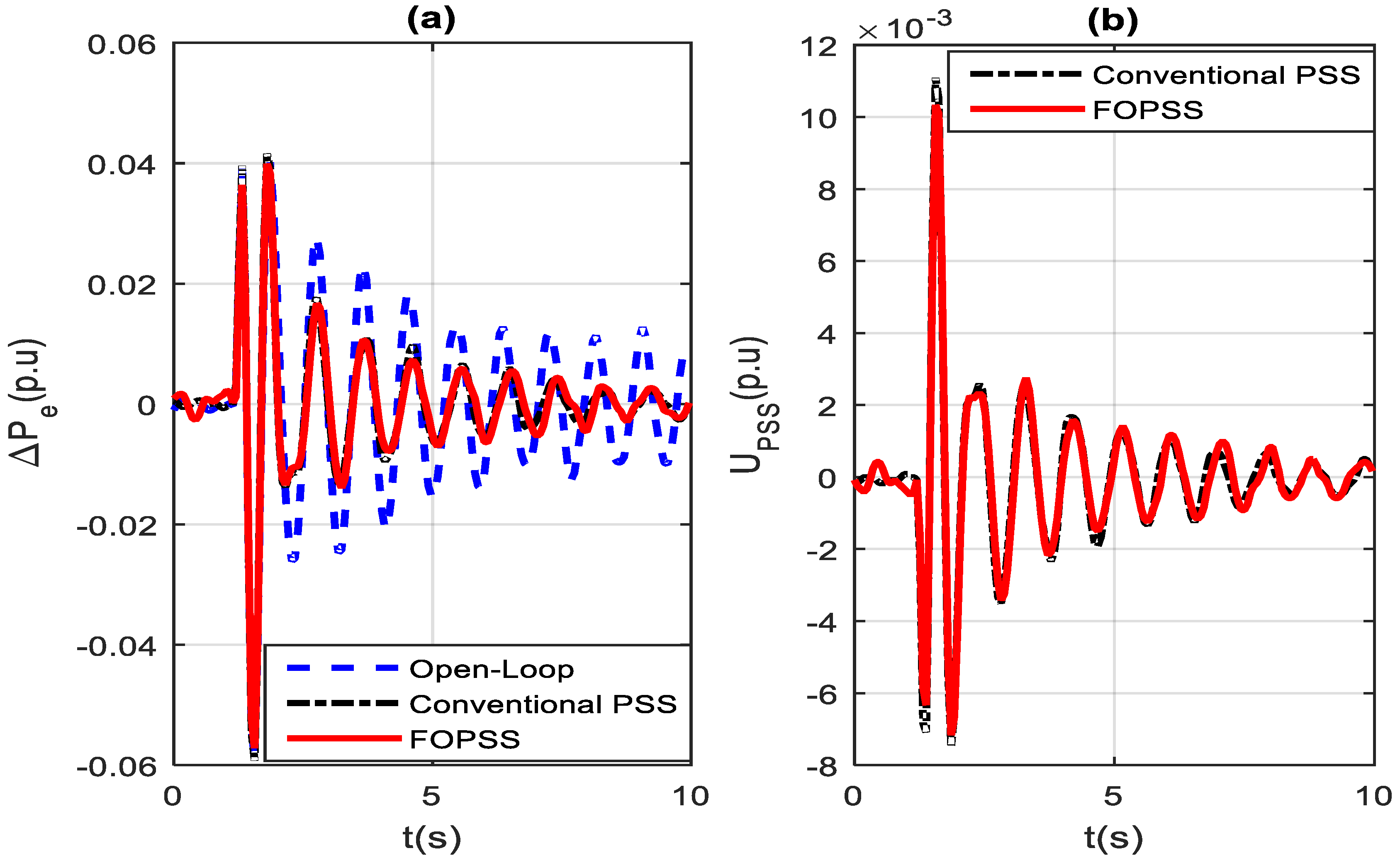
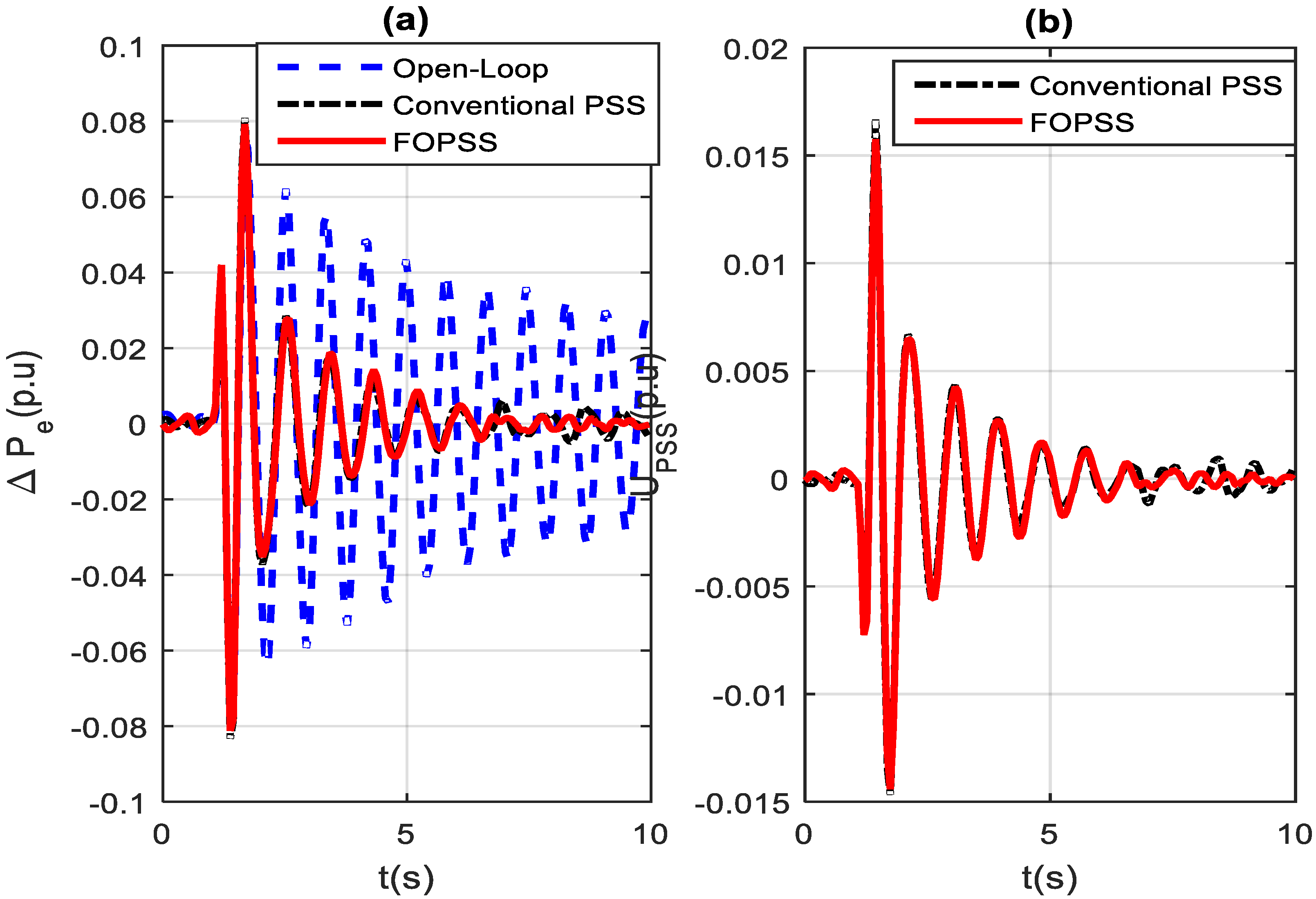
7. Practical Tests Performance Evaluation
7.1. Experimental Field Tests
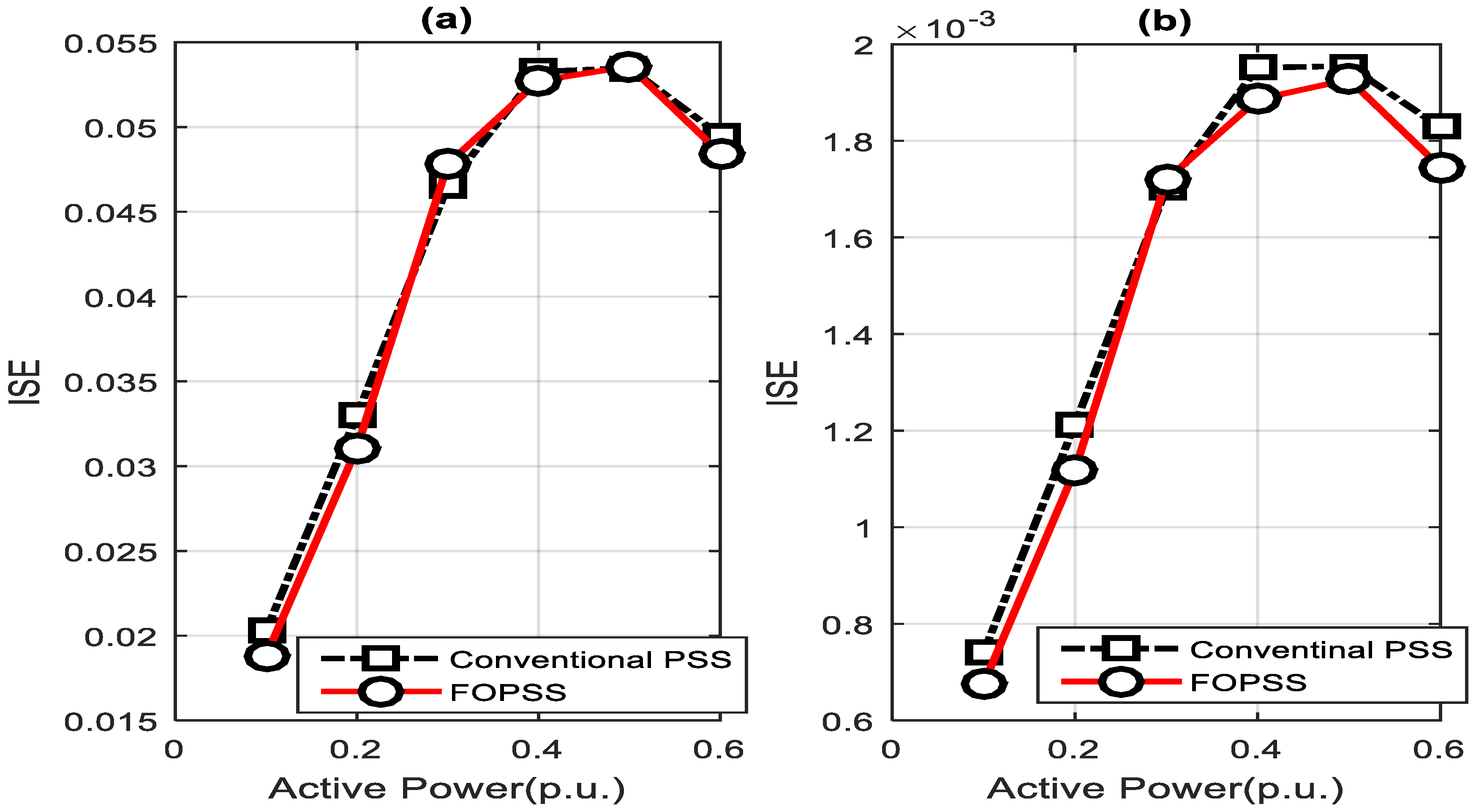
7.2. Cost Function Evaluation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kundur, P. Power System Stability and Control; McGraw-Hill: Toronto, ON, Canada, 1994; pp. 699–825. [Google Scholar]
- Peter, W.S.; Pai, M.A. Power System Dynamics and Stability; Stipes Publishing: Upper Saddle River, NJ, USA, 1998; pp. 221–282. [Google Scholar]
- Barreiros, J.A.L.; Silva, A.S.; Costa, J.A.S. A self-tuning generalized predictive power system stabilizer. Electr. Power Energy Syst. 1998, 20, 213–219. [Google Scholar]
- Fabrício, G.N.; Walter, B.J.; Carlos, T.C.J.; Anderson, R.B.M.; Marcus, C.M.G; Janio, J.L. Design and Experimental Evaluation Tests of a Takagi-Sugeno Power System Stabilizer. IET. Gener. Trans. Distrib. 2013, 8, 451–462. [Google Scholar]
- Gustavo, K.D.; Aguinaldo, S.S. Robust Design of Power System Controllers Based on Optimization of Pseudospectral Functions. IEEE Trans. Power. Syst. 2013, 28, 1756–1765. [Google Scholar]
- Concepción, A.M.; Blas, M.V.; Vicente, F.; Yangquan, C. Tuning and Auto-tuning of Fractional Order Controllers for Industry Applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar]
- Xue, D.; Zhao, C.; Chen, Y. Fractional Order PID Control of DC-Motor with Elastic Shaft: A Case Study. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 3182–3187. [Google Scholar]
- Ali, A.J.; Shabnam, K. Tuning of FOPID Controller Using Taylor Series Expansion. Int. J. Sci Commer. Eng. Res. 2011, 2, 1–5. [Google Scholar]
- Majid, Z.; Masoud, K.G.; Nasser, S.; Mostafa, P. Design of a Fractional Order PID Controller for an AVR Using Particle Swarm Optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar]
- Mohammad, R.F.; Abbas, N. On Fractional-Order PID Design. Appl. MATLAB Sci. Eng. 2011. [CrossRef]
- Riccardo, C.; Giovanni, D.; Luigi, F.; Ivo, P. Fractional Order Systems: Modeling and Control Applications; World scientific: Hackensack, NJ, USA, 2010; pp. 1–30. [Google Scholar]
- Larsen, E.V.; Swann, D.A. Applying Power System Stabilizers Part II: Performance Objectives and Tuning Concepts. IEEE Trans. Power Deliv. 1981, PAS-100, 3025–3033. [Google Scholar] [CrossRef]
- Duarte, V.; Jose, S.C. An Introduction to Fractional Control; IET: London, UK, 2013; pp. 79–106. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional Order Control Systems, Fundamentals and Applications; Springer: London, UK, 2010; pp. 133–140. [Google Scholar]
- Landau, I.D.; Zito, G. Digital Control Systems: Design, Identification and Implementation; Springer: London, UK, 2006; pp. 201–245. [Google Scholar]
- Ayres Junior, F.A.d.C. Controle de Ordem Fracionária Aplicadas ao Amortecimento de Oscilações Eletromecânicas em Sistemas Elétricos de Potência. Master's Thesis, Universidade Federal do Pará, Belém, Brazil, August 2014. [Google Scholar]
- Takenori, A.; William, M. Modified Bode Plots for Robust Performance in SISO Systems with Structured and Unstructured Uncertainties. IEEE Trans. Control Syst. Technol. 2012, 20, 356–368. [Google Scholar]
- John, C.D.; Bruce, A.F.; Allen, R.T. Feedback Control Theory; Macmillan Publications: New York, NY, USA, 1992. [Google Scholar]




| Resistance and Reactance (p.u.) | ||||||
|---|---|---|---|---|---|---|
| Ra | Xd | Xq | X’d | X’’d | X’’q | |
| Values | 0.048 | 1.058 | 0.693 | 0.169 | 0.0736 | 0.0736 |
| Time Constants (s) | ||||||
| T’d0 | T’’d0 | T’’q0 | H | |||
| 0.490 | 0.019 | 0.019 | 3.861 | |||
| Low Loading (Pe = 0.3 p.u) P1 | B(q−1) Coefficients Pe = 0.3 p.u. | |||
| b1 | b2 | b3 | b4 | |
| 0.012276 | 0.143705 | −0.075265 | −0.111931 | |
| A(q−1) Coefficients Pe = 0.3 p.u. | ||||
| a1 | a2 | a3 | a4 | |
| −2.586840 | 3.020355 | −1.832865 | 0.555510 | |
| Medium loading (Pe = 0.5 p.u) P2 | B(q−1) Coefficients Pe = 0.5 p.u. | |||
| b1 | b2 | b3 | b4 | |
| 0.019359 | 0.152224 | -0.085471 | -0.117924 | |
| A(q−1) Coefficients Pe = 0.5 p.u. | ||||
| a1 | a2 | a3 | a4 | |
| −2.585856 | 3.014485 | −1.819959 | 0.550024 | |
| High loading (Pe = 0.65 p.u) P3 | B(q−1) Coefficients Pe = 0.65 p.u. | |||
| b1 | b2 | b3 | b4 | |
| 0.017439 | 0.132755 | −0.039632 | −0.134924 | |
| A(q−1) Coefficients Pe = 0.65 p.u. | ||||
| a1 | a2 | a3 | a4 | |
| −2.485972 | 2.763681 | −1.590566 | 0.474089 | |
| Eigenvalue | Local Model P1 | Local Model P2 | Local Model P3 |
|---|---|---|---|
| λ1 | ξ1 = 0.072, ω1 = 7.93 rad/s | ξ2 = 0.063, ω2 = 8.03 rad/s | ξ3 = 0.071, ω3 = 8.01 rad/s |
| λ2 | ξ1 = 0.072, ω1 = 7.93 rad/s | ξ2 = 0.063, ω2 = 8.03 rad/s | ξ3 = 0.071, ω3 = 8.01 rad/s |
| λ3 | ξ1 = 0.258, ω1 = 16.80 rad/s | ξ2 = 0.267, ω2 = 16.80 rad/s | ξ3 = 0.321, ω3 = 17.60 rad/s |
| λ4 | ξ1 = 0.258, ω1 = 16.80 rad/s | ξ2 = 0.267, ω2 = 16.80 rad/s | ξ3 = 0.321, ω3 = 17.60 rad/s |
| Parameters Values | Conventional PSS | |||
| KPSS | T1 | T2 | N | |
| 0.2849 | 0.2000 s | 0.2556 s | 2 | |
| FOPSS | ||||
| KPSS | T1 | T2 | α | |
| 0.2429 | 0.2000s | 0.0783 s | −0.4587 | |
| Pole 1 | Pole 2 | Pole 3 | Pole 4 | Pole 5 | Pole 6 | |
|---|---|---|---|---|---|---|
| Classic PSS eigenvalues (rad/s) | 3.38 | 4.19 | 8.54 | 8.54 | 15.9 | 15.9 |
| Relative damping ξ | 1.0 | 1.0 | 0.183 | 0.183 | 0.225 | 0.225 |
| FOPSS Eigenvalues (rad/s) | 5.35 | 8.57 | 8.57 | 9.73 | 15.9 | 15.9 |
| Relative damping ξ | 1.0 | 0.185 | 0.185 | 1.0 | 0.231 | 0.231 |
| Parameters | PSS | FOPSS |
|---|---|---|
| r0 | 0.1850 | 0.1721 |
| r1 | −0.2718 | −0.1902 |
| r2 | 0.0998 | 0.0513 |
| s1 | −1.5724 | −1.2407 |
| s2 | 0.6181 | 0.3777 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayres Junior, F.A.d.C.; Costa Junior, C.T.d.; Medeiros, R.L.P.d.; Barra Junior, W.; Neves, C.C.d.; Lenzi, M.K.; Veroneze, G.D.M. A Fractional Order Power System Stabilizer Applied on a Small-Scale Generation System. Energies 2018, 11, 2052. https://doi.org/10.3390/en11082052
Ayres Junior FAdC, Costa Junior CTd, Medeiros RLPd, Barra Junior W, Neves CCd, Lenzi MK, Veroneze GDM. A Fractional Order Power System Stabilizer Applied on a Small-Scale Generation System. Energies. 2018; 11(8):2052. https://doi.org/10.3390/en11082052
Chicago/Turabian StyleAyres Junior, Florindo A. de C., Carlos T. da Costa Junior, Renan L. P. de Medeiros, Walter Barra Junior, Cleonor C. das Neves, Marcelo K. Lenzi, and Gabriela De M. Veroneze. 2018. "A Fractional Order Power System Stabilizer Applied on a Small-Scale Generation System" Energies 11, no. 8: 2052. https://doi.org/10.3390/en11082052





