Stability Analysis of Grid-Connected Converters with Different Implementations of Adaptive PR Controllers under Weak Grid Conditions
Abstract
:1. Introduction
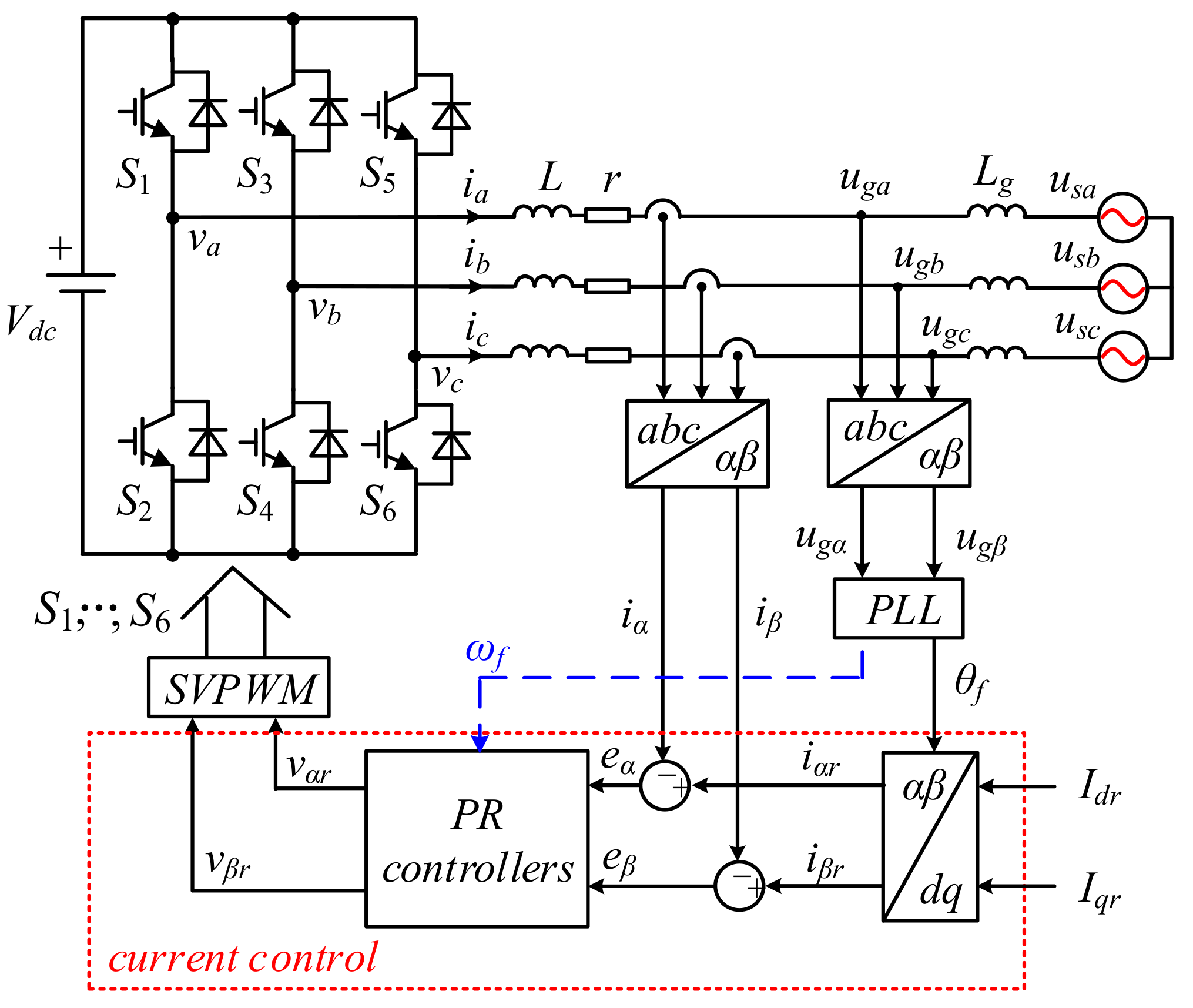
2. VSC with Adaptive PR Current Controllers
2.1. Adaptive PR Controller
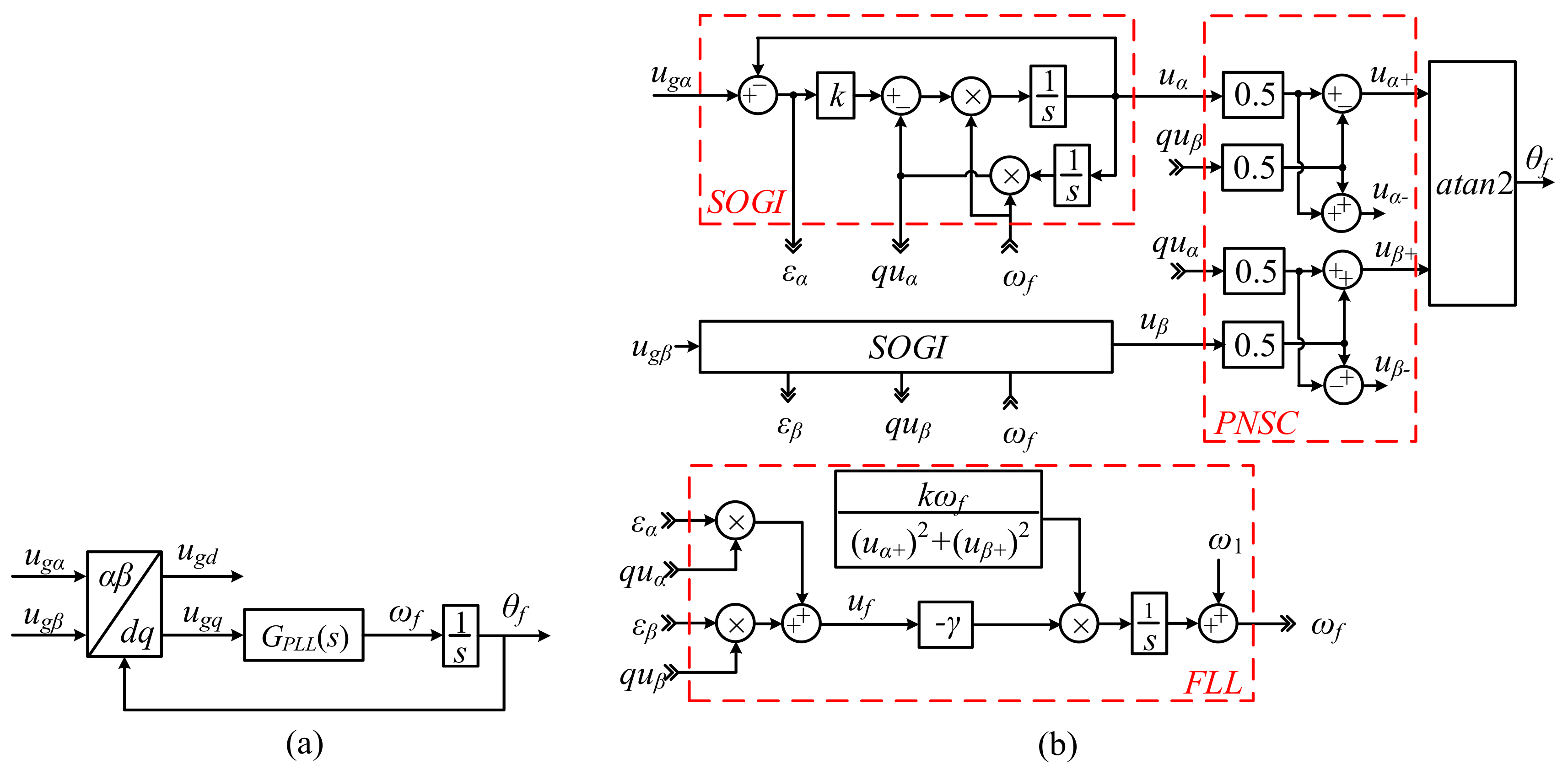
2.2. Grid Synchronization Methods
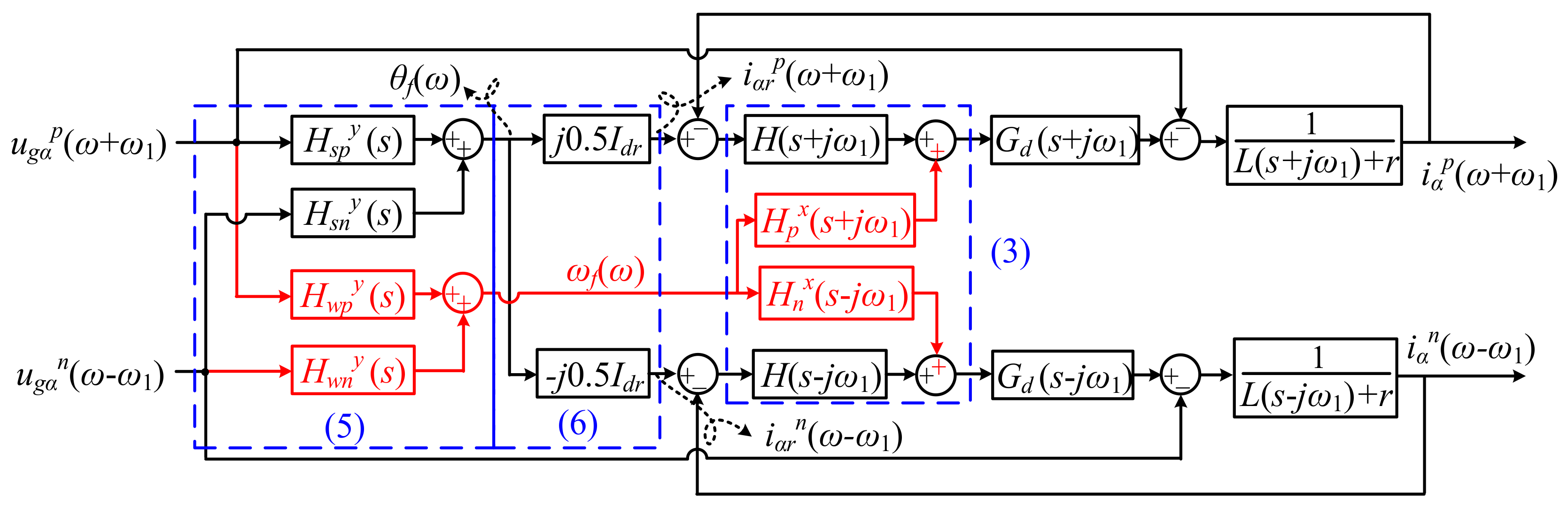
3. Impedance Modeling
3.1. Model of the Adaptive PR Controllers
3.2. Model of the PLL System
3.3. Model of the Current References
3.4. Model of the Grid Current Loop
3.5. Admittance Matrix
4. Impedance-Based Stability Analysis
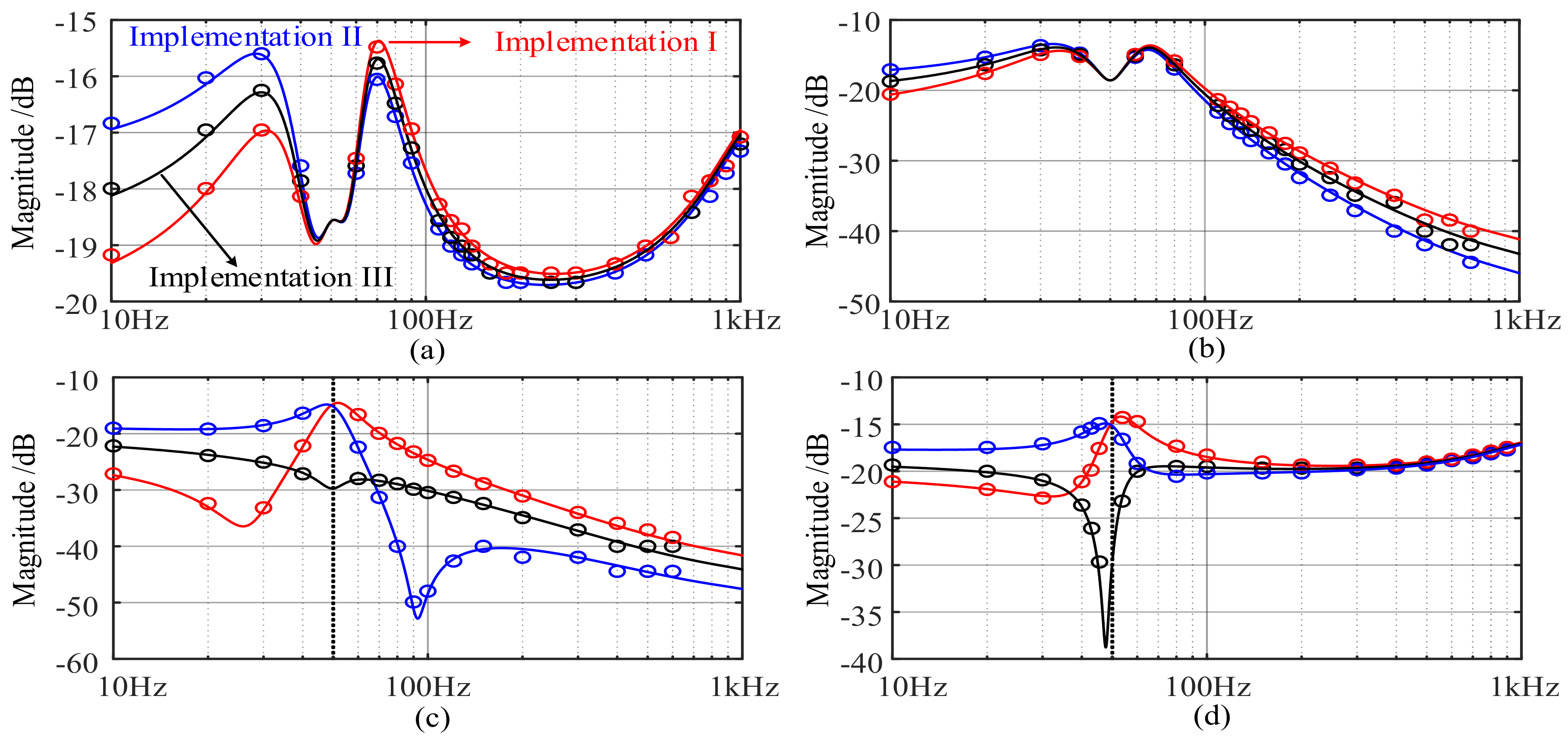
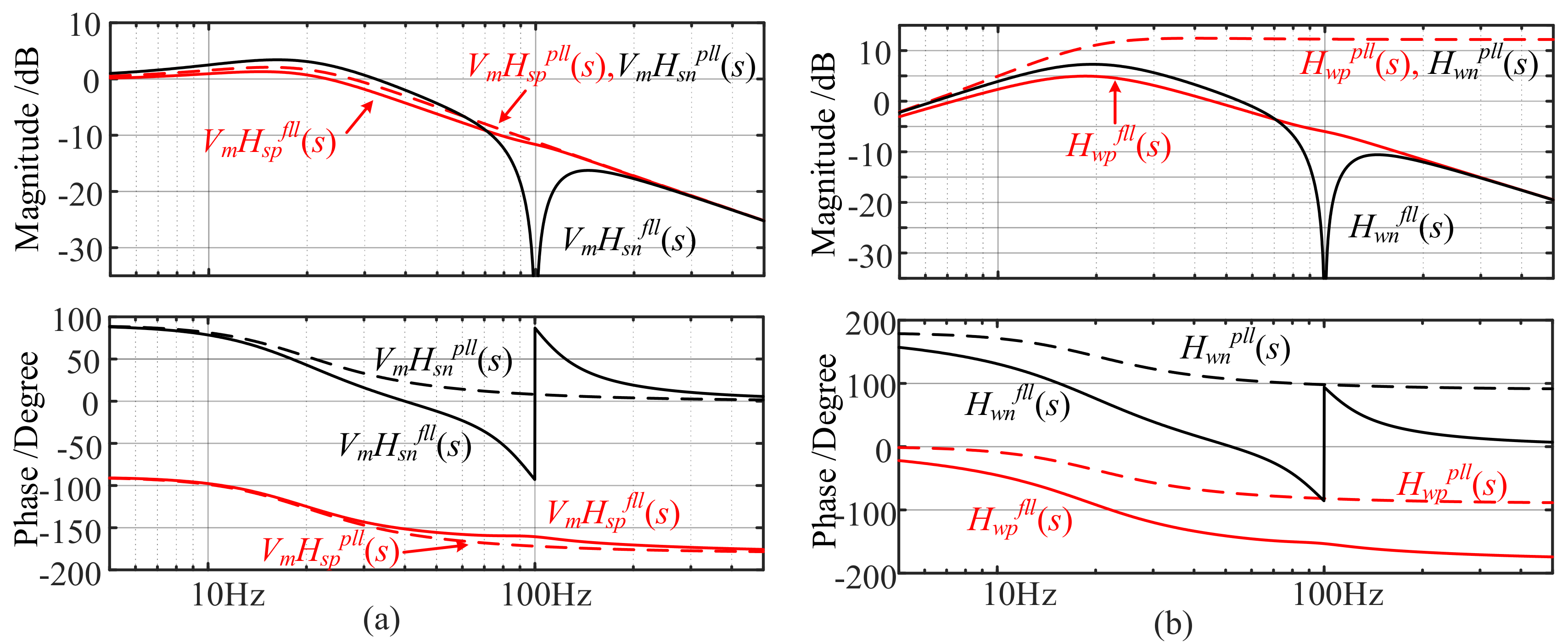
4.1. Addmittances Analysis and Verifications
4.1.1. SRF-PLL is Used for Grid Synchronization
4.1.2. DSOGI-FLL is Used for Grid Synchronization
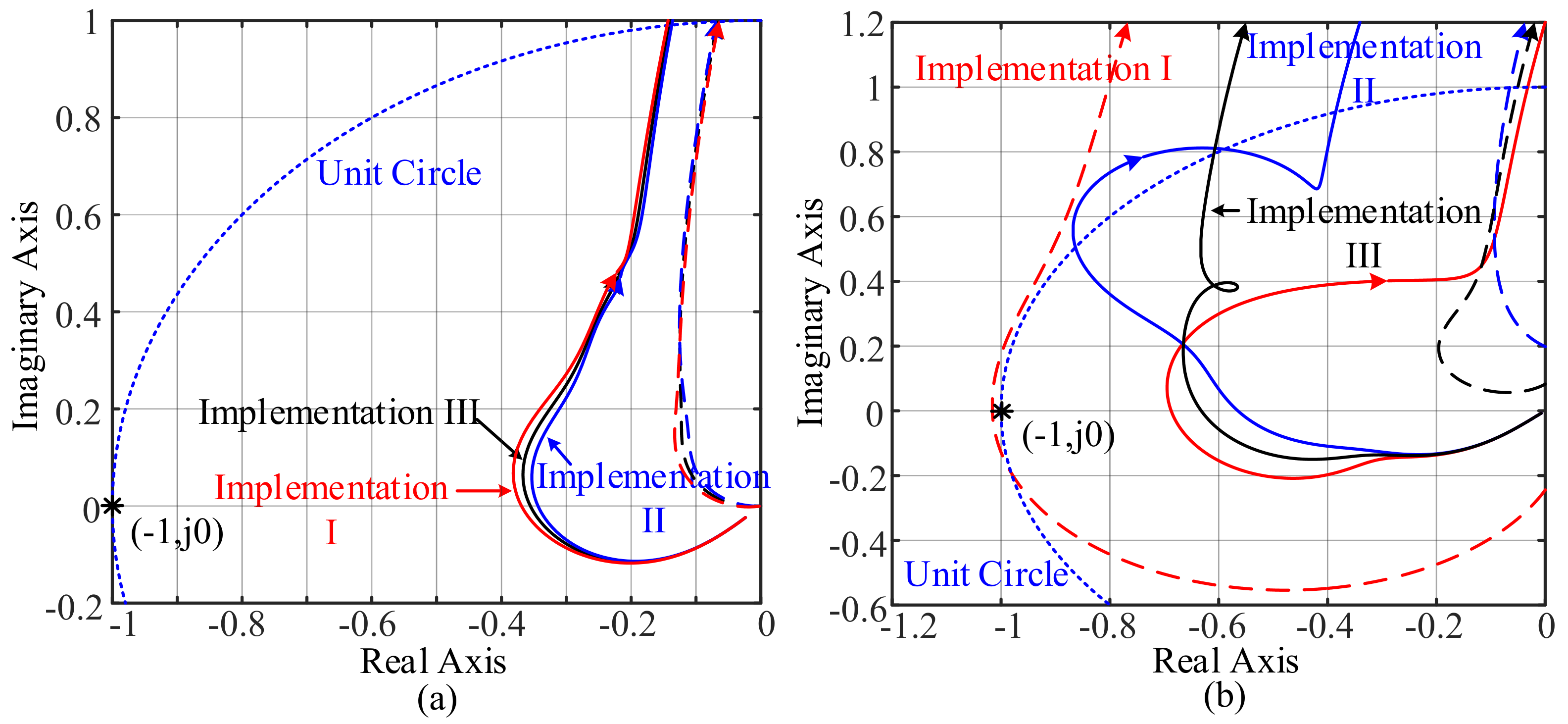
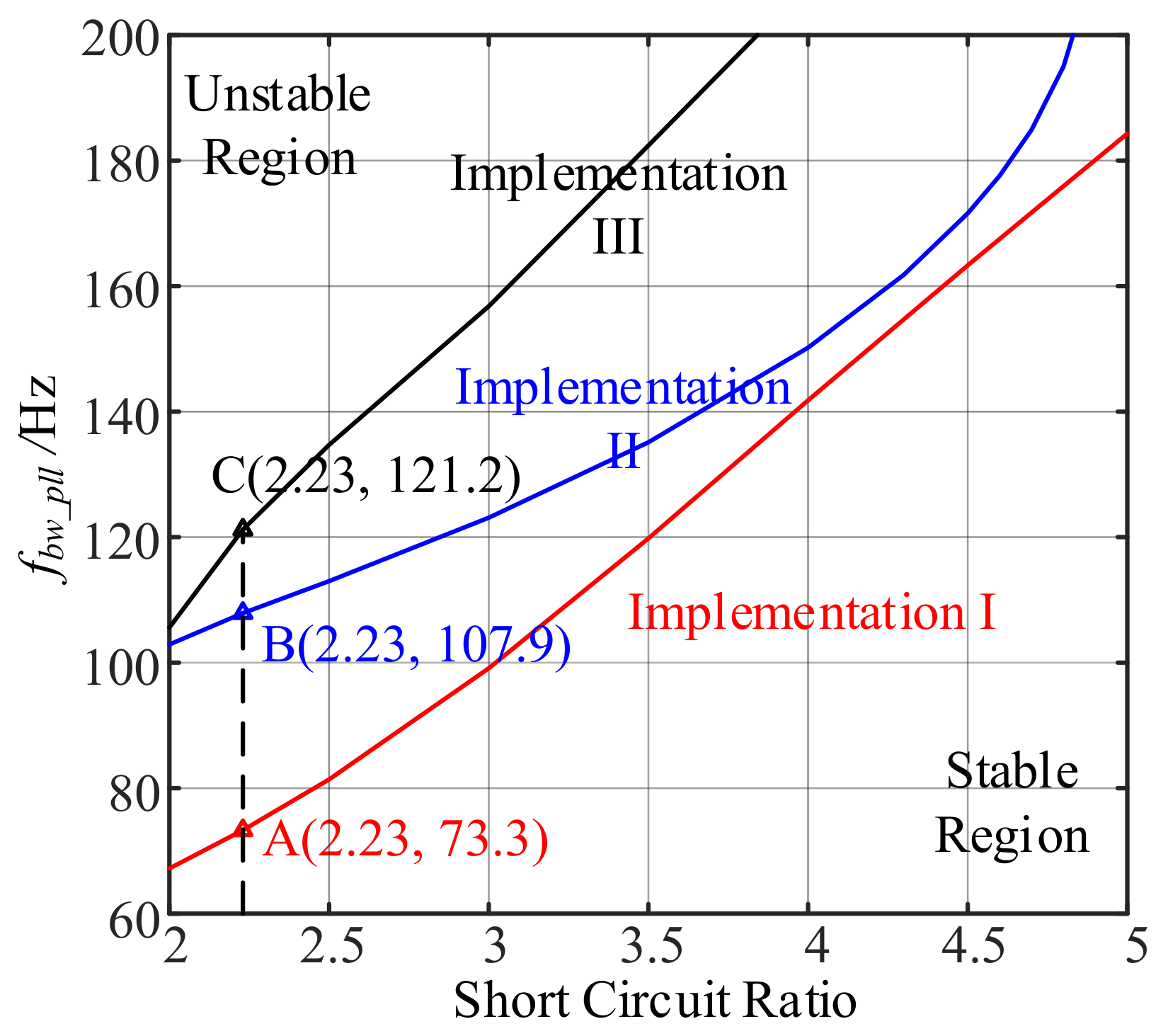
4.2. Stability Analysis
4.2.1. Stability Criterion
4.2.2. Stability Analysis with Different PLLs
4.2.3. Comparison with Different PLLs
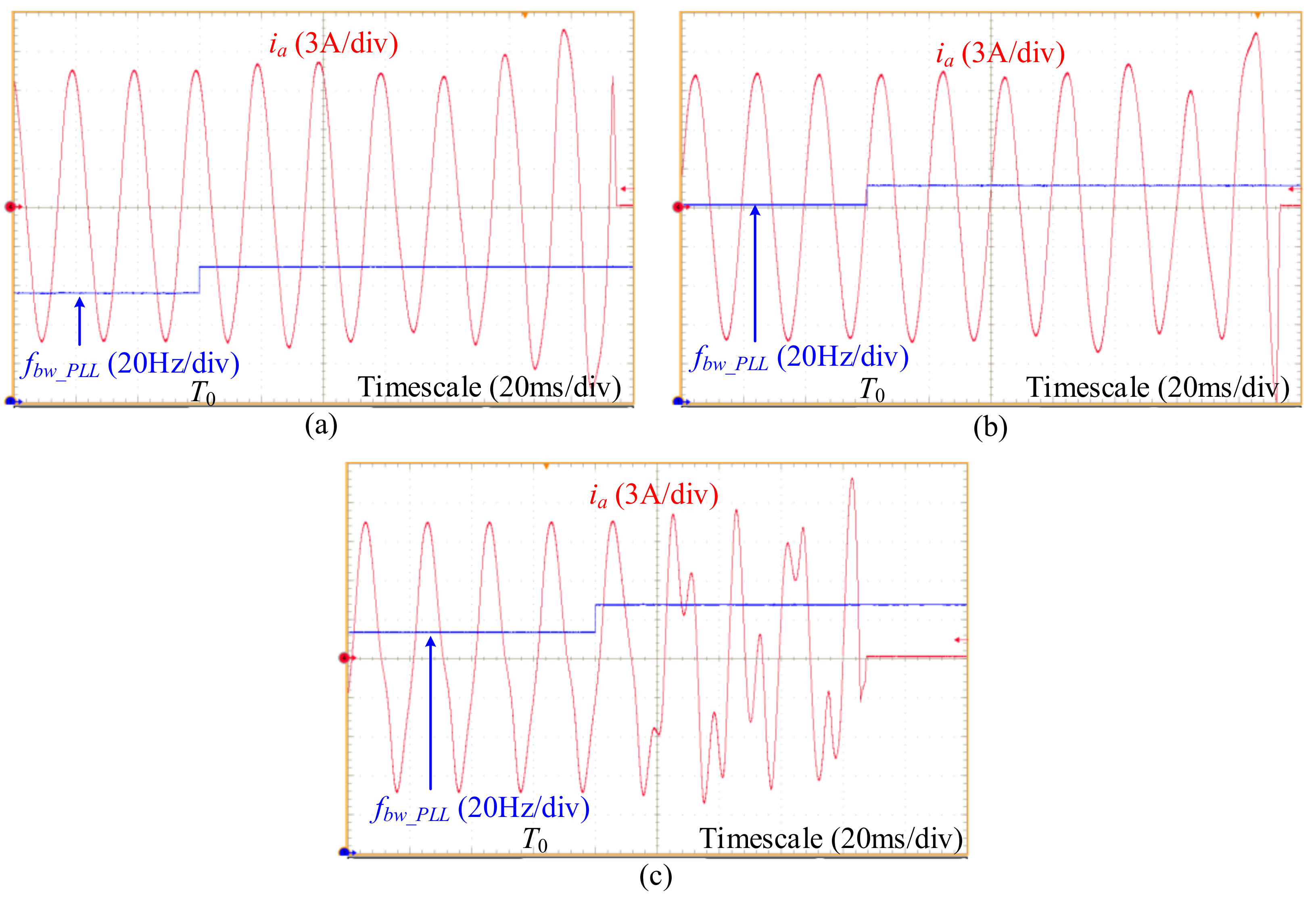
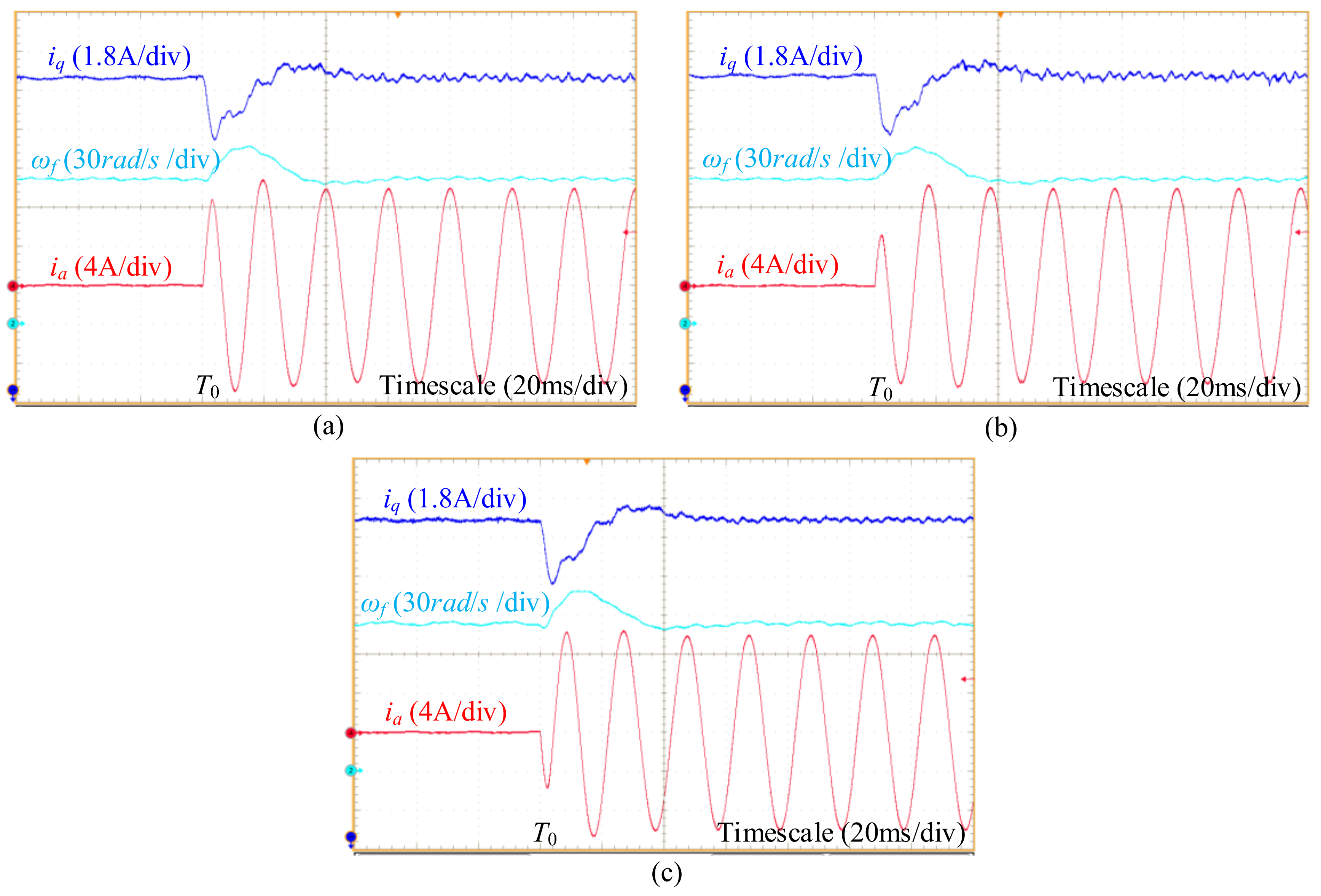
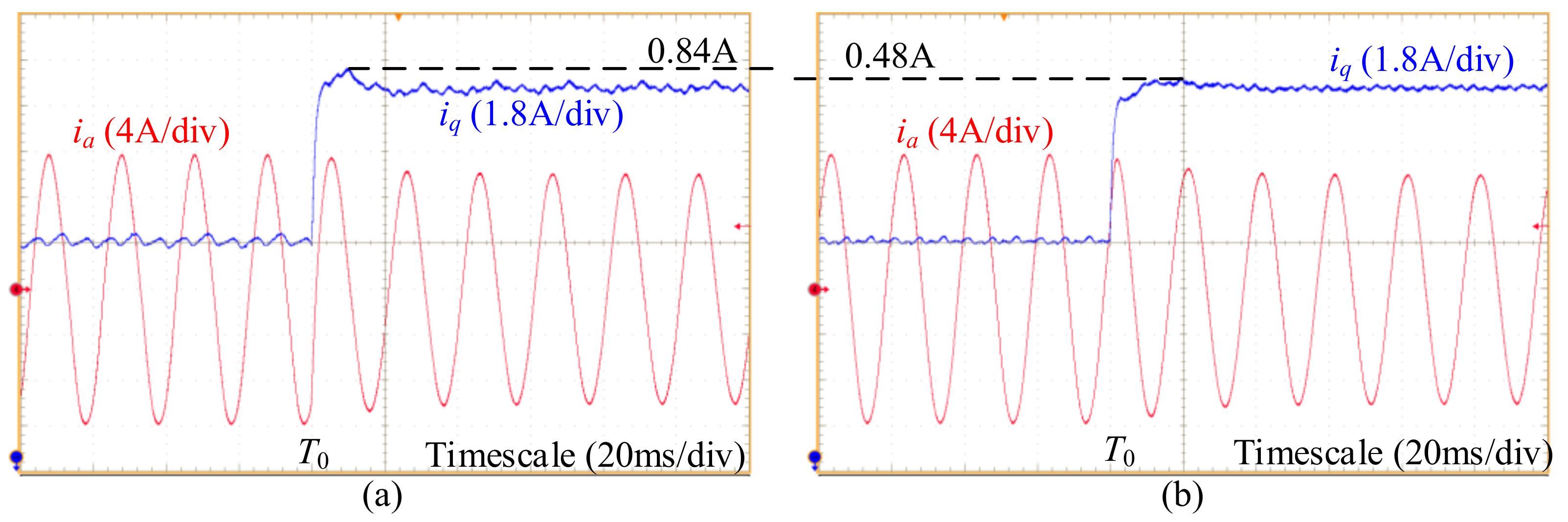
5. Experimental Verifications
6. Conclusions
- (1)
- If a SRF-PLL is used for grid synchronization, the system using implementation III of the resonant controller has the best stability margin, while the system using implementation I has the worst stability margin under weak grid conditions.
- (2)
- If a DSOGI-FLL is used for grid synchronization, the systems using implementation I, II, and III of the resonant controller have similar stability margins.
- (3)
- The system using a DSOGI-FLL for grid synchronization has a larger stability margin than that of the system using a SRF-PLL if the dynamic property of the output angle of the two synchronization methods are similar.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Modeling of the SRF-PLL
Appendix A.2. Modeling of the DSOGI-FLL
Appendix A.2.1. Modeling of the SOGIs
Appendix A.2.2. Modeling of the PNSC
Appendix A.2.3. Modeling of the FLL
Appendix A.2.4. Modeling of the Output Angle
References
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Dash, P.P.; Kazerani, M. Dynamic modeling and performance analysis of a grid-connected current-source inverter-based photovoltaic system. IEEE Trans. Sustain. Energy 2011, 2, 443–450. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Gandoy, J.D.; Lopez, O.; Malvar, J.; Comesana, P.F. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1772. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Enhancing the Frequency Adaptability of Periodic Current Controllers with a Fixed Sampling Rate for Grid-Connected Power Converters. IEEE Trans. Power Electron. 2016, 31, 7232–7285. [Google Scholar] [CrossRef]
- Bojoi, R.I.; Griva, G.; Bostan, V.; Guerriero, M.; Farina, F.; Profumo, F. Current Control Strategy for Power Conditioners Using Sinusoidal Signal Integrators in Synchronous Reference Frame. IEEE Trans. Power Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F.; Wang, D.; Zhang, B. Frequency Adaptive Selective Harmonic Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2015, 30, 3912–3924. [Google Scholar] [CrossRef] [Green Version]
- Cadaval, E.R.; Spagnuolo, G.; Franquelo, L.G.; Paja, C.A.R.; Suntio, T.; Xiao, W.M. Grid-connected photovoltaic generation plants: Components and operation. IEEE Ind. Electron. Mag. 2013, 7, 6–20. [Google Scholar] [CrossRef] [Green Version]
- Espin, F.G.; Garcera, G.; Patrao, I.; Figueres, E. An adaptive control system for three-phase photovoltaic inverters working in a polluted and variable frequency electric grid. IEEE Trans. Power Electron. 2012, 27, 4248–4261. [Google Scholar] [CrossRef]
- Herran, M.A.; Fischer, J.R.; Gonzalez, S.A.; Judewicz, M.G.; Carugati, I.; Carrica, D.O. Repetitive control with adaptive sampling frequency for wind power generation systems. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 58–69. [Google Scholar] [CrossRef]
- Jorge, S.G.; Busada, C.A.; Solsona, J.A. Frequency-adaptive current controller for three-phase grid-connected converters. IEEE Trans. Ind. Electron. 2013, 60, 4169–4177. [Google Scholar] [CrossRef]
- Timbus, A.V.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Adaptive Resonant Controller for Grid-Connected Converters in Distributed Power Generation Systems. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006; pp. 1601–1606. [Google Scholar]
- Chung, S.K. A phase tracking system for three phase utility interface inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Aguilar, R.S.M.; Otadui, I.E.; Teodorescu, R.; Blaabjerg, F. A Stationary Reference Frame Grid Synchronization System for Three-Phase Grid-Connected Power Converters under Adverse Grid Conditions. IEEE Trans. Power Electron. 2012, 27, 99–112. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and analysis of harmonic stability in an AC power-electronics-based power system. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Alawasa, K.M.; Mohamed, Y.A.R.I.; Xu, W. Active mitigation of subsynchronous interactions between PWM voltage-source converters and power networks. IEEE Trans. Power Electron. 2014, 29, 121–134. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Alvarez, A.E.; Fekriasl, S.; Hassan, F.; Bellmunt, O.G. Advanced Vector Control for Voltage Source Converters Connected to Weak Grids. IEEE Trans. Power Syst. 2015, 30, 3072–3081. [Google Scholar] [CrossRef]
- Li, X.; Lin, H. Multifrequency Small-Signal Model of Voltage Source Converters Connected to a Weak Grid for Stability Analysis. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 728–732. [Google Scholar]
- Cho, Y.; Lee, C.; Hur, K.; Kang, Y.C.; Muljadi, E. Impedance-Based Stability Analysis in Grid Interconnection Impact Study Owing to the Increased Adoption of Converter-Interfaced Generators. Energies 2017, 10, 1355. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Rygg, A.; Monlinas, M.; Zhang, C.; Cai, X. A modified sequence domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of ac power electronic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1383–1396. [Google Scholar] [CrossRef]
- Bakhshizadeh, M.K.; Wang, X.; Blaabjerg, F.; Hjerrild, J.; Kocewiak, L.; Bak, C.L.; Hesselbaek, B. Couplings in Phase Domain Impedance Modeling of Grid-Connected Converters. IEEE Trans. Power Electron. 2016, 31, 6792–6796. [Google Scholar]
- Timbus, A.; Liserre, M.; Teodoresce, R.; Rodriguez, P.; Blaabjerg, F. Evaluation of current controllers for distributed power generation systems. IEEE Trans. Power Electron. 2009, 24, 654–664. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. Grid synchronization PLL based on cascaded delayed signal cancellation. IEEE Trans. Power Electron. 2001, 26, 1987–1997. [Google Scholar] [CrossRef]
- Yi, H.; Wang, X.; Blaabjerg, F.; Zhou, F. Impedance Analysis of SOGI-FLL-Based Grid Synchronization. IEEE Trans. Power Electron. 2017, 32, 7409–7413. [Google Scholar] [CrossRef]




| X | i | ii | iii |
|---|---|---|---|
| Symbol | Description | Value |
|---|---|---|
| V1 | Grid phase-neutral peak voltage | 30√2 V |
| ω1 | Grid angular frequency | 2π × 50 rad/s |
| fs | Switching frequency | 10 kHz |
| Vdc | Dc-link voltage | 130 V |
| L | Inductance of the L-type filter | 2 mH |
| r | Resistance of the filter | 0.2 Ω |
| αc | Current control loop bandwidth | 2π × 833 rad/s |
| ki | Proportional gain of ac/dc current controller | 10.47 |
| kr | R parameter of ac/dc current controller | 1047 |
| Idr | D channel current reference of VSC | 10 A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lin, H. Stability Analysis of Grid-Connected Converters with Different Implementations of Adaptive PR Controllers under Weak Grid Conditions. Energies 2018, 11, 2004. https://doi.org/10.3390/en11082004
Li X, Lin H. Stability Analysis of Grid-Connected Converters with Different Implementations of Adaptive PR Controllers under Weak Grid Conditions. Energies. 2018; 11(8):2004. https://doi.org/10.3390/en11082004
Chicago/Turabian StyleLi, Xing, and Hua Lin. 2018. "Stability Analysis of Grid-Connected Converters with Different Implementations of Adaptive PR Controllers under Weak Grid Conditions" Energies 11, no. 8: 2004. https://doi.org/10.3390/en11082004





