An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment
Abstract
:1. Introduction
2. Uncertainty Representation with Renewable Generation
2.1. VAR Calculation
- Step 1.
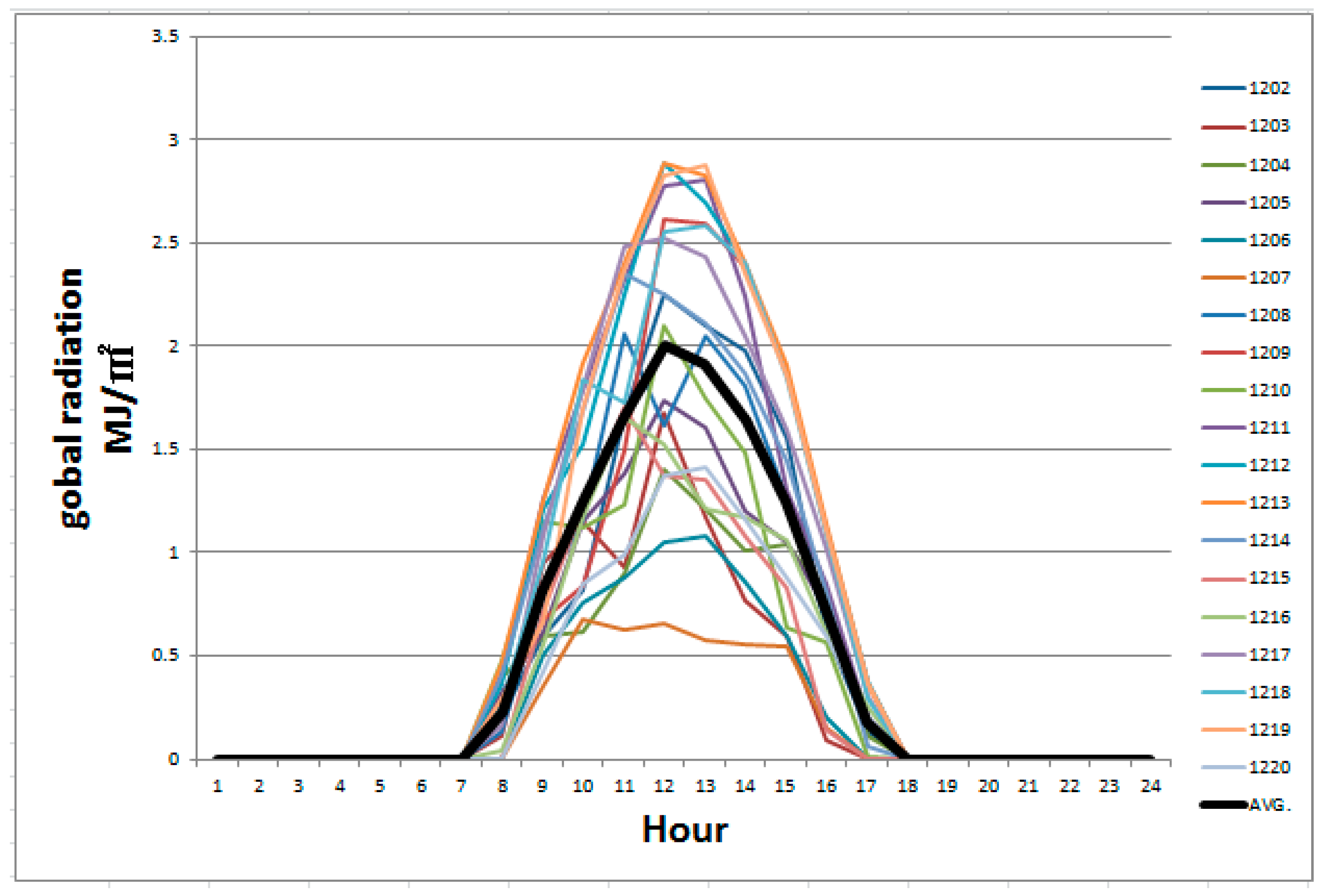
- Retrieve the historical data:The wind speed and global irradiance for the WTs and PVs were retrieved from the historical data.
- Step 2.
- Calculate the rate of change for the wind speed/global irradiance:: The wind speed or global irradiance at time t.
- Step 3.
- Sort the rate of change from small to large.
- Step 4.
- Calculate the critical value of the rate of change in a confidence value, α%
- Step 5.
- Multiply the critical value of the rate of change by the wind speed/global irradiance value to derive the VAR (
- Step 6.
- Combine the EWMAA and decay factor, so that the VAR of the following data is calculated. When all historical data are completed, the operation stops. If the pre-set target is not yet attained, go back to Step (1) and repeat the operation. In this paper, there were 720 items of historical data.
2.2. The Power Output of the WT Uncertainty
2.3. The Power Output of the PV Uncertainty
2.4. The Fuel Cost of Diesel Oil Unit
2.5. Model for Battery Storage
- If the battery is charging:
- If the battery is discharging:where and are the charging efficiency and the discharging efficiency, respectively. is the electrical power of the battery output at the hour. is the aggregated capacity of the batteries at hour. is the rated maximum storage energy. / is the maximum portion of the rated capacity that can be added to/withdrawn from storage in an hour. is the scheduling hour. In this paper, was equal to 1 h.
3. Mathematical Formulation
- (a)
- Load balance:
- (b)
- Unit power generation limitation:
- (c)
- Ramp up rate:
- (d)
- Ramp down rate:
- (e)
- Electricity bought/sold of utility:
4. Methodology
4.1. Initial Solutions
4.2. Employed Bee Phase
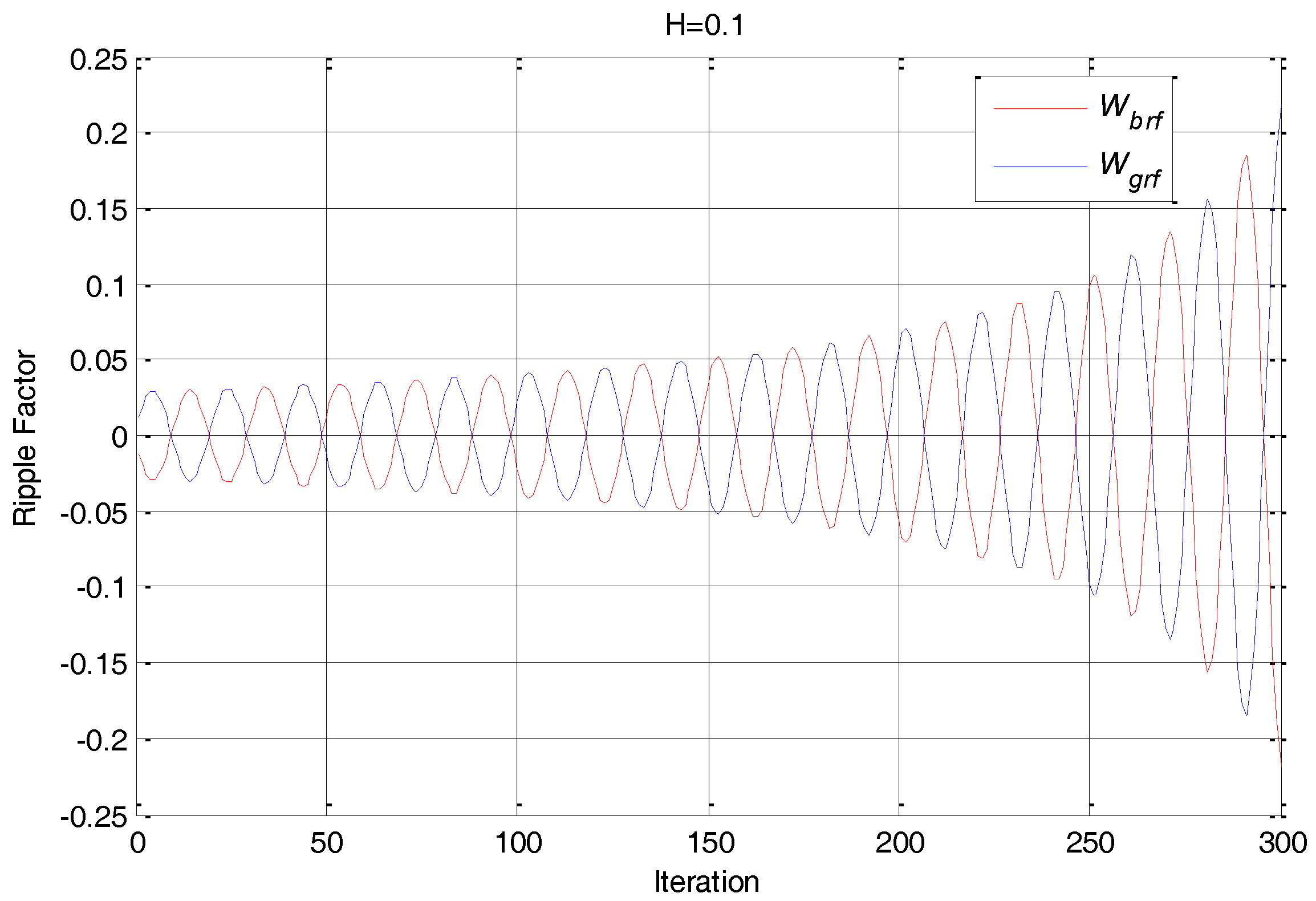
4.2.1. Sin-Wave Weight Factor (SWF)
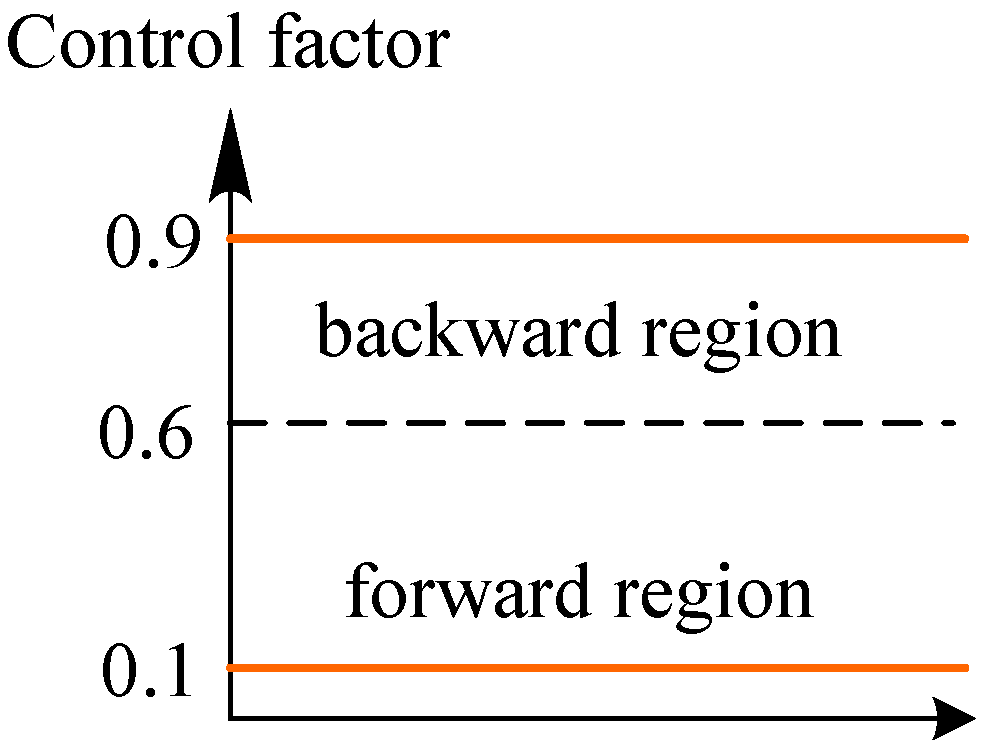
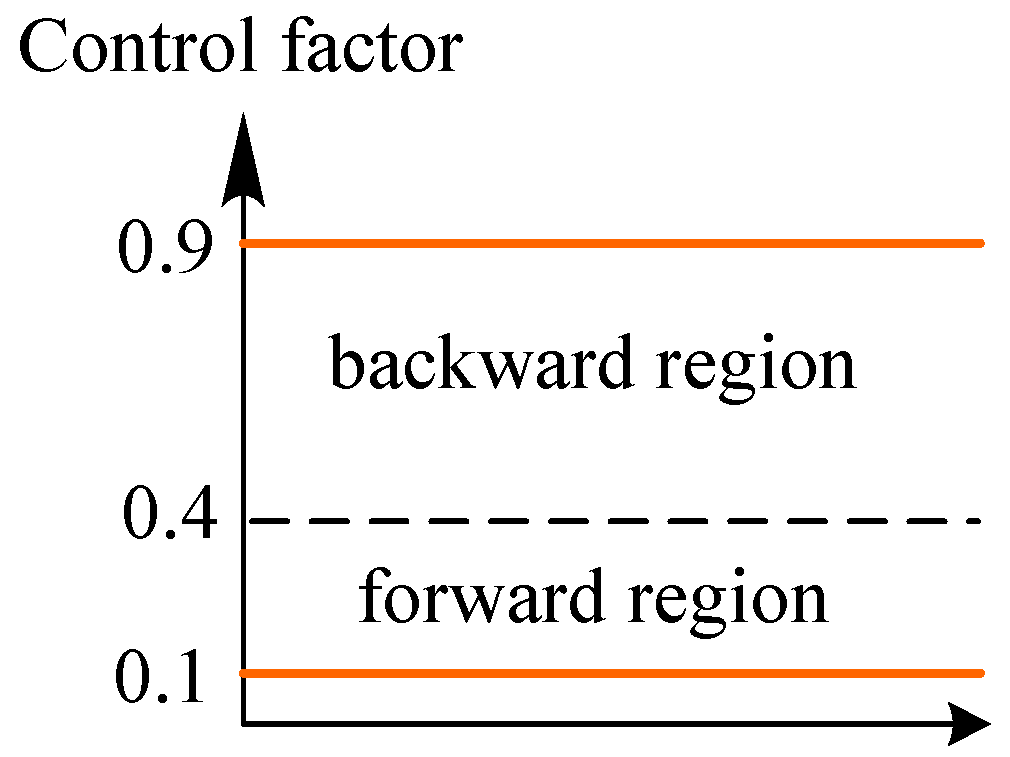
4.2.2. Forward-Backward Control Factor (FBCF)
4.3. Onlooker Bees
4.4. Scout Bees
4.5. Stop Condition
5. Simulation Results
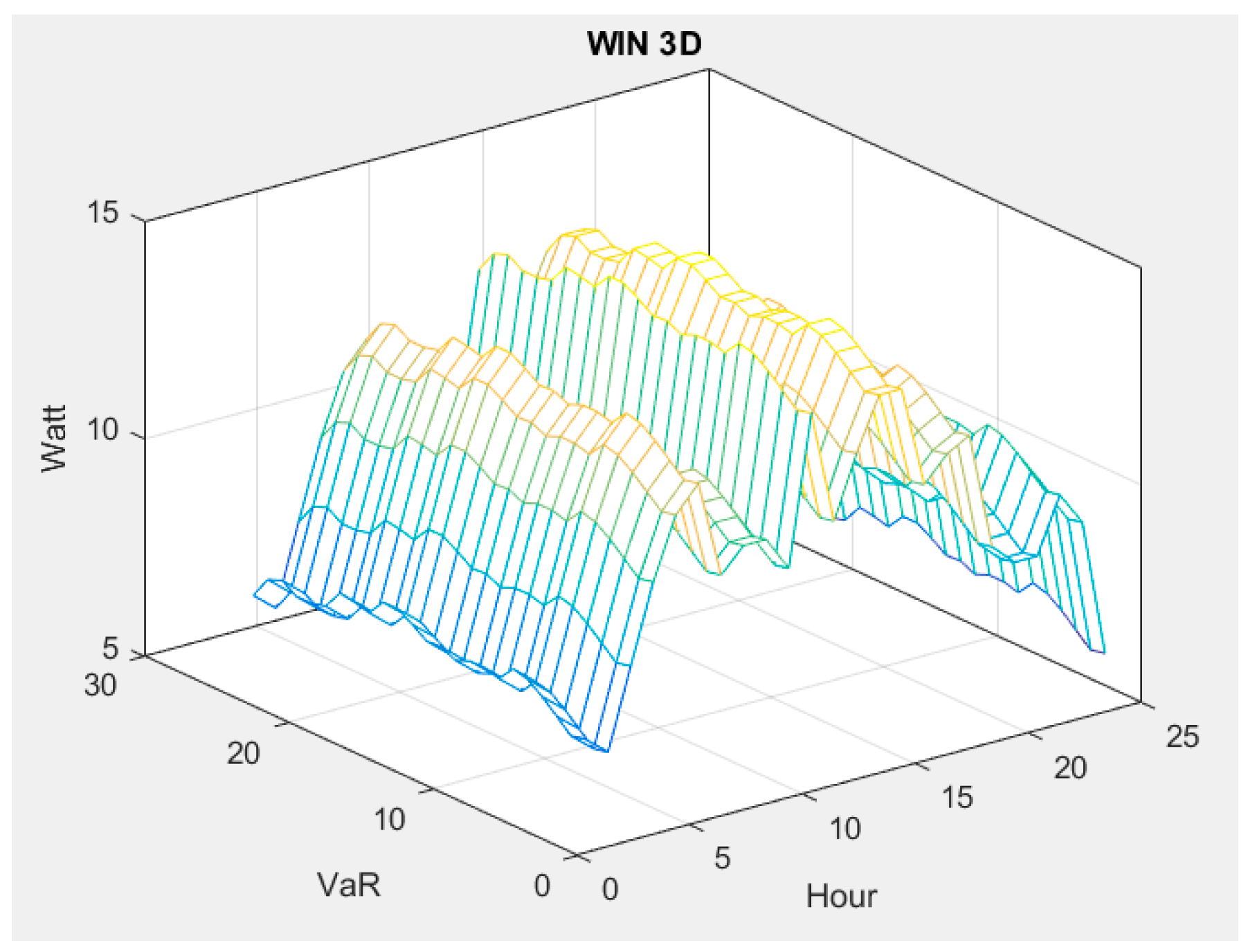
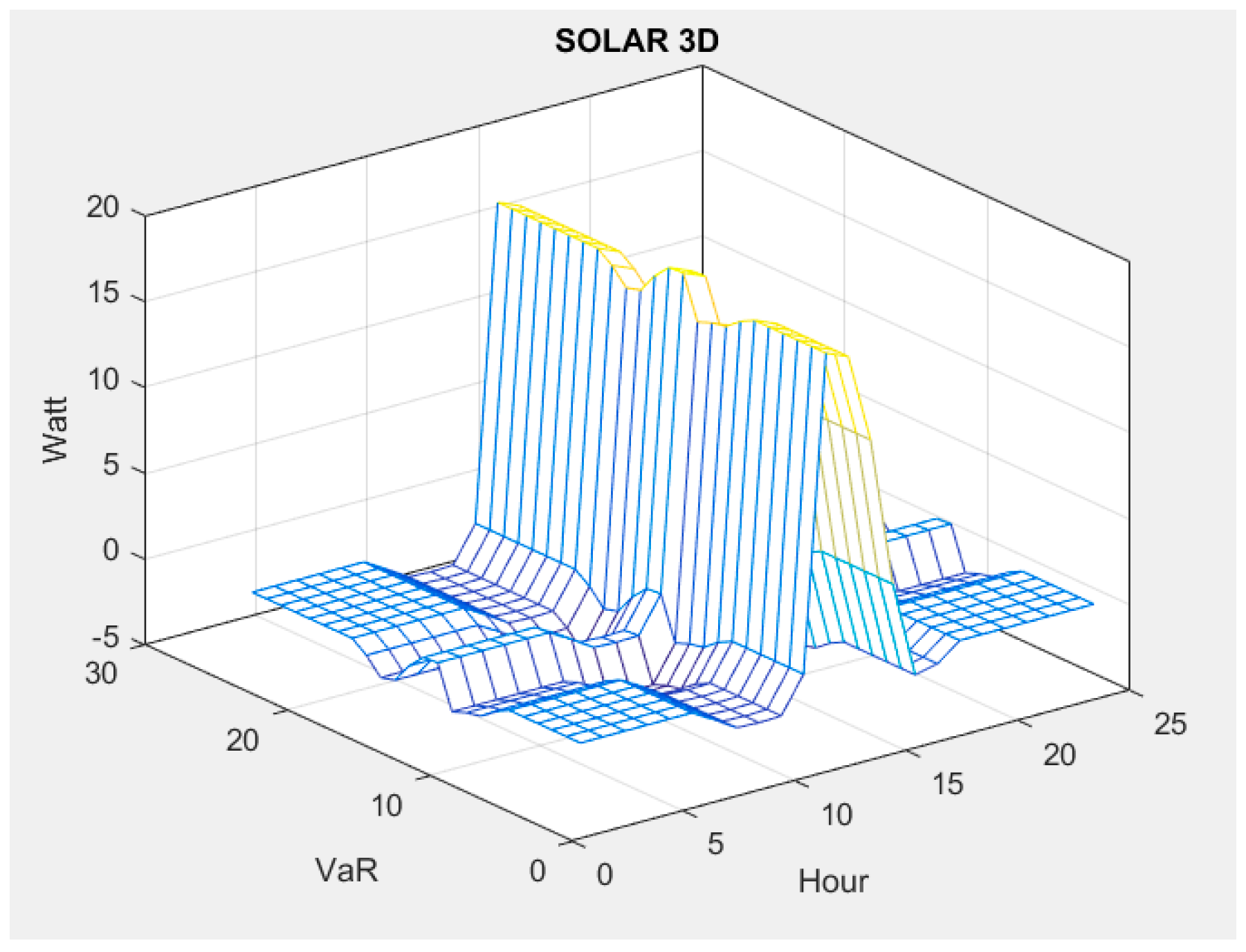
5.1. VAR of WTs and PVs’ Generation in Different Scenarios
5.2. Results in the Grid-Connected Scenario
5.3. Results in the Stand-Alone Scenario
5.4. Convergence Test
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Huang, J.; Jiang, C.; Xu, R. A review on distributed energy resources and Microgrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Manag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Faber, I.; Lane, W.; Pak, W.; Prakel, M.; Rocha, C.; Farr, J.V. Micro-energy markets: The role of a consumer preference pricing strategy on microgrid energy investment. Energy 2014, 74, 567–575. [Google Scholar] [CrossRef]
- Hopkins, M.D.; Pahwa, A.; Easton, T. Intelligent Dispatch for Distributed Renewable Resources. IEEE Trans. Smart Grid 2012, 3, 1047–1054. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Dong, X.; Luan, W.; Bornemann, X. Short-term operation scheduling in renewable-powered microgrids: A duality-based approach. IEEE Trans. Sustain. Energy 2014, 5, 209–217. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy management of microgrid in grid-connected and stand-alone modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Bonucci, F. Micro-grid operation analysis for cost-effective battery energy storage and RES plants integration. Energy 2016, 113, 831–844. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Abdelsalam, A.A. Microgrid energy management in grid-connected and islanding modes based on SVC. Energy Convers. Manag. 2014, 86, 964–972. [Google Scholar] [CrossRef]
- Juan, M.; Lujano, R.; Dufo-López, R.; José, L.; Eduardo, M.G. Operating conditions of lead-acid batteries in the optimization of hybrid energy systems and microgrids. Appl. Energy 2016, 179, 590–600. [Google Scholar]
- Zhong, H.; Xia, Q.; Xia, Y.; Kang, C.; Xie, L. Integrated dispatch of generation and load: A pathway towards smart grids. Electr. Power Syst. Res. 2015, 120, 206–213. [Google Scholar] [CrossRef]
- Rémy, R.M.; Bruno, S.; Xavier, R.; Christophe, T. Optimal power dispatching strategies in smart-microgrids with storage. Renew. Sustain. Energy Rev. 2014, 40, 649–658. [Google Scholar] [Green Version]
- Agamah, S.U.; Ekonomou, L. Energy storage system scheduling for peak demand reduction using evolutionary combinatorial optimization. Sustain. Energy Technol. Assess. 2017, 23, 73–82. [Google Scholar]
- Al Ghaithi, H.M.; Fotis, G.P.; Vita, V. Techno-economic assessment of hybrid energy off-grid system—A case study for Masirah island in Oman. Int. J. Power Energy Res. 2017, 1, 103–116. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Ekonomou, L.; Mastorakis, N.E. Economic analysis of energy storage system integration with a grid connected intermittent power plant, for power quality purposes. WSEAS Trans. Power Syst. 2016, 11, 65–71. [Google Scholar]
- Nieto, A.; Vita, V.; Maris, T.I. Power quality improvement in power grids with the integration of energy storage systems. Int. J. Eng. Res. Technol. 2016, 5, 438–443. [Google Scholar]
- El-Hendawi, M.; Gabbar, H.A.; El-Saady, G.; Ibrahim, E.A. Control and EMS of a Grid-Connected Microgrid with Economical Analysis. Energies 2018, 11, 129. [Google Scholar] [CrossRef]
- Zhang, N. A convex model of risk-based unit commitment for day-ahead market clearing considering wind power uncertainty. IEEE Trans. Power Syst. 2015, 30, 1582–1592. [Google Scholar] [CrossRef]
- Alexander, C. Risk Management and Analysis—Volume 1 Measuring and Modeling Financial Risk; John Wiley & Sons Ltd.: Chichester, UK, 1998. [Google Scholar]
- Ji, L.; Huang, G.; Xie, Y.; Zhou, Y.; Zho, J. Robust cost-risk tradeoff for day-ahead schedule optimization in residential microgrid system under worst-case conditional value-at-risk consideration. Energy 2018, 153, 324–337. [Google Scholar] [CrossRef]
- Shen, J.; Jiang, C.; Liu, Y.; Wang, X. A microgrid energy management system and risk management under an electricity market environment. IEEE Acess 2016, 3, 2349–2356. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Integration of renewable generation uncertainties into stochastic unit commitment considering reserve and risk: A comparative study. Energy 2016, 103, 735–745. [Google Scholar] [CrossRef]
- Asensio, M.; Contreras, J. Stochastic unit commitment in isolated systems with renewable penetration under cavr assessment. IEEE Trans. Smart Grid 2016, 7, 1356–1367. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Wang, J.; Wei, W.; Mei, S. Risk-based admissibility assessment of wind generation integrated into a bulk power system. IEEE Trans. Sustain. Energy 2016, 7, 325–336. [Google Scholar] [CrossRef]
- Pousinho, H.M.I.; Mendes, V.M.F.; Catalao, J.P.S. A risk-averse optimization model for trading wind energy in a market environment under uncertainty. Energy 2011, 36, 4935–4942. [Google Scholar] [CrossRef] [Green Version]
- Pinto, M.S.S.; Miranda, V.; Saavedra, O.R. Risk and unit commitment decisions in scenarios of wind power uncertainty. Renew. Energy 2016, 97, 550–558. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Deng, W.; Zhang, K. Application of cost-cvar model in determining optimal spinning reserve for wind power penetrated system. Int. J. Electr. Power Energy Syst. 2015, 66, 110–115. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Seifi, A.; Niknam, T. Multi-operation management of a typical micro-grids using Particle Swarm Optimization: A comparative study. Renew. Sustain. Energy Rev. 2012, 16, 1268–1281. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ito, T.; Senjyu, T.; Saber, A.Y. Intelligent Economic Operation of Smart-Grid Facilitating Fuzzy Advanced Quantum Evolutionary Method. IEEE Trans. Sustain. Energy 2013, 4, 905–916. [Google Scholar] [CrossRef]
- Liao, G.C. Solve environmental economic dispatch of Smart MicroGrid containing distributed generation system—Using chaotic quantum genetic algorithm. Int. J. Electr. Power Energy Syst. 2012, 43, 779–787. [Google Scholar] [CrossRef]
- Firouzi, B.B.; Farjah, E.; Abarghooee, R.A. An efficient scenario-based and fuzzy self-adaptive learning particle swarm optimization approach for dynamic economic emission dispatch considering load and wind power uncertainties. Energy 2013, 50, 232–244. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Guerrero, J.M. An optimal energy management system for islanded microgrids based on multiperiod artificial bee colony combined with markov chain. IEEE Syst. J. 2015, 99, 1–11. [Google Scholar] [CrossRef]
- Marrison, C. Fundamentals of Risk Measurement; McGraw-Hill Companies, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Slootweg, J.G.; Haan, S.W.H.; Polinder, H.; Kling, W.L. General model for representing variable speed wind turbines in power system dynamics simulations. IEEE Trans. Power Syst. 2003, 18, 144–151. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, X.; Yang, H.; Kong, S. Design and Realization of Microgrid Composing of Photovoltaic and Energy Storage System. Energy Procedia 2011, 12, 1008–1014. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener. 2011, 6, 258–267. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. J. Appl. Math. Comput. 2009, 2014, 108–132. [Google Scholar] [CrossRef]








| Unit | The Number of Unit | Capacity/Unit (MW) | Total Capacity |
|---|---|---|---|
| Jianshan Plant | 12 | 11 | 121 |
| Chongtun WT | 8 | 0.6 | 4.8 |
| Huhs WT | 6 | 0.9 | 5.4 |
| Jianshan PV | 1 | 0.1 | 0.1 |
| Cimei PV | 1 | 0.2 | 0.2 |
| Tai-pen power line | 1 | 100 | 100 |
| Battery storage | 1 | 20 | 20 |
| Time | α = 95% | α = 90% | α = 85% |
|---|---|---|---|
| 1 | 90,455 | 89,576 | 89,166 |
| 2 | 79,409 | 79,158 | 78,975 |
| 3 | 74,640 | 74,442 | 74,298 |
| 4 | 71,932 | 71,750 | 71,618 |
| 5 | 73,911 | 73,698 | 73,543 |
| 6 | 71,347 | 71,151 | 71,007 |
| 7 | 80,250 | 80,042 | 79,900 |
| 8 | 126,592 | 126,254 | 126,033 |
| 9 | 165,173 | 164,815 | 164,570 |
| 10 | 210,630 | 210,218 | 208,611 |
| 11 | 223,932 | 223,424 | 227,057 |
| 12 | 202,373 | 214,050 | 210,144 |
| 13 | 233,289 | 239,982 | 229,980 |
| 14 | 251,213 | 258,779 | 250,429 |
| 15 | 237,691 | 237,273 | 238,393 |
| 16 | 243,499 | 237,487 | 235,574 |
| 17 | 188,989 | 180,220 | 179,592 |
| 18 | 180,828 | 172,106 | 171,833 |
| 19 | 184,866 | 184,799 | 187,371 |
| 20 | 201,678 | 203,469 | 192,526 |
| 21 | 192,914 | 185,583 | 192,343 |
| 22 | 103,460 | 98,745 | 102,822 |
| 23 | 94,632 | 97,177 | 94,581 |
| 24 | 84,864 | 84,381 | 76,354 |
| Total | 3,668,568 | 3,654,917 | 3,622,124 |
| Time | α = 95% | α = 90% | α = 85% |
|---|---|---|---|
| 1 | 297,176 | 296,582 | 296,091 |
| 2 | 249,432 | 248,510 | 247,916 |
| 3 | 249,425 | 248,746 | 248,251 |
| 4 | 249,425 | 248,770 | 248,297 |
| 5 | 242,642 | 242,087 | 241,572 |
| 6 | 235,717 | 234,532 | 234,022 |
| 7 | 235,718 | 234,607 | 234,206 |
| 8 | 234,976 | 238,187 | 237,810 |
| 9 | 280,813 | 279,107 | 278,710 |
| 10 | 280,805 | 282,627 | 282,181 |
| 11 | 330,239 | 323,518 | 322,935 |
| 12 | 285,731 | 285,029 | 284,512 |
| 13 | 285,731 | 285,672 | 285,004 |
| 14 | 285,732 | 286,969 | 286,328 |
| 15 | 285,735 | 283,001 | 282,323 |
| 16 | 281,554 | 280,635 | 280,163 |
| 17 | 281,556 | 281,580 | 281,115 |
| 18 | 292,229 | 295,140 | 294,788 |
| 19 | 292,220 | 292,755 | 292,454 |
| 20 | 339,723 | 341,522 | 341,242 |
| 21 | 339,722 | 339,276 | 338,967 |
| 22 | 334,643 | 334,271 | 334,005 |
| 23 | 320,622 | 320,240 | 319,994 |
| 24 | 303,793 | 303,339 | 303,040 |
| Total | 6,815,360 | 6,807,893 | 6,797,139 |
| Algorithm | Maximal Converged Cost (NT$) | Minimal Converged Cost (NT$) | Average Converged Cost (NT$) | Average Number of Generations to Converge | No. of Trials Reaching Optimum | Average Execution Time (s) |
|---|---|---|---|---|---|---|
| EP | 3,683,693 | 3,665,990 | 3,673,568 | 195 | 5 | 0.57 |
| GA | 3,684,978 | 3,669,434 | 3,675,568 | 197 | 7 | 1.56 |
| PSO | 3,676,768 | 3,665,594 | 3,672,568 | 194 | 54 | 0.68 |
| BSO | 3,675,155 | 3,665,436 | 3,671,568 | 172 | 50 | 0.73 |
| IBSO | 3,673,609 | 3,665,347 | 3,668,568 | 153 | 77 | 0.80 |
| Algorithm | Maximal Converged Cost (NT$) | Minimal Converged Cost (NT$) | Average Converged Cost (NT$) | Average Number of Generations to Converge | No. of Trials Reaching Optimum | Average Execution Time (s) |
|---|---|---|---|---|---|---|
| EP | 6,871,663 | 6,781,284 | 6,825,732 | 201 | 1 | 2.11 |
| GA | 6,899,863 | 6,808,210 | 6,829,203 | 202 | 2 | 6.06 |
| PSO | 6,868,878 | 6,798,868 | 6,824,748 | 195 | 31 | 2.22 |
| BSO | 6,868,689 | 6,802,491 | 6,820,079 | 191 | 37 | 2.27 |
| IBSO | 6,821,787 | 6,810,424 | 6,815,360 | 176 | 55 | 2.47 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-M.; Yang, C.-Y.; Tu, C.-S.; Tsai, M.-T. An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment. Energies 2018, 11, 1423. https://doi.org/10.3390/en11061423
Lin W-M, Yang C-Y, Tu C-S, Tsai M-T. An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment. Energies. 2018; 11(6):1423. https://doi.org/10.3390/en11061423
Chicago/Turabian StyleLin, Whei-Min, Chung-Yuen Yang, Chia-Sheng Tu, and Ming-Tang Tsai. 2018. "An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment" Energies 11, no. 6: 1423. https://doi.org/10.3390/en11061423
APA StyleLin, W.-M., Yang, C.-Y., Tu, C.-S., & Tsai, M.-T. (2018). An Optimal Scheduling Dispatch of a Microgrid under Risk Assessment. Energies, 11(6), 1423. https://doi.org/10.3390/en11061423




