Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid
Abstract
:1. Introduction
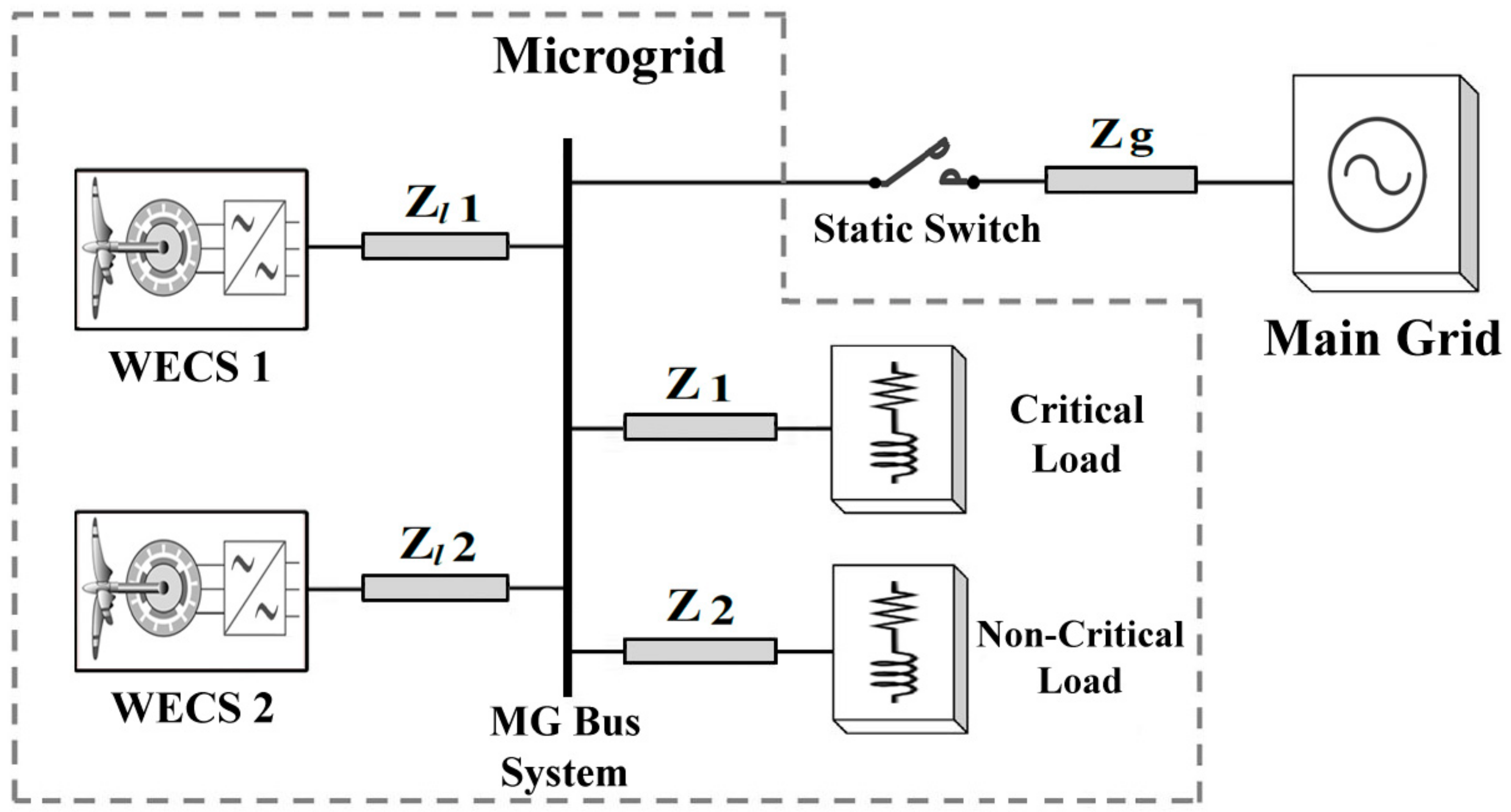
2. Structure of WECS-Based Microgrid
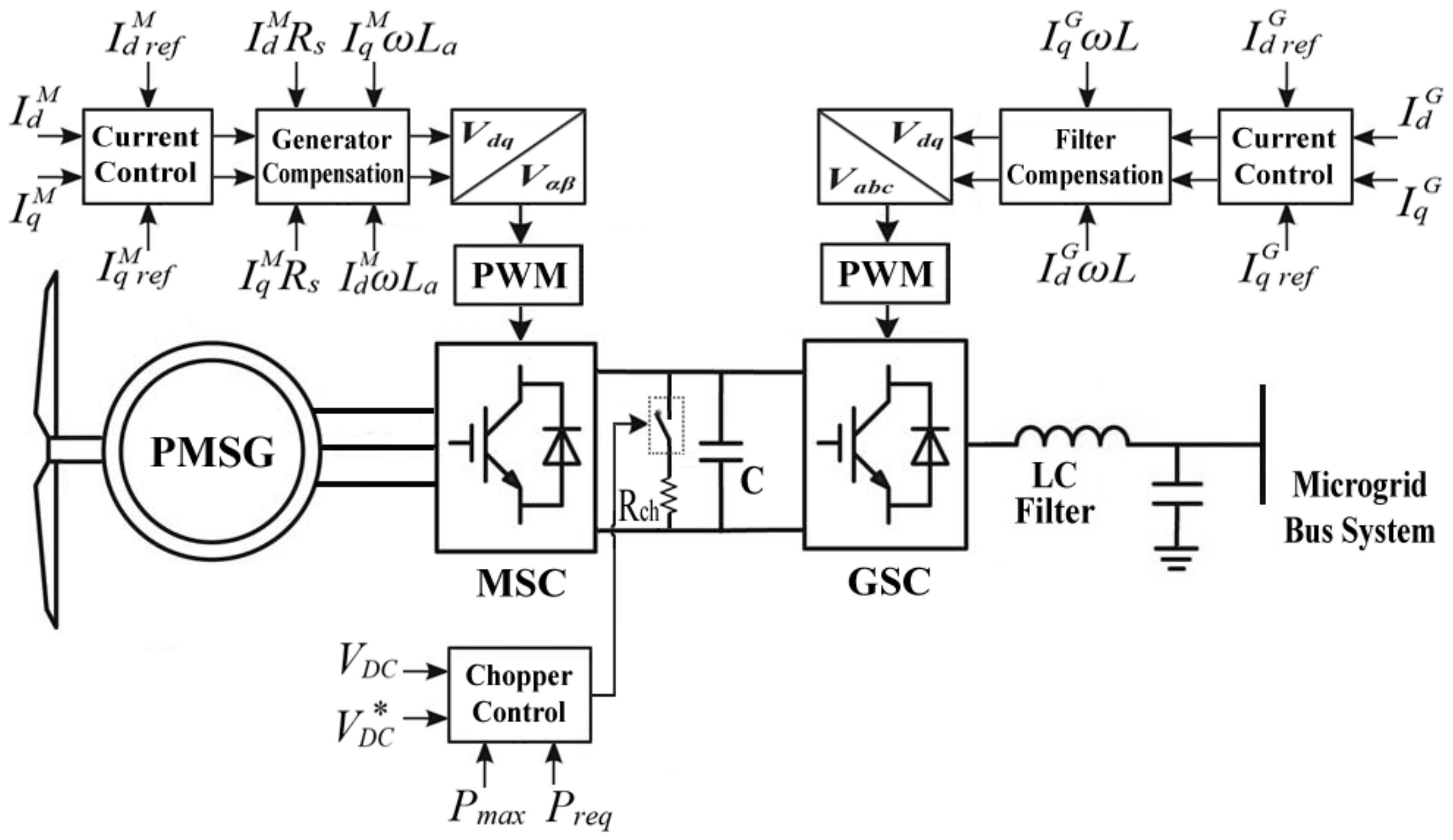
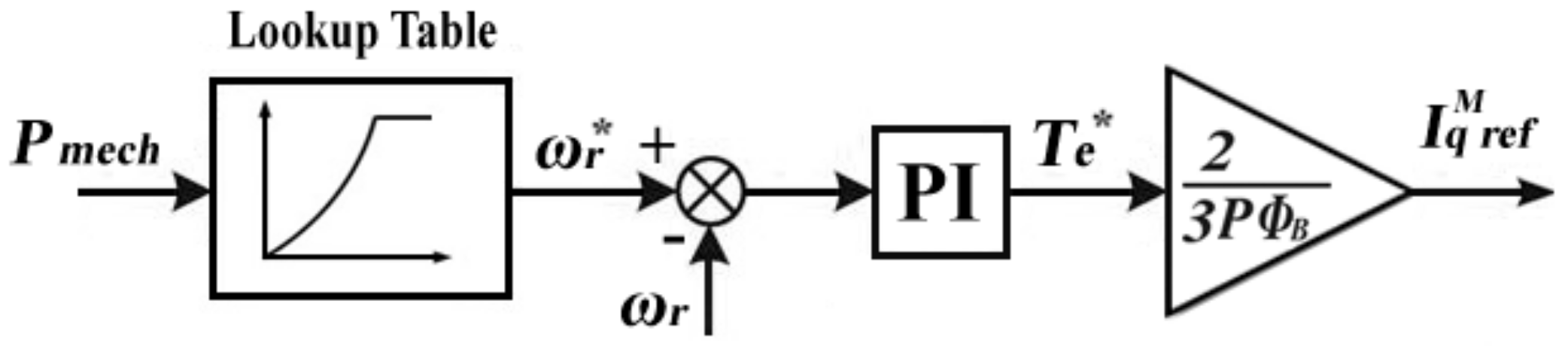
2.1. WECS 1: Battery-Backed WECS
2.2. WECS 2: WECS Supported by Adaptive Operation
3. Two-Stage Hierarchical Control System
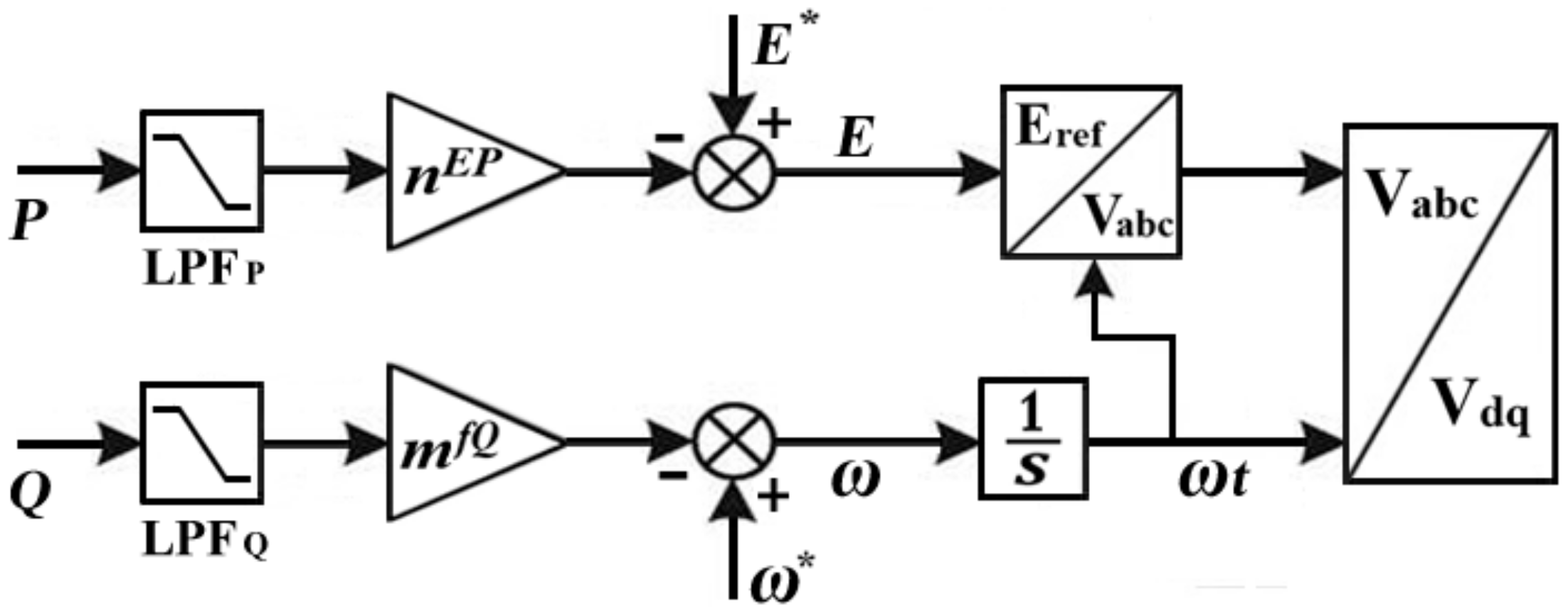
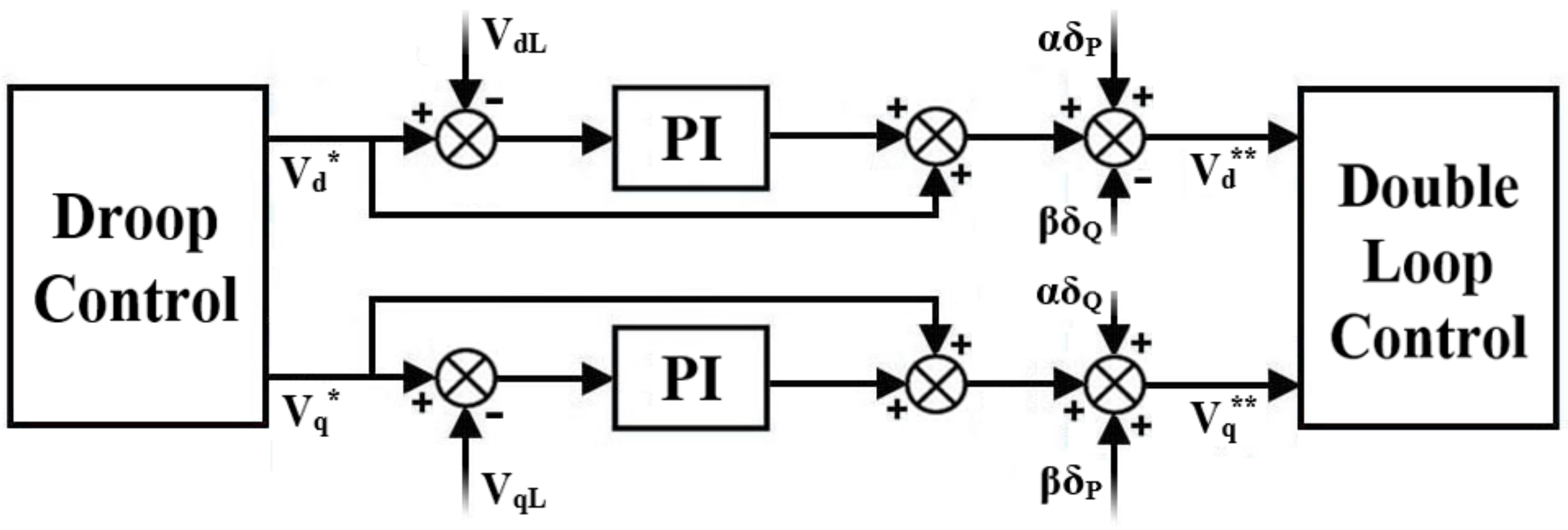
3.1. Primary Stage
3.2. Secondary Stage
3.3. Small Signal Analysis
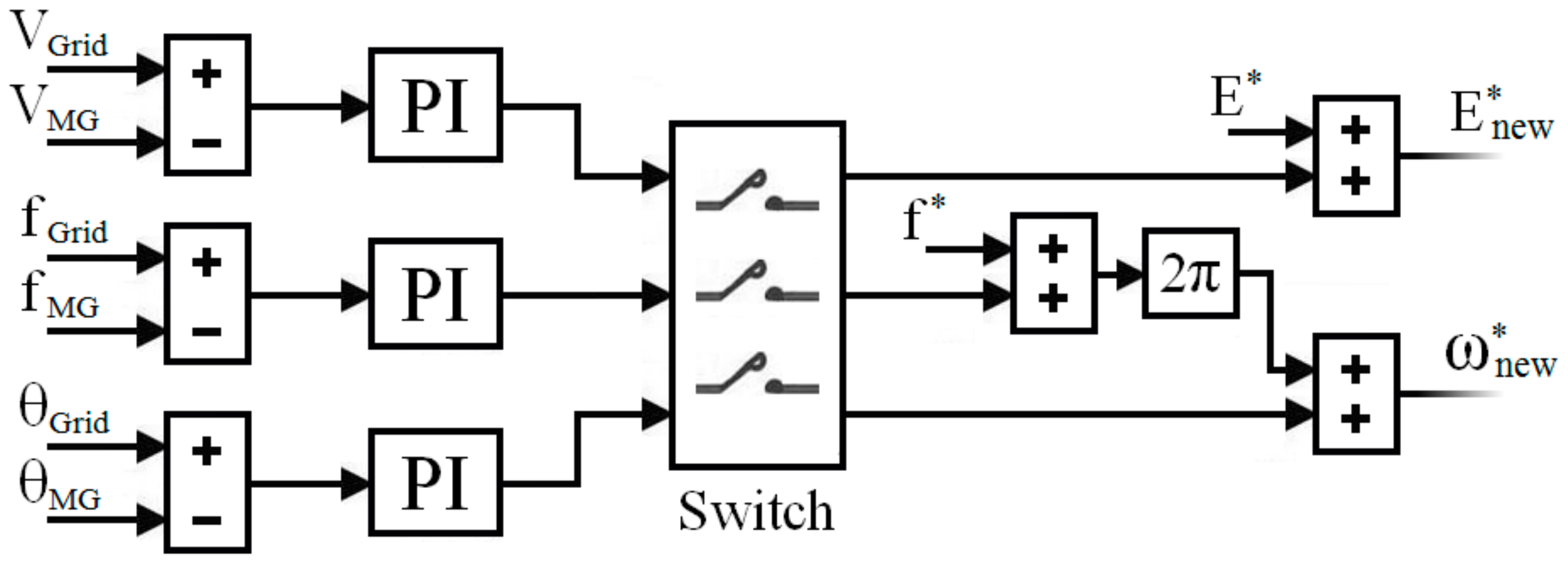
4. Formulation of Mode Transition
4.1. From Grid-Tied to Autonomous
4.2. From Autonomous to Grid-Tied
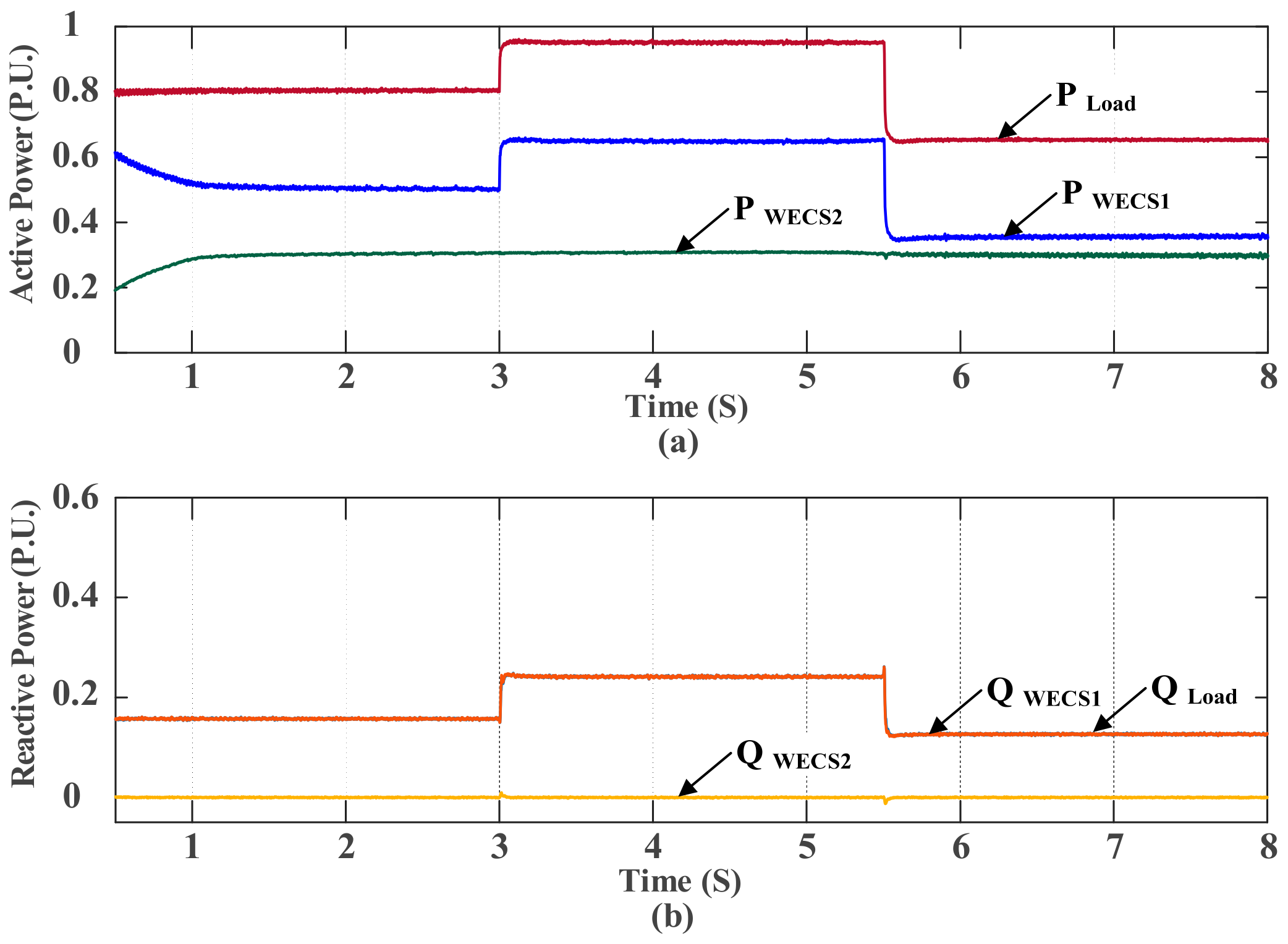
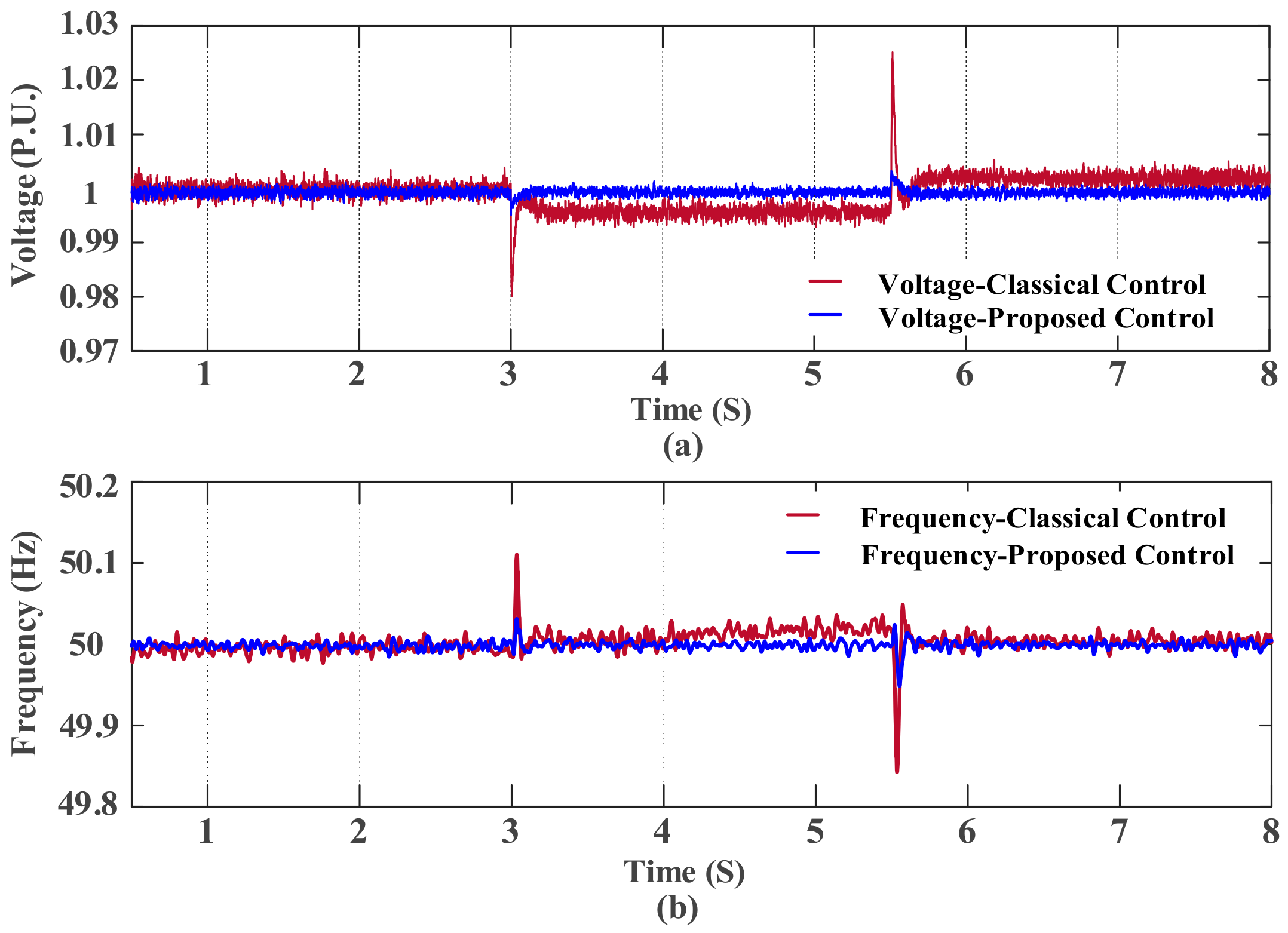
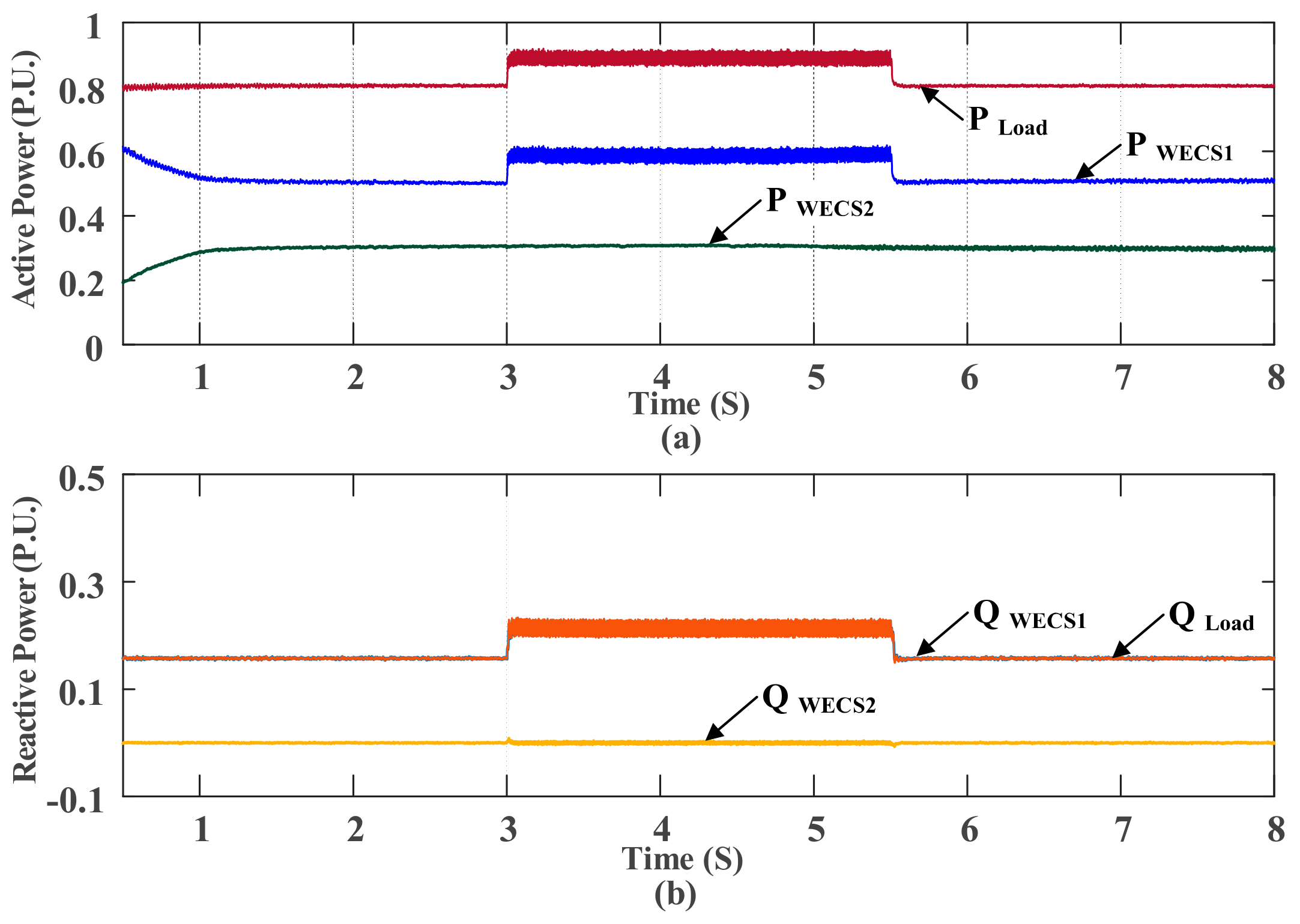
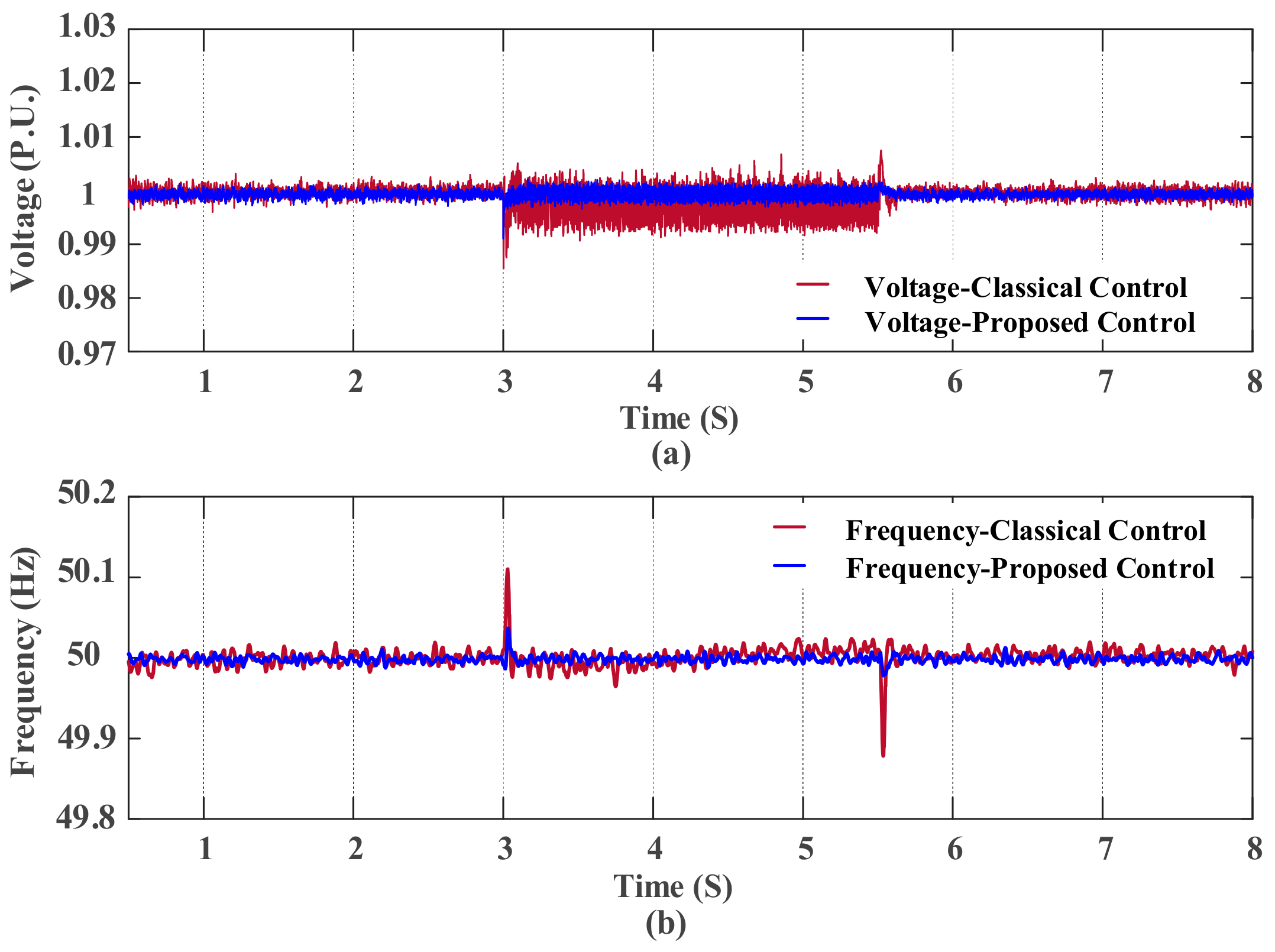
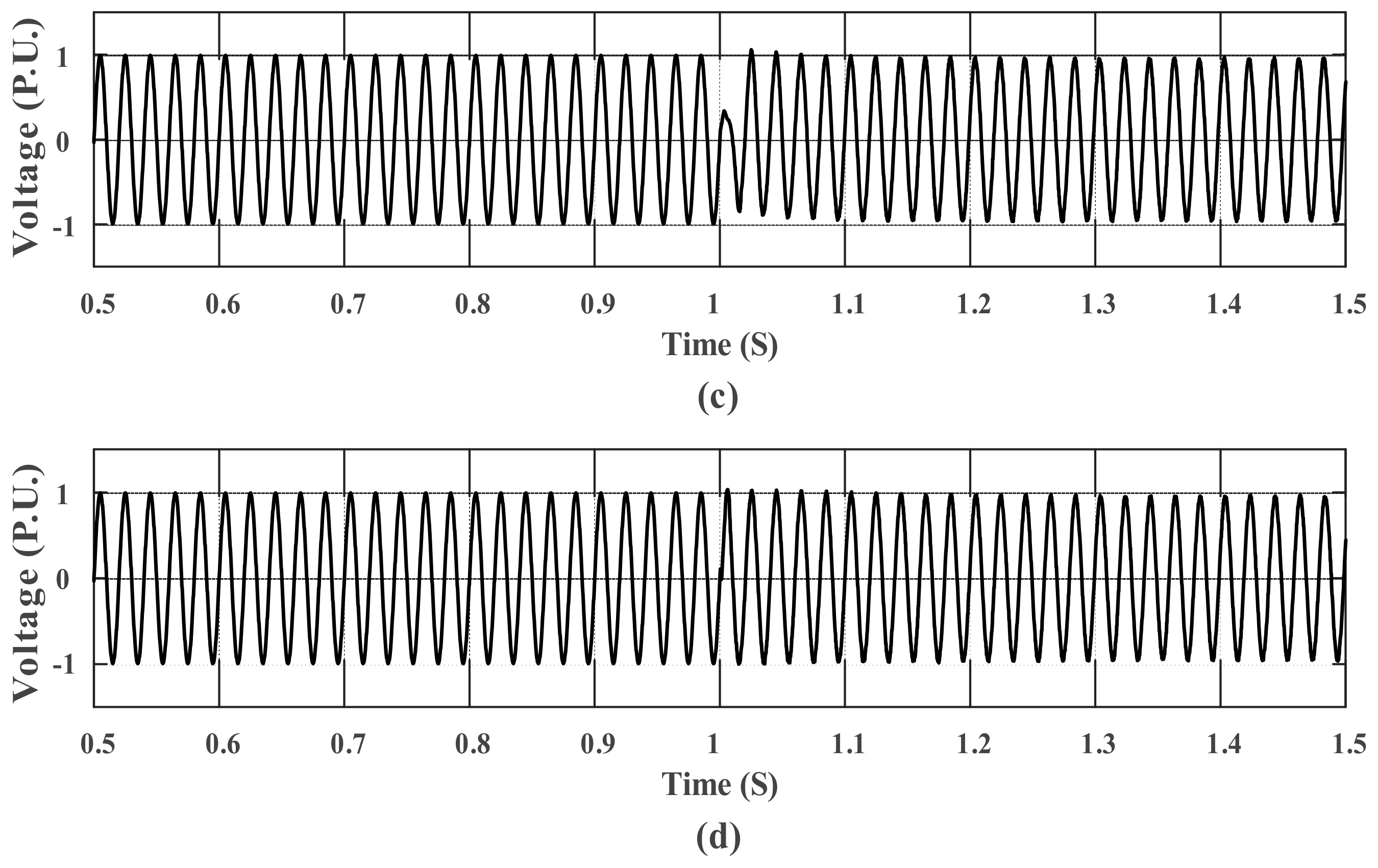
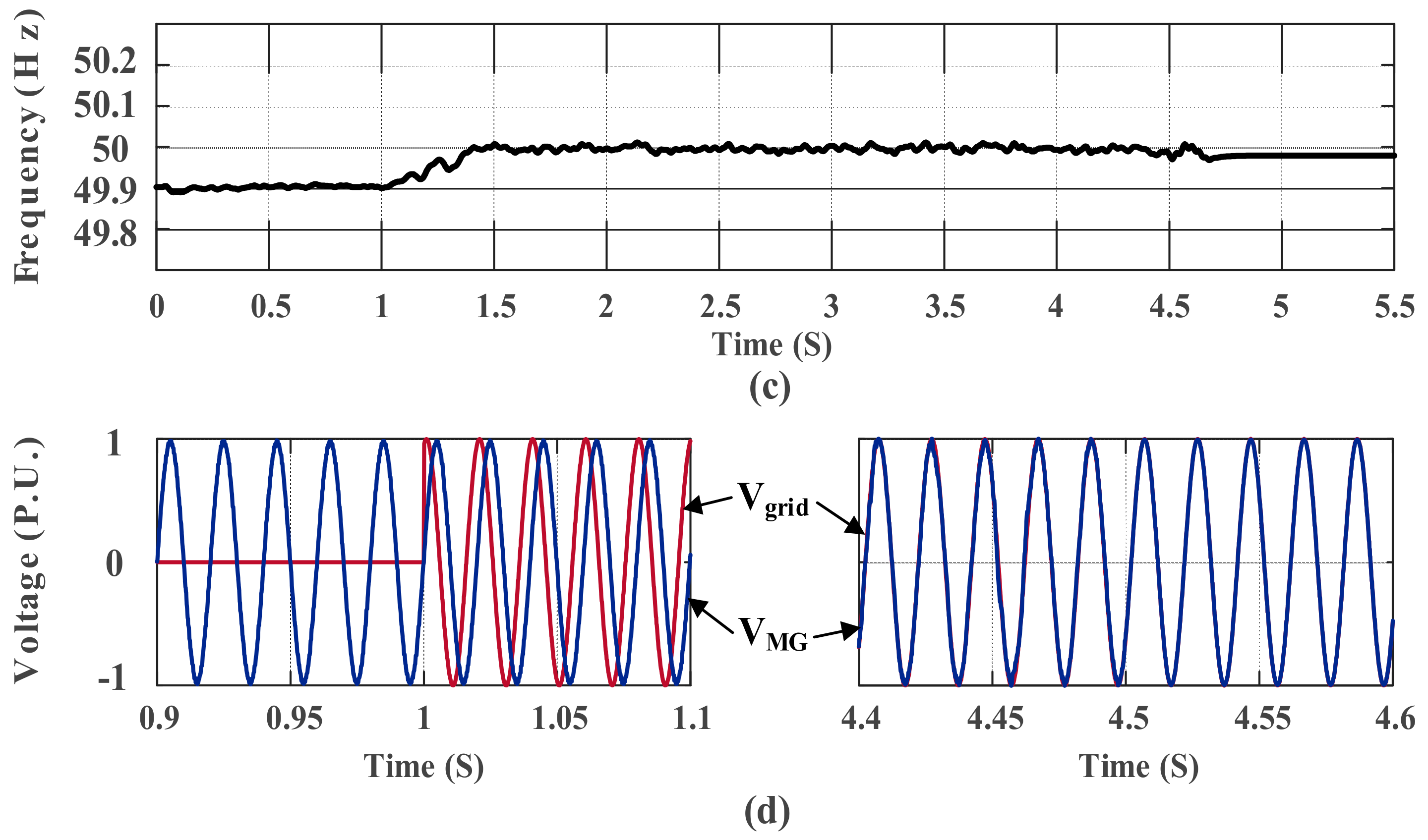
5. Simulation Results
5.1. Mitigate the Deviations during Large Changes in Load
5.2. Smooth Mode Transition between Grid-Tied and Autonomous
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Singh, M.; Chandra, A. Application of adaptive network-based fuzzy inference system for sensorless control of PMSG-based wind turbine with nonlinear-load-compensation capabilities. IEEE Trans. Power Electron. 2011, 26, 165–175. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Giraldo, J.; Mojica-Nava, E.; Quijano, N. Synchronization of isolated microgrids with a communication infrastructure using energy storage systems. Int. J. Electron. Power Energy Syst. 2014, 63, 71–82. [Google Scholar] [CrossRef]
- Tang, X.; Hu, X.; Li, N.; Deng, W.; Zhang, G. A novel frequency and voltage control method for islanded microgrid based on multienergy storages. IEEE Trans. Smart Grid 2016, 7, 410–419. [Google Scholar] [CrossRef]
- Mahmud, M.; Hossain, M.; Pota, H.; Oo, A. Robust nonlinear distributed controller design for active and reactive power sharing in islanded microgrids. IEEE Trans. Energy Convers. 2014, 29, 893–903. [Google Scholar] [CrossRef]
- Savaghebi, M.; Vasquez, J.C.; Jalilian, A.; Guerrero, J.M.; Lee, T.L. Selective compensation of voltage harmonics in grid-connected microgrids. Math. Comput. Simul. 2013, 91, 211–228. [Google Scholar] [CrossRef]
- Avelar, H.J.; Parreira, W.A.; Vieira, J.B.; de Freitas, L.C.G.; Coelho, E.A.A. A state equation model of a single-phase grid-connected inverter using a droop control scheme with extra phase shift control action. IEEE Trans. Ind. Electron. 2012, 59, 1527–1537. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Castilla, M.; de Vicuña, L.G. Control strategy for flexible microgrid based on parallel line-interactive UPS systems. IEEE Trans. Ind. Electron. 2009, 56, 726–736. [Google Scholar] [CrossRef]
- Xin, H.; Zhang, L.; Wang, Z. Control of island AC microgrids using a fully distributed approach. IEEE Trans. Smart Grid 2015, 6, 943–945. [Google Scholar] [CrossRef]
- Arboleya, P.; Gonzalez-Moran, C.; Coto, M.; Falvo, M.C.; Martirano, L.; Sbordone, D.; Bertini, I.; Di Pietra, B. Efficient energy management in smart micro-grids: ZERO grid impact buildings. IEEE Trans. Smart Grid 2015, 6, 1055–1063. [Google Scholar] [CrossRef]
- Ding, G.; Gao, F.; Zhang, F. Control of hybrid AC/DC microgrid under islanding operational conditions. J. Mod. Power Syst. Clean Energy 2014, 2, 223–232. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation. IEEE Trans. Ind. Appl. 2011, 47, 2525–2538. [Google Scholar] [CrossRef]
- Liu, Q.; Tao, Y.; Liu, X.H.; Deng, Y.; He, X.G. Voltage unbalance and harmonics compensation for islanded microgrid inverters. IET Power Electron. 2013, 7, 1055–1063. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, Q.W.; Deng, Y.; Liu, X.H.; He, X.G. Analysis and mitigation of inverter output impedance impacts for distributed energy resource interface. IEEE Trans. Power Electron. 2015, 30, 3563–3576. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. An enhanced microgrid load demand sharing strategy. IEEE Trans. Power Electron. 2012, 27, 3984–3995. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Reactive power sharing in islanded microgrids using adaptive voltage droop control. IEEE Trans. Smart Grid 2015, 6, 3052–3060. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids—A novel approach. IEEE Trans. Power Electron. 2014, 29, 1018–1031. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C.; Teodorescu, R.; Huang, L. Hierarchical control of parallel AC-DC converter interfaces for hybrid microgrids. IEEE Trans. Smart Grid 2014, 5, 683–692. [Google Scholar] [CrossRef]
- Savaghebi, M.; Hashempour, M.M.; Guerrero, J.M. Hierarchical coordinated control of distributed generators and active power filters to enhance power quality of microgrids. In Proceedings of the 2014 55th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 14 October 2014; pp. 259–264. [Google Scholar]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Power calculation using RBF neural networks to improve power sharing of hierarchical control scheme in multi-DER microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1217–1225. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.; Guerrero, J. Autonomous active power control for islanded ac microgrids with photovoltaic generation and energy storage system. IEEE Trans. Energy Convers. 2014, 29, 882–892. [Google Scholar] [CrossRef]
- Han, H.; Liu, Y.; Sun, Y.; Su, M.; Guerrero, J.M. An improved droop control strategy for reactive power sharing in islanded microgrid. IEEE Trans. Power Electron. 2015, 30, 3133–3141. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Guerrero, J.M.; Xu, Z.; Green, T.C. Multiple-time-scales hierarchical frequency stability control strategy of medium-voltage isolated microgrid. IEEE Trans. Power Electron. 2016, 31, 5974–5991. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.-L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Han, Y.; Shen, P.; Zhao, X.; Guerrero, J.M. Control strategies for islanded microgrid using enhanced hierarchical control structure with multiple current-loop damping schemes. IEEE Trans. Smart Grid 2017, 8, 1139–1153. [Google Scholar] [CrossRef]
- Guerrero, J.; Matas, J.; de Vicuna, L.G.; Castilla, M.; Miret, J. Decentralized control for parallel operation of distributed generation inverters using resistive output impedance. IEEE Trans. Ind. Electron. 2007, 54, 994–1004. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Wong, K.P. Advanced control strategies of PMSG-based wind turbines for system inertia support. IEEE Trans. Power Syst. 2017, 32, 3027–3037. [Google Scholar] [CrossRef]
- Mozayan, S.M.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M. Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law. IEEE Trans. Ind. Electron. 2016, 63, 6148–6159. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- La Bella, A.; Cominesi, S.R.; Sandroni, C.; Scattolini, R. Hierarchical Predictive Control of Microgrids in Islanded Operation. IEEE Trans. Autom. Sci. Eng. 2017, 14, 536–546. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; De Kooning, J.D.M.; Meersman, B.; Guerrero, J.M.; Vandevelde, L. Automatic power-sharing modification of P/V droop controllers in low-voltage resistive microgrids. IEEE Trans. Power Deliv. 2012, 27, 2318–2325. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Lu, Z.; Wang, Y.; Benbouzid, M.; Moreau, L. Virtual Synchronous Generator Based Hierarchical Control Scheme of Distributed Generation Systems. Energies 2017, 10, 2049. [Google Scholar] [CrossRef]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small-signal stability for parallel-connected inverters in stand-alone AC supply systems. IEEE Trans. Ind. Appl. 2002, 38, 533–542. [Google Scholar] [CrossRef]
- Zhang, T.; Yue, D.; O’Grady, M.J.; O’Hare, G.M.P. Transient oscillations analysis and modified control strategy for seamless mode transfer in micro-grids: A wind-PV-ES hybrid system case study. Energies 2015, 8, 13758–13777. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, W.; Cai, J.Q.; Cai, T.; Xu, Z.Q.; Yan, N. A synchronization control method for micro-grid with droop control. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 519–524. [Google Scholar]




| Parameter | Symbol | Value |
|---|---|---|
| Cut-off frequency of measuring filter | ωc | 12π rad/s |
| Voltage droop slope | nEP | 0.0008 V/W |
| Frequency droop slope | mfQ | 0.0006 rad/s/VAr |
| Proportional gain-D axis-Secondary controller | Kpdsec | 2.4 |
| Integral gain-D axis-Secondary controller | Kidsec | 10 |
| Proportional gain-Q axis-Secondary controller | Kpqsec | 1.8 |
| Integral gain-Q axis-Secondary controller | Kiqsec | 8 |
| Preset voltage of droop control | E* | 390 V |
| Parameter | Value |
|---|---|
| System Sizing | |
| WECS1 | 360 kVA |
| WECS2 | 300 kVA |
| Battery | 400 kWh |
| System Parameters | |
| Grid voltage (L-L) | 480 V |
| Grid frequency | 50 Hz |
| Line impedance (Zl1) | 0.14 + j0.021 Ω |
| Line impedance (Zl2) | 0.12 + j0.018 Ω |
| Line impedance (Z1) | 0.09 + j0.017 Ω |
| Line impedance (Z2) | 0.09 + j0.017 Ω |
| WECS1 LC filter | 3 mH, 60 μF |
| WECS2 LC filter | 3 mH, 60 μF |
| Parameter | Value |
|---|---|
| WECS1-GSC-Current regulator-D axis Kp, Ki | 3.26, 40 |
| WECS1-GSC-Current regulator-Q axis Kp, Ki | 1.8, 65 |
| WECS1-GSC-Voltage regulator-D axis Kp, Ki | 0.85, 48 |
| WECS1-GSC-Voltage regulator-Q axis Kp, Ki | 0.66, 74.5 |
| WECS1-Boost DC current regulator Kp, Ki | 0.58, 13.6 |
| WECS1-Buck/Boost DC current regulator Kp, Ki | 4.5, 60 |
| WECS2-GSC-Current regulator-D axis Kp, Ki | 5.2, 84 |
| WECS2-GSC-Current regulator-Q axis Kp, Ki | 10.5, 63 |
| WECS2-GSC-DC voltage regulator Kp, Ki | 20, 76 |
| WECS2-Chopper voltage regulator Kp, Ki | 0.2, 6.9 |
| WECS2-MSC-Current regulator-D axis Kp, Ki | 4, 12 |
| WECS2-MSC-Current regulator-Q axis Kp, Ki | 4, 12 |
| WECS2-MSC-Torque generator Kp, Ki | 0.6, 0.5 |
| Current compensator for unplanned outage Kp, Ki | 5, 50 |
| Pre-synch. control-Voltage component Kp, Ki | 0.2, 4 |
| Pre-synch. control-Frequency component Kp, Ki | 4.1, 2 |
| Pre-synch. control-Phase angle component Kp, Ki | 12, 7.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, R.M.; Wang, S. Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid. Energies 2018, 11, 1270. https://doi.org/10.3390/en11051270
Imran RM, Wang S. Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid. Energies. 2018; 11(5):1270. https://doi.org/10.3390/en11051270
Chicago/Turabian StyleImran, Rasool M., and Shaorong Wang. 2018. "Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid" Energies 11, no. 5: 1270. https://doi.org/10.3390/en11051270
APA StyleImran, R. M., & Wang, S. (2018). Enhanced Two-Stage Hierarchical Control for a Dual Mode WECS-Based Microgrid. Energies, 11(5), 1270. https://doi.org/10.3390/en11051270





