1. Introduction
Most of the solar radiation coming towards the Earth’s surface is reflected back as shortwave or longwave radiation by the Earth’s surface. However, some gases called “greenhouse gases” in the lower atmosphere behave as a blanket for this longwave radiation, because these gases adsorb and re-emit the solar radiation back towards the Earth’s surface within the thermal infrared range. This is commonly known as the “greenhouse gas effect” and results in the increasing global temperature effect called “global warming”, one of the most debated topics among researchers. The dangerous consequences of global warming have now been reported worldwide [
1]. According to Le-Treut et al. [
2], if no greenhouse gas effect existed, the average world temperature would be around 33 °C lower than the present temperature. During the last century, the average world temperature has risen by around 1 °C as a result of global warming [
3] and this number is continuously rising with the human activities associated with rapid industrial development. The use of fossil fuels and deforestation are the main causes of increased atmospheric CO
2 levels and to date around 35% increment in CO
2 levels has been recorded in the industrialized areas of the world [
2]. Global warming has therefore become a challenging issue which requires the contribution of scientists to overcome it. As a result, a diverse range of greenhouse gas mitigation and global warming control techniques have been tested throughout the world.
The most common types of greenhouse gases are carbon dioxide (CO2), methane, and nitrous oxide, and the most abundant greenhouse gas in the atmosphere is CO2, as it is a by-product of many industrial applications, such as coal-fired power generation. Therefore, scientists’ main concern has been attracted by the mitigation of atmospheric CO2 levels, as every day the entire world is releasing vast amounts of CO2 into the world’s atmosphere.
Of the suitable CO
2 mitigation initiatives, CO
2 capture and storage (CCS) has been shown to offer a viable path to reduce the CO
2 emissions into the atmosphere. According to scientific predictions, it is necessary to capture and store CO
2 at a 5.1 Gt annual rate by 2050, which is 14% of the total needed for global temperature stabilisation [
4]. According to the ETP BLUE Map scenario [
5], global CO
2 emissions can be reduced by 50% in 2015 with emission reduction strategies at a cost of up to US
$200 per 1 ton of CO
2. This includes around 19% CO
2 emission reduction through CCS and if CCS were not employed, the annual cost for the emission reduction in 2050 would be increased by around 71% [
6].
In the CCS process, deep brine aquifers are identified as suitable geological structures, in which CO
2 can be stored, since they are widely distributed and have large storage capacity in their pores [
7,
8]. Also, CO
2 geo-sequestration in subsurface systems has been identified as an effective option, due to its ability to release tightly bonded productive gas, largely methane, from the reservoir. Importantly, CO
2 geo-sequestration in deep coal seams can be considered as economical way of reducing the atmospheric carbon content when consider its ability to enhance the coal seam gas production while storing carbon dioxide and when the two process considered together is called enhanced coal bed methane recover (ECBM). However, CO
2 behaviour in coal seams is quite complicated due to its chemically reactive nature with the coal matrix and the associated modifications of the coal mass chemical and physical structure. These factors have led to unpredictable CO
2 injectivity into deep coal seams after CO
2 injection in field CO
2 sequestration projects [
9,
10], and the potential phase transition of injected CO
2 in the seam (from liquid or gas to super critical CO
2) has caused these complications related to CO
2 sequestration/ECBM to become more critical [
3]. The aim of this paper is to provide a comprehensive review of current findings on CO
2 flow behaviour in deep coal seams under various in-situ conditions.
2. Natural Permeability of Preferable Coal Seams for CO2 Sequestration
Since permeability quantifies flow ability through any coal seam [
11], it is clearly one of the most critical parameters affecting CO
2 sequestration in coal, in terms of CO
2 injectability. Generally, natural coal seams have quite low permeability values, which significantly affect the CO
2 sequestration process in the seam. As a result, precise prediction of permeability is necessary for the effective planning of any CO
2 sequestration process. The permeability of natural coal seams is influenced by a broad range of factors, including the geological stress field of the coal seam, the seam temperature and its moisture content, and the degree of maturity or coal rank.
It is important to understand the permeability measurement techniques used by different researchers for different types of coal seam. Several techniques have been used to precisely measure the permeability values of coal samples under laboratory conditions. Tri-axial experiments on undisturbed core samples is the common technique as it approximately represents the in situ conditions and natural porosity and cleat system of the coal seam. Pulse decay method is an extended technique, which measures the effective permeability and diffusivity of adsorptive gases. Several other techniques such as gas expansion techniques, onsite drill-core desorption tests, mercury intrusion curves have been used for the permeability measurements under different experimental conditions [
12,
13]. Moreover, stochastic simulations are widely used for coal sample characterization and permeability evaluation. Using advanced techniques like X-ray imaging and modelling, the heterogeneity and the complexity of coal seam can be accurately evaluated and thus the permeability can be predicted [
14,
15].
The pore space or porosity of the coal mass is the main factor governing its flow ability or permeability, because highly porous media have higher tendency to offer easy flow paths for fluid movement in coal. A direct relationship between coal permeability and porosity has been proposed in existing studies (Equation (1)), and the n value can be theoretically taken as 3 [
16], although it may exceed 3 in actual situations [
17]:
where
k is the coal permeability,
ko is the initial permeability,
is the seam porosity,
is the initial porosity and
n is a constant.
The main factor that controls porosity and therefore permeability in a reservoir is the magnitude of the net stress or effective stress acting on the coal mass. Effective stress can be predicted based on the simple force-balance between the confining pressure and the pore pressure (Equation (2)), as pore pressure and confining pressure have opposite effects on the pore volume:
where
is the differential pressure,
is the confining pressure,
is the pore pressure and
is the effective stress coefficient.
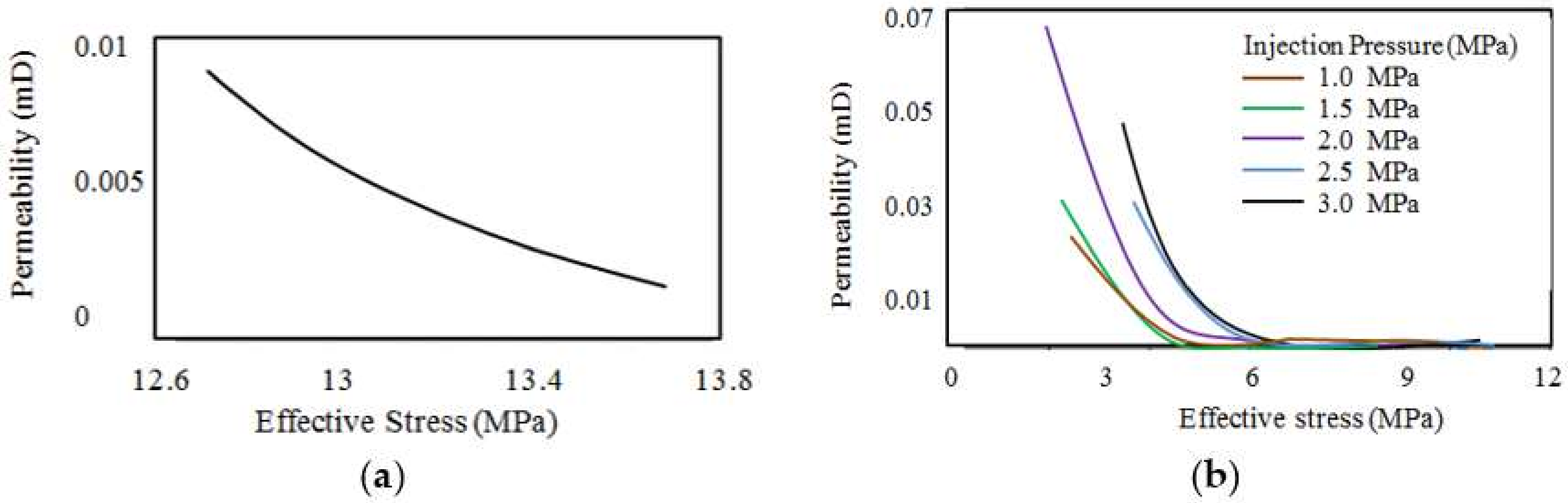
Being a type of relatively weak and compressible rock, coal’s pore structure varies greatly with the changing of the applying effective stresses on it. According to Somerton et al. [
18], increasing the effective stress acting on any coal mass causes the fissures and pores of that coal body to close, which increases the tortuosity for fluid flow movement inside the coal mass and therefore reduces the permeability. In Somerton’s et al. [
18] experimental study on a range of coal samples (with 0.1 and 100 mD permeability), increasing the effective stress upon load application during coal failure caused the permeability to be reduced by 1 to 2 orders of magnitude and effective stress was found to have a negative exponential relationship with coal permeability. Interestingly, permeability of high rank coal is more greatly affected by effective stress changes compared to low rank coal, where low rank coal show about an order of permeability reduction with the effective stress increment and high rank coal show two orders of permeability reduction. This negative exponential relationship between coal permeability with effective stress has been confirmed by many researchers, including Durucan and Edwards [
19]. According to the experimental results of Durucan and Edwards [
19], permeability reduction in coal with effective stress increment exhibits an initial steep gradient followed by a gentle gradient and eventually reaches a residual value. According to these researchers, this initial steep gradient is due to the immediate closure of existing micro-fractures under very low stresses.
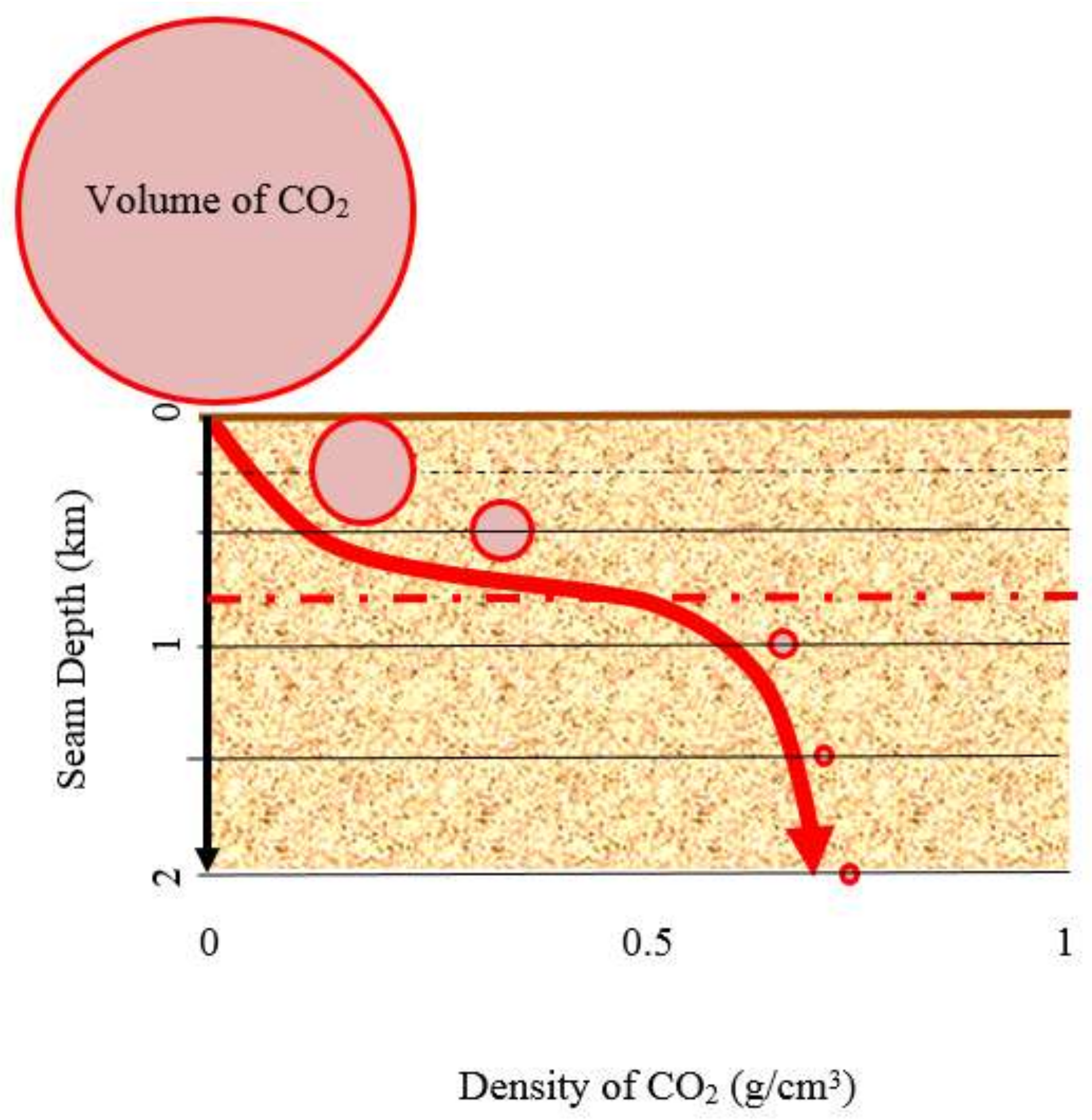
It is known that the effective stress applying on any coal seam is increasing with increasing the seam depth, as it causes to generate greater confining stresses on the seam. Deeper coal seams therefore exhibit much lower permeability compared to shallow seams. Most of the deep coal seams normally have high temperatures and a greater amount of water in their pores, thus it is generally expected to have higher degree of water saturations. Therefore, the combined effects on permeability need to be considered.
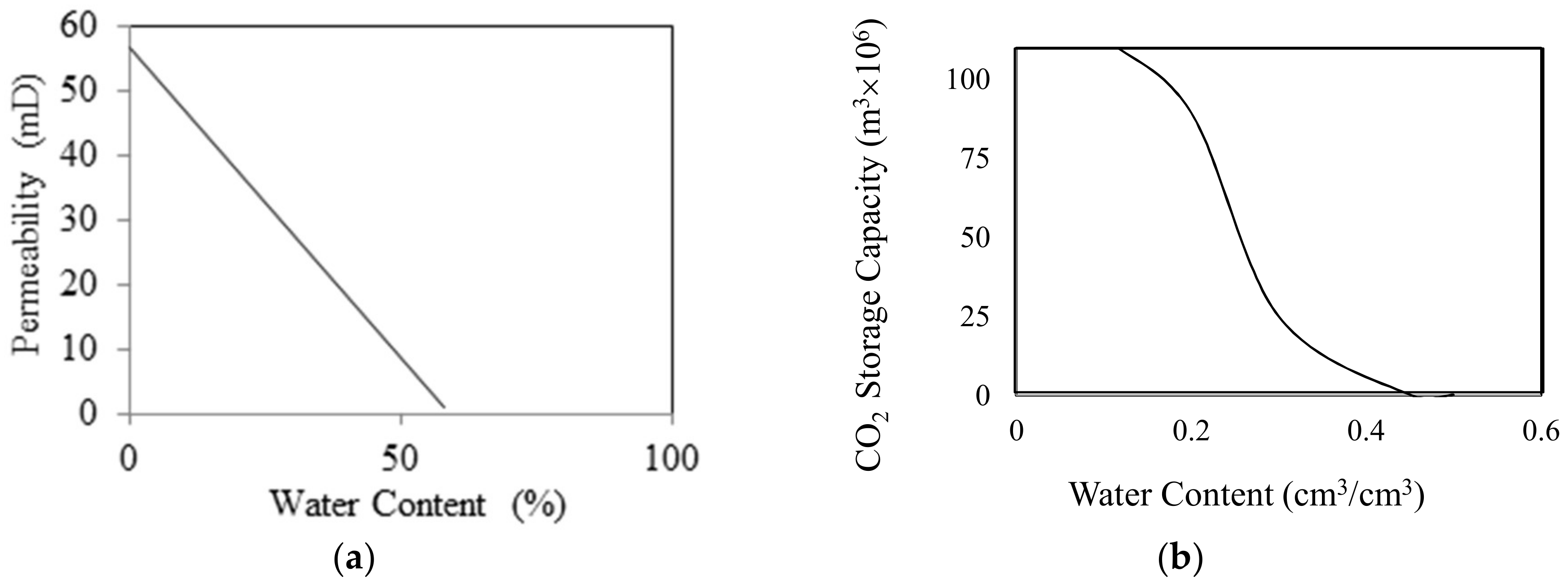
In relation to coal permeability variation with moisture content, the coal mass tends to shrink with the reduction of its moisture content, creating permeability enhancement in the coal seam [
20]. The moisture in the coal mass pore structure occupies the pore space available for fluid movement and the adsorption of that water in the coal matrix induces significant matrix swelling, both of which obstruct the flow paths available in the coal matrix and therefore cause the reduction of overall coal seam permeability [
20]. The variation of coal seam permeability and gas storage capacity with the natural moisture content have been studied by Skawinski et al. [
20] and Perera et al. [
21] and the results are shown in
Figure 1. Regarding the moisture content effect, deeper coal seams generally have water-saturated conditions compared with shallow seams and thus are expected to have low permeability.
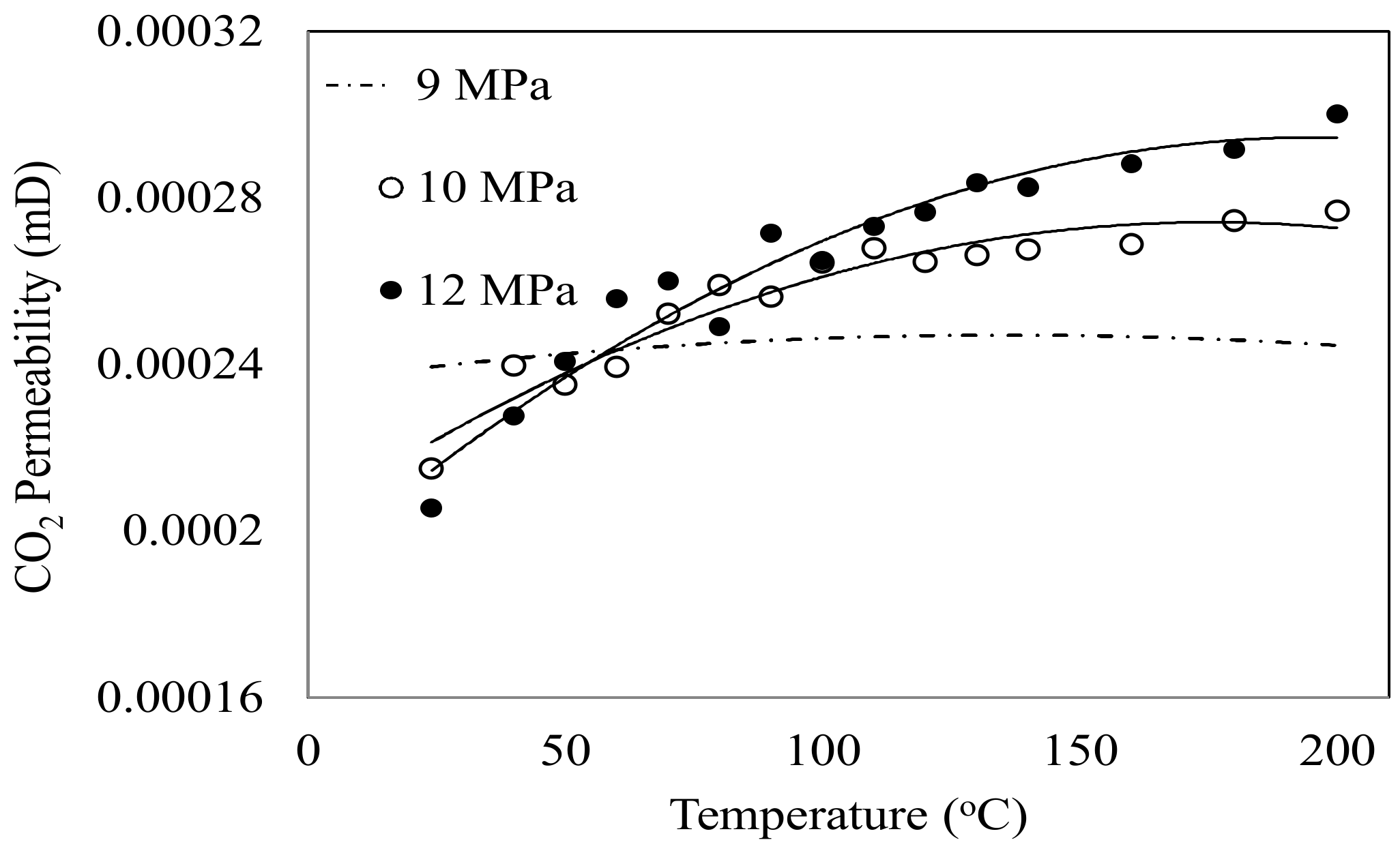
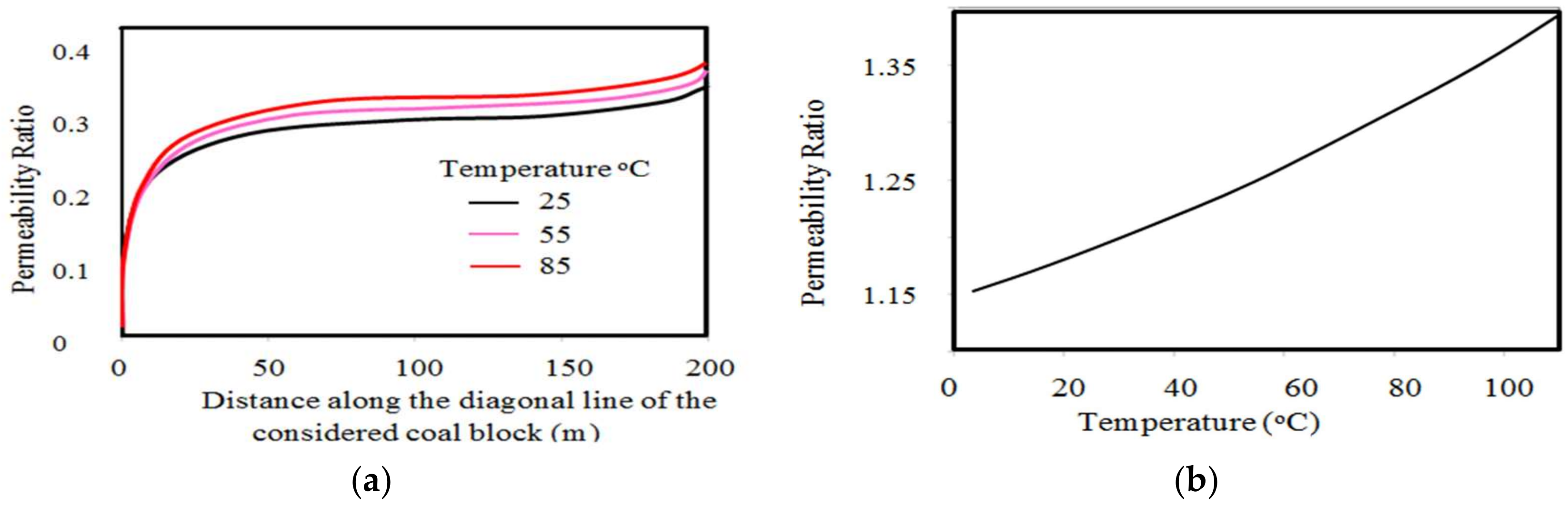
In relation to the temperature effect on coal seam permeability, according to De Silva et al. [
22], the average thermal gradient available underground is around 25–30 °C/km increment from the ground surface. Therefore, preferable coal seams for CO
2 sequestration or ECBM process (>0.8 km depth) possibly have considerably high temperatures. The high temperatures create thermal expansion in the coal matrix that reduces the available pore space and therefore its permeability [
23]. In contrast, high temperature also creates thermal cracks in the coal matrix, thus increasing its pore space and permeability. Therefore, the combined effects of each of these factors must be considered in order to determine the influence of temperature on coal seam permeability.
Further, deeper coal seams normally contain higher-rank coal, as that coal has more opportunities to be subjected to greater pressure and temperature variations [
24]. In simple theory, the higher the burial depth, the higher the stress applying on the coal mass. Thus, the coal mass pore structure shrinks with increasing rank, due to the increment of the stress applying on the mass, resulting in a permeability reduction. This was proved both experimentally and numerically by many researchers, in which they have shown that the permeability decreases significantly with the increase of effective stress applied on the coal mass [
25,
26,
27]. This is because high-rank coal has been subjected to greater stresses and temperature variations and therefore is a tight, low porous medium with a greater proportion of micro-pores [
28]. In contrast, low-rank coal has only been subjected to lower stresses and temperatures and is therefore a less compacted highly porous medium with a greater proportion of macro-pores. Therefore, the burial depth or the rank of the coal seam also has a significant influence on its permeability, and a permeability reduction trend can be expected with increasing coal rank.
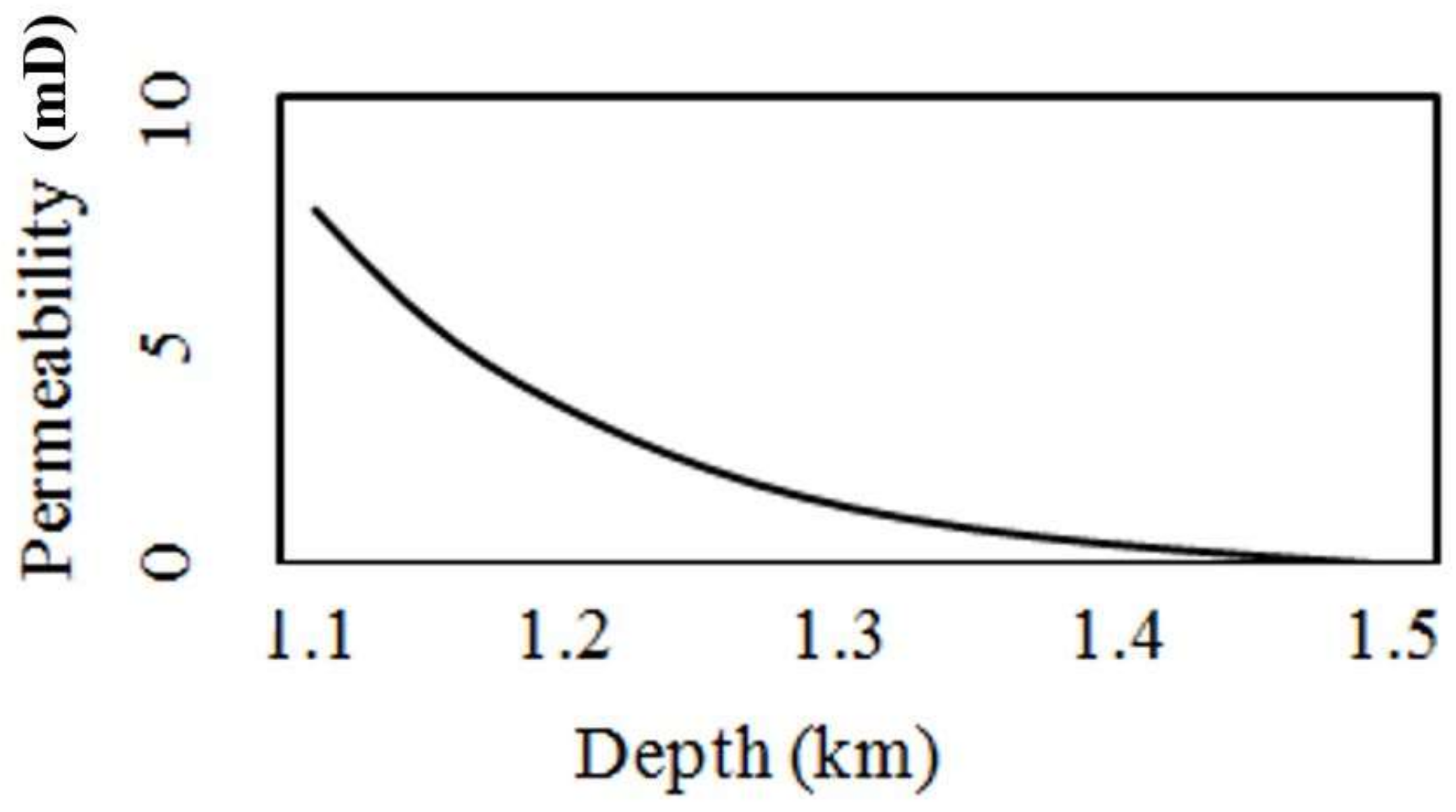
On the basis of all of these facts, since deeper coal seams have greater effective stresses, higher-rank coals and water saturation condition, deep coal seams generally have very low permeability values. However, the temperature influence is the opposite, and most available coal seams have less than 0.001 mD extremely low permeability values [
29]. The variation of coal seam permeability with depth predicted by Korre et al. [
30] is shown in
Figure 2.
3. CO2 Injection-Created Natural Coal Seam Permeability Alterations
The permeability of a coal seam is thought to be independent of the flowing fluid properties. However, the strong dependence of coal mass permeability on the structure of its connected pore spaces causes coal permeability to be dependent on any factor that may contribute to changes in its pore structure. The significant reduction of coal mass pore space with the swelling induced by CO
2 injection and the mobilisation of the hydrocarbons in the seam with CO
2 interaction have been recorded [
31]. The corresponding blockage of flow paths by the adsorbed CO
2-induced swelling and the mobilized hydrocarbons from the coal matrix leads to a significant reduction in coal mass flow ability or permeability, which eventually reduces CO
2 injectability into the coal seam. This has been widely experienced in field CO
2 sequestration projects. For example, the CO
2 injection rate was reduced by around 50% during the first six months of CO
2 injection in the San Juan Basin, USA field CO
2 sequestration project [
32], and by around 70% during the first twelve months of CO
2 injection in the Ishikari basin, Japan [
33].
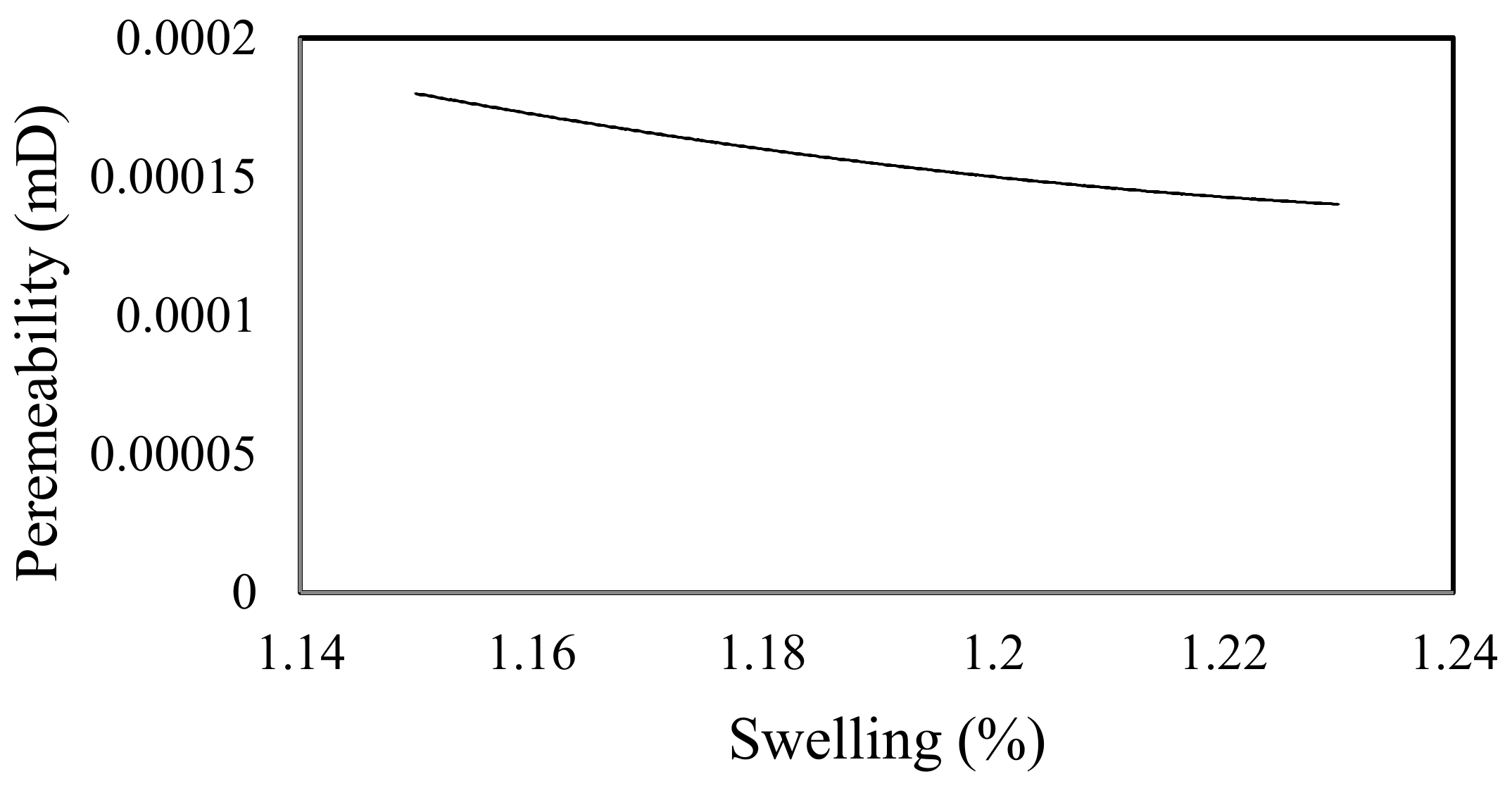
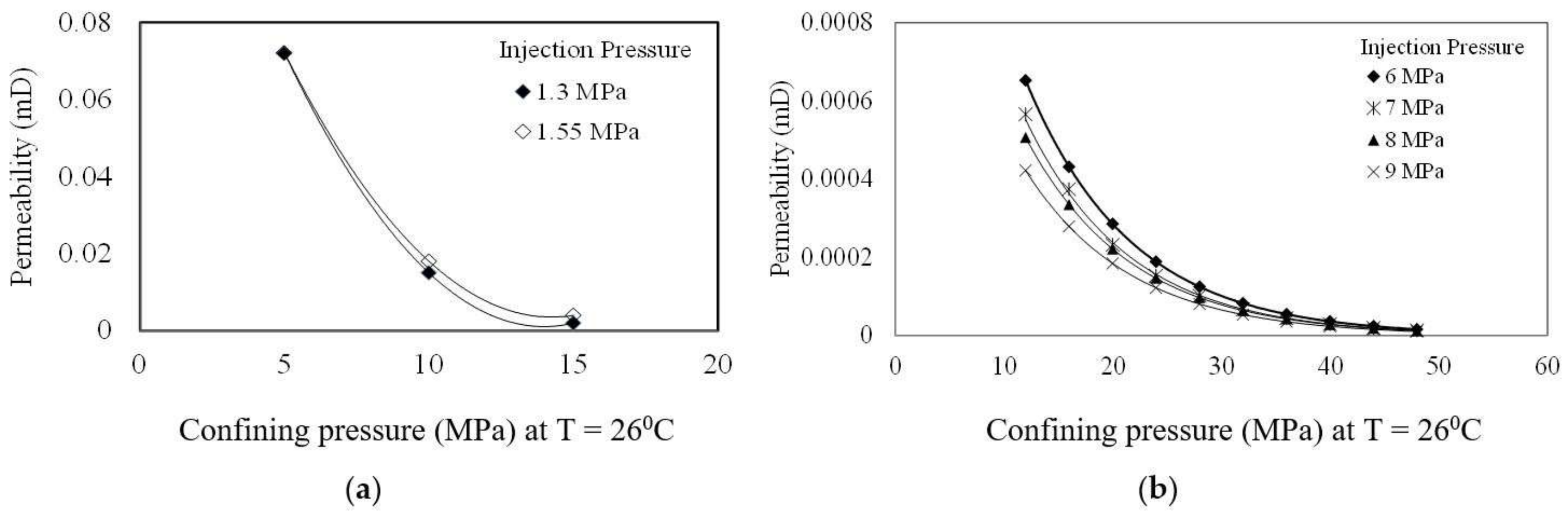
Pekot and Reeves [
34] have shown how coal permeability is reduced with coal matrix swelling and the results are summarised in
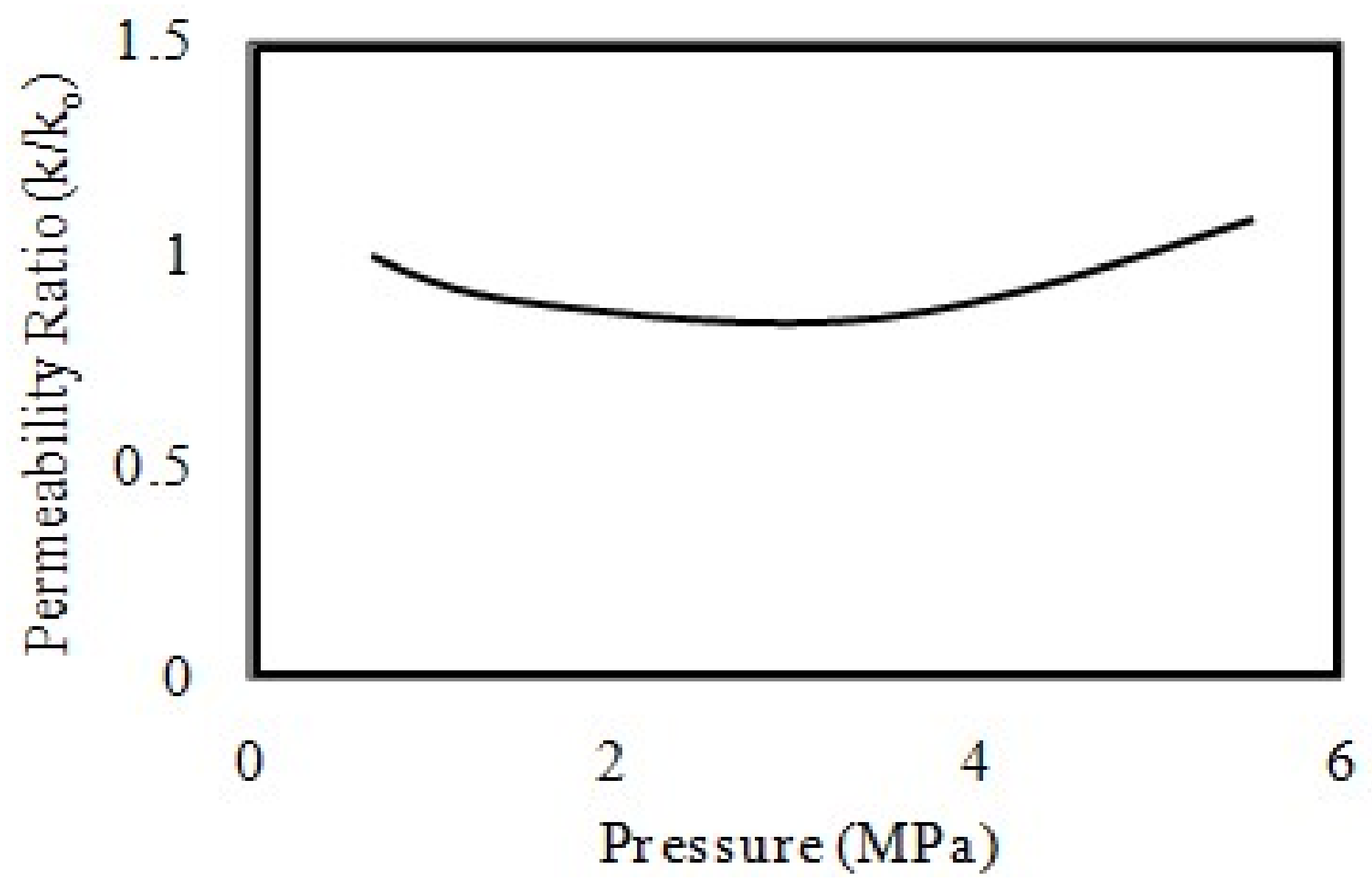
Figure 3. A direct relationship between CO
2 adsorption-induced coal matrix swelling and coal permeability has been shown by many researchers [
35,
36] and one of the results is shown in
Figure 4.
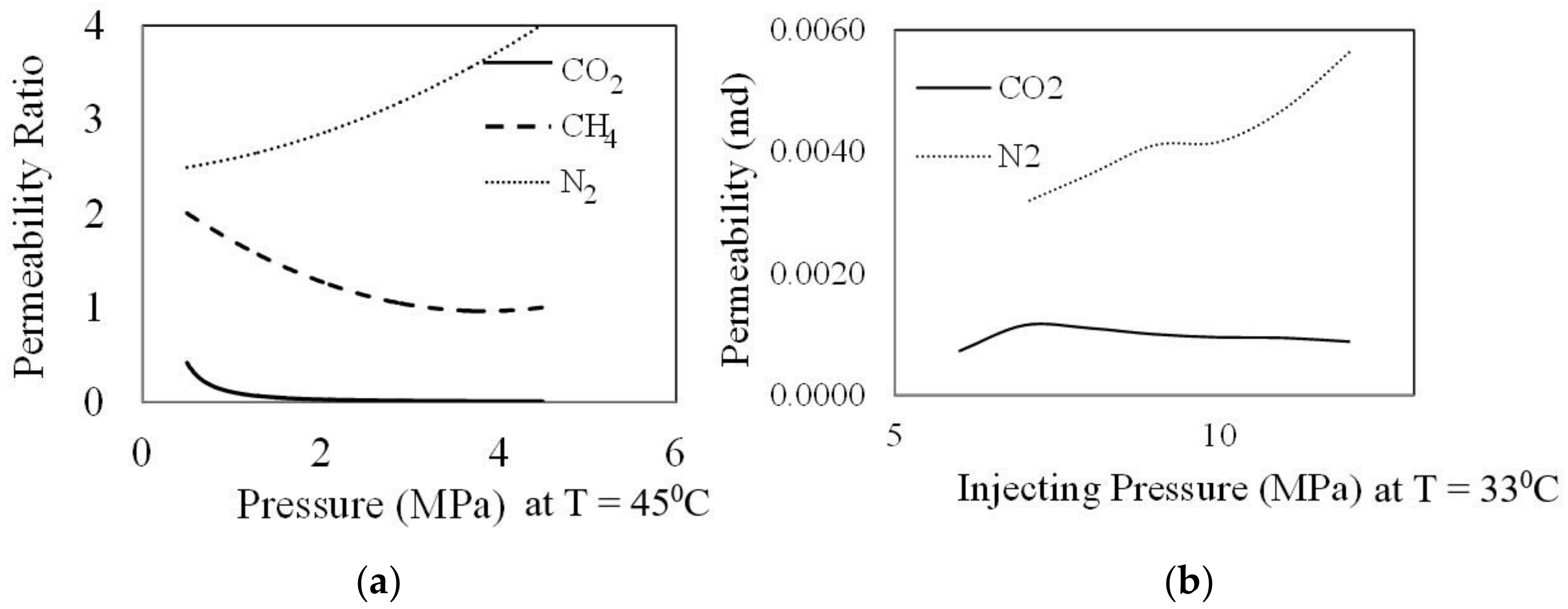
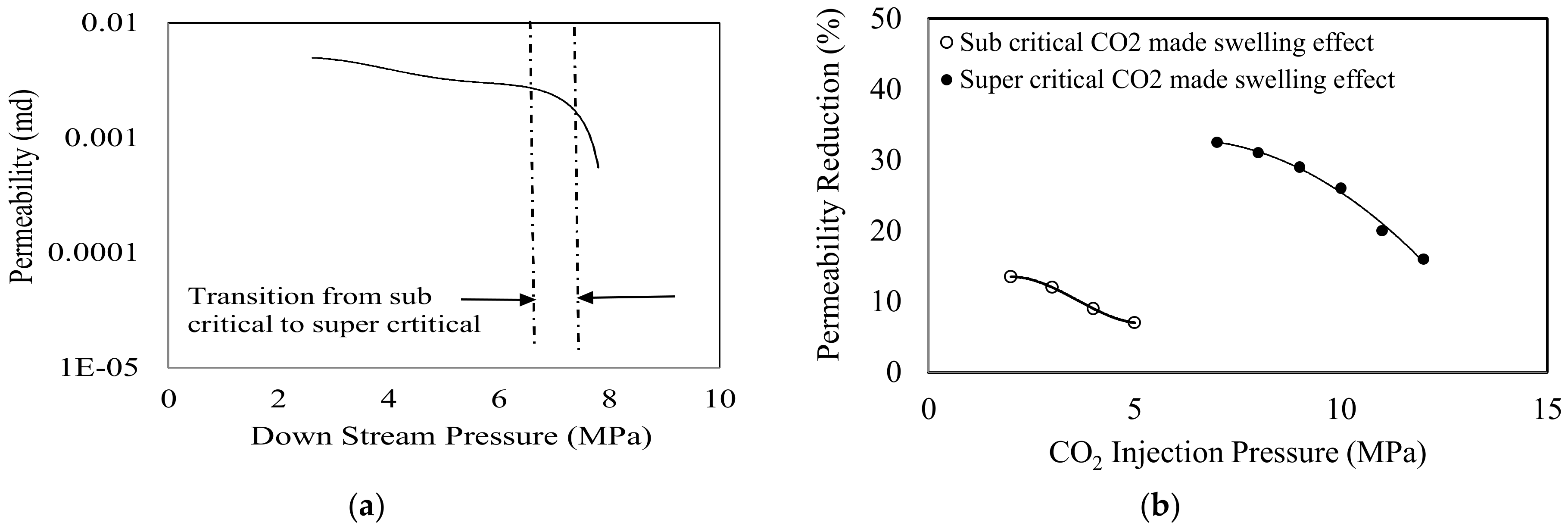
According to the figure, swelling significantly reduces the deep coal seams permeability, and therefore CO
2 flow behaviour in natural coal seams varies significantly from the flow behaviours of other types of gases such as N
2 in them. This unique flow behaviour of CO
2 in coal compared to other types of gases has been shown by many researchers. Cui et al. [
37] analyzed the adsorption and transport of CO
2 and N
2 in coal particles with numerical modelling and found that CO
2 can permeate in to ultra-micro pores, resulting in a higher diffusivity in coal matrix, than CH
4 or N
2. This is due to relatively smaller kinetic diameter, linear shape and the high affinity of CO
2, which allow it to permeate not only to macro pores but also to micro and ultra-micro pores as well [
38,
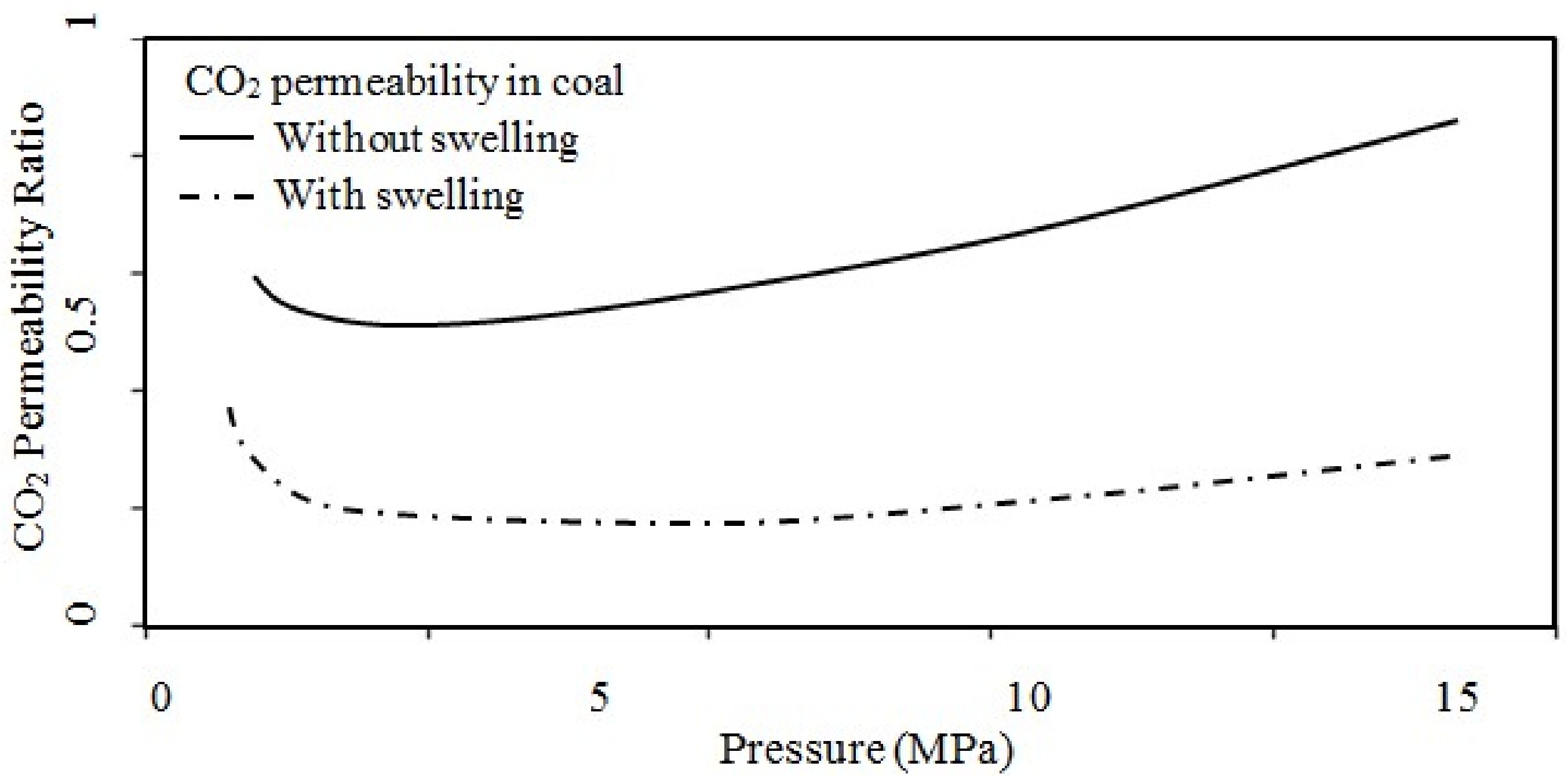
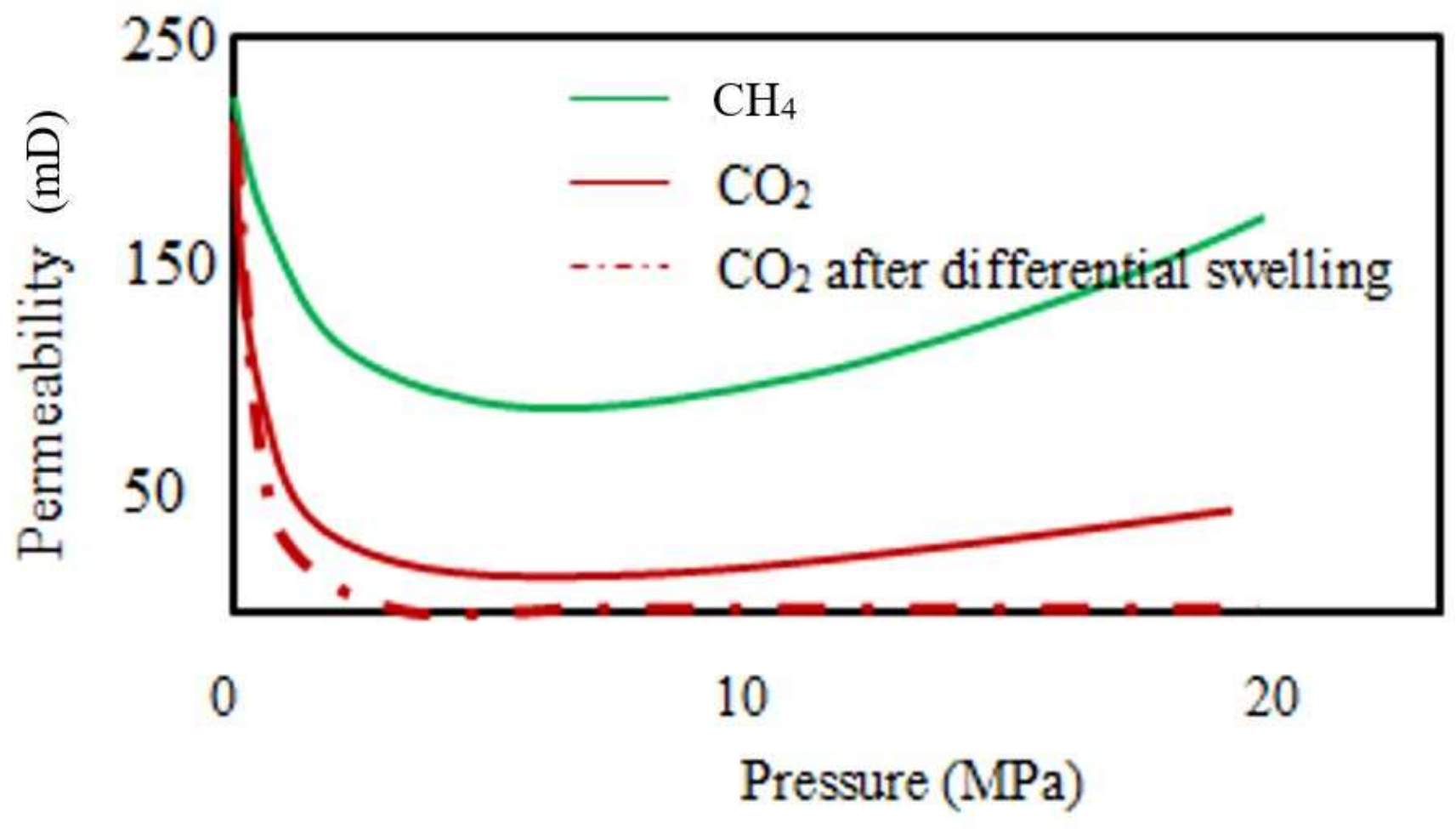
39]. Also the significantly reduced coal mass permeability upon CO
2 movement compared to other gases has been clearly shown (
Figure 5) and CO
2-induced coal matrix swelling was found to be the main cause for this reduction [
3,
35,
40,
41].
Figure 5a shows that CH
4 has lower permeability values compared to N
2 and for this reason CH
4 causes a considerable swelling effect in coal. However, the swelling-related issues caused by CO
2 are much greater than those caused by CH
4. According to Larsen [
42], the coal mass can swell by up to 4% of its volume due to CO
2 adsorption, which pressures the fractures and cleats in the coal mass, thereby reducing its permeability. For example, the Tahmoor and North Cliff Mines in the Bulli seam exhibited lower gas drainage capabilities due to the available high carbon dioxide concentrations in their coal seam gas [
43].
5. Simulation of CO2 Flow Behaviour in Coal
To date, many permeability models have been proposed for gas movement in coal and most have been developed by assessing the effect of stress on coal permeability. One of the earliest studies was by Somerton et al. [
18], who considered N
2 and CH
4 gas flow injection into three different types of fractured coal samples taken from different locations in USA (Pittsburgh, Virginia Pocahontas, and Greenwich Colleries) under various axial and radial stress conditions. Their experimental results reveal the importance of stress history on coal permeability and the negligible influences of loading sequence and direction of stress application on it. Based on these observations, they proposed an equation for coal permeability as a function of effective principal stress, as follows (Equation (8)):
where
is the permeability under stress (mD),
is the permeability under zero stress (mD) and
is mean stress (psi).
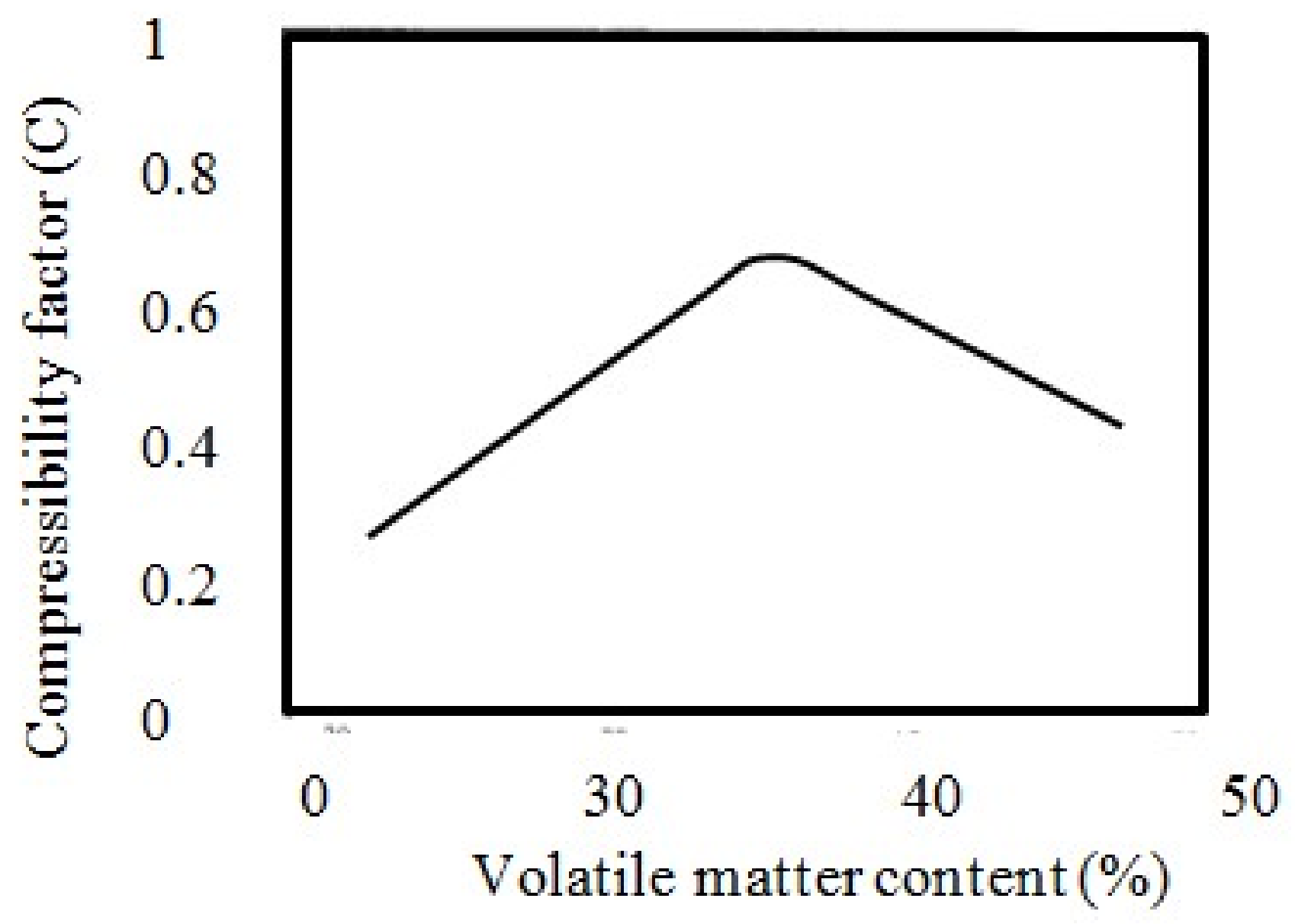
In 1986, Durucan et al. [
19] proposed a somewhat different relationship among coal permeability and effective stresses, considering the radial stress applied on the coal mass and the permeability behaviour of fractured coal samples taken from seven different locations (Acilik, Caydamar, Barnsley, Cockhead, Banbury, Dunsil and Deep Hard):
where
σ3 is radial stress (MPa),
K is permeability (mD),
C and
Ki are constants, where
Ki is the relative incidence of excising fissures and fractures of coal and
C is the volatile matter content-dependent compressibility factor of the coal (
Figure 15).
The main limitation in this equation is the finding of Ki. Although it has been defined as the relative incidence of existing fissures and fractures of coal, insufficient details have been given to find it in practice. Without knowing the way of finding the value of Ki, it is difficult to use this equation to find the permeability. Further, in this research the researchers maintained the σ1 = 3σ3 relationship throughout each test (σ1 is the major principal stress and σ3 is the minor principal stress acting on the coal sample) and therefore the influence of the major principal stress (σ1) on permeability is clear and therefore needs to be incorporated for the precise estimation of permeability.
Another coal permeability relationship with applying stresses has been proposed by Gray [
65], who conducted tri-axial experiments on CH
4 injection into several coal types under various isotropic confined stress levels (Equation (10)):
where
K is permeability (mD) and
σ is confining stress (MPa), which is proposed to be estimated using Equation (11) to account for the effect of matrix shrinkage and pore pressure:
where,
is the change in equal sorption pressure (MPa),
is the strain caused by a unit change in equivalent pressure,
is the Poisson’s ratio,
is the initial pressure (MPa),
is the pressure (MPa),
is the initial confining stress (MPa) and
is the confining stress after the changes caused by pore pressure and matrix shrinkage (MPa). In Equation (11), the first term provides the pore pressure influence and the second term describes the pore pressure reduction creating matrix shrinkage influence on cleat permeability. However, this equation was developed based on the basic assumption that coal matrix shrinkage is proportional to the reduction in equivalent sorption pressure, and cannot predict the initial permeability increment in coal seam gas recovery at the primary stage.
In the same study, the researcher showed the applicability of the well-known Darcy equation for predicting coal permeability (Equation (12)) with assuming a linear laminar behavior of CO
2 in coal:
where
q is the flow rate (m
3/s),
Po is the outlet pressure (MPa),
L is the length of core (m),
µ is the viscosity of the flow (Pa.s),
A is the area of core sample (cm
2) and
Pi is the inlet pressure (MPa).
In 2011, Jasinge et al. [
36] proposed the following simplified Darcy permeability equation for use in laboratory data analysis:
where
and
are two known flow rates for known confining pressures and gas injection pressures
and
, where
and
are the corresponding outlet pressures.
However, there are some limitations when applying this simplified Darcy equation for actual reservoir conditions. The empirical equation was developed by testing natural and reconstituted brown coal samples in laboratory conditions. The equation does not address the effect of natural cleat system in high rank coals and the influence of coal matrix swelling. Importantly, it is not possible to expect the linear laminar condition of the flow in deep coal seams during the CO
2 sequestration process, particularly close to the injection point, and flow through the seam may be in a turbulent, non-Darcy state. In such situations it is necessary to use a more accurate approach as shown below to predict permeability [
66]:
where
is the pressure gradient,
is the velocity,
is the flowing fluid density,
is the flowing fluid viscosity,
is the non-Darcy permeability and
is the non-Darcy coefficient of the porous medium.
The pore pressure effect on permeability has also been studied by Harpalani and Zhao [
46], who proposed a fully empirical relation for coal permeability with pore pressure as follows:
where
A,
B and
C are constants and
is the pore pressure. Although this model is easy to use due to its simplicity, it does not precisely describe the pore pressure effect on coal permeability, as the first and third terms in the right-hand side of the equation describe opposite pore pressure influences on coal permeability.
In 1992, Seidle [
67] proposed a new relationship among coal cleat permeability with effective stress and pore pressure, using two types of coal taken from the Black Warrior and San Juan Basins (Equations (16) and (17)):
where
is the cleat permeability (mD),
is the cleat volume compressibility (kPa
−1),
is the hydrostatic stress (kPa),
E is the elastic modulus of coal and
pp is the pore pressure of the coal mass. However, since these relations are based on the data of only two different types of coal samples, Seidle [
67] suggested more studies using a variety of coal samples taken from different locations to check the accuracy of this model as the universal model for coal.
In 1995, Seidle and Huitt [
68] proposed a descriptive model for coal porosity considering the effect of coal matrix shrinkage on gas desorption (matrix shrinkage expands the pore space in coal and therefore enhances coal mass permeability), based on the experimental data of highly volatile bituminous coal samples taken from the San Juan Basin. This relationship more precisely describes the influence of coal matrix deformations (which occur through sorption and desorption during CH
4 and CO
2 gas flows) on coal mass pore space:
where
is the coal bed porosity after sorption/desorption of gases,
is the initial coalbed porosity,
is the strain and b is a constant. This equation can be used to predict coal permeability with the assistance of the basic porosity-permeability cubic law for porous media:
However, this equation concerns only the effect of matrix shrinkage on permeability and does not consider the influence of effective stress.
In 1990, Sawyer et al. [
69] developed the following widely-used equation for coal permeability (commonly called the ARI model):
where
is the pore volume compressibility,
is the matrix shrinkage compressibility (
according to McKee et al. [
16]),
is the pressure change per
concentration variation and
is the initial gas concentration. Here, the first term describes the porosity changes due to pore pressure and the second term describes the porosity changes due to matrix shrinkage.
Later, Palmer and Mansoori [
50] proposed the following equation for coal permeability based on the theoretical evaluation of the effects of matrix shrinkage and effective stress on coal permeability, and proposed a new model for coal permeability as a function of both matrix shrinkage and effective stress (commonly known as the P & M model):
where:
where
is the porosity difference,
is the pore pressure difference (md),
is the Langmuir volume,
b is the Langmuir constant (describes the effect of grain compression),
K and
M are bulk and the constrained axial modulus, respectively and can be given as functions of Poisson’s ratio as follows:
Integration of Equation (21) gives:
where
,
and
and are the original reservoir porosity, the original pressure (MPa) and the matrix shrinkage compressibility, respectively. This equation also can be used to predict permeability by combining it with Equation (19). Here, the first terms describe the effective stress influence and the last term describes the matrix shrinkage influence. According to the researchers, this equation can be reduced to the following simpler model if the compressibility factor,
is constant, although it will not be constant practically as it varies with medium porosity and Young’s modulus:
However, it should be noted that Equation (25) can only be used under constant applied pressure conditions (only the flow effect is considered) as the effect of stress variation is not considered. To date, this model has been widely used in coal bed methane simulators. However, all the coal permeability models described above have been developed for methane production and CO2 injection has been ignored.
Therefore, Pekot et al. [
51] studied both the ARI and the P & M models and showed the importance of adding a new term to account for the effect of differential shrinkage of coal mass due to CO
2 movement. This is because, based on their experimental study, they found that greater strain (swelling) was developed by CO
2 in coal compared to CH
4, which causes greater porosity and permeability reductions and is called “differential swelling”. The proposed new equation for coal porosity after adding the differential swelling term is shown below:
where
is the differential swelling coefficient. The effect of differential swelling on coal permeability reported by Pekot et al. [
51] is shown in
Figure 16.
In 2000, Gilman and Beckie [
70] developed a theoretical approach to coal permeability for methane movement, considering the regular cleat system in coal, adsorptive gas storage, the extremely slow mechanism of methane release from the coal matrix to cleats and the significant permeability changes caused by this desorption. Here, they considered two different types of methane gas flow mechanisms inside the coal mass: (a) in fractures, modelled using Darcy’s law and, (b) in coal mass micro-pores, modelled using the Knudsen diffusion formula (coupled with ideal gas flow), to derive the following equation for coal seam permeability:
where
is the change in effective stress and
is the fracture’s Young’s modulus. This equation was then converted into a more comprehensive form by adding the matrix shrinkage/swelling effects as follows, showing both effective stress and the matrix shrinkage effects. Here two basic assumptions have been made; (1) the coal mass is a homogeneous isotropic elastic medium and (2) zero lateral strain occurs in it:
where
is the change of adsorbed mass,
is the volumetric swelling coefficient,
is the Poisson’s ratio,
is the pore pressure and
E is the coal mass Young’s modulus.
A similar but more advanced and precise theoretical approach to simulate the CO
2 flow behaviour in coal has been proposed by Wang et al. [
71], based on some basic assumptions: (1) non-water flow in the fluid phase, (2) the adsorbed phase is in equilibrium and (3) the system is isothermal, (4) zero lateral strain occurs in it:
where
where
is the coal mass Young’s modules,
is the Young’s modulus of the coal matrix,
τf is the tortuosity,
So and
S are the initial and final adsorbed mass, and
k(
so) and
k(
s) are the initial and final permeability values.
However, all the models described above have been developed based on one common assumption: that lateral stain is zero. Although this is applicable for field coal seams with hydrostatic stress, the use of this assumption for laboratory-scale coal sample testing such as tri-axial testing is not correct, as there is considerable lateral strain in the coal sample under such conditions. Therefore, in 2013, Perera et al. [
48] derived the following more compressive equation to predict coal seam permeability in coal under tri-axial, non-zero lateral strain conditions:
where
k is the permeability of the coal mass,
ko is the initial permeability of the coal mass,
E is the coal mass Young’s modulus,
Ef is the fracture Young’s modulus,
ϑ is the Poisson’s ratio of the coal mass,
ϑf is the Poisson’s ratio of fractures,
is the bulk modulus of the coal mass,
is the CO
2 injection pressure,
σA is the axial stress,
σc is the confining pressure,
εv is the volumetric strain,
αs is the volumetric swelling coefficient for coal, and Δ
S is the change of adsorption mass.
7. Conclusions
The permeability of natural coal seams is influenced by the geological stress field of the coal seam, its temperature and moisture content, and the coal maturity or rank. Coal permeability is basically dependent on the porosity of the coal mass, as highly porous media have higher capability to offer easy flow paths. Therefore, the factors affecting coal mass porosity have a direct impact on its flow ability or permeability. In this respect, effective stress plays a major role, because being a type of relatively weak and compressible rock, coal’s pore structure is greatly reduced with increasing effective stresses applied on it, because it causes the fissures/pores of the coal mass to close, increasing the tortuosity. For this reason, deep coal seams generally have much lower permeability values than shallow seams.
Coal tends to become more permeable with the reduction of its moisture content, because moisture occupies the pore space available in the coal mass for fluid movement and adsorption of that water into the coal matrix induces significant matrix swelling, both of which obstruct the flow paths in the coal matrix. Preferable coal seams for CO2 sequestration/ECBM have considerably high temperatures due to their deep depths. Although high temperatures cause thermal expansion in the coal matrix with resulting its permeability reduction, extremely high temperatures may create thermal cracks in the coal matrix, thus increasing permeability. Deeper coal seams normally contain higher ranked coal as that coal had more opportunities to be subjected to greater pressure and temperature variations and much lower permeability can be expected in deeper coal seams. Based on all of these facts, since deeper coal seams have greater effective stresses, higher ranked coals and potential water saturation conditions, deep coal seams generally have very low permeability values, although the effect of temperature is the opposite.
Flowing CO2 inside a coal seam during CO2 sequestration/ECBM has a significant influence on its natural existing permeability through CO2 adsorption-induced swelling and hydrocarbon mobilisation in the seam, which have been widely experienced in field CO2 sequestration projects, and the CO2 injection rate has been greatly reduced after the initial stage of CO2 injection in many field projects.
However, CO2 flow behaviour can vary from seam to seam, and deeper coal seams generally have lower CO2 flow ability due to the shrunken pore structure due to the available greater pressures and temperatures. This low CO2 permeability existing at greater depths has created serious issues in large-scale sequestration projects, as critically high injection pressures are required to achieve sufficient CO2 injection into them, which is an expensive task and also involves some risks associated with CO2 leakage. Therefore, the combined influences of high temperatures (thermal cracks and thermal expansion), changes in adsorption behaviour and therefore swelling and the associated phase transition need to be studied to precisely identify the influence of temperature on coal permeability. Coal permeability for CO2 reduces with increasing CO2 pressure due to the swelling effect and the slip-flow effect. The change of CO2 phase condition from gas/liquid state to super-critical state in deep seams has a significant influence on swelling. Since super-critical CO2 occupies much smaller space in the seam, generally it is planned to target deep seams for CCS projects. However, super-critical CO2 is more chemically reactive and creates a significantly higher swelling effect in coal and has much reduced flow ability. Gas CO2 flow through coal occurs along very narrow and complex paths and in theory extremely low permeability creates very high sorption capacity in coal. However, this does not happen due to the Klinkenberg slip-flow effect, which causes greater permeability for gas in coal compared to liquid/super-critical CO2.
Theoretical and empirical models play very important roles in predicting CO2 flow behaviour in order to identify the coal mass properties in deep coal seams, considering the factors affecting it, including porosity, effective stress, and swelling /shrinkage.