A Distributed Robust Dispatch Approach for Interconnected Systems with a High Proportion of Wind Power Penetration
Abstract
:1. Introduction
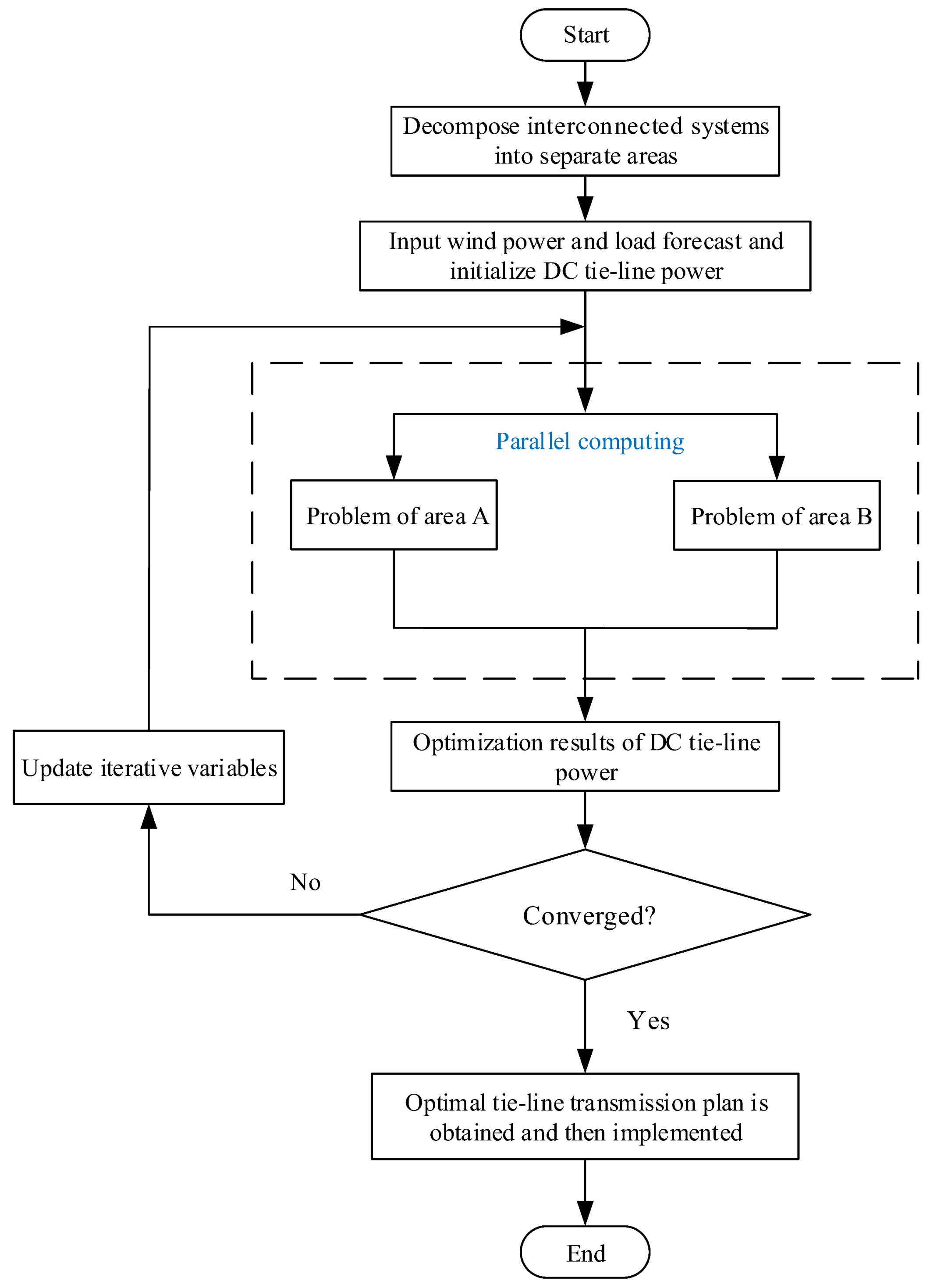
2. Basic Principle of SADMM
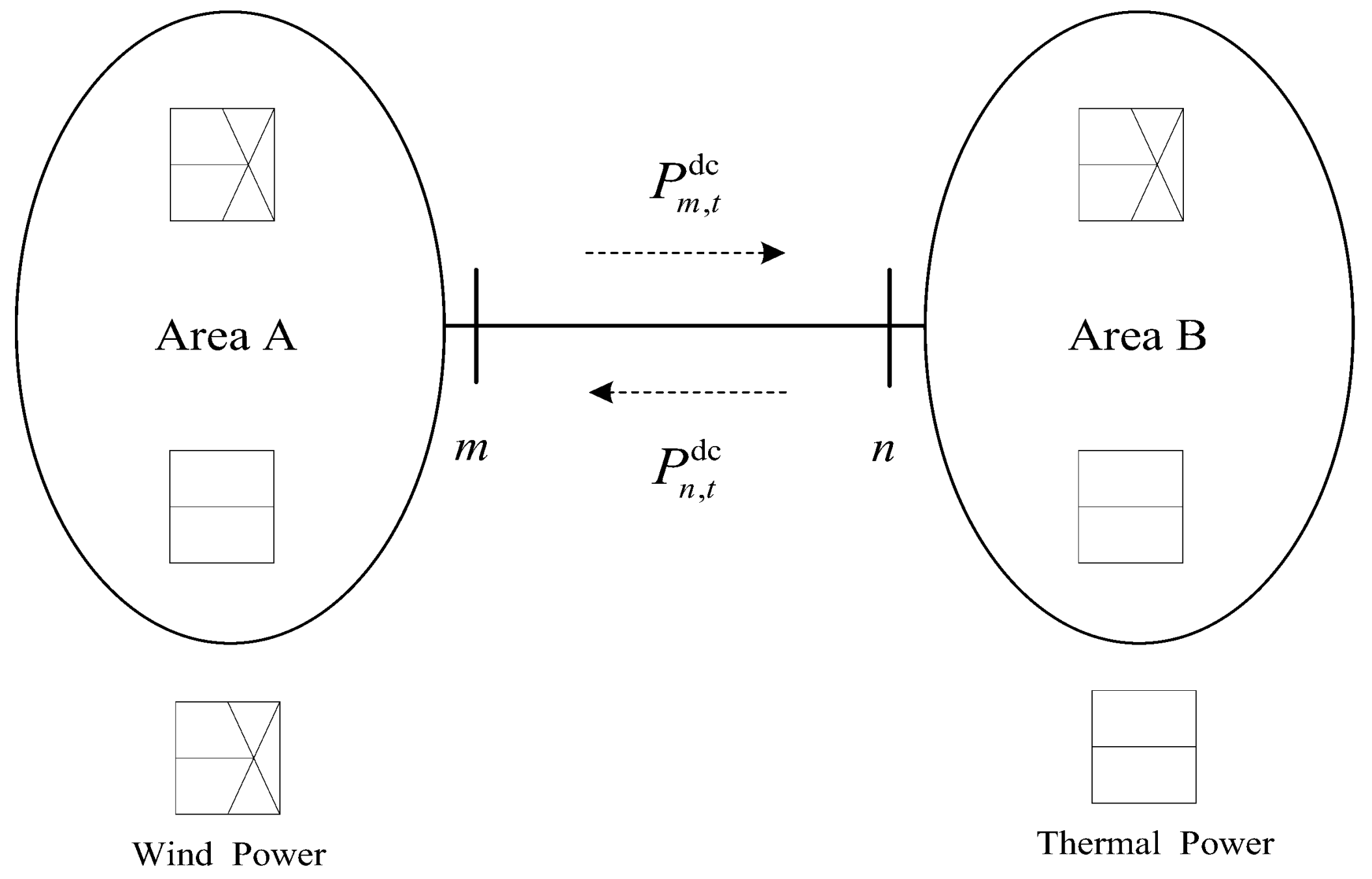
3. Decentralized Economic Dispatch Model of the Interconnected Power System
3.1. Modeling of Wind Power Output
3.2. The Objective Function
3.3. The Constraints
4. Model Solving and Case Study
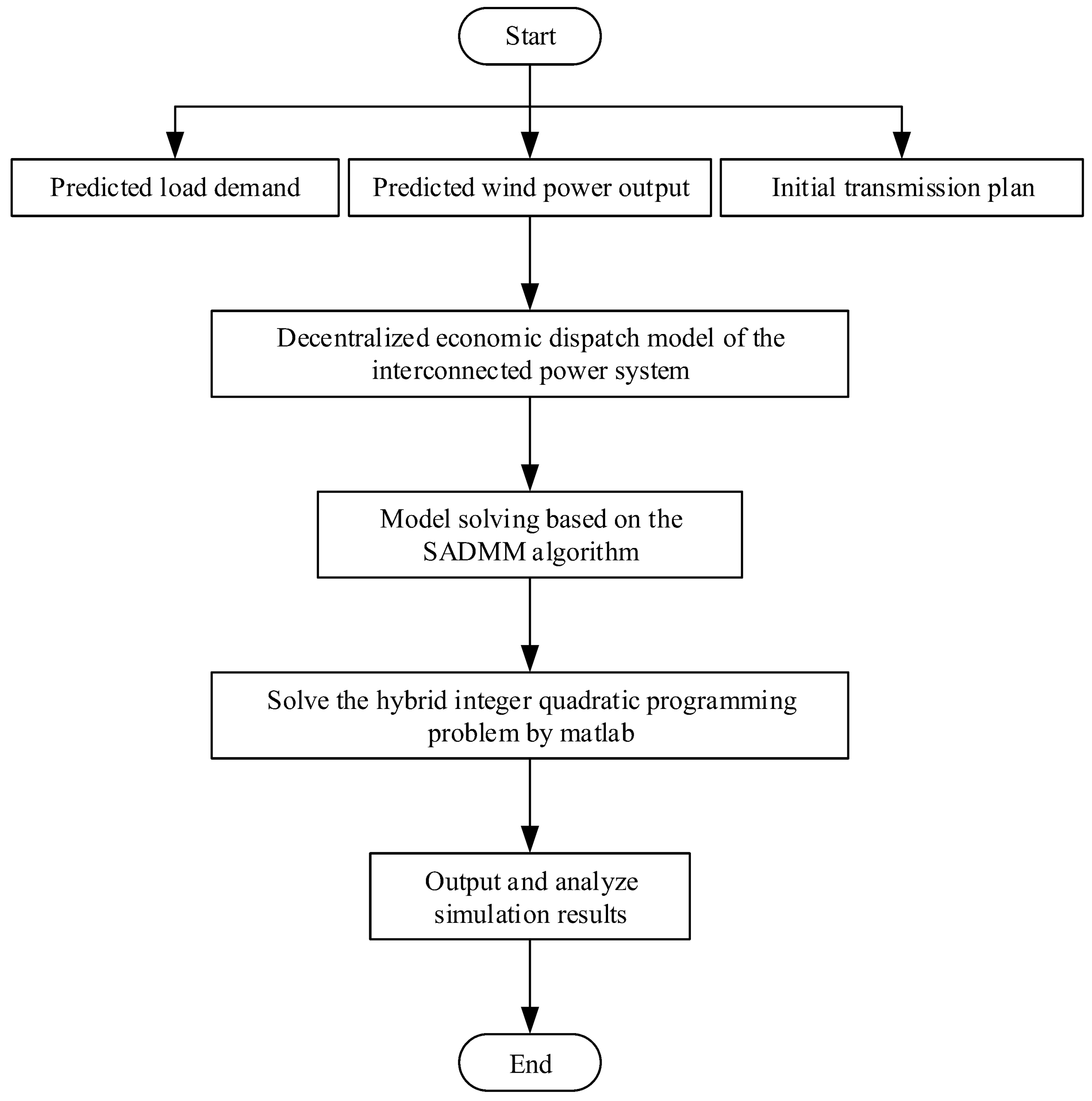
4.1. Integrated Schematic of the Whole Study
- Step 1:
- Input the predicted load demand, predicted wind power output, and initial transmission plan.
- Step 2:
- Propose a distributed robust dispatch model to solve the economic dispatch problem of the interconnected power system with a high proportion of wind power penetration.
- Step 3:
- Solve the model by using the SADMM algorithm.
- Step 4:
- Solve the hybrid integer quadratic programming problem on the Matlab2016a platform.
- Step 5:
- Output and analyze the simulation results.
4.2. Flow Chart of Model Solving Based on the SADMM
4.3. Case Study
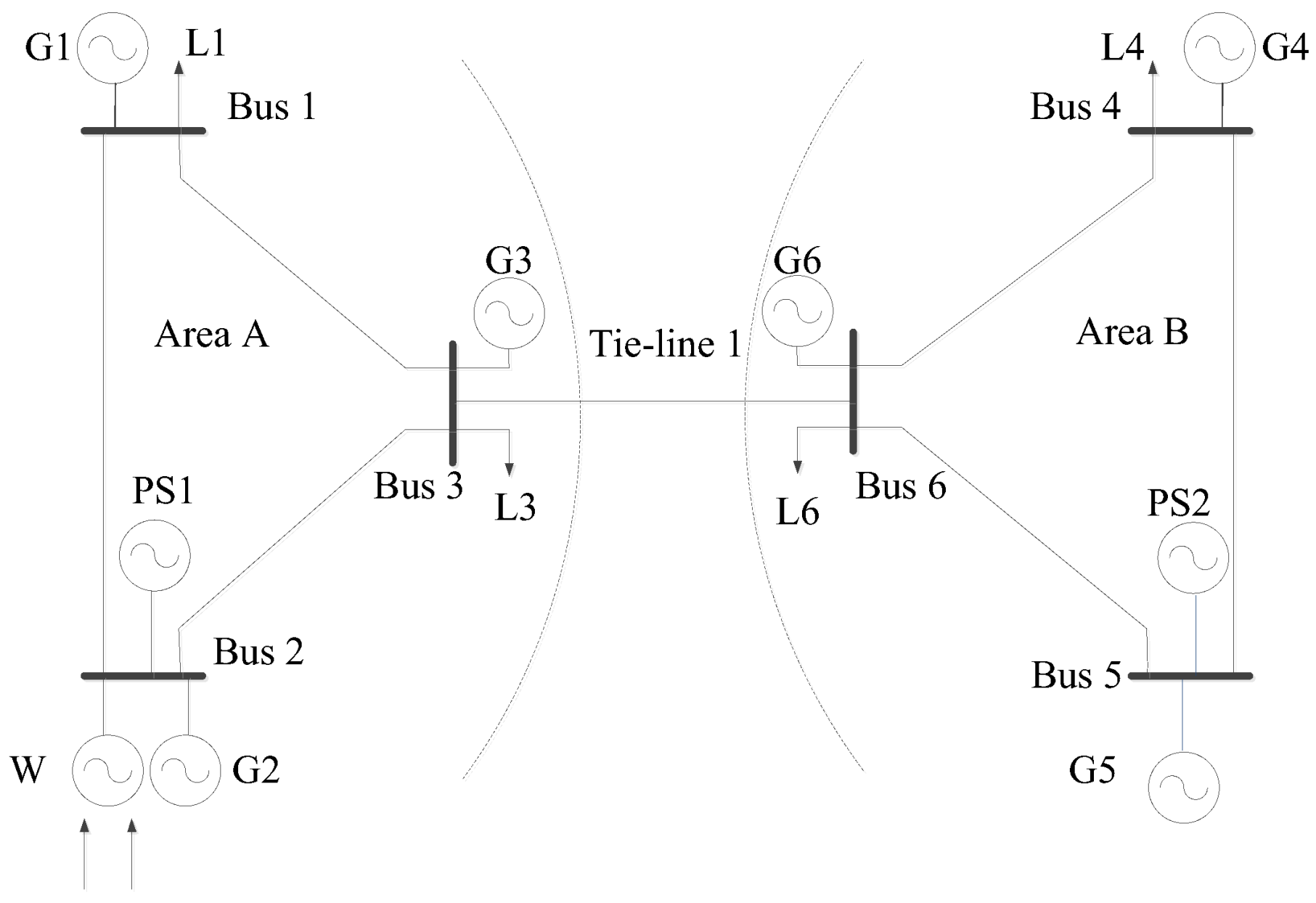
4.3.1. A 2-Area 6-Node System
4.3.2. Interconnection of Several Modified New England 39-Node Systems
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| The objective function of region A | |
| The objective function of region B | |
| , | The coupling coefficient matrice between the regions, respectively |
| The number of iterations | |
| The introduced Lagrange multiplier vector | |
| A positive constant | |
| The maximal output of wind farm in the period of | |
| The minimal output of wind farm in the period of | |
| The upper limit of the overall deviation of all wind power output predictions in each dispatch period | |
| The upper limit of the overall deviation of all wind power output predictions in all the periods for a particular wind farm | |
| The identification quantities of positive deviation of the wind power predictions | |
| The identification quantities of negative deviation of the wind power predictions | |
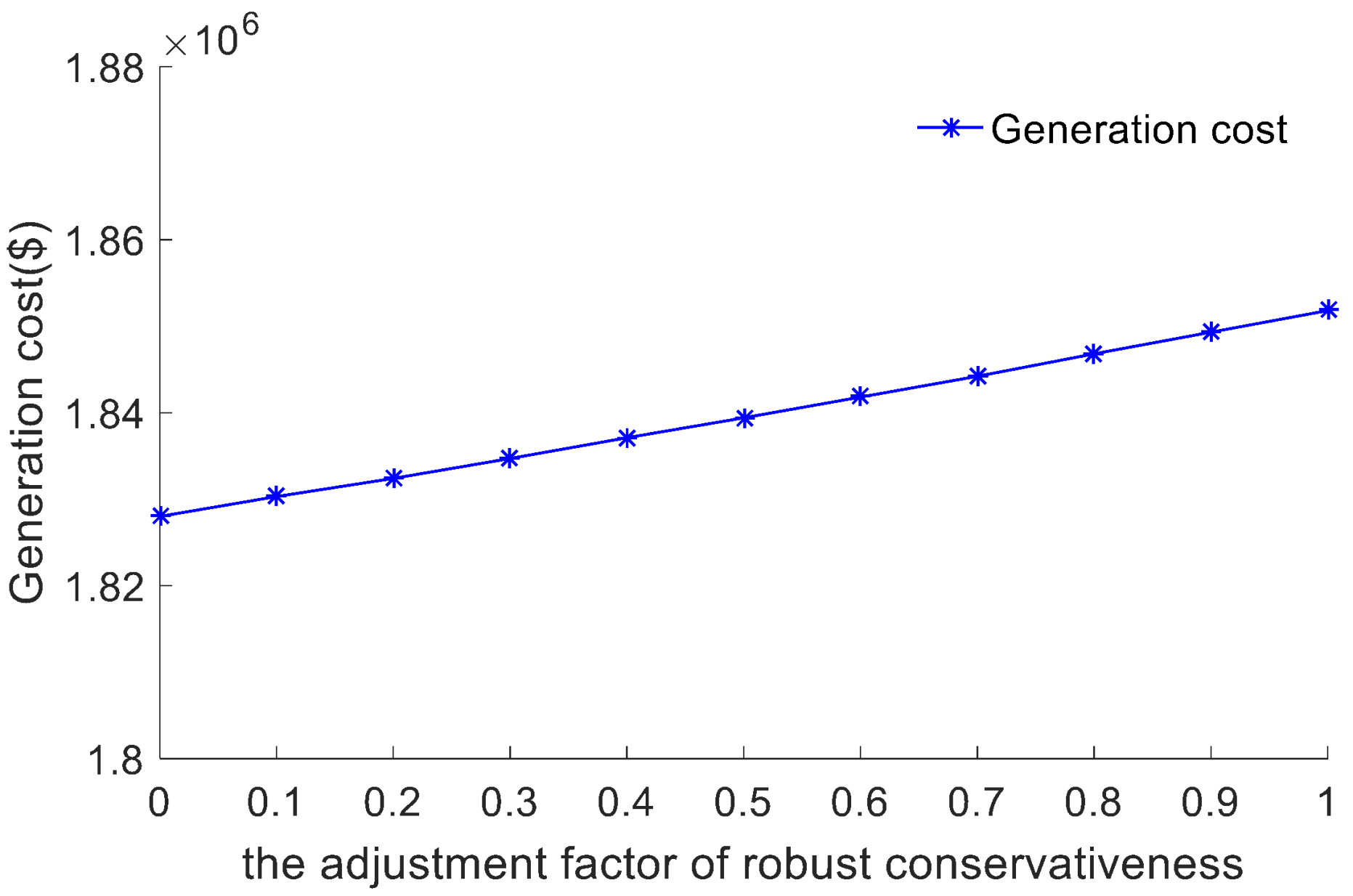
| The adjustment factor of robust conservativeness | |
| The set of thermal power units in region A | |
| The operation cost of the thermal power unit | |
| The output of the thermal power unit in the period | |
| The set of wind turbines in region A | |
| The penalty cost coefficient of the abandoned wind power | |
| The power of the abandoned wind of wind turbine in the period | |
| The output of wind turbine in the period | |
| The wind power actually invoked by the power grid of wind turbine in the period | |
| The optimized power of the DC tie line for the time segment in region A | |
| The arithmetic mean of the optimized power of DC tie line in region A and B in the iteration processed by SADMM | |
| The introduced additional term using the SADMM algorithm | |
| The set of load nodes in region A | |
| The predicted value of the load in region A in the period | |
| The maximal output of the thermal power unit in region A in the period | |
| The maximal and minimal output of the thermal power unit in region A in the period | |
| The limit of upward climbing rate of the thermal power unit | |
| The limit of downward climbing rate of the thermal power unit | |
| The climbing rate of the thermal power unit | |
| The landslide rate of the thermal power unit | |
| The response time of the positive spinning reserve | |
| The upper limit of the output of DC tie line in the period | |
| The lower limit of the output of DC tie line in the period | |
| The positive spinning reserve capacity in the period | |
| The demand coefficient of the load for positive spinning reserve in region A | |
| The demand coefficient of wind power for positive spinning reserve in region A | |
| The demand coefficient of wind power for negative spinning reserve in region A | |
| The flow transfer distribution factor of the thermal power unit | |
| The flow transfer distribution factor of the wind turbine unit | |
| The flow transfer distribution factor of DC tie line | |
| The flow transfer distribution factor of load | |
| The maximal transmission power of line | |
| 0–1 variables which are utilized to indicate whether the DC tie lines climb in the period | |
| 0–1 variables which are utilized to indicate whether the DC tie lines landslide in the period | |
| The maximal adjustment of the output power of the DC tie lines in the period | |
| The maximal and minimal adjustment of the output power of the DC tie lines in the period | |
| The maximal number of the adjustments of the output power of the DC tie lines in the dispatch period | |
| The total number of periods in the dispatch period | |
| The total planned outbound power of the DC tie lines in the dispatch period | |
| The single time interval during which the unit is operating | |
| The number of iterations | |
| The convergence accuracy |
References
- Doostizadeh, M.; Aminifar, F.; Ghasemi, H.; Lesani, H. Energy and reserve scheduling under wind power uncertainty: An adjustable interval approach. IEEE Trans. Smart Grid 2016, 7, 2943–2952. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Xia, Q.; Liang, J. Modeling conditional forecast error for wind power in generation scheduling. IEEE Trans. Power Syst. 2014, 29, 1316–1324. [Google Scholar] [CrossRef]
- Nikoobakht, A.; Mardaneh, M.; Aghaei, J.; Guerrero-Mestre, V.; Contreras, J. Flexible power system operation accommodating uncertain wind power generation using transmission topology control: An improved linearised AC SCUC model. IET Gener. Transm. Dis. 2017, 11, 142–153. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Wang, J.; Qiu, F.; Wei, W.; Mei, S.; Lei, S. Robust risk-constrained unit commitment with large-scale wind generation: An adjustable uncertainty set approach. IEEE Trans. Power Syst. 2017, 32, 723–733. [Google Scholar] [CrossRef]
- Gill, S.; Kockar, I.; Ault, G. Dynamic optimal power flow for active distribution networks. IEEE Trans. Power Syst. 2014, 29, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wu, W.; Shahidehpour, M.; Zhang, B. Adaptive robust tie-line scheduling considering wind power uncertainty for interconnected power systems. IEEE Trans. Power Syst. 2016, 31, 1351–1361. [Google Scholar] [CrossRef]
- Zhao, F.; Litvinov, E.; Zheng, T. A marginal equivalent decomposition method and its application to multi-area optimal power flow problems. IEEE Trans. Power Syst. 2014, 29, 53–61. [Google Scholar] [CrossRef]
- Ahmadi-Khatir, A.; Conejo, A.; Cherkaoui, R. Multi-area energy and reserve dispatch under wind uncertainty and equipment failures. IEEE Trans. Power Syst. 2013, 28, 4373–4383. [Google Scholar] [CrossRef]
- Kargarian, A.; Hug, G.; Mohammadi, J. A multi-time scale co-optimization method for sizing of energy storage and fast-ramping generation. IEEE Trans. Sustain. Energy 2016, 7, 1351–1361. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y.; Gao, D.; Lin, J.; Cheng, L. A versatile probability distribution model for wind power forecast errors and its application in economic dispatch. IEEE Trans. Power Syst. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Saha, T.; Eghbal, M. Wind power offering strategy in day-ahead markets: Employing demand response in a two-stage plan. IEEE Trans. Power Syst. 2015, 30, 1888–1896. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Zhou, X.; Watada, J. Two-stage multi-objective unit commitment optimization under hybrid uncertainties. IEEE Trans. Power Syst. 2016, 31, 2266–2277. [Google Scholar] [CrossRef]
- Toulabi, M.; Bahrami, S.; Ranjbar, A. An input-to-state stability approach to inertial frequency response analysis of doubly-fed induction generator-based wind turbines. IEEE Trans. Energy Convers. 2017, 32, 1418–1431. [Google Scholar] [CrossRef]
- Amini, M.; Boroojeni, K.; Iyengar, S.; Pardalos, P.; Blaabjerg, F.; Madni, A. Sustainable Interdependent Networks: From Theory to Application; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Bahrami, S.; Wong, V. Security-constrained unit commitment for ac-dc grids with generation and load uncertainty. IEEE Trans. Power Syst. 2017. [Google Scholar] [CrossRef]
- Mohammadi, A.; Mehrtash, M.; Kargarian, A. Diagonal quadratic approximation for decentralized collaborative TSO+DSO optimal power flow. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Amini, M.; Nabi, B.; Haghifam, M. Load management using multi-agent systems in smart distribution network. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Bahrami, S.; Amini, M.; Shafie-khah, M.; Catalao, J. A decentralized electricity market scheme enabling demand response deployment. IEEE Trans. Power Syst. 2017. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhou, B.; Zhang, M. Parallel augment Lagrangian relaxation method for transient stability constrained unit commitment. IEEE Trans. Power Syst. 2013, 28, 1140–1148. [Google Scholar] [CrossRef]
- Ahmadi-Khatir, A.; Conejo, A.; Cherkaoui, R. Multi-area unit scheduling and reserve allocation under wind power uncertainty. IEEE Trans. Power Syst. 2014, 29, 1701–1710. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Shahidehpour, M.; Zhang, B.; Wang, B. Decentralized multi-area dynamic economic dispatch using modified generalized benders decomposition. IEEE Trans. Power Syst. 2016, 31, 526–538. [Google Scholar] [CrossRef]
- Kargarian, A.; Fu, Y.; Li, Z. Distributed security-constrained unit commitment for large-scale power systems. IEEE Trans. Power Syst. 2015, 30, 1925–1936. [Google Scholar] [CrossRef]
- Zhou, M.; Zhai, J.; Li, G.; Ren, J. Distributed dispatch approach for bulk AC/DC hybrid systems with high wind power penetration. IEEE Trans. Power Syst. 2017. [Google Scholar] [CrossRef]
- Bakirtzis, A.; Biskas, P. A decentralized solution to the DC-OPF of interconnected power systems. IEEE Trans. Power Syst. 2003, 18, 1007–1013. [Google Scholar] [CrossRef]
- Zheng, W.; Wu, W.; Zhang, B.; Sun, H.; Liu, Y. A fully distributed reactive power optimization and control method for active distribution networks. IEEE Trans. Smart Grid 2016, 7, 1021–1033. [Google Scholar] [CrossRef]
- Loukarakis, E.; Bialek, J.; Dent, C. Investigation of maximum possible OPF problem decomposition degree for decentralized energy markets. IEEE Trans. Power Syst. 2015, 30, 2566–2578. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wang, S. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response. IEEE Trans. Power Syst. 2017, 8, 2637–2647. [Google Scholar] [CrossRef]
- Zhang, Y.; Giannakis, G. Distributed stochastic market clearing with high-penetration wind power. IEEE Trans. Power Syst. 2016, 31, 895–899. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Wolsey, L. Integer Programming; Wiley Inter-Science: New York, NY, USA, 1998. [Google Scholar]
- Ongsaul, W.; Petcharks, N. Unit commitment by enhanced adaptive Lagragian relaxation. IEEE Trans. Power Syst. 2004, 19, 620–628. [Google Scholar] [CrossRef]
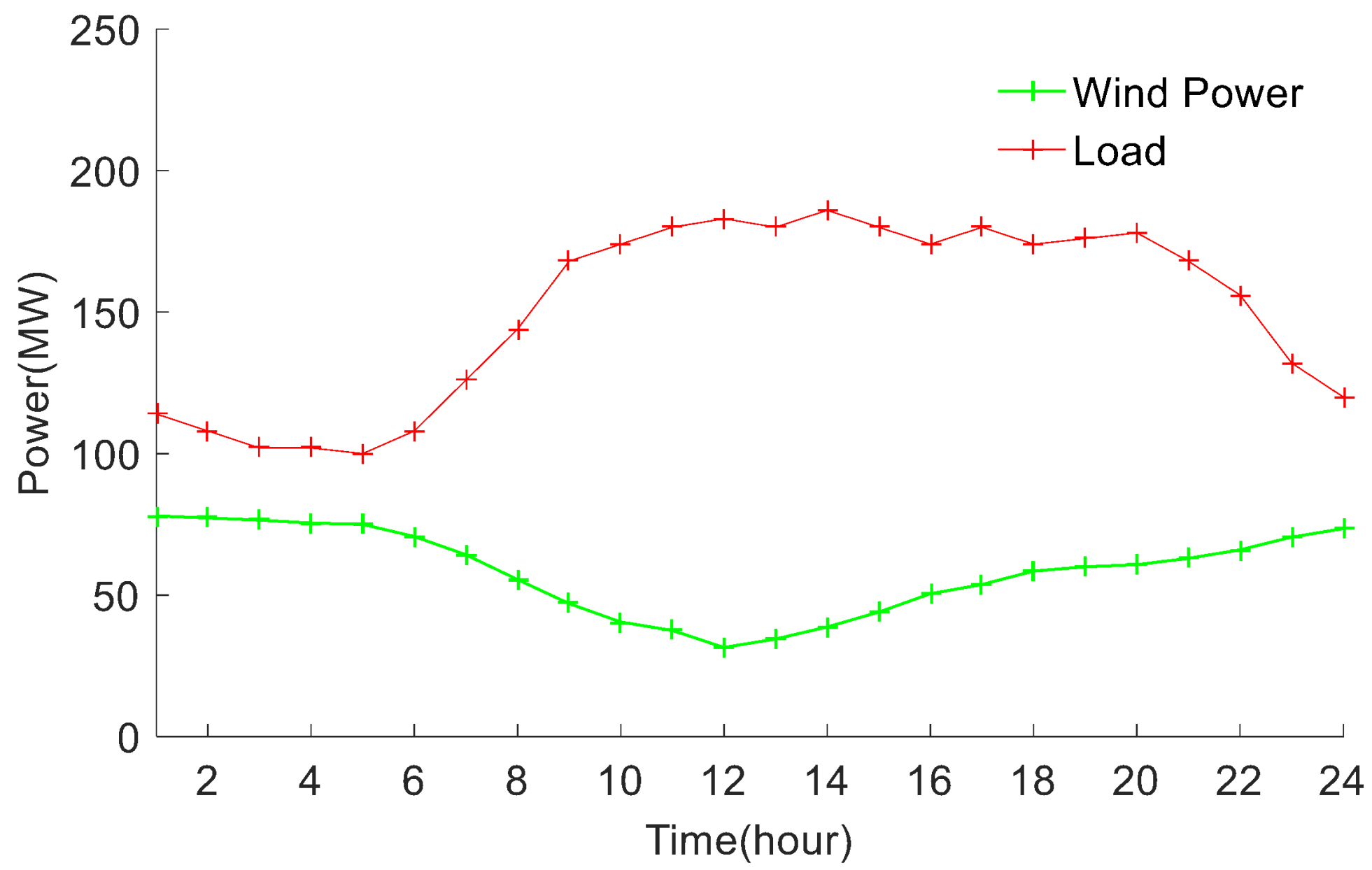
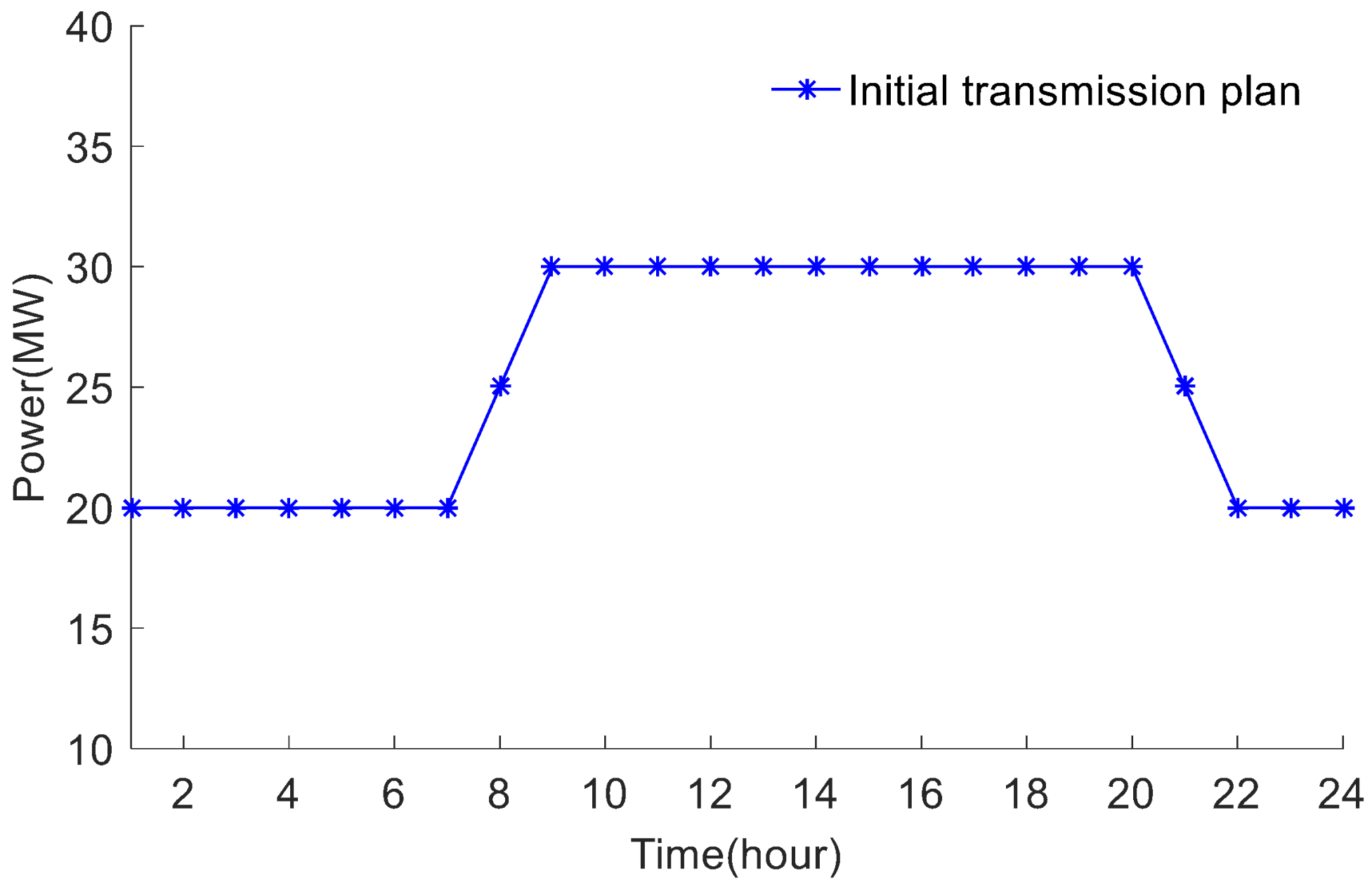
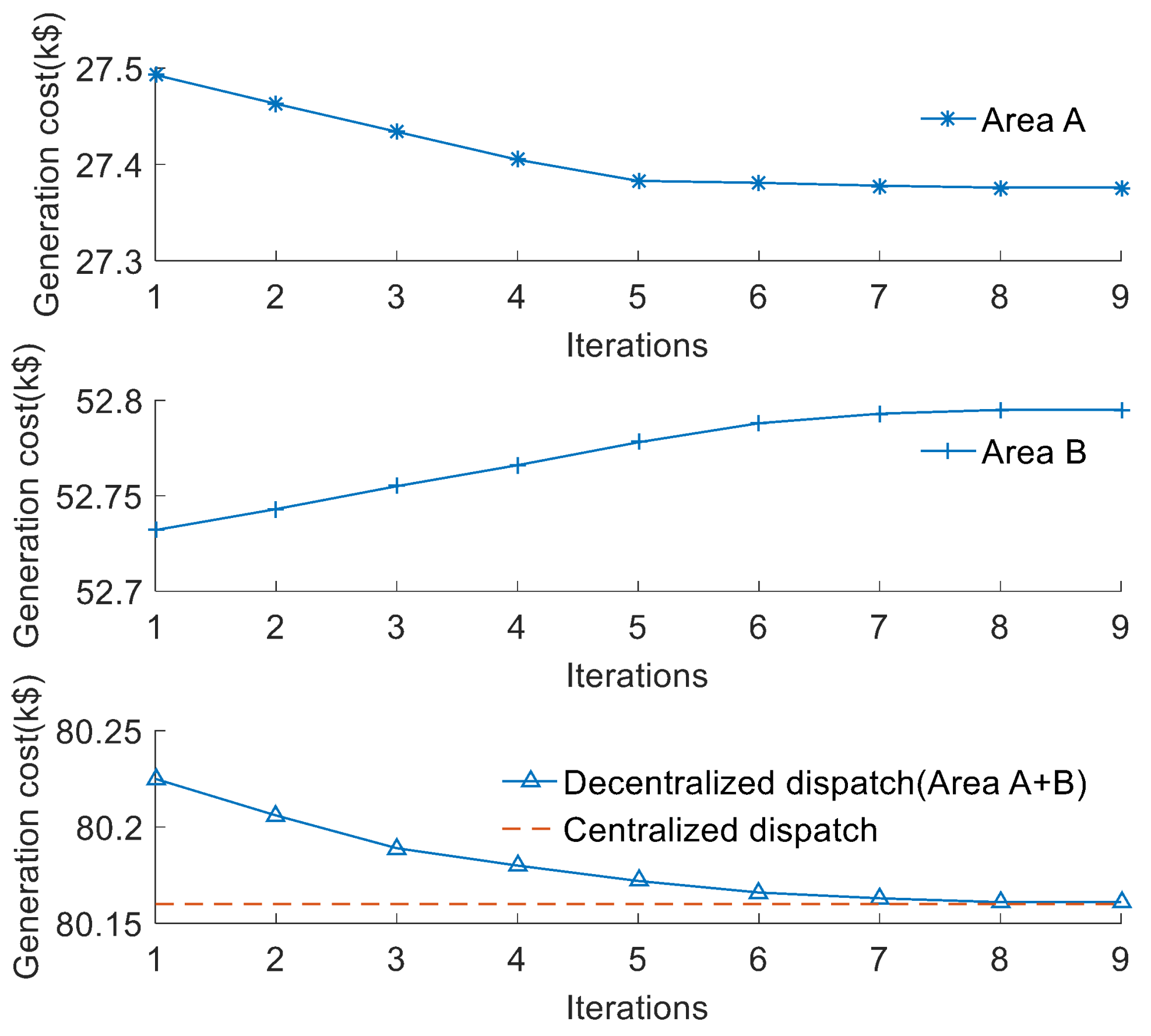
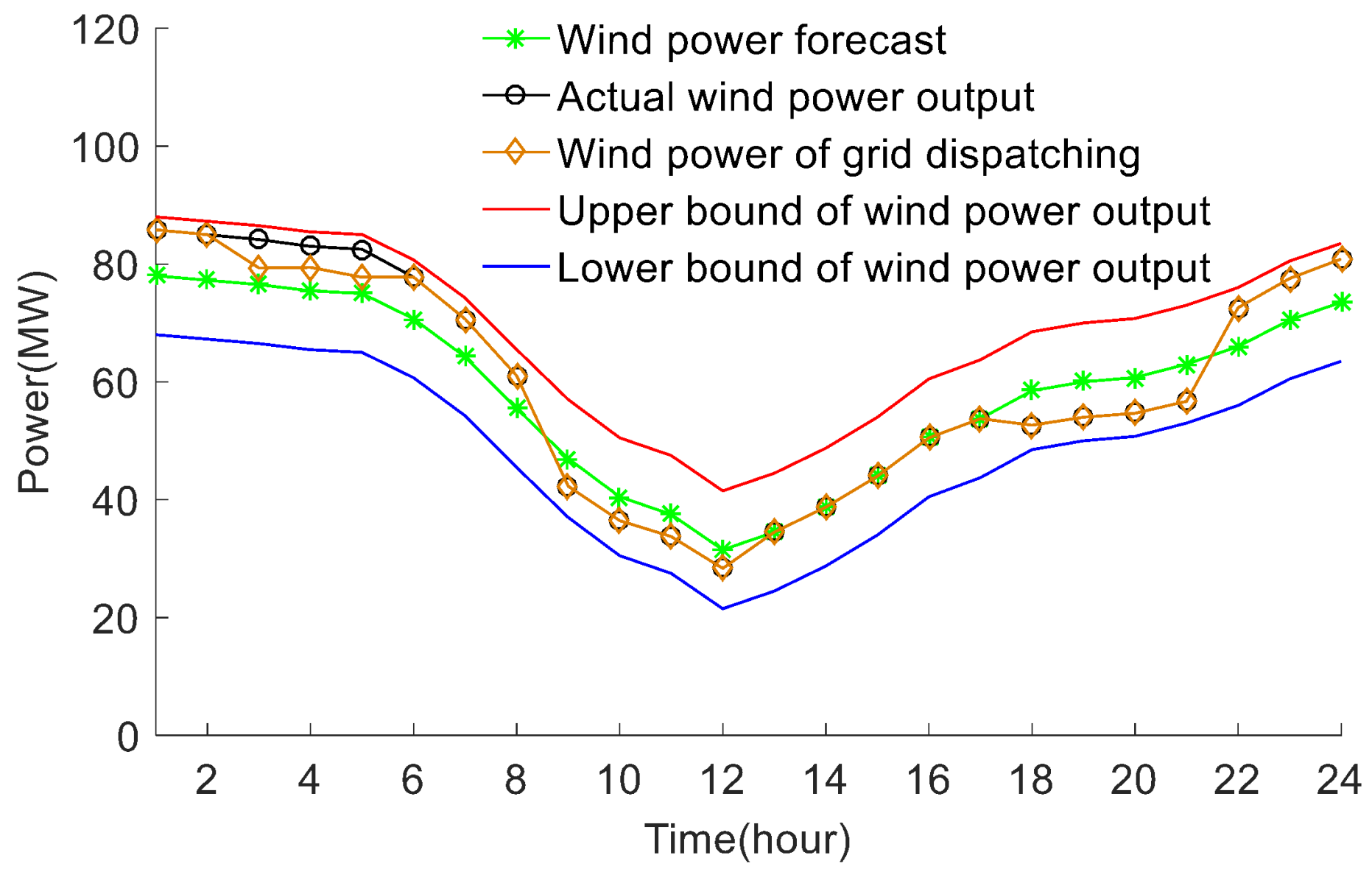
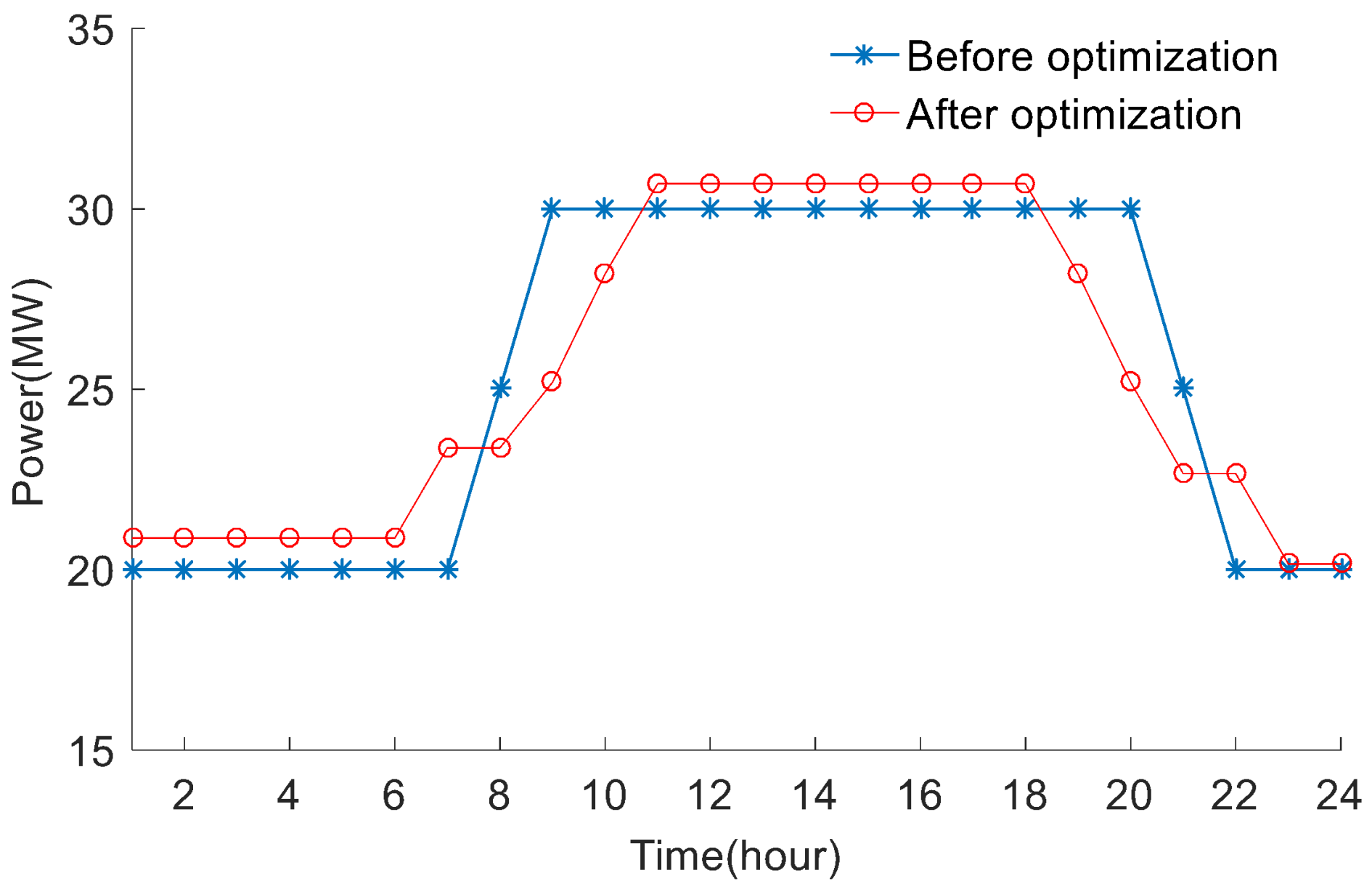
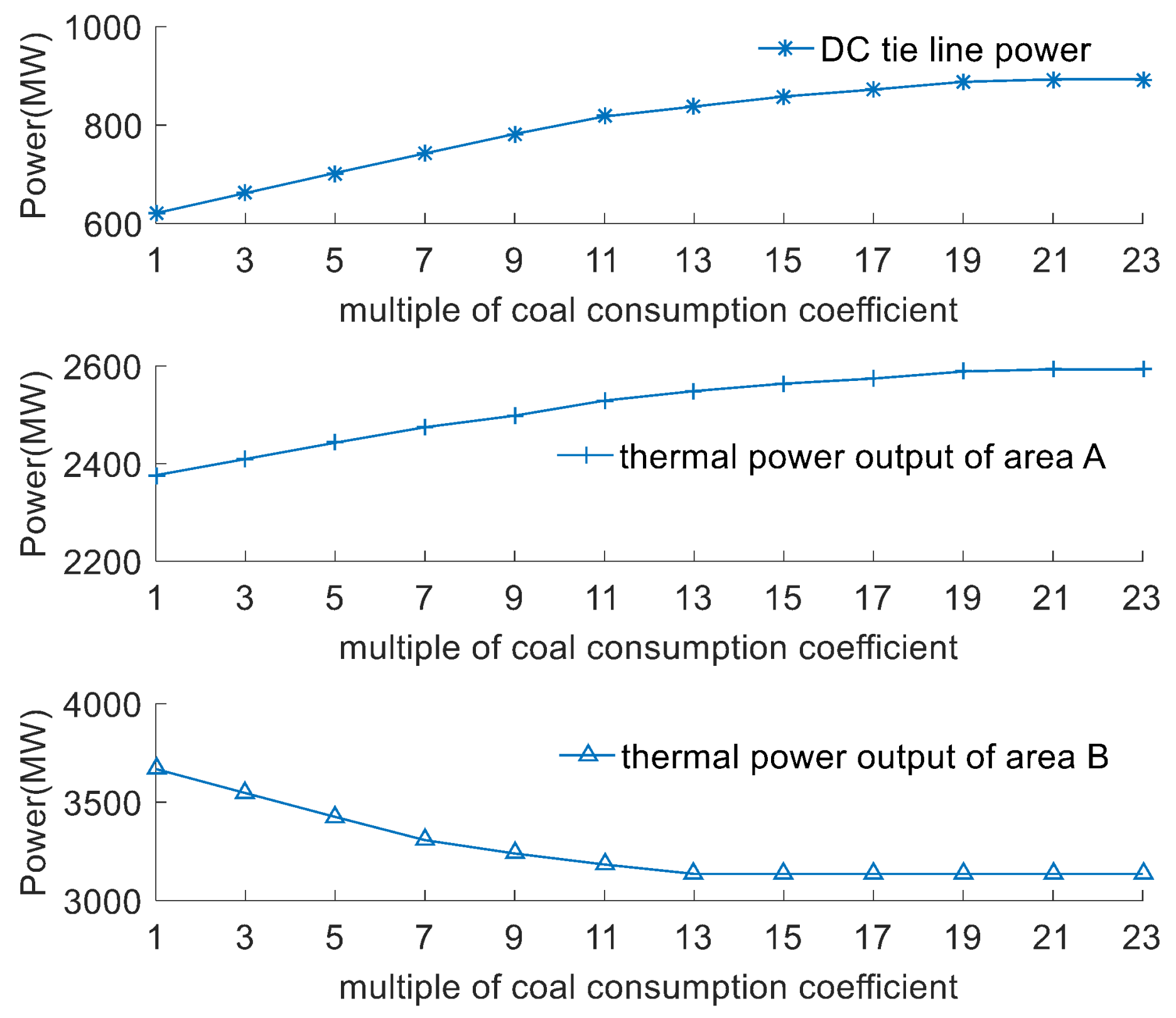
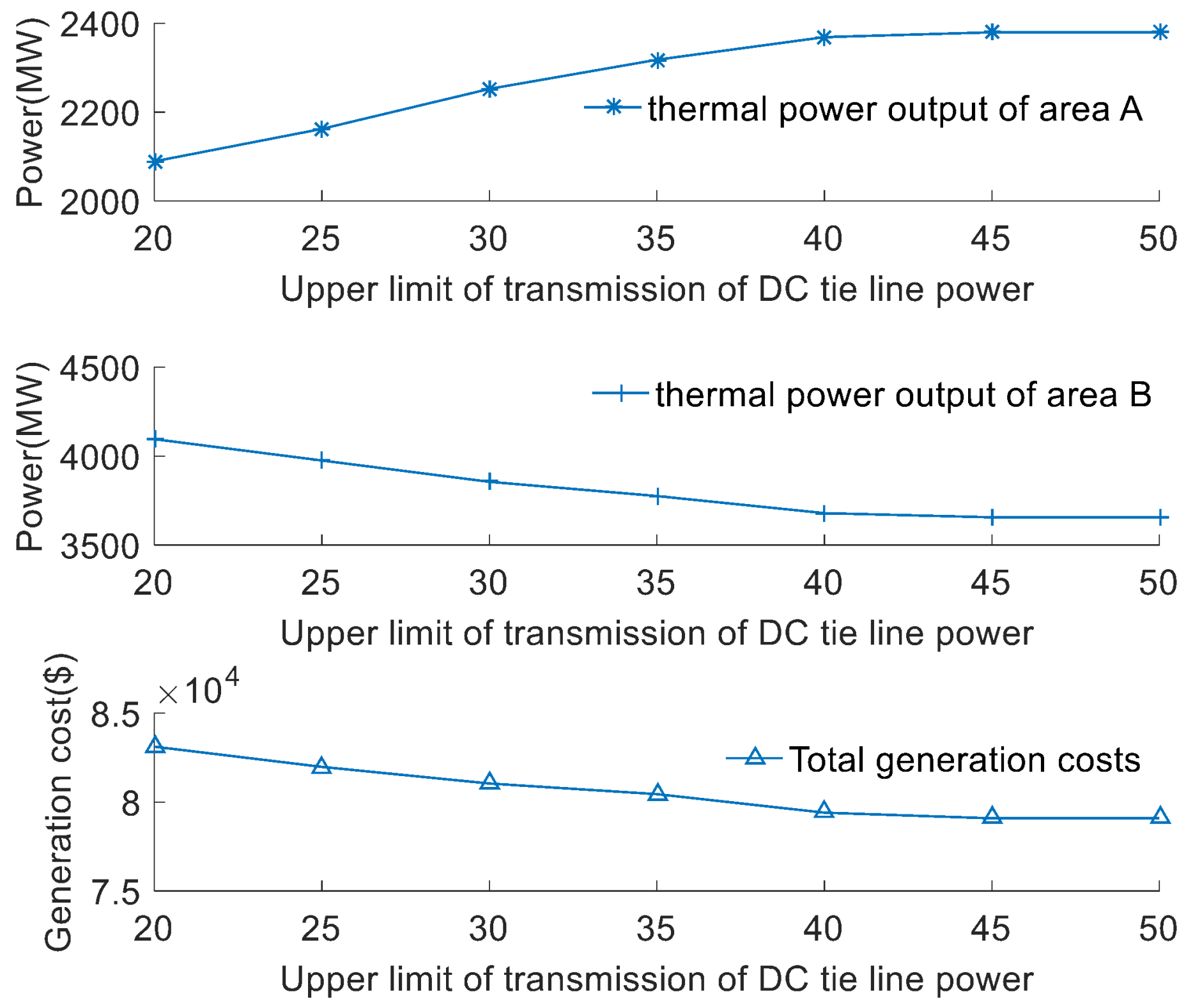
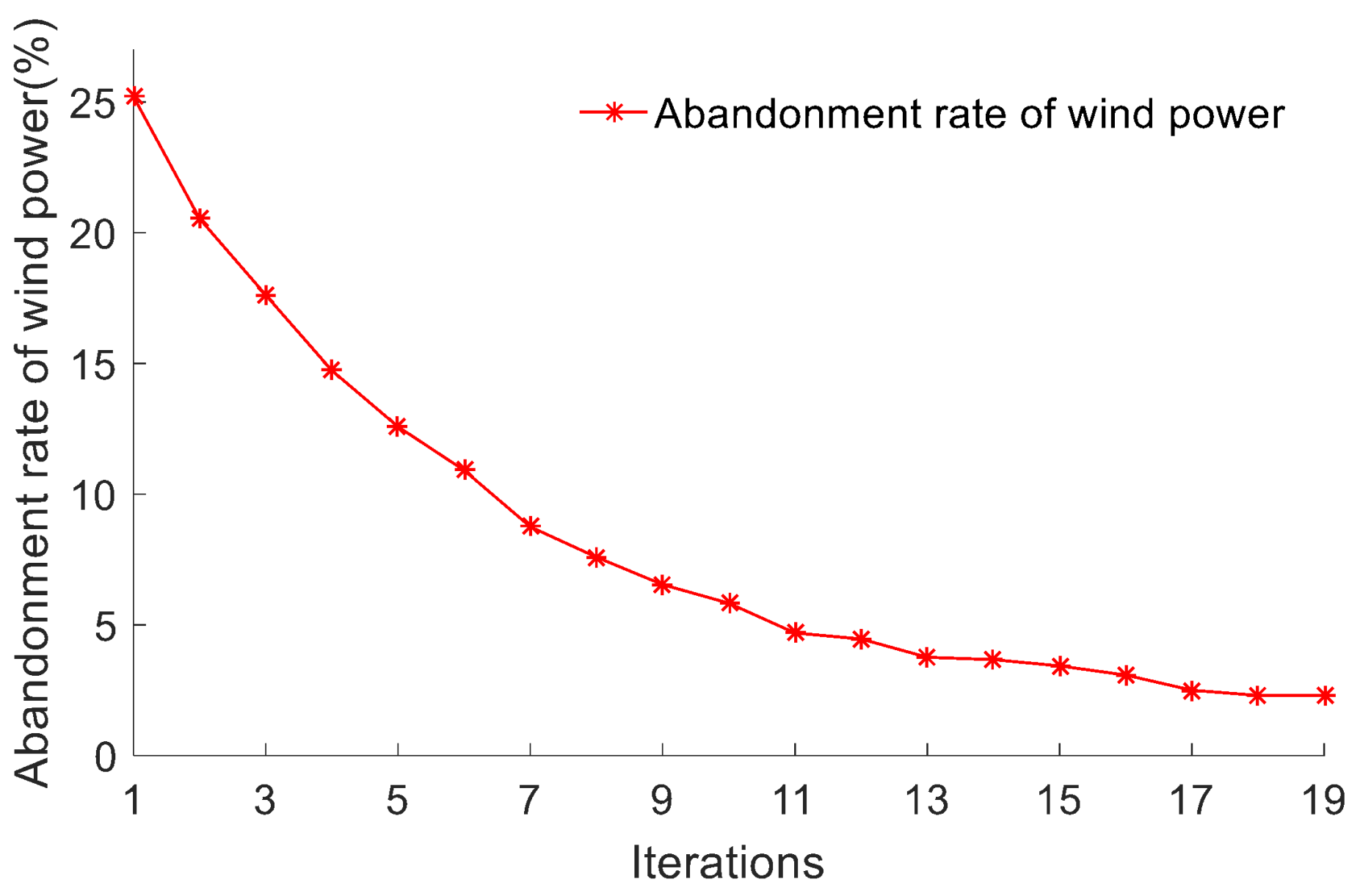
| Generator | (MW) | (MW) | ($/h) | ($/MW·h) | ($/MW·h2) |
|---|---|---|---|---|---|
| G1 | 10 | 100 | 100 | 30 | 0.3 |
| G2 | 10 | 75 | 100 | 40 | 0.8 |
| G3 | 10 | 50 | 100 | 20 | 0.2 |
| G4 | 10 | 100 | 200 | 60 | 0.6 |
| G5 | 10 | 75 | 200 | 80 | 1.6 |
| G6 | 10 | 50 | 200 | 40 | 0.4 |
| Dispatch Method | Abandonment Rate of Wind Power (%) | Generation Cost ($) | Time (s) |
|---|---|---|---|
| Centralized dispatch | 1.9 | 79,309.1 | 14.2 |
| Decentralized dispatch | 1.9 | 80,161.3 | 130.1 |
| Number of Regions | Abandonment Rate of Wind Power (%) | Generation Cost ($) | Time (s) | |||
|---|---|---|---|---|---|---|
| Centralize | Decentralize | Centralize | Decentralize | Centralize | Decentralize | |
| 2 | 2.3 | 2.3 | 1,810,496.6 | 1,839,402.3 | 90.4 | 314.9 |
| 3 | 0 | 0 | 2,912,026.3 | 2,938,421.8 | 352.8 | 462.3 |
| 8 | 0 | 0 | 6,243,526.8 | 6,276,134.5 | 1446.5 | 1269.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Xu, Y.; Wang, S. A Distributed Robust Dispatch Approach for Interconnected Systems with a High Proportion of Wind Power Penetration. Energies 2018, 11, 835. https://doi.org/10.3390/en11040835
Ren J, Xu Y, Wang S. A Distributed Robust Dispatch Approach for Interconnected Systems with a High Proportion of Wind Power Penetration. Energies. 2018; 11(4):835. https://doi.org/10.3390/en11040835
Chicago/Turabian StyleRen, Jianwen, Yingqiang Xu, and Shiyuan Wang. 2018. "A Distributed Robust Dispatch Approach for Interconnected Systems with a High Proportion of Wind Power Penetration" Energies 11, no. 4: 835. https://doi.org/10.3390/en11040835
APA StyleRen, J., Xu, Y., & Wang, S. (2018). A Distributed Robust Dispatch Approach for Interconnected Systems with a High Proportion of Wind Power Penetration. Energies, 11(4), 835. https://doi.org/10.3390/en11040835




