Adaptive Stabilization and Dynamic Performance Preservation of Cascaded DC-DC Systems by Incorporating Low Pass Filters
Abstract
:1. Introduction
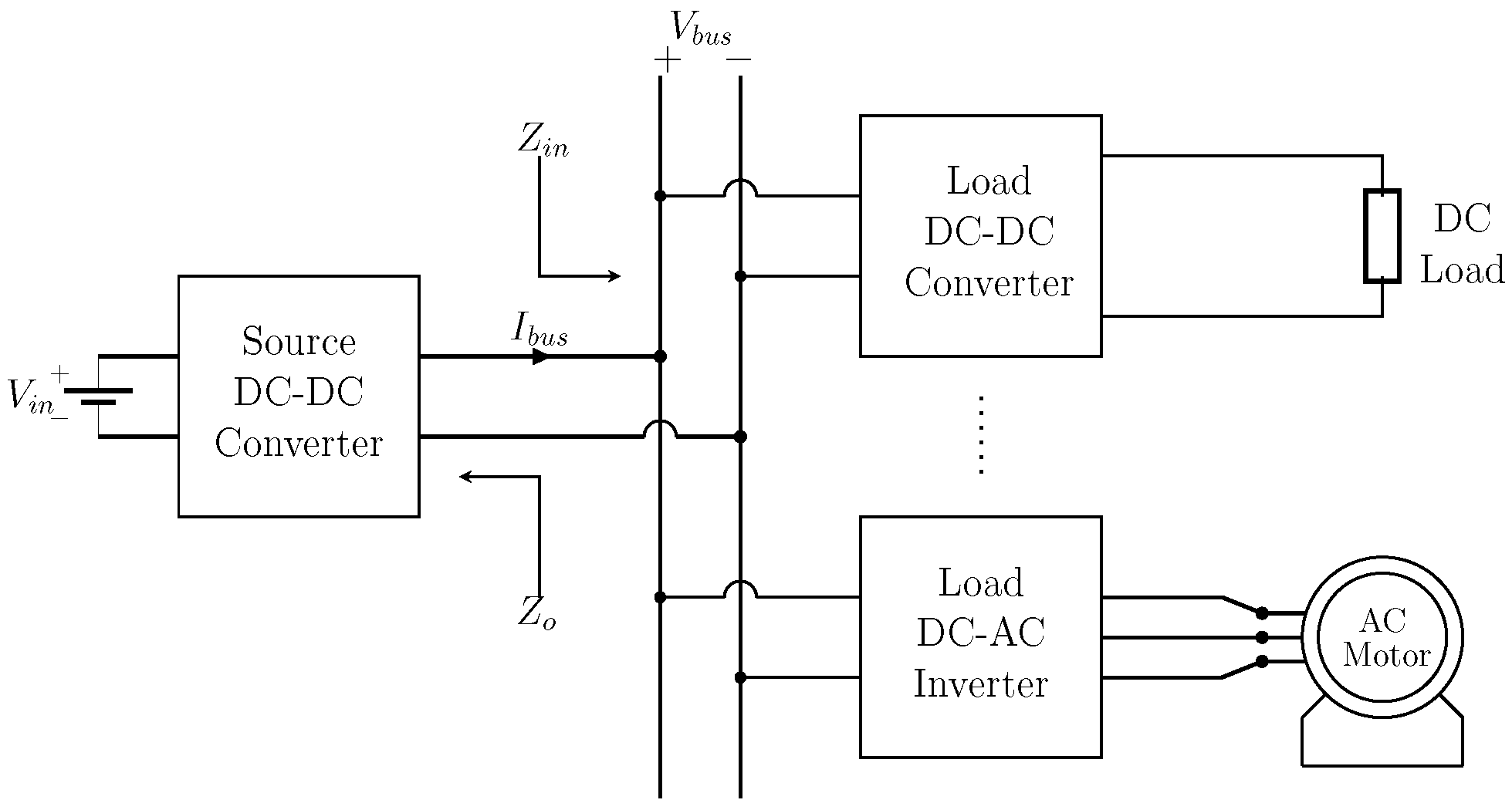
2. Stability and Performance of Cascaded DC-DC Systems
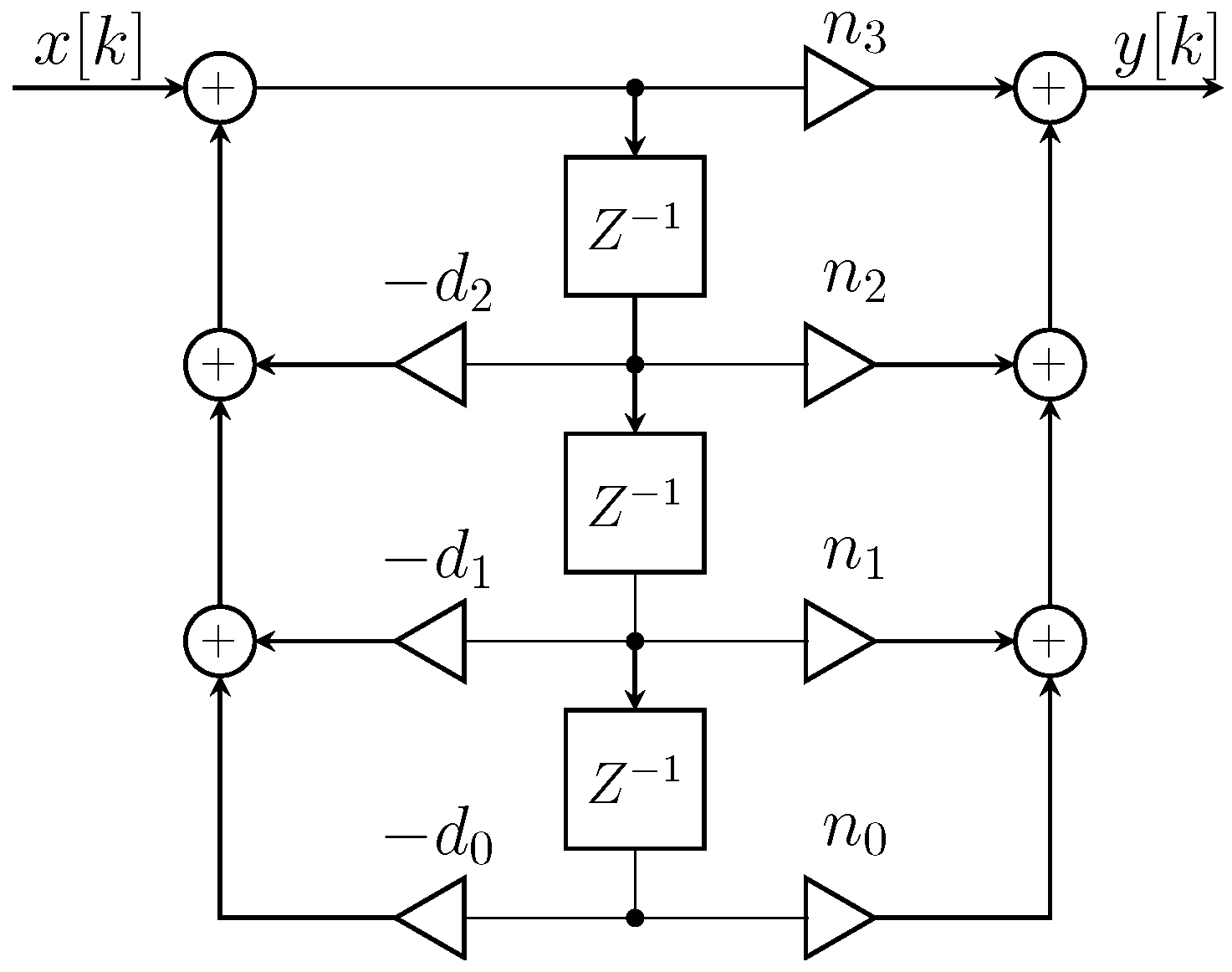
3. The Controller Design
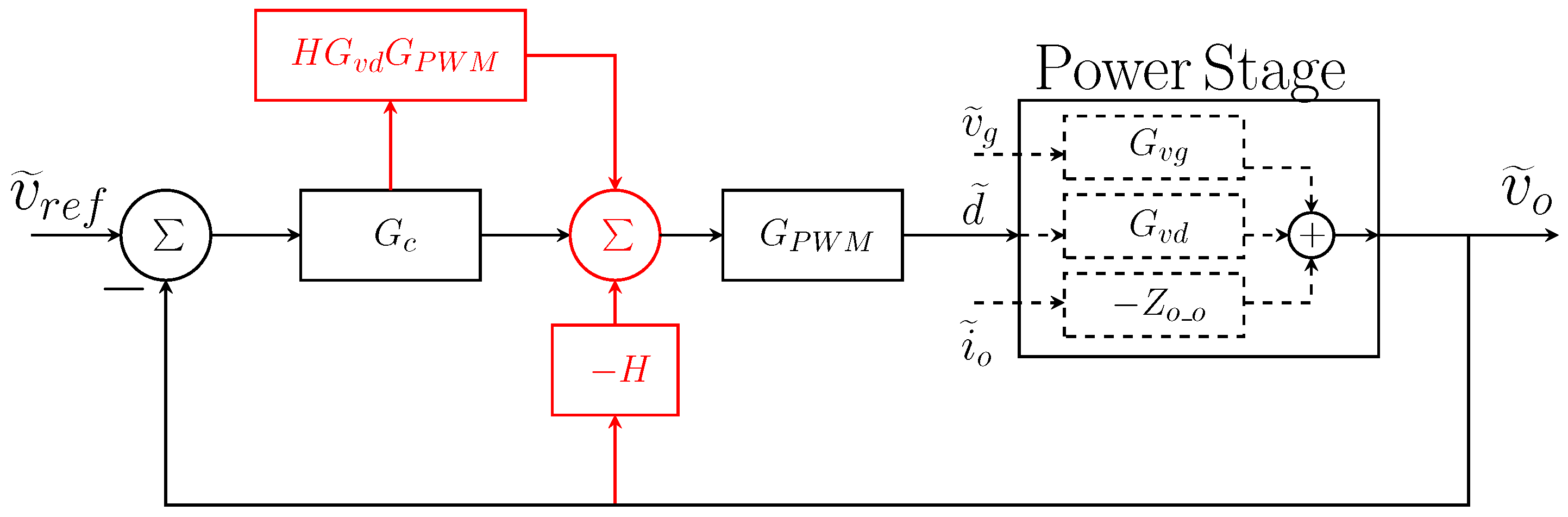
3.1. The Proposed Reshaping
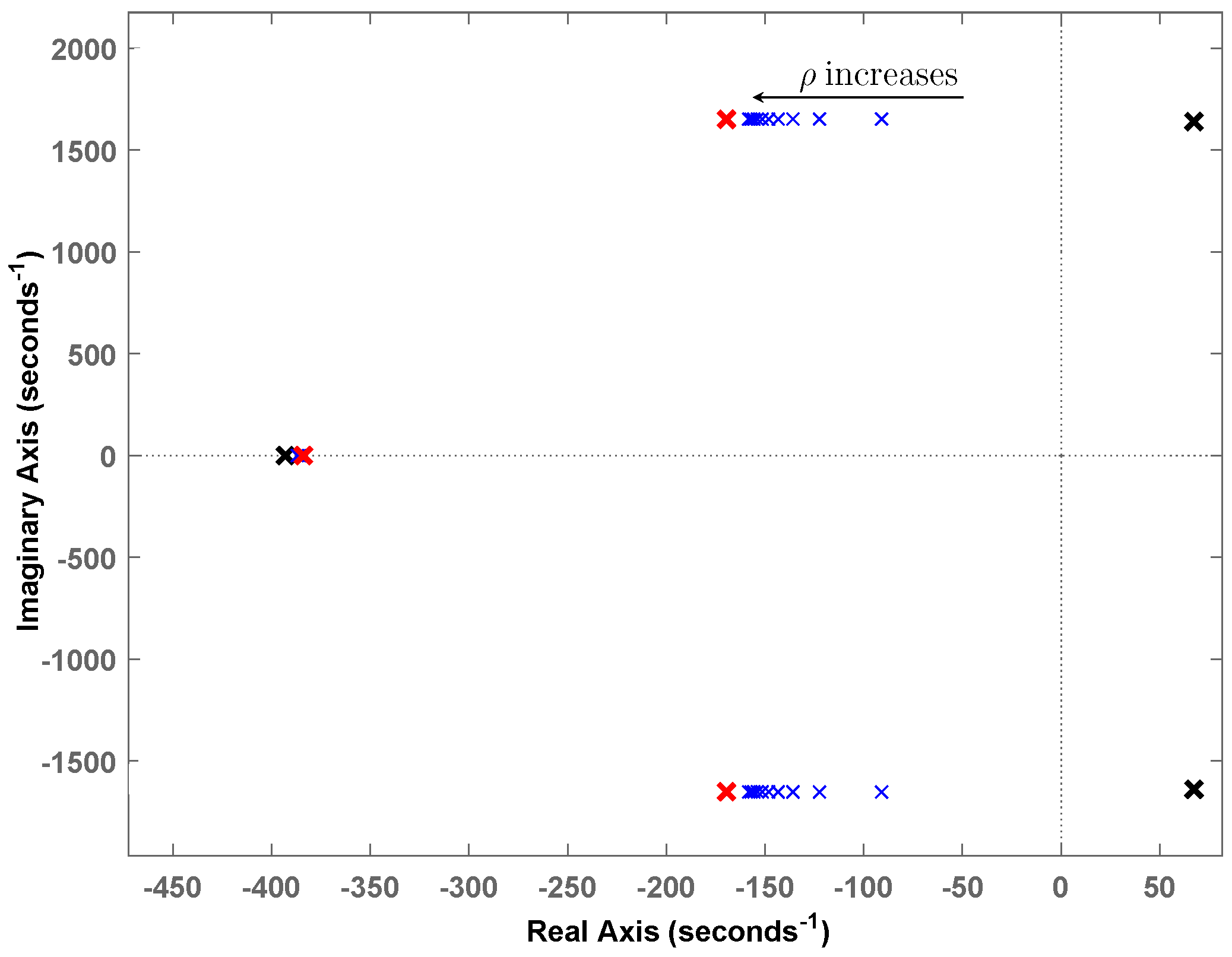
3.2. The Adaptivity
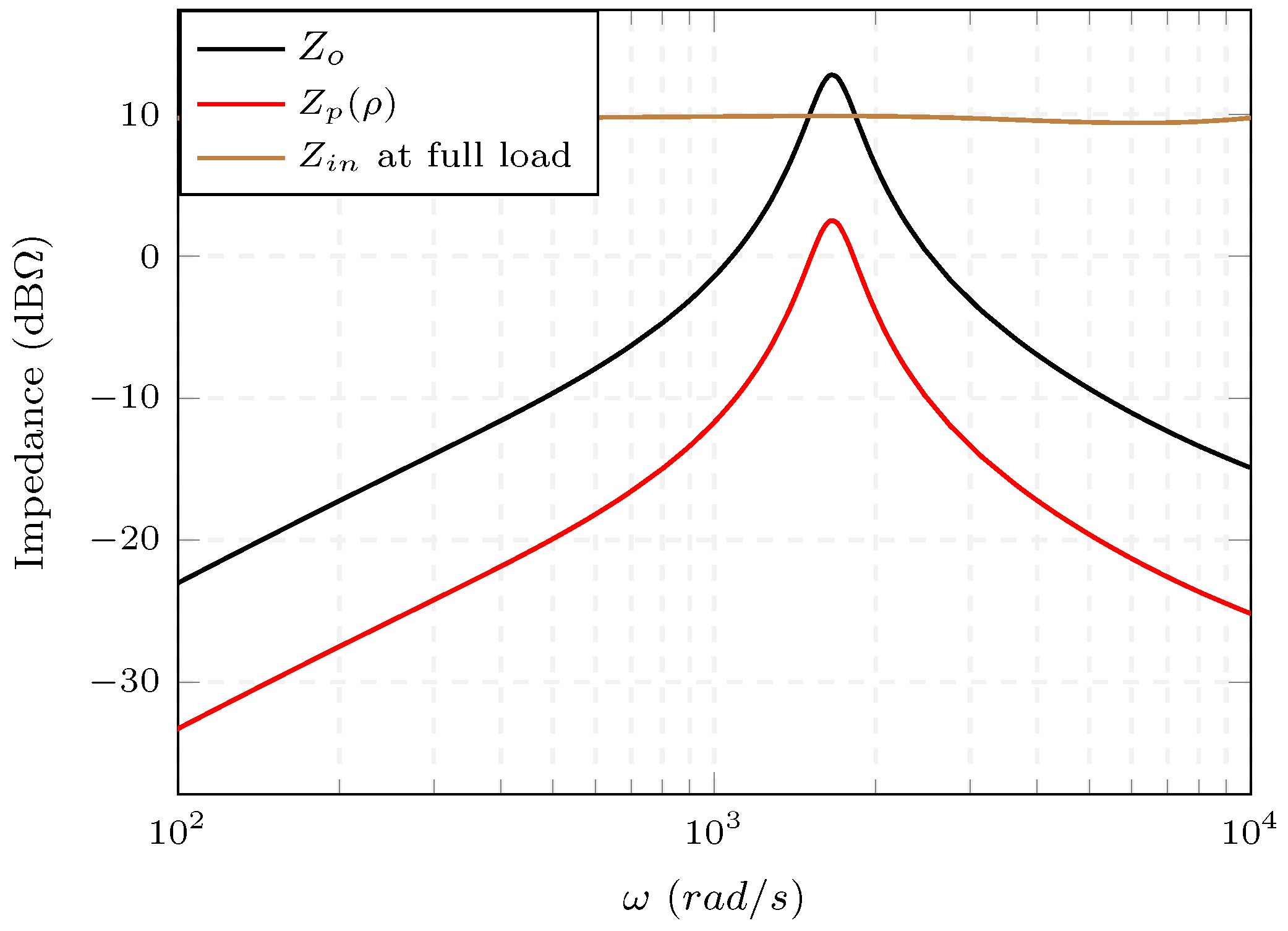
3.3. Determining the Low Pass Filter Corner Frequency
3.4. Modification for Non-Minimum Phase Converters
4. Minimum-Phase Cascaded System
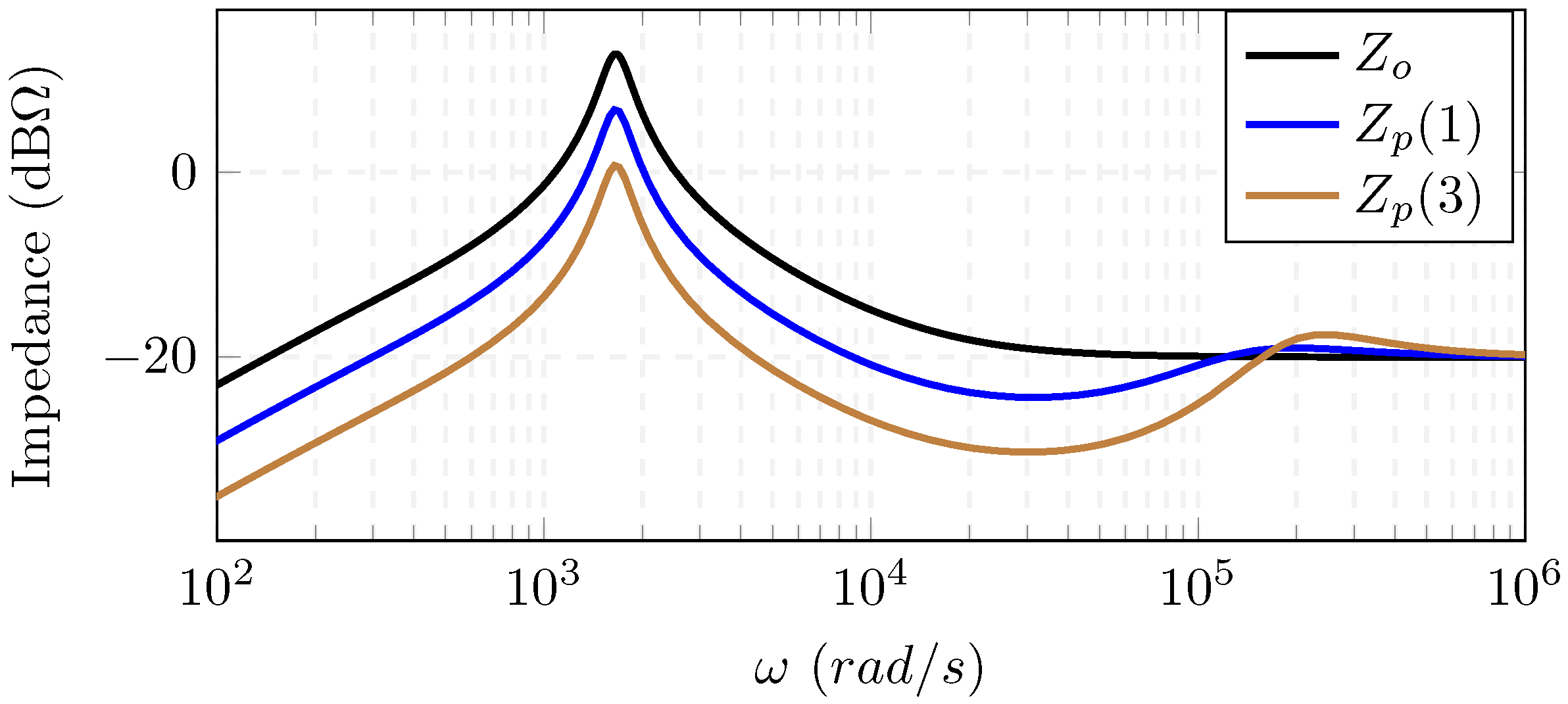
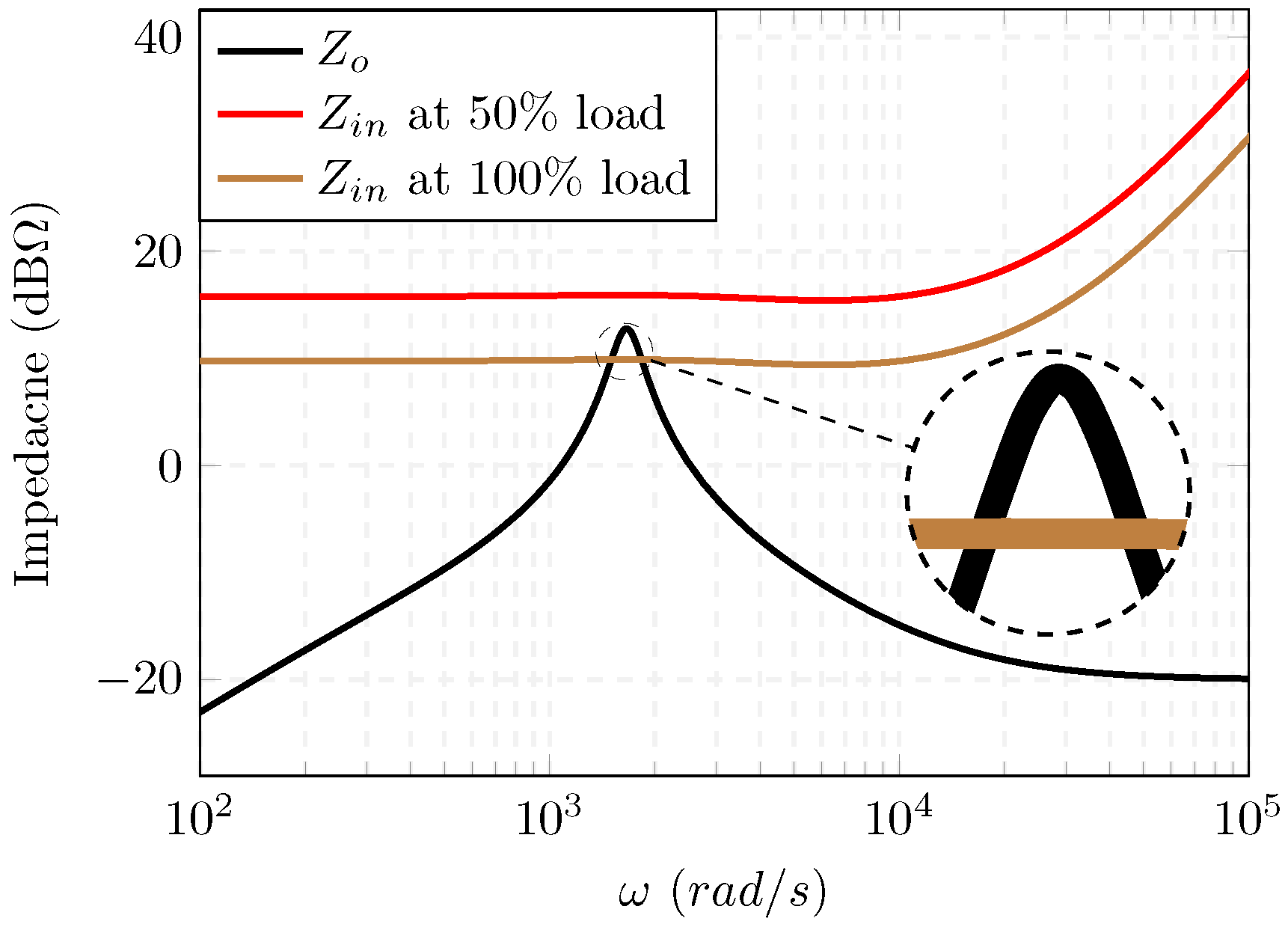
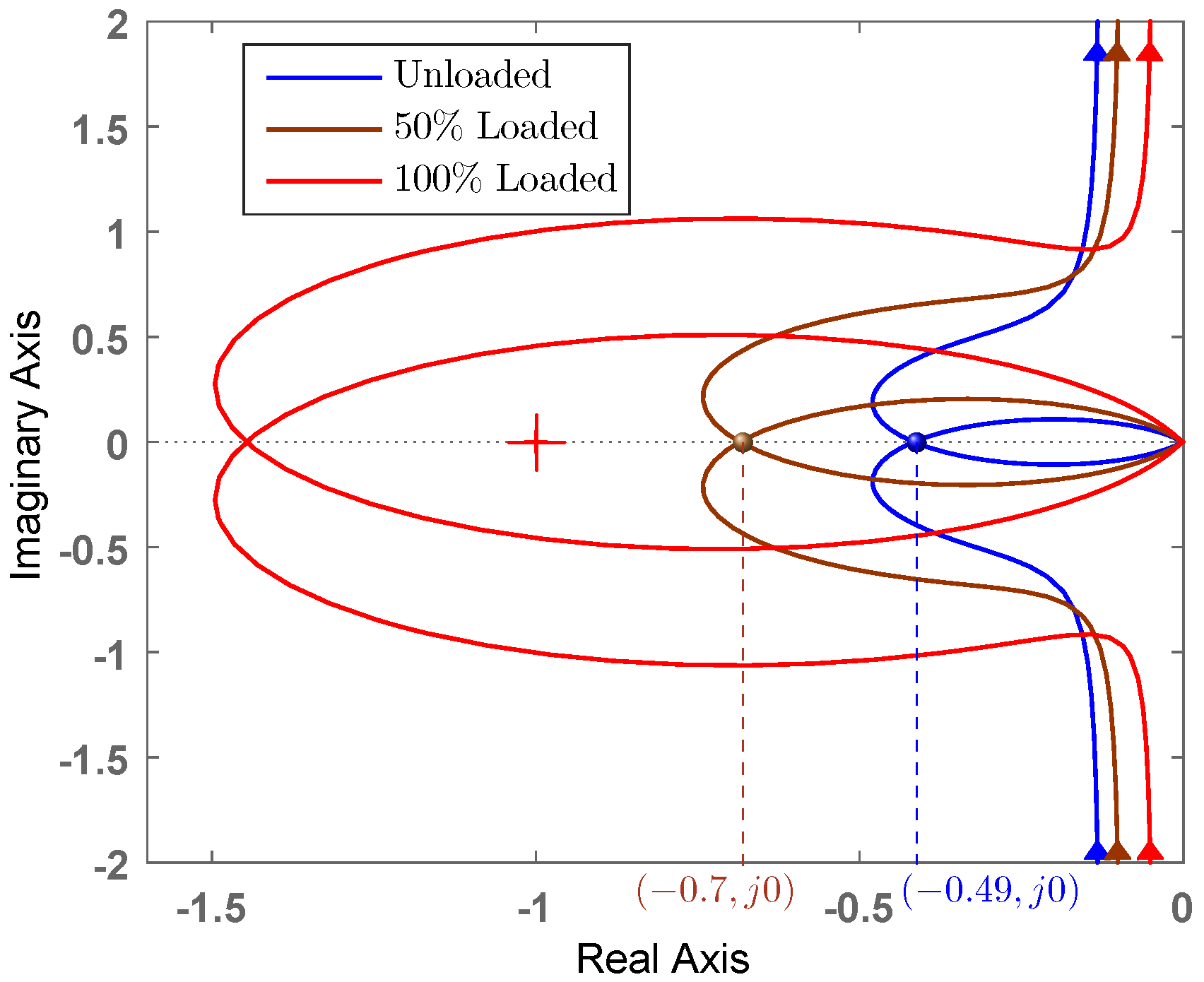
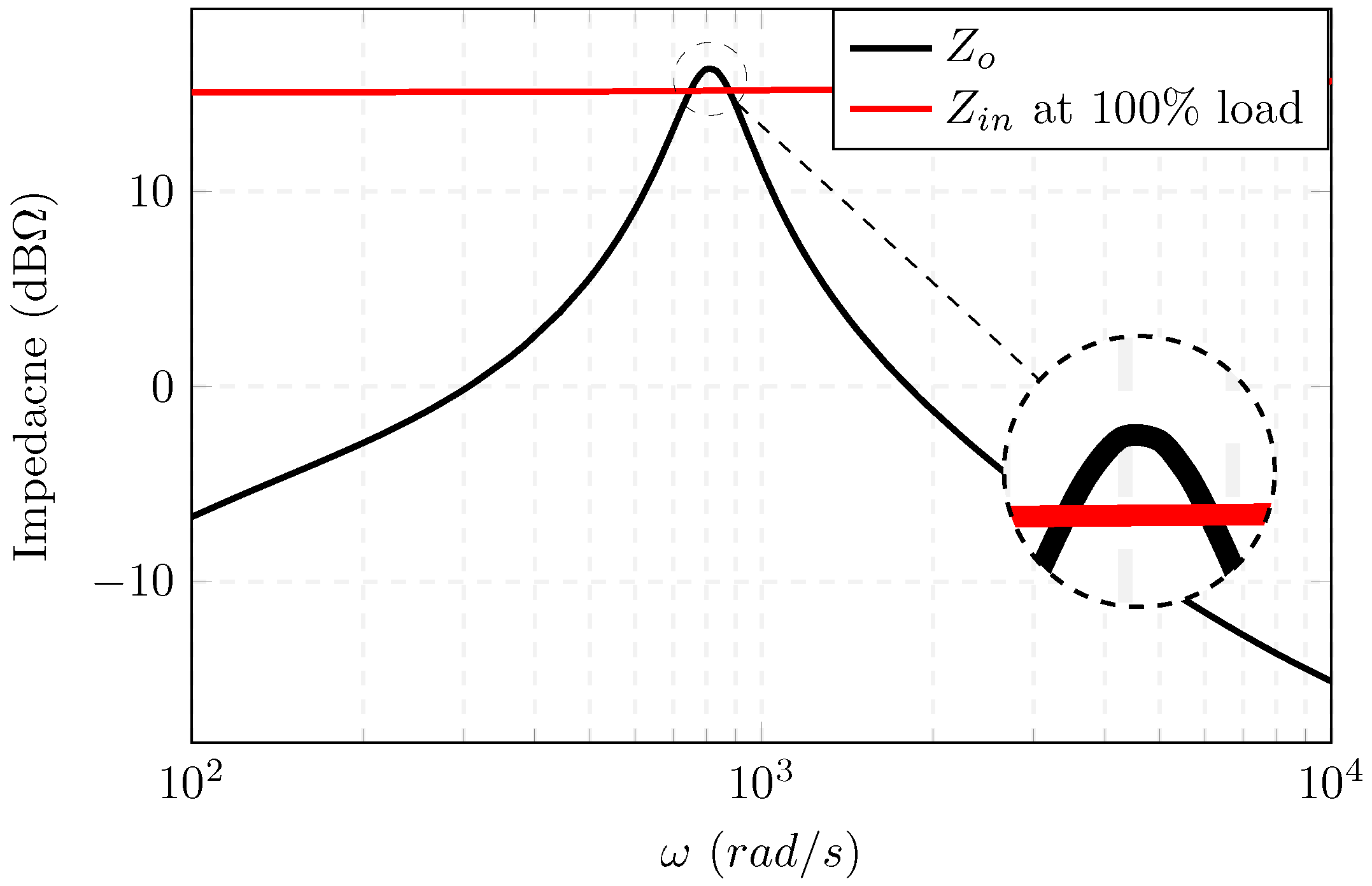
4.1. Theoretical Analysis
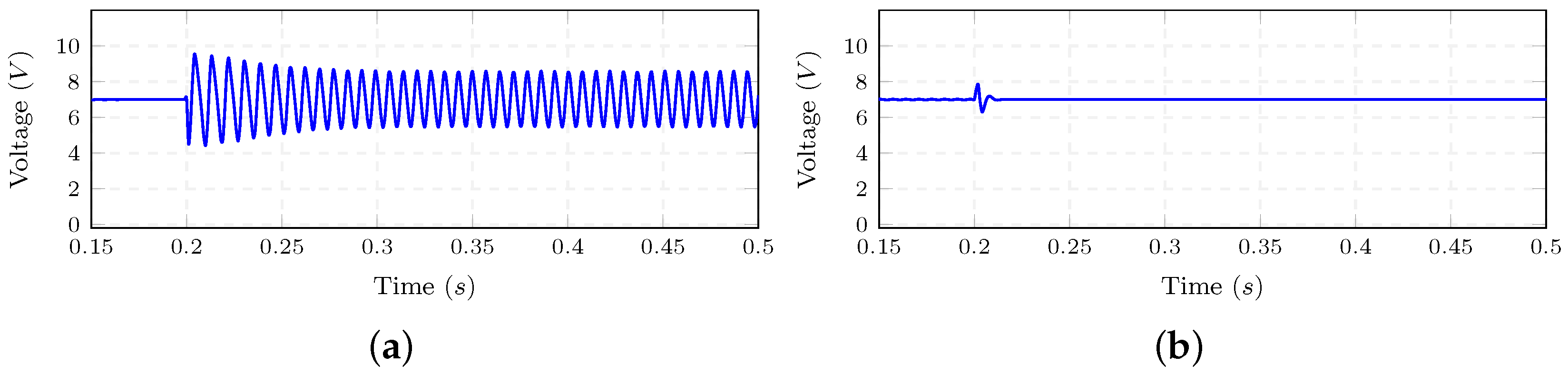
4.2. Simulation Case Studies
4.3. Experiment
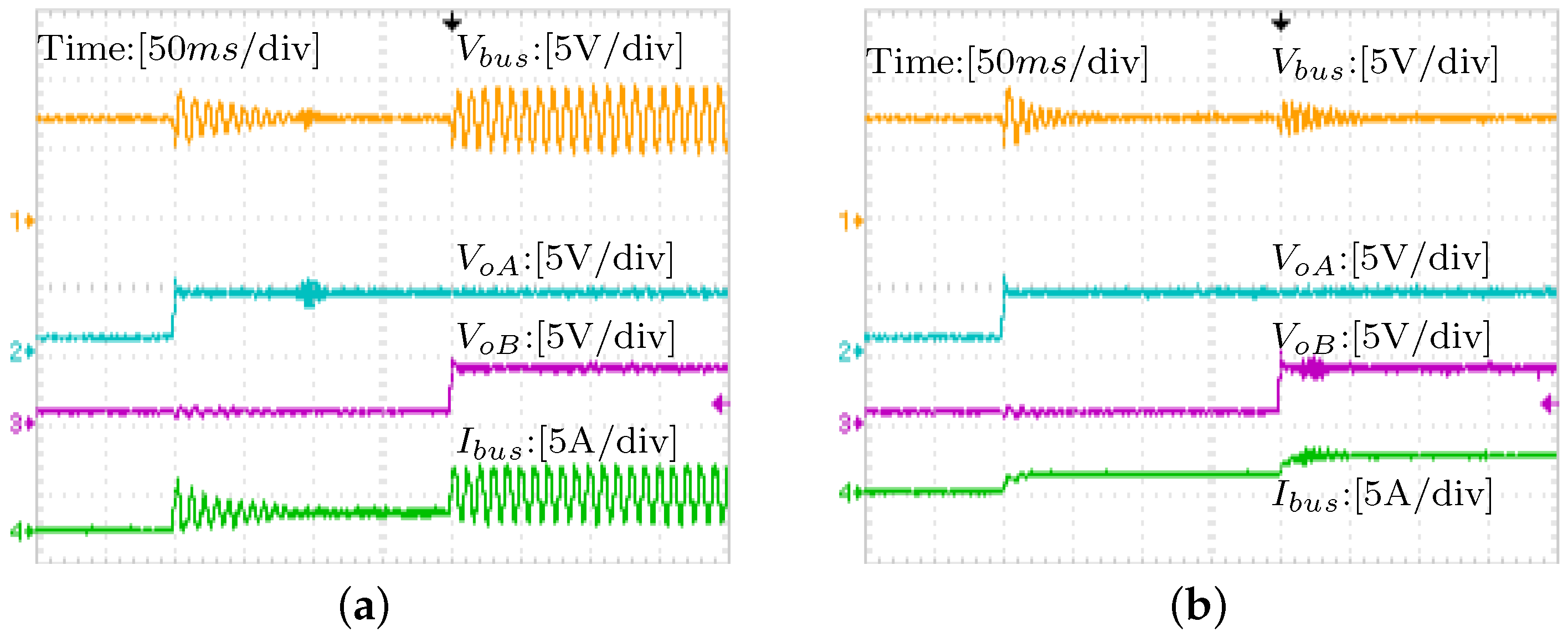
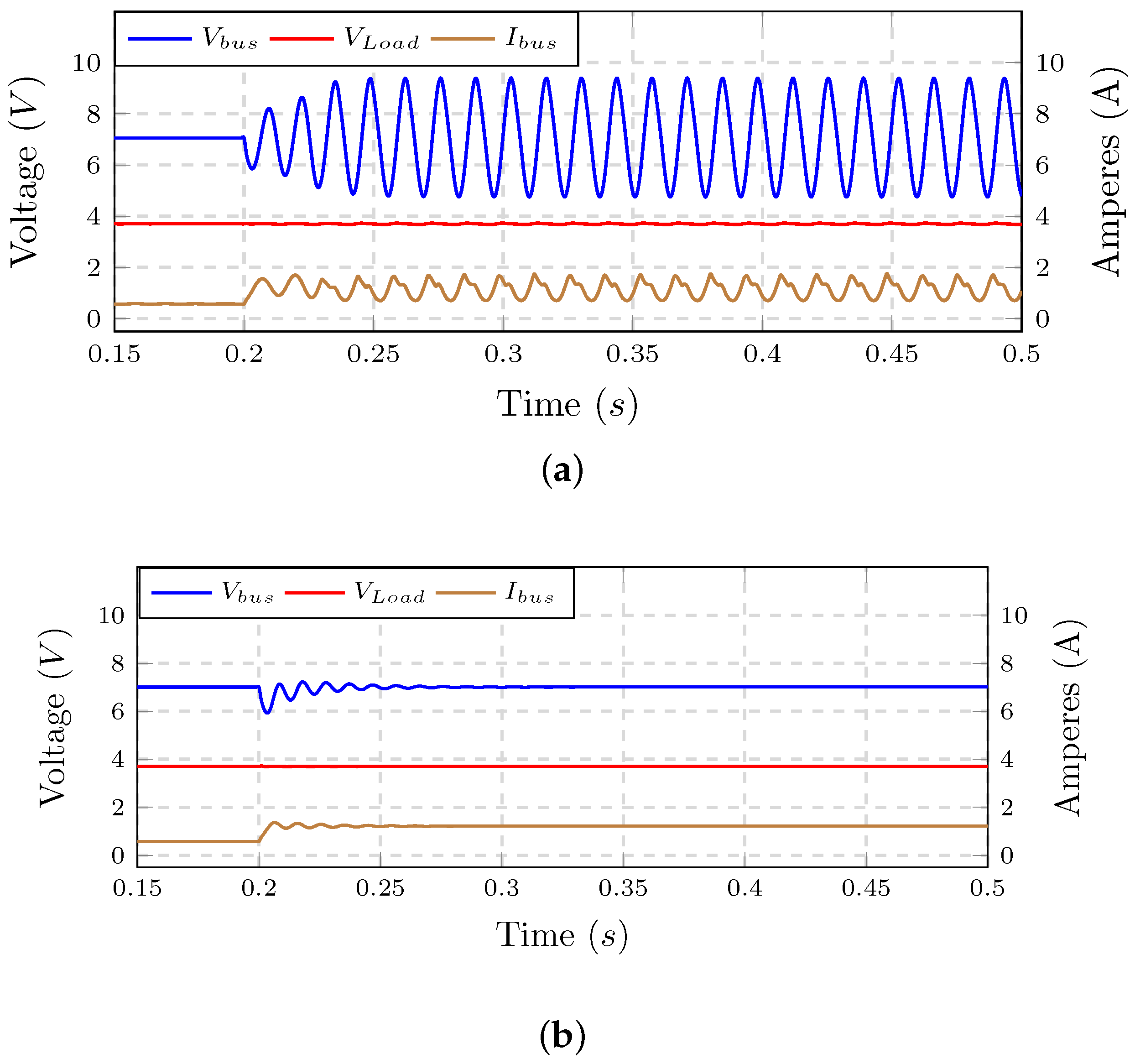
4.3.1. Sequential Connection
4.3.2. Simultaneous Testing
5. Non-Minimum Phase Cascaded System
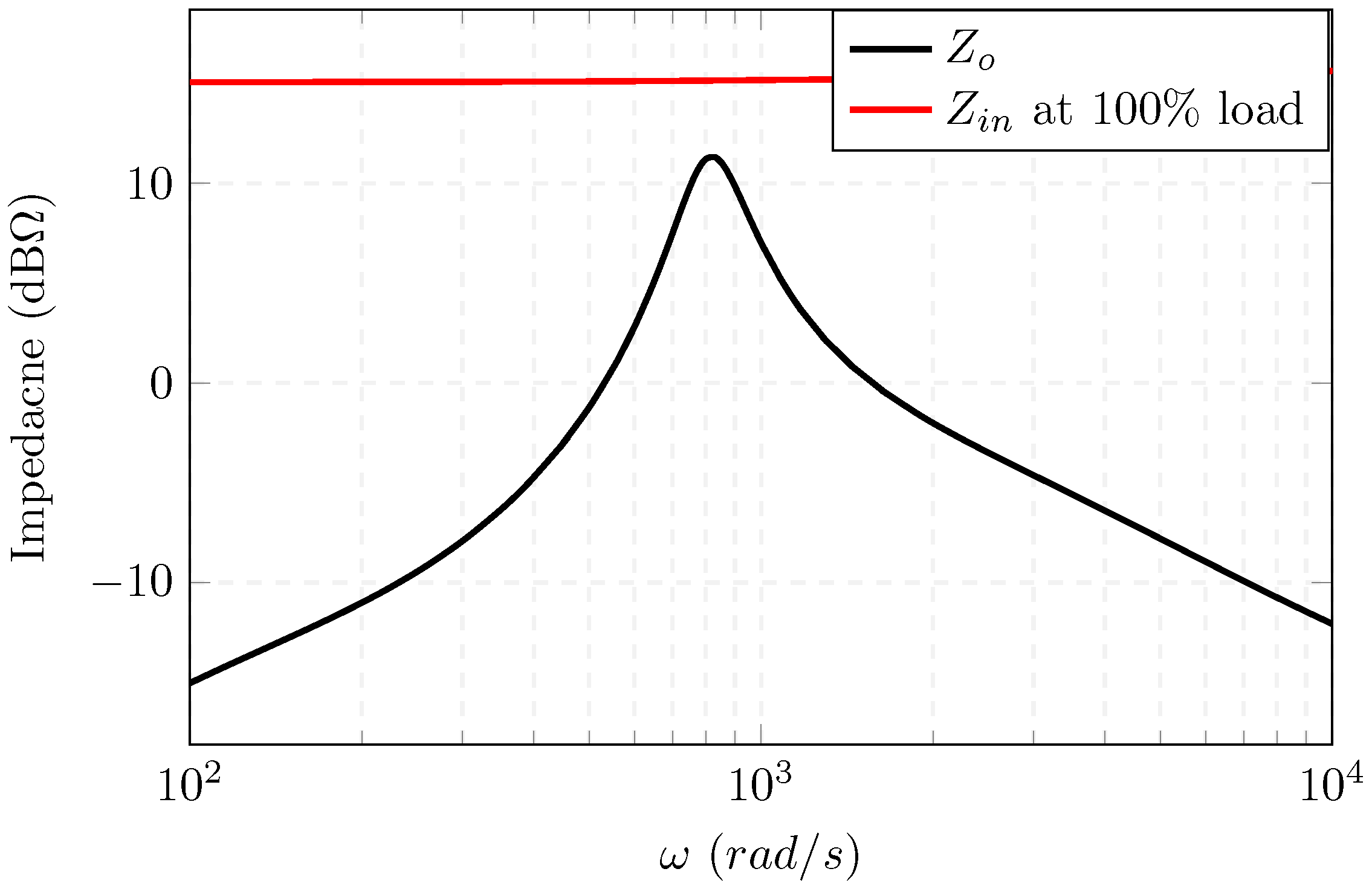
5.1. Theoretical Analysis
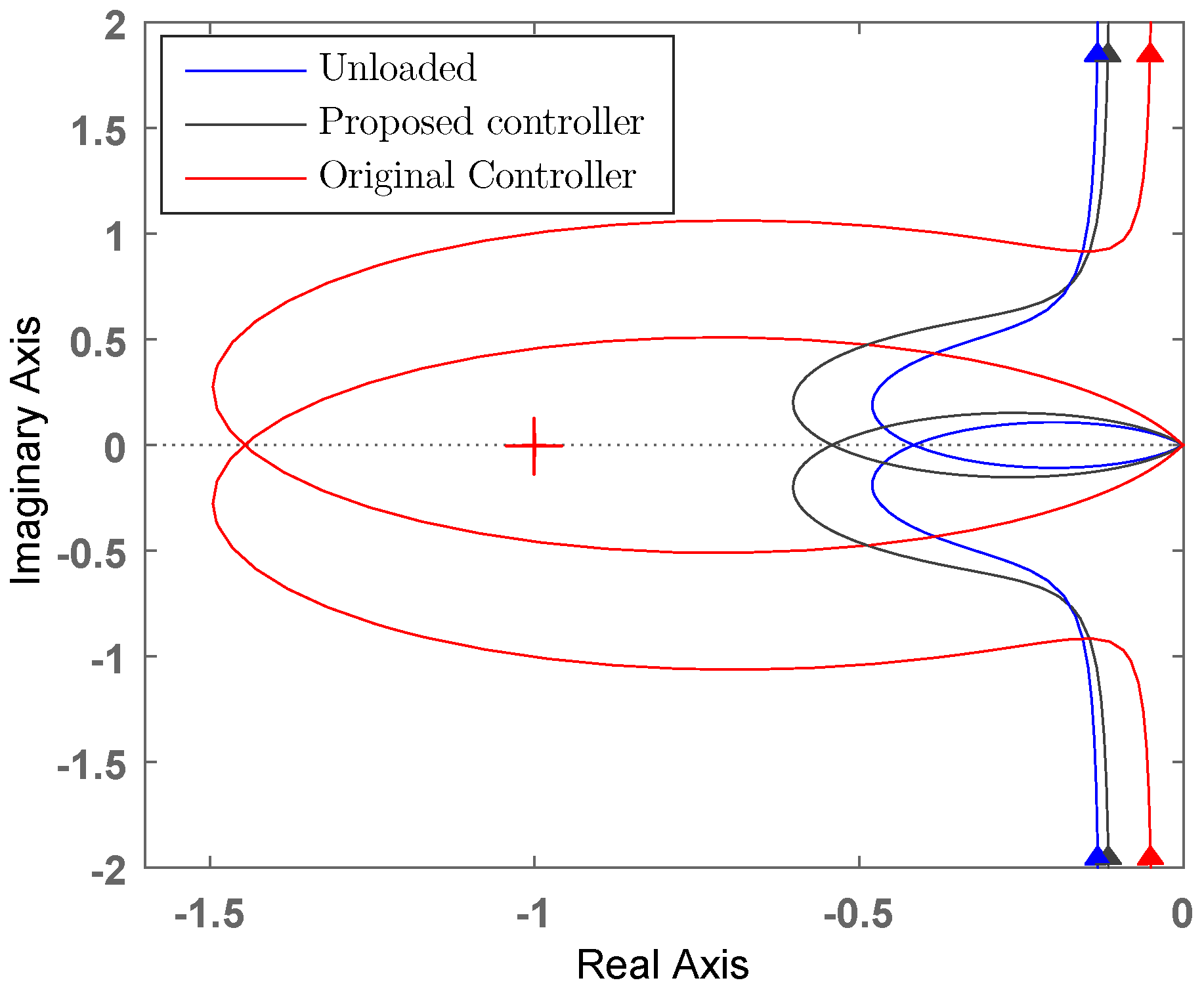
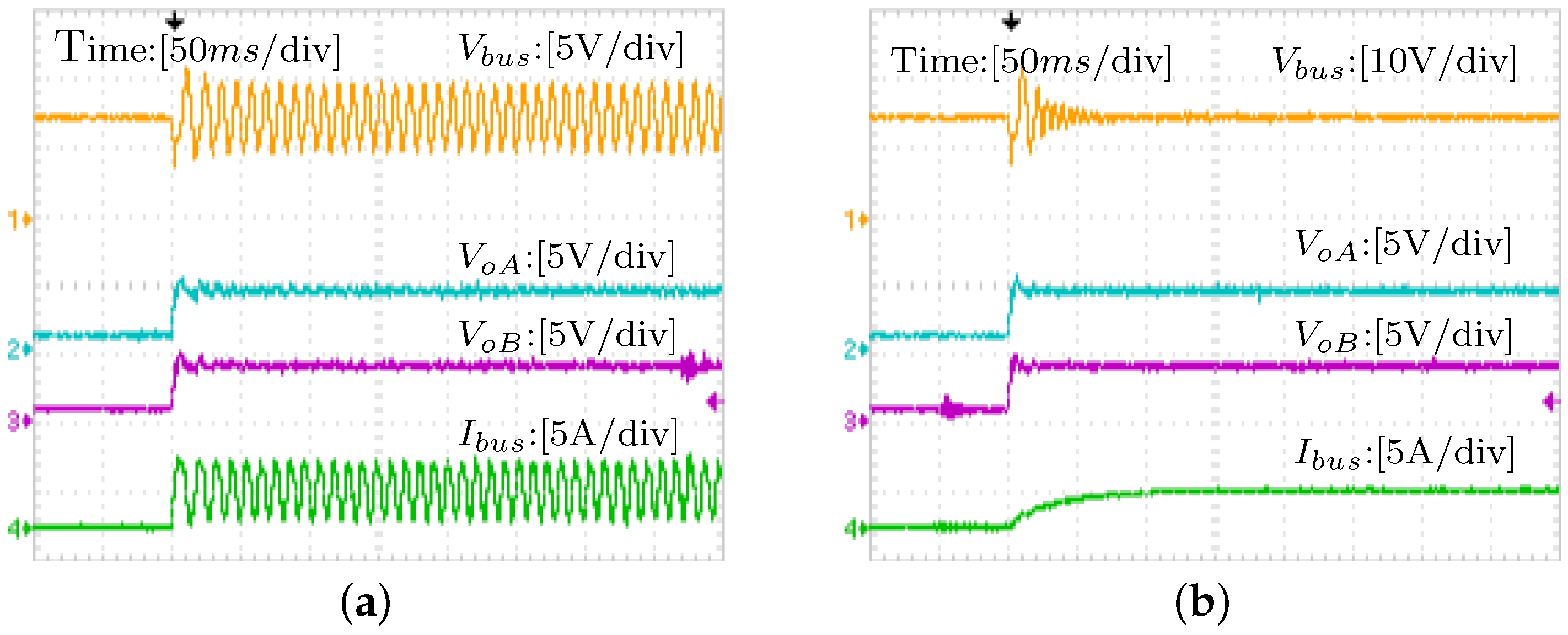
5.2. Simulation Case Studies
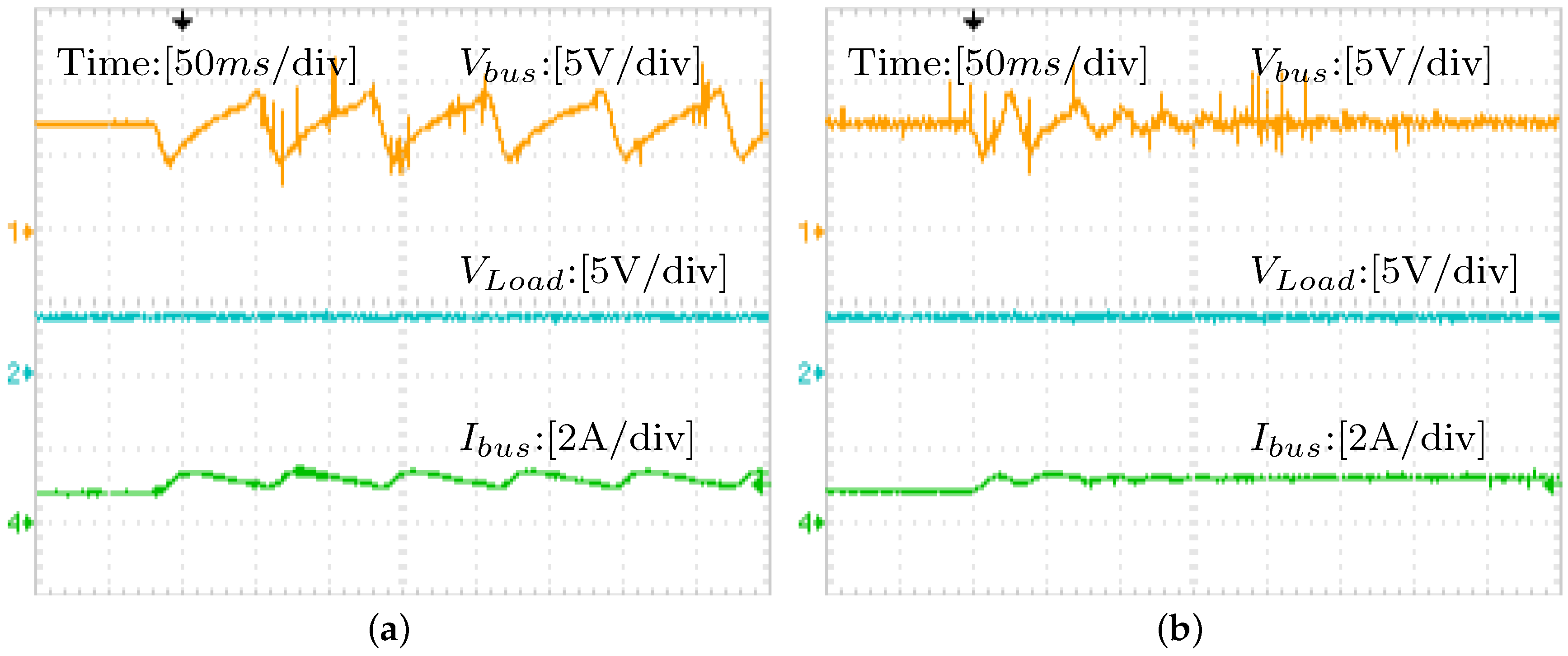
5.3. Experiment
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
References
- Luo, S. A review of distributed power systems part I: DC distributed power system. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 5–16. [Google Scholar] [CrossRef]
- Riccobono, A.; Santi, E. Comprehensive Review of Stability Criteria for DC Power Distribution Systems. IEEE Trans. Ind. Appl. 2014, 50, 3525–3535. [Google Scholar] [CrossRef]
- Yi, Z. Solar Photovoltaic (PV) Distributed Generation Systems—Control and Protection. Ph.D Thesis, The George Washington University, Washington, DC, USA, 2017. [Google Scholar]
- Ahmadi, R. Dynamic Modeling, Stability Analysis, and Controller Design for DC Distribution Systems. Ph.D Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2013. [Google Scholar]
- Muroyama, S.; Sakakibara, K.; Yamashita, T. Transient Voltage Analysis of DC Power Distribution Systems. In Proceedings of the Fifth International Telecommunications Energy Conference, 1983, INTELEC ’83, Tokyo, Japan, 18–21 October 1983; pp. 315–321. [Google Scholar]
- Emadi, A.; Ehsani, M.; Miller, J.M. Vehicular Electric Power Systems: Land, Sea, Air, and Space Vehicles; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Yi, Z.; Etemadi, A.H. Line-to-Line Fault Detection for Photovoltaic Arrays Based on Multiresolution Signal Decomposition and Two-Stage Support Vector Machine. IEEE Trans. Ind. Electron. 2017, 64, 8546–8556. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Input Filter Considerations in Design and Application of Switching Regulators. IEEE Ind. Appl. Soc. Annu. Meet. 1976, 11, 366–382. [Google Scholar]
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids-Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar] [CrossRef]
- Wildrick, C.M.; Lee, F.C.; Cho, B.H.; Choi, B. A method of defining the load impedance specification for a stable distributed power system. In Proceedings of the 24th Annual IEEE Power Electronics Specialists Conference, 1993. PESC ’93 Record, Seattle, WA, USA, 20–24 June 1993; pp. 826–832. [Google Scholar]
- Feng, X.; Ye, Z.; Xing, K.; Lee, F.C.; Borojevic, D. Impedance specification and impedance improvement for DC distributed power system. In Proceedings of the 30th Annual IEEE, Power Electronics Specialists Conference (PESC 99), Charleston, SC, USA, 1 July 1999; Volume 2, pp. 889–894. [Google Scholar]
- Sudhoff, S.D.; Glover, S.F.; Lamm, P.T.; Schmucker, D.H.; Delisle, D.E. Admittance space stability analysis of power electronic systems. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 965–973. [Google Scholar] [CrossRef]
- Suntio, T. Dynamic Profile of Switched-Mode Converter: Modeling, Analysis and Control; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Wang, X.; Yao, R.; Rao, F. Three-step impedance criterion for small-signal stability analysis in two-stage DC distributed power systems. IEEE Power Electron. Lett. 2003, 1, 83–87. [Google Scholar] [CrossRef]
- Riccobono, A.; Santi, E. A novel Passivity-Based Stability Criterion (PBSC) for switching converter DC distribution systems. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 2560–2567. [Google Scholar]
- Hankaniemi, M. Dynamical Profile of Switched-Mode Converter—Fact or Fiction? Ph.D Thesis, Tampere University of Technology, Tampere, Finland, 2007. [Google Scholar]
- Cai, W.; Yi, F.; Cosoroaba, E.; Fahimi, B. Stability Optimization Method Based on Virtual Resistor and Nonunity Voltage Feedback Loop for Cascaded DC DC Converters. IEEE Trans. Ind. Appl. 2015, 51, 4575–4583. [Google Scholar] [CrossRef]
- Wu, M.; Lu, D.D.C. A Novel Stabilization Method of LC Input Filter With Constant Power Loads Without Load Performance Compromise in DC Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4552–4562. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Zhong, Q.C. Improving the Stability of Cascaded DC/DC Converter Systems via Shaping the Input Impedance of the Load Converter With a Parallel or Series Virtual Impedance. IEEE Trans. Ind. Electron. 2015, 62, 7499–7512. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Kim, H.; Tse, C.K. Adaptive Active Capacitor Converter for Improving Stability of Cascaded DC Power Supply System. IEEE Trans. Power Electron. 2013, 28, 1807–1816. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Q.C.; Ming, W.L. Stabilization of a Cascaded DC Converter System via Adding a Virtual Adaptive Parallel Impedance to the Input of the Load Converter. IEEE Trans. Power Electron. 2016, 31, 1826–1832. [Google Scholar] [CrossRef]
- Ahmadi, R.; Ferdowsi, M. Improving the Performance of a Line Regulating Converter in a Converter-Dominated DC Microgrid System. IEEE Trans. Smart Grid 2014, 5, 2553–2563. [Google Scholar] [CrossRef]
- Ahmadi, R.; Ferdowsi, M. Controller design method for a cascaded converter system comprised of two DC-DC converters considering the effects of mutual interactions. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1838–1844. [Google Scholar]
- Erickson, R.W.; Dragan, M. Fundamentals of Power Electronics; Kluwer Academic: Norwell, MA, USA, 2001. [Google Scholar]
- Basso, C.P. Designing Control Loops for Linear and Switching Power Supplies: A Tutorial Guide; Artech House: Norwood, MA, USA, 2012. [Google Scholar]
- Ang, S.S. Power-Switching Converters; M. Dekker: New York, NY, USA, 1995. [Google Scholar]
- Ahmadi, R.; Paschedag, D.; Ferdowsi, M. Analyzing stability issues in a cascaded converter system comprised of two voltage-mode controlled dc-dc converters. In Proceedings of the 2011 Twenty-Sixth Annual IEEE, Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 1769–1775. [Google Scholar]
- Wildrick, C.M. Stability of Distributed Power Supply Systems. Ph.D Thesis, Virginia Polytechnic and State University, Blacksburg, VA, USA, 1993. [Google Scholar]
- Pidaparthy, S.K.; Choi, B. Stability analysis of PWM converters connected to general load subsystems. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 1033–1040. [Google Scholar]
- Cao, L.; Loo, K.H.; Lai, Y.M. Systematic Derivation of a Family of Output-Impedance Shaping Methods for Power Converters—A Case Study Using Fuel Cell-Battery-Powered Single-Phase Inverter System. IEEE Trans. Power Electron. 2015, 30, 5854–5869. [Google Scholar] [CrossRef]
- Cao, L.; Loo, K.H.; Lai, Y.M. Output-Impedance Shaping of Bidirectional DAB DC - DC Converter Using Double-Proportional-Integral Feedback for Near-Ripple-Free DC Bus Voltage Regulation in Renewable Energy Systems. IEEE Trans. Power Electron. 2016, 31, 2187–2199. [Google Scholar] [CrossRef]
- Aldhaheri, A.; Etemadi, A. Impedance Decoupling in DC Distributed Systems to Maintain Stability and Dynamic Performance. Energies 2017, 10, 470. [Google Scholar] [CrossRef]
- Braatz, R.D. On Internal Stability and Unstable Pole-Zero Cancellations [Feedback]. IEEE Control Syst. 2012, 32, 15–16. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, Binder Version; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sudhoff, S.D.; Corzine, K.A.; Glover, S.F.; Hegner, H.J.; Robey, H.N. DC link stabilized field oriented control of electric propulsion systems. IEEE Trans. Energy Conver. 1998, 13, 27–33. [Google Scholar] [CrossRef]
- Manolakis, D.G.; Ingle, V.K. Applied Digital Signal Processing: Theory and Practice; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]







| Parameter | Source | Load A | Load B |
|---|---|---|---|
| 20 | 7 | 7 | |
| 7 | 4 | 4 | |
| 510 | 390 | 400 | |
| 0.05 | 0.01 | 0.04 | |
| 697 | 697 | 697 | |
| 0.1 | 0.1 | 0.1 | |
| ⋯ | 2 | 2 | |
| 100 | |||
| 1 | |||
| Source Controller | |||
| Parameter | Boost | Buck |
|---|---|---|
| 5 | 7 | |
| 7 | 3.6 | |
| 930 | 390 | |
| 0.05 | 0.01 | |
| 697 | 697 | |
| 0.1 | 0.1 | |
| ⋯ | 1.4 | |
| 100 | ||
| 1 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldhaheri, A.; Etemadi, A. Adaptive Stabilization and Dynamic Performance Preservation of Cascaded DC-DC Systems by Incorporating Low Pass Filters. Energies 2018, 11, 440. https://doi.org/10.3390/en11020440
Aldhaheri A, Etemadi A. Adaptive Stabilization and Dynamic Performance Preservation of Cascaded DC-DC Systems by Incorporating Low Pass Filters. Energies. 2018; 11(2):440. https://doi.org/10.3390/en11020440
Chicago/Turabian StyleAldhaheri, Ahmed, and Amir Etemadi. 2018. "Adaptive Stabilization and Dynamic Performance Preservation of Cascaded DC-DC Systems by Incorporating Low Pass Filters" Energies 11, no. 2: 440. https://doi.org/10.3390/en11020440





