Improved Adaptive Backstepping Sliding Mode Control of Static Var Compensator
Abstract
:1. Introduction
2. Model of MSIB System with SVC and Control Objective
2.1. Model of SMIB System with SVC
2.2. The Statement of Problem and Control Objective
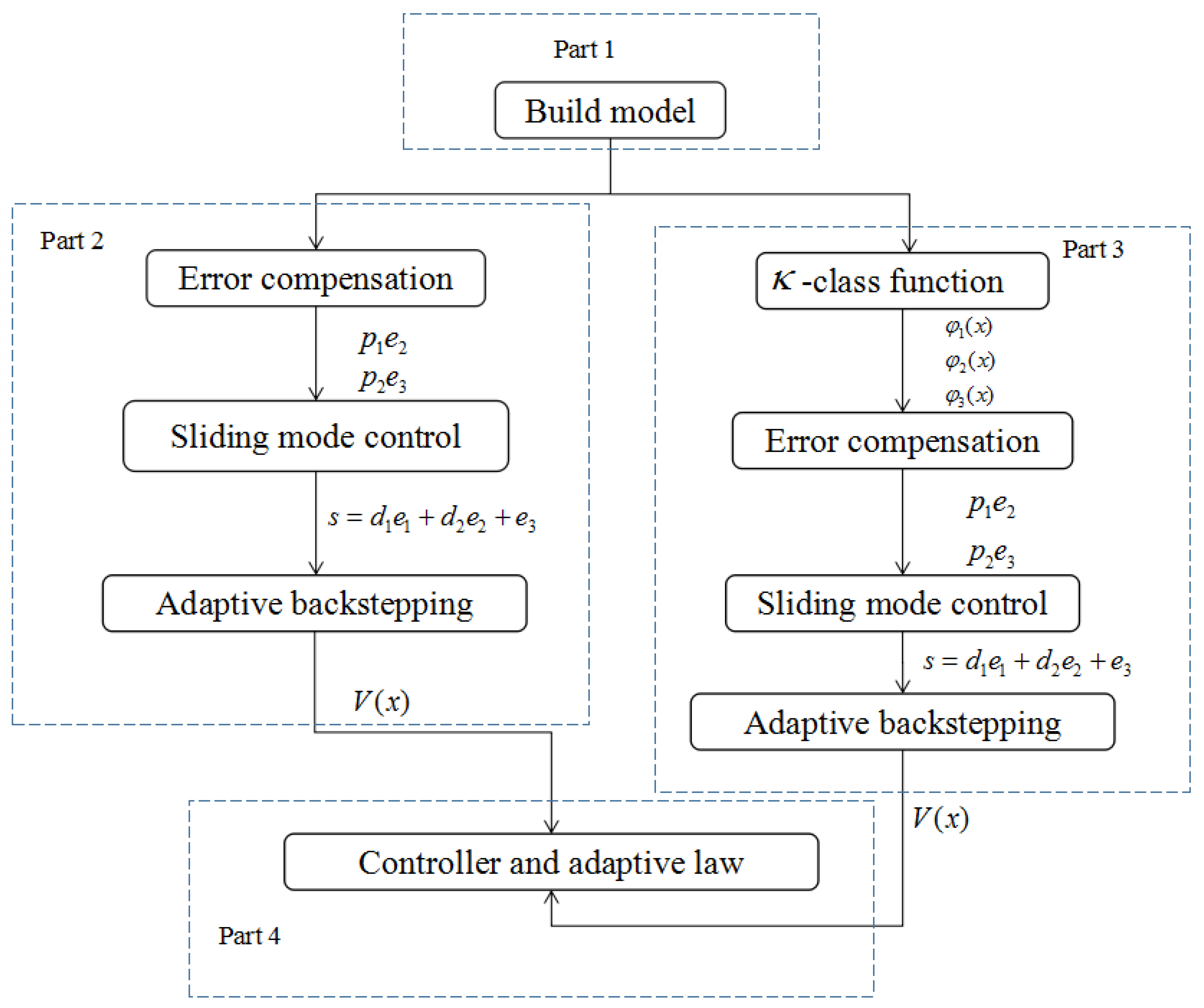
3. Design of Adaptive Backstepping Controller Based on Error Compensation
4. Design of Adaptive Backstepping Sliding Mode Variable Structure Controller Based on Error Compensation
- (1)
- (2)
- (3)
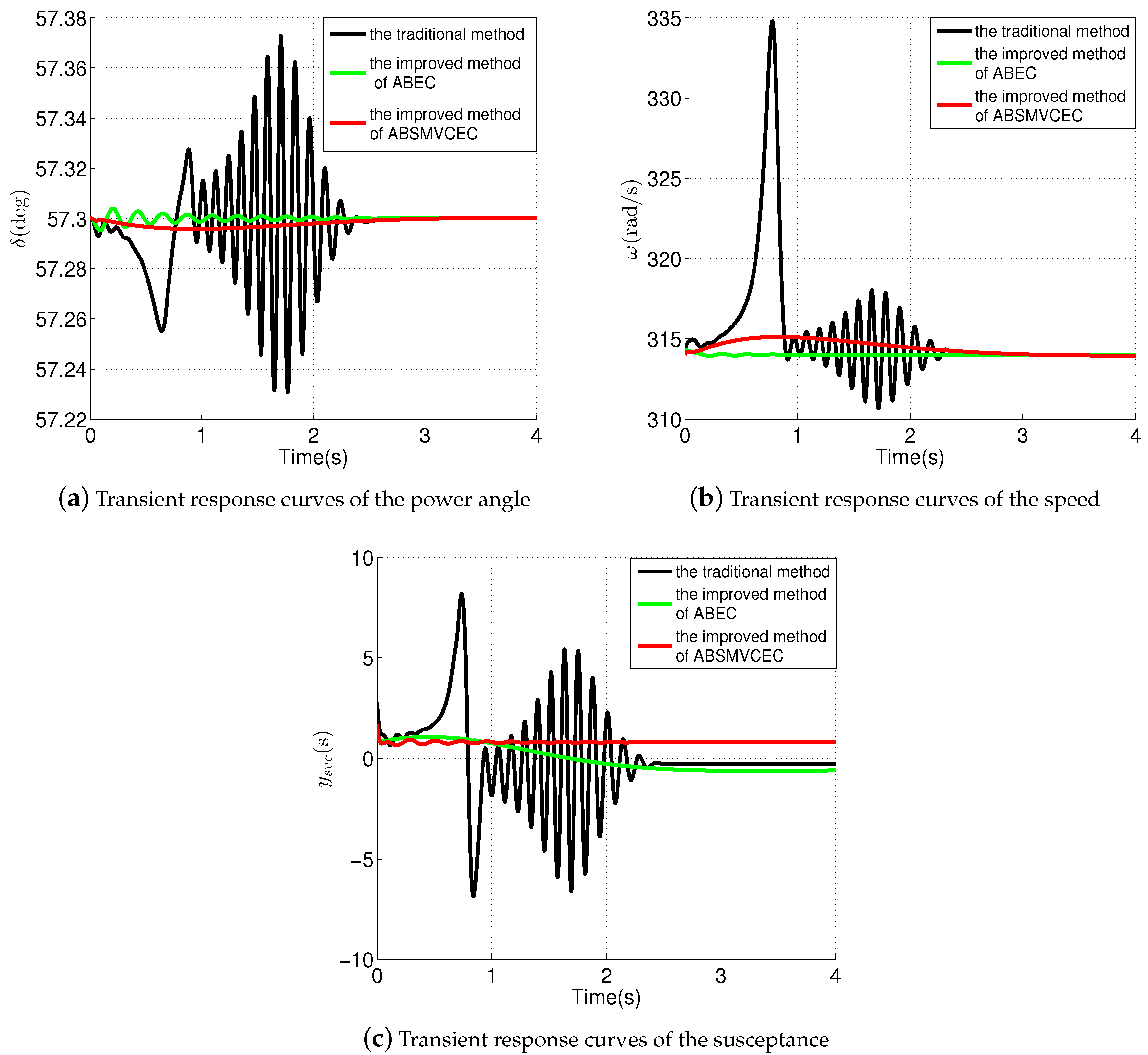
5. Simulation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SVC | Static Var Compensator |
| ABSMVCEC | Adaptive Backstepping Sliding Mode Variable Control Based On Error Compensation |
| PID | Proportion Integral And Differential |
| ABEC | Adaptive Backstepping Method Based On Error Compensation |
| SMIB | Single Machine Infinite Bus |
References
- Benidris, M.; Elsaiah, S.; Sulaeman, S.; Mitra, J. Transient Stability of Distributed Generators in the Presence of Energy Storage Devices. In Proceedings of the 44th IEEE North American Power Symposium, Champaign, IL, USA, 9–11 September 2012. [Google Scholar]
- Caciotta, M.; Leccese, F.; Trifiro, A. From power quality to perceived power quality. In Proceedings of the IASTED International Conference on Energy and Power Systems, Chiang Mai, Thailand, 29–31 March 2006; pp. 94–102. [Google Scholar]
- De Araujo, V.V.; Simas Filho, E.F.; Oliveira, A.; de Oliveira, W.L.A.; Esteves, L.T.C. Integrated circuit for real-time poly-phase power quality monitoring. Microelectron. J. 2018, 79, 57–63. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; Et Power Electronics; McGraw-Hill Education: New York, NY, USA, 2007; Volume 7, pp. 100–103. [Google Scholar]
- Su, J.; Chen, C. Study on SVC control for power system with nonlinear loads. Autom. Electri. Power Syst. 2002, 26, 12–15. [Google Scholar]
- Li, S.; Su, Z. Static state feedback control for saddle-node bifurcation in a simple power system. In Proceedings of the International Conference on Power Electronics and Intelligent Transportation System, Shenzhen, China, 19–20 December 2010; pp. 158–160. [Google Scholar]
- Hwang, Y.H.; Park, K.K.; Yang, H.W. Robust adaptive backstepping control for efficiency optimization of induction motors with uncertainties. In Proceedings of the ieee International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 878–883. [Google Scholar]
- Okano, K.; Hagino, K. Adaptive control design approximating solution of Hamilton-Jacobi-Bellman equation for nonlinear strict-feedback system with uncertainties. In Proceedings of the Annual Conference on Sice Conference, Tokyo, Japan, 20–22 August 2008; pp. 204–208. [Google Scholar]
- Modi, P.K.; Singh, S.P.; Sharma, J.D. Fuzzy neural network based voltage stability evaluation of power systems with SVC. Appl. Soft Comput. 2008, 8, 657–665. [Google Scholar] [CrossRef]
- Dimirovski, G.; Yuan, W.; Wen, L. Adaptive Back-Stepping Design of TCSC Robust Nonlinear Control for Power Systems. Intell. Autom. Soft Comput. 2006, 12, 75–87. [Google Scholar] [CrossRef]
- Shang, A.L.; Wang, Z. Adaptive backstepping second order sliding mode control of non-linear systems. Int. J. Model. Identif. Control 2013, 19, 195–201. [Google Scholar] [CrossRef]
- Shi, C.X.; Yang, G.H.; Li, X.J. Robust adaptive backstepping control for hierarchical multi-agent systems with signed weights and system uncertainties. IET Control Theory Appl. 2017, 11, 2743–2752. [Google Scholar] [CrossRef]
- Mitra, A.; Mukherjee, M.; Naik, K. Enhancement of power system transient stability using a novel adaptive backstepping control law. In Proceedings of the Third International Conference on Computer, Communication, Control and Information Technology, West-Bengal, India, 7–8 February 2015; pp. 1–5. [Google Scholar]
- Manosa, V.; Ikhouane, F.; Rodellar, J. Control of uncertain non-linear systems via adaptive backstepping. J. Sound Vib. 2005, 280, 657–680. [Google Scholar]
- Wang, H.M.; Huang, T.L.; Tsai, C.M. Power system stabilizer design using adaptive backstepping controller. In Proceedings of the Fifth International Conference on Power Electronics and Drive Systems, Singapore, 17–20 November 2003. [Google Scholar]
- Benayache, R.; Chrifialaoui, L.; Bussy, P. Adaptive backstepping sliding mode control for hydraulic system without overparametrisation. Int. J. Model. Identif. Control 2012, 16, 60–69. [Google Scholar] [CrossRef]
- Sun, L.-Y. Based on the Backstepping Method of Power System Nonlinear Robust Adaptive Control Design; Northeastern University: Boston, MA, USA, 2009; pp. 50–56. [Google Scholar]
- Zhang, T.; Dong, C. Compound control system design based on adaptive backstepping theory. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 902–906. [Google Scholar]
- Mao, J.; Sun, Y.-K.; Wu, G.-Q.; Liu, X.-F. A variable structure robust control method in SVC application for performance improvement. In Proceedings of the 2007 Chinese Control Conference, Harbin, China, 7–11 August 2006; pp. 67–70. [Google Scholar]
- Hagras, A.; Zaid, S.; Ekousy, A.A. Performance comparison of shunt active power filter for interval type-2 fuzzy and adaptive backstepping controllers. Int. J. Model. Identif. Control 2014, 21, 270–287. [Google Scholar] [CrossRef]
- Salma, K.; Nouha, B.; Souhir, S.; Larbi, C.-A.; MBA, K. Transient stability enhancement and voltage regulation in SMIB power system using SVC with PI controller. In Proceedings of the International Conference on Systems and Control, Wuhan, China, 7–9 May 2017; pp. 115–120. [Google Scholar]
- Yimin, L.; Yang, Y.; Li, L. Adaptive Backstepping Fuzzy Control Based on Type-2 Fuzzy System. J. Appl. Math. 2012, 2012, 295–305. [Google Scholar]
- Lin, F.J.; Shen, P.H.; Hsu, S.P. Adaptive backstepping sliding mode control for linear induction motor drive. Proc. Electr. Power Appl. 2002, 149, 184–194. [Google Scholar] [CrossRef]
- Yu, H.; Wang, J.; Deng, B. Adaptive backstepping sliding mode control for chaos synchronization of two coupled neurons in the external electrical stimulation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1344–1354. [Google Scholar] [CrossRef]
- Song, Z.; Sun, K. Adaptive backstepping sliding mode control with fuzzy monitoring strategy for a kind of mechanical system. ISA Trans. 2014, 53, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Zou, T.; Li, S. Adaptive backstepping sliding mode control for leader-follower multi-agent systems. Control Theory Appl. IET 2012, 6, 1109–1117. [Google Scholar] [CrossRef]
- Gong, X.; Hou, Z.C.; Zhao, C.J. Adaptive Backstepping Sliding Mode Trajectory Tracking Control for a Quad-rotor. Int. J. Autom. Comput. 2012, 9, 555–560. [Google Scholar] [CrossRef]
- Dong, L.; Tang, W.C. Adaptive backstepping sliding mode control of flexible ball screw drives with time-varying parametric uncertainties and disturbances. ISA Trans. 2014, 53, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Schilling, K.; Schmid, C. Adaptive Backstepping Sliding Mode Control with Gaussian Networks for a Class of Nonlinear Systems with Mismatched Uncertainties. In Proceedings of the IEEE 2005 and 2005 European Control Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 5504–5509. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Q.; Dong, F.; Shen, X. Improved Adaptive Backstepping Sliding Mode Control of Static Var Compensator. Energies 2018, 11, 2750. https://doi.org/10.3390/en11102750
Su Q, Dong F, Shen X. Improved Adaptive Backstepping Sliding Mode Control of Static Var Compensator. Energies. 2018; 11(10):2750. https://doi.org/10.3390/en11102750
Chicago/Turabian StyleSu, Qingyu, Fei Dong, and Xueqiang Shen. 2018. "Improved Adaptive Backstepping Sliding Mode Control of Static Var Compensator" Energies 11, no. 10: 2750. https://doi.org/10.3390/en11102750



