Multi-Time Scale Model Order Reduction and Stability Consistency Certification of Inverter-Interfaced DG System in AC Microgrid
Abstract
:1. Introduction
2. IIDG Multi-Time Scale Model Based on Droop Control
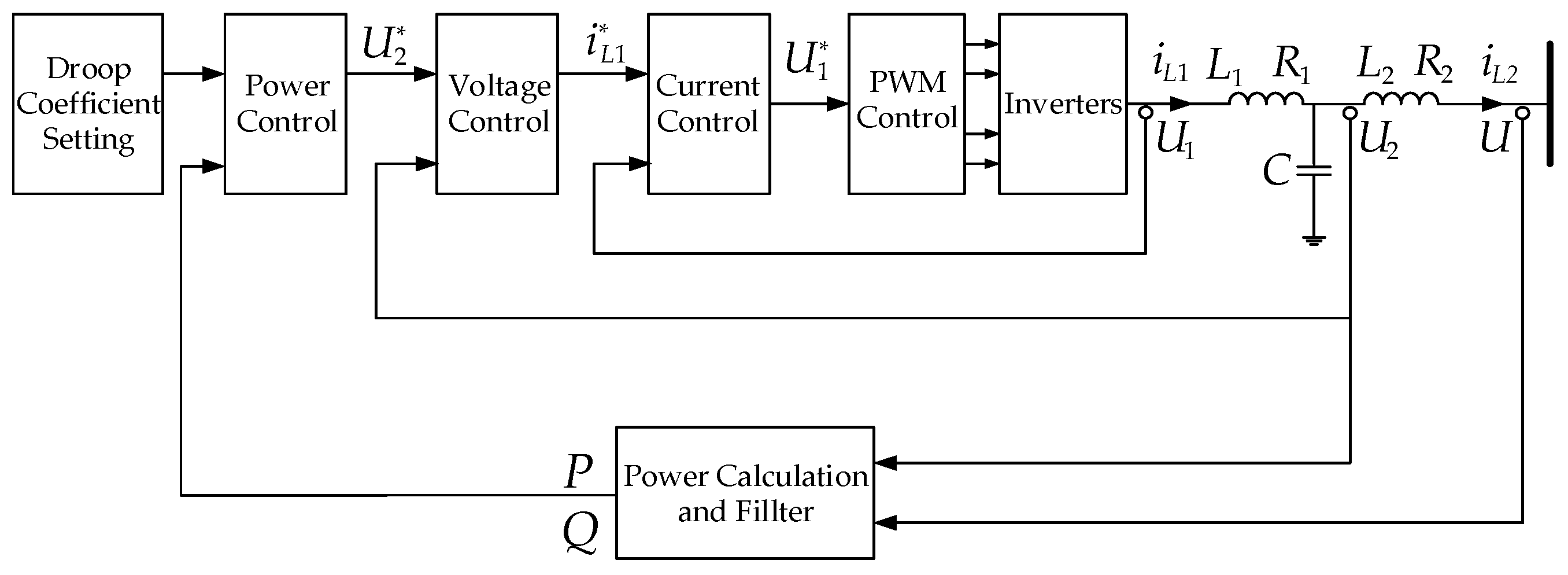
2.1. IIDG Full Model Based on Droop Control
2.2. Multi-Time Scale Decomposition of IIDG System
2.3. Order Reduction Form of Neglecting Fast Dynamics for IIDG System
3. Stability Consistency Proof of IIDG Model Order Reduction
3.1. Consistency Proof of Static Stability before and after Order Reduction
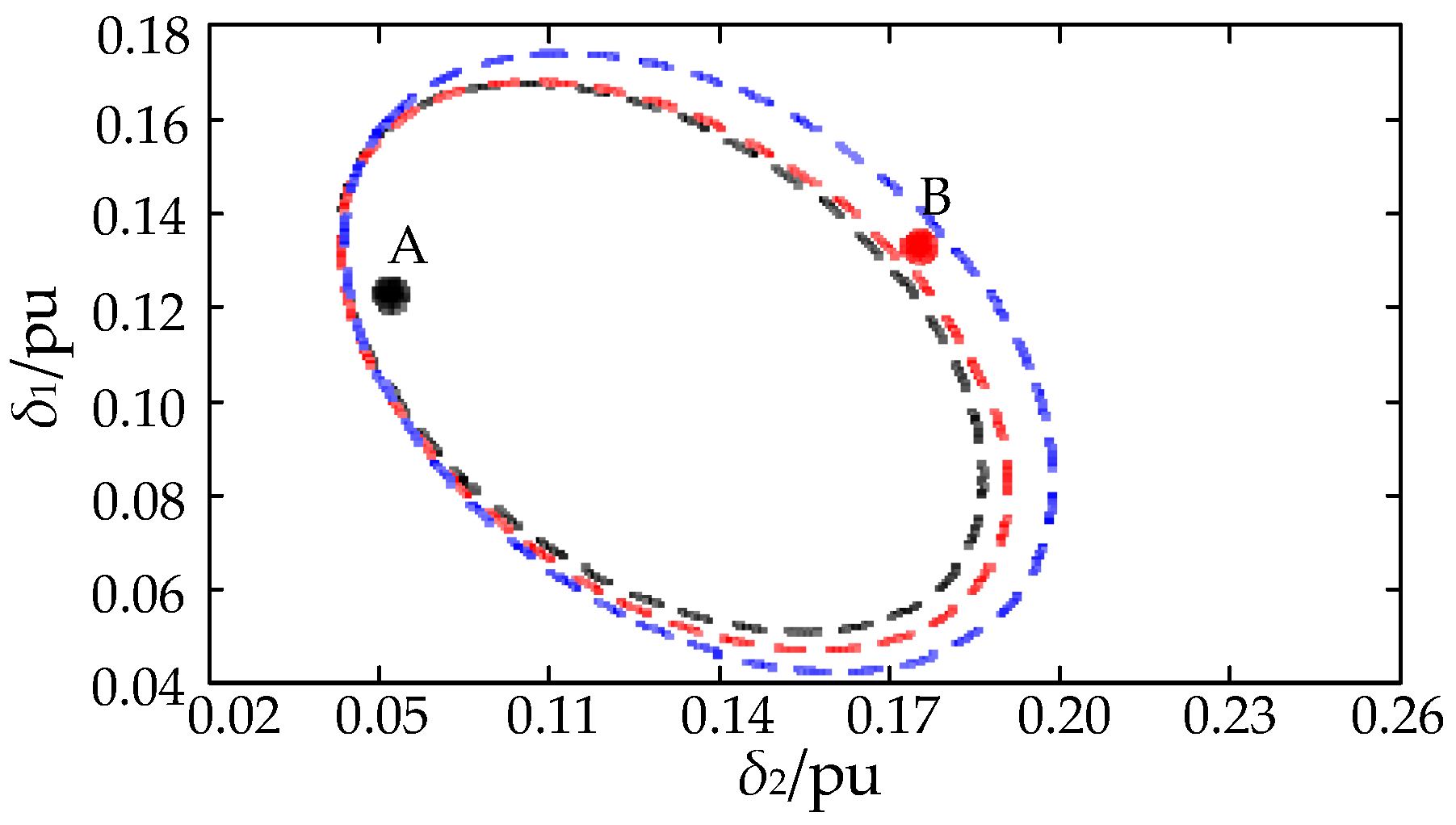
3.2. Consistency Proof of Transient Stability before and after Order Reduction
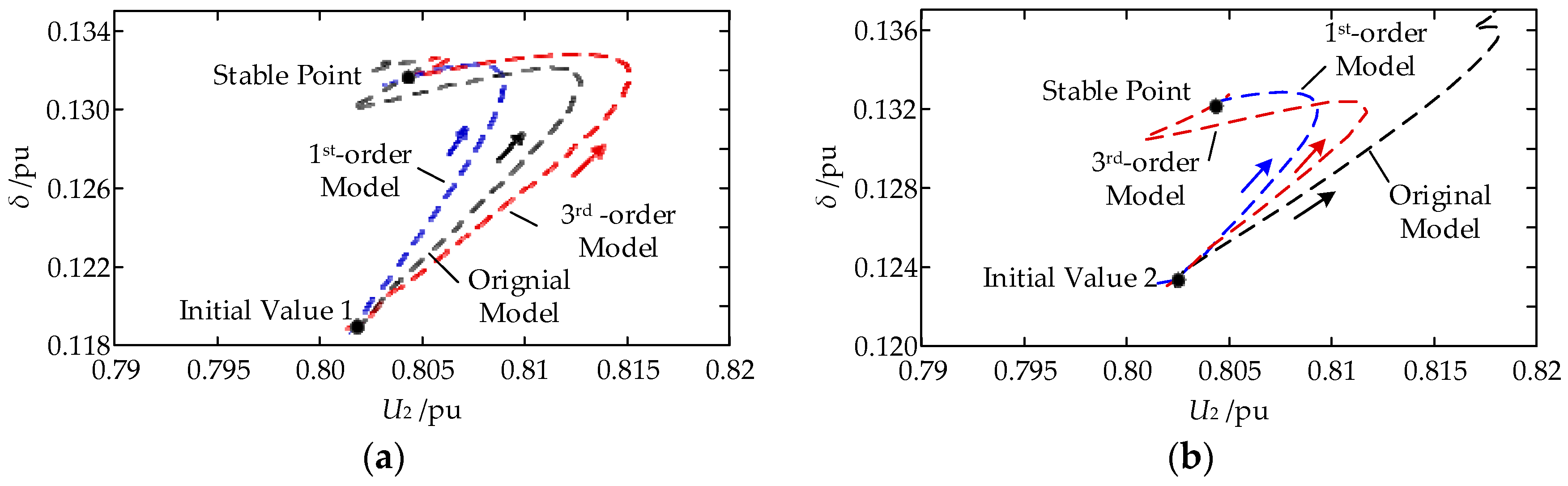
3.3. Consistency Evaluation of Dynamic Response before and after Order Reduction
4. Simulation Studies
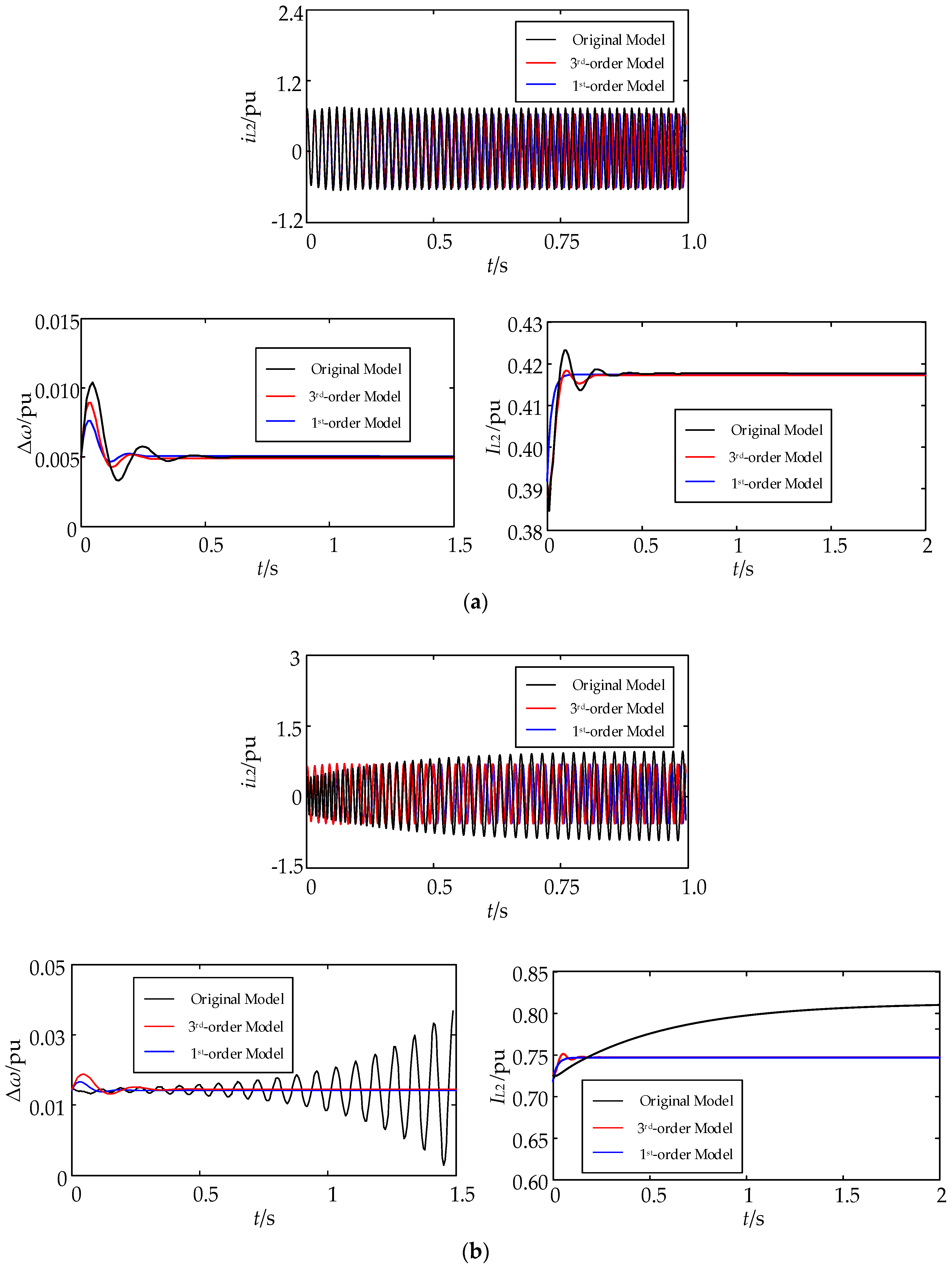
4.1. Stand-Alone System (System 1)
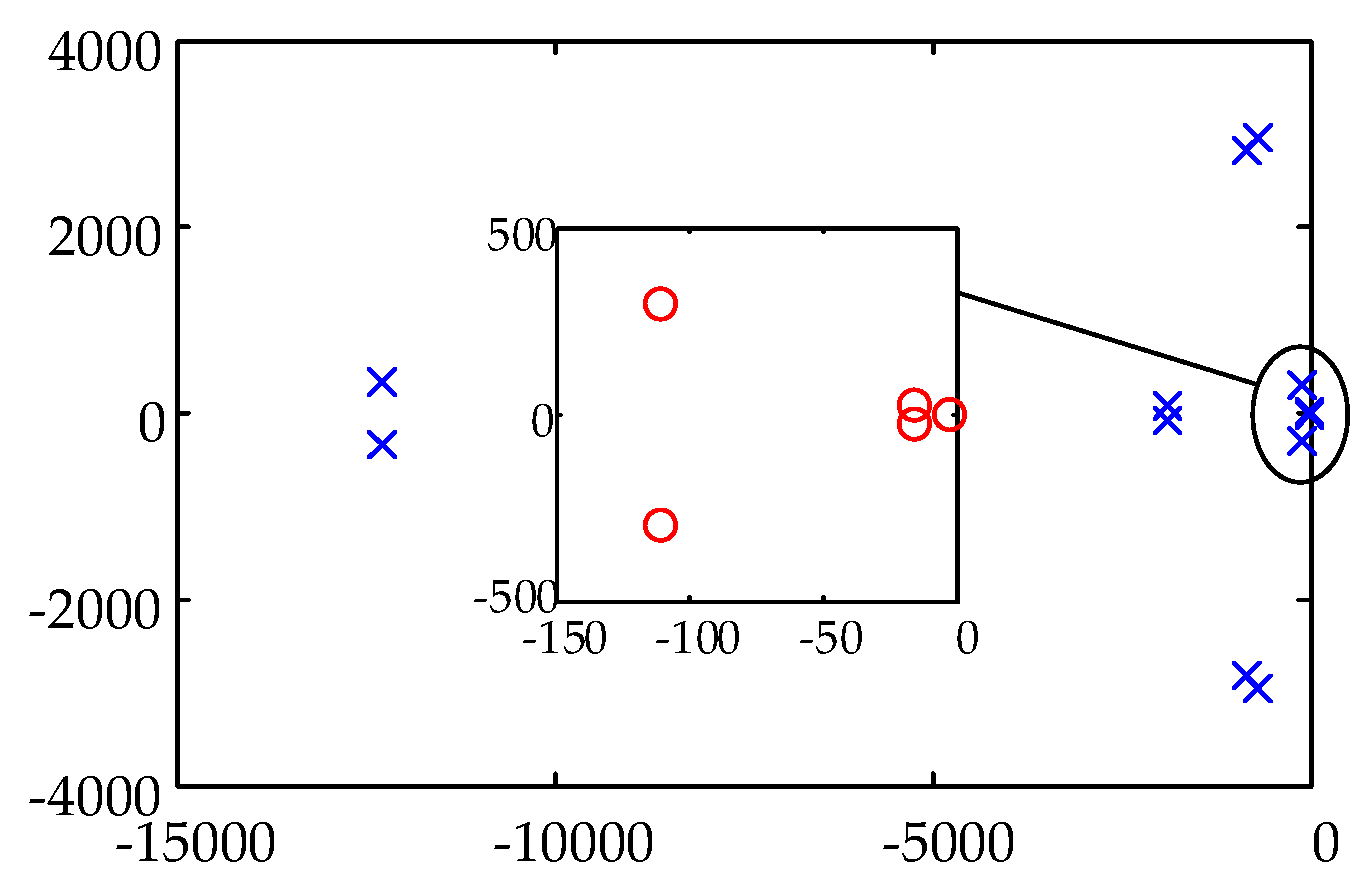
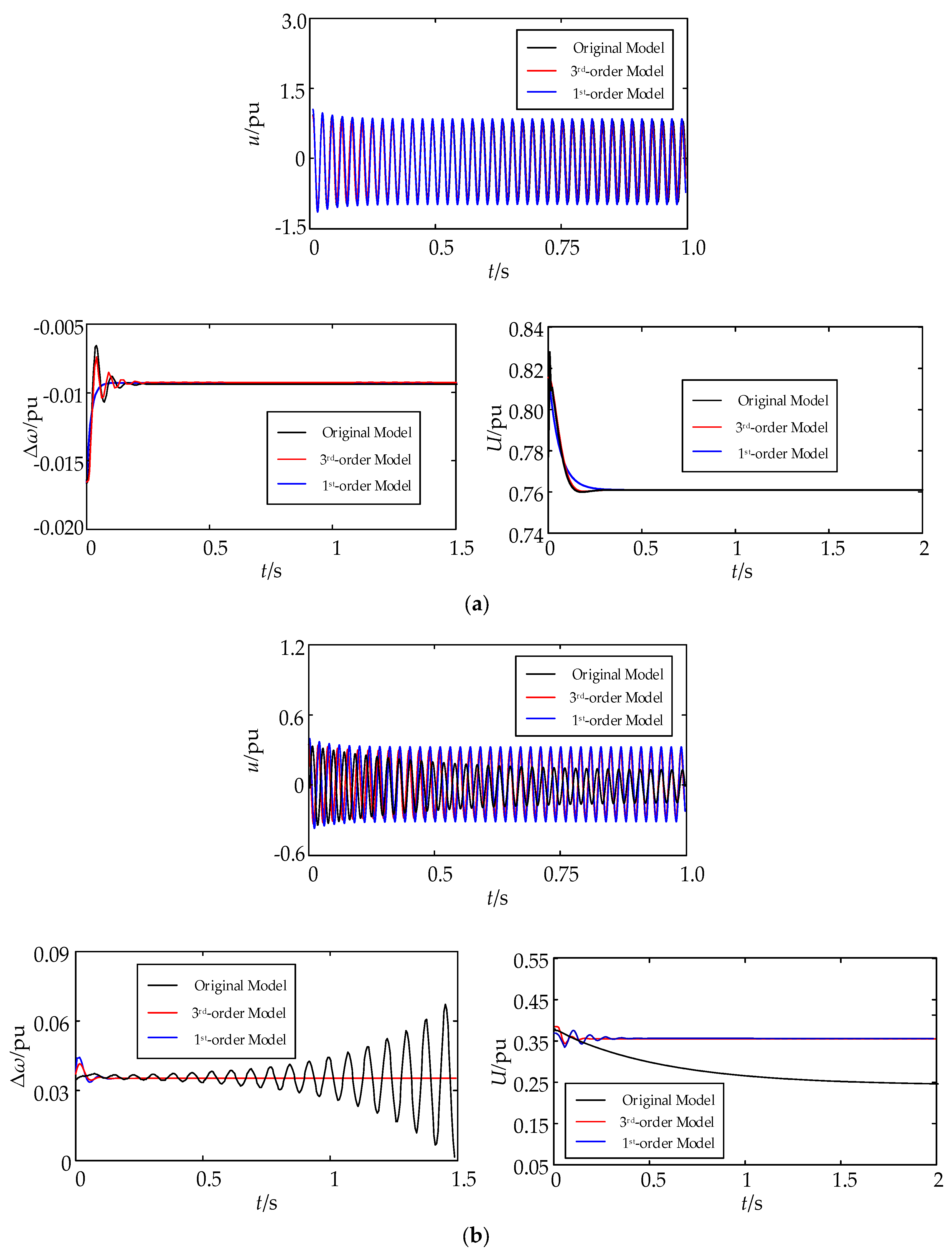
4.2. Three-IIDG Microgrid Pilot Project System (System 2)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. IIDG Parameters
Appendix A.2. IIDG Detailed Model
Appendix B
| Eigenvalues | Values |
|---|---|
| λ1,2 | −1.2277 × 104 ± 0.0332 × 104i |
| λ3,4 | −0.0689 × 104 ± 0.2954 × 104i |
| λ5,6 | −0.085 × 104 ± 0.281 × 104i |
| λ7,8 | −0.189 × 104 ± 0.007 × 104i |
| λ9,10 | −0.011 × 104 ± 0.030 × 104i |
| λ11,12 | −16 ± 25i |
| λ13 | −3 |
State Matrix of the IIDG Complete Model
Appendix C
Appendix D
Parameters of Three-IIDG Microgrid Pilot Project System
References
- Pogaku, N.; Milan, P.; Timothy, C.G. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids-A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Hu, B.; Wang, H.; Yao, S. Optimal economic operation of isolated community micro-grid incorporating temperature controlling devices. Prot. Control Mod. Power Syst. 2017, 2, 6. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q small-signal impedance of grid-tied inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Wang, X.; Yu, H.; Xing, Z. Analysis and design of current control schemes for LCL-type grid-connected inverter based on a generalmathematical model. IEEE Trans. Power Electron. 2017, 32, 4395–4410. [Google Scholar] [CrossRef]
- Qi, J.; Wang, J.; Liu, H.; Dimitrovski, A.D. Nonlinear model reduction in power systems by balancing of empirical controllability and observability covariances. IEEE Trans. Power Syst. 2017, 32, 114–126. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.M.; Savaghebi, M.; Eloy-Garcia, J.; Teodorescu, R. Modeling, analysis, and design of stationary-reference-frame droop-controlled parallel three-phase voltage source inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar] [CrossRef]
- Gutierrez, B.; Kwak, S.S. Modular multilevel converters (MMCs) controlled by model predictive control with reduced calculation burden. IEEE Trans. Power Electron. 2018, in press. [Google Scholar] [CrossRef]
- Kahrobaeian, A.; Mohamed, Y.A.R.I. Analysis and mitigation of low-frequency instabilities in autonomous medium-voltage converter-based microgrids with dynamic loads. IEEE Trans. Ind. Electron. 2014, 61, 1643–1658. [Google Scholar] [CrossRef]
- Cao, W.; Ma, Y.; Liu, Y.; Wang, F.; Tolbert, L.M. D-Q Impedance Based Stability Analysis and Parameter Design of Three-Phase Inverter-Based AC Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 6017–6028. [Google Scholar] [CrossRef]
- Arani, M.F.M.; El-Saadany, E.F. Implementing virtual inertia in DFIG-based wind power generation. IEEE Trans. Power Syst. 2013, 28, 1373–1384. [Google Scholar] [CrossRef]
- Tang, X.; Hu, X.; Li, N.; Deng, W.; Zhang, G. A novel frequency and voltage control method for islanded microgrid based on multienergy storages. IEEE Trans. Smart Grid 2016, 7, 410–419. [Google Scholar] [CrossRef]
- Levron, Y.; Belikov, J. Reduction of power system dynamic models using sparse representations. IEEE Trans. Power Syst. 2017, 32, 3893–3900. [Google Scholar] [CrossRef]
- Li, X.Y.; Chen, X.H.; Tang, G.Q. Output feedback control of doubly-fed induction generator based on multi-time scale model. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 2798–2802. [Google Scholar]
- Ramirez, A.; Mehrizi-Sani, A.; Hussein, D.; Matar, M.; Abdel-Rahman, M.; Chavez, J.J.; Davoudi, A.; Kamalasadan, S. Application of balanced realizations for model-order reduction of dynamic power system equivalents. IEEE Trans. Power Deliv. 2016, 31, 2304–2312. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, A.R.I.; El-Saadany, E.F. Analysis and mitigation of the impacts of asymmetrical virtual inertia. IEEE Trans. Power Syst. 2014, 29, 2862–2874. [Google Scholar] [CrossRef]
- Gu, Y.; Bottrell, N.; Green, T.C. Reduced-order models for representing converters in power system studies. IEEE Trans. Power Electron. 2018, 33, 3644–3654. [Google Scholar] [CrossRef]
- Ye, Y.; Wei, L.; Ruan, J.; Li, Y.; Lu, Z.; Qiao, Y. A generic reduced-order modeling hierarchy for power-electronic interfaced generators with the quasi-constant-power feature. Proc. CSEE 2017, 14, 3993–4001. (In Chinese) [Google Scholar]
- Davoudi, A.; Jatskevich, J.; Chapman, P.L.; Bidram, A. Multiresolution modeling of power electronics circuits using model-order reduction techniques. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 810–823. [Google Scholar] [CrossRef]
- Kodra, K.; Zhong, N.; Gajić, Z. Model order reduction of an islanded microgrid using singular perturbations. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3650–3655. [Google Scholar]
- Luo, L.; Dhople, S.V. Spatiotemporal model reduction of inverter-based islanded microgrids. IEEE Trans. Energy Convers. 2014, 29, 823–832. [Google Scholar] [CrossRef]
- Ma, F.; Fu, L. Principle of multi-time scale order reduction and its application in AC/DC hybrid power systems. In Proceedings of the IEEE 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 3951–3956. [Google Scholar]
- Saxena, S.; Hote, Y.V. Load frequency control in power systems via internal model control scheme and model-order reduction. IEEE Trans. Power Syst. 2013, 28, 2749–2757. [Google Scholar] [CrossRef]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Small signal stability assessment of power systems with increased penetration of photovoltaic generation: A case study. IEEE Trans. Sustain. Energy 2013, 4, 960–967. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Guerrero, J.M.; Xu, Z.; Green, T.C. Multiple-time-scales hierarchical frequency stability control strategy of medium-voltage isolated microgrid. IEEE Trans. Power Electron. 2016, 31, 5974–5991. [Google Scholar] [CrossRef]
- Kokotovic, P.V.; Sauer, P.V. Integral manifold as a tool for reduced-order modeling of nonlinear systems: A synchronous machine case study. IEEE Trans. Circuit Syst. 1989, 36, 403–410. [Google Scholar] [CrossRef]
- Chiang, H.D.; Chu, C.C. Theoretical foundation of the BCU method for direct stability analysis of network-reduction power system. Models with small transfer conductance. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1992, 42, 252–265. [Google Scholar] [CrossRef]
- Chiang, H.D.; Wu, F.F.; Varaiya, P.P. A BCU method for direct analysis of power system transient stability. IEEE Trans. Power Syst. 1994, 9, 1194–1208. [Google Scholar] [CrossRef]
- Zhao, S.; Loparo, K.A. Forward and backward extended prony (FBEP) method for power system small-signal stability analysis. IEEE Trans. Power Syst. 2017, 32, 3618–3626. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, W.; Zhang, B. A fast method to identify the order of frequency-dependent network equivalents. IEEE Trans. Power Syst. 2016, 31, 54–62. [Google Scholar] [CrossRef]

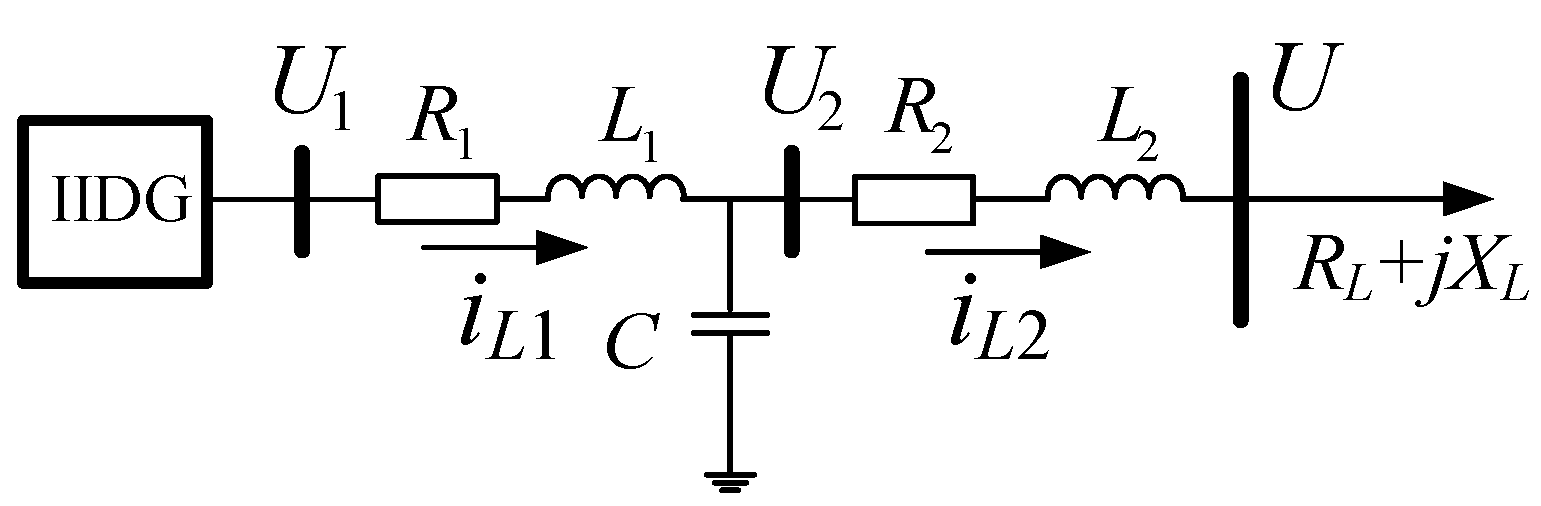
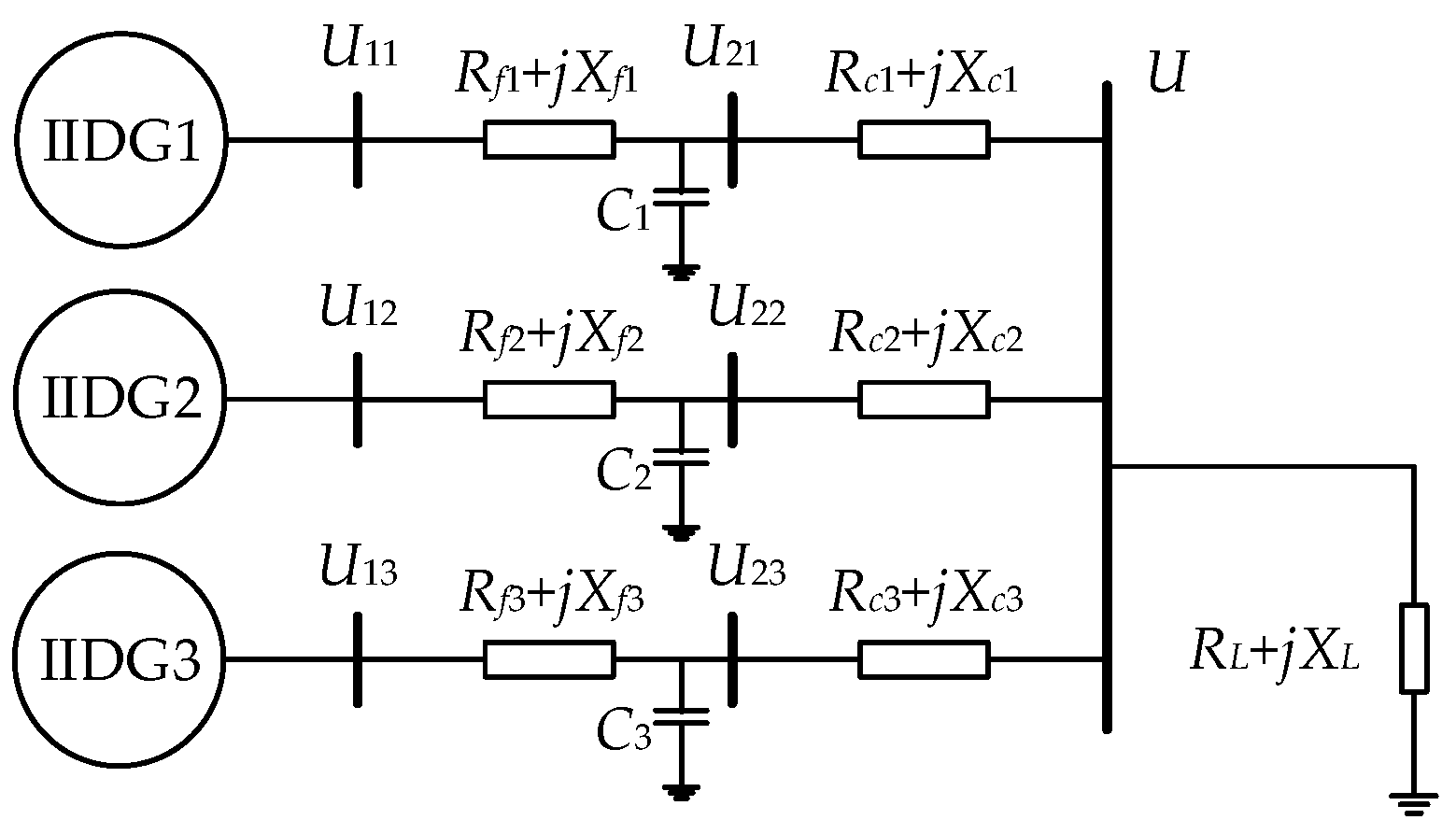
| Boundary Layer System | Original System | Order Reduction System | Transient Stability Index | Transient Stability Consistency |
|---|---|---|---|---|
| Stable | Stable | Stable | Both positive numbers | Conformity |
| Stable | Unstable | Unstable | Both negative numbers | Conformity |
| Unstable | Unstable | Stable | Opposite sign | Inconformity |
| Unstable | Unstable | Unstable | Both negative numbers | Conformity |
| State Variables | Initial Value 1/pu | Initial Value 2/pu | SEP/pu | UEP/pu |
|---|---|---|---|---|
| δ | 0.1189 | 0.1237 | 0.1319 | 0.1626 |
| P | 0.5000 | 0.5590 | 0.5817 | 0.6844 |
| Q | 0.0500 | 0.1118 | 0.0500 | 0.1118 |
| ϕd | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ϕq | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| λd | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| λq | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| iL1d | 0.5256 | 0.4393 | 0.6770 | 0.5286 |
| iL1q | 0.3426 | 0.5531 | 0.3105 | 0.5067 |
| u2d | 0.7164 | 0.6229 | 0.7572 | 0.6413 |
| u2q | 0.3604 | 0.5160 | 0.2815 | 0.4710 |
| iL2d | 0.5290 | 0.4441 | 0.6797 | 0.5330 |
| iL2q | 0.3359 | 0.5474 | 0.3036 | 0.5009 |
| System Eigenvalues | Order Reduction Form | |
|---|---|---|
| 3rd Order (ε2 = 0) | 1st Order (ε1 = 0, ε2 = 0) | |
| Fast subsystem σ(A22) | −12,277 ± 331i −687± 2952i −849 ± 2813i −1889 ± 73i −101 ± 294i | −12,277 ± 332i −689 ± 2954i −850 ± 2811i −1888 ± 74i −109 ± 298i −29 −10 |
| Slow subsystem σ(An) | −18.41 ± 25.96i −2.568 | −8.367 |
| Original system σ(A) | −12,277 ± 332i −689 ± 2954i −850 ± 2811i −1888 ± 74i −111 ± 297i −16 ± 25i −3 | |
| Order Reduction Form | Transient Stability Analysis Result under Initial Value 3 | Transient Stability Analysis Result under Initial Value 4 | ||||
|---|---|---|---|---|---|---|
| Original Model | 3rd Order Model | 1st Order Model | Original Model | 3rd Order Model | 1st Order Model | |
| Transient Stability Index IQ | 0.7989 | 0.8240 | 0.6241 | −0.0033 | 0.0054 | 0.2080 |
| Stability Consistency | / | √ | √ | / | × | × |
| Calculation Time | 24 s | 18 s | 5 s | 27 s | 15 s | 3 s |
| IIDG Output Current at Stable Point | Frequency Consistency Index | Damping Consistency Index | Amplitude Consistency Index | |||
| 3rd Order Model | 1st Order Model | 3rd Order Model | 1st Order Model | 3rd Order Model | 1st Order Model | |
| 98.26% | 95.34% | 96.14% | 93.58% | 95.31% | 91.71% | |
| State Variable | IV3/pu | IV4/pu | SEP/pu | UEP/pu | State Variable | IV3/pu | IV4/pu | SEP/pu | UEP/pu | State Variable | IV3/pu | IV4/pu | SEP/pu | UEP/pu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| δ1 | 0.129 | 0.139 | 0.132 | 0.156 | δ2 | 0.053 | 0.142 | 0.123 | 0.183 | δ3 | 0.058 | 0.144 | 0.129 | 0.187 |
| P1 | 0.526 | 0.559 | 0.660 | 0.695 | P2 | 0.263 | 0.280 | 0.312 | 0.342 | P3 | 0.263 | 0.280 | 0.315 | 0.345 |
| Q1 | 0.050 | 0.150 | 0.050 | 0.150 | Q2 | 0.050 | 0.112 | 0.050 | 0.112 | Q3 | 0.050 | 0.112 | 0.050 | 0.112 |
| ϕd1 | 0.000 | 0.000 | 0.000 | 0.000 | ϕd2 | 0.000 | 0.000 | 0.000 | 0.000 | ϕd3 | 0.000 | 0.000 | 0.000 | 0.000 |
| ϕq1 | 0.000 | 0.000 | 0.000 | 0.000 | ϕq2 | 0.000 | 0.000 | 0.000 | 0.000 | ϕq3 | 0.000 | 0.000 | 0.000 | 0.000 |
| λd1 | 0.000 | 0.000 | 0.000 | 0.000 | λd2 | 0.000 | 0.000 | 0.000 | 0.000 | λd3 | 0.000 | 0.000 | 0.000 | 0.000 |
| λq1 | 0.000 | 0.000 | 0.000 | 0.000 | λq2 | 0.000 | 0.000 | 0.000 | 0.000 | λq3 | 0.000 | 0.000 | 0.000 | 0.000 |
| iL1d1 | 0.554 | 0.473 | 0.665 | 0.549 | iL1d2 | 0.133 | 0.113 | 0.178 | 0.140 | iL1d3 | 0.136 | 0.116 | 0.180 | 0.141 |
| iL1q1 | 0.375 | 0.581 | 0.260 | 0.453 | iL1q2 | 0.096 | 0.136 | 0.125 | 0.093 | iL1q3 | 0.091 | 0.131 | 0.122 | 0.091 |
| u2d1 | 0.734 | 0.670 | 0.624 | 0.506 | u2d2 | 0.686 | 0.623 | 0.737 | 0.651 | u2d3 | 0.679 | 0.612 | 0.732 | 0.649 |
| u2q1 | 0.394 | 0.540 | 0.454 | 0.632 | u2q2 | 0.380 | 0.533 | 0.282 | 0.482 | u2q3 | 0.385 | 0.537 | 0.284 | 0.483 |
| iL2d1 | 0.541 | 0.461 | 0.719 | 0.638 | iL2d2 | 0.139 | 0.117 | 0.182 | 0.133 | iL2d3 | 0.142 | 0.120 | 0.183 | 0.136 |
| iL2q1 | 0.379 | 0.585 | 0.267 | 0.469 | iL2q2 | 0.089 | 0.124 | 0.080 | 0.103 | iL2q3 | 0.086 | 0.121 | 0.078 | 0.101 |
| Order Reduction Form | Eigenvalues | ||
|---|---|---|---|
| Original model (dominant poles) | −14.70 ± 25.01i −2.93 | −14.38 ± 16.91i −9.43 | −14.34 ± 16.98i −9.41 |
| Adopting 3rd-order model | −18.41 ± 25.96i −2.57 | −14.84 ± 16.56i −9.57 | −14.85 ± 16.52i −9.54 |
| Adopting 1st-order model | −8.36 | −16.89 | −16.86 |
| Order Reduction Form | Eigenvalues | ||
|---|---|---|---|
| Original model (dominant poles) | −3.23 ± 48.34i 3.01 | −10.14 ± 39.02i −0.55 | −9.43 ± 38.68i −0.56 |
| Adopting 3rd-order model | −17.63 ± 53.64i 2.53 | −17.82 ± 40.98i −0.48 | −17.94 ± 40.94i −0.49 |
| Adopting 1st-order model | −0.65 | −3.89 | −3.86 |
| Order Reduction Form | Transient Stability Analysis Result under Initial Value 3 | Transient Stability Analysis Result under Initial Value 4 | ||||
|---|---|---|---|---|---|---|
| Original Model | 3rd Order Model | 1st Order Model | Original Model | 3rd Order Model | 1st Order Model | |
| Transient Stability Index IQ | 0.7309 | 0.7211 | 0.5387 | −0.1028 | −0.0532 | 0.0122 |
| Stability Consistency | / | √ | √ | / | √ | × |
| Calculation Time | 124 s | 48 s | 10 s | 128 s | 52 s | 5 s |
| Microgrid PCC Voltage at Stable Point | Frequency Consistency Index | Damping Consistency Index | Amplitude Consistency Index | |||
| 3rd Order Model | 1st Order Model | 3rd Order Model | 1st Order Model | 3rd Order Model | 1st Order Model | |
| 98.51% | 94.87% | 97.94% | 96.21% | 96.38% | 92.14% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Wang, Q.; Zhou, N.; Xiao, S.; Chi, Y. Multi-Time Scale Model Order Reduction and Stability Consistency Certification of Inverter-Interfaced DG System in AC Microgrid. Energies 2018, 11, 254. https://doi.org/10.3390/en11010254
Meng X, Wang Q, Zhou N, Xiao S, Chi Y. Multi-Time Scale Model Order Reduction and Stability Consistency Certification of Inverter-Interfaced DG System in AC Microgrid. Energies. 2018; 11(1):254. https://doi.org/10.3390/en11010254
Chicago/Turabian StyleMeng, Xiaoxiao, Qianggang Wang, Niancheng Zhou, Shuyan Xiao, and Yuan Chi. 2018. "Multi-Time Scale Model Order Reduction and Stability Consistency Certification of Inverter-Interfaced DG System in AC Microgrid" Energies 11, no. 1: 254. https://doi.org/10.3390/en11010254






