1. Introduction
Increasing power demands due to continuous population growth and industrial needs, and depleting fossil fuel reserves and environmental concerns have led to the use of renewable energy sources, particularly to solar energy. Solar energy, being pollution free, renewable and freely available, has attracted great attention all around the world.
Photovoltaic (PV) solar cells are used to harvest energy from solar radiation and convert it into electric energy. These cells are made up of semiconductor materials, traditionally silicon. The low efficiency, high cost and physical barriers of silicon limit the use of traditional solar cells. Extensive research has been carried out to improve the conversion efficiency of a solar cell; special attention has been paid to the materials used in the manufacture of solar cells. A new generation of solar cells, known as the 3rd generation solar cells, has evolved, which make use of sustainable materials and flexible architectures like dye-sensitized solar cells (DSSCs). DSSCs operate as an artificial photosynthetic system to convert solar light into electricity, and are reported to provide efficiencies of up to 14% [
1]. More insights on the materials and coatings employed for efficient DSSCs can be found in [
2,
3,
4].
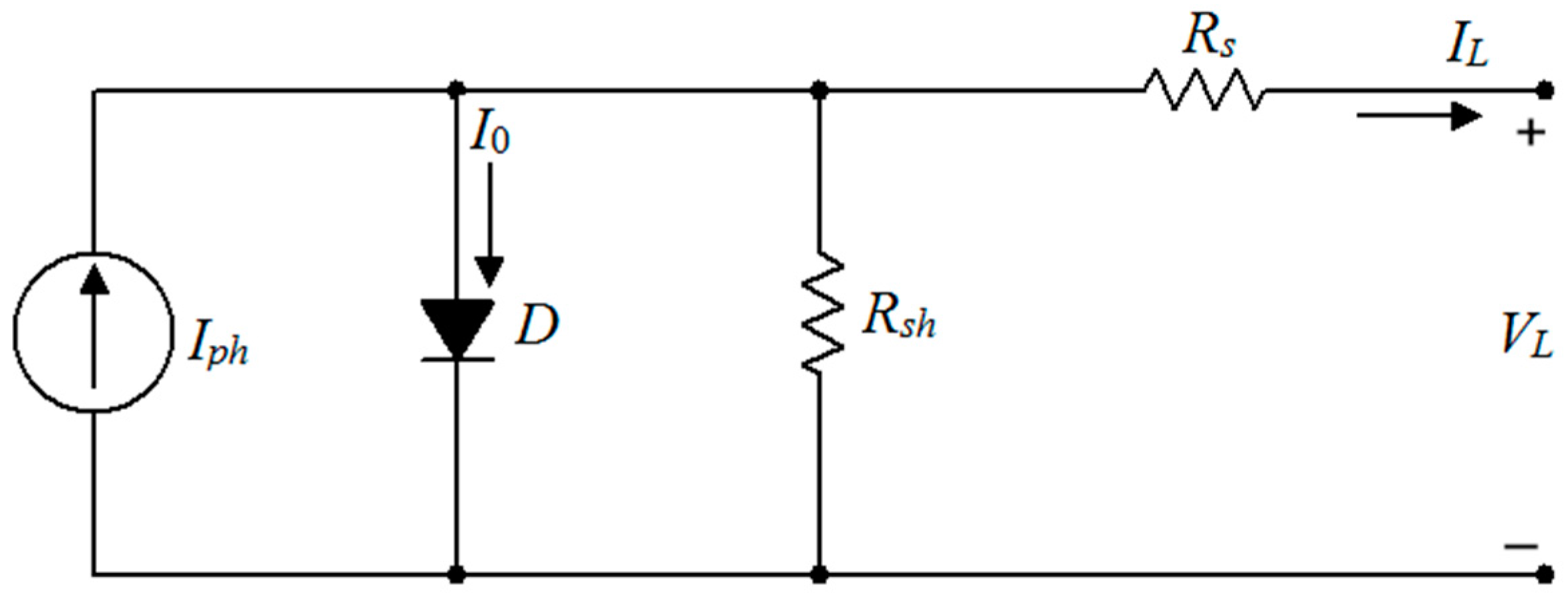
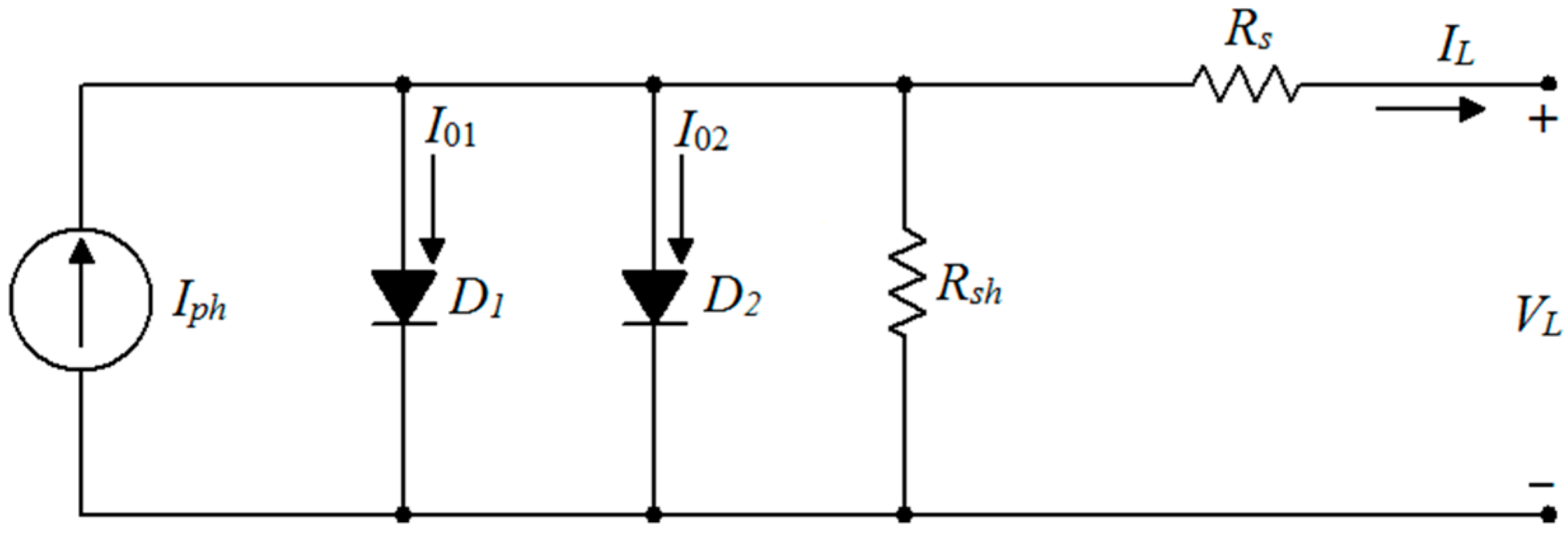
These cells are connected in series and parallel combinations to construct a solar module. Accurate modeling of solar cells is necessary to evaluate and forecast the performance of the PV systems. Many circuit models have been proposed. Among them, single diode models (SDM) and double diode models (DDM) are prominent and widely used for PV system modeling. For a simulation model to perform characteristics like the real one, precise model parameter estimation is required. An optimized parameter estimation strategy should be adopted to achieve the PV model
I-V characteristics to closely track the experimentally measured
I-V characteristics. Many methods have been used for parameter estimation of solar cells including classical methods such as the Newton-Raphson method [
5], and Lambert function [
6]-based method; but these methods are highly prone to being trapped into a local minimum [
7].
Metaheuristics have been widely applied in solving nonlinear multimodal optimization problems in recent years. The literature describes many similar methods applied successfully for solar PV cell parameter estimation. The applied methods include genetic algorithm (GA) [
8], differential evolution (DE) [
9], particle swarm optimization (PSO) [
10], simulated annealing (SA) [
11], harmony search (HS) [
12], artificial bee colony (ABC) [
13], cuckoo search (CS) [
14], pattern search (PS) [
15], etc.
Ishaque et al. [
9] proposed a penalty-based differential evolution method to estimate the parameters of multi-crystalline, mono-crystalline, and thin-film PV modules.
I-V test data were obtained synthetically using DDM. The results confirmed the outperformance of the method over GA, SA and PSO.
Ye et al. [
10] applied PSO to parameter estimation of SDM and DDM PV models. To check the ability of the PSO, synthesized and experimental
I-V data were used. The results indicated that the PSO outperformed GA in terms of parameter precision and computational efficiency.
Alrashidi et al. [
11] applied SA for parameter estimation of solar PV cells. Summation of individual absolute errors (IAE) was used as the objective function to be minimized. A 57 mm diameter commercial (RTC France) silicon solar cell under 1 sun (1000 W/m
2) at 33 °C was used for parameter estimation of SDM and DDM. The results showed the superiority of the SA over PS and gradient based methods.
Askarzadeh et al. [
12] investigated three different variants of HS algorithm for parameter estimation of SDM and DDM employing experimental data for a commercial solar cell (RTC France). The HS variants outperformed GA, chaos particle swarm optimization (CPSO) and PS in terms of precision.
Wang et al. [
13] provided improved ABC (IABC) for parameter identification of SDM and DDM. IABC outperformed artificial bee colony algorithm, DE, PSO and ABSO algorithms in terms of error residuals.
Ma et al. [
14] applied CS to estimate the parameters of the solar cell and solar module. A commercial 57 mm diameter solar cell (RTC France) was employed for SDM parameter estimation. The results showed that the CS performed better than CPSO, GA and PS.
Metaheuristics present a fairly acceptable solution to optimization problems; but the problem of premature convergence still endures. Premature convergence makes a metaheuristic easily become trapped in a local optimum which leads to a local solution. In order to alleviate the problem of premature convergence, recently, a trend is seen in hybridizing a swarm-based algorithm with a point to point based algorithm [
11,
12,
13,
14]. SA is a point to point based metaheuristic which requires less computation time, easy implementation and strong local search ability [
16]. These make it suitable for hybridization with swarm based optimization algorithms. In reference [
17], the authors hybridized PSO with SA and applied the concept to commonly used benchmark functions to evaluate the performance of the hybrid algorithms; the hybrid strategy presented promising results when compared with conventional PSO. Junghans et al. [
18] proposed a hybrid optimization approach using GA and modified SA for building optimization; idea behind the approach was that the best solution from GA has been improved by SA. Fang et al. [
19] described a hybrid algorithm of particle swarm optimization (PSO) and tabu search (TS) for distribution network reconfiguration problem; the algorithm demonstrated fast computation speed and ability to avoid premature convergence. Carapellucci et al. [
20] described a hybrid parameter estimation strategy for estimation of energy generation island using GA and SA.
This paper attempts to mitigate the problem of premature convergence. Each global best solution from PSO undergoes SA to further improve the solution in terms of better objective values. This approach sufficiently eliminated the premature convergence problem and achieved a better solution in less iteration. This paper is organized as follows:
Section 2 discusses the solar cell modeling and formulation of the parameter estimation problem.
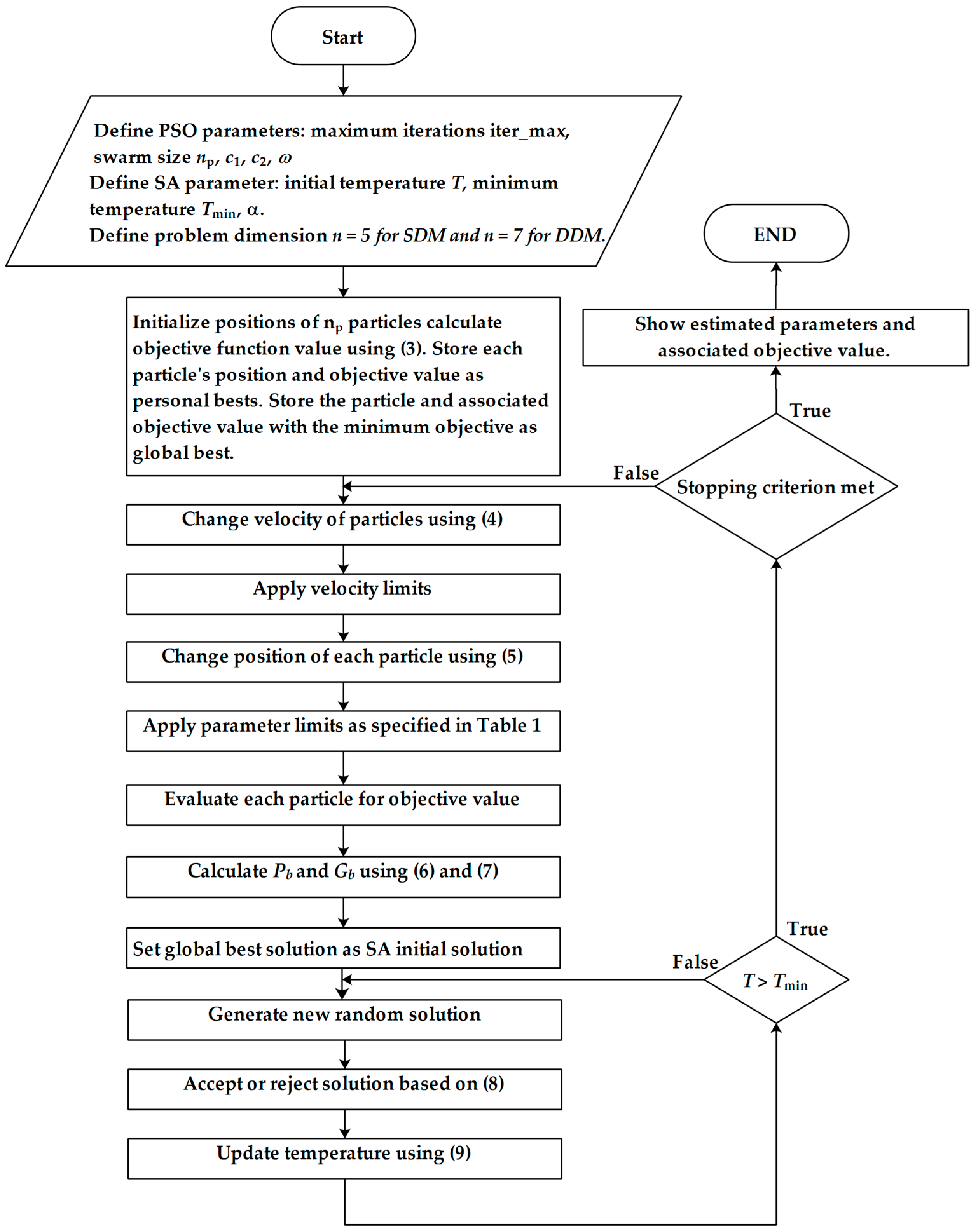
Section 3 provides details of the HPSOSA algorithm. Simulation results are discussed in
Section 4 along with analysis on the results.
Section 5 provides concluding remarks on the research work.
4. Experimental Results and Discussions
The HPSOSA algorithm described above is used to estimate the parameters of a commercial silicon solar cell (RTC France, city, country); the experimental data were obtained at an irradiance of 1000 W/m
2 and temperature of 33 °C [
24]. For HPSOSA, initially,
is set as 0.9 and decreased monotonically with a factor of 0.9, at each iteration. Both
and
are set as 2. The number of particles is set as 500 for SDM as well as for DDM.
for SA is set as 100 and
is set as 0.99. Termination criterion is set by maximum number of iterations; algorithm stops when it reaches 100 iterations. The HPSOSA is compared with conventional particle swarm optimization (CPSO) as described in [
25], HS, IABC, SA and PS algorithms to authenticate its performance. In an attempt to evaluate the quality of the estimated model, two basic measures of accuracy namely root mean square error
and mean absolute error
are calculated based on Equations (10) and (11):
Another test of quality of the estimated model is to calculate residual autocorrelation function
that describes that the estimated model satisfactorily defines a given set of data. The test is implemented in two steps: (1) Examination of the estimated residuals described by
. (2) Calculation of
RACF at different time lags using the following expression:
where
k is the time lag, and
t is the time index. The
value ranges from −1 to +1. If a given value is significantly different from zero, it will fall outside a confidence level.
4.1. Results for Single Diode PV Model
The algorithm has been run for 20 times to curtail the effect of randomness implicit in the results. Statistics of 20 runs for SDM have been computed and tabulated in
Table 2.
It is evident from
Table 2 that HPSOSA performs better than CPSO in terms of the average, best, worst, standard deviation, and median of the objective values in all 20 runs. The HPSOSA achieved the average, minimum, maximum and median of objective values as low as 7.7301 × 10
−4. HPSOSA achieved a standard deviation of 4.0768 × 10
−17; obviously it is far better than the standard deviation calculated for CPSO. The best values of the estimated parameters of SDM have been tabulated in
Table 3 along with
and
values. It can be seen that HPSOSA stands out as superior among all the algorithms with
and
values as low as 7.7301 × 10
−4 and 6.7818 × 10
−4, respectively.
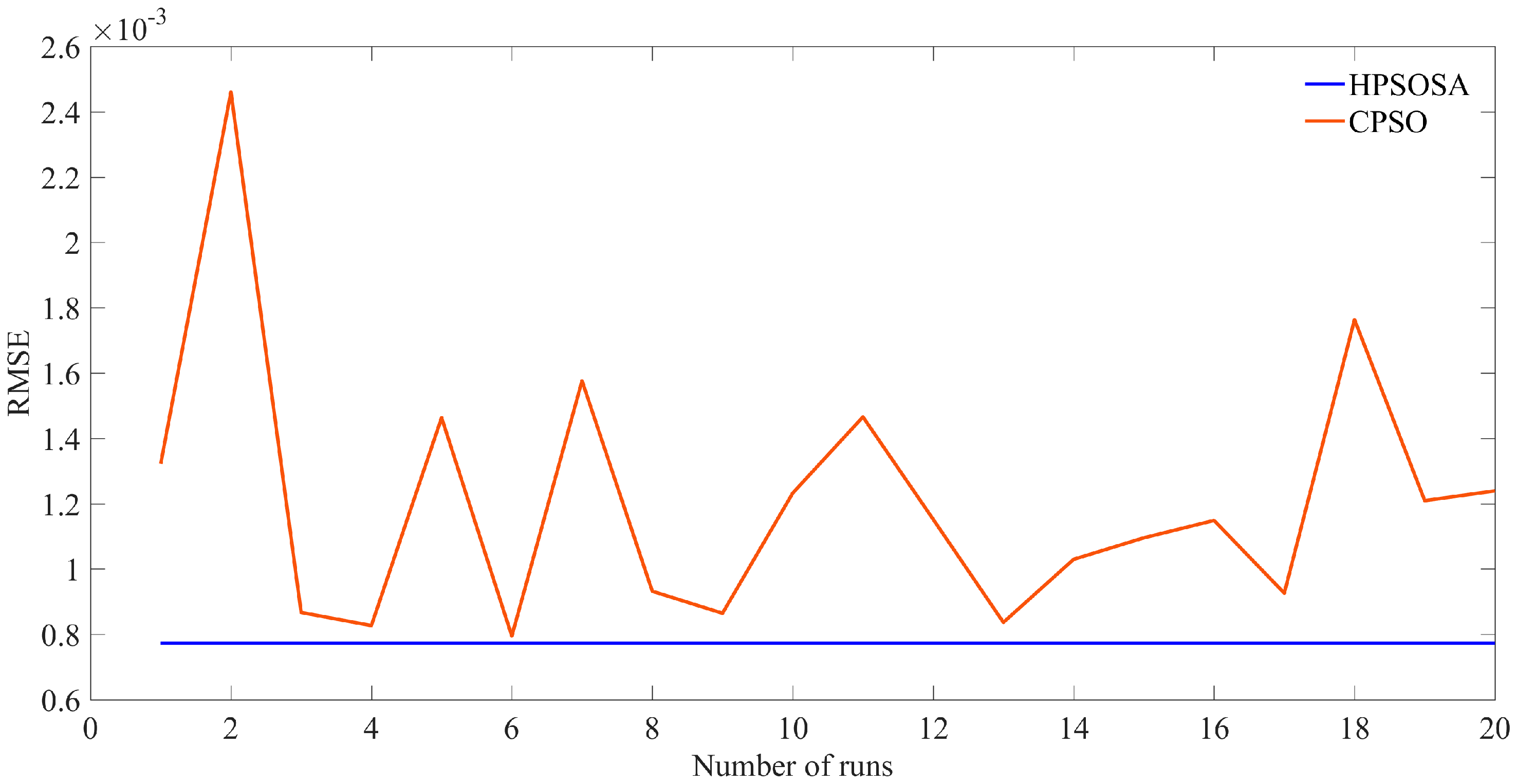
A measure of robustness of the HPSOSA and CPSO for 20 runs is shown in
Figure 4. It is apparent from
Figure 4 that the HPSOSA is able to achieve a minimum
RMSE value in all 20 iterations and presents a robust solution for the parameter estimation problem. Whereas CPSO reached only once in the proximity of the minimum
RMSE, achieved by HPSOSA.
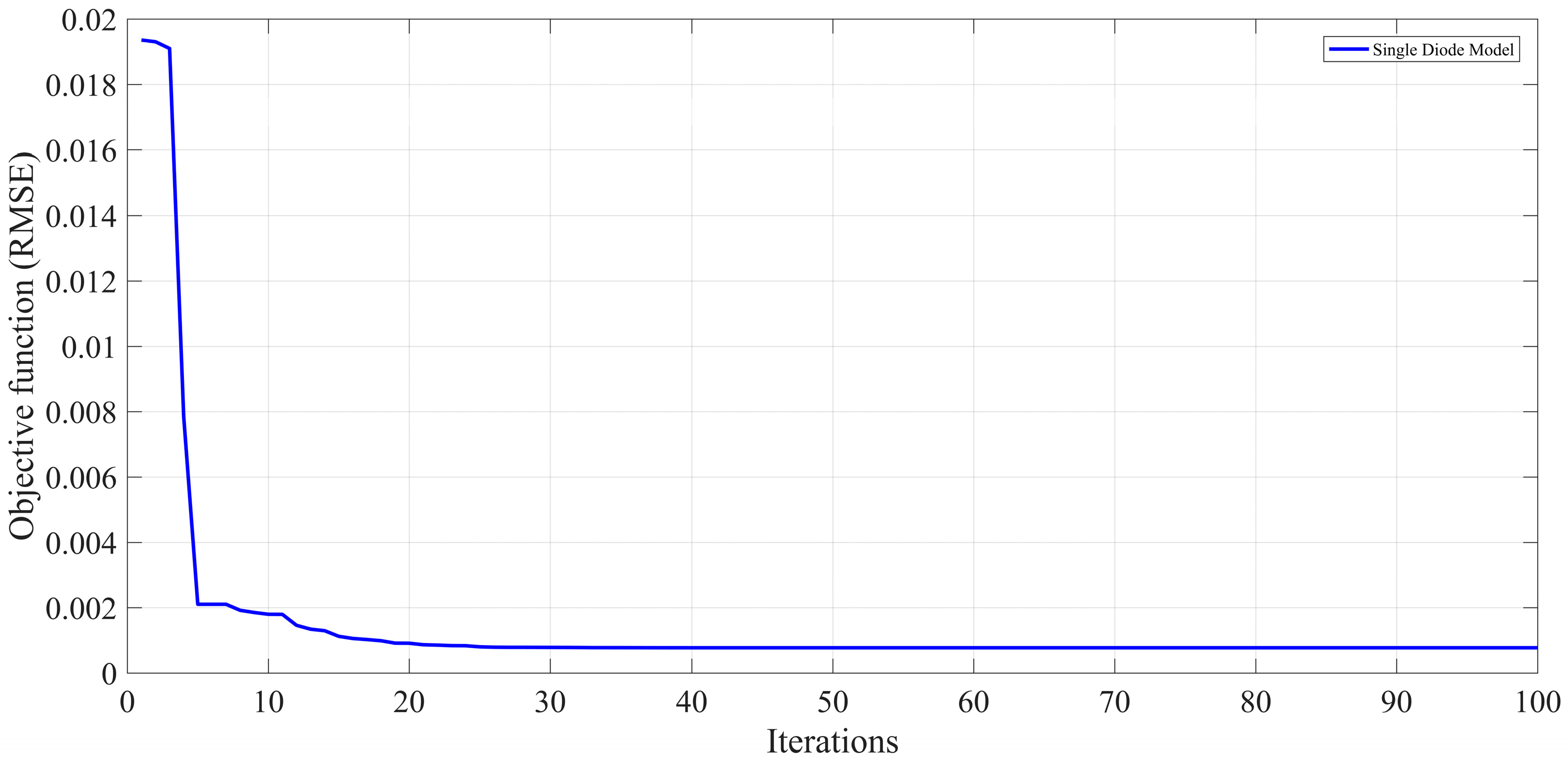
Objective function convergence curve for the best run of HPSOSA has been shown in
Figure 5. It is evident from the figure that the HPSOSA is able to attain a stable minimum objective value in less than 20 iterations.
A further insight of how close the estimated values are with the experimental values has been given in
Table 4,
Figure 6 and
Figure 7. Experimentally measured voltage, current and the error between measured current and estimated current, calculated by
, have been tabulated in
Table 4.
Table 4 shows that very low error values portray high precision of the estimated parameters.
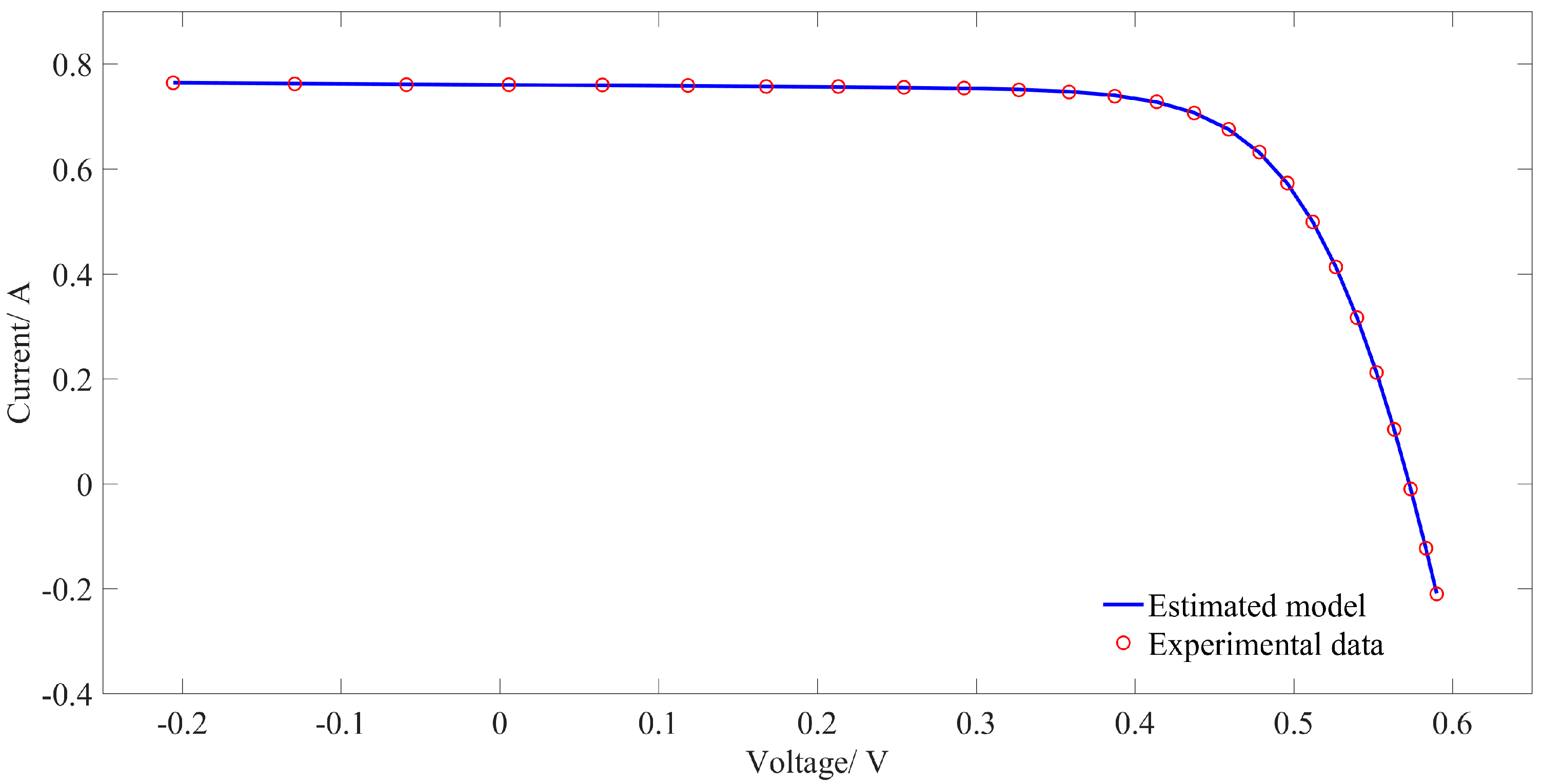
Figure 6 plots experimentally measured
I-V data points and
I-V data obtained by estimated parameters.
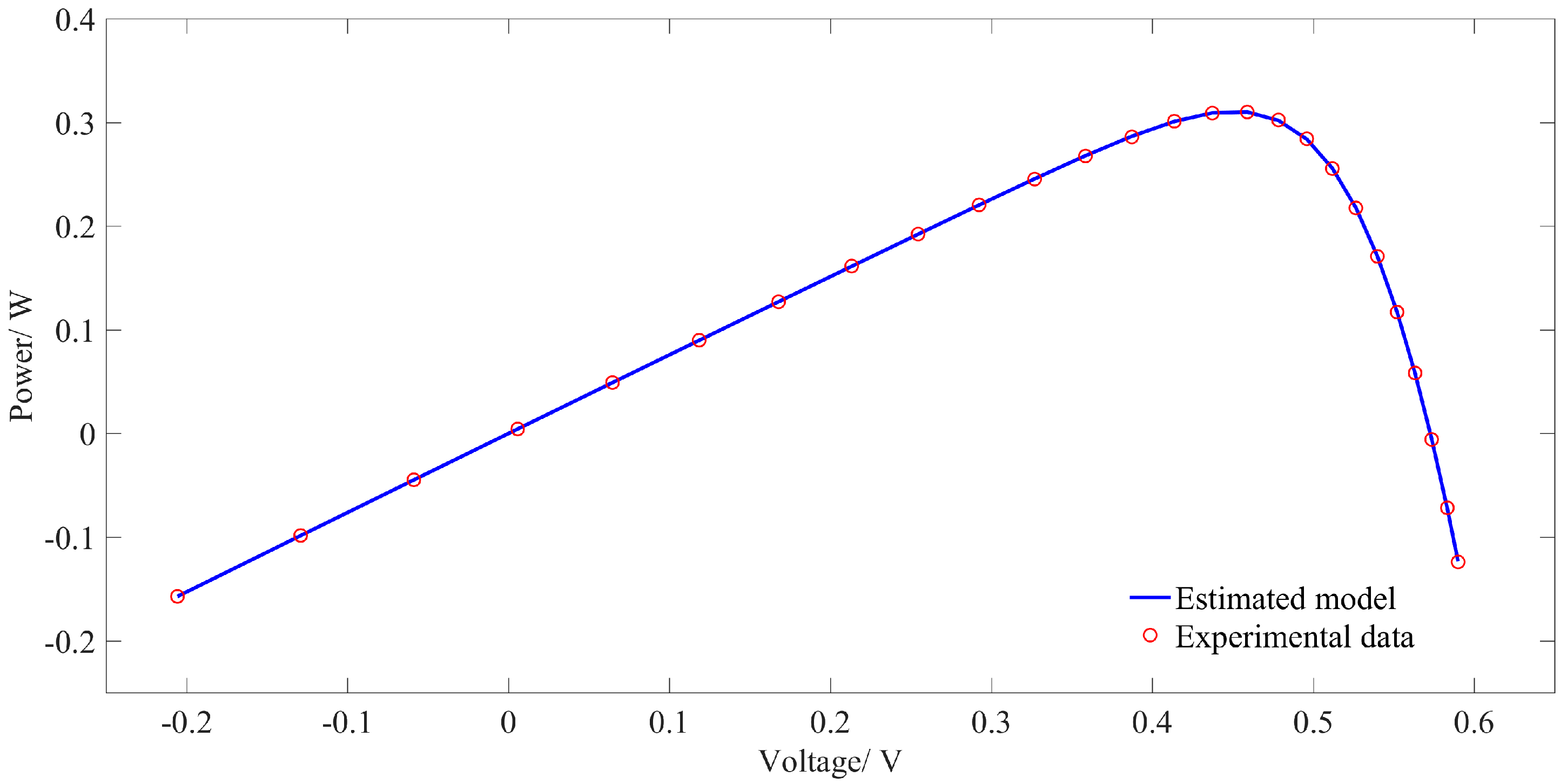
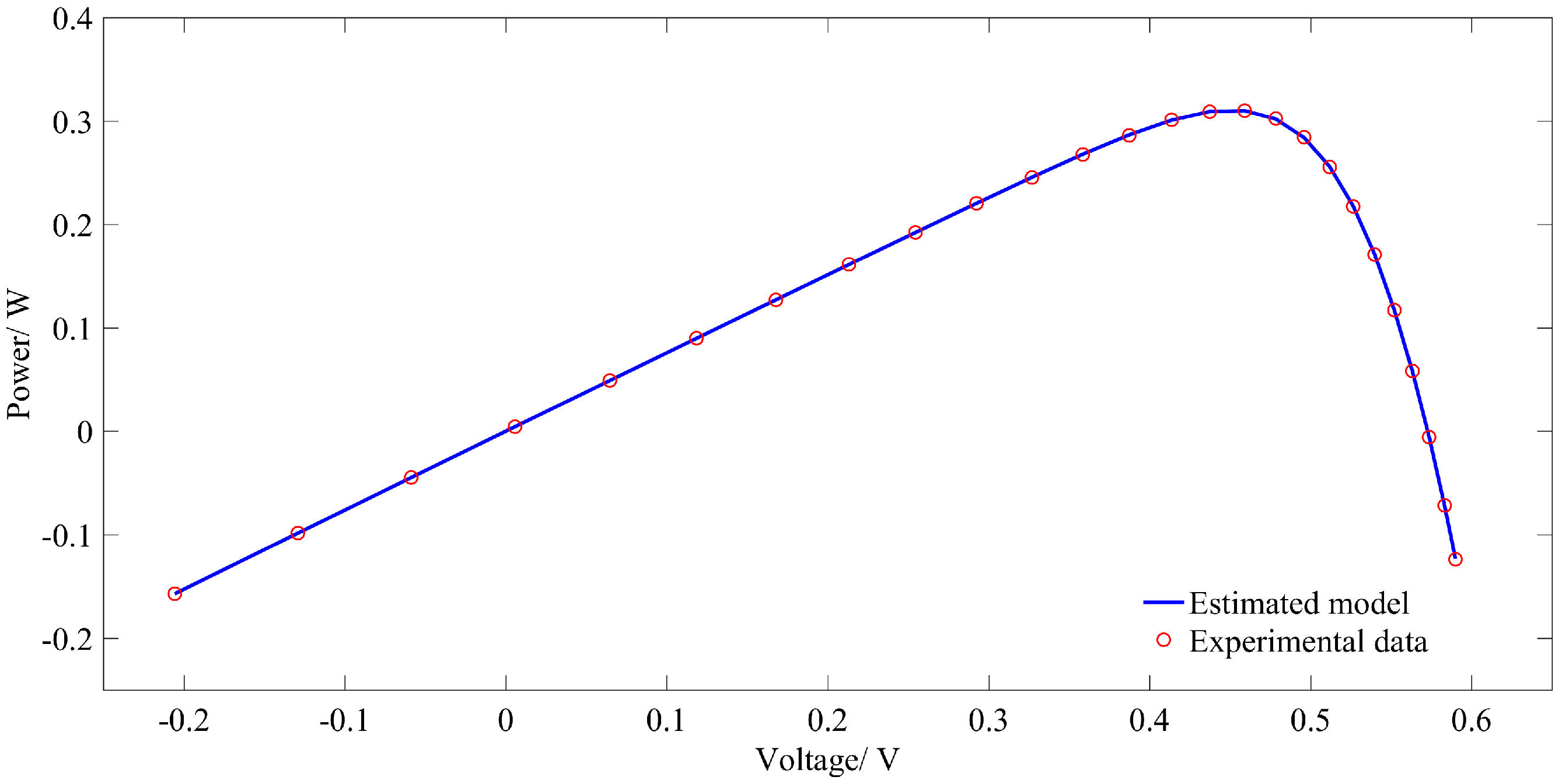
Figure 7 plots experimentally measured
P-V (power-voltage) data points and
P-V data obtained by estimated parameters.
Figure 6 and
Figure 7 clearly portray that the estimated data is in close agreement with the experimentally measured data.
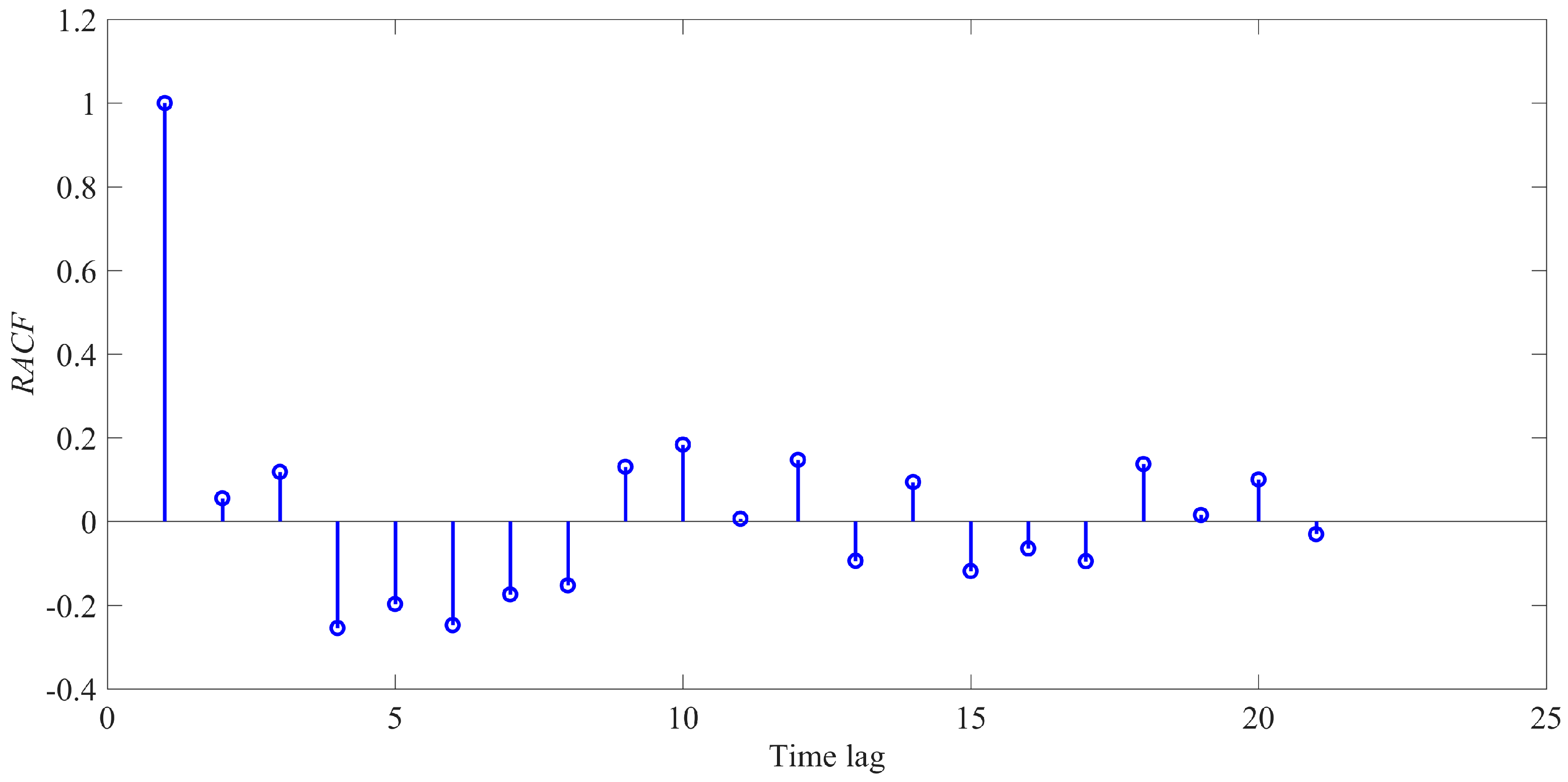
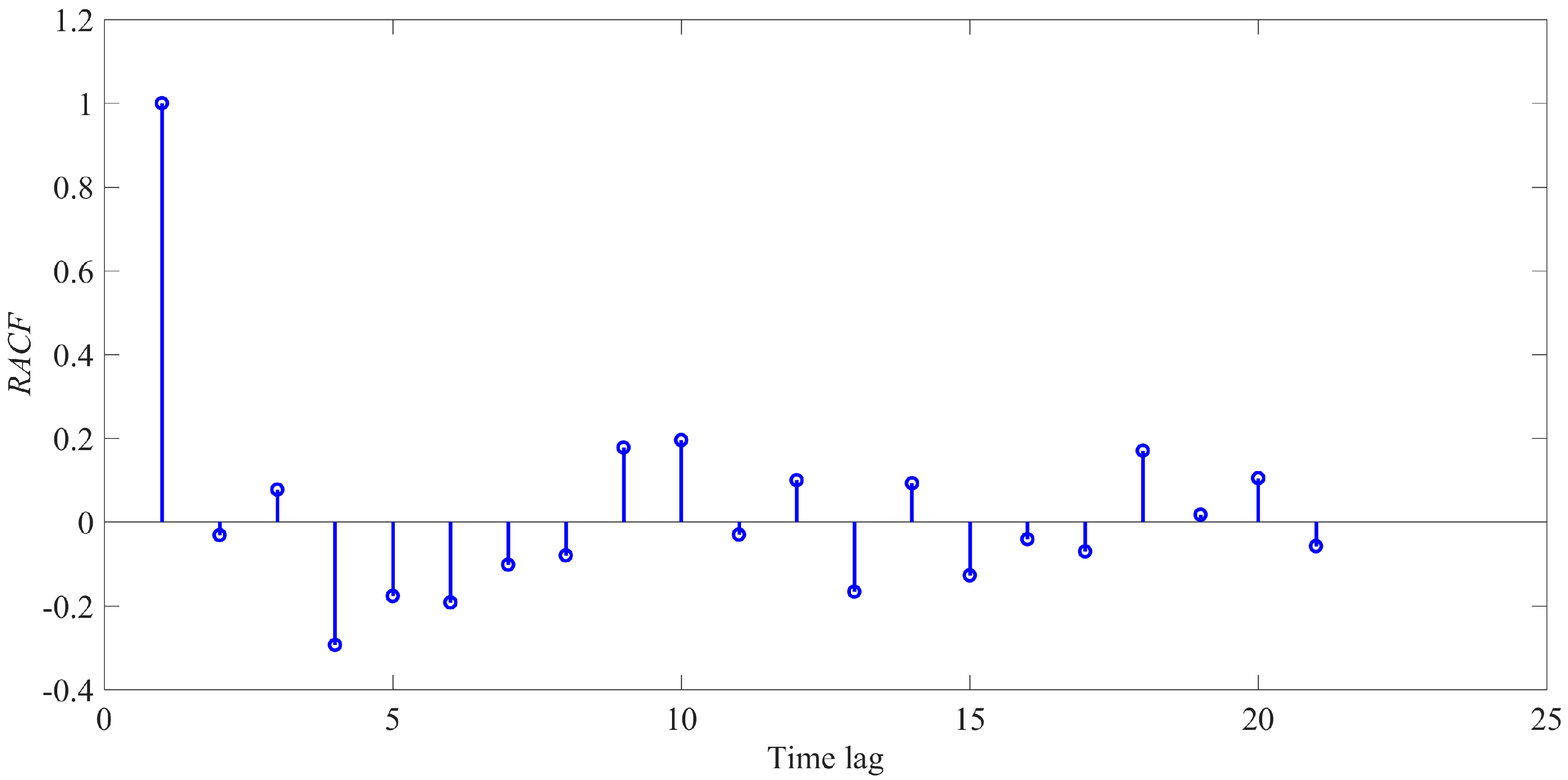
The
result for SDM using the HPSOSA is shown in
Figure 8. The estimated SDM qualifies the test as the values are in the range of –1 and +1.
4.2 Results for Double Diode PV Model
For the double diode model of the PV cell, statistics of 20 runs are tabulated in
Table 5. It is obvious from
Table 5 that the HPSOSA presented better statistics when compared with CPSO. The HPSOSA attains a best
RMSE value of 7.4532 × 10
−4, which is far better than the best
RMSE value attained by CPSO. The HPSOSA outperforms CPSO in all means of average, best, maximum, standard deviation and median. The HPSOSA achieved a good standard deviation of 5.8569 × 10
−5 while CPSO achieved a standard deviation of 5.0461 × 10
−4.
Table 6 lists the best values of parameters estimated by HPSOSA and other five optimization algorithms along with
and
.
Table 6 is evident of the superiority of the HPSOSA compared with other algorithms. It is obvious that the HPSOSA achieved significantly low values of
and
, 7.453163 × 10
−4 and 6.5556 × 10
−4 respectively.
To further examine that how close the currents are calculated by the HPSOSA with the experimentally measured currents,
Figure 9 and
Figure 10 have been shown.
Figure 9 plotted the
I-V characteristics of the estimated model and the experimental data while
Figure 10 plotted the
P-V characteristics of the estimated model and the experimental data. It is clear from
Figure 9 and
Figure 10 that the current and power estimated by the HPSOSA closely trace the experimentally measured data.
Table 7 shows another measure of how close are the estimated model and the experimentally measured data by virtue of error between them. Experimentally measured voltage, current and the error between the experimental current and the calculated current have been listed in
Table 7. The very low error is an indication of the accuracy of the HPSOSA.
The
result for DDM using the HPSOSA has been shown in
Figure 11. The estimated DDM qualifies the test as the values are in the range of –1 and +1.
5. Conclusions
This paper has presented a hybrid optimization approach using particle swarm optimization and simulated annealing for parameter estimation of photovoltaic solar cell single diode and double diode models. Experimentally measured data of a silicone solar cell (RTC France), measured at an irradiance of 1000 W/m2 and a temperature of 33 °C, were used to estimate the models. The approach significantly improves the problem of premature convergence. The applied approach is compared with different metaheuristic algorithms, namely CPSO, IABC, HS, SA and PS. The HPSOSA outperformed all the compared algorithms by all means of statistical analysis used in this paper, i.e., average, best, maximum, standard deviation and median. The HPSOSA achieved very low values of RMSE and MAE comparatively. The HPSOSA successfully passed the RACF test and the test values lie within the confidence interval.