Design of a Control System for a Maglev Planar Motor Based on Two-Dimension Linear Interpolation
Abstract
:1. Introduction
2. Analysis Model of Maglev Planar Motor
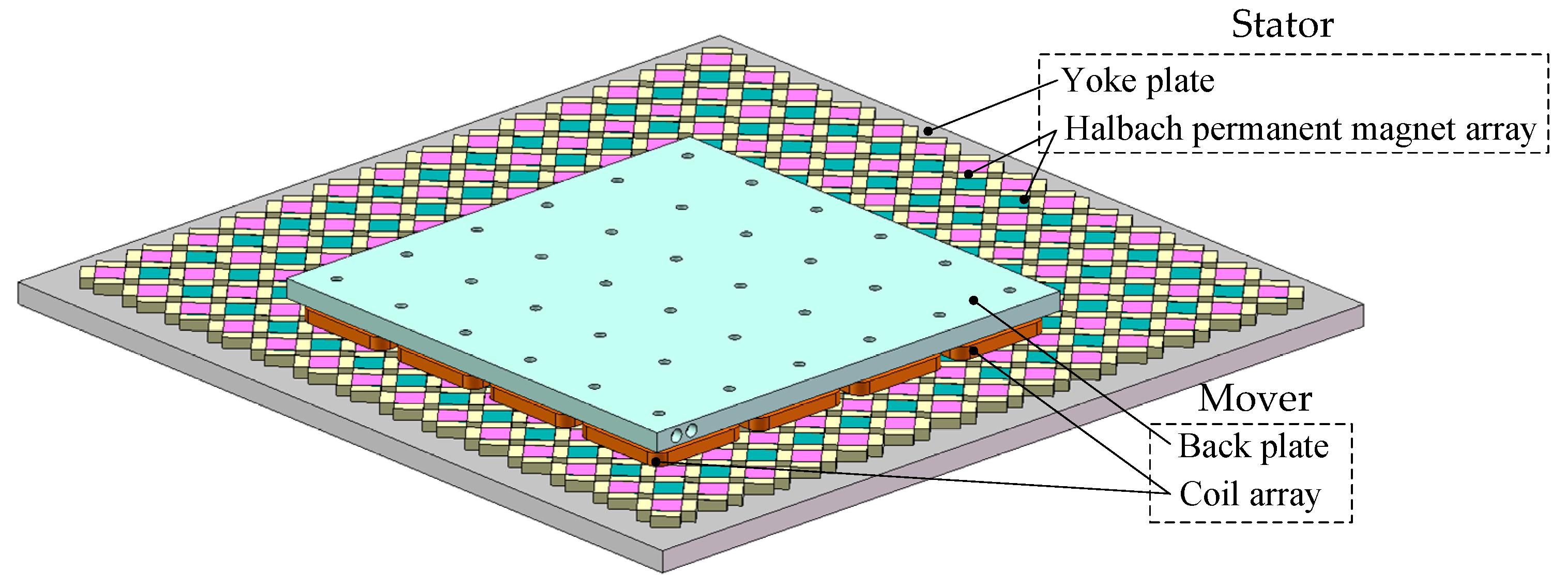
2.1. Structure and Working Principle
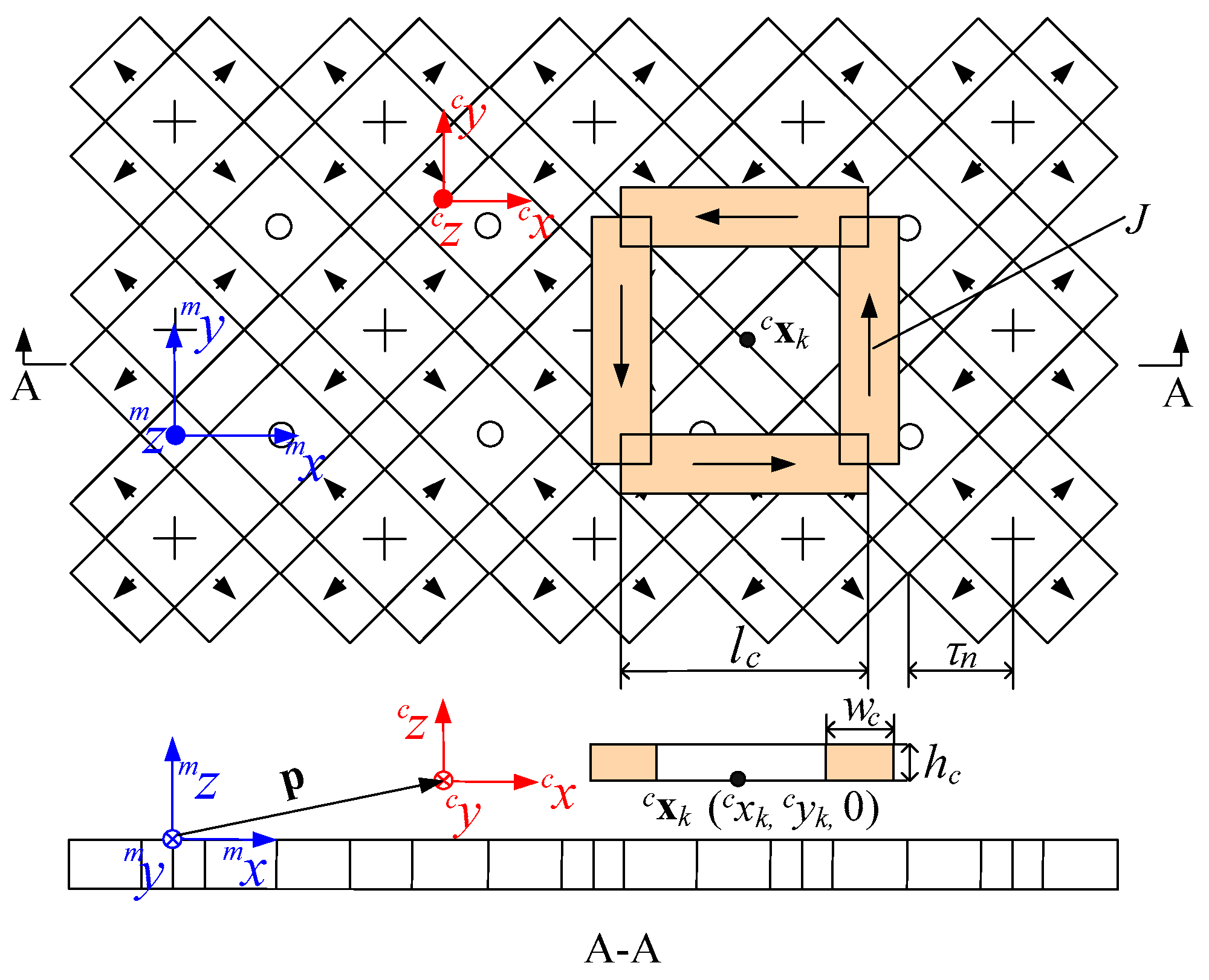
2.2. Coordinate Definition and Transformation
2.3. Electromagnetic Force and Torque
3. Design of the Control System
3.1. Electromagnetic Model Based on Two-Dimensional Linear Interpolation
3.1.1. Interpolation Region Partition
3.1.2. Interpolation Calculation
3.2. Current Decoupling
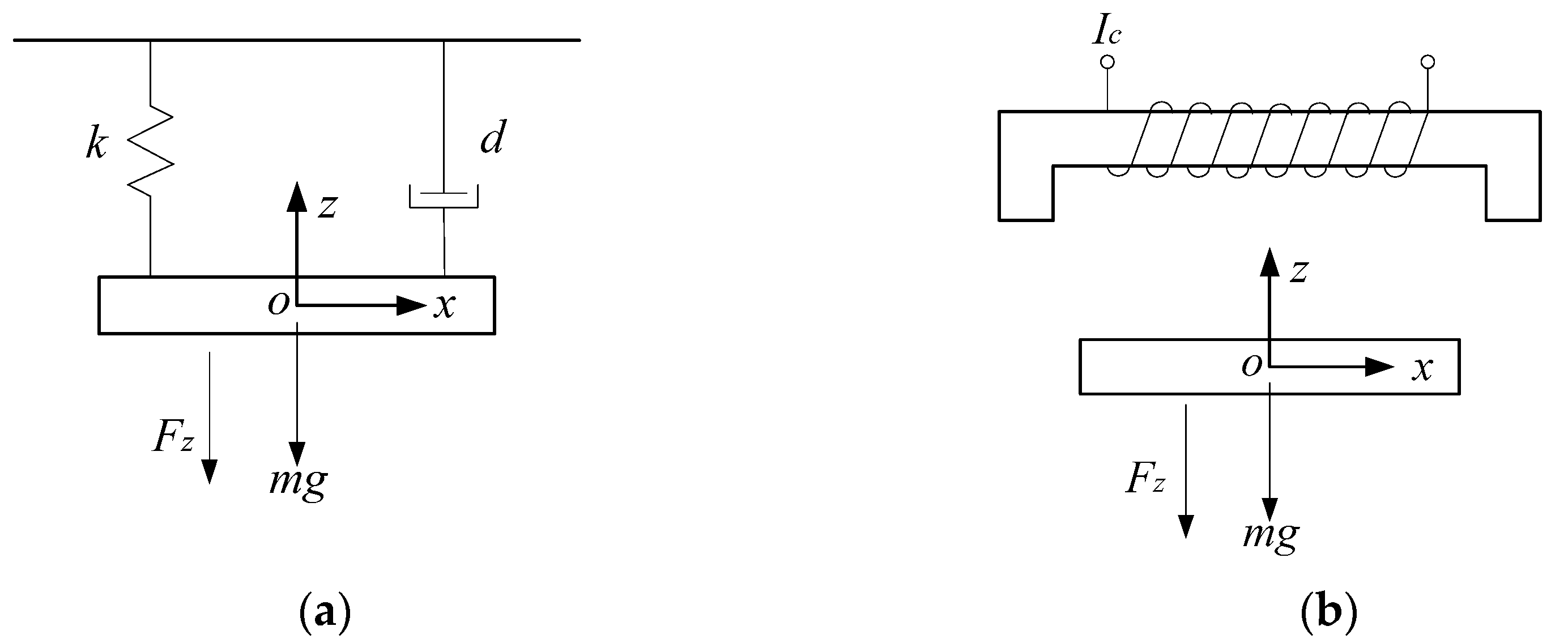
3.3. Dynamic Model
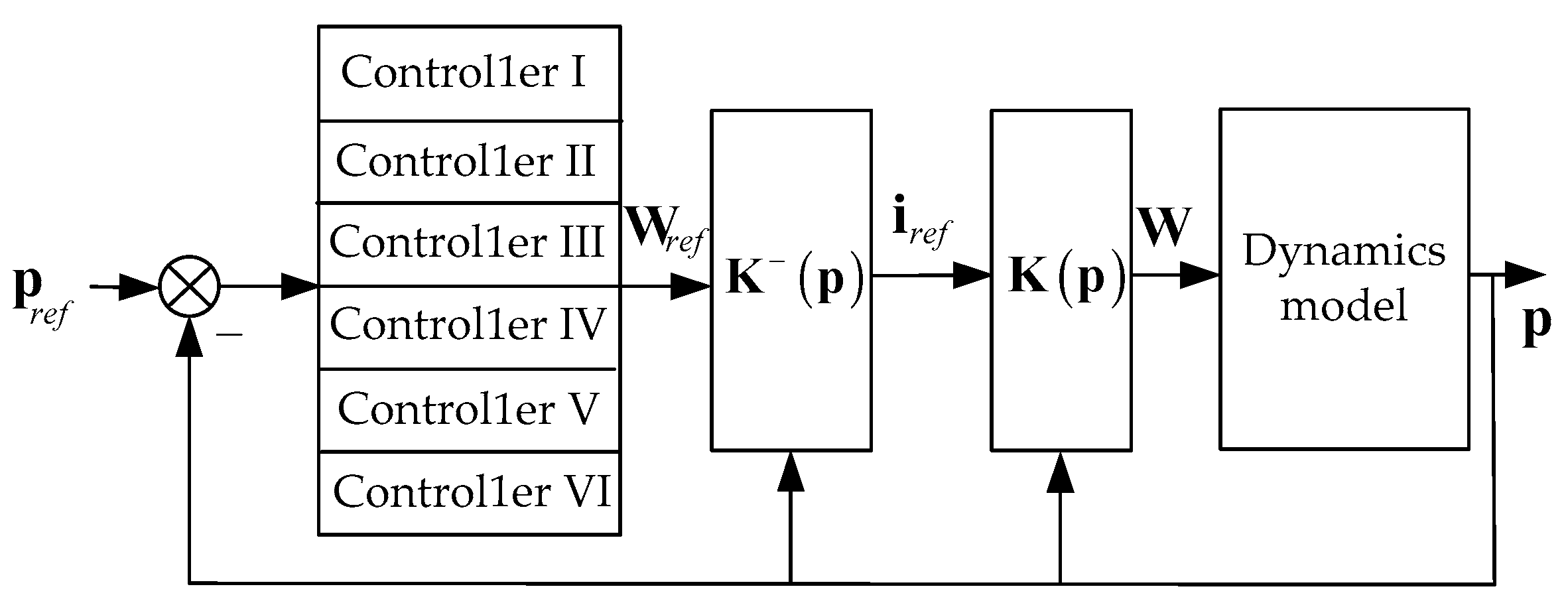
3.4. Control System Structure
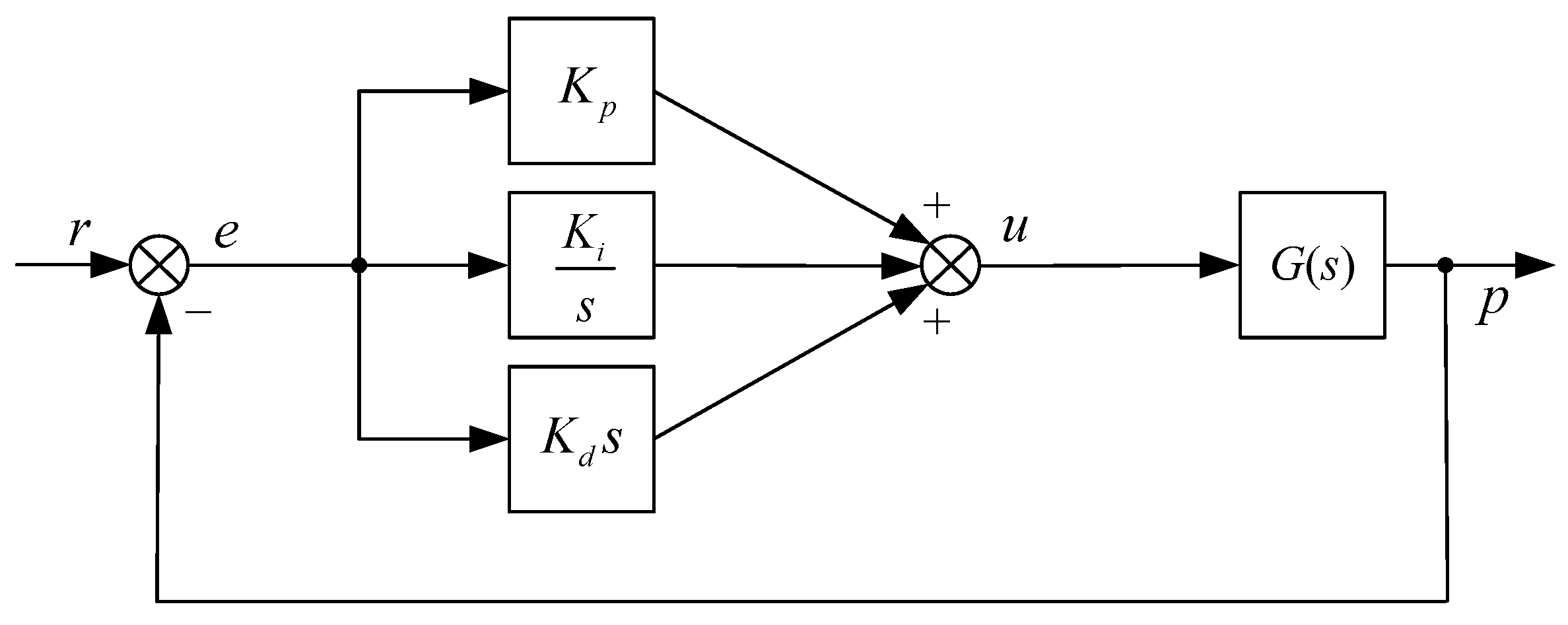
3.5. Controller Design
3.5.1. Control Law Analysis
3.5.2. Controller Struture
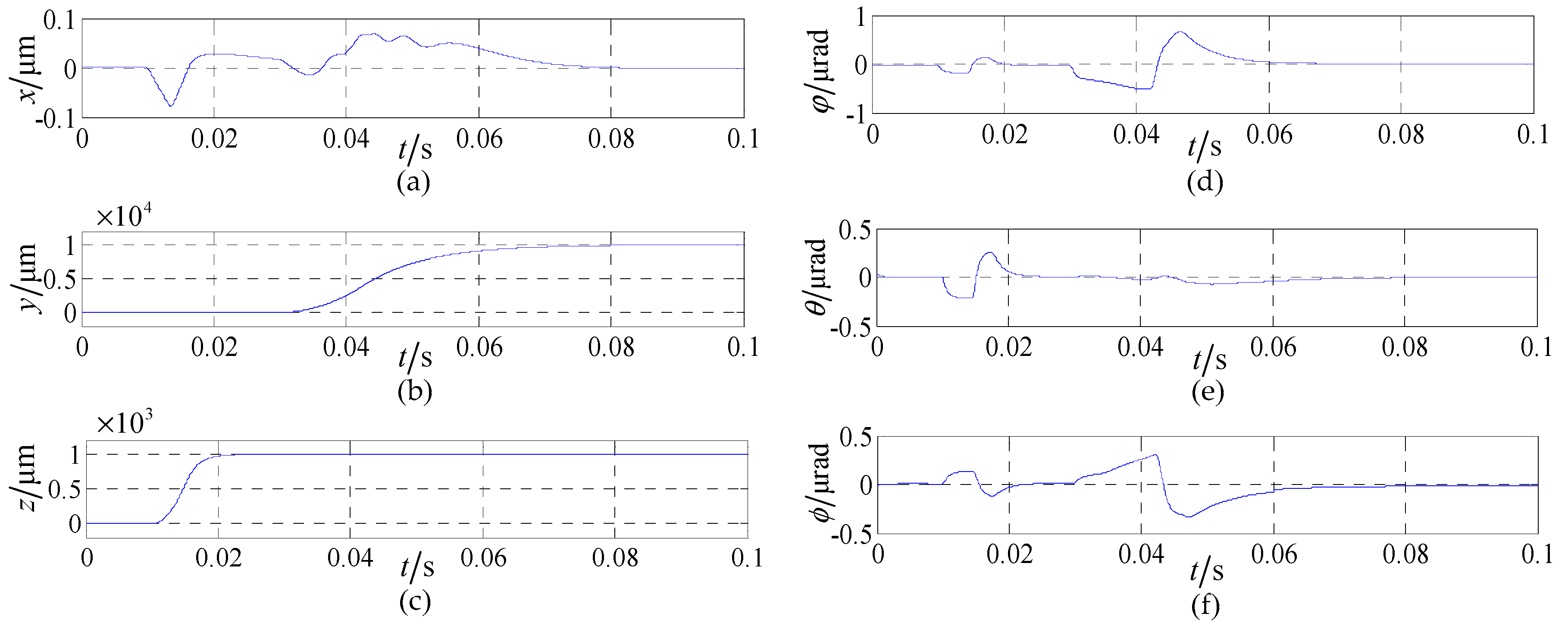
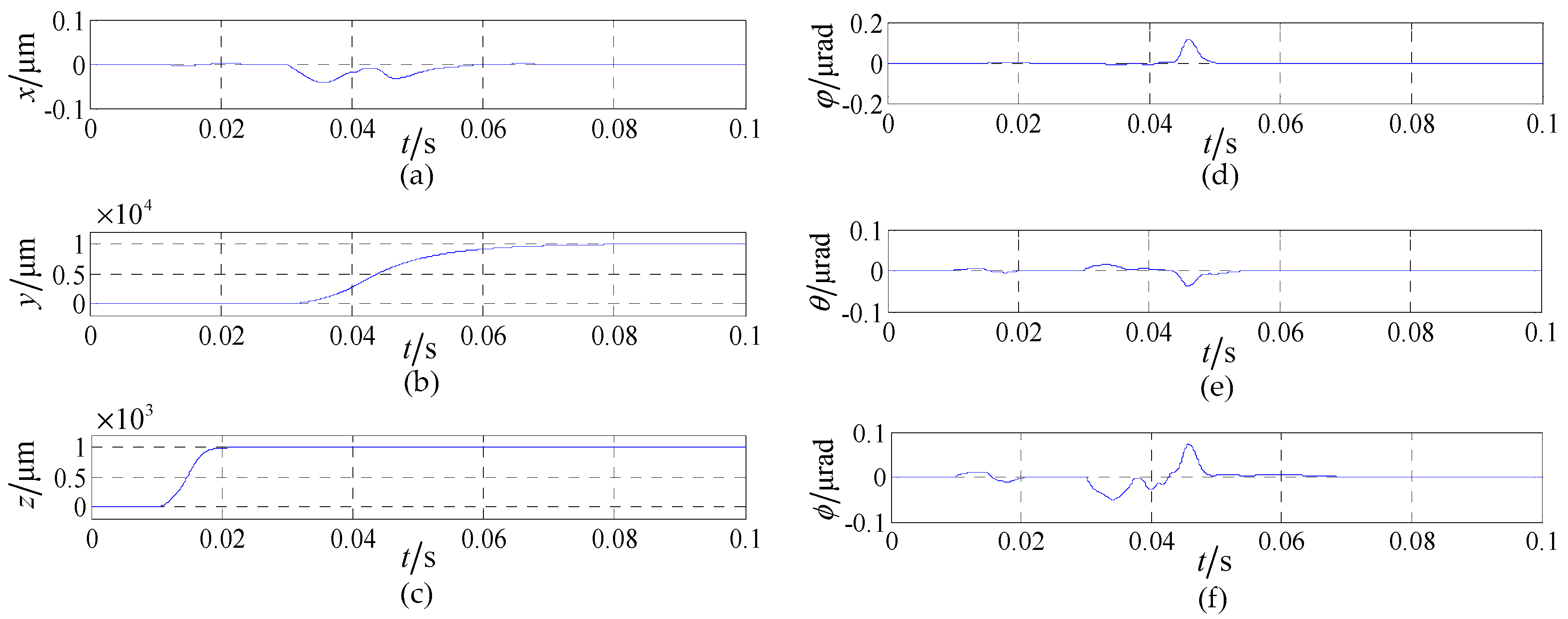
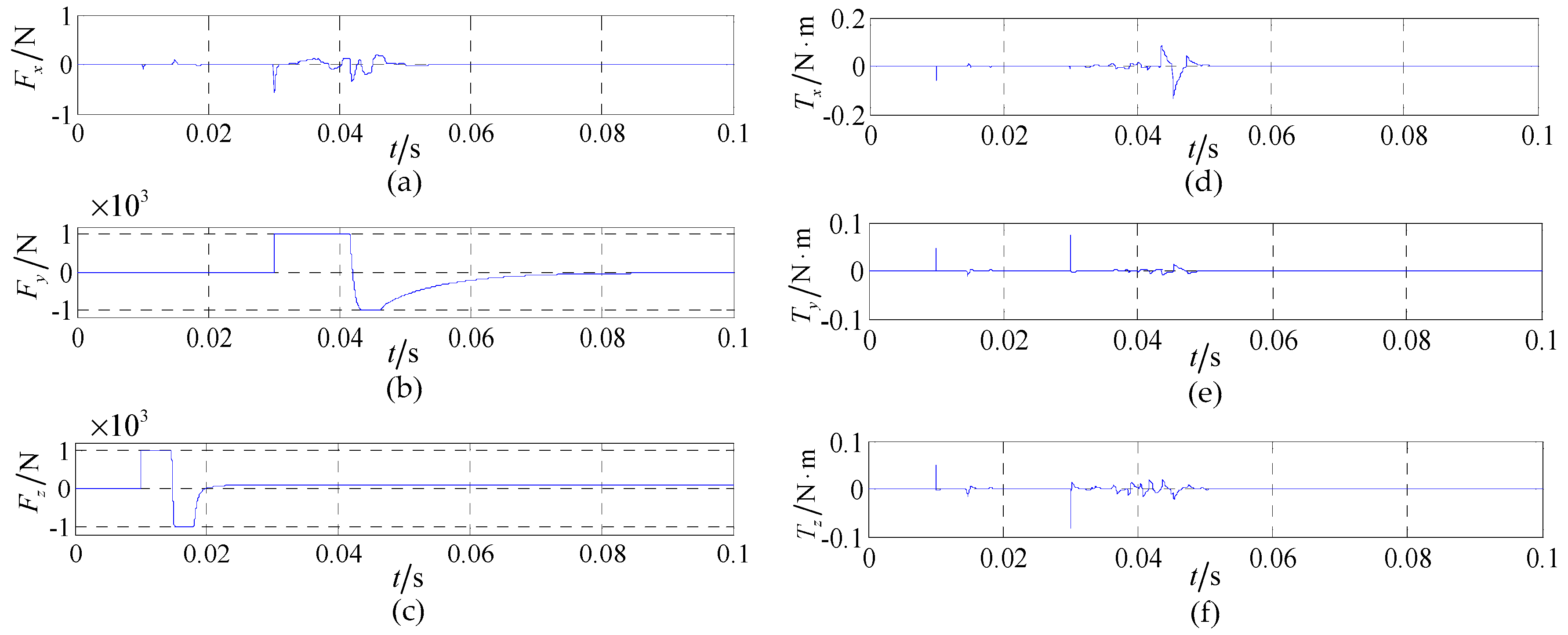
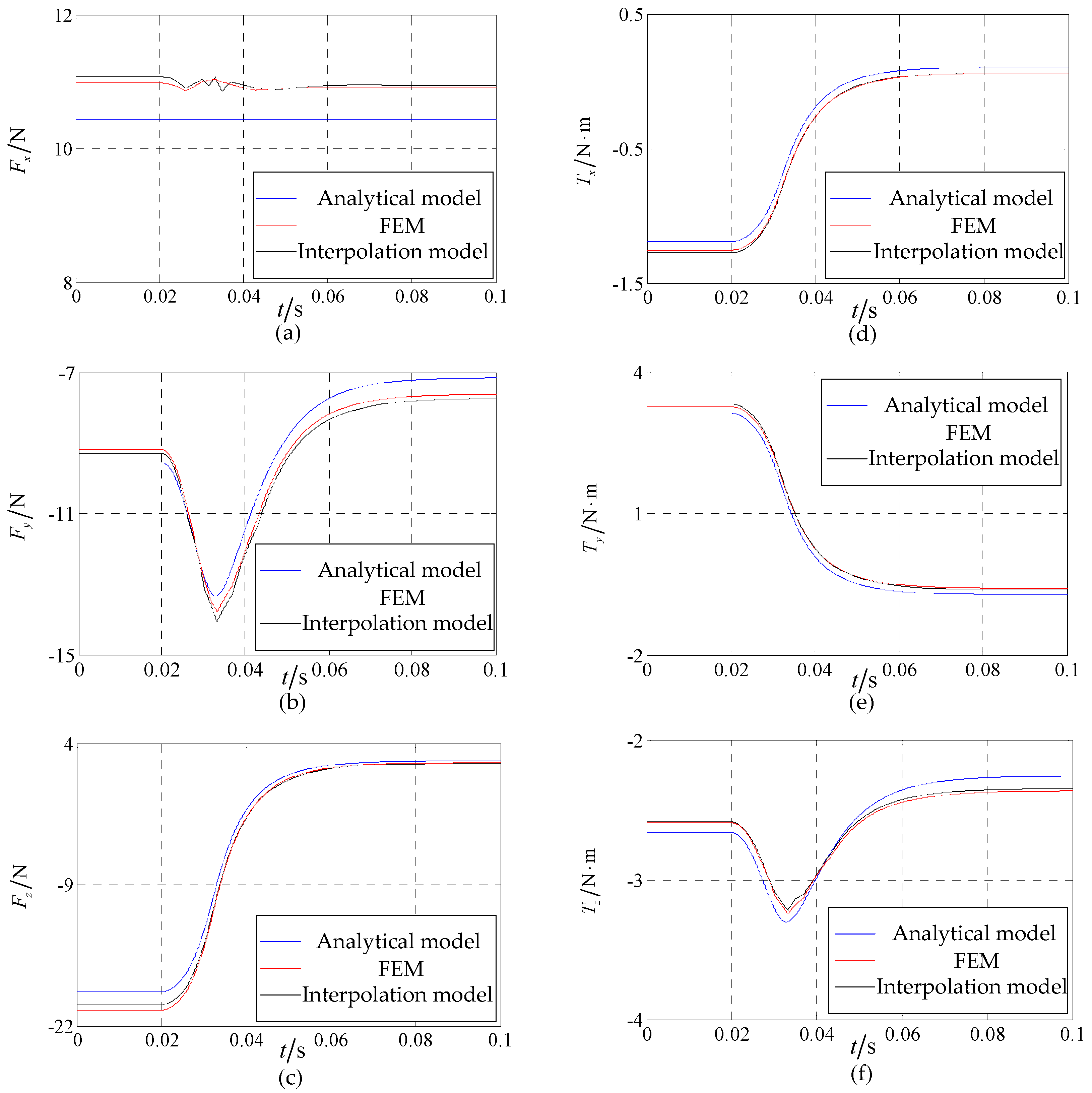
4. Validation and Analysis
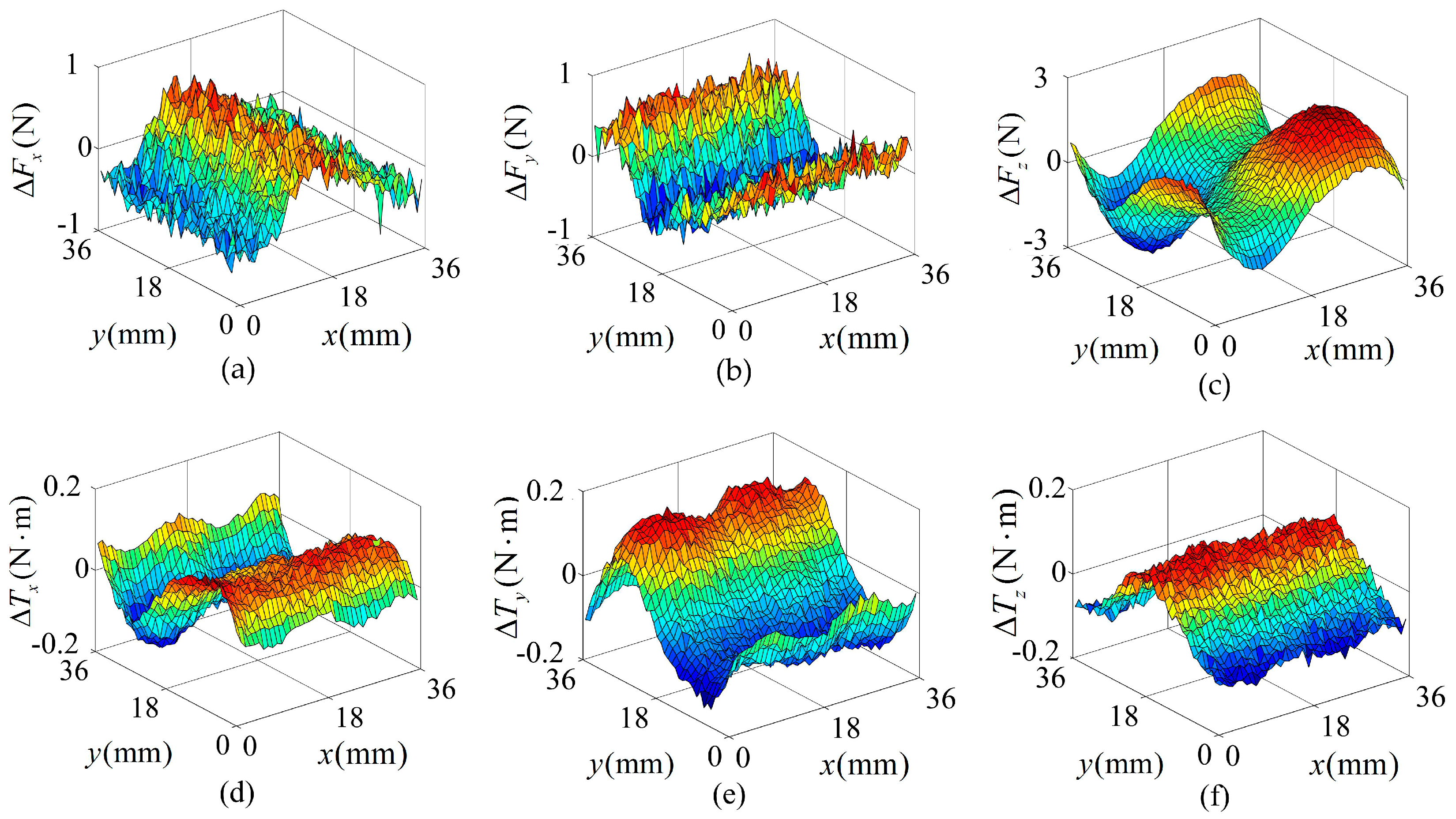
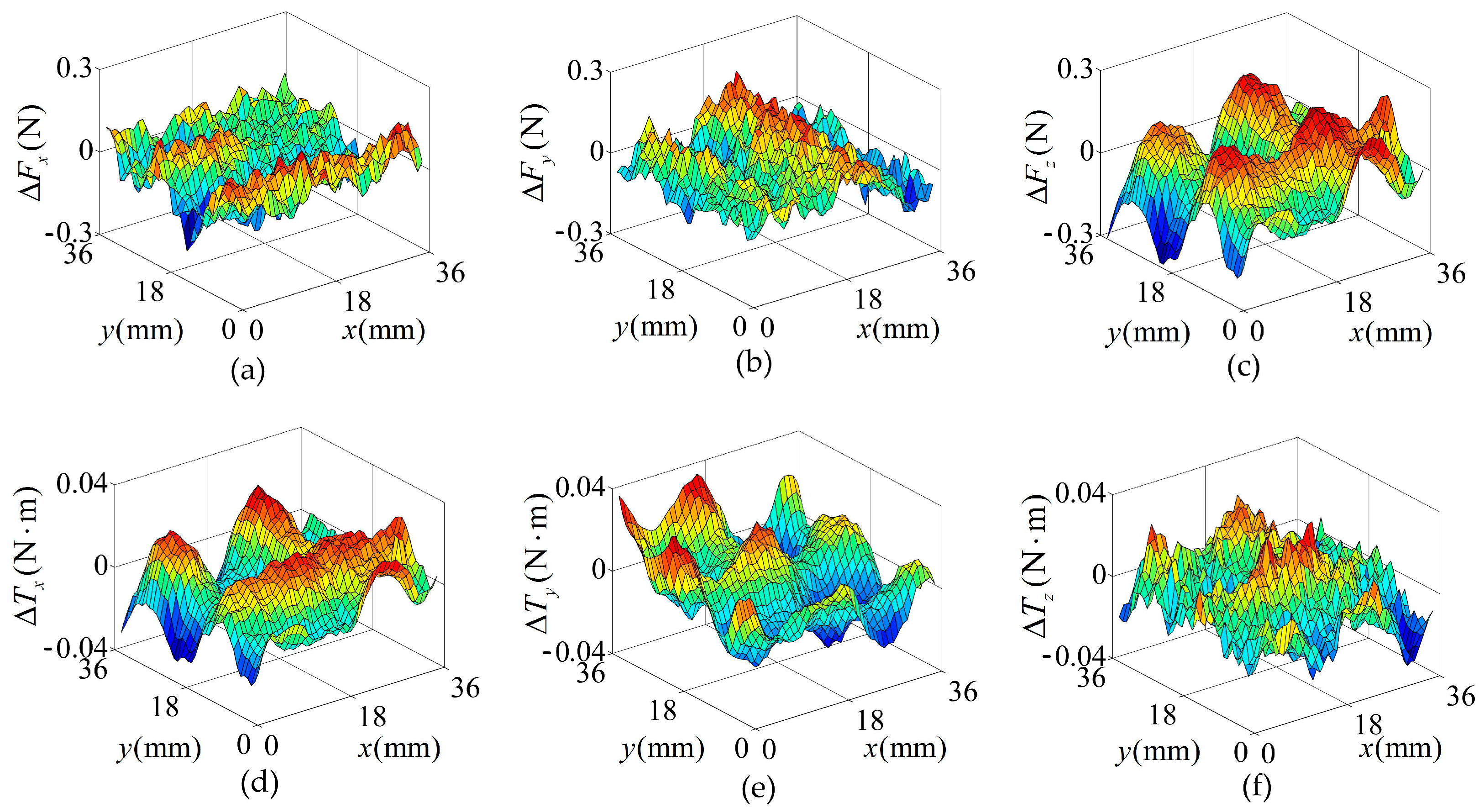
4.1. Model Accuracy Analysis
4.2. System Precision Analysis
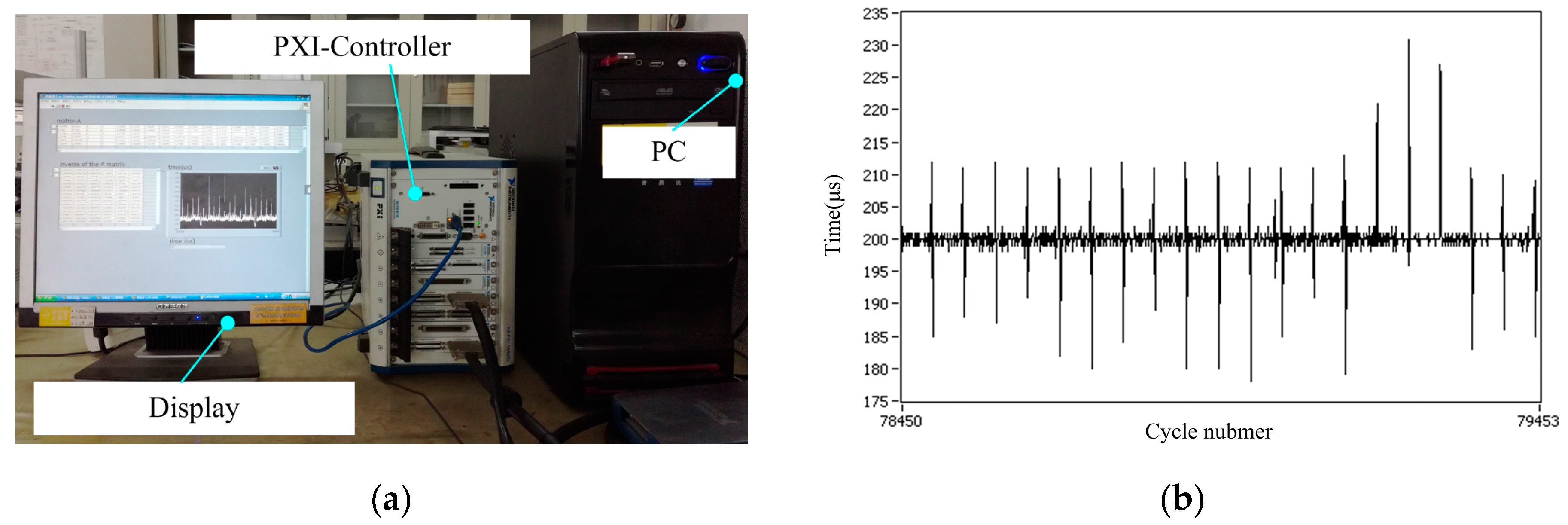
4.3. Model Real-Time Verification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rovers, J.M.M.; Jansen, J.W.; Compter, J.C.; Lomonova, E.A. Analysis method of the dynamic force and torque distribution in the magnet array of a commutated magnetically levitated planar actuator. IEEE Trans. Ind. Electron. 2012, 59, 2157–2166. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Kim, W.J. Design and control of a compact lightweight planar position moving over a concentrated-field magnet matrix. IEEE Trans. Mechatron. 2013, 18, 1090–1099. [Google Scholar] [CrossRef]
- Jansen, J.W.; Lomonova, E.A.; Vandenput, A.J.A.; Van Lierop, C.M.M. Analytical model of a magnetically levitated linear actuator. In Proceedings of the Fourtieth IAS Annual Meeting, IEEE Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 2107–2113. [Google Scholar]
- Jansen, J.W.; Smeets, J.P.C.; Overboom, T.T. Overview of analytical models for the design of linear and planar motors. IEEE Trans. Magn. 2014, 50, 39–52. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.Q.; Li, L.Y. Modeling and design of an integrated winding synchronous permanent magnet planar motor. IEEE Trans. Plasma Sci. 2013, 41, 1214–1219. [Google Scholar] [CrossRef]
- Ueda, Y.; Ohsaki, H. A Planar actuator with a small mover traveling over large yaw and translational displacements. IEEE Trans. Magn. 2008, 44, 609–616. [Google Scholar] [CrossRef]
- Christian, S.R.J.; Kim, W.J. Multivariable control and optimization of a compact 6-DOF precision positioner with hybrid H2/H∞ and digital filtering. IEEE Trans. Control Syst. Technol. 2013, 21, 1641–1651. [Google Scholar]
- Jansen, J.W.; van Lierop, C.M.M.; Lomonova, E.A. Magnetically levitated planar actuator with moving magnets. IEEE Trans. Ind. Appl. 2008, 44, 1108–1115. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.Q.; Zhang, H.; Guo, S.L. Characteristic analysis of a long-stroke synchronous permanent magnet planar motor. IEEE Trans. Magn. 2012, 48, 4658–4661. [Google Scholar] [CrossRef]
- Jansen, J.W. Magnetically Levitated Planar Actuator with Moving Magnets: Electromechanical Analysis and Design. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2007. [Google Scholar]
- Hamers, H.R. Actuation Principles of Permanent Magnet Synchronous Planar Motors: A Literature Survey; Working Paper; Eindhoven University of Technology: Eindhoven, The Netherlands, 2005. [Google Scholar]
- Van Lierop, C.M.M.; Jansen, J.W.; Damen, A.A.H.; Lomonova, E.A.; van den Bosch, P.P.J.; Vandenput, A.J.A. Model-based commutation of a long-stroke magnetically levitated linear actuator. IEEE Trans. Ind. Appl. 2009, 45, 1982–1990. [Google Scholar] [CrossRef]
- Peng, J.R.; Zhou, Y.F.; Liu, G.D. Calculation of a new real-time control model for the magnetically levitated ironless planar motor. IEEE Trans. Magn. 2013, 49, 1416–1422. [Google Scholar] [CrossRef]
- Xu, F.Q.; Dinavahi, V.; Xu, X.Z. Parallel computation of wrench model for commutated magnetically levitated planar actuator. IEEE Trans. Ind. Electron. 2016, 63, 7621–7631. [Google Scholar] [CrossRef]
- Jansen, J.W.; van Lierop, C.M.M.; Lomonova, E.A.; Vandenput, A.J.A. Modeling of magnetically levitated planar actuators with moving magnets. IEEE Trans. Magn. 2007, 43, 15–25. [Google Scholar] [CrossRef]
- Verma, S.; Shakir, H.; Kim, W.J. Novel electromagnetic actuation scheme for multiaxis nanopositioning. IEEE Trans. Magn. 2006, 42, 2052–2062. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Teo, T.J.; Pang, C.K. Design and modeling of a six degrees-of-freedom magnetically levitated positioner using square coils and 1D halbach arrays. IEEE Trans. Ind. Electron. 2016, 64, 440–450. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, Q.B.; Jin, Y.X.; Zhang, H.L. Modeling and analysis of a new cylindrical magnetic levitation gravity compensator with low stiffness for the 6-DOF fine stage. IEEE Trans. Ind. Electron. 2015, 62, 3629–3639. [Google Scholar] [CrossRef]
- Berkelman, P.; Dzadovsky, M. Magnetic levitation over large translation and rotation ranges in all directions. IEEE/ASME Trans. Mechatron. 2013, 18, 44–52. [Google Scholar] [CrossRef]
- Lai, Y.C.; Lee, Y.L.; Yen, J.Y. Design and servo control of a single-deck planar maglev stage. IEEE Trans. Magn. 2007, 43, 2600–2602. [Google Scholar] [CrossRef]
- Zeng, Z.P.; Triozon, F.; Barraud, S.; Niquet, Y.M. A Simple interpolation model for the carrier mobility in trigate and gate-all-around silicon NWFETs. IEEE Trans. Electron. Devices 2017, 64, 2485–2491. [Google Scholar] [CrossRef]
- Chen, Y.D.; Li, L. Smooth geodesic interpolation for five-axis machine tools. IEEE/ASME Trans. Mechatron. 2016, 21, 1592–1603. [Google Scholar] [CrossRef]
- Tang, J.J.; Ni, F.; Ponci, F.; Monti, A. Dimension-adaptive sparse grid interpolation for uncertainty quantification in modern power systems: Probabilistic power flow. IEEE Trans. Power Syst. 2016, 31, 907–919. [Google Scholar] [CrossRef]
- Huang, X.D.; Jing, S.X.; Wang, Z.H.; Xu, Y.; Zheng, Y.Q. Closed-form FIR filter design based on convolution window spectrum interpolation. IEEE Trans. Signal Process. 2016, 64, 1173–1186. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; pp. 19–48. [Google Scholar]
- Jansen, J.W.; van Essen, J.M.; van Lierop, C.M.M.; Lomonova, E.A.; Vandenput, A.J.A. Design and test of an ironless, three degree-of-freedom, magnetically levitated linear actuator with moving magnets. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 858–865. [Google Scholar]
- Li, D.Q. Encyclopedia of Microfluidics and Nanofluidics; Springer Science & Business Media: New York, NY, USA, 2008; p. 47. [Google Scholar]
- Press, W.H. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 110–196. [Google Scholar]
- Wang, J.S.; Yang, G.H. Data-driven output-feedback fault-tolerant compensation control for digital PID control systems with unknown dynamics. IEEE Trans. Ind. Electron. 2016, 63, 7029–7039. [Google Scholar] [CrossRef]
- Song, Y.D.; Huang, X.; Wen, C.Y. Robust adaptive fault-tolerant PID control of MIMO nonlinear systems with unknown control direction. IEEE Trans. Ind. Electron. 2017, 64, 4876–4884. [Google Scholar] [CrossRef]
- Pounds, P.E.I.; Dollar, A.M. Stability of helicopters in compliant contact under PD-PID control. IEEE Trans. Robot. 2014, 30, 1472–1486. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Singhal, R.; Padhee, S.; Kaur, G. Design of fractional order PID controller for speed control of DC motor. Int. J. Sci. Res. Publ. 2012, 2, 1–8. [Google Scholar]
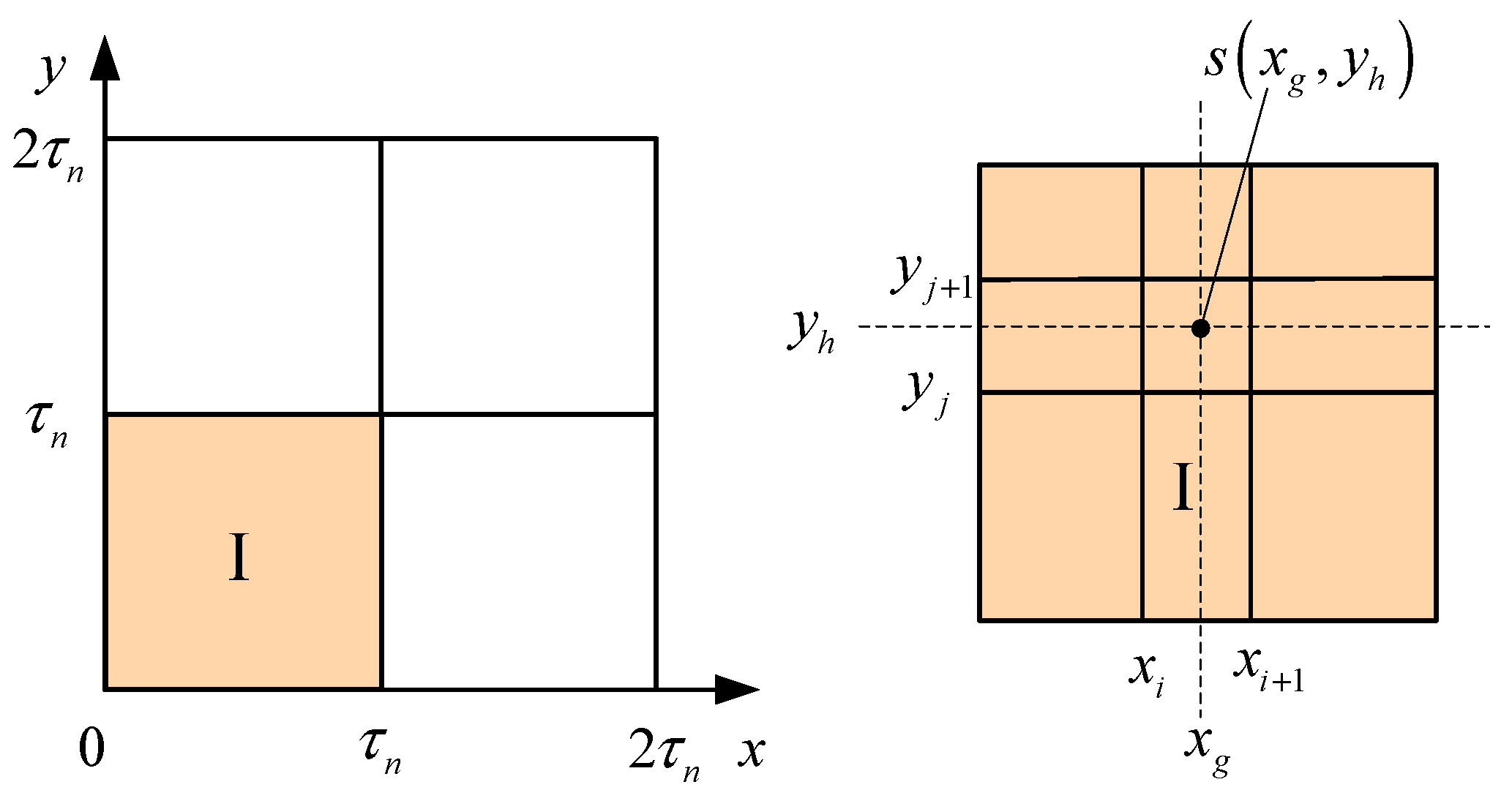

| Symbol | Quantity | Value |
|---|---|---|
| τn | pole pitch | 17.7 mm |
| wc | coil width | 11.8 mm |
| hc | coil height | 10 mm |
| hm | permanent magnet thickness | 20 mm |
| h | air gap | 1 mm |
| lc | coil length of the straight coil segment | 53.1 mm |
| Bz | magnetic flux density vertical component | 0.81 T |
| Nc | number of turns | 218 |
| m | mover mass | 20 kg |
| Ix | x-axis moment of inertia | 0.268 kg·m2 |
| Iy | y-axis moment of inertia | 0.268 kg·m2 |
| Iz | z-axis moment of inertia | 0.533 kg·m2 |
| g | acceleration of gravity | 9.8 m/s2 |
| Method | Time |
|---|---|
| FEM | 1 h |
| analytical method | 200 μs |
| interpolation method | 200 μs |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, F.; Kou, B.; Zhang, L.; Yin, X.; Zhou, Y. Design of a Control System for a Maglev Planar Motor Based on Two-Dimension Linear Interpolation. Energies 2017, 10, 1132. https://doi.org/10.3390/en10081132
Xing F, Kou B, Zhang L, Yin X, Zhou Y. Design of a Control System for a Maglev Planar Motor Based on Two-Dimension Linear Interpolation. Energies. 2017; 10(8):1132. https://doi.org/10.3390/en10081132
Chicago/Turabian StyleXing, Feng, Baoquan Kou, Lu Zhang, Xiangrui Yin, and Yiheng Zhou. 2017. "Design of a Control System for a Maglev Planar Motor Based on Two-Dimension Linear Interpolation" Energies 10, no. 8: 1132. https://doi.org/10.3390/en10081132





