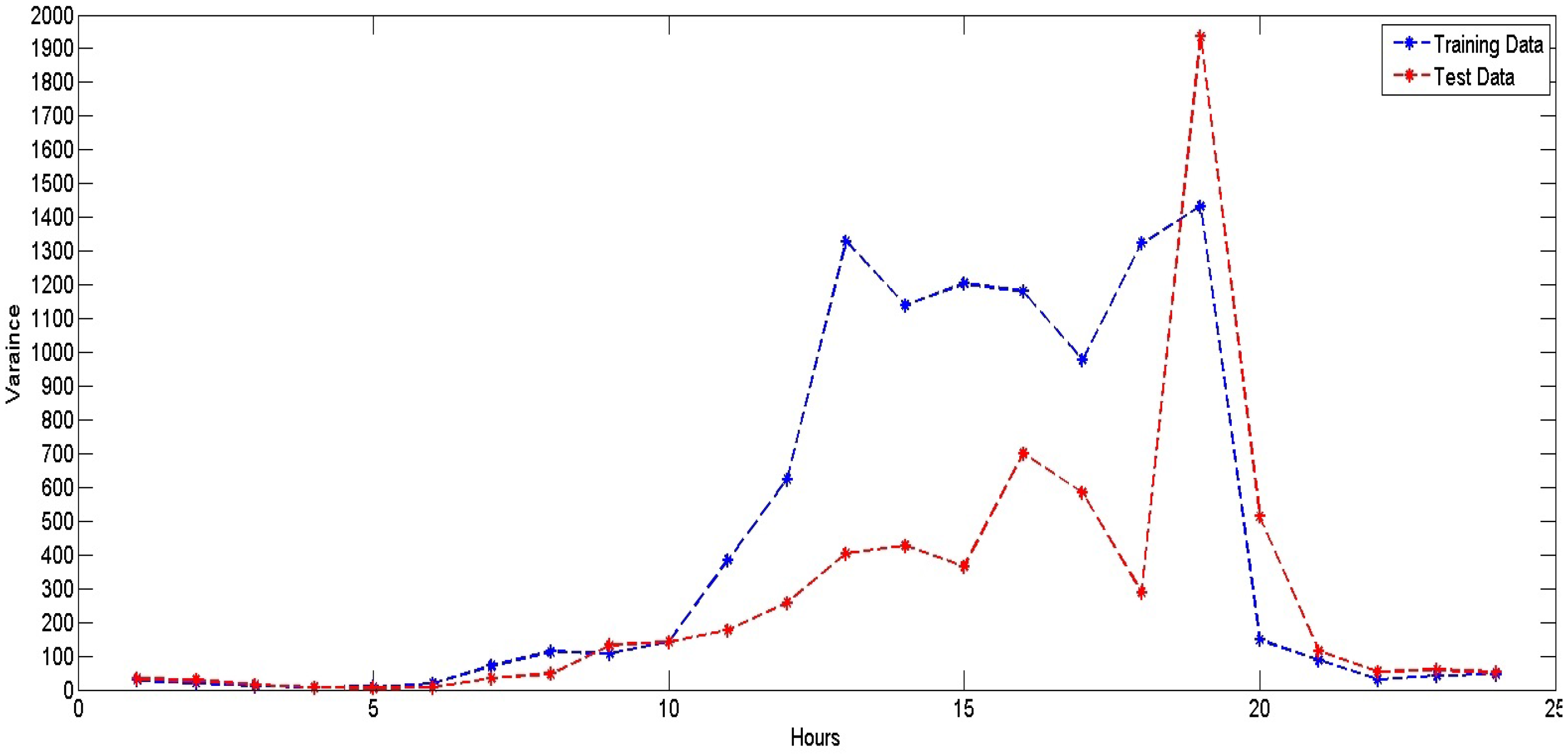
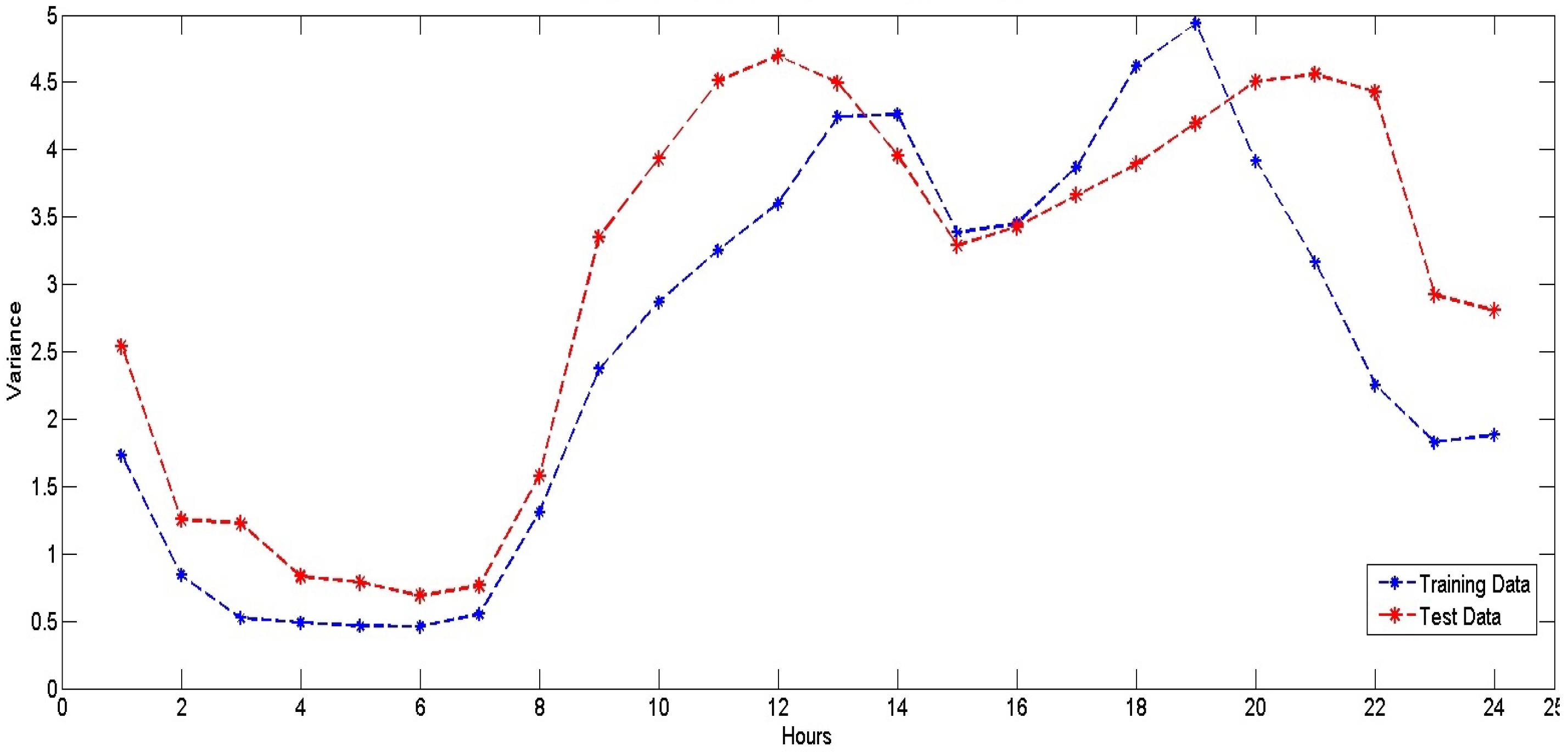
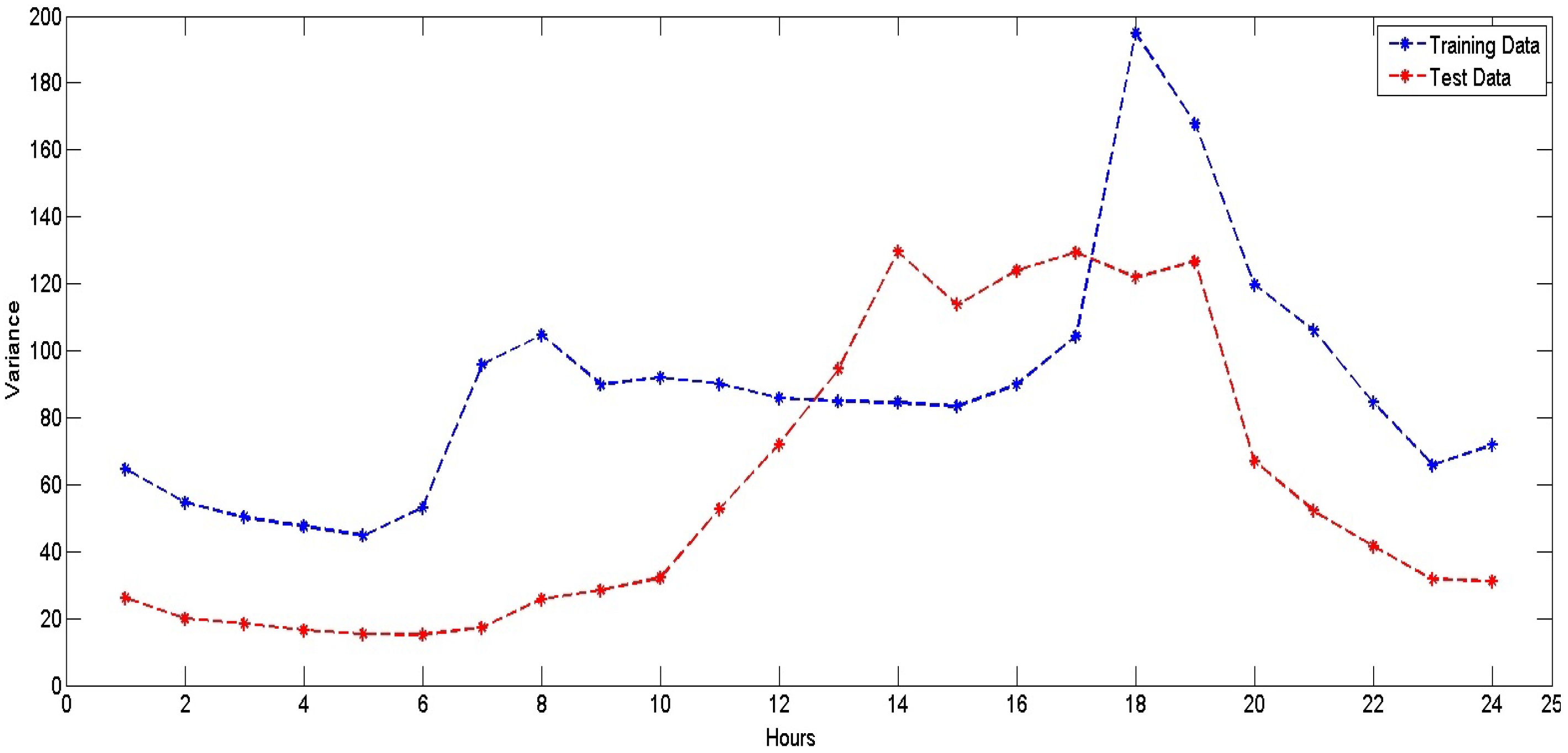
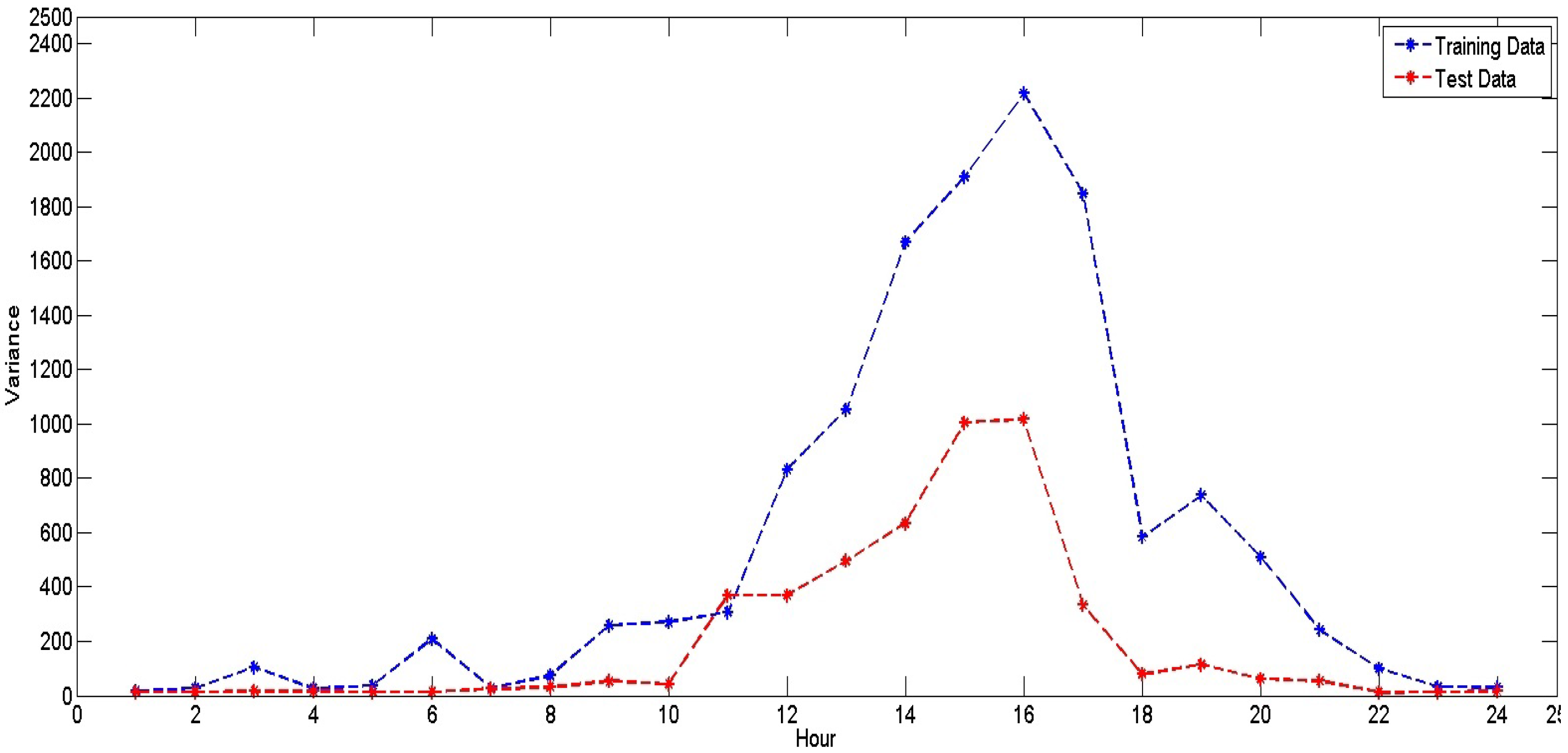
Our objective is to develop a robust model that can sustain its good performance irrespective of various uncertainty factors. For that, we propose an ensemble prediction model that provides flexibility in choosing the type of algorithm for price prediction. This flexibility enables the user to choose the algorithm based on available resources, time constraints and computational complexity.
We believe that incorporating the modified ensemble learning [
42] scenario into the well-known prediction methods will help to improve the performance of the prediction model. With the current research on price prediction, machine learning algorithms, like Artificial Neural Network (ANN) [
43], Support Vector Regression (SVR) [
44] and Random Forest (RF) [
45] showed promising results. Hence, this paper proposes an ensemble learning strategy with ANN, SVR and RF as the members of the expert algorithm that learn from the environment and update their parameters based on the information they have collected.
3.1. Model Formulation
Consider a wholesale electricity market where a retailer proposes an hour-ahead bidding price based only on information that is available at the present moment. Once the actual price is known, the retailer is able to evaluate the validity of the predictions and will seek to minimize the difference between the actual and predicted market prices.
Now, let us consider an ensemble forecasting model involving a number of forecasting algorithms. Let denote a set of participating forecasting algorithms, where n is the number of participating algorithms and is an individual participating algorithm.
Each hour of the day is treated separately, such that, in total, 24 separate ensemble forecasting models are constructed, one for each hour . For the sake of simplicity, we omit this hour parameter in our description of the proposed model below. Therefore, unless stated otherwise, all variables used below belong to an individual hour h of the day.
The prediction error of an algorithm
is defined as follows:
where
P is the actual price and
is the price predicted by algorithm
x. Let
(
) be the past performance “weight” of algorithm
(the performance weights are calculated using one of two algorithms, the Fixed Weight Method (FWM) or the Varying Weight Method (VWM), which will be explained in detail later).
The algorithm whose past performance weight
is the highest on a given day is selected as the “expert” algorithm for that day and is denoted as
.
In most cases, we will use the forecasts produced by the expert algorithm as our final prediction result. This is due to our expectation that the algorithm with the highest performance weight (i.e., the one that has performed the best recently) will also give us the best prediction result for today. However, this expectation might not always be realistic. For example, if the best performing algorithm is rotating among all of the participating algorithms, the recent best performer may not be today’s best performer, and consequently, the expert algorithm we have selected for today may not be actually optimal for today. Thus, in order to alleviate this effect and to make sure that the our prediction result of our ensemble algorithm on average is at least as good as that of the best individual algorithm, we include the following fallback mechanism.
Suppose we make the observations of our forecasting process for
m number of days. Then, we have a list
of containing
m expert algorithms.
Our expectation is that over
m days, the overall performance of the list
’s expert algorithms on their corresponding days should be superior to that of any individual participating algorithm acting alone. In order words, the cumulative prediction error incurred by our selected expert algorithms should be less than that of any individual algorithm. Formally, we should have:
Therefore, in the proposed algorithms, the constraint in Equation (
4) above is checked at every round. If the past cumulative prediction error of the selected expert algorithms over
m days exceeds that of any of the individual algorithms, the forecasts produced by the best individual algorithm are then used as the final prediction result. In addition, all participating algorithms are constantly re-trained using all available data to date to address the problem of concept drift [
46], which often occurs in time-series data like electricity prices.
3.2. Model Architecture
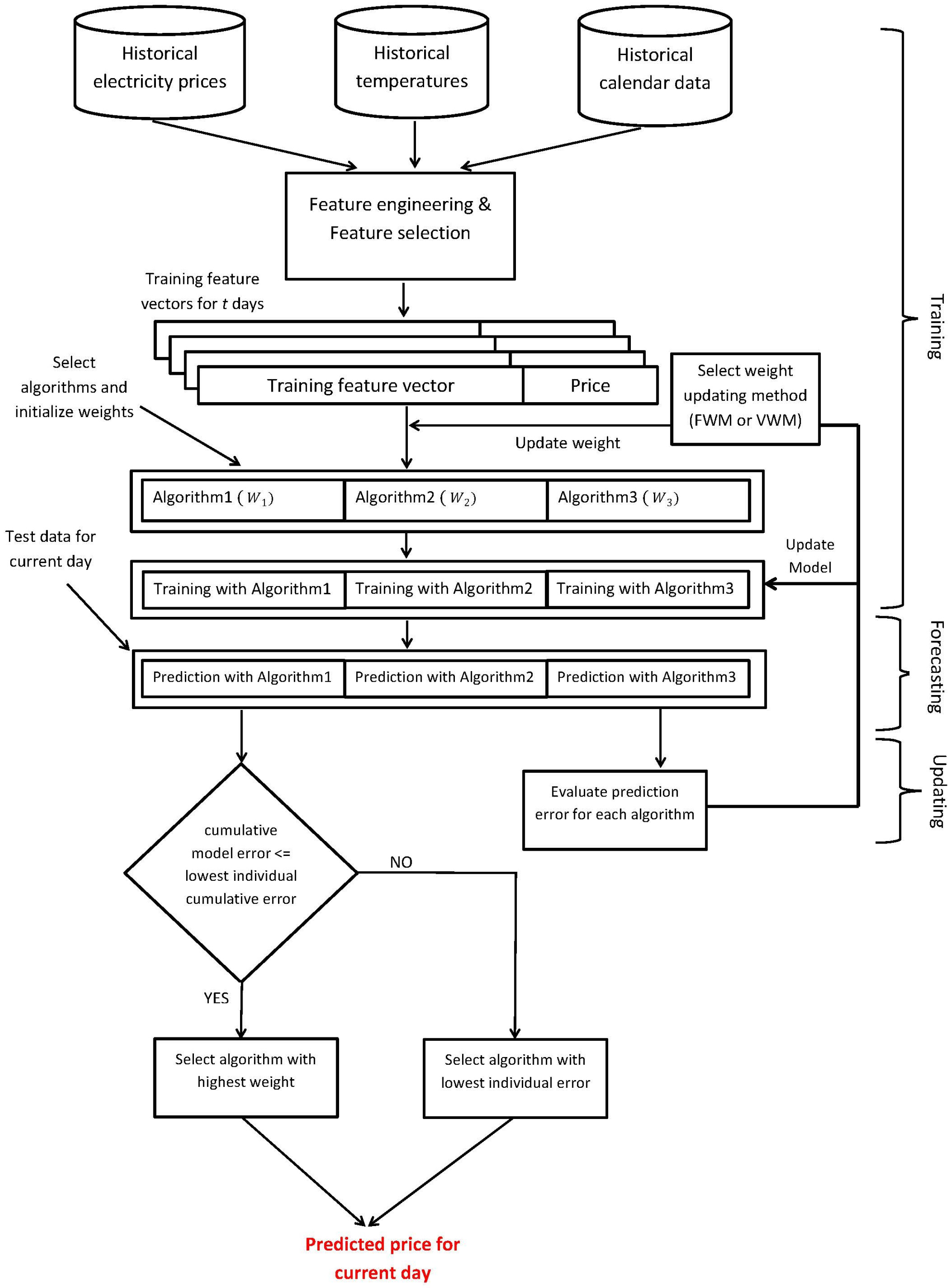
The proposed model for electricity price prediction is presented in
Figure 1. We have to recruit prediction algorithms that exhibit promising results when utilized separately to participate in our ensemble model. Here, we show three participating algorithms for demonstration purposes (in theory, any number of different algorithms can be used under this model depending on the processing power and time available). The proposed model performs feature engineering on the price data along with the corresponding temperature and calendar data collected from a de-regulated electricity market, which is followed by feature selection, learning, predicting and model updating steps.
All of the participating algorithms will generate predictions, but the actual decision will be made by the algorithm whose performance was best recently in the previous days. On the first day of the model deployment, the expert algorithm will be chosen randomly. From the second day onward, for each hour of the day, the performance of each algorithm will be evaluated, and the best algorithm will be chosen based on the past prediction accuracy. The best predictor will be the expert predictor, whose predicted value for the next day will be the decisive value. At the end of each day when the actual price becomes available, every algorithm will analyze its own performance for that day. If the performance is within the range of the threshold, the models are maintained. Otherwise, the models are updated by re-training them with all of the available data up to date. The proposed ensemble models, using fixed weights and varying weights respectively, are described in Algorithms 1 and 2.
It should be noted that both algorithms are designed for each individual hour of the day. Therefore, for each algorithm, we need to run 24 separate instances of it to forecast the electricity prices for 24 h.
3.2.1. Algorithm 1: Fixed Weight Method
The Fixed Weight Method (FWM) is described in Algorithm 1. Briefly, FWM is initialized by assigning a weight of zero to all participating algorithms, except for one randomly-chosen expert algorithm, whose weight is set to one. Models for each participating algorithm are then built using the training dataset and are used to predict the target electricity prices for the unseen test data. Once we obtain the prediction from each model, the constraint in Equation (
4) is checked as a fallback procedure, and the final predicted value is decided. Then, the weight of each participating algorithm is updated based on the respective prediction accuracy. The weight for the model with the highest prediction accuracy is set to one, and zero is assigned to the weights of the rest of the models. The model with weight equal to one will be the expert model for the next day. If the performance of the expert model is below that of an individual model acting alone, a re-train signal is sent to the system, which will initiate the retraining of all of the individual models. Newly built models will replace the old models, but will maintain the weights of the previous models.
| Algorithm 1 Fixed weight method (, ) |
- 1:
choose the set A of n participating algorithms: - 2:
; /* initialize list of experts */ - 3:
; ; /* randomly select an algorithm as expert and assign its weight as 1 */ - 4:
for to n do - 5:
if then - 6:
; /* initialize weights of all algorithms except expert’s as 0 */ - 7:
end if - 8:
; /* build prediction model by training algorithm using data in the training set for days */ - 9:
; /* initialize cumulative prediction error of all algorithms as 0 */ - 10:
end for - 11:
; /* initialize cumulative prediction error of list of experts as 0 */ - 12:
FALSE; - 13:
- 14:
for to m do - 15:
/* for all m number of days in , do the following three steps */ - 16:
- 17:
/* Step 1: carrying out prediction */ - 18:
for to n do - 19:
/* apply prediction model of algorithm using data in the training set plus those in the testing set up until previous day */ - 20:
; - 21:
if then - 22:
; /* if weight is 1, then it is the current expert */ - 23:
add to list ; /* insert the current expert into list of experts */ - 24:
; /* tentatively, predicted price will be output of the current expert */ - 25:
end if - 26:
end for - 27:
- 28:
/* Step 2: fallback procedure and reporting */ - 29:
; /* l is index of algorithm with lowest cumulative error */ - 30:
if then - 31:
; /* take algorithm l’s output instead of expert algorithm’s */ - 32:
TRUE; /* all models must be updated later */ - 33:
end if - 34:
report ; /* report predicted price for j-th day as our output */ - 35:
- 36:
/* Step 3: prediction error calculation and updating — after actual price P of day j is known */ - 37:
; /* calculate expert algorithm’s prediction error */ - 38:
; - 39:
for to n do - 40:
; /* calculate all algorithms’ prediction errors */ - 41:
; - 42:
end for - 43:
; /* reset weight of old expert to 0 */ - 44:
; /* select algorithm with lowest error for j-th day as new expert for -th day */ - 45:
; /* set weight of new expert as 1 */ - 46:
/* re-train models if required */ - 47:
if TRUE then - 48:
for to n do - 49:
; /*update all models using the latest available data till now */ - 50:
end for - 51:
FALSE; /* reset flag */ - 52:
end if - 53:
end for
|
3.2.2. Algorithm 2: Varying Weight Method
Algorithm 2 describes the steps for the Varying Weight Method (VWM). VWM follows a similar approach as proposed in FWM, with few changes in updating the weight of participating algorithm. In this model, the weight of each participating algorithm varies based on the prediction accuracy achieved by the respective algorithm in all of the previous predictions made by it, whereas in FWM, the weight of the algorithm is either zero or one based on its previous day performance. At the beginning, the weight for all participating algorithms is set to one, and randomly, one algorithm is chosen to be the expert algorithm for the first day. These models are used to predict the electricity prices for the unseen test data. Once we obtain the prediction value from each model and come to know the actual price, we evaluate the performance of each model and update the weight based on the function of their prediction accuracy and learning rate λ. The algorithm with the highest accuracy (lowest prediction error) will have its weight increased, and the other algorithms with lower accuracy will have their weight decreased based on the prediction accuracy achieved by them. The main benefit of this model is that it considers the individual prediction error value when updating the weight. Therefore, the weight of any algorithm is dependent on the cumulative error and number of times it has been the best predictor.