1. Introduction
In this paper, we investigate the risk–return relationship, along with the impact of volatility feedback, by estimating a Bayesian nonparametric model of the joint distribution of market excess returns and realized variance. In contrast to the existing risk–return literature where the conditional mean of excess stock market returns is modeled as a linear relationship with the conditional volatility, we allow the observed monthly returns and realized variances calculated from daily returns to determine the relationship between the conditional mean of excess returns and the contemporaneous log-realized variance.
1 Distinguishing between lagged and contemporaneous relationships has implications for the risk–return relationship which can be indirectly derived from the contemporaneous model.
Past risk–return research finds conflicting evidence on the direction and level of significance a change in a GARCH model’s conditional variance can have on the conditional mean return.
2 Recent results on risk and return has helped to resolve some of these conflicts.
Scruggs (
1998) and
Guo and Whitelaw (
2006) show that additional predetermined conditional variables can affect the sign and significance of risk.
Lundblad (
2007) argues that longer samples are necessary in order to find a significant relationship between the market risk premium and expected volatility with GARCH specifications.
Bandi and Perron (
2008) document a long-run relationship between expected excess market returns and past market variance, while
Maheu and McCurdy (
2007) find the long-run component of realized variance is priced in annual data. Recently,
Ghysels et al. (
2013) established a positive risk and return relationship over sample periods that excluded financial crises.
3Most of the research on risk–return assumes excess returns are conditionally normally distributed.
Harvey (
2001) argues one should dispense with the parametric assumptions around the conditional expectations given the contemporaneous log realized variance that normality assumes. Gaussianity also ignores the potential role higher order moments like skewness and leptokurtosis play in the predictability of returns (see
Campbell and Hentschel 1992). Using daily data,
Maheu et al. (
2013) find the conditional variance and conditional skewness, due to jumps in returns, is significantly priced. Hence, ignoring the higher ordered moments for excess returns may confound the evidence of a positive risk and return relation.
In this paper, we relax the normality assumption and let the data determine the joint distribution between excess returns and volatility.
4 This borrows from the parametric approach of
Brandt and Kang (
2004) by jointly modeling the distribution of returns and log-volatility but now nonparametrically. A nonparametric estimate of the joint distribution also allows us to study the risk–return relationship from a flexible uninformed standpoint and to avoid having to address those issues pointed out by
Scruggs (
1998) and
Guo and Whitelaw (
2006) over which predetermined conditioning variables to include.
Our nonparametric estimator is an extension of the Bayesian Dirichlet process mixture (DPM) model (see
Lo (
1984)). Most DPM models consist of an infinite mixture of normal distributions whose means, covariances, and mixture probabilities are estimated by applying the relatively uninformative Dirichlet process (DP) prior to the infinite number of unknowns (see
Ferguson (
1973)). Being almost surely a discrete distribution, the DP prior essentially shrinks the number of unknowns down to just a few important mixture clusters, thus enabling us to overcome the common nonparametric problem of having more unknowns than observations. For conditional distributions, which govern the risk–return relationship, the DPM is an infinite mixture of conditional normals but whose mixture probabilities, means and variances all depend on the value of the conditioning variables (see
Muller et al. (
1996) and
Taddy and Kottas (
2010)). The DPM representation and estimation of the conditional distribution allows for a more flexible relationship between the conditional mean of excess returns and contemporaneous realized variance than is possible under Gaussianity.
Because of its straightforward nature and good empirical performance, the DPM approach has become the gold standard for Bayesian nonparametric estimation of unknown distributions.
5 For investigating the risk–return relationship, we extend the DPM by assuming the means of the infinite mixture of normals depend on intertemporal variables. Rather than modelling the joint distribution of excess returns and log realized variances as a mixture over the unconditional bivariate mean vectors, we include contemporaneous and lagged excess returns and log realized variances in the means and mix over each covariates coefficient. By including contemporaneous and lagged variables in the mixture, our bivariate DPM model is a semi-nonparametric estimator since it accounts for structural economic relationships like volatility feedback and known empirical regularities like persistence in volatility, while not imposing any fixed parametric relationship over the risk premium or volatility feedback. We design a Markov chain Monte Carlo (MCMC) algorithm that uses the slice sampler methodology of
Walker (
2007) to deliver posterior draws of the unknowns from which estimates are obtained that account for uncertainty in the risk–return trade-off and volatility effect through the unknown joint distribution.
Volatility feedback is the causal relationship between the variance and price changes and can be an important source of asymmetry in returns.
Campbell and Hentschel (
1992) show that volatility feedback plays an important role in finding a positive risk and return relationship. They find a positive relationship with a model derived from economic restrictions that linearly relate log-returns to log-prices and log-dividends.
6Our nonparametric approach differs in several important ways from the existing volatility feedback literature. First, while almost all the literature has studied volatility feedback from a tightly parameterized model, we use a flexible approach with no economic restrictions. Second, we use realized variance which is an accurate ex post measure of the variance of returns and permits the joint modelling of returns and variance. Third, we nonparametrically model the relationship between contemporaneous excess returns and log-realized variance. Volatility feedback implies an instantaneous causal relationship between volatility innovations and price levels or returns and our contemporaneous model is designed to investigate this relationship directly. Fourth, our nonparametric approach allows for conditioning on predetermined conditioning variables.
Using a long calender span of monthly US stock market data, we find strong robust evidence of volatility feedback. Expected excess returns are always positive when volatility shocks are small; however, they become negative once the volatility shock becomes larger. This risk–return relationship is very nonlinear and depends on the current level of expected volatility. Ignoring these dynamics will result in confounding evidence for risk and return. Once volatility feedback is accounted for, there is an unambiguous positive relationship between expected excess returns and expected log-realized variance. Conditional quantile and contour plots support these findings and display significant deviations from the monotonic changes in the conditional distribution of the parametric model. We find strong evidence of the volatility feedback affecting the whole distribution of excess returns and not just its conditional mean.
This paper is organized as follows. The data and construction of realized variance are discussed in the next section followed by
Section 3, which motivates our model and the link to risk and return and volatility feedback. The nonparametric model for excess market returns and log-realized variance is introduced in
Section 4.
Section 5 discusses estimation of the conditional distribution and conditional mean of excess returns given log-realized variance. Empirical results are found in
Section 6 followed by the conclusions.
2. Return and Realized Variance Data
Using high frequency daily returns permits the construction of monthly realized variance—an ex post, observable variance that is the focus of our study. Although the realized variance has been used in empirical finance for some time
French et al. (
1987), there exists a strong theoretical foundation for using it as an essentially nonparametric measure of ex post volatility (for recent reviews, see
Andersen and Benzoni (
2008) and
McAleer and Medeiros (
2008)). For example, in the factor analysis investigation of the risk–return trade-off by
Ludvigson and Ng (
2007), the nonparametric realized variance affords them the luxury of not having to specify a potentially restrictive parametric form for volatility. For our purpose, the strength of realized variance is it being a consistent estimate of return volatility. This property means that we can directly model the distribution of return volatility by treating the realized variances as a time series of observed volatilities.
To compute the monthly realized variances, we obtain daily price data from Bill Schwert
7 for February 1885–December 1925, and from CRSP for January 1926–December 2011 on the value-weighted portfolio with distributions for the S&P500. The price data is converted to continuously compounded daily returns. If
denotes the continuously compounded return for day
in month
t, then we compute month
t’s realized variance according to
where
denotes the number of daily returns in month
t. This estimate of return volatility contains a bias adjustment of order
q to account for market microstructure dynamics and stale prices and follows
Hansen and Lunde (
2006). The Bartlett weights in Equation (
1) ensure that
is always positive. In this paper, we set
and let
.
Monthly returns are taken from the associated monthly files from Schwert and CRSP S&P500. The risk-free rate is obtained from Amit Goyal’s website for February 1885–December 1925, and, after this time period, the risk-free rate equals the one-month rate from the CRSP Treasury bill file.
Our risk–return analysis dataset thus consists of monthly excess returns and monthly realized variance from January 1885–December 2011 for a total of 1519 monthly observations. Returns are scaled by 12 and by 144 in order for our findings to be interpreted in terms of annual returns. When estimating the model, we reserve the first 22 observations as conditioning variables. The information set is denoted by , for .
Table 1 reports various summary statistics for monthly excess returns and realized variance. Compared to squared returns, realized variance is less noisy. Returns standardized by realized variance are approximately normal with sample skewness of 0.003 and sample kurtosis of 2.6856. Log-realized variance is closer to being bell-shaped than the levels of
.
Figure 1 displays a scatter plot of market excess returns and
which is the basis of our time-series models.
4. Nonparametric Model of Market Excess Returns and Realized Variance
In this section, we provide the intuition behind the nonparametric model that we will use to flexibly estimate the joint relationship between excess returns and contemporaneous realized variance. As pointed out by
Brandt and Kang (
2004), there are no theoretical reasons that a particular parametric relationship should hold between the conditional mean and variance of excess returns. Without a theoretical relationship to guide us, we choose to let the data inform us about the risk–return trade-off by modeling the joint probability distribution of excess returns and realized variance as an unknown distribution and fitting it nonparametrically.
Our nonparametric approach consists of approximating the unknown joint distribution’s density with the infinite mixture of bivariate densities
where
are the mixture probabilities such that
,
, and
, and
are the mixture parameters. The function
is the
jth mixture components smooth, bivariate, probability density function given the mixture parameter
and information set
.
It it well understood that any continuous bivariate distribution can be approximated to arbitrary accuracy by selecting an appropriate density function for
and by estimating the unknown mixture weights
and mixture parameters
, for
(
Ghosal et al. 1999). In the next section, we discuss how the infinite number of unknowns can be estimated with a finite number of observation. For now, we only consider how we can obtain a nonparametric representation of the risk–return relationship from Equation (
3) through the conditional distribution of excess returns given log-realized variance. To reduce the clutter from carrying around excessive notation on the conditional mixture arguments, we drop
and
from
when it is clear to do so.
By the law of total probability, the joint distribution in Equation (
3) can be written as the product of the marginal and conditional distributions
Drawing on the theoretical considerations of
Andersen et al. (
2003), the known empirical bell-shaped distribution of
, and the approximately normally distributed standardized excess returns, we choose to let the conditional and marginal probability density functions be
where
is the normal density function with mean
and variance
. The
jth-cluster’s mixture parameter vector is
and the conditioning set is
. Although the
jth mixture component in Equations (
5) and (
6) are normally distributed, mixing them over the infinite set of different valued
s produces joint distributions of excess returns and log-realized variances with non-zero higher ordered moments, multiple modes, and a wide variety of curvatures.
What is novel about Equations (
5) and (
6) is that their mixture locations and scales are functions of contemporaneous and lagged realized variances and lagged returns. Previous infinite mixture models directly mix over the conditional means and variances and do not allow for covariates in the mixture moments. By including contemporaneous and intertemporal variables, our mixture model’s means and covariances explicitly depend on intertemporal values of returns and volatility and contemporaneous values of volatility. For example, the values of
can impact the mixture means and variances of excess returns. Note that, under certain conditions,
will be an unbiased estimate of the variance of returns, but we allow for deviations that are captured by the
s in the mixture model.
Although not the focus of this study, the model allows for a leverage effect or asymmetric response of past return shocks to future
. This occurs in Equation (
6) through the terms
and
and, since this enters the mixture, allows for a general nonlinear leverage effect.
The intertemporal form of Equations (
5) and (
6) is not based on theory, but on empirical regularities known to exist in stock market returns and their volatility. For instance, the conditional mean of
in Equation (
6) is along the lines of the models found in
Andersen et al. (
2007),
Corsi (
2009) and the joint models of
Maheu and McCurdy (
2007,
2011), as adapted to monthly data. It features an expected volatility comprised of an intertemporal six month component that captures the significant persistence known to exist in realized variances.
8 The last two terms of the conditional mean in Equation (
5) also accounts for an asymmetric volatility relationship by including an asymmetric response in the mixture means of log-realized variances to lagged returns.
In the conditional density of Equation (
5), any potentially nonlinear function of
can be conditioned on; e.g.,
or
. This conditional density function of excess returns captures the empirical regularity of excess returns being normally distributed when standardized by
. The conditional mixture mean implicitly includes a risk–return relationship (positive) as well as a volatility feedback effect (positive or negative).
9 As a result, the signs of the mixture parameters
s are left ambiguous. Essentially, we are nonparametrically modeling through Equation (
3),
Campbell and Hentschel (
1992) reduced form equation of excess returns without imposing any theoretical restrictions. For this reason, we place no restrictions on the
and
,
. The implications for the risk–return trade-off can be indirectly derived from the contemporaneous model and are discussed later.
4.1. Conditional Distribution of Returns Given Realized Variance
From the mixture representation of the joint distribution of excess returns and realized variances in Equation (
3), it directly holds that the probability density function of excess returns conditional on contemporaneous log-realized variance equals
where
is the conditional probability density function of the
jth cluster and
is the associated marginal density function for
.
The mixture weights in Equation (8) have the particular form
so that they sum to one. From Equation (10), we see that those clusters providing a better
fit of
receive more weight in the mixture representation. Components whose
and
result in larger likelihoods play a bigger role in accounting for the risk–return trade-off and the volatility feedback effect. Note that different values of
produce smooth changes in the conditional distribution of excess returns and, hence, in its mean.
Our interest rests in the risk–return and volatility feedback relationship; in other words, the conditional expectation of market excess returns given log-realized volatility. Since the expectation of a mixture distribution is equivalent to the mixture of the expectations, from the conditional mixture means of excess returns in Equation (
5), the expectation of Equation (8) is the conditional expectation
A linear parametric risk–return relationship is nested in Equation (11) by simply letting there be only one mixture component. As more mixture components are added and a greater mixture of differently valued s and s are included, the conditional mean of excess returns as a function of , moves away from linearity. This mixing allows Equation (11) to become more flexible and capable of modeling a wider array of different types of risk–return and volatility feedback relationships.
Being a function of realized variance, the mixture representation in Equation (11) differs from previous work by nonparametrically modelling excess returns and ex post variance. The conditional mean of excess returns given realized variance will contain an ex ante risk–return component and an ex post volatility feedback component.
A plot of the conditional expectation of excess returns as a function of will be a smoothly changing function that weights each of the cluster specific conditional expectations according to how the weight function changes as changes. This is true even if each cluster’s expectation, , is constant. In this way, we can see the contemporaneous relationship of log-volatility on the conditional mean of excess returns. As mentioned above, volatility feedback occurs simultaneously and this specification is designed to shed light on it.
4.2. Dirichlet Process Prior for the Infinite Number Of Unknowns
Because our nonparametric model of excess returns and log-realized variance joint probability distribution consists of an infinite number of unknown mixture weights,
, and parameter vectors,
, we resort to a Bayesian prior to shrink the number of unknowns to a feasible number while not forsaking the flexibility that comes from an infinite mixture model. The prior we choose is the Dirichlet process prior (DP). The Dirichlet process prior has a long history, beginning with
Ferguson (
1973), of use in Bayesian nonparametric problems. It was used as a prior in countable infinite mixtures for density estimation in
Ferguson (
1983) and
Lo (
1984), but applications were limited until modern computational techniques. The seminal paper by
Escobar and West (
1995) shows how to perform Bayesian nonparametric density estimation with Gibbs sampling.
The DP prior essentially partitions the parameter space into a finite number of sets such that parameter vectors drawn from a particular set all have the same unique value. Such a prior promotes clustering among the mixture components resulting in only having to estimate a few unknown mixture parameter vectors. The probability of a particular mixture parameter vector occurring is equal to the probability over a member set of the partition as defined by the DP prior.
To be explicit, we assume the Dirichlet process prior,
, for the unknown
and
,
of Equation (
3).
Sethuraman (
1994) shows that a
prior for the mixture unknowns has the representation of being almost surely draws from
for
. In Equation (13), each mixture cluster parameter vector
is a unique vector independently drawn from the base distribution
. This base distribution is our best guess at how the
s are distributed. In Equation (
12), the mixture weights are drawn from what is referred to as a stick breaking process since the unit interval is successively broken into the mixture weights,
,
, by breaking off random
portions of the remaining part of the unit length stick. This stick breaking process ensures the mixture weights sum to one while also promoting clustering in the
s.
The positive scalar , known as the Dirichlet processes’ concentration parameter, controls the degree of clustering in the mixture components. A close to zero results in only a few mixture weights being nonzero, putting most of the weight on only a few unique draws from . As gets larger more s become nonzero, and, hence, there is less clustering and more unique s. In the limit as approaches infinity, the partition of the mixture parameter space is no longer finite and discrete. Instead, the parameter sets within the partition becomes so fine and large in number that the s no longer cluster to a finite set of unique value but instead will be continuously distributed as . In other words, when , the mixture weights are uniformly distributed, no clustering occurs and the prior for the s is essentially .
4.3. Hierarchical Representation
The Dirichlet process mixture model defined in Equations (
3)–(
6), (
12) and (13) also has the hierarchical representation where
is distributed
In Equation (15), the distribution of the parameter vector
is the unknown distribution,
G, whose prior is modeled in Equation (16) by the Dirichlet process prior
. Given the stick breaking definition of the Dirichlet process in Equations (
12) and (13), the prior distribution for
G is almost surely equal to the discrete distribution
where
denotes a point mass at
, and
and
are the random realizations defined in Equations (
12) and (13).
Equation (
17) helps us better appreciate the clustering behavior of the DP prior. Since
G is almost surely a discrete distribution, there will be duplicates among the
,
. As a result, several of the observations will share the same mixture parameter vector,
.
If volatility risk is priced, a positive volatility shock requires an increase in returns which discounts all future cash flows at a higher rate. This discounting results in a drop in the current price. As a result, if any unexpected news arrives be it good or bad, uncertainty increases causing the innovation to volatility, , to be positive. If a volatility feedback effect exists the effect good news has on returns will be dampened, whereas the effect of the bad news will be amplified. Therefore, a price increase from good news will be less than what would occur without volatility feedback while a price decrease from bad news will be steeper. Dynamics of this sort occur when is negative. On the other hand, if volatility shocks are small, the net impact on the conditional mean of excess returns will be a reward for risk which can be captured by a positive .
By connecting the clustering property of the DP with the volatility feedback parameter, , our nonparametric model will have a unique during similar market environments. Two months with similar market behavior will have the same volatility feedback, . However, the volatility feedback for months where the market dynamics are different will not equal .
4.4. Posterior Simulation
To sample the posterior density of our nonparametric joint distribution model, we will exploit the mixture representation in Equation (
3) and a slice sampler based on
Walker (
2007);
Kalli et al. (
2011); and
Papaspiliopoulos (
2008).
10 This Markov chain Monte Carlo (MCMC) algorithm introduces a random auxiliary, latent, variable,
, which slices away any mixtures clusters with a weight
less than
. In this way, the infinite mixture model is reduced to a finite mixture.
Introducing the latent variable
, we define the joint conditional density of the observed variables
and
as,
This infinite mixture is truncated to only include alive clusters with while dead clusters have a weight of 0 and can be ignored. If has a uniform distribution, then integration of with respect to gives back the original model . On the other hand, the marginal density of is .
We augment the parameter space to include estimation of
. Let
,
and
, then the full likelihood is
and the joint posterior is
where the number of mixture clusters,
K, is the smallest natural number that satisfies the condition
. This value of
K ensures that there are no
for
. In other words, we have the set of all clusters that are alive,
.
Posterior simulation consists of sampling from the following densities:
, , .
, , with
, .
Find the smallest K such that .
, RV.
where and .
The first step depends on the model and the base density
to the DP priors’ base measure,
. For the kernel densities in Equations (
5) and (
6), specifying a normal prior for the regression coefficients and an independent inverse gamma prior for the variance, in other words, defining
, we can employ standard Gibbs sampling techniques in Step 1 (see
Greenberg (
2013) for details on the exact form of these conditional distributions). Step 2 results from the conjugacy of the generalized Dirichlet distribution and multinomial sampling
Ishwaran and James (
2001). Given
and
S, each
is uniformly distributed on
. The next step updates the truncation parameter
K. If
K is incremented, Step 4 will also involve drawing additional
and
from the DP prior. The final step is a multinomial draw of the cluster assignment variable
based on a mixture with equal weights.
Repeating all these steps forms one iteration of the sampler. The MCMC sampler yields the following set of variables at each iteration
i,
Note that
, implies
, through Equation (
12). After dropping the burn-in phase from the above sampler, we collect
samples.
Each
ith iteration of the algorithm produces a draw of the unknown mixing distribution
G from its posterior
as
We will make use of these posterior realizations of G to form the predictive density and conditional expectations.
5. Nonparametric Conditional Density Estimation
To flexibly estimate the conditional density
found in Equation (8), or the conditional mean in Equation (11), we use the method of
Muller et al. (
1996). This is an elegant approach to nonparametric estimation that allows the conditional density and expectation of excess returns to depend on covariates, in this case
. The method requires the joint modeling of the predictor variable and its covariates and uses well know estimation methods for Dirichlet process mixture models. We extend
Muller et al. (
1996) to the slice sampler to accommodate the non-Gaussian data densities and nonconjugate priors found in our nonparametric model of market excess returns and realized variances.
11Based on the previous section, and given
, the
ith realization from the posterior of the joint conditional predictive density for the generic return, log-realized variance combination,
, is
where the predictive is conditional on the information set
.
Substituting in the stick breaking representation for
found in Equation (
22), the posterior draw of the predictive density has the equivalent representation
where
is the expectation of Equation (
14) over
. To integrate out the uncertainty associated with
G, one averages Equation (
24) over the posterior realizations,
,
, to obtain the posterior predictive density
Now, the predictive density of
r given
can be estimated as well. For each draw of
, we have
where
is the conditional density of Equation (
5),
is the marginal density of Equation (
6) and
The denominator of
is the marginal of Equation (
24) obtained by integrating out
r.
is the marginal data density of
for the
jth cluster with the marginal cluster parameter
and
is the marginal data density with mixing over the base measure. The terms in Equations (
26) and (
27) involving
are defined as follows:
Assuming that the marginal data density
is available in analytic form, both of these expressions can be approximated by the usual MCMC methods. For instance,
, where
, with a similar expression for the numerator of Equation (
28).
The posterior predictive conditional density is estimated by averaging Equation (
26) over the posterior simulations of
as
Using this approximation, features of the conditional distribution such as conditional quantiles can be derived.
Nonparametric Conditional Mean Estimation
Our focus will be on the conditional expectation that can be estimated from these results. First, the conditional expectation of
r given
,
and the information set
is
where
is taken with respect to Equation (
28). Note that this final term is only a function of
and can be computed once, at the start of estimation, for a grid of values of
. It is estimated as
12
for
,
.
Given
, Equation (
31) shows the conditional expectation of
r is a convex combination of cluster specific conditional expectations
,
, along with the expectation taken with respect to the base measure
. The weighting function changes with the conditioning variable
, which in turn changes for each
.
Finally, with this, we can obtain the posterior predictive conditional mean estimate by averaging over Equation (
31) as follows:
in order to integrate out uncertainty concerning
G.
13 Point-wise density intervals of the conditional mean can be estimated from the quantiles of
.
We evaluate the predictive conditional mean for a grid of values over . This will produce a smooth curve and we will have a unique curve for each information set in our sample .
6. Empirical Findings
For our empirical analysis, we specify the following priors. The base measure
contains priors for each regression parameter in Equations (
5) and (
6) as independent
while
and
,
, where
denotes a gamma distribution with mean
. Note that we expect the
s to be close to 1 and the prior reflects this with
but allows for deviations from this. These prior beliefs cover a wide range of empirically realistic values and robustness to other choices is discussed below. The concentration parameter of the Dirichlet process,
, is estimated and has a prior
. Each cluster contains the nine parameters found in
.
We use 5000 initial iterations of the posterior sampler for burn-in and then collect the following 20,000 for posterior inference. The Markov chain mixes well and the posterior mean (0.95 density interval) for is , and the posterior mean (0.95 density interval) for the number of alive clusters is , . In other words, about 2.6 components are used to fit the joint model of and .
Before we turn to the estimates from our nonparametric DPM model, a parametric version of the model is reported in
Table 2. This is a one state model. The coefficient
on
in the excess return equation is significantly negative and hence evidence of the volatility feedback mechanism at work.
is close to 1 and indicates no systematic bias in
. The estimates of
and
indicate persistence in
. The lagged standardized excess return terms entering the log-volatility equation show asymmetry. A negative return shock results in a larger conditional mean for log-volatility next period compared to a positive shock.
Figure 2 displays the contemporaneous relationship between expected excess returns and
for the estimated parametric model.
14 The conditional expectation of excess returns given log-realized variance is computed over a grid of 100 log-variance values between
to 2.0. Using a straight line, we interpolate between the values of
at the different values of log variance in order to approximate the smooth relationship between
and
. Although the estimated model is a fixed linear relationship between excess returns and
, this parametric model yields the nonlinear relations between the conditional mean of excess returns and log-realized variance found in
Figure 2.
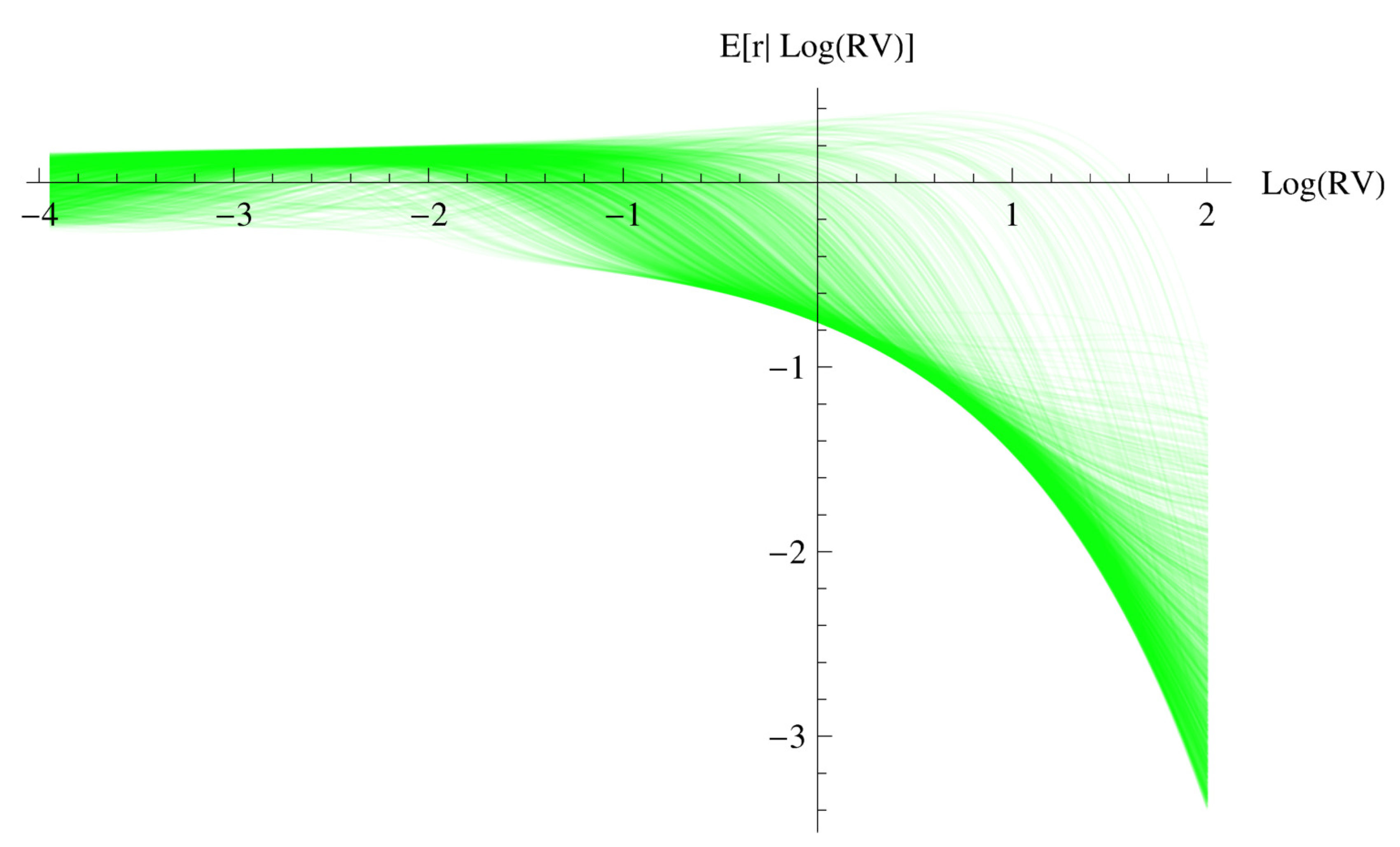
In
Figure 3, the conditional expectation of excess returns as a function of log-realized variance for our nonparametric model is plotted for every information set,
,
, in our dataset. Note that the parametric relationship in
Figure 2 is the same for every information set and is not affected by low or high volatility periods. Overall, there is a general increase in the conditional mean of excess returns in
Figure 3 as log-realized variance increases from low levels of volatility to a point where expected returns become negative. This is a general pattern found in all of the plots of
Figure 3. However, the log-variance argument that causes the conditional mean of excess returns to begin to decline does differ for the different information sets
. It is clear that, if one averaged over these expectations, you could obtain a positive value for expected excess returns or a negative value.
15 To really understand the relationship between the conditional mean of excess returns and log-realized variance, we need to consider the conditional expectation and the innovation of log-volatility as well.
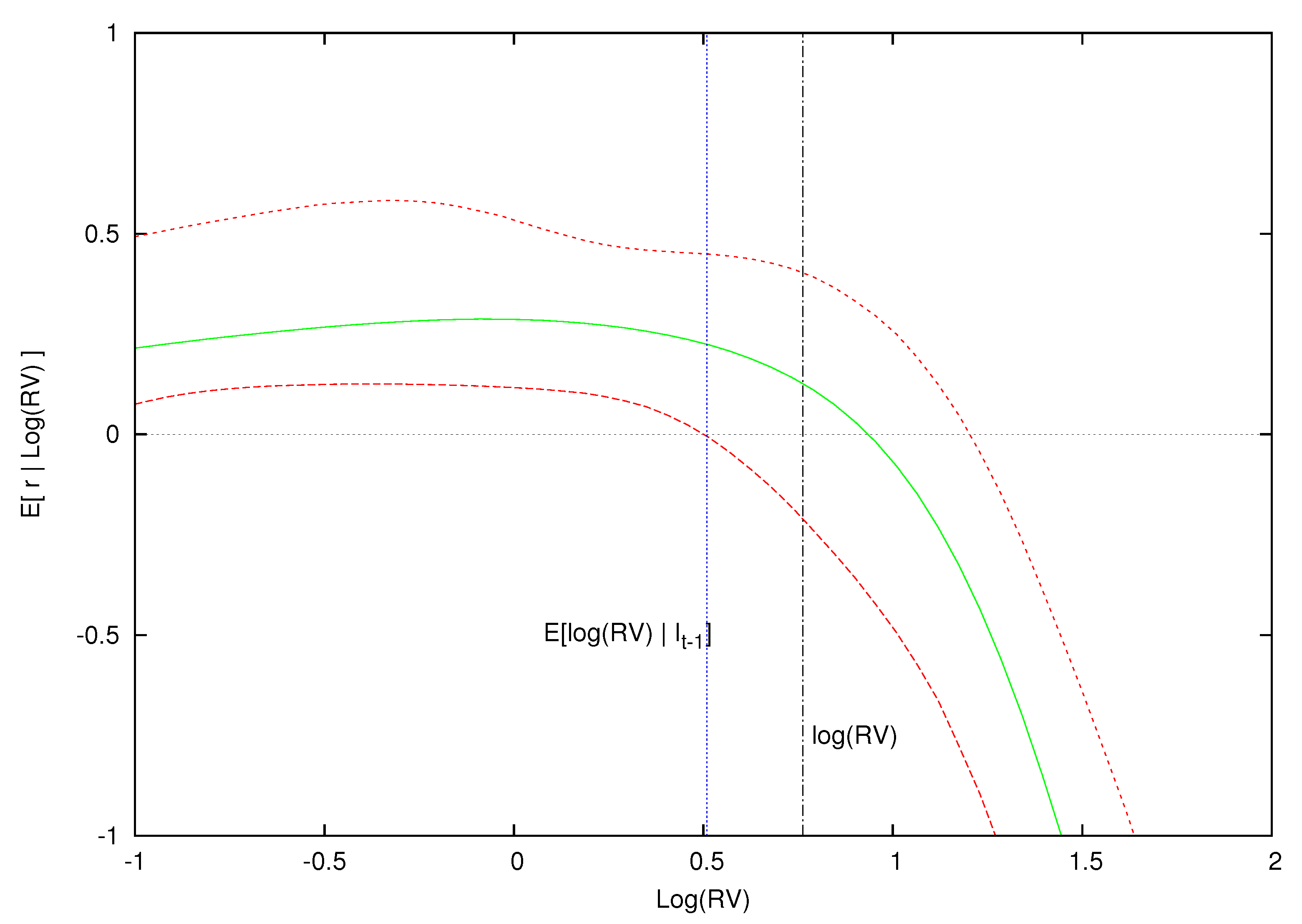
To do this, we isolate three months in our sample where market volatility is low (October, 1964), average (February, 1996) and high (December, 2008) and plot in
Figure 4,
Figure 5 and
Figure 6 the conditional expectations of excess returns against different values of log-realized variance during these three months. In addition to plotting the conditional expectation of market excess returns, the three figures also include the conditional expectation of log-realized variance,
, as a vertical blue line, and the observed realized value of log-realized variance for that month,
, as a vertical dashed line. Point-wise 90% probability density intervals are included for the expected excess return.
6.1. Volatility Effect
Recalling our discussion on volatility feedback, if volatility is priced and a positive volatility shock arrives, then, all things being equal, the required rate of return increases which discounts all future cash flows at a higher rate and results in a simultaneous drop in the current price so as to deliver a higher future return consistent with the increase in risk. Only when the observed log-variance is equal to its expected value will the volatility feedback effect be zero. Hence, if volatility risk is priced, values of log-variance greater (less) than its expected value will cause current prices to fall (rise).
This is exactly what we find in
Figure 4,
Figure 5 and
Figure 6 for an unexpected positive volatility shock where log-variance is greater than the expected value of log-realized variance. For instance, consider
Figure 4, which conditions on the low volatility information set,
.
16 In this month of low market volatility, the model’s expected log-realized variance is
. The expected excess return is positive for values of log-variance below and slightly above this expected value, but eventually the expected excess return becomes negative as
increases above
. In other words, when market volatility is low, if the volatility shock is sufficiently larger than zero, we expect a contemporaneous decrease in prices from the volatility feedback effect.
Figure 5 displays a similar pattern for the month where volatility is not unusual but typical for the equity market. The period is for the information set
and our model finds the expected value of
to be
. As before, expected excess returns are positive for values of log-variance less than and slightly greater than
, but eventually becomes negative when log-realized variance is larger than
. If the log-volatility shock is sufficiently large (about +0.68), then the expected excess return is negative and continues to decrease as the size of the volatility shock grows. In addition, notice that the whole posterior curve of
has shifted rightward as the expected
has increased from
Figure 4 to
Figure 5 (low to average
). This suggests an increase in compensation for the higher perceived volatility risk when the market moves from an unusually calm market to one that is typical.
A highly volatility market corresponding to the information set
is found in
Figure 6. Just as before,
is essentially linear and flat for values of
smaller than
. In other words, the expected excess returns do not respond to negative volatility shocks. However, for values of
greater than
, expected excess returns start to decline and become negative when log-realized variance is almost one.
17 This is consistent with the volatility feedback effect. Note that, in each of these three figures, the effect of volatility feedback on returns gets stronger where the impact of a positive volatility shock on expected returns increases as the the market moves from a low volatility state to a market with average volatility and then to a market where volatility is exceptionally high.
Figure 7 plots
for each of the three information sets,
and
. As
increases, the conditional expectation of excess returns shifts rightward and up. This is consistent with a positive and increasing reward for bearing higher levels of risk.
In summary, we find a robust volatility feedback effect that is most notable for positive shocks to volatility. Expected excess returns are positive below but after this value eventually become negative. Thus, small news events have little effect on expected returns, whereas large news events cause expected excess returns to decline. This suggests that risk is priced and the previous figure is consistent with this.
6.2. Risk and Return Trade-Off
To focus on risk and return, we need to account for the volatility feedback effect. In each of our figures, the point on the line that corresponds to is exactly the point with no volatility feedback. This point is where the investor receives exactly the reward for risk with no adjustment for volatility feedback because the volatility shock is zero. This will be at a different place in each of our curves of . Using interpolation between each of the grid values, we can estimate the value of at for each time period t. This represents a pure risk and return relationship which nets out volatility feedback.
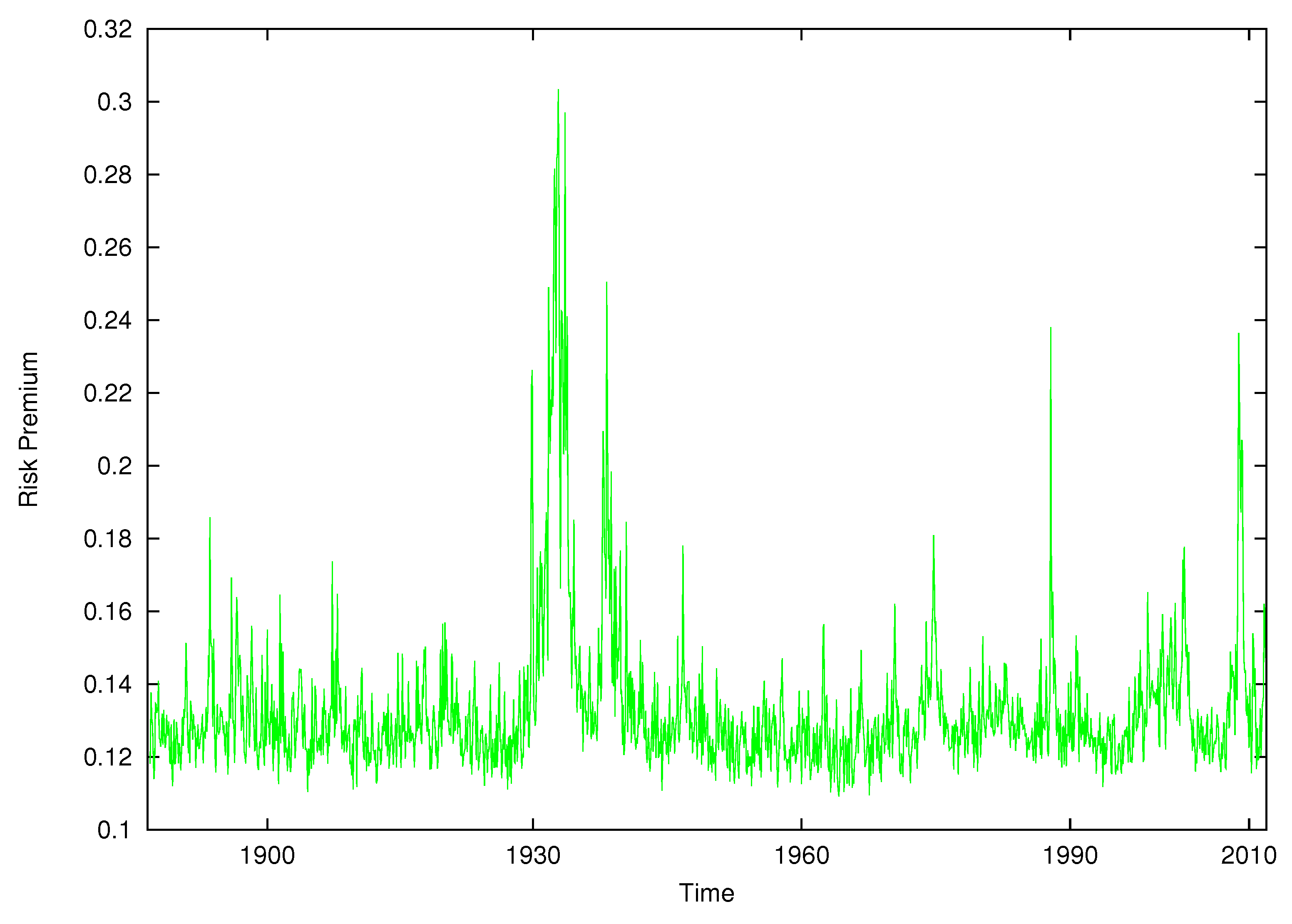
Figure 8 displays the equity risk premium over time from the nonparametric model when volatility feedback has been removed. The premium is everywhere positive.
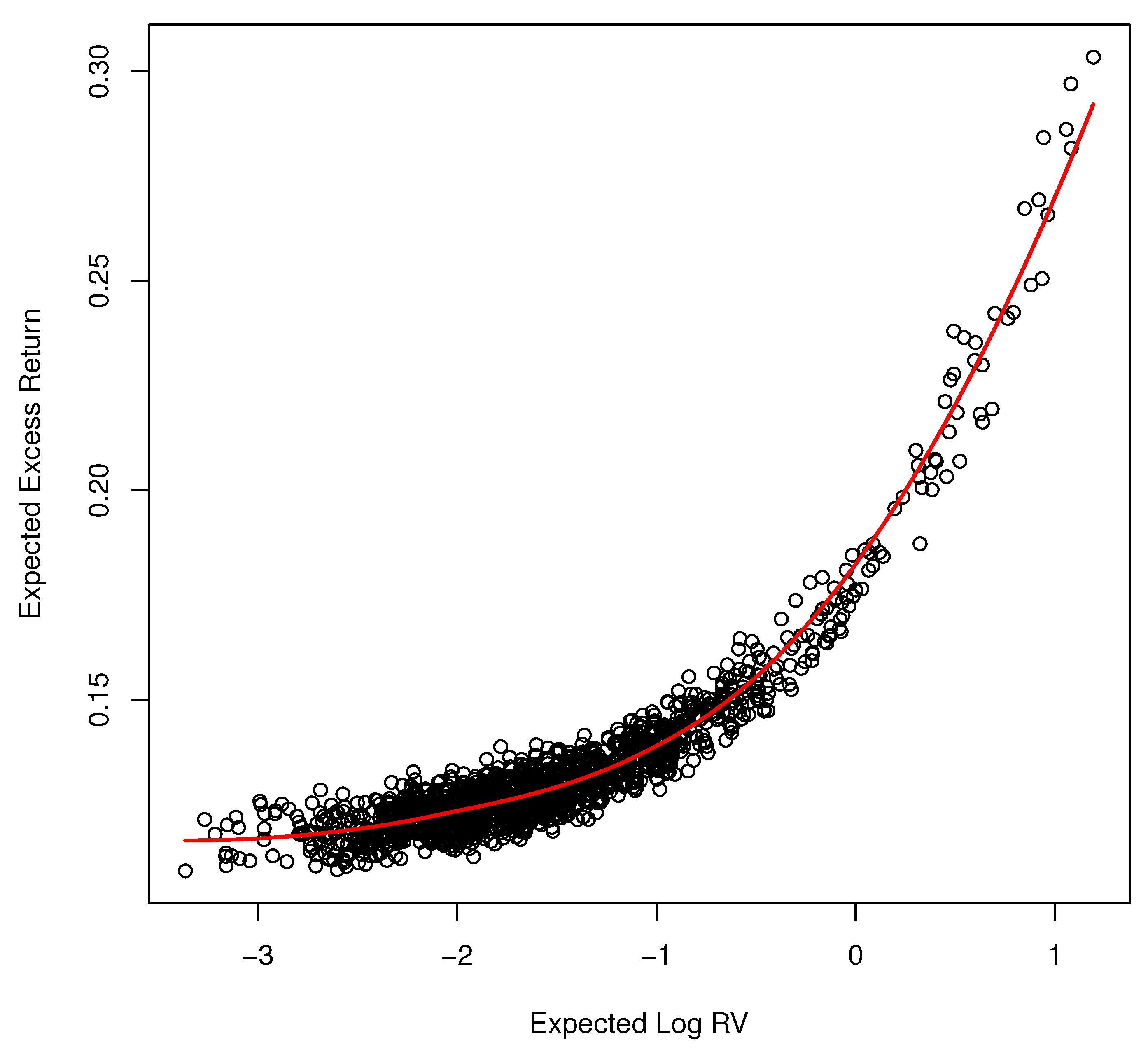
Figure 9 displays the pure risk and return relationship. It shows the expected excess return as a function of expected log-realized variance according to our model estimates when volatility feedback is removed. Each dot represents the point of
in which volatility feedback is zero given the information set
. The relationship is unambiguously positive and increasing in
which accords with theory. The relationship is nonlinear. It is approximately linear for a small value of log-volatility but increases sharply as expected log-volatility surpasses zero.
In contrast to
Campbell and Hentschel (
1992) and the subsequent literature on volatility feedback, we find evidence of a positive risk and return relationship and a volatility feedback effect without imposing any economic restrictions. The key is flexibly modeling the contemporaneous distribution of market excess returns and log-realized variance and accounting for the volatility shock.
6.3. Conditional Quantiles and Contour Plots
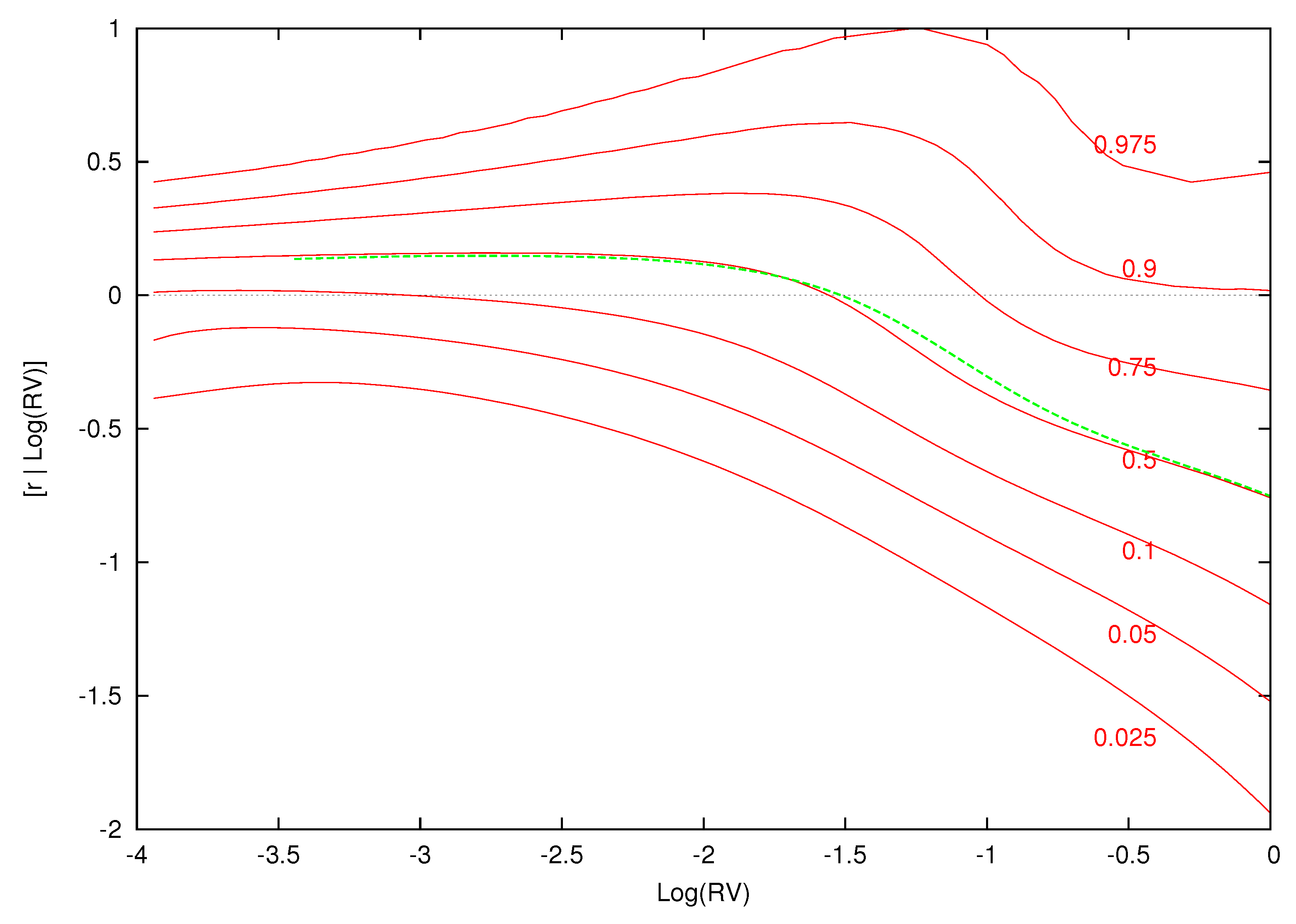
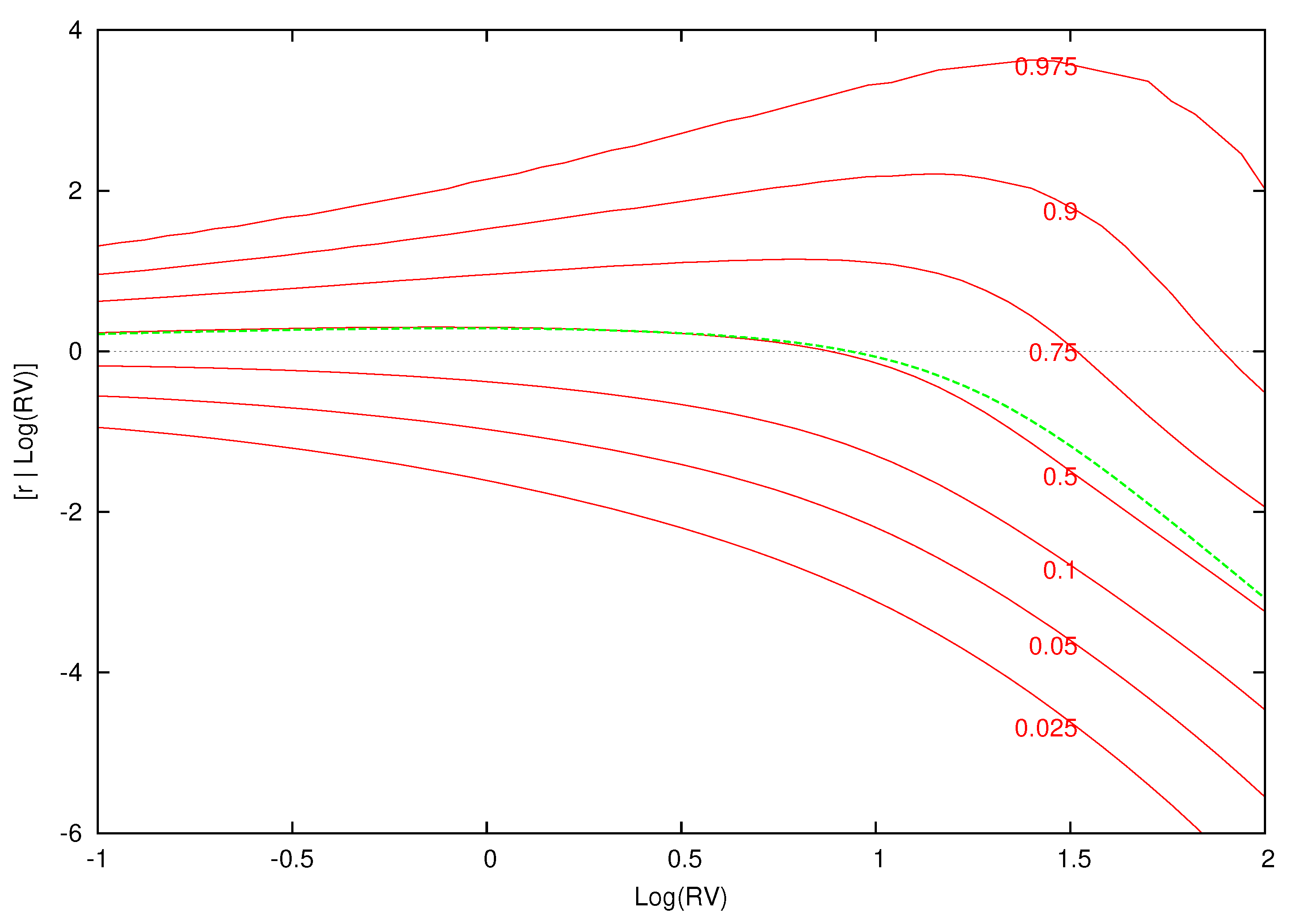
Figure 10,
Figure 11,
Figure 12 and
Figure 13 display conditional quantile plots of the distribution of excess returns given different values of
for the parametric model and several cases of the nonparametric model. In each figure, the green line is the conditional mean that was discussed above.
For the parametric model, as before, the conditional quantiles do not change for different information sets. The estimated weights and component densities in the mixture model of Equation (8), however, are sensitive to the information set and result in very different conditional distributions. Each of the conditional quantile plots show a highly nonlinear distribution that is at odds with the parametric model.
Recall from the previous discussion that the conditional expectations of the low, average and high levels of
were
,
and
, respectively. In
Figure 11,
Figure 12 and
Figure 13, the bulk of the distribution is above zero at each of these points. Investors are most likely to receive a positive excess return from the market at the value of the expected value of log-realized variance. As
increases and the volatility shock becomes larger, most of the mass in each conditional density is over a negative range of excess returns. Here, investors are likely to have a loss from investing in the market.
The upper quantiles show the most nonlinear behavior given low (
Figure 11) and average (
Figure 12) levels of volatility. Volatility feedback has an impact on the whole distribution and not just the conditional mean. The changes in the density, as
increases, are non-monotonic. In
Figure 11 and
Figure 12, there is an increase in the spread of the density followed by a decrease and final increase. The point of these changes in the conditional density is to the right of the conditional mean of
. The parametric quantile plot is inconsistent with these features.
Although volatility feedback is the most likely explanation of our results,
Veronesi (
1999) shows that, in the presence of uncertainty about the economic regime, prices overreact to bad news in good times and underreact to good news in bad times. This results in negative returns coupled with high volatility such as seen in the conditional quantile plots.
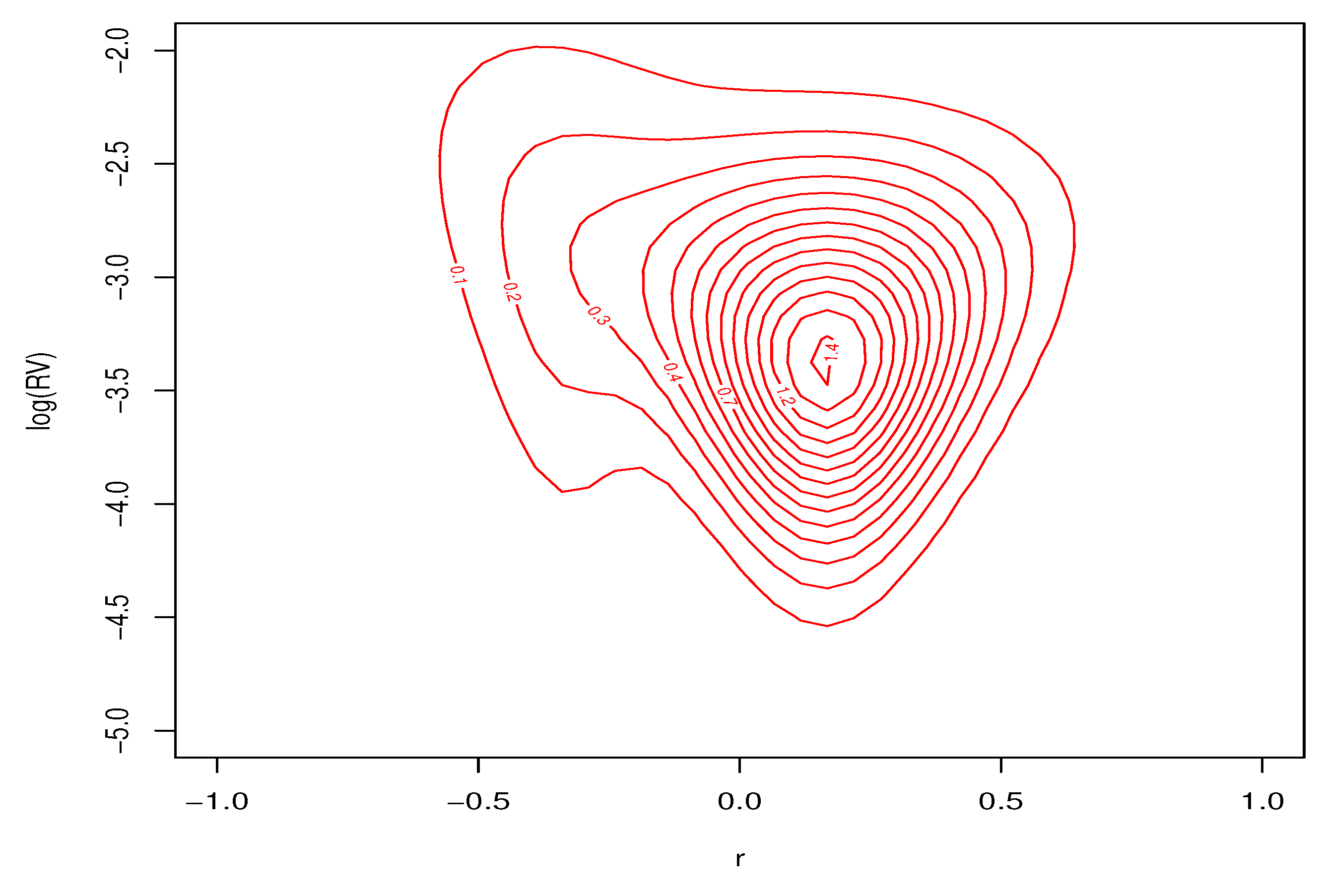
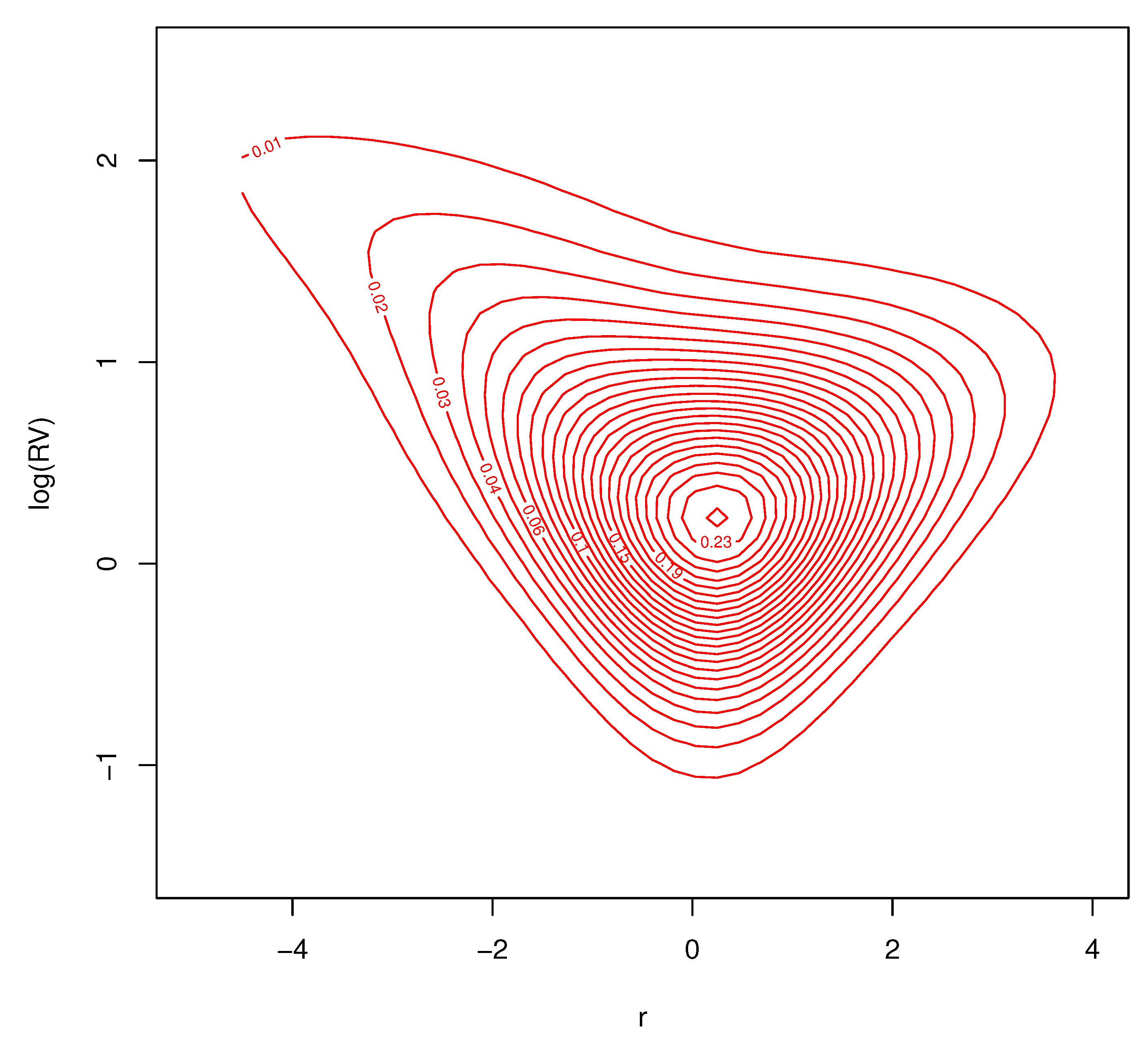
Contour plots of the conditional joint predictive density for excess returns and log-realized variances, for the three different months of market volatility, are found in
Figure 14,
Figure 15 and
Figure 16. Each of the figures are consistent with deviations from Gaussian behavior in the conditional bivariate distribution. It is clear that the conditional distribution changes a great deal over time and is not a result of changes in location and/or scale. There is a thick tail for small values of
r and larger values of
in each figure, but the shape of the distributions tail is very different depending on
. These important changes in the conditional density are the features that our nonparametric model are designed to capture. Conventional parametric approaches cannot accommodate these features.
6.4. Parameter Estimates and Robustness
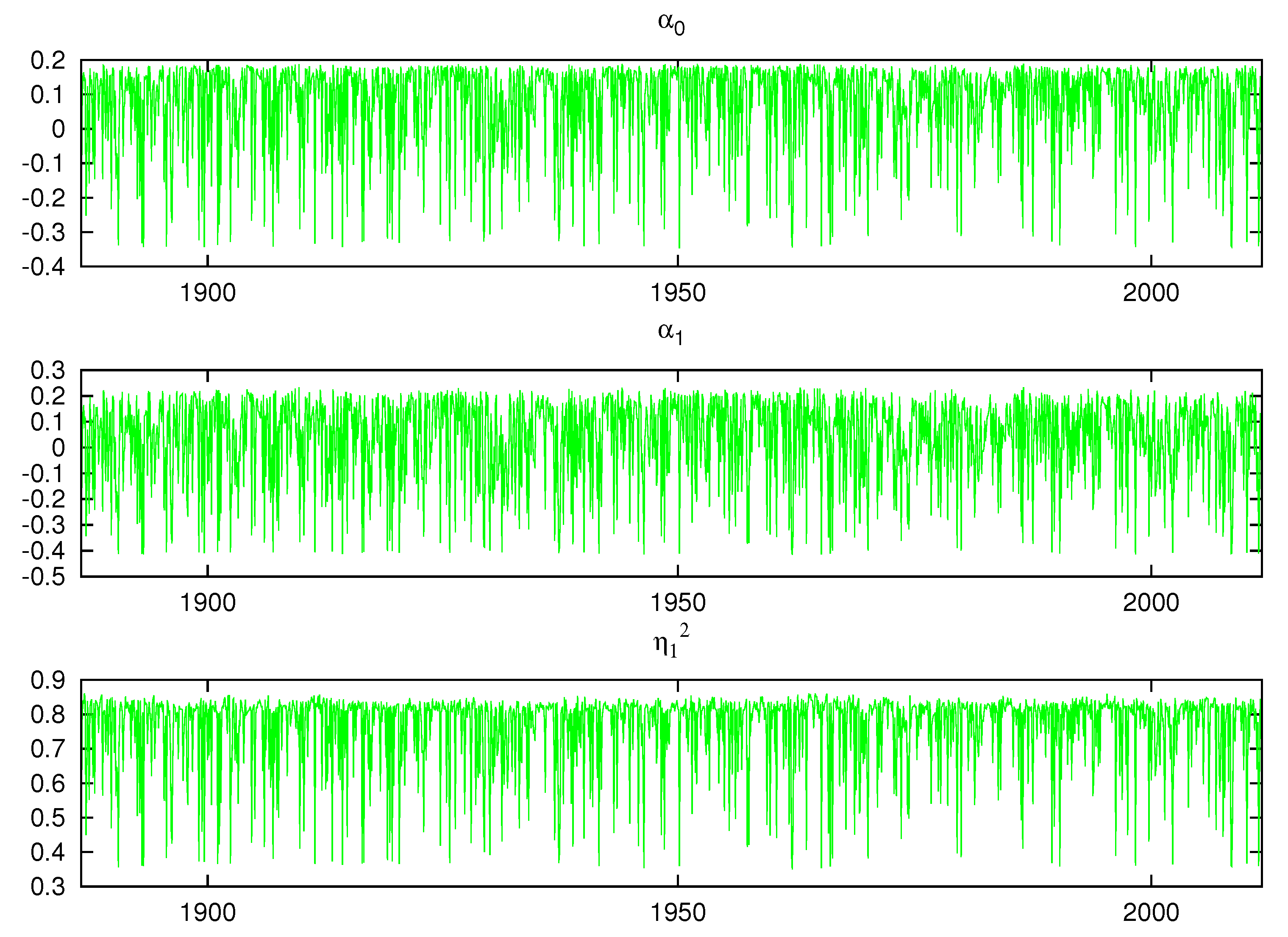
Figure 17 and
Figure 18 display the posterior mean of each of the model parameters contained in the vector
for
. A parametric model would be a straight line. We see considerable switching between clusters in all the plots and the size of the change between the cluster’s parameter values is often large. This shows that multiple mixture components in our nonparametric model is a significant feature of the data. Compared to the parametric model results found in
Table 2,
, the coefficient on
is negative and positive over different time periods. The variability of the parameters in the figures is well beyond the 95% density intervals for the parametric model reported in
Table 2. Although the parametric model estimate of
is close to one, the nonparametric parameter estimates,
,
, varies between 0.4 to 0.85. This is due to the significantly improved fit that the nonparametric model offers in the conditional mean, which contributes to a lower innovation variance.
Our results are robust to changes in the priors and the model for the data density. For instance, we obtain the same qualitative results for
if we omit from Equation (
5)
by setting
,
, or drop the lagged return terms from Equation (
6) by making
for
. Although our priors are quite diffuse and provide a wide range of empirically realistic parameter values, making them more diffuse produces similar results, but the density intervals for
are generally larger. If
is replaced by
in the conditional mean of excess returns (
5), we obtain the same results for
.