Modeling Heterogeneity in Direct Infectious Disease Transmission in a Compartmental Model
Abstract
:1. Introduction
2. Methods
2.1. NBD Transmission Function
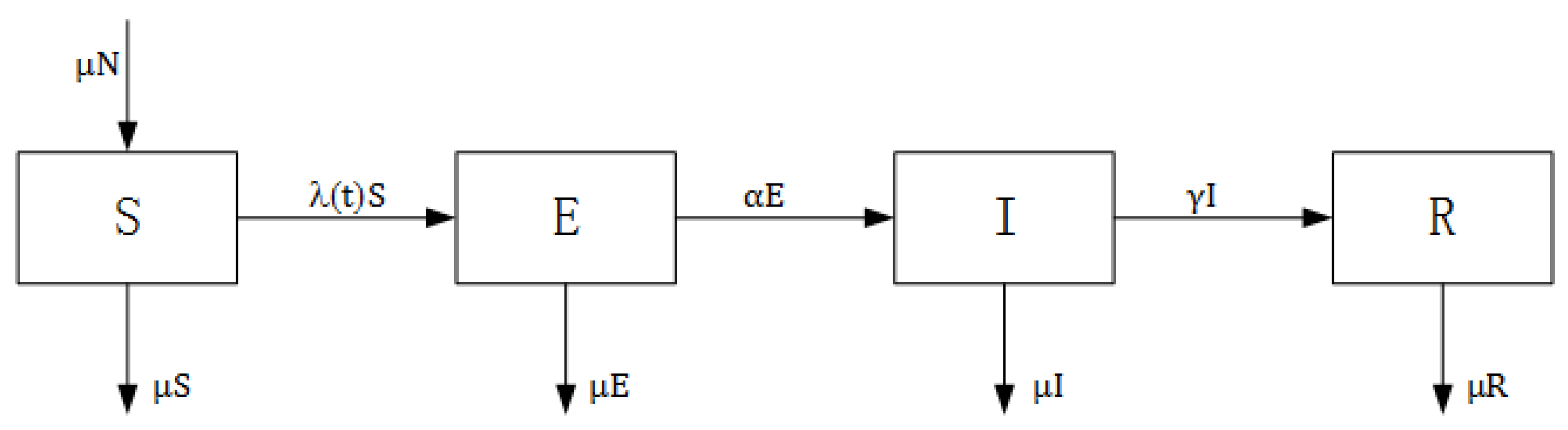
2.2. NBD Compartmental Model
3. Results
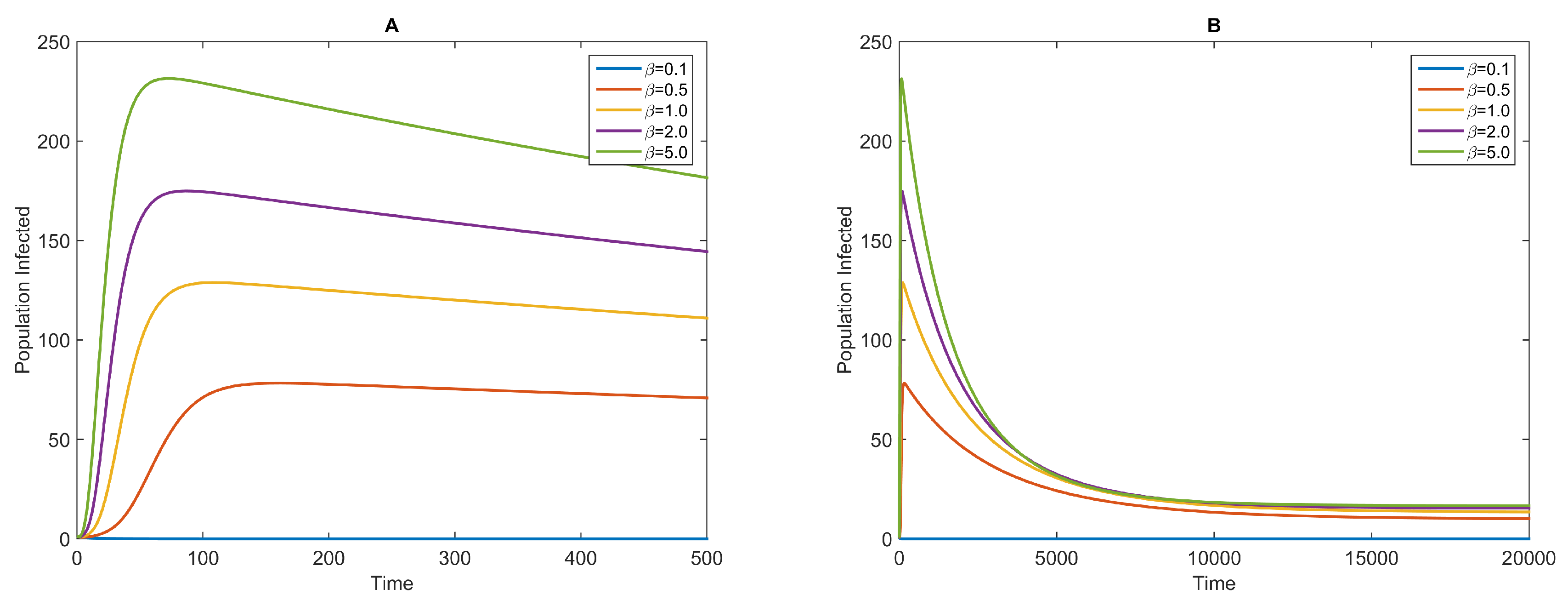
3.1. Dynamics of the NBD Model
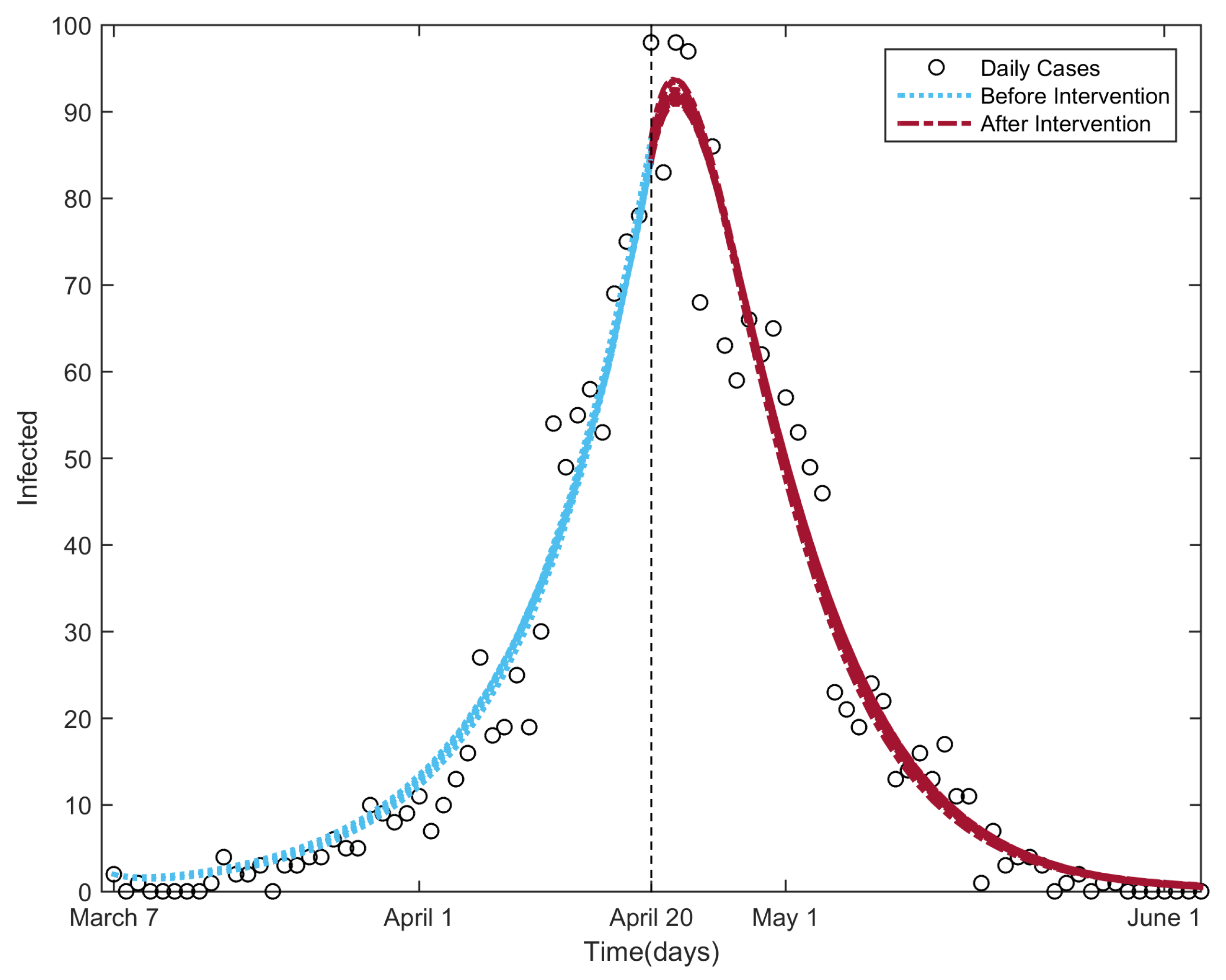
3.2. Fitting the NBD Model to the 2003 Beijing SARS Outbreak Data
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Appendix A. R 0 Expression for the Model
Appendix B. Endemic Equilibrium
References
- Anderson, R.; May, R. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: New York, NY, USA, 1991. [Google Scholar]
- Hethcote, H. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Grassly, N.C.; Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 2008, 6, 477–487. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Rodriguez, D.; Torres-Sorando, L. Models of infectious diseases in spatially heterogeneous environments. Bull. Math. Biol. 2001, 63, 547–571. [Google Scholar] [CrossRef] [PubMed]
- Bansal, S.; Grenfell, B.T.; Meyers, L.A. When individual behaviour matters: Homogeneous and network models in epidemiology. J. R. Soc. Interface 2007, 4, 879–891. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.M.; Hethcote, H.W.; Levin, S.A. Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 1987, 25, 359–380. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, M. Nonlinear transmission rates and the dynamics of infectious-disease. J. Theor. Biol. 1991, 153, 301–321. [Google Scholar] [CrossRef]
- Stroud, P.D.; Sydoriak, S.J.; Riese, J.M.; Smith, J.P.; Mniszewski, S.M.; Romero, P.R. Semi-empirical power-law scaling of new infection rate to model epidemic dynamics with inhomogeneous mixing. Math. Biosci. 2006, 203, 301–318. [Google Scholar] [CrossRef] [PubMed]
- May, R.; Anderson, R. The transmission dynamics of human immunodeficiency virus (HIV). Philos. Trans. R. Soc. B Bio. Sci. 1988, 321, 565–607. [Google Scholar] [CrossRef]
- Babad, H.R.; Nokes, D.J.; Gay, N.J.; Miller, E.; Morgancapner, P.; Anderson, R.M. Predicting the impact of measles vaccination in England and Wales: Model validation and analysis of policy options. Epidemiol. Infect. 1995, 114, 319–344. [Google Scholar] [CrossRef] [PubMed]
- Schenzle, D. An age-structured model of pre- and post-vaccination measles transmission. IMA J. Math. Appl. Med. Biol. 1984, 1, 169–191. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Eames, K.T. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Danon, L.; Ford, A.P.; House, T.; Jewell, C.P.; Keeling, M.J.; Roberts, G.O.; Ross, J.V.; Vernon, M.C. Networks and the epidemiology of infectious disease. Interdiscip. Perspect. Infect. Dis. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Roche, B.; Drake, J.M.; Rohani, P. An agent-based model to study the epidemiological and evolutionary dynamics of influenza viruses. BMC Bioinform. 2011, 12. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.; Cao, Z.; Ge, Y.; Qiu, X. Modeling and simulation for the spread of H1N1 influenza in school using artificial societies. In Intelligence and Security Informatics; Chau, M., Wang, G., Zheng, X., Chen, H., Zeng, D., Mao, W., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany; Heidelberg, Germany, 2011; Volume 6749, pp. 121–129. [Google Scholar]
- Dunham, J.B. An agent-based spatially explicit epidemiological model in MASON. J. Artif. Soc. Soc. Simul. 2006, 9, 1. [Google Scholar]
- Keeling, M. The implications of network structure for epidemic dynamics. Theor. Popul. Biol. 2005, 67, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Roy, M.; Pascual, M. On representing network heterogeneities in the incidence rate of simple epidemic models. Ecol. Complex. 2006, 3, 80–90. [Google Scholar] [CrossRef]
- Aparicio, J.P.; Pascual, M. Building epidemiological models from R-0: An implicit treatment of transmission in networks. Proc. R. Soc. B Biol. Sci. 2007, 274, 505–512. [Google Scholar] [CrossRef]
- Abbey, H. An examination of the Reed-Frost theory of epidemics. Hum. Biol. 1952, 24, 201–233. [Google Scholar] [PubMed]
- Vynnycky, E.; White, R. An Introduction to Infectious Disease Modelling; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Bury, K. Statistical Distributions in Engineering; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lloyd-Smith, J.; Schreiber, S.; Kopp, P.; Getz, W. Superspreading and the effect of individual variation on disease emergence. Nature 2005, 438, 355–359. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Host-parasitoid systems in patchy environments: A phenomenological model. J. Anim. Ecol. 1978, 47, 833–844. [Google Scholar] [CrossRef]
- Godfray, H.C.J.; Hassell, M.P. Discrete and continuous insect populations in tropical environments. J. Anim. Ecol. 1989, 58, 153–174. [Google Scholar] [CrossRef]
- Briggs, C.J.; Godfray, H.C.J. The dynamics of insect-pathogen interactions in stage-structured populations. Am. Nat. 1995, 145, 855–887. [Google Scholar] [CrossRef]
- Barlow, N. Non-linear transmission and simple models for bovine tuberculosis. J. Anim. Ecol. 2000, 69, 703–713. [Google Scholar] [CrossRef]
- Hoch, T.; Fourichon, C.; Viet, A.F.; Seegers, H. Influence of the transmission function on a simulated pathogen spread within a population. Epidemiol. Infect. 2007, 136, 1374–1382. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J.; Lewis, T.; Martin, C.F.; Jones, M.A.; Lo, C.K.; Stamp, M.; Mundel, G.; Way, A.B. Analysis of a measles epidemic. Stat. Med. 1993, 12, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Al-Showaikh, F.; Twizell, E. One-dimensional measles dynamics. Appl. Math. Comput. 2004, 152, 169–194. [Google Scholar] [CrossRef]
- Chen, S.C.; Chang, C.F.; Jou, L.J.; Liao, C.M. Modelling vaccination programmes against measles in Taiwan. Epidemiol. Infect. 2007, 135, 775–786. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Hethcote, H. Simulations of rubella vaccination strategies in China. Math. Biosci. 2006, 202, 371–385. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B. A simple analysis of vaccination strategies for rubella. Math. Biosci. Eng. 2011, 8, 677–687. [Google Scholar] [CrossRef] [PubMed]
- Grais, R.; Ellis, J.; Glass, G. Assessing the impact of airline travel on the geographic spread of pandemic influenza. Eur. J. Epidemiol. 2003, 18, 1065–1072. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.C.; Liao, C.M. Modelling control measures to reduce the impact of pandemic influenza among schoolchildren. Epidemiol. Infect. 2008, 136, 1035–1045. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.; Ma, S.; James, L.; Gopalakrishna, G.; Chew, S.; Tan, C.; Samore, M.; Fisman, D.; Murray, M. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; McMichael, A.J.; Meng, B.; Becker, N.G.; Han, W.; Glass, K.; Wu, J.; Liu, X.; Liu, J.; Li, X.; Zheng, X. Spatial dynamics of an epidemic of severe acute respiratory syndrome in an urban area. Bull. World Health Organ. 2006, 84, 965–968. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Hagenaars, T.; Donnelly, C.; Ferguson, N. Spatial heterogeneity and the persistence of infectious diseases. J. Theor. Biol. 2004, 229, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Zhu, Z.; Guo, J.; Liu, Z.; He, X.; Zhou, W.; Chin, D.P.; Schuchat, A. Severe acute respiratory syndrome, Beijing, 2003. Emerg. Infect. Dis. J. 2004, 10, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Pang, X.; Zhu, Z.; Xu, F.; Guo, J.; Gong, X.; Liu, D.; Liu, Z.; Chin, D.; Feikin, D. Evaluation of control measures implemented in the severe acute respiratory syndrome outbreak in Beijing, 2003. J. Am. Med. Assoc. 2003, 290, 3215–3221. [Google Scholar] [CrossRef] [PubMed]
- Puska, S.M. Chinese National Security: Decisionmaking Under Stress; Strategic Studies Institute of the US Army War College (SSI): Carlisle, PA, USA, 2005; pp. 85–133. [Google Scholar]
- MathWorks. Global Optimization Toolbox. Available online: http://cn.mathworks.com/help/gads/index.html (accessed on 16 February 2016).
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Marti, R. Scatter search and local NLP solvers: A multistart framework for global optimization. Inf. J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- MathWorks. Goodness of Fit between Test and Reference Data. Available online: http://cn.mathworks.com/help/ident/ref/goodnessoffit.html (accessed on 16 February 2016).
- Beijing Municipal Bureau of Statistics NBS Survey Office in Beijing. Beijing Statistical Yearbook 2014; China Statistics Press: Beijing, China, 2014. [Google Scholar]
- Centers for Disease Control and Prevention (America). Frequently Asked Questions about SARS. Available online: http://www.cdc.gov/sars/about/faq.html (accessed on 16 February 2016).
- Barthelemy, M.; Barrat, A.; Pastor-Satorras, R.; Vespignani, A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. J. Theor. Biol. 2005, 235, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Volz, E. SIR dynamics in random networks with heterogeneous connectivity. J. Math. Biol. 2008, 56, 293–310. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.C.; Slim, A.C.; Volz, E.M. Edge-based compartmental modelling for infectious disease spread. J. R. Soc. Interface 2011, 9, 890–906. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.C.; Volz, E.M. Incorporating disease and population structure into models of SIR disease in contact networks. PLoS ONE 2013, 8, e69162. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Biological Meaning | Bound/Value | Source |
|---|---|---|---|
| Heterogeneity level before intervention | Assumed | ||
| Heterogeneity level after intervention | Assumed | ||
| β | Transmission rate | Assumed | |
| Latent period | days | [48] | |
| Infectious period | days | [48] | |
| Expected human lifetime | 70 years | Assumed |
| Parameter | Minimum | Maximum | Mean | Standard Variance |
|---|---|---|---|---|
| β | ||||
| α | ||||
| γ | ||||
| NRMSE |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Wang, J.; Han, W.; Cao, Z. Modeling Heterogeneity in Direct Infectious Disease Transmission in a Compartmental Model. Int. J. Environ. Res. Public Health 2016, 13, 253. https://doi.org/10.3390/ijerph13030253
Kong L, Wang J, Han W, Cao Z. Modeling Heterogeneity in Direct Infectious Disease Transmission in a Compartmental Model. International Journal of Environmental Research and Public Health. 2016; 13(3):253. https://doi.org/10.3390/ijerph13030253
Chicago/Turabian StyleKong, Lingcai, Jinfeng Wang, Weiguo Han, and Zhidong Cao. 2016. "Modeling Heterogeneity in Direct Infectious Disease Transmission in a Compartmental Model" International Journal of Environmental Research and Public Health 13, no. 3: 253. https://doi.org/10.3390/ijerph13030253






