Dynamic Hierarchical Sleep Scheduling for Wireless Ad-Hoc Sensor Networks
Abstract
:1. Introduction
2. Literature Review
3. Dynamic Sensor Scheduling Algorithms
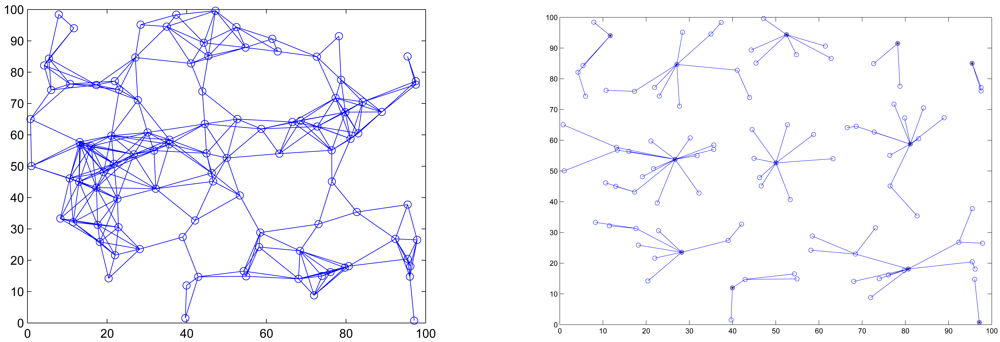
3.1. Cluster Formation for Scheduling Management
3.2. Centralized Adaptive Scheduling Algorithm (CASA)
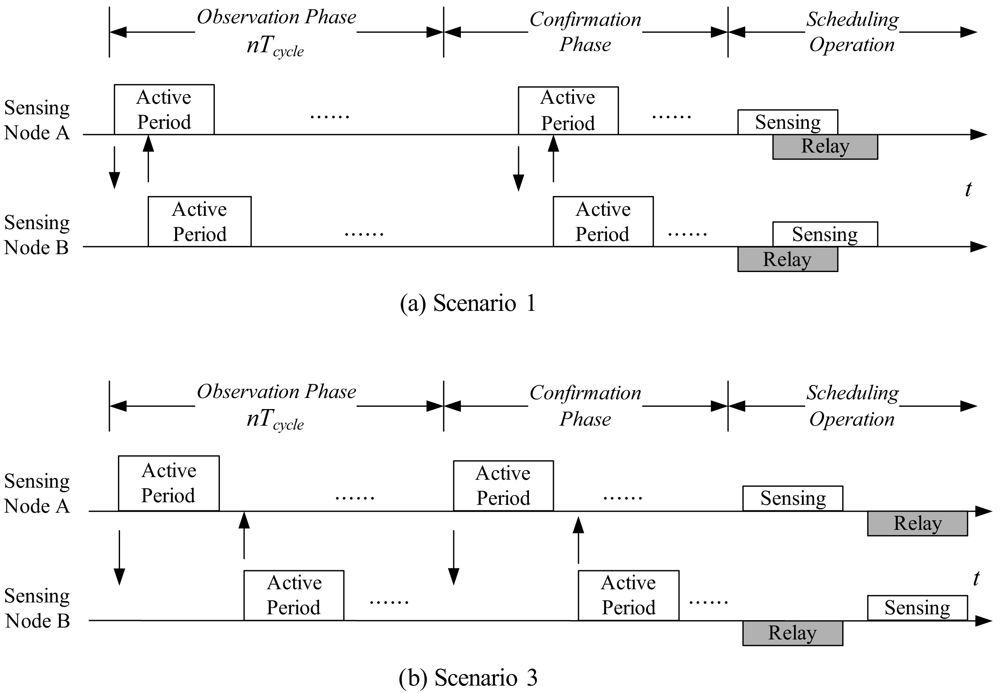
The Scheduling Scheme
Maintenance of Network Connectivity
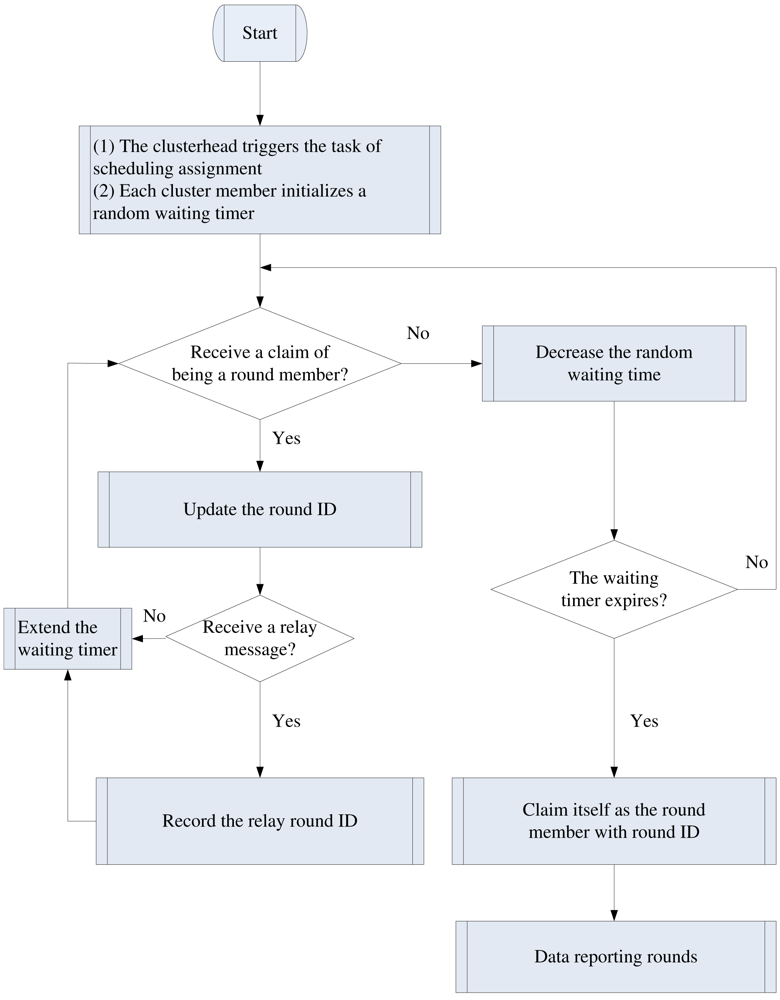
3.3. Distributed Adaptive Scheduling Algorithm (DASA)
The Setting of Waiting Timer
The Scheduling Scheme
4. Analysis
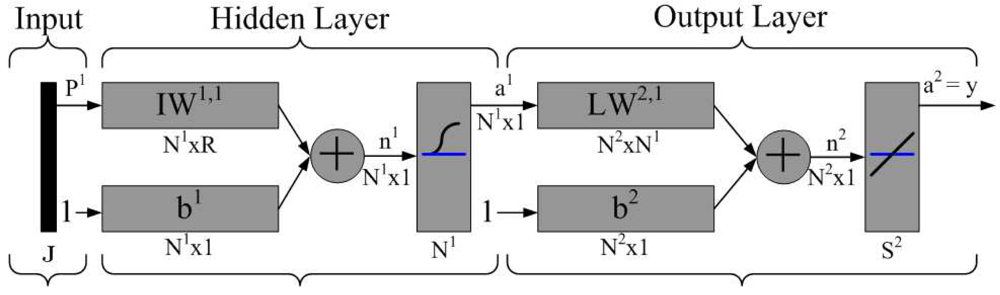
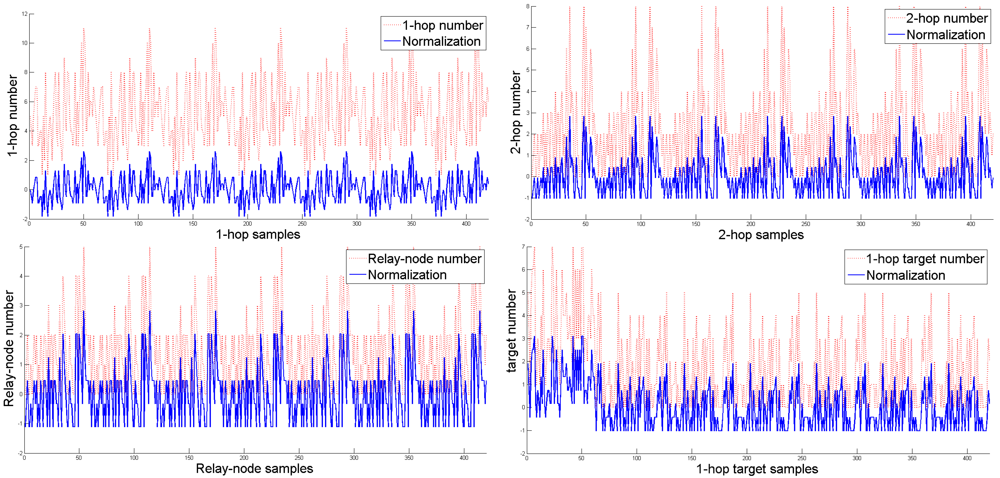
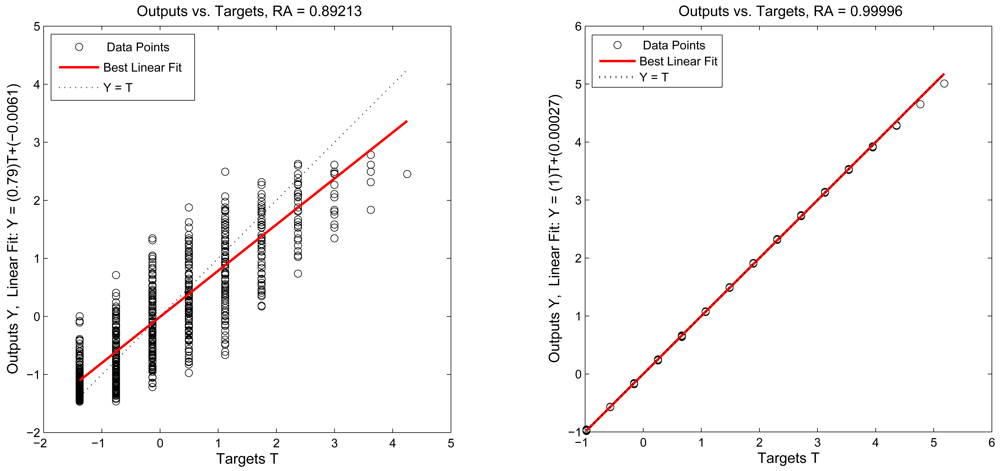
4.1. Neural Networking for the Centralized Approach
Backpropagation Learning Algorithm
 be sample representation of the unknown function f : n → p:
be sample representation of the unknown function f : n → p:
 (·) is the signal function, and η is the learning rate in the back-propagation algorithm.
(·) is the signal function, and η is the learning rate in the back-propagation algorithm.Estimation of the Number of Sensing Rounds
4.2. Probabilistic Model (PM) for the Distributed Approach
Overlap of Geometrical Figures
Theorem 1
Lindeberg Theorem
Theorem 2
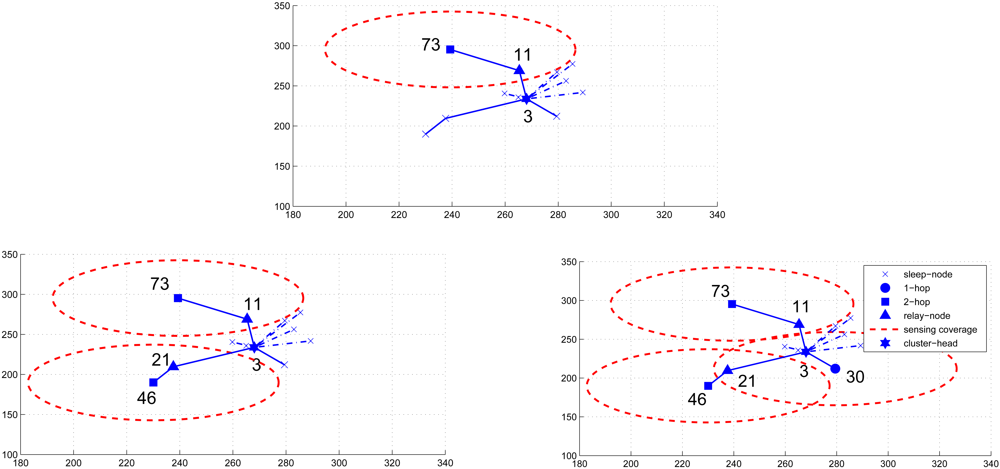
Estimation of the Number of Sensing Rounds
4.3. Sensor Lifetime and Cluster Lifetime
4.4. Complexity Analysis
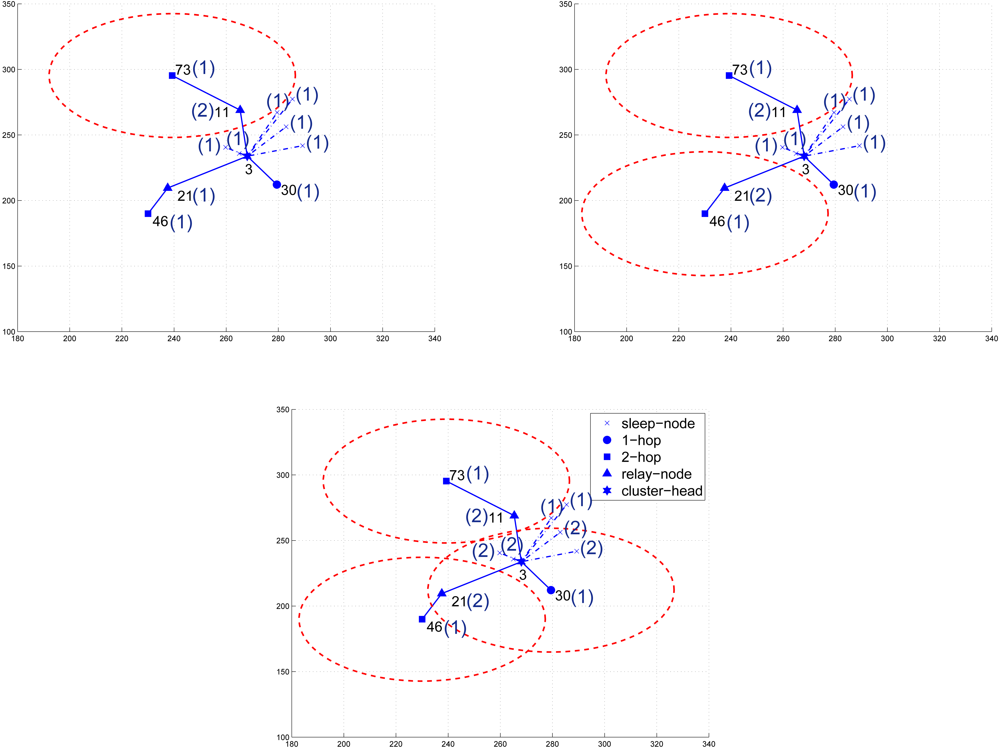
CASA Scheme
 (2) rounds. Next, the clusterhead triggers two rounds of 1-hop flooding for broadcasting the sensor scheduling information throughout the cluster. At last, two rounds of 1-hop flooding is performed for determining the gateway nodes. Thus, the time complexity is
(2) rounds. Next, the clusterhead triggers two rounds of 1-hop flooding for broadcasting the sensor scheduling information throughout the cluster. At last, two rounds of 1-hop flooding is performed for determining the gateway nodes. Thus, the time complexity is
 (6) rounds.
(6) rounds. (NC). Moreover, when operating the sensing task, the energy consumption is related to the number of active sensors in a round. Therefore, the communication complexity for collecting sensing data is
(NC). Moreover, when operating the sensing task, the energy consumption is related to the number of active sensors in a round. Therefore, the communication complexity for collecting sensing data is
 (MRG), where MRG is the number of round members in the cluster.
(MRG), where MRG is the number of round members in the cluster.DASA Scheme
 (7) rounds.
(7) rounds. (NC), NC is the number of sensors in the cluster. Similar to the CASA scheme, when operating the sensing task, the energy consumption is related to the number of active sensors. Therefore, the communication complexity for collecting sensing data is
(NC), NC is the number of sensors in the cluster. Similar to the CASA scheme, when operating the sensing task, the energy consumption is related to the number of active sensors. Therefore, the communication complexity for collecting sensing data is
 (MRG), where MRG is the number of members in each round in the cluster.
(MRG), where MRG is the number of members in each round in the cluster. (NC). For the cluster members, they need to initialize a waiting time, to check if a claim of being a round member is received, to update the round ID, to extend the waiting time, and to check if the waiting timer expires. Therefore, the computation complexity for scheduling management in a cluster member is
, where
is the number of the neighboring cluster members of sensor j.
(NC). For the cluster members, they need to initialize a waiting time, to check if a claim of being a round member is received, to update the round ID, to extend the waiting time, and to check if the waiting timer expires. Therefore, the computation complexity for scheduling management in a cluster member is
, where
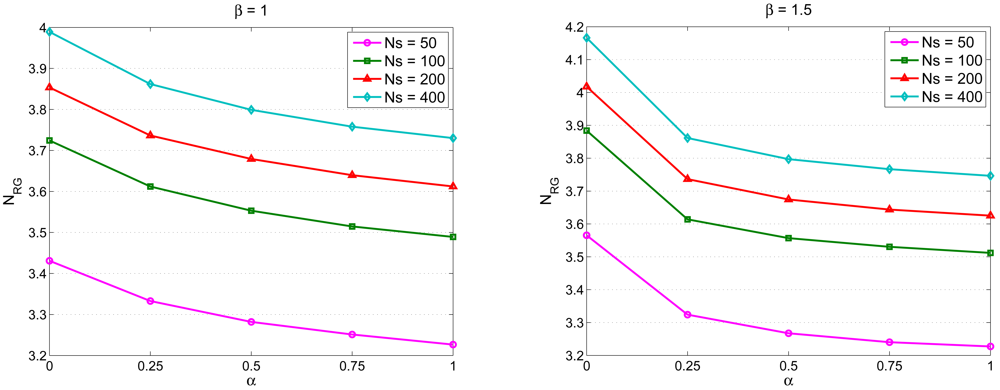
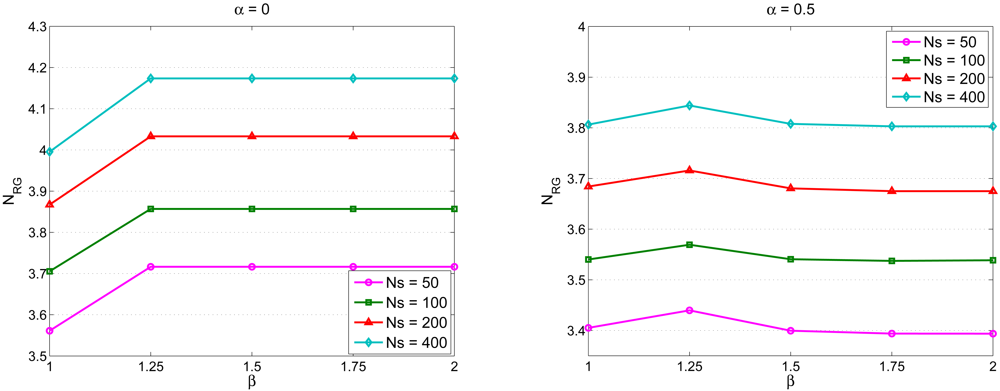
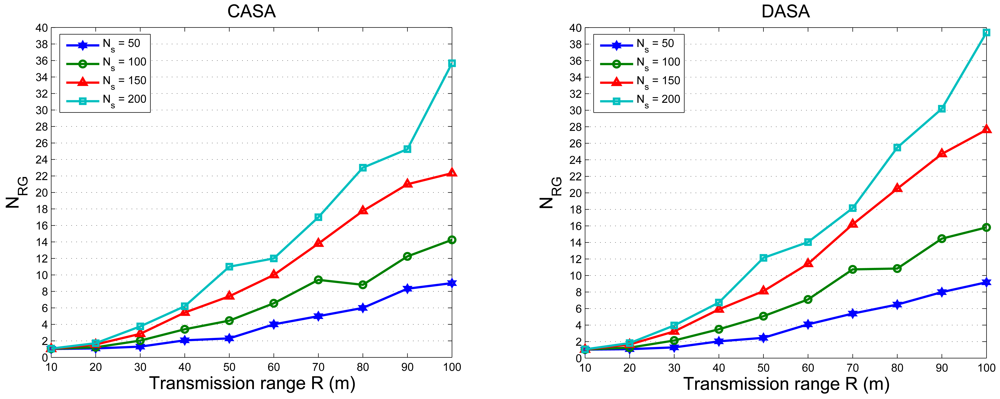
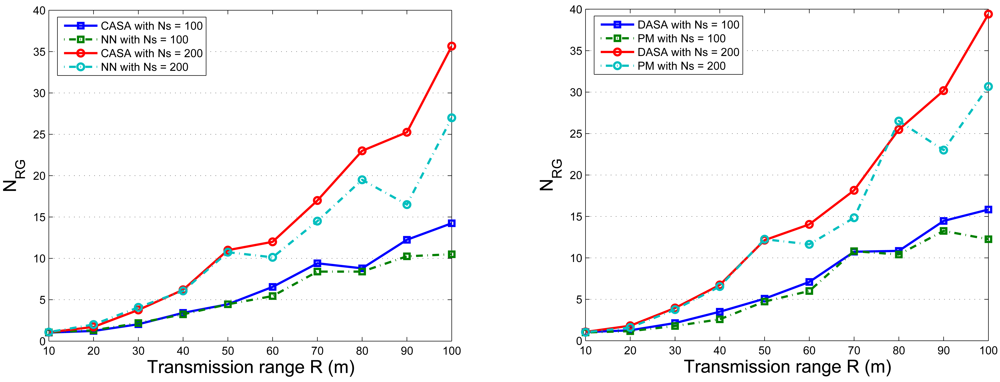
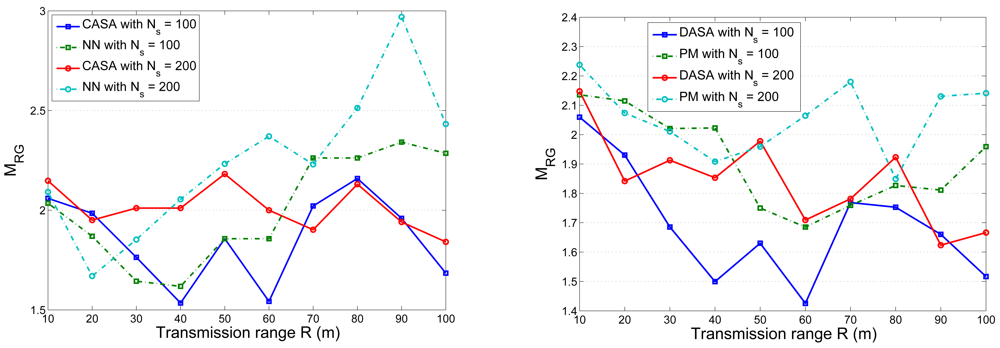
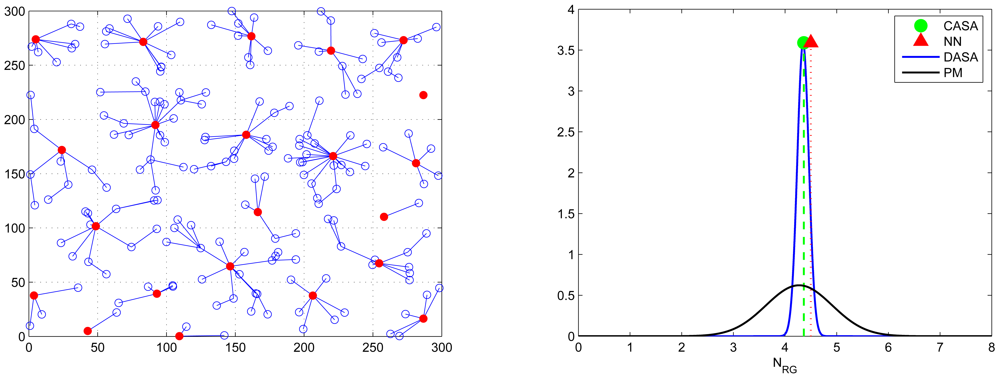
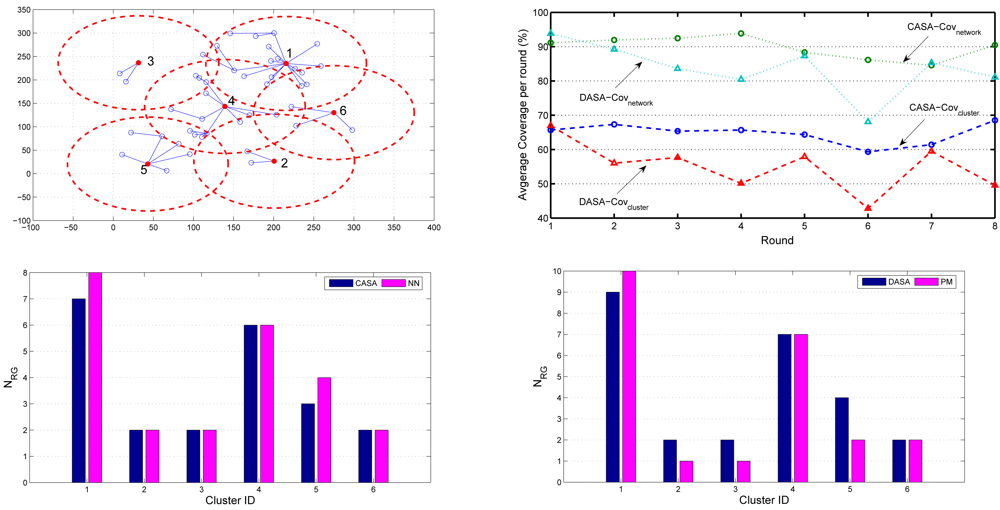
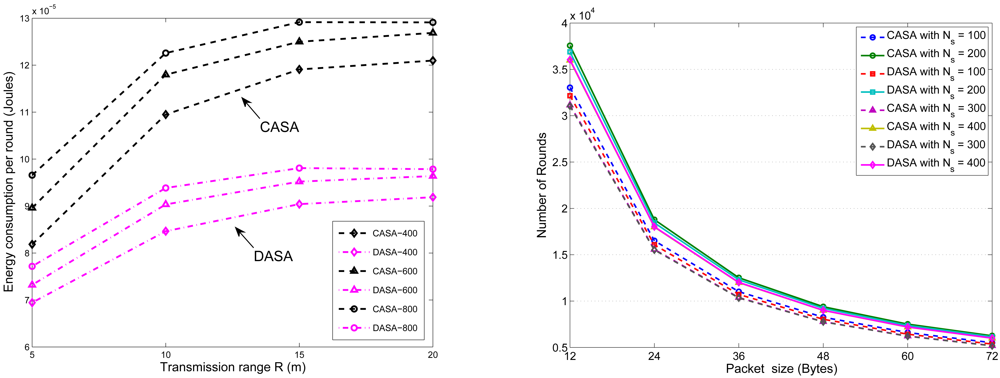
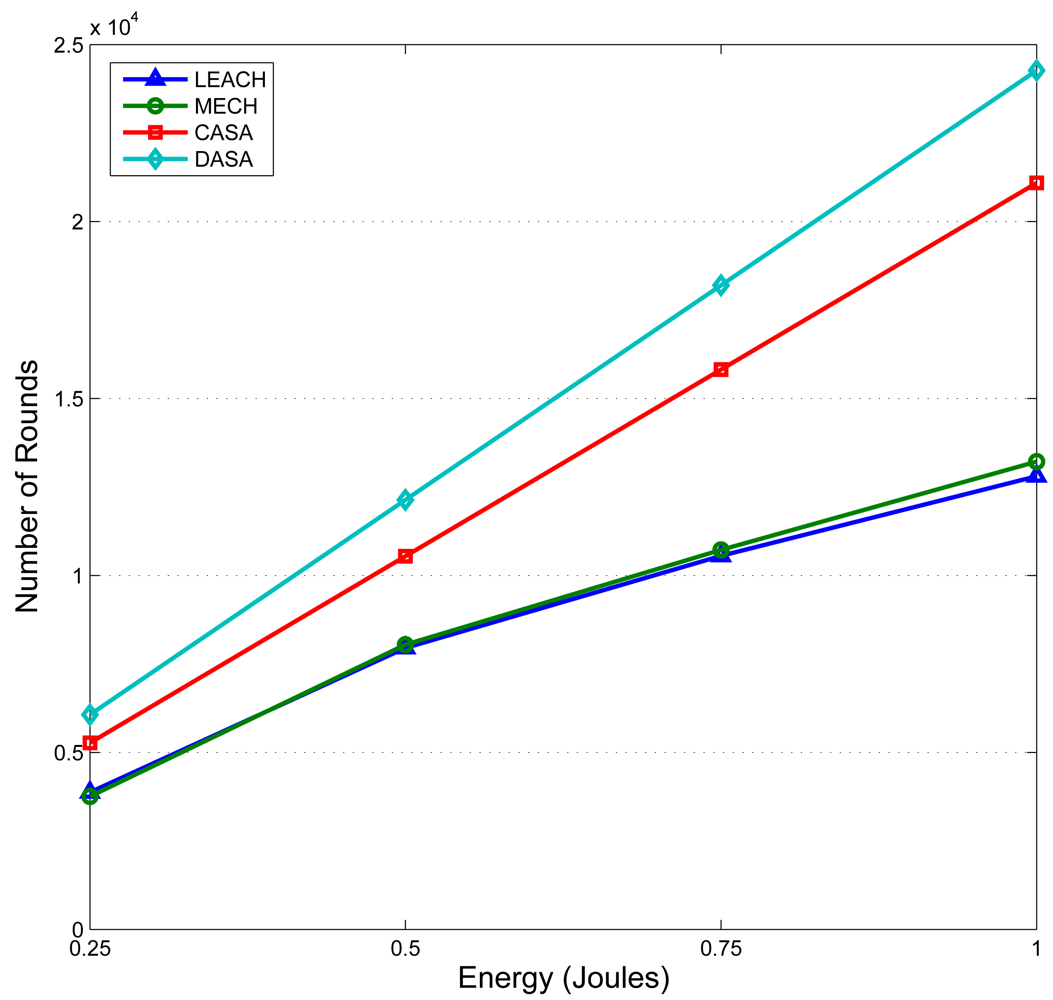
is the number of the neighboring cluster members of sensor j.5. Experimental Results
6. Conclusions
References and Notes
- Yan, T.; He, T.; Stankovic, J. Differentiated surveillance for sensor networks. 2003; pp. 51–62. [Google Scholar]
- Liu, B.; Towsley, D. A study on the coverage of large-scale sensor networks. Proc. of the First IEEE International Conf. Mobile Ad-Hoc and Sensor Systems, Fort Lauderdale, FL, USA; 2004; pp. 475–483. [Google Scholar]
- Ren, S.; Li, Q.; Wang, H.; Chen, X.; Zhang, X. Design and analysis of sensing scheduling algorithms under partial coverage for object detection in sensor networks. IEEE Trans. Parallel Distrib. Syst. 2007, 18, 334–350. [Google Scholar]
- Turau, V.; Weyer, C. Scheduling transmission of bulk data in sensor networks using a dynamic tdma protocol. Proc. of the International Workshop on Data Intensive Sensor Networks, Mannheim, Germany; 2007; pp. 321–325. [Google Scholar]
- Hohlt, B.; Doherty, L.; Brewer, E. Flexible power scheduling for sensor networks. Proc. of the 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA; 2004; pp. 205–214. [Google Scholar]
- Schrage, D.; Gonsalves, P.G. Sensor scheduling using ant colony optimization. Proc. of the 6th International Conference of Information Fusion, Vol. 1. Cairns, Australia; 2003; pp. 379–385. [Google Scholar]
- Decker, C.; Riedel, T.; Peev, E.; Beigl, M. Adaptation of on-line scheduling strategies for sensor network platforms. Proc. of the Third IEEE International Conference on Mobile Ad-hoc and Sensor Systems, Vancouver, Canada; 2006; pp. 534–537. [Google Scholar]
- Chamberland, J.-F.; Veeravalli, V.V. The art of sleeping in wireless sensing systems. Proc. of the IEEE Workshop on Statistical Signal Processing, St. Louis, Missouri, USA; 2003; pp. 17–20. [Google Scholar]
- Tian, D.; Georganas, N.D. A node scheduling scheme for energy conservation in large wireless sensor networks. Wirel. Commun. Mob. Comput. 2003, 3, 271–290. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. Proc. of the 33rd Hawaii International Conference on System Sciences, Hawaii, USA; 2000; pp. 1–10. [Google Scholar]
- Chang, R.-S.; Kuo, C.-J. An energy efficient routing mechanism for wireless sensor networks. Proc. of the 20th International Conference on Advanced Information Networking and Applications, Vienna, Austria; 2006; pp. 308–312. [Google Scholar]
- Cheng, C.T.; Tse, C.K.; Lau, F.C.M. A bio-inspired scheduling scheme for wireless sensor networks. Proc. of IEEE 67th Vehicular Technology Conference, Singapore, Singapore; 2008; pp. 223–226. [Google Scholar]
- Premkumar, K.; Kumar, A. Optimal sleep-wake scheduling for quickest intrusion detection using sensor networks. Proc. of IEEE INFOCOM, Phoenix, AZ, USA; 2008; pp. 2074–2082. [Google Scholar]
- Xiao, Y.; Zhang, Y.; Sun, X.; Chen, H. Asymptotic coverage and detection in randomized scheduling algorithm in wireless sensor networks. Proc. of IEEE ICC, Glasgow, Scotland; 2007; pp. 3541–3545. [Google Scholar]
- Xiao, Y.; Chen, H.; Zhang, Y.; Du, X.; Sun, B.; Wu, K. Intrusion objects with shapes under randomized scheduling algorithm in sensor networks. Proc. of the 28th International Conference on Distributed Computing Systems Workshops, Beijing, China; 2008; pp. 315–320. [Google Scholar]
- Abrams, Z.; Goel, A.; Plotkin, S. Set k-cover algorithms for energy efficient monitoring in wsns. Proc. of IPSN, Berkeley, CA, USA; 2004; pp. 424–432. [Google Scholar]
- Meguerdichian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M. Coverage problems in wireless ad-hoc sensor networks. Proc. of IEEE INFOCOM, Anchorage, Alaska, USA; 2001; pp. 1380–1387. [Google Scholar]
- Wu, K.; Gao, Y.; Li, F.; Xiao, Y. Lightweight deploymentaware scheduling for wsns. ACM/Springer Mobile Networks and Applications (MONET) 2005, 10, 837–852. [Google Scholar]
- Ye, F.; Zhong, G.; Cheng, J.; Lu, S.; Zhang, L. Peas: A robust energy conserving protocol for long-lived sensor networks. Proc. of ICNP, Riverside, CA, USA; 2002; pp. 28–37. [Google Scholar]
- Slijepcevic, S.; Potkonjak, M. Power efficient organization of wsns. Proc. of ICC, Vol. 2. Helsinki, Finland; 2001; pp. 472–476. [Google Scholar]
- Liu, C.; Wu, K.; Xiao, Y.; Sun, B. Random coverage with guaranteed connectivity: Joint scheduling for wsns. IEEE Trans. Parallel Distrib. Syst. 2006, 17, 562–575. [Google Scholar]
- Gupta, V.; Chung, T.H.; Hassibi, B.; Murray, R.M. On a stochastic sensor selection algorithm with applications in sensor scheduling and sensor coverage. Automatica 2006, 42, 251–260. [Google Scholar]
- Shakkottai, S.; Srikant, R.; Shroff, N. Unreliable sensor grids: Coverage, connectivity and diameter. Proc. of INFOCOM, San Francisco, CA, USA; 2003; pp. 1073–1080. [Google Scholar]
- Zhang, H.; Hou, J. Maintaining coverage and connectivity in large sensor networks. Ad Hoc Sens. Wirel. Netw. 2004, 1, 89–123. [Google Scholar]
- Choi, W.; Das, S.K. Coverage-adaptive random sensor scheduling for application-aware data gathering in wireless sensor networks. Comput. Commun. 2006, 29, 3467–3482. [Google Scholar]
- Wang, L.; Xiao, Y. A survey of energy-efficient scheduling mechanisms in sensor networks. Mob. Netw. Appl. 2006, 11, 723–740. [Google Scholar]
- Wen, C.-Y.; Sethares, W.A. Automatic decentralized clustering for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2005, 5, 686–697. [Google Scholar]
- Sun, K.; Ning, P.; Wang, C. Fault-tolerant cluster-wise clock synchronization for wireless sensor networks. IEEE Trans. Dependable Secure Comput. 2005, 2, 177–189. [Google Scholar]
- Billingsley, P. Probability and Measure; John-Wiley & Sons: NY, USA, 1979. [Google Scholar]
- Kumar, S. Neural Networks: A Classroom approach; McGraw-Hill: Singapore, 2005. [Google Scholar]
- Garwood, F. The variance of the overlap of geometrical figures with reference to a bombing problem. Biometrika 1947, 34, 1–17. [Google Scholar]
- Robbins, H.E. On the measure of a random set. i. Ann. Math. Statist. 1944, 15, 70–74. [Google Scholar]
- Chatterjee, M.; Das, S.K.; Turgut, D. Wca: A weighted clustering algorithm for mobile ad hoc networks. J. Cluster Comput. 2002, 5, 193–204. [Google Scholar]
- Demuth, H.; Beale, M.; Hagan, M. Neural Network Toolbox 6: User's Guide; The Math Works, Inc.: MA, USA, 2008. [Google Scholar]
- Santi, P. Topology Control in Wireless Ad Hoc and Sensor Networks; John-Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Joa-Ng, M.; Lu, I.-T. A peer-to-peer zone-based two-level link state routing for mobile ad hoc networks. IEEE J. Sel. Areas Commun. 1999, 17, 1415–1425. [Google Scholar]









| Assign NRG = 0, ℓ = 1; |
| while (U ≠ ϕ) do |
| { |
| ; |
| RGℓ = ϕ; |
| \* Selecting 2-hop round members *\ |
| if (H2 ≠ ϕ) |
| { |
| i = argmaxk|H1(k)|, ∀ k ∈ H2; |
| RGℓ = {i}; |
| ; |
| H2 = H2 − i; |
| } |
| \* Selecting 1-hop round members *\ |
| while do |
| { |
| Pick sensor m, ; |
| RGℓ = RGℓ ∪ m; |
| ; |
| H1 = H1 − m; |
| } |
| U = U − RGℓ; |
| ℓ = ℓ + 1; |
| NRG = NRG + 1; |
| } |
|
| * ⌈·⌉ is the ceiling function. |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wen, C.-Y.; Chen, Y.-C. Dynamic Hierarchical Sleep Scheduling for Wireless Ad-Hoc Sensor Networks. Sensors 2009, 9, 3908-3941. https://doi.org/10.3390/s90503908
Wen C-Y, Chen Y-C. Dynamic Hierarchical Sleep Scheduling for Wireless Ad-Hoc Sensor Networks. Sensors. 2009; 9(5):3908-3941. https://doi.org/10.3390/s90503908
Chicago/Turabian StyleWen, Chih-Yu, and Ying-Chih Chen. 2009. "Dynamic Hierarchical Sleep Scheduling for Wireless Ad-Hoc Sensor Networks" Sensors 9, no. 5: 3908-3941. https://doi.org/10.3390/s90503908





