Modeling and Control of the Redundant Parallel Adjustment Mechanism on a Deployable Antenna Panel
Abstract
:1. Introduction
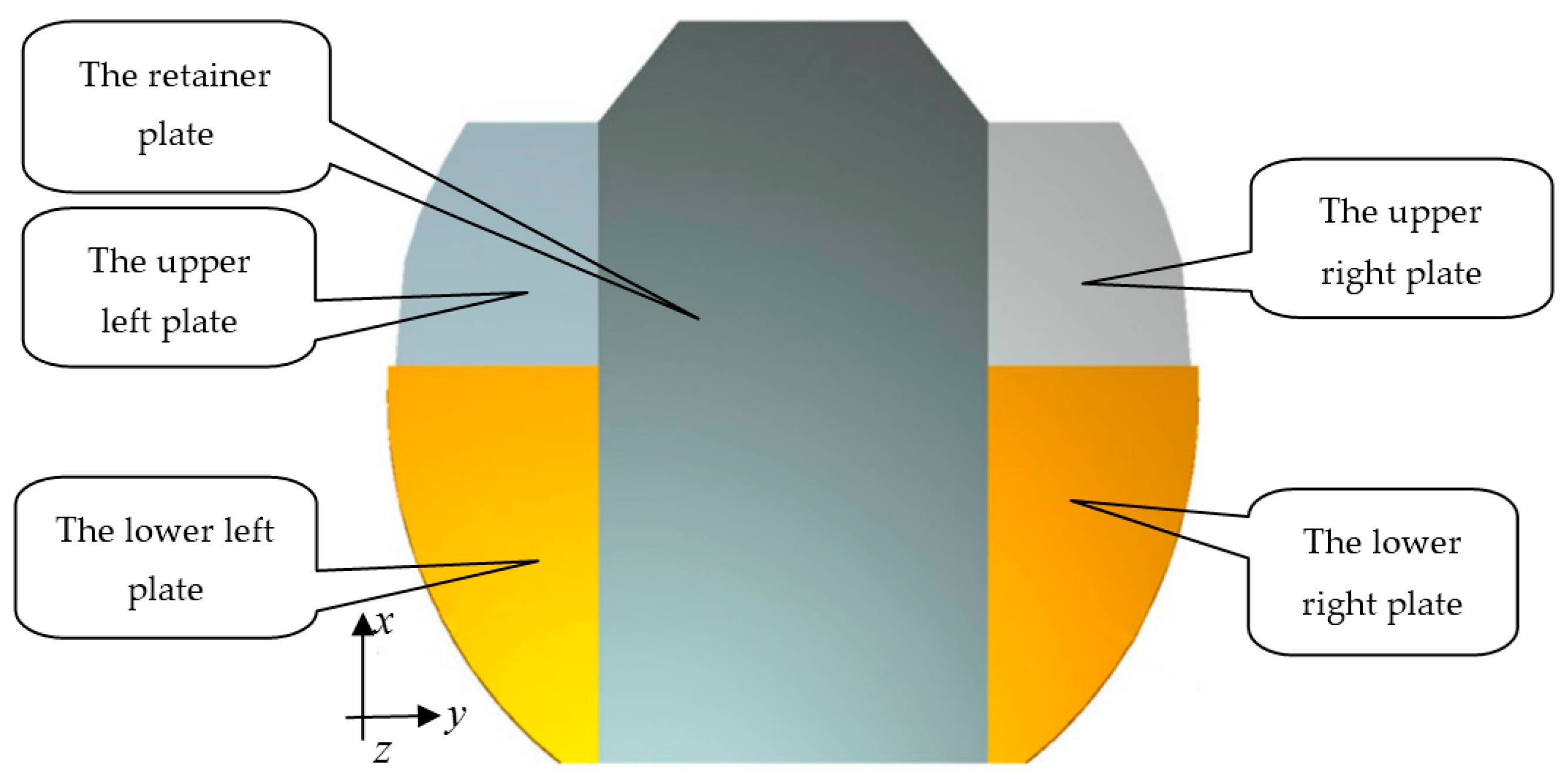
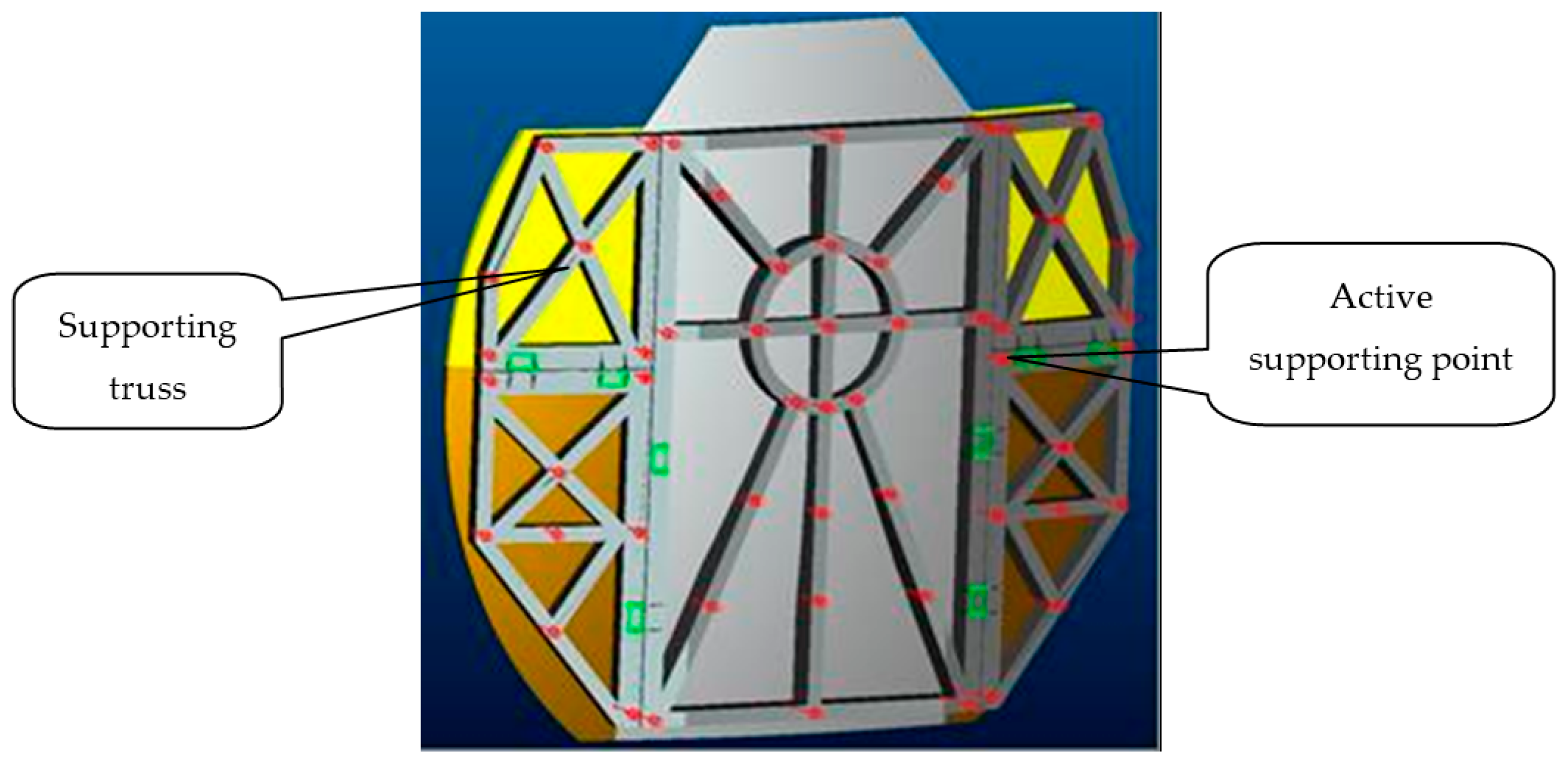
2. Materials and Methods
2.1. Modeling Based on Hamilton Principle
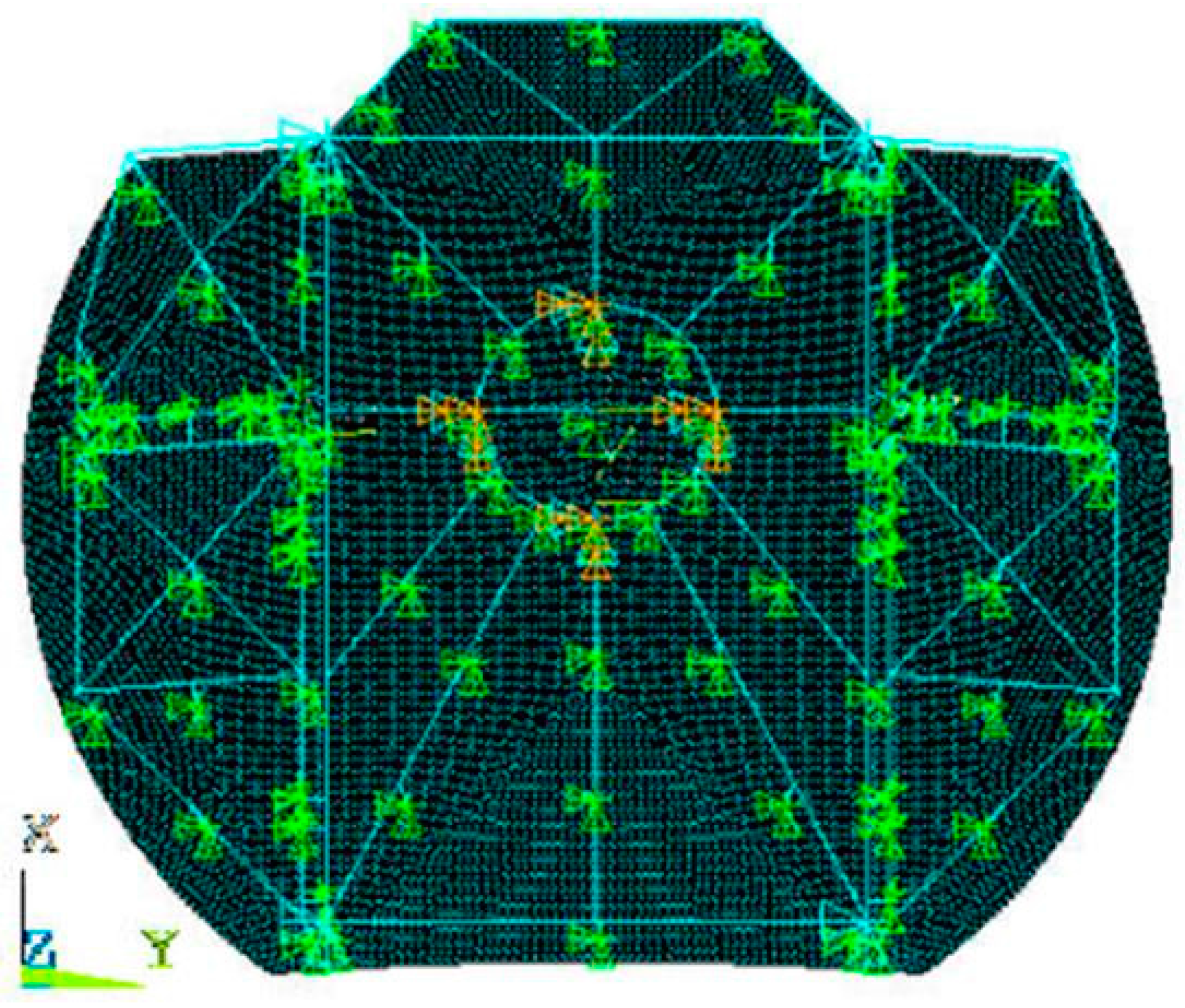
2.2. Modal Analysis
3. Controller Design
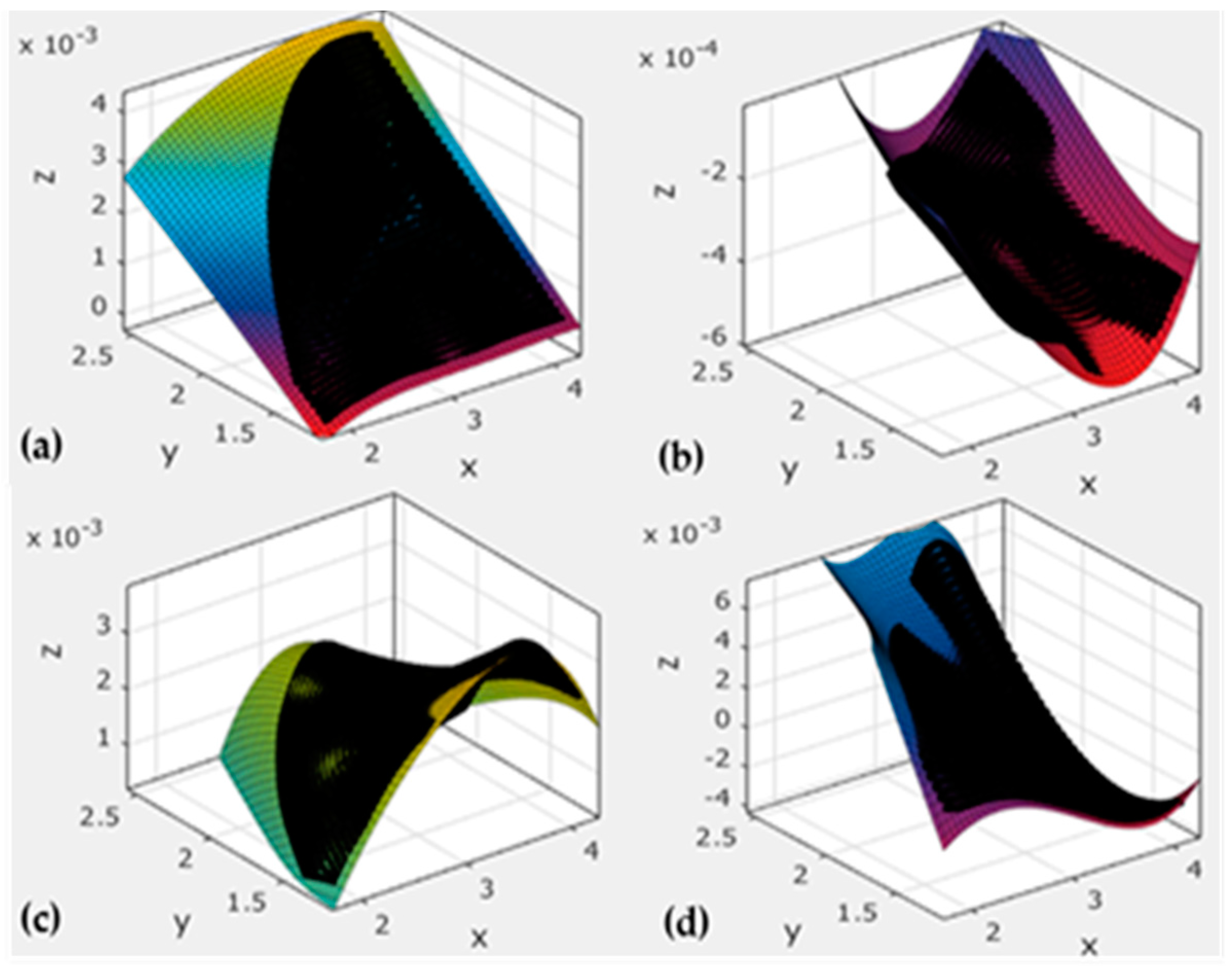
4. Simulations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Duan, B. Optimization Analysis and Measurement of Antenna Structure; Xidian University Press: Xi’an, China, 1998. [Google Scholar]
- Natori, M.; Takano, T.; Noda, T.; Tashima, T.; Tabata, M. Ground adjustment procedure of a deployable high accuracy mesh antenna for space VLBI mission. In Proceedings of the Structures, Structural Dynamics, and Materials Conference and Exhibit, Long Beach, CA, USA, 8–11 April 2013.
- Liu, M. Shape accuracy adjustment of a flexible mesh antenna reflector. J. Astronaut. 2001, 22, 72–77. [Google Scholar]
- Zhao, D.S. Study on the shape accuracy adjustment technology of mesh deployable antenna reflector. Machinery 2010, 37, 31–33. [Google Scholar]
- Jiang, T. Modeling, Simulation and Experimental Research of Flexible Manipulator. Ph.D. Dissertation, Tianjin University, Tianjin, China, 1996. [Google Scholar]
- Tan, H. Research on Hybrid Control Method of Mechanical Force/Position. Master’s Thesis, Chongqing University, Chongqing, China, 2013. [Google Scholar]
- Gawronski, W.; Souccar, K. Control System of the Large Millimeter Telescope. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation Conference, Glasgow, UK, 21–25 June 2004.
- Gawronski, W.; Mellstrom, J.A. Modeling and Simulations of the DSS13 Antenna Control System; TDA Progress Report 42-106; NASA: Greenbelt, MD, USA, 1991; pp. 205–248.
- Fehr, J.; Eberhard, P. Simulation process of flexible multibody systems with non-modal model order reduction techniques. Multibody Syst. Dyn. 2011, 25, 313–334. [Google Scholar] [CrossRef]
- Gawronski, W.; Mellstrom, J.A. Elevation Control System Model for the DSS13 Antenna; TDA Progress Report 42-105; NASA: Greenbelt, MD, USA, 1991; pp. 83–85.
- Gawronski, W.; Bartos, R. Communications Ground System Section, Modeling and Analysis of the DSS-14 Antenna Control System; TDA Progress Report 42-124; NASA: Greenbelt, MD, USA, 1996; pp. 113–142.
- Emde, P.; Süß, M.; Eisenträger, P.; Moik, R.; Kärcher, H. Design of the solar telescope GREGOR under dynamic wind loads. In Proceedings of the Optical Materials and Structures Technologies, International Symposium on Optical Science and Technology, San Diego, CA, USA, 3–8 August 2003.
- Li, H.; Wang, J. Thin Mirror Active Optics Experiment System; Opto-Electronic Engineering: Chengdu, China, 2009. [Google Scholar]
- Ye, M.; Xiao, L. Mechanical Analysis; Tianjin University Press: Tianjin, China, 2001; pp. 54–83. [Google Scholar]
- Wang, Z. Mechanical Analysis; Science Press: Beijing, China, 2002; pp. 125–132. [Google Scholar]
- Li, S.; Tang, B.; Wu, G. Experimental study on the static and dynamic characteristics of the piezoelectric actuator. J. Hehai Univ. (Changzhou Campus) 2002, 16, 12–22. [Google Scholar]
- Zhang, Z.; Xu, M.; Shao, C. Application of piezoelectric actuator in active vibration control of flexible ring antenna. Intensity Environ. 2013, 40, 21–27. [Google Scholar]
- Liu, B. Modern Control Theory; Machinery Industry Press: Beijing, China, 2000; pp. 210–220. [Google Scholar]
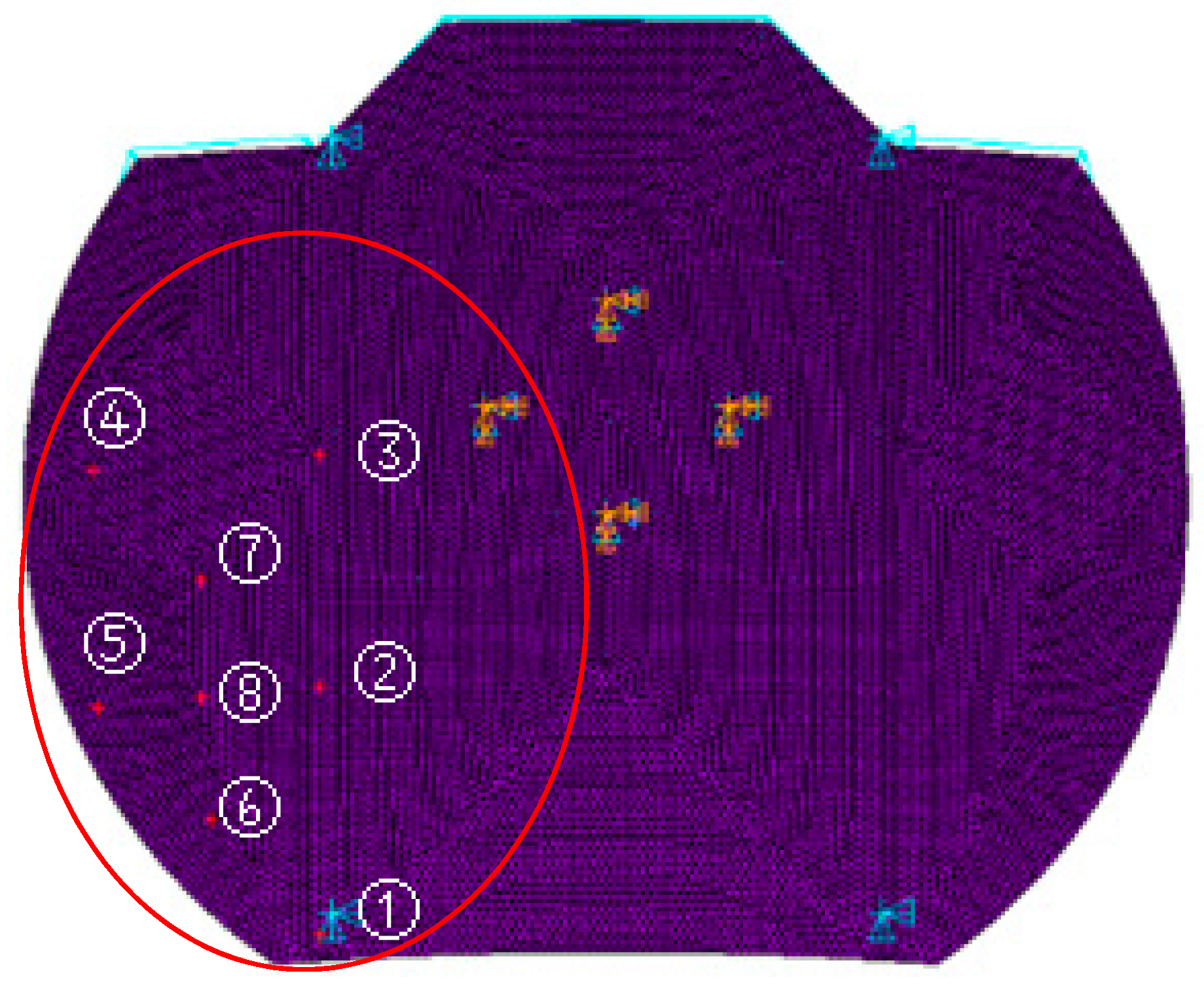

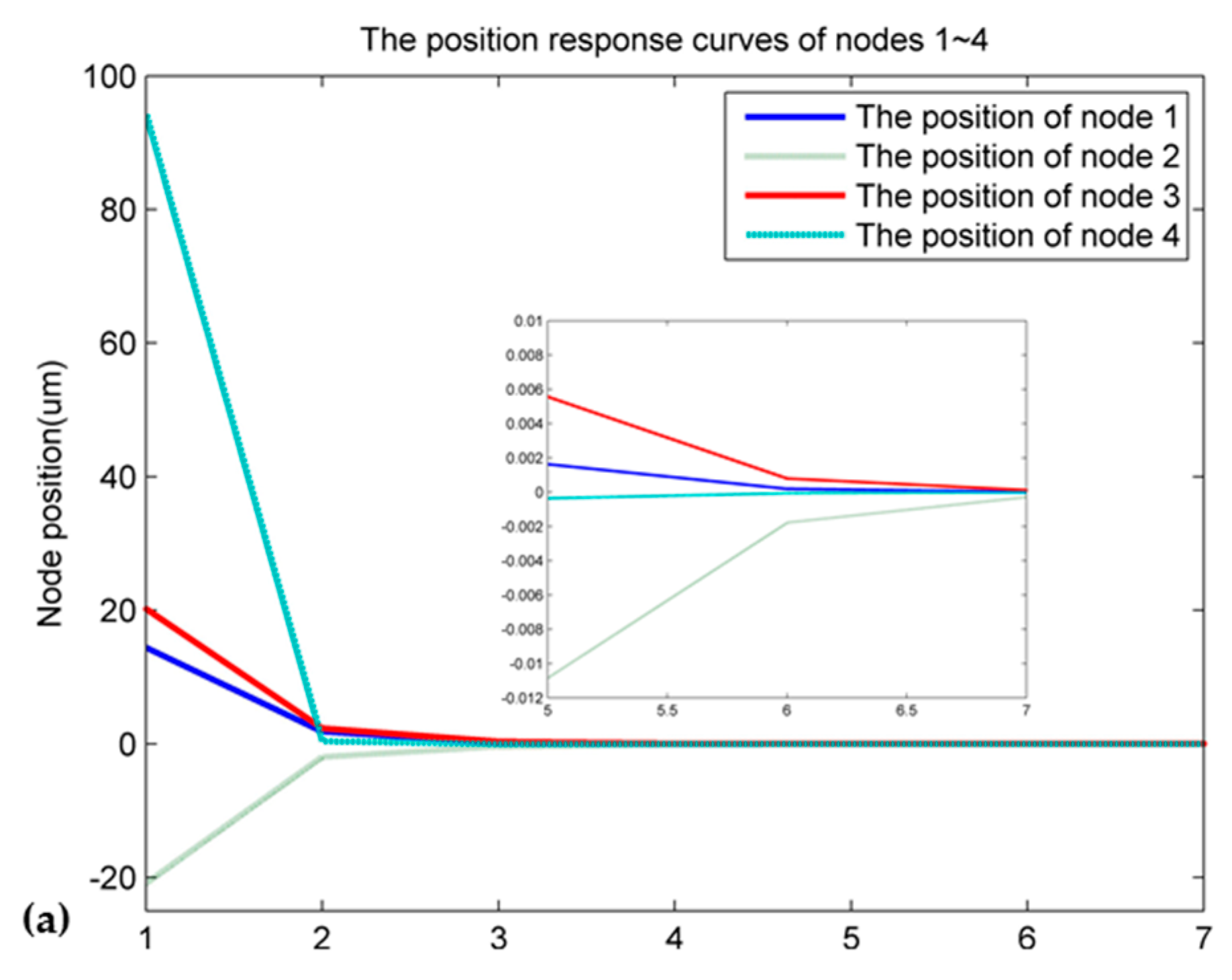
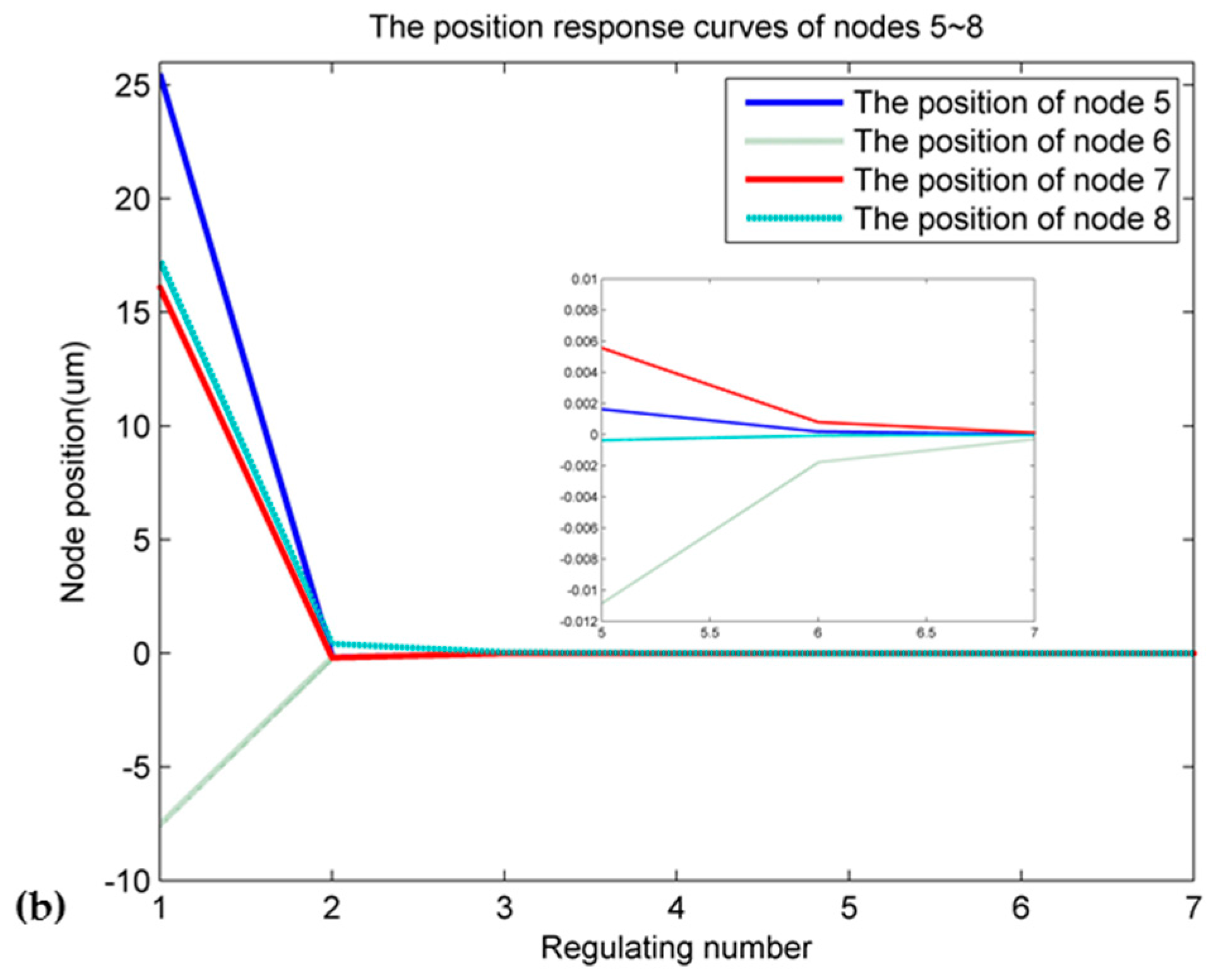
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0525 | 0.0084 | −0.0054 | −0.0110 | 0.0109 | 0.0282 | 0.0003 | 0.0103 |
| 2 | 0.0159 | 0.1496 | 0.0767 | 0.1016 | 0.1156 | 0.0767 | 0.1149 | 0.1272 |
| 3 | −0.0066 | 0.0679 | 0.1310 | 0.1565 | 0.1099 | 0.0529 | 0.1193 | 0.0904 |
| 4 | −0.0377 | 0.0674 | 0.1311 | 1.2854 | 1.1341 | 0.5207 | 0.6880 | 0.6321 |
| 5 | −0.0009 | 0.0963 | 0.0993 | 1.1489 | 1.2822 | 0.6277 | 0.6924 | 0.7184 |
| 6 | 0.0287 | 0.0696 | 0.0546 | 0.5478 | 0.6400 | 0.4287 | 0.3442 | 0.3723 |
| 7 | −0.0044 | 0.1027 | 0.1159 | 0.7100 | 0.6995 | 0.3391 | 0.4702 | 0.4207 |
| 8 | 0.0083 | 0.1177 | 0.0897 | 0.6568 | 0.7283 | 0.3698 | 0.4233 | 0.4854 |
| Forced Number | Force (N) | Approximate Model (mm) | ANSYS Model (mm) |
|---|---|---|---|
| 1 | 1000 | 0.1300 | 0.07527 |
| 2 | −500 | 0.0512 | 0.11062 |
| 3 | 1000 | 0.3795 | 0.25606 |
| 4 | −500 | 0.1831 | 0.06539 |
| 5 | 1000 | 1.0748 | 0.85711 |
| 6 | −500 | 0.9403 | 0.80501 |
| 7 | 1000 | 0.5097 | 0.52377 |
| 8 | −500 | 0.5132 | 0.46679 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 18.7700 | −1.1285 | 0.5362 | 0.8827 | 0.8241 | −3.5113 | 0.2569 | −0.3165 |
| 2 | −1.0920 | 12.8232 | −3.4966 | 2.1748 | 3.3688 | −0.5431 | −4.3024 | −6.2003 |
| 3 | 0.4759 | −3.3923 | 11.8982 | −1.0247 | 2.8461 | 0.0475 | −4.6879 | −0.3009 |
| 4 | 0.8858 | 2.2394 | −0.9862 | 5.7688 | −2.6642 | 0.5768 | −5.7366 | 0.3834 |
| 5 | 0.8321 | 3.7598 | 2.8797 | −2.6517 | 12.1776 | −4.8199 | −4.6021 | −8.3840 |
| 6 | −3.5954 | −0.5427 | −0.0066 | 0.5836 | −4.8108 | 9.8095 | 0.2140 | −1.0532 |
| 7 | 0.2784 | −4.5508 | −5.0232 | −5.7180 | −4.5889 | 0.2099 | 22.1431 | −2.8526 |
| 8 | −0.2797 | −6.7561 | −0.0268 | 0.3542 | −8.3148 | −1.0323 | −2.9019 | 18.9238 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, L.; Bao, H.; Wang, M.; Duan, X. Modeling and Control of the Redundant Parallel Adjustment Mechanism on a Deployable Antenna Panel. Sensors 2016, 16, 1632. https://doi.org/10.3390/s16101632
Tian L, Bao H, Wang M, Duan X. Modeling and Control of the Redundant Parallel Adjustment Mechanism on a Deployable Antenna Panel. Sensors. 2016; 16(10):1632. https://doi.org/10.3390/s16101632
Chicago/Turabian StyleTian, Lili, Hong Bao, Meng Wang, and Xuechao Duan. 2016. "Modeling and Control of the Redundant Parallel Adjustment Mechanism on a Deployable Antenna Panel" Sensors 16, no. 10: 1632. https://doi.org/10.3390/s16101632





