Effects of Dispersal-Related Factors on Species Distribution Model Accuracy for Boreal Lake Ecosystems
Abstract
:1. Introduction
2. Methods
2.1. Study Area and Sampling
| Median | Mean | Min | Max | |
|---|---|---|---|---|
| altitude (m a.s.l.) | 169 | 250 | 15 | 1,138 |
| catchment area (km2) | 5.6 | 75.5 | 0.26 | 2,902 |
| lake area (km2) | 0.6 | 1.9 | 0.02 | 52.2 |
| lake depth (m) | 10 | 12 | 1 | 36 |
| color (filtered absorbance) | 0.10 | 0.14 | 0.0 | 0.59 |
| pH | 6.67 | 6.56 | 5.03 | 8.27 |
| precipitation per year (mm) | 750 | 752 | 550 | 1,150 |
| temperature July (°C) | 16 | 15 | 8 | 17 |
| total nitrogen (µg/L) | 387 | 430 | 54 | 1,345 |
| total phosphorus (µg/L) | 7.6 | 11.6 | 1.8 | 67.6 |
| catchment agriculture (%) | 0.0 | 3.1 | 0.0 | 54.4 |
| catchment coniferous forest (%) | 3.3 | 14.2 | 0.0 | 75.9 |
| catchment deciduous forest (%) | 0.6 | 2.3 | 0.0 | 19.6 |

| environmental factor | unit | |
|---|---|---|
| water chemistry | total phosphorus concentration | µg/L |
| total nitrogen concentration | µg/L | |
| pH | ||
| total organic carbon | mg/L | |
| calcium concentration | meq/L | |
| magnesium concentration | meq/L | |
| potassium concentration | meq/L | |
| alkalinity | meq/L | |
| catchment land cover | water color1 coniferous forest | km2 |
| deciduous forest | km2 | |
| mixed forest | km2 | |
| water | km2 | |
| wetland | km2 | |
| agriculture | km2 | |
| pasture | km2 | |
| altitude | m above sea level | |
| geographical | longitude latitude | |
| catchment area | km2 | |
| lake area | km2 | |
| lake depth | meter | |
| precipitation2 | mm | |
| climate | air temperature July2 | Celsius |
| length of vegetation period | days |
| source | |
|---|---|
| lake size | Digital maps from the National Land Survey of Sweden [24] |
| catchment size | Digital maps from the National Land Survey of Sweden [24] |
| water in catchment-lake area | Corine land cover [28] |
| altitude | Digital elevation model from the National Land Survey of Sweden [24] |
| distance to 1st, 5th and 10th lake | Distance to outlet coordinate, using database from Swedish institute for metrology and hydrology [25] containing 105,645 lakes with area ≥ 1 hectare |
| N lakes within 100, 200, 500, 1,000, 5,000 and 10,000 m buffers | Using database from Swedish institute for metrology and hydrology [25] containing 105,645 lakes with area ≥ 1 hectare |
2.2. Modeling
2.3. Evaluation of Model Accuracy
2.3.1. Invertebrate Flight Ability
2.3.2. Ecosystem Connectivity
3. Results
3.1. Effect of Connectivity and Ecosystem Size on Assemblage Prediction Accuracy
| littoral | profundal | phytoplankton | |
|---|---|---|---|
| lake area | 0.07 | 0.18 | 0.46*** |
| catchment area | 0.03 | 0.24* | 0.43*** |
| water (excl. study lake) | 0.07 | 0.03 | 0.37*** |
| altitude | −0.33*** | 0.00 | −0.07 |
| distance neighbor 1 | 0.13 | −0.02 | 0.18 |
| distance neighbor 2 | 0.12 | 0.04 | 0.23* |
| distance neighbor 5 | 0.15 | 0.08 | 0.30** |
| distance neighbor 10 | 0.19* | 0.11 | 0.22* |
| N lakes 100 m | 0.00 | 0.04 | 0.03 |
| N lakes 200 m | 0.08 | 0.14 | 0.07 |
| N lakes 500 m | 0.00 | 0.03 | 0.13 |
| N lakes 1,000 m | −0.05 | −0.07 | 0.08 |
| N lakes 5,000 m | −0.17 | −0.06 | −0.07 |
| N lakes 10,000 m | −0.22* | −0.01 | −0.02 |

3.2. Effect of Flight Ability on Invertebrate Distribution Prediction Accuracy
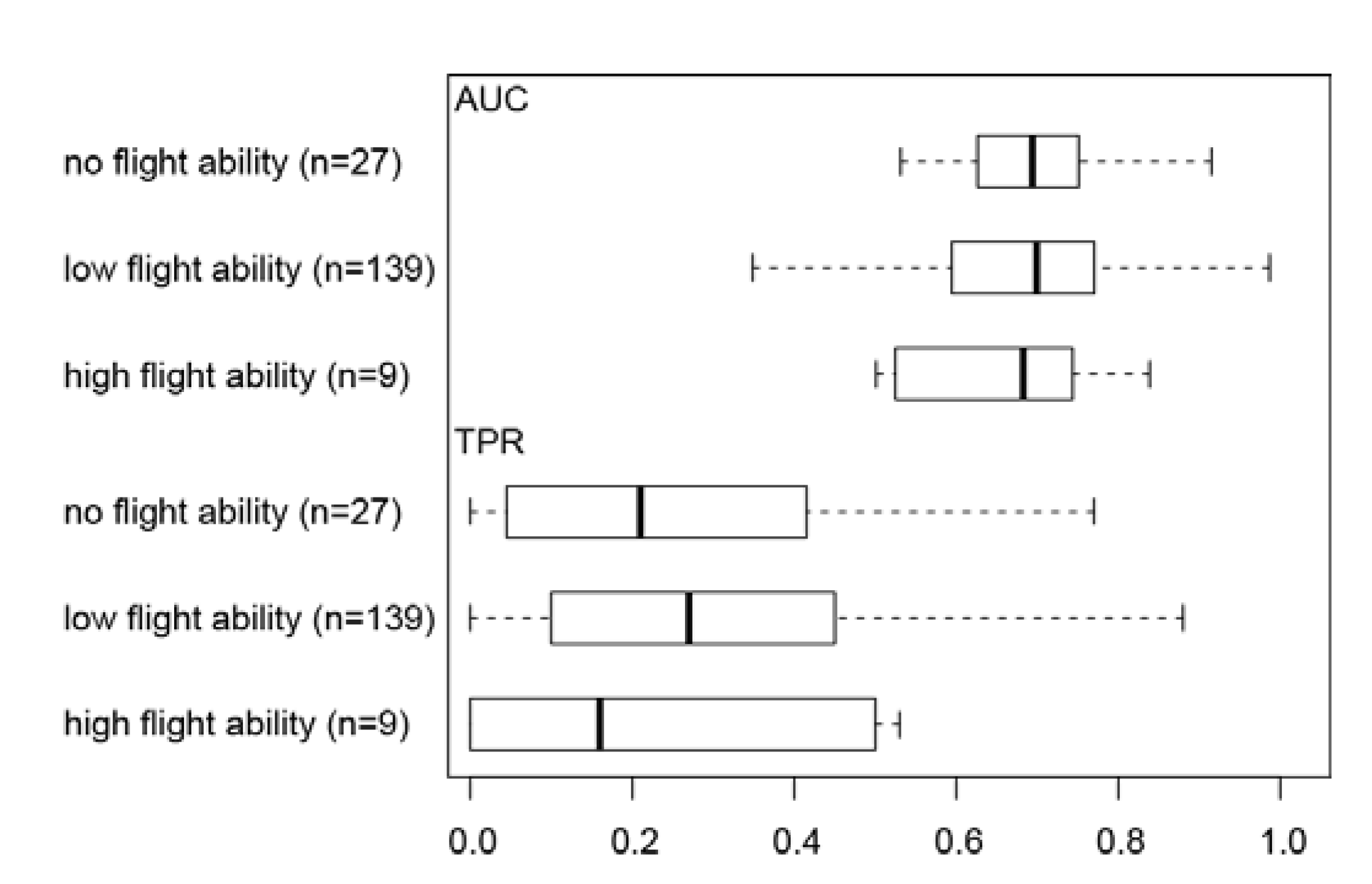
3.3. Importance of Predictor Variables
| littoral | profundal | phytoplankton | |||||
|---|---|---|---|---|---|---|---|
| environmental variables | Q75 | max | Q75 | max | Q75 | max | |
| water chemistry | total phosphorus concentration | 0.05 | 1.58 | 0.10 | 1.09 | 0.27 | 1.07 |
| total nitrogen concentration | 0.01 | 1.11 | 0.02 | 1.13 | 0.04 | 1.33 | |
| pH | 0.06 | 1.20 | 0.06 | 1.15 | 0.25 | 1.34 | |
| TOC | 0.36 | 1.62 | 0.36 | 1.21 | 0.32 | 1.42 | |
| calcium concentration | 0.02 | 1.15 | 0.03 | 1.09 | 0.04 | 1.13 | |
| magnesium concentration | 0.01 | 1.50 | 0.00 | 1.08 | 0.03 | 1.46 | |
| potassium concentration | 0.01 | 1.19 | 0.01 | 1.24 | 0.01 | 1.14 | |
| water color | 0.03 | 1.42 | 0.10 | 1.04 | 0.10 | 1.11 | |
| land use | coniferous forest | 0.01 | 1.09 | 0.04 | 1.09 | 0.01 | 1.01 |
| deciduous forest | 0.01 | 1.09 | 0.01 | 0.93 | 0.00 | 1.01 | |
| mixed forest | 0.01 | 0.97 | 0.01 | 0.78 | 0.00 | 1.39 | |
| wetland | 0.01 | 1.16 | 0.00 | 0.95 | 0.00 | 0.90 | |
| agriculture | 0.00 | 1.15 | 0.00 | 0.74 | 0.00 | 1.13 | |
| pasture | 0.00 | 1.04 | 0.00 | 1.10 | 0.00 | 1.04 | |
| geographical | altitude | 0.20 | 1.21 | 0.06 | 1.05 | 0.04 | 1.18 |
| catchment area | 0.01 | 1.12 | 0.06 | 1.23 | 0.01 | 1.14 | |
| lake area | 0.12 | 1.13 | 0.01 | 1.07 | 0.01 | 1.73 | |
| lake depth | 0.01 | 1.22 | 0.45 | 1.14 | 0.01 | 1.14 | |
| climate | precipitation | 0.00 | 0.93 | 0.00 | 0.75 | 0.00 | 1.08 |
| length of vegetation period | 0.00 | 1.20 | 0.00 | 1.09 | 0.00 | 1.00 | |
4. Discussion
4.1. Effect of Connectivity and Ecosystem Size on Assemblage Prediction Accuracy
4.2. Effect of Flight Ability on Invertebrate Distribution Prediction Accuracy
5. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Moore, K.A.; Elmendorf, S.C. Propagule vs. niche limitation: untangling the mechanisms behind plant speciesʼ distributions. Ecol. Lett. 2006, 9, 797–804. [Google Scholar] [CrossRef]
- Thuiller, W.; Lavorel, S.; Araujo, M.B.; Sykes, M.T.; Prentice, I.C. Climate change threats to plant diversity in Europe. Proc. Natl. Acad. Sci. USA 2005, 102, 8245–8250. [Google Scholar] [CrossRef]
- Thomas, C.D.; Cameron, A.; Green, R.E.; Bakkenes, M.; Beaumont, L.J.; Collingham, Y.C.; Erasmus, B.F.N.; de Siqueira, M.F.; Grainger, A.; Hannah, L.; et al. Extinction risk from climate change. Nature 2004, 427, 145–148. [Google Scholar] [CrossRef] [Green Version]
- Peterson, A.T.; Vieglais, D.A. Predicting species invasions using ecological niche modeling: new approaches from bioinformatics attack a pressing problem. Bioscience 2001, 51, 363–371. [Google Scholar] [CrossRef]
- Hawkins, C.P.; Norris, R.H.; Hogue, J.N.; Feminella, J.W. Development and evaluation of predictive models for measuring the biological integrity of streams. Ecol. Appl. 2000, 10, 1456–1477. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Concluding remarks Cold Spring Harbor Symp. Quantitative Biol. 1957, 22, 415–427. [Google Scholar] [CrossRef]
- Leibold, M.A.; Holyoak, M.; Mouquet, N.; Amarasekare, P.; Chase, J.M.; Hoopes, M.F.; Holt, R.D.; Shurin, J.B.; Law, R.; Tilman, D.; et al. The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 2004, 7, 601–613. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.H.; Anderson, R.P.; Dudik, M.; Ferrier, S.; Guisan, A.; Hijmans, R.J.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; Li, J.; et al. Novel methods improve prediction of speciesʼ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E.; Elith, J.; Graham, C.H.; Phillips, S.; Peterson, A.T. What matters for predicting the occurrences of trees: Techniques, data, or speciesʼ characteristics? Eco. Monogr. 2007, 77, 615–630. [Google Scholar] [CrossRef]
- Thuiller, W. BIOMOD-optimizing predictions of species distributions and projecting potential future shifts under global change. Global Change Biol. 2003, 9, 1353–1362. [Google Scholar] [CrossRef]
- Marmion, M.; Parviainen, M.; Luoto, M.; Heikkinen, R.K.; Thuiller, W. Evaluation of consensus methods in predictive species distribution modelling. Divers. Distrib. 2009, 15, 59–69. [Google Scholar] [CrossRef]
- Kadmon, R.; Farber, O.; Danin, A. A systematic analysis of factors affecting the performance of climatic envelope models. Ecol. Appl. 2003, 13, 853–867. [Google Scholar] [CrossRef]
- Newbold, T.; Reader, T.; Zalat, S.; El-Gabbas, A.; Gilbert, F. Effect of characteristics of butterfly species on the accuracy of distribution models in an arid environment. Biodiver. Conserv. 2009, 18, 3629–3641. [Google Scholar] [CrossRef]
- Göthe, E.; Angeler, D.G.; Sandin, L. Metacommunity structure in a small boreal stream network. J. Anim. Ecol. 2013, 82, 449–458. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Wilson, E.O. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Allouche, O.; Steinitz, O.; Rotem, D.; Rosenfeld, A.; Kadmon, R. Incorporating distance constraints into species distribution models. J. Appl. Ecol. 2008, 45, 599–609. [Google Scholar] [CrossRef]
- Vaughan, I.P.; Ormerod, S.J. The continuing challenges of testing species distribution models. J. Appl. Ecol. 2005, 42, 720–730. [Google Scholar] [CrossRef]
- Vaughan, I.P.; Ormerod, S.J. Increasing the value of principal components analysis for simplifying ecological data: a case study with rivers and river birds. J. Appl. Ecol. 2005, 42, 487–497. [Google Scholar] [CrossRef]
- Johnson, R.K. Regional Representativeness of Swedish Reference Lakes. Environ. Manage. 1999, 23, 115–124. [Google Scholar] [CrossRef]
- Throndsen, J. Preservation and storage. In Phytoplankton Manual Monographs on Oceanographic Methodology; Sournia, A., Ed.; UNESCO: Paris, France, 1978; pp. 70–71. [Google Scholar]
- Olrik, K.P.; Blomqvist, P.; Brettum, P.; Cronberg, G.; Eloranta, P. Methods for Quantitative Assessment of Phytoplankton in Freshwaters, Part I; Report 4860; Swedish Environmental Protection Agency: Stockholm, Sweden, 1989.
- European Committee for Standardization, Water Quality-Methods for Biological Sampling-Guidance on Handnet Sampling of Aquatic Benthic Macro-Invertebrates; CEN: Brussels, Belgium, 1994.
- Wilander, A.; Johnson, R.K.; Goedkoop, W. Riksinventering 2000: En synoptisk studie av vattenkemi och bottenfauna i svenska sjöar och vattendrag (in Swedish); Department of Environmental Assessment: Uppsala, Sweden, 2003.
- National land survey of Sweden. Available online: www.lantmateriet.se/ (accessed on 1 April 2013).
- Swedish institute for metrology and hydrology. Available online: www.smhi.se/ (accessed on 1 April 2013).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar]
- ESRI homepage. Available online: http://www.esri.com/ (accessed on 1 April 2013).
- Heymann, Y.; Steenmans, C.; Croissille, G.; Bossard, M. Corine Land Cover; Technical Guide; Office for Official Publications of the European Communities: Luxembourg, Luxembourg, 1994. [Google Scholar]
- Thuiller, W.; Lafourcade, B.; Engler, R.; Araújo, M.B. BIOMOD-a platform for ensemble forecasting of species distributions. Ecography 2009, 32, 369–373. [Google Scholar] [CrossRef]
- R Development Core Team, R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2007.
- Jiménez-Valverde, A.; Lobo, J.M. Threshold criteria for conversion of probability of species presence to either–or presence–absence. Acta Oecol. 2007, 31, 361–369. [Google Scholar] [CrossRef]
- Illies, J. Limnofauna Europaea; Gustav Fisher Verlag: Stuttgart, Germany, 1978. [Google Scholar]
- NCAR-Research Application Program. Verification: Forecast verification utilities. Available online: http://CRAN.R-project.org/package=verification/ (accessed on 1 April 2013).
- JMP homepage. Available online: http://www.jmp.com/ (accessed on 1 April 2013).
- Kovats, Z.E.; Ciborowski, J.J.H.; Corkum, L.D. Inland dispersal of adult aquatic insects. Freshwater Biol. 1996, 36, 265–276. [Google Scholar] [CrossRef]
- Vanschoenwinkel, B.; Gielen, S.; Seaman, M.; Brendonck, L. Wind mediated dispersal of freshwater invertebrates in a rock pool metacommunity: differences in dispersal capacities and modes. Hydrobiologia 2009, 635, 363–372. [Google Scholar] [CrossRef]
- Hanspach, J.; Kuhn, I.; Pompe, S.; Klotz, S. Predictive performance of plant species distribution models depends on species traits. Perspect Plant Ecol. 2010, 12, 219–225. [Google Scholar] [CrossRef]
- Poyry, J.; Luoto, M.; Heikkinen, R.K.; Saarinen, K. Species traits are associated with the quality of bioclimatic models. Global Ecol. Biogeogr. 2008, 17, 403–414. [Google Scholar] [CrossRef]
- Raybould, A.F.; Clarke, R.T.; Bond, J.M.; Welters, R.E.; Gliddon, C.J. Inferring patterns of dispersal from allele frequency data. In Dispersal ecology; Bullock, J.M., Kenward, R.E., Hails, R.S., Eds.; Blackwell Science: Oxford, UK, 2002; pp. 89–110. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hallstan, S.; Johnson, R.K.; Sandin, L. Effects of Dispersal-Related Factors on Species Distribution Model Accuracy for Boreal Lake Ecosystems. Diversity 2013, 5, 393-408. https://doi.org/10.3390/d5020393
Hallstan S, Johnson RK, Sandin L. Effects of Dispersal-Related Factors on Species Distribution Model Accuracy for Boreal Lake Ecosystems. Diversity. 2013; 5(2):393-408. https://doi.org/10.3390/d5020393
Chicago/Turabian StyleHallstan, Simon, Richard K. Johnson, and Leonard Sandin. 2013. "Effects of Dispersal-Related Factors on Species Distribution Model Accuracy for Boreal Lake Ecosystems" Diversity 5, no. 2: 393-408. https://doi.org/10.3390/d5020393





