1. Introduction
The estimated volume of forest trees is fairly sensitive, despite the research and development of cubage made in the timber trade. Taking into account the commercial considerations always omnipresent, it returns to the forest manager, not a research institute, to choose the appropriate method of scaling during sales or inventory management. However, comparisons between “management” and “research” cubage are inevitable when field data, such as price per cubic meter, are used in applied research.
Indeed, wood cubage is used to determine the volume of the logs. This is very important for sale, because it is one of the essential elements of wood value. This volume is the basis of the commercial transaction between buyers and sellers of wood. It is also useful in forest management and monitoring. Finally, it is necessary for resource assessment and forest production, which contribute to evaluating strategic guidance at every level. Thus, the sustainable management of forest resources requires appropriate data collection [
1]. One of the most widely used indicators is cubage. Prediction of individual volume and merchantable volume of the trunk is necessary in the management of forestry. In order to do this, sample-based inventory procedures are used, in which tree volume is determined through volumetric equations and other procedures, such as volume ratio or taper models [
2]. The most widely used procedure is that of volumetric equations, usually adjusted by using data from scaling of the sample trees. In scaling, stem volume may be obtained through water displacement (xylometer), which considers the real volume, or through mathematical equations, such as Huber’s, Newton’s, Smalian’s, Hohenald’s, Pressler’s, the centroid method and Hossfeld’s equation, among others, all of which are estimative of the real volume [
3,
4,
5]. In volumes of log calculation, there are two major sources that contribute to the total error in volume estimation [
6]. First, there is the choice of the equation used in determining volume. The accuracy of a volume equation's prediction depends upon the underlying shape of the log (geometric solid). A second source of error is introduced when diameters and lengths of logs are not accurately measured.
Opinions regarding the most precise formulas for carrying out scaling differ among authors. The most widely used are Newton’s, Huber’s and Smalian’s formulas [
7]. Goulding [
8] and Husch
et al. [
9] affirm that Newton’s is the most precise formula, as it takes into account the different forms the tree stem can assume: cone, paraboloid, Neloïd and cylinder. Finger [
7] highlights that the Huber and Smalian formulas are precise only when the stem resembles a paraboloid.
There is also a difference in use of formulas according to continents and countries. Huber’s formula is more used in Europe due to its accuracy, while the Smalian is preferred in the USA due to its practicality, especially if the aim is also to quantify the logs piled together [
3]. In Brazil, the Smalian formula is widely used to determine tree volume and to adjust volumetric equations of different native and exotic species [
10,
11,
12,
13,
14,
15,
16,
17]. According to Machado and Figueiredo Filho [
5], this is due more to practicality than to accuracy.
In Benin, the difficulty of having an appropriate cubage pushes managers to use only formulas established for tropical trees by Dawkings [
18] to estimate the total volume or marketable volume. For Dawkings [
18], the value of the form factor of tropical species is 0.55 to estimate the total volume and 0.70 for stem volume. These values are not consistent with the morphology of the trees in the Sudanian zone. Fonton
et al. [
19] noted an underestimation of about 10% of the volume four species (
Isoberlinia doka,
Isoberlinia tomentosa,
Anogeissus leiocarpa and
Daniellia oliveri) with the form factor proposed by Dawkins [
18]. Consequently, sometimes significant discrepancies can be observed between the mensuration characteristics estimated and the real characteristics of the stands, hence errors in estimation and forest planning.
The study aims to evaluate the influence of the log length in determining the volume of teak trees. The choice of this species is justified by the fact that, during the past few decades, many private operators interest is more to install teak plantation, given its technological quality. According to the increase of production, Benin is currently an exporter of teak wood. Teak is, therefore, the best opportunity for producing tropical timber quality [
20,
21].
4. Discussions
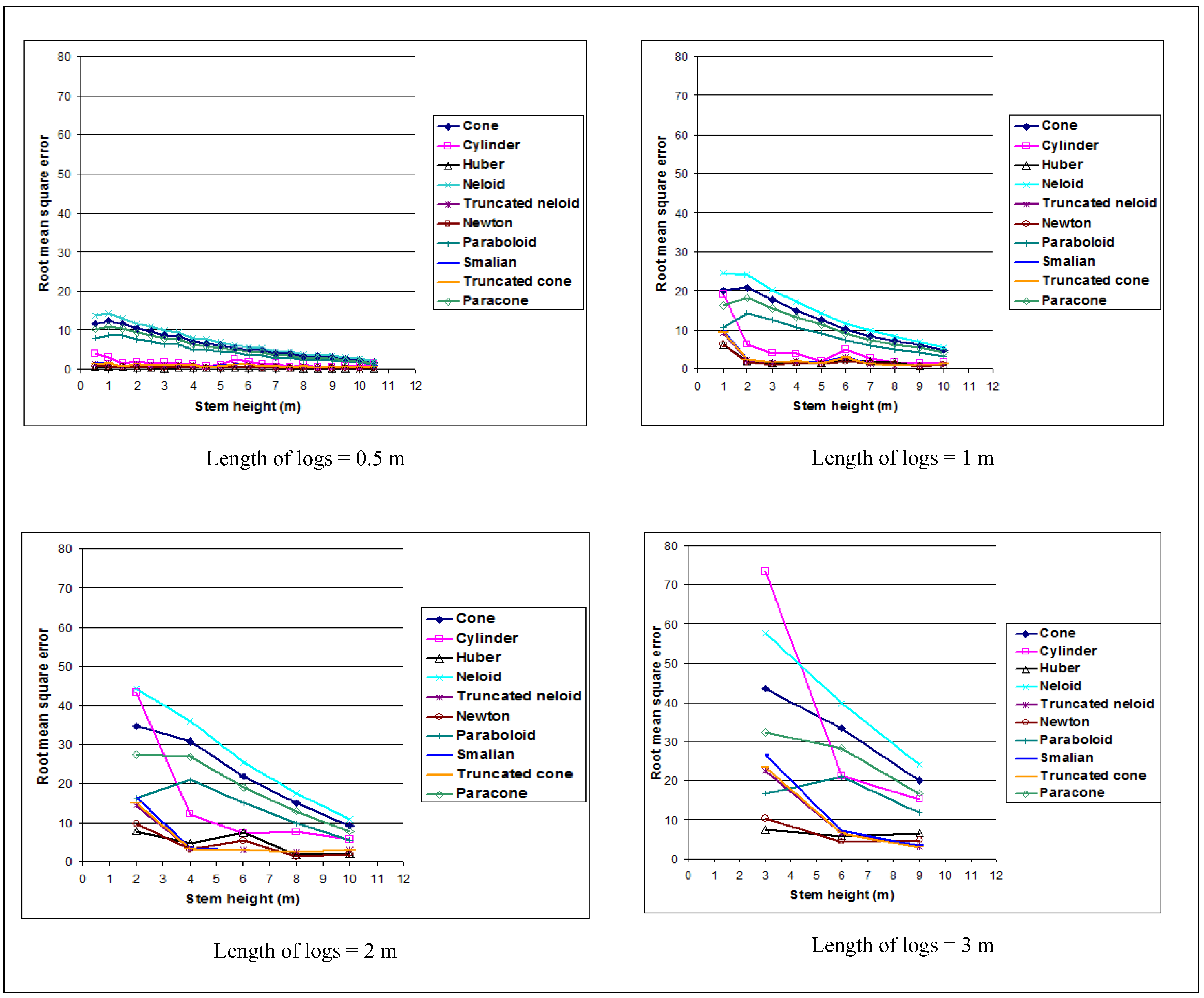
In the literature, many approaches are used to determine the real volume value of logs. In this study, the approach is based on the scaling technique of dividing the stem into several logs section of 0.5 m and determining the real volume of logs by the xylometer technique. The advantage of this approach is to have a high accuracy of the real volume value in contrast to the approach of estimating the volume by the simple scaling formulas, e.g., Huber, Smalian or Newton formulas proposed by [
3,
4,
5,
22]. Bigin [
6] mentioned that if volume is being determined via water displacement, there can be other sources of measurement error if water adheres to the log. The use of plastic film can minimize this source of error.
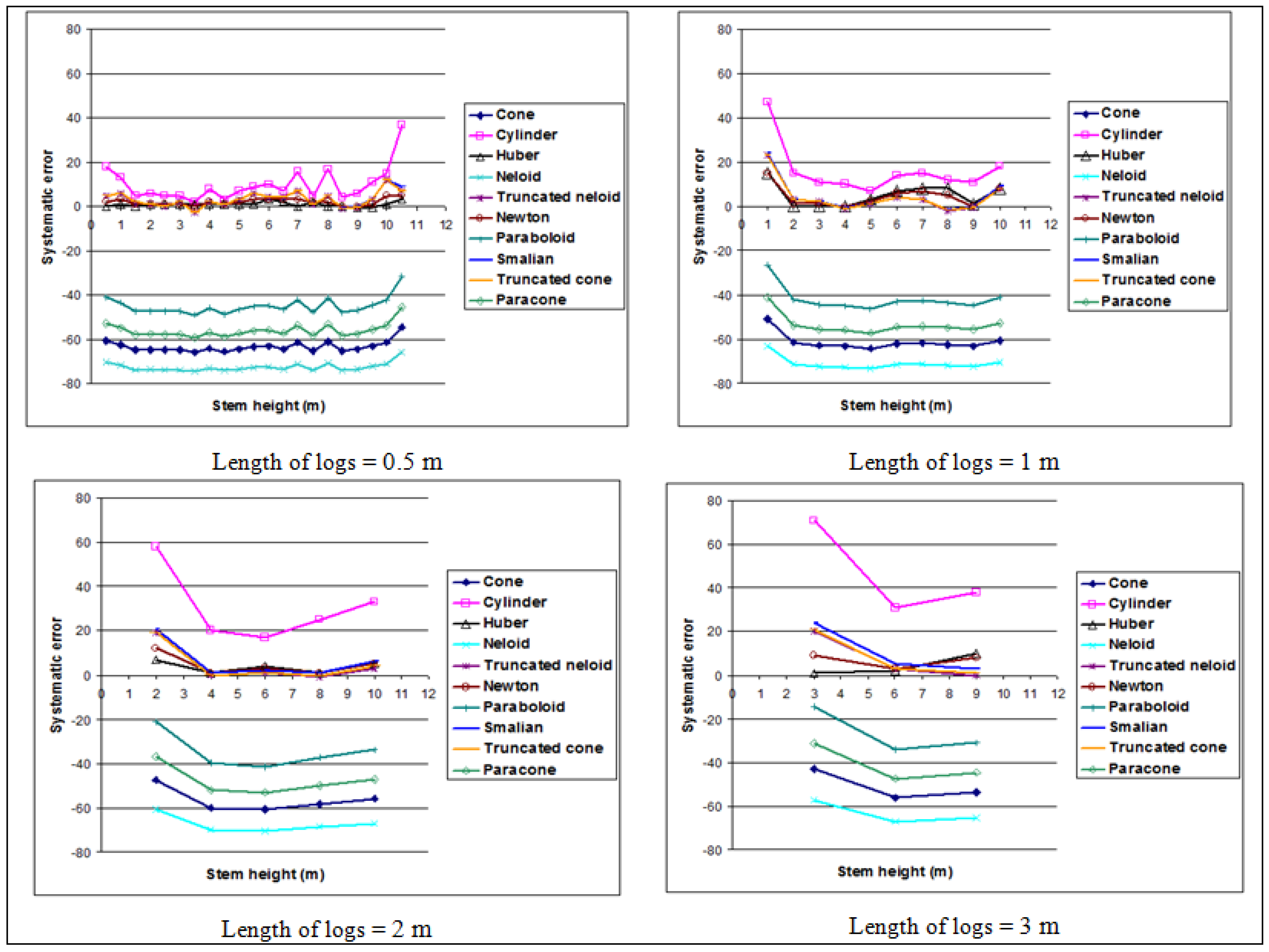
Huber’s formula has the lowest values of the squared error and systematic error along the stem of the tree for logs of 0.5 m. It adapts to the length of logs of 1, 2 and 3 m from the base of the stem (stem height less than or equal to 4 m). Beyond this height (stem height greater than 4 m), the formulas of Newton, truncated cone and Smalian are more precise for logs of 1 m, and Newton’s formula is suitable for logs of 2 m. For logs of 3 m, Newton's formula is suitable for logs in the center of the stem (3 to 6 m) and the truncated cone formula bolts at the top of the stem (6 to 9 m). Similar results were obtained by other authors, including [
24], comparing the accuracy of different volume equations on
Pinus elliottii trees, believes that Huber’s formula is more efficient than other approaches for estimating the volume of any length of ridge considered. These authors also noted that Huber's formula is the formula most accurate on several species, whatever the age of the trees and geographic region.
Fonton
et al. [
19] mentioned the hypothesis of the succession of truncated cones along the stem of four species
(Isoberlinia doka, Isoberlinia tomentosa, Anogeissus leiocarpa and
Daniellia oliveri) and think that it is more reasonable, because it is less dependent on the length of the logs and more suited to the general taper of a tree [
25,
26,
27].
Whatever the length of the log, mean square error decreases from the bottom to the top of the stem. Altherr [
28] also showed in a study of 15,000 trees the influence of the length of the logs. He finds that the use of logs of 2 m along the stem leads to a systematic error of 1%, compared to the volume obtained for logs of 1 m. He also demonstrates that the error focuses on the first five meters of the trunk, while it is almost zero for the central part of the stem and very low for the last five meters. This fact can be explained by the irregularities of the stem, which are larger at the base than the upper end of the shaft. These irregularities can be explained by the plantation regime and type of thinning performed. Indeed, the plantations from which come the trees of the present study Huber are coppice and the type of thinning is selective. The results of research on pre-commercial and commercial thinning demonstrated the relationship between crown length and stem taper. Barbour
et al. [
29] found in red spruce
(Picea rubens Sarg.), following a pre-commercial thinning conducted in Nova Scotia fifteen years ago, that the crown was longer and that higher stems taper in thinned stands. According to Thomson and Barclay [
30], a strong commercial thinning reduces pruning at the base of the crown. After treatment, more light can enter in the stand, and lower branches remain active for photosynthesis. This results in a slower crown recession in individual trees of thinned stands. The radial growth in the lower part of the stem is therefore increased, since the auxin fall faster across the stem, resulting in a greater scroll [
31]
. Newnham [
32] also observed that when the cover is released, the stem have a form, which is closer to a cone or Neloïd form, due to a more pronounced extension of the crown.
According to Viens [
33], four hypotheses can be used to explain the differences in the shape and distribution of growth on the stem. One hypothesis, which is connected to a mechanical compensation order, has been described by [
34]. It states that the external mechanical stress tends to alter and change the shape of the stem.
Two mechanical forces influence the straightness of a stem [
34]. The first is the vertical force, which is the weight of the stem itself plus the weight of snow and ice. The second is the horizontal force imposed by the wind. Therefore, the greatest growth observed at the base of the stem of trees from thinned stands may be due to increased wind penetration in the canopy and lower mutual support of the stems, which leads to the formation of the reaction wood [
33].
A second hypothesis relates to the conductivity of the water [
34,
35]. Assuming that the shape of the stem is a response to the needs of the hydraulic tree, thinning causes a rise of the surface conduction of the water in the non-leaves of the rod, due to an increase in photosynthetic activity and transpiration.
The third hypothesis, posed by Pressler, offers another explanation of the changes of form caused by thinning [
34]. This assumption is based only on the fact that radial growth is connected to the leaf biomass. He mentioned that the radial growth at a location on the stem is a function of leaf biomass present above this point. Also, the point where the maximum radial growth is to be located lower on the stem of trees treated as thinning induces a decrease in the height of the crown base.
Finally, the changes of form after thinning would not necessarily be due to a change in tree growth, but may be caused by the morphology of residual trees. For example, at a low thinning, the dominant trees are preserved, which artificially increases the average scroll of the stem [
34]. A strong low thinning will therefore select trees with a scroll larger than lower thinning [
34].
Models expressing the volume as a function of the square of the diameter are most relevant for estimating the volume of individual trees [
27,
36,
37,
38]. However, the models obtained for scaling the entire tree in this study express the logarithm of the volume (total and merchantable volume) according to the logarithm of the diameter and height. These models have the best fit parameters (residual error and adjusted coefficient of determination).


















 is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):
is the angular coefficient of the straight line passing through the origin and expressing the test volume according to the reference volume (the real volume):


 , the real volume of logs i at position i of the stem i and,
, the real volume of logs i at position i of the stem i and,  , its estimate by one of the formulas.
, its estimate by one of the formulas.