The Relation between Evenness and Diversity
1. Introduction
2. Theoretical Background
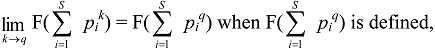
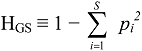

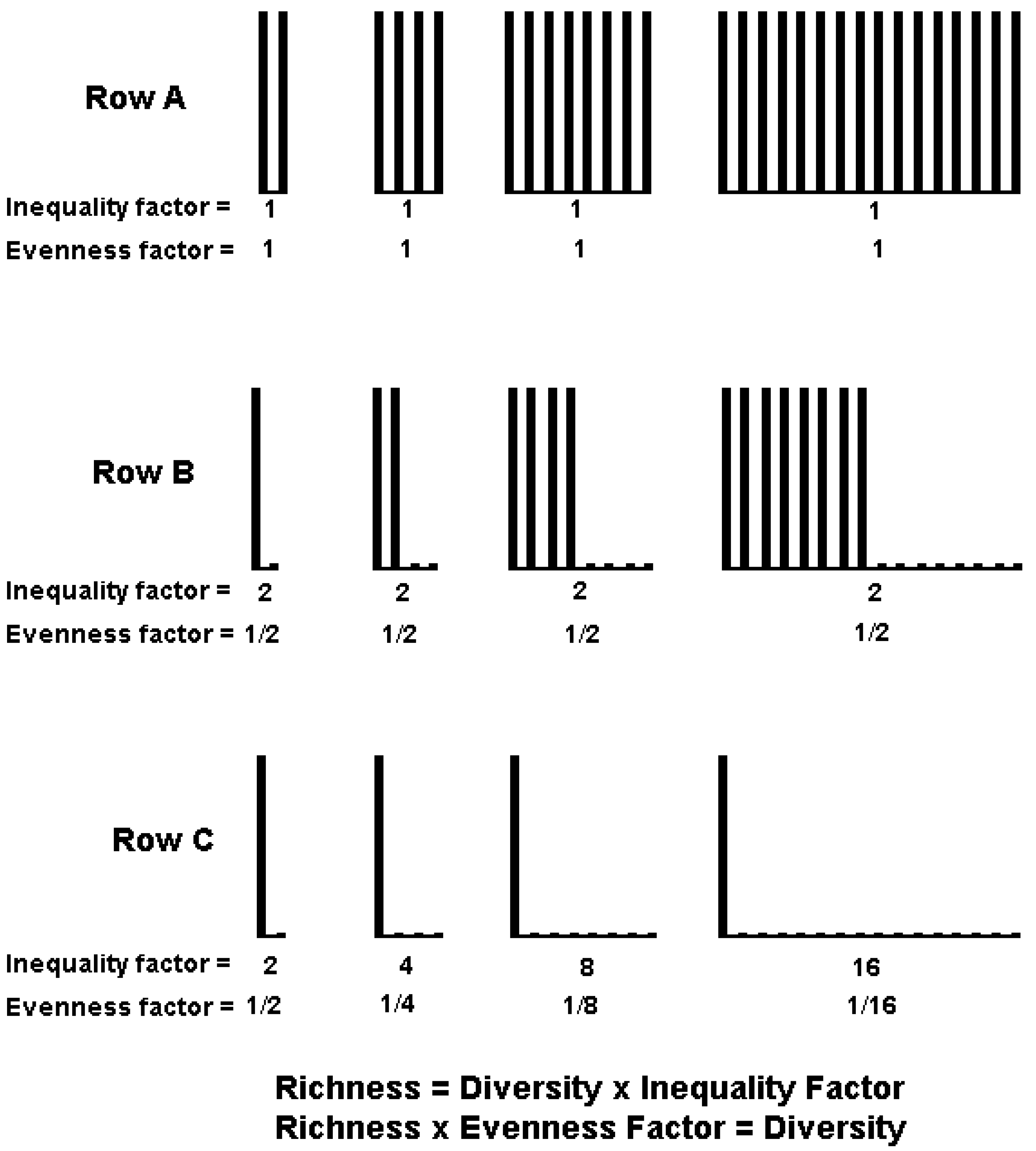
3. Evenness, Richness, Diversity: Which Two Are Independent?
3.1. Diversity Cannot Be Decomposed into Independent Richness and Evenness Components
3.2. Derivation of Evenness and Inequality Measures from the Partitioning Theorem
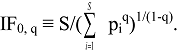
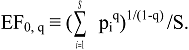
4. IF0, q and EF0, q Satisfy Common Requirements for Evenness and Inequality Measures
5. Interpretation of Evenness and Inequality Factors
5.1. Interpretation in Terms of Proportion of Dominant Species
5.2. Interpretation in Terms of Equivalent Maximally Uneven Communities
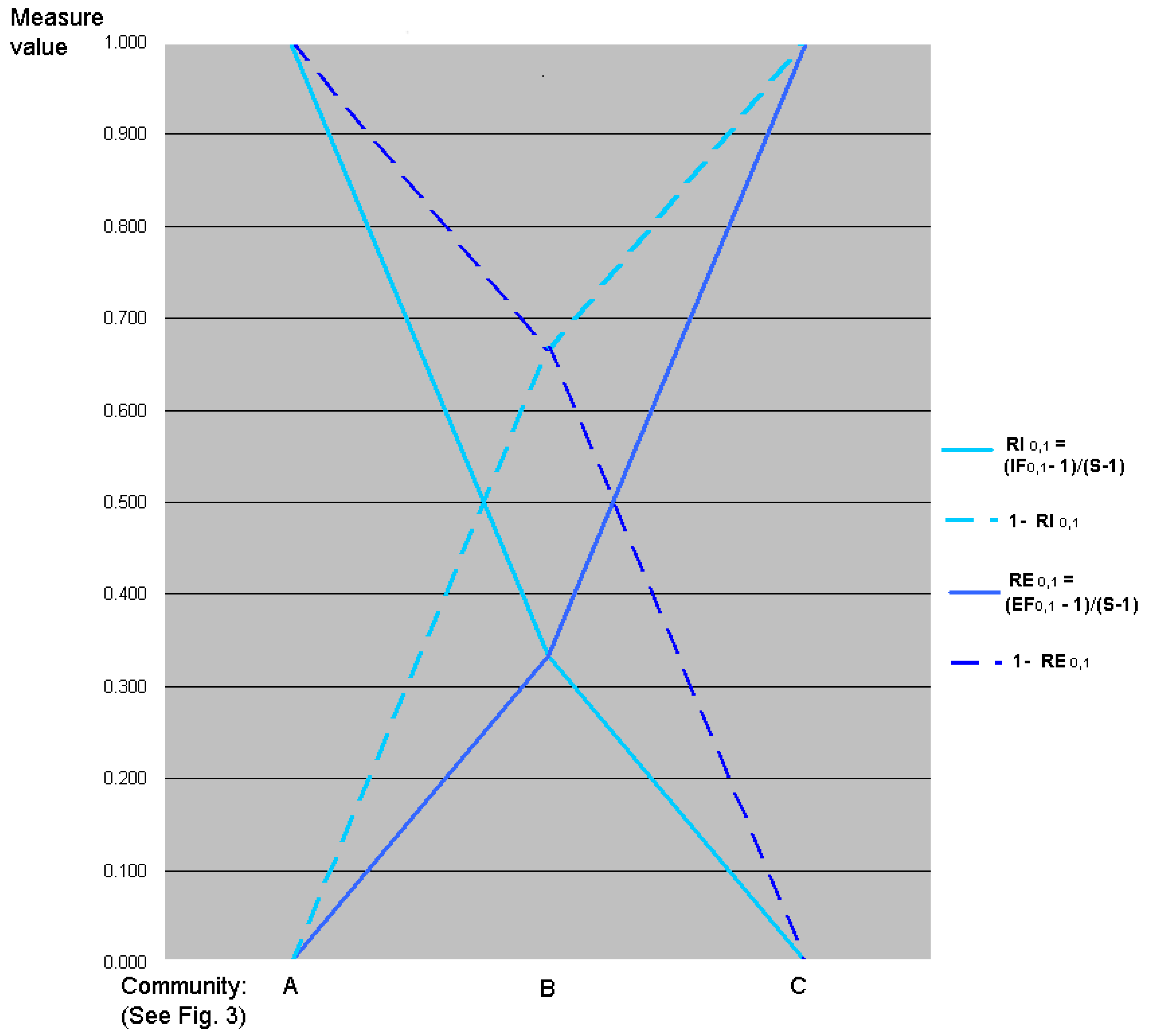
5.3. Graphic Interpretation
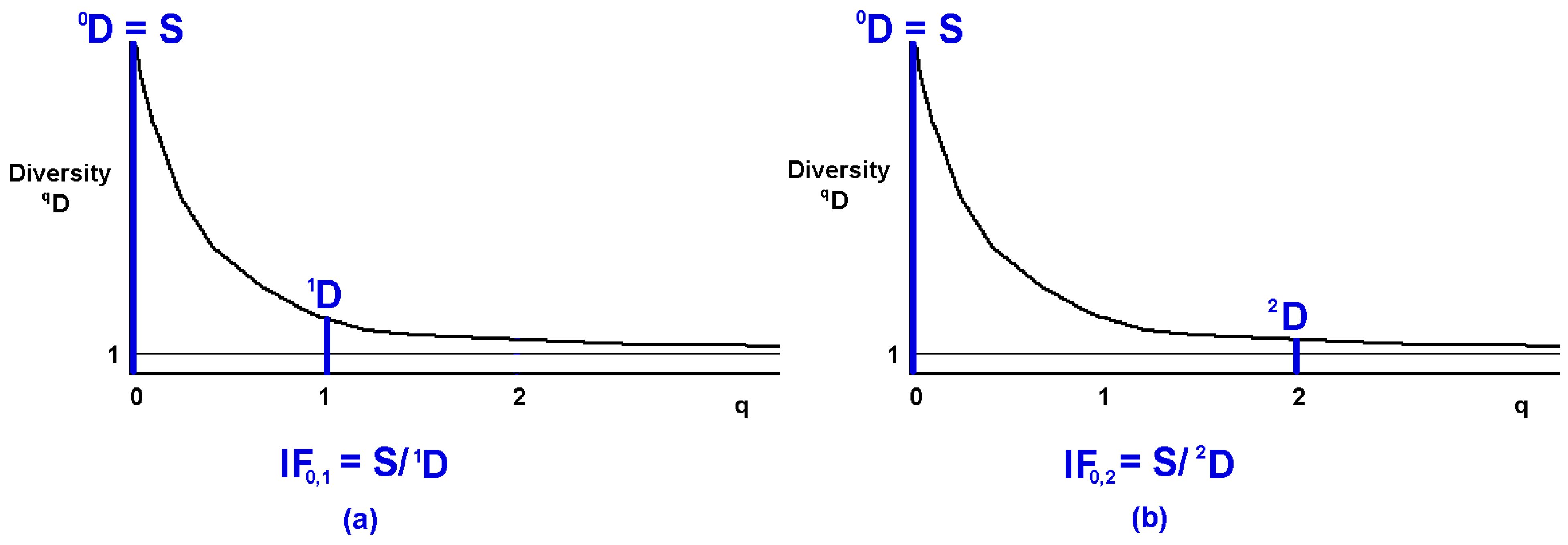
5.4. Interpretation in Terms of Mean Deviation from Equiprobability
6. Monotonic Transformations of the Evenness and Inequality Factors
6.1. Motivation
6.2. Theil Entropy Inequality Measure

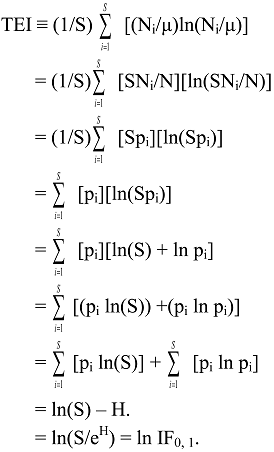
6.3. Logarithmic Transformations of General IF0, q
6.4. Deformed Logarithmic Transformations

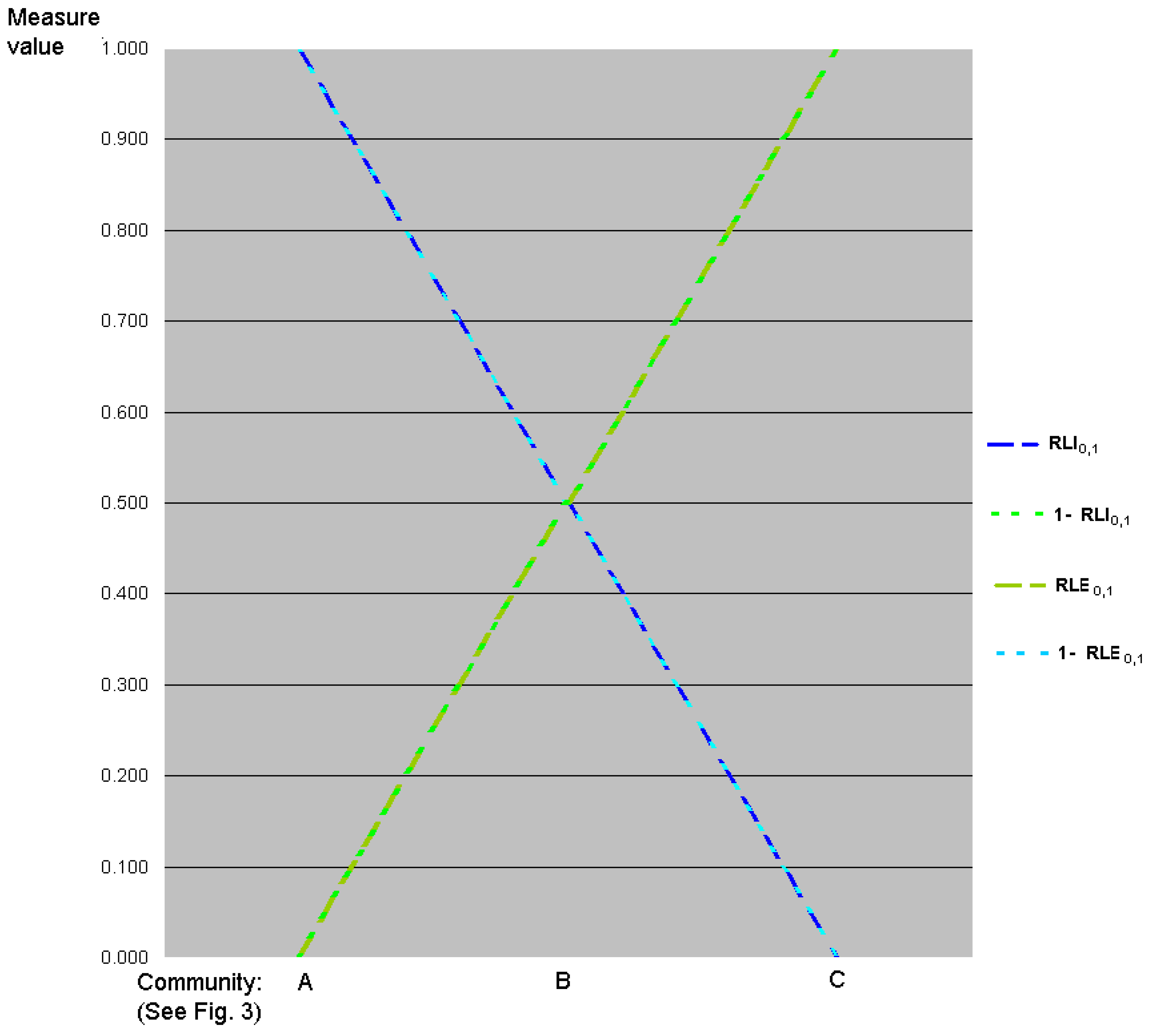
7. Relative Inequality and Evenness
7.1. Motivation
7.2. Linear Transformations of Evenness and Inequality Factors


7.3. Transformations of Logarithms of Evenness and Inequality Factors
= (ln qD – ln S + ln S) / ln S
= ln qD / ln S.
= (ln S – ln qD)/ ln S
= 1 − RLE 0, q
7.4. Slope of Chord of Renyi Spectrum
= (ln S – ln qD)/ln S
= RLI 0, q.
= ln qD/ln S
= RLE 0, q.
7.5. Relative Evenness Measures Cannot and Should Not Be Replication Invariant
8. Statistical Concerns
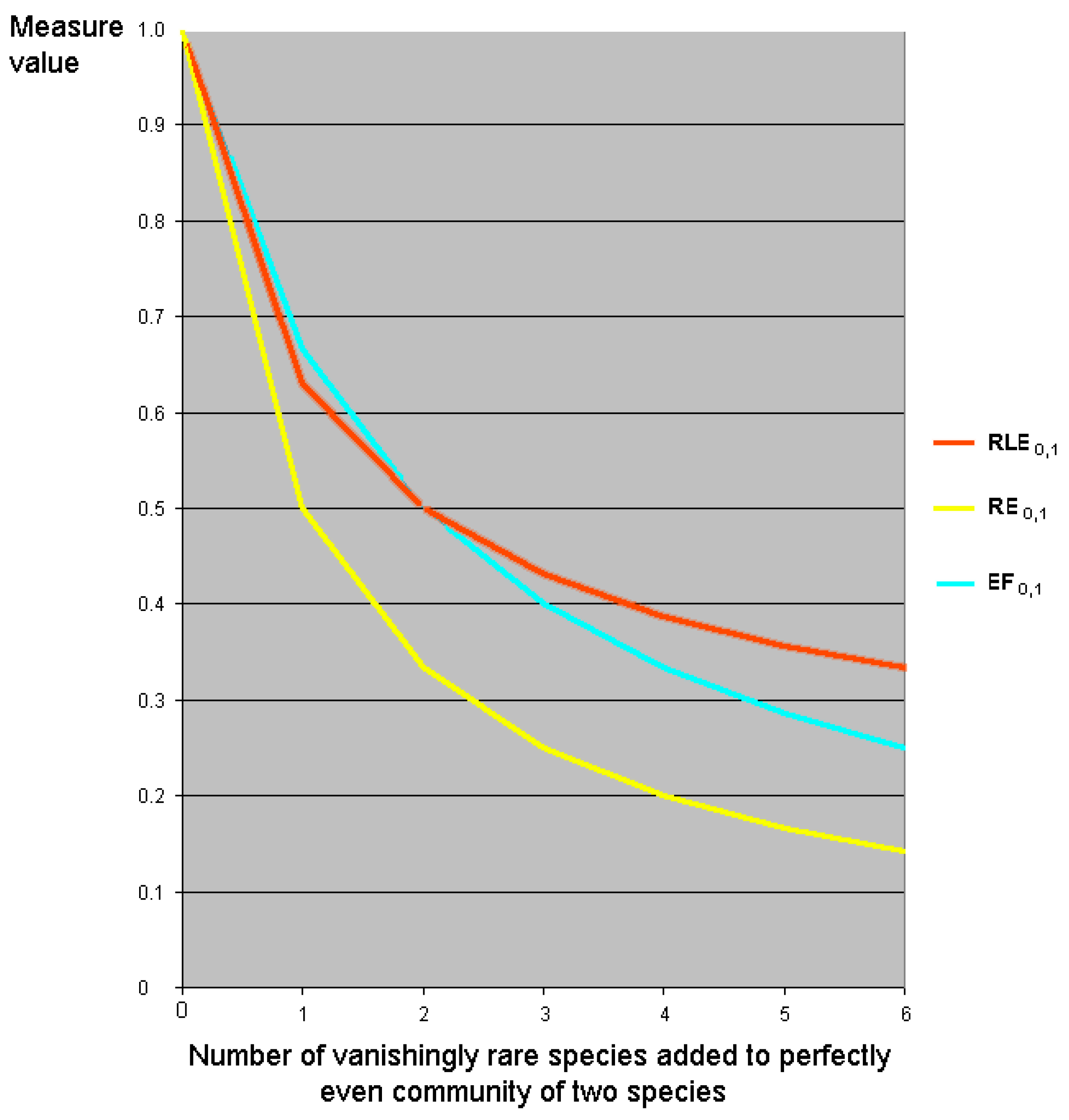
8.2. Partitioning Higher-Order Diversity Measures
= (2D − 1)/(1D − 1).
= [ln 2D – ln 1D + ln1D)]/[ln 1D]
= [ln 2D]/[ln 1D].
8.3. An Estimable Evenness Measure
9. Discussion
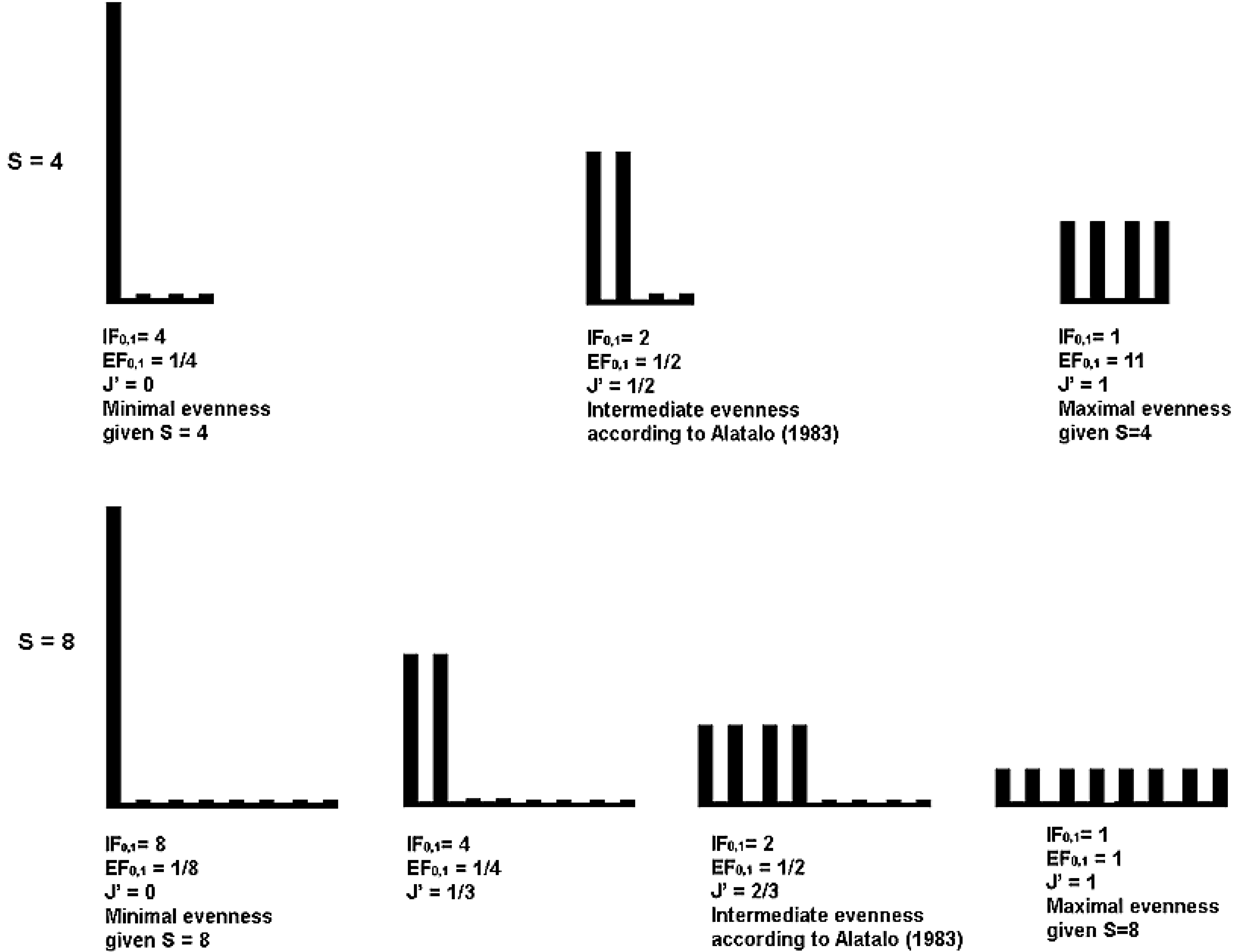
9.1. Relative versus Absolute Evenness and Inequality
| Maximally uneven | Intermediate according | Completely even | |||||||
|---|---|---|---|---|---|---|---|---|---|
| to Alatalo [26] | |||||||||
| RichnesS | J | IF0,1 | EF0,1 or 1/IF0,1 | J | IF0,1 | EF0,1 or 1/IF0,1 | J | IF0,1 | EF0,1 or 1/IF0,1 |
| 4 | 0 | 4 | 0.25 | 0.5 | 2 | 0.5 | 1 | 1 | 1 |
| 8 | 0 | 8 | 0.125 | 0.67 | 2 | 0.5 | 1 | 1 | 1 |
| 16 | 0 | 16 | 0.0625 | 0.75 | 2 | 0.5 | 1 | 1 | 1 |
| 512 | 0 | 512 | 0.002 | 0.89 | 2 | 0.5 | 1 | 1 | 1 |
9.2. An Alternative Evenness Concept
10. Conclusion
Acknowledgements
References and Notes
- Pielou, E. The measurement of diversity in different types of biological collections. J. Theor. Biol. 1966, 13, 131–144. [Google Scholar] [CrossRef]
- Heip, C. A new index measuring evenness. J. Marine Biol. Ass. UK 1974, 54, 555–557. [Google Scholar] [CrossRef]
- Smith, B.; Wilson, J. A consumer’s guide to evenness indices. Oikos 1996, 76, 70–82. [Google Scholar] [CrossRef]
- Gosselin, F. Lorentz partial order: the best known logical framework to define evenness indices. Community Ecol. 2001, 2, 197–207. [Google Scholar] [CrossRef]
- Gosselin, F. An assessment of the dependence of evenness indices on species richness. J. Theor. Biol. 2006, 242, 591–597. [Google Scholar] [CrossRef]
- Jost, L. Partitioning diversity into independent alpha and beta components. Ecology 2007, 88, 2427–2439. [Google Scholar] [CrossRef]
- Ricotta, C. A recipe for unconventional evenness measures. Acta Biotheor. 2004, 52, 95–104. [Google Scholar] [CrossRef]
- Patil, G.; Taillie, C. Diversity as a concept and its measurement. J. Amer. Statist. Assn. 1982, 77, 548–561. [Google Scholar] [CrossRef]
- Adelman, M. Comment on the H-concentration measure as a numbers-equivalent. Rev. Econ. Statist. 1969, 51, 99–101. [Google Scholar] [CrossRef]
- Hill, M. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Jost, L. GST and its relatives do not measure differentiation. Mol. Ecol. 2008, 17, 4015–4026. [Google Scholar] [CrossRef]
- Jost, L. Mismeasuring biological diversity: Response to Hoffmann and Hoffmann (2008). Ecol. Econ. 2009, 68, 925–928. [Google Scholar] [CrossRef]
- Jost, L.; DeVries, P.; Walla, T.; Greeney, H.; Chao, A.; Ricotta, C. Partitioning diversity for conservation analyses. Divers. Distrib. 2010, 16, 65–76. [Google Scholar] [CrossRef]
- Taillie, C. Species equitability: a comparative approach. In Ecological Diversity in Theory and Practice; Grassle, F., Patil, G., Smith, W., Taillie, C., Eds.; International Co-operative Publishing House: Fairland, MD, USA, 1979. [Google Scholar]
- Jost, L.; Chao, A. Diversity Analysis; Taylor and Francis: London, UK. (In preparation)
- Routledge, R. Evenness indices: are any admissible? Oikos 1983, 40, 149–151. [Google Scholar] [CrossRef]
- Theil, A. Economics and Information Theory; Rand McNally and Company: Chicago, IL, USA, 1967. [Google Scholar]
- Buzas, M.; Hayek, L. Biodiversity resolution: an integrated approach. Biodivers. Lett. 1996, 3, 40–43. [Google Scholar] [CrossRef]
- Tsallis, C.; Rapisarda, A.; Latora, V.; Baldovin, F. Nonextensivity: From low-dimensional maps to Hamiltonian systems. In Dynamics and Thermodynamics of Systems with Long-Range Interactions; Dauxois, T., Ruffo, S., Arimundo, E., Wilkens, M., Eds.; Lecture Notes in Physics 602; Springer: Berlin, Germany, 2002. [Google Scholar]
- Hoffmann, S. Generalized distribution based diversity measurement: Survey and unification. FEMM Working Paper. Otto-von-Guericke-University: Magdeburg, Germany, 2007. [Google Scholar]
- Bajo, O.; Salas, R. Inequality foundations of concentration measures: an application to the Hannah-Kay indices. Span. Econ. Rev. 2002, 4, 311–316. [Google Scholar] [CrossRef]
- Hubbell, S.P.; Condit, R.; Foster, R.B. Barro Colorado Forest Census plot data. Available online: http://ctfs.si.edu/datasets/bci.
- Song, K.-S. Renyi information, loglikelihood and an intrinsic distribution measure. J. Statist. Plan. Infer. 2001, 93, 51–69. [Google Scholar] [CrossRef]
- Chao, A.; Shen, T. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 2003, 10, 429–433. [Google Scholar] [CrossRef]
- Alatalo, R.V. Problems in the measurement of evenness in ecology. Oikos 1981, 37, 199–204. [Google Scholar] [CrossRef]
- Chao, A.; Shen, T. SPADE. Available online: http://chao.stat.nthu.edu.tw/download.html.
- Chao, A.; Colwell, R.; Lin, C.-W.; Gotelli, N. Sufficient sampling for asymptotic minimum species richness estimators. Ecology 2009, 90, 1125–1133. [Google Scholar] [CrossRef]
- Good, I.J. The population frequencies of species and the estimation of population parameters. Biometrika 1953, 40, 237–264. [Google Scholar] [CrossRef]
- Good, I.J.; Toulmin, G. The number of new species, and the increase in population coverage, when a sample is increased. Biometrika 1956, 43, 45–63. [Google Scholar] [CrossRef]
- Rasmussen, S.; Starr, N. Optimal and adaptive stopping in the search for new species. J. Amer. Statist. Assn. 1979, 74, 661–667. [Google Scholar] [CrossRef]
- Engen, S. Some basic concepts of ecological equitability. In Ecological Diversity in Theory and Practice; Grassle, F., Patil, G., Smith, W., Taillie, C., Eds.; International Co-operative Publishing House: Fairland, MD, USA, 1979. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jost, L. The Relation between Evenness and Diversity. Diversity 2010, 2, 207-232. https://doi.org/10.3390/d2020207
Jost L. The Relation between Evenness and Diversity. Diversity. 2010; 2(2):207-232. https://doi.org/10.3390/d2020207
Chicago/Turabian StyleJost, Lou. 2010. "The Relation between Evenness and Diversity" Diversity 2, no. 2: 207-232. https://doi.org/10.3390/d2020207
APA StyleJost, L. (2010). The Relation between Evenness and Diversity. Diversity, 2(2), 207-232. https://doi.org/10.3390/d2020207