The Regulatory Roles of Intrinsically Disordered Linker in VRN1-DNA Phase Separation
Abstract
:1. Introduction
2. Results
2.1. The Effective Local Concentration Effect of IDL has Essential Influence on the Binding Affinity between VRN1 and DNA
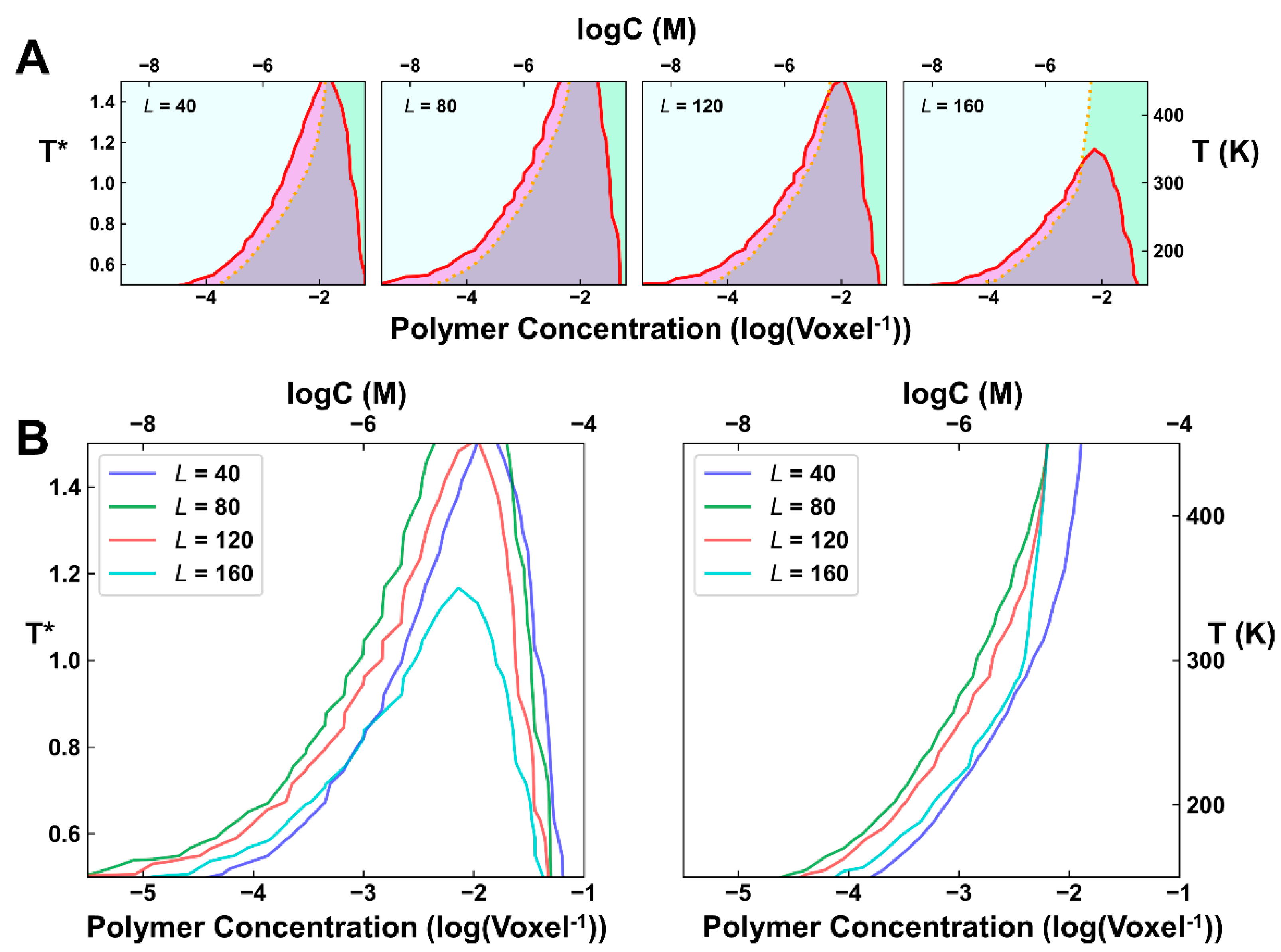
2.2. Simulations of Phase Separation under Different IDL Lengths
2.3. Simulations of Phase Separation for Systems with Charged Patches in Linker
3. Discussion
4. Materials and Methods
4.1. Fitting VRN1 Linker to WLC Model and RMC Model
4.2. Lattice-Based Coarse-Grained Monte-Carlo Simulations of Phase Diagrams
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feric, M.; Misteli, T. Phase separation in genome organization across evolution. Trends. Cell Biol. 2021, 31, 671–685. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, L.; Quan, H.; Tian, H.; Meng, L.; Yang, L.; Feng, H.; Gao, Y.Q. From 1D sequence to 3D chromatin dynamics and cellular functions: A phase separation perspective. Nucleic Acids Res. 2018, 46, 9367–9383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lytle, T.K.; Chang, L.W.; Markiewicz, N.; Perry, S.L.; Sing, C.E. Designing electrostatic interactions via polyelectrolyte monomer sequence. ACS Cent. Sci. 2019, 5, 709–718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bajpai, G.; Amiad Pavlov, D.; Lorber, D.; Volk, T.; Safran, S. Mesoscale phase separation of chromatin in the nucleus. eLife 2021, 10, e63976. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Jiang, H. Nuclear protein condensates and their properties in regulation of gene expression. J. Mol. Biol. 2021, 167151. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Eckmann, C.R.; Courson, D.S.; Rybarska, A.; Hoege, C.; Gharakhani, J.; Julicher, F.; Hyman, A.A. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 2009, 324, 1729–1732. [Google Scholar] [CrossRef]
- Yeong, V.; Werth, E.G.; Brown, L.M.; Obermeyer, A.C. Formation of biomolecular condensates in bacteria by tuning protein electrostatics. ACS Cent. Sci. 2020, 6, 2301–2310. [Google Scholar] [CrossRef]
- Cohan, M.C.; Pappu, R.V. Making the case for disordered proteins and biomolecular condensates in bacteria. Trends Biochem. Sci. 2020, 45, 668–680. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Xu, A.; Cai, M.; Cao, J.; Zhu, H.; Yang, B.; Shao, X.; Ying, M.; He, Q. Protein phase separation: A novel therapy for cancer? Br. J. Pharmacol. 2020, 177, 5008–5030. [Google Scholar] [CrossRef]
- Tsang, B.; Pritišanac, I.; Scherer, S.W.; Moses, A.M.; Forman-Kay, J.D. Phase separation as a missing mechanism for interpretation of disease mutations. Cell 2020, 183, 1742–1756. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.; Liu, Z.; Lippincott-Schwartz, J. Biomolecular condensates and their links to cancer progression. Trends Biochem. Sci. 2021, 46, 535–549. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wang, X.; Dou, Z.; Yang, W.; Huang, B.; Lou, J.; Zhang, Z. Protein databases related to liquid-liquid phase separation. Int. J. Mol. Sci. 2020, 21, 6796. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Peng, X.; Li, Y.; Tang, W.; Zhu, J.; Huang, J.; Qi, Y.; Zhang, Z. LLPSDB: A database of proteins undergoing liquid–liquid phase separation in vitro. Nucleic Acids Res. 2020, 48, D320–D327. [Google Scholar] [CrossRef]
- Ning, W.; Guo, Y.; Lin, S.; Mei, B.; Wu, Y.; Jiang, P.; Tan, X.; Zhang, W.; Chen, G.; Peng, D.; et al. DrLLPS: A data resource of liquid-liquid phase separation in eukaryotes. Nucleic Acids Res. 2020, 48, D288–D295. [Google Scholar] [CrossRef]
- Mészáros, B.; Erdős, G.; Szabó, B.; Schád, É.; Tantos, Á.; Abukhairan, R.; Horváth, T.; Murvai, N.; Kovács, O.P.; Kovács, M.; et al. PhaSePro: The database of proteins driving liquid–liquid phase separation. Nucleic Acids Res. 2020, 48, D360–D367. [Google Scholar] [CrossRef]
- You, K.; Huang, Q.; Yu, C.; Shen, B.; Sevilla, C.; Shi, M.; Hermjakob, H.; Chen, Y.; Li, T. PhaSepDB: A database of liquid-liquid phase separation related proteins. Nucleic Acids Res. 2020, 48, D354–D359. [Google Scholar] [CrossRef]
- Shen, B.; Chen, Z.; Yu, C.; Chen, T.; Shi, M.; Li, T. Computational screening of phase-separating proteins. Genom. Proteom. Bioinf. 2021, 19, 13–24. [Google Scholar] [CrossRef]
- Chu, X.; Sun, T.; Li, Q.; Xu, Y.; Zhang, Z.; Lai, L.; Pei, J. Prediction of liquid-liquid phase separating proteins using machine learning. BMC Bioinform. 2022, 23, 72. [Google Scholar] [CrossRef]
- Schmit, J.D.; Feric, M.; Dundr, M. How hierarchical interactions make membraneless organelles tick like clockwork. Trends Biochem. Sci. 2021, 46, 525–534. [Google Scholar] [CrossRef]
- Dignon, G.L.; Best, R.B.; Mittal, J. Biomolecular phase separation: From molecular driving forces to macroscopic properties. Annu. Rev. Phys. Chem. 2020, 71, 53–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Das, S.; Lin, Y.H.; Vernon, R.M.; Forman-Kay, J.D.; Chan, H.S. Comparative roles of charge, p, and hydrophobic interactions in sequence-dependent phase separation of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2020, 117, 28795–28805. [Google Scholar] [CrossRef]
- Wei, M.T.; Elbaum-Garfinkle, S.; Holehouse, A.S.; Chen, C.C.; Feric, M.; Arnold, C.B.; Priestley, R.D.; Pappu, R.V.; Brangwynne, C.P. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem. 2017, 9, 1118–1125. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Li, M.; Lai, L.; Liu, Z. Allostery of multidomain proteins with disordered linkers. Curr. Opin. Struct. Biol. 2020, 62, 175–182. [Google Scholar] [CrossRef]
- Li, M.; Cao, H.; Lai, L.; Liu, Z. Disordered linkers in multidomain allosteric proteins: Entropic effect to favor the open state or enhanced local concentration to favor the closed state? Protein Sci. 2018, 27, 1600–1610. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Wang, L.; Tian, Y.; Xia, X.; Chen, Z. Structure and regulation of the chromatin remodeller ISWI. Nature 2016, 540, 466–469. [Google Scholar] [CrossRef]
- Anthis, N.J.; Clore, G.M. The length of the calmodulin linker determines the extent of transient interdomain association and target affinity. J. Am. Chem. Soc. 2013, 135, 9648–9651. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.X. Quantitative account of the enhanced affinity of two linked scFvs specific for different epitopes on the same antigen. J. Mol. Biol. 2003, 329, 1–8. [Google Scholar] [CrossRef]
- Harmon, T.S.; Holehouse, A.S.; Rosen, M.K.; Pappu, R.V. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. eLife 2017, 6, e30294. [Google Scholar] [CrossRef]
- McCarty, J.; Delaney, K.T.; Danielsen, S.P.O.; Fredrickson, G.H.; Shea, J.E. Complete phase diagram for liquid-liquid phase separation of intrinsically disordered proteins. J. Phys. Chem. Lett. 2019, 10, 1644–1652. [Google Scholar] [CrossRef] [PubMed]
- Schuster, B.S.; Dignon, G.L.; Tang, W.S.; Kelley, F.M.; Ranganath, A.K.; Jahnke, C.N.; Simpkins, A.G.; Regy, R.M.; Hammer, D.A.; Good, M.C.; et al. Identifying sequence perturbations to an intrinsically disordered protein that determine its phase-separation behavior. Proc. Natl. Acad. Sci. USA 2020, 117, 11421–11431. [Google Scholar] [CrossRef]
- Dzuricky, M.; Rogers, B.A.; Shahid, A.; Cremer, P.S.; Chilkoti, A. De novo engineering of intracellular condensates using artificial disordered proteins. Nat. Chem. 2020, 12, 814–825. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.M.; Holehouse, A.S.; Pappu, R.V. Physical principles underlying the complex biology of intracellular phase transitions. Annu. Rev. Biophys. 2020, 49, 107–133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, J.M.; Dar, F.; Pappu, R.V. LASSI: A lattice model for simulating phase transitions of multivalent proteins. PLoS Comput. Biol. 2019, 15, e1007028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borcherds, W.; Bremer, A.; Borgia, M.B.; Mittag, T. How do intrinsically disordered protein regions encode a driving force for liquid-liquid phase separation? Curr. Opin. Struct. Biol. 2021, 67, 41–50. [Google Scholar] [CrossRef]
- Ruff, K.M.; Dar, F.; Pappu, R.V. Ligand effects on phase separation of multivalent macromolecules. Proc. Natl. Acad. Sci. USA 2021, 118, e2017184118. [Google Scholar] [CrossRef]
- Cohan, M.C.; Eddelbuettel, A.M.P.; Levin, P.A.; Pappu, R.V. Dissecting the functional contributions of the intrinsically disordered C-terminal tail of Bacillus subtilis FtsZ. J. Mol. Biol. 2020, 432, 3205–3221. [Google Scholar] [CrossRef]
- Singh, K.; Rabin, Y. Sequence effects on internal structure of droplets of associative polymers. Biophys. J. 2020, 120, 1210–1218. [Google Scholar] [CrossRef]
- Levy, Y.Y.; Mesnage, S.; Mylne, J.S.; Gendall, A.R.; Dean, C. Multiple roles of Arabidopsis VRN1 in vernalization and flowering time control. Science 2002, 297, 243–246. [Google Scholar] [CrossRef]
- Bastow, R.; Mylne, J.S.; Lister, C.; Lippman, Z.; Martienssen, R.A.; Dean, C. Vernalization requires epigenetic silencing of FLC by histone methylation. Nature 2004, 427, 164–167. [Google Scholar] [CrossRef] [PubMed]
- Mylne, J.S.; Barrett, L.; Tessadori, F.; Mesnage, S.; Johnson, L.; Bernatavichute, Y.V.; Jacobsen, S.E.; Fransz, P.; Dean, C. LHP1, the Arabidopsis homologue of HETEROCHROMATIN PROTEIN1, is required for epigenetic silencing of FLC. Proc. Natl. Acad. Sci. USA 2006, 103, 5012–5017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, H.; Song, Z.; Zhong, S.; Zuo, L.; Qi, Z.; Qu, L.J.; Lai, L. Mechanism of DNA-induced phase separation for transcriptional repressor VRN1. Angew. Chem. Int. Ed. 2019, 58, 4858–4862. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, H.; Sun, X.; Huang, Q.; Li, S.; Liu, Z.; Zhang, C.; Lai, L. Charge segregation in the intrinsically disordered region governs VRN1 and DNA liquid-like phase separation robustness. J. Mol. Biol. 2021, 433, 167269. [Google Scholar] [CrossRef] [PubMed]
- Staller, M.V.; Ramirez, E.; Kotha, S.R.; Holehouse, A.S.; Pappu, R.V.; Cohen, B.A. Directed mutational scanning reveals a balance between acidic and hydrophobic residues in strong human activation domains. Cell Syst. 2022, 13, 334–345. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.X. Loops in proteins can be modeled as worm-like chains. J. Phys. Chem. B 2001, 105, 6763–6766. [Google Scholar] [CrossRef]
- Zhou, H.X. The affinity-enhancing roles of flexible linkers in two-domain DNA-binding proteins. Biochemistry 2001, 40, 15069–15073. [Google Scholar] [CrossRef]
- Zhou, H.X. Single-chain versus dimeric protein folding: Thermodynamic and kinetic consequences of covalent linkage. J. Am. Chem. Soc. 2001, 123, 6730–6731. [Google Scholar] [CrossRef]
- Mariottini, D.; Idili, A.; Nijenhuis, M.A.D.; de Greef, T.F.A.; Ricci, F. DNA-based nanodevices controlled by purely entropic linker domains. J. Am. Chem. Soc. 2018, 140, 14725–14734. [Google Scholar] [CrossRef]
- Feric, M.; Vaidya, N.; Harmon, T.S.; Mitrea, D.M.; Zhu, L.; Richardson, T.M.; Kriwacki, R.W.; Pappu, R.V.; Brangwynne, C.P. Coexisting liquid phases underlie nucleolar subcompartments. Cell 2016, 165, 1686–1697. [Google Scholar] [CrossRef] [Green Version]
- Guillen-Boixet, J.; Kopach, A.; Holehouse, A.S.; Wittmann, S.; Jahnel, M.; Schlussler, R.; Kim, K.; Trussina, I.; Wang, J.; Mateju, D.; et al. RNA-induced conformational switching and clustering of G3BP drive stress granule assembly by condensation. Cell 2020, 181, 346–361. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, Z. Dimensions, energetics, and denaturant effects of the protein unstructured state. Protein Sci. 2016, 25, 734–747. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Huang, Y. Advantages of proteins being disordered. Protein Sci. 2014, 23, 539–550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whyte, W.A.; Orlando, D.A.; Hnisz, D.; Abraham, B.J.; Lin, C.Y.; Kagey, M.H.; Rahl, P.B.; Lee, T.I.; Young, R.A. Master transcription factors and mediator establish super-enhancers at key cell identity genes. Cell 2013, 153, 307–319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaret, K.S. Pioneer transcription factors initiating gene network changes. Annu. Rev. Genet. 2020, 54, 367–385. [Google Scholar] [CrossRef] [PubMed]
- Capasso Palmiero, U.; Kuffner, A.M.; Krumeich, F.; Faltova, L.; Arosio, P. Adaptive chemoenzymatic microreactors composed of inorganic nanoparticles and bioinspired intrinsically disordered proteins. Angew. Chem. Int. Ed. 2020, 59, 8138–8142. [Google Scholar] [CrossRef]
- van Dongen, E.; Evers, T.H.; Dekkers, L.M.; Meijer, E.W.; Klomp, L.W.J.; Merkx, M. Variation of linker length in ratiometric fluorescent sensor proteins allows rational tuning of Zn(II) affinity in the picomolar to femtomolar range. J. Am. Chem. Soc. 2007, 129, 3494–3495. [Google Scholar] [CrossRef]
- Borcherds, W.; Becker, A.; Chen, L.; Chen, J.; Chemes, L.B.; Daughdrill, G.W. Optimal affinity enhancement by a conserved flexible linker controls p53 mimicry in MdmX. Biophys. J. 2017, 112, 2038–2042. [Google Scholar] [CrossRef] [Green Version]
- Krishnamurthy, V.M.; Semetey, V.; Bracher, P.J.; Shen, N.; Whitesides, G.M. Dependence of effective molarity on linker length for an intramolecular protein-ligand system. J. Am. Chem. Soc. 2007, 129, 1312–1320. [Google Scholar] [CrossRef] [Green Version]

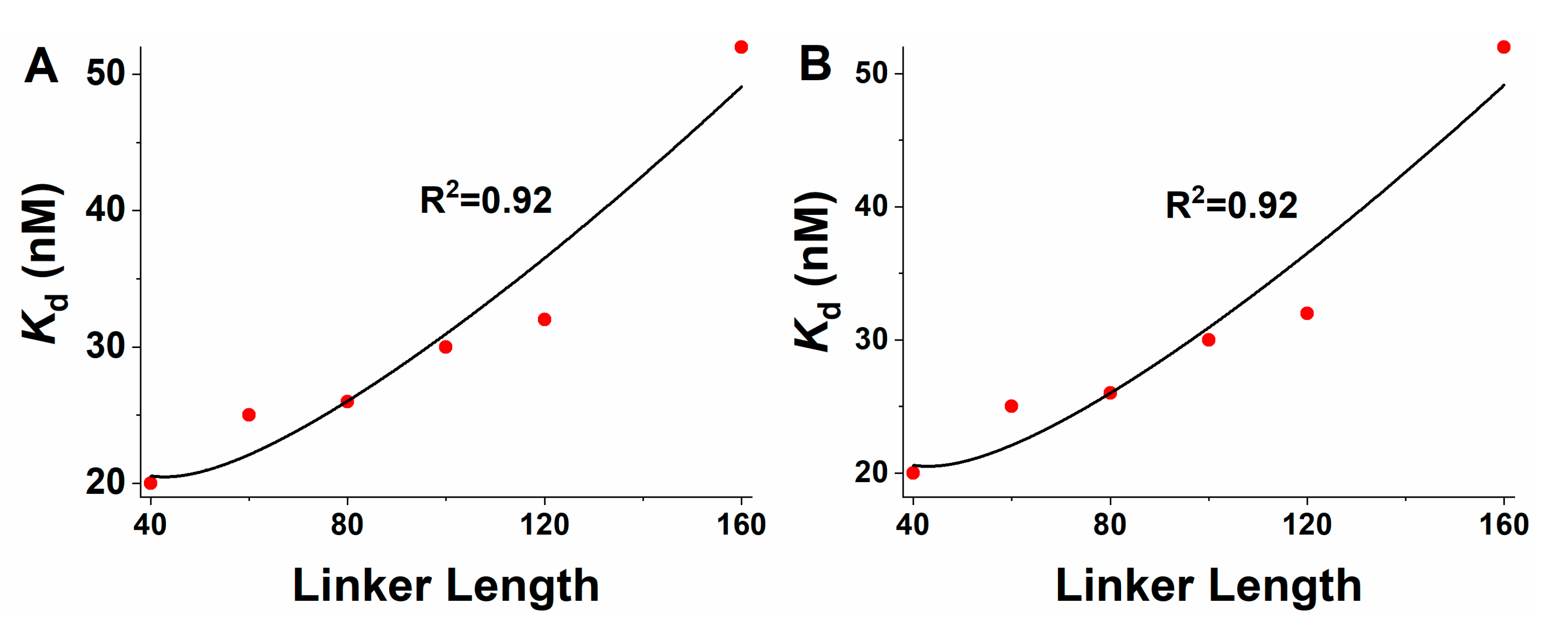



| Name | Apparent Kd from Ref. [44] (nM) | Ceff (mM) a | RMC-Kd | RMC-Ceff | WLC-Kd | WLC-Ceff |
|---|---|---|---|---|---|---|
| Single B3 | 753 | |||||
| PSN40 | 20 | 0.0284 | 21.4 | 0.0265 | 21.4 | 0.0265 |
| PSN60 | 25 | 0.0227 | 21.8 | 0.0260 | 21.7 | 0.0261 |
| PSN80 | 26 | 0.0218 | 24.9 | 0.0227 | 24.9 | 0.0227 |
| PSN100 | 30 | 0.0189 | 29.2 | 0.0194 | 29.2 | 0.0194 |
| PSN120 | 32 | 0.0177 | 34.1 | 0.0166 | 34.1 | 0.0166 |
| PSN160 | 52 | 0.0109 | 45.2 | 0.0125 | 45.2 | 0.0126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Wang, Y.; Liu, Z.; Lai, L. The Regulatory Roles of Intrinsically Disordered Linker in VRN1-DNA Phase Separation. Int. J. Mol. Sci. 2022, 23, 4594. https://doi.org/10.3390/ijms23094594
Huang Q, Wang Y, Liu Z, Lai L. The Regulatory Roles of Intrinsically Disordered Linker in VRN1-DNA Phase Separation. International Journal of Molecular Sciences. 2022; 23(9):4594. https://doi.org/10.3390/ijms23094594
Chicago/Turabian StyleHuang, Qiaojing, Yanyan Wang, Zhirong Liu, and Luhua Lai. 2022. "The Regulatory Roles of Intrinsically Disordered Linker in VRN1-DNA Phase Separation" International Journal of Molecular Sciences 23, no. 9: 4594. https://doi.org/10.3390/ijms23094594







