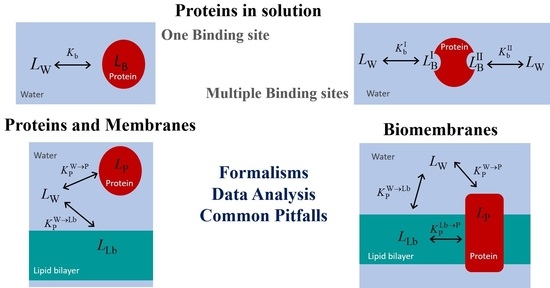
Analysis of the Equilibrium Distribution of Ligands in Heterogeneous Media–Approaches and Pitfalls
Abstract
:1. Introduction
2. Proteins in Solution
2.1. Proteins with a Single Binding Site
2.1.1. Analytical Solution of the Full Equation
2.1.2. Approximations Commonly Used
2.2. Proteins with More than One Binding Site
2.2.1. Formalism—Microscopic and Macroscopic Association Constants
2.2.2. Characterization of the Binding Parameters from Protein Saturation Curves
2.2.3. Scatchard Plots and Evaluation of Cooperativity
2.2.4. Indirect Characterization of the Binding Parameters Indirectly from Changes in a Protein Property
2.3. Quenching of Protein Fluorescence: Stern–Volmer Plots
2.4. Characterization of the Binding Parameters from Ligand Saturation Curves
2.4.1. Ligand Binding to Proteins with Multiple Binding Sites
2.4.2. Ligand Binding as a Partition Coefficient
3. Ligand Distribution in the Presence of Proteins and Membranes
3.1. Lipid Membranes and Proteins in Solution
3.2. Membranes Containing Lipids and Membrane Proteins
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tanford, C. Hydrophobic Free-Energy, Micelle Formation and Association of Proteins with Amphiphiles. J. Mol. Biol. 1972, 67, 59. [Google Scholar] [CrossRef]
- Southall, N.T.; Dill, K.A.; Haymet, A.D.J. A view of the hydrophobic effect. J. Phys. Chem. B 2002, 106, 521–533. [Google Scholar] [CrossRef]
- Creighton, T.E. Proteins. Structures and Molecular Properties; W. H. Freeman and Company: New York, NY, USA, 1993. [Google Scholar]
- Klotz, I.M.; Hunston, D.L. Protein Interactions with Small Molecules—Relationships Between Stoichiometric Binding Constants, Site Binding Constants, and Empirical Binding Parameters. J. Biol. Chem. 1975, 250, 3001–3009. [Google Scholar] [CrossRef]
- Cera, E.D. Mechanisms of ligand binding. Biophys. Rev. 2020, 1, 011303. [Google Scholar] [CrossRef] [PubMed]
- Gennis, R.B. Biomembranes. Molecular Structure and Function; Springer: New York, NY, USA, 1989. [Google Scholar]
- Singer, S.J.; Nicolson, G.L. Fluid Mosaic Model of Structure of Cell-Membranes. Science 1972, 175, 720. [Google Scholar] [CrossRef]
- Deyoung, L.R.; Dill, K.A. Solute Partitioning Into Lipid Bilayer-Membranes. Biochemistry 1988, 27, 5281–5289. [Google Scholar] [CrossRef]
- Seelig, A.; Allegrini, P.R.; Seelig, J. Partitioning of Local-Anesthetics Into Membranes—Surface-Charge Effects Monitored by the Phospholipid Headgroup. Biochim. Biophys. Acta 1988, 939, 267–276. [Google Scholar] [CrossRef]
- Santos, N.C.; Prieto, M.; Castanho, M.A.R.B. Quantifying molecular partition into model systems of biomembranes: An emphasis on optical spectroscopic methods. Biochim. Biophys. Acta-Biomembr. 2003, 1612, 123–135. [Google Scholar] [CrossRef]
- Melo, E.; Freitas, A.A.; Chang, Y.W.; Quina, F.H. On the significance of the solubilization power of detergents. Langmuir 2001, 17, 7980–7981. [Google Scholar] [CrossRef]
- Melo, E.C.C.; Costa, S.M.B. A Critical Evaluation of Partition Constants in Nonionic Micelles. J. Phys. Chem. 1987, 91, 5635–5640. [Google Scholar] [CrossRef]
- Lopes, A.; Demelo, J.S.; Martins, A.J.; Macanita, A.L.; Pina, F.S.; Wamhoff, H.; Melo, E. Partition of Pesticides of the Coumarin Family between Water and Amphiphilic Aggregates. Environ. Sci. Technol. 1995, 29, 562–570. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.J. Kinetics of Bimolecular Reactions with Stochastic Effects and Dimensional Constraints; Universidade Nova de Lisboa: Oeiras, Portugal, 2000. [Google Scholar]
- Moreno, M.J.; Herrmann, C.; Ivo, R.; Lourtie, I.M.G.; Wamhoff, H.; Melo, E. Consequences of the Partition between Water and Molecular Aggregates on the Photodegradation Pattern and Kinetics of a Pesticide of the Coumarin Family. Environ. Sci. Technol. 1995, 29, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.J.; Lourtie, I.M.G.; Melo, E. Stochastic effects on the time-dependent rate constant of photodimerization of 12-(9-anthroyloxy)stearic acid in micelles. J. Phys. Chem. 1996, 100, 18192–18200. [Google Scholar] [CrossRef]
- Berberansantos, M.N.; Prieto, M.J.E. Energy-Transfer in Spherical Geometry—Application to Micelles. J. Chem. Soc.-Faraday Trans. Ii 1987, 83, 1391–1410. [Google Scholar] [CrossRef]
- Matsuoka, K.; Moroi, Y. Micelle formation of sodium deoxycholate and sodium ursodeoxycholate (Part 1). Biochim. Biophys. Acta 2002, 1580, 189–199. [Google Scholar] [CrossRef]
- Tanford, C. Thermodynamics of Micelle Formation—Prediction of Micelle Size and Size Distribution. Proc. Natl. Acad. Sci. USA 1974, 71, 1811–1815. [Google Scholar] [CrossRef]
- Oliver, R.C.; Lipfert, J.; Fox, D.A.; Lo, R.H.; Doniach, S.; Columbus, L. Dependence of Micelle Size and Shape on Detergent Alkyl Chain Length and Head Group. PLoS ONE 2013, 8, 2488. [Google Scholar] [CrossRef]
- Davis, H.T. Factors Determining Emulsion-Type—Hydrophile-Lipophile Balance and Beyond. Colloids Surf. A 1994, 91, 9–24. [Google Scholar] [CrossRef]
- Menger, F.M.; McCreery, M.J. Kinetic Characterization of Bile-Salt Micelles. J. Am. Chem. Soc. 1974, 96, 121–126. [Google Scholar] [CrossRef]
- Bolt, J.D.; Turro, N.J. Measurement of the Rates of Detergent Exchange Between Micelles and the Aqueous Phase Using Phosphorescent Labeled Detergents. J. Phys. Chem. 1981, 85, 4029–4033. [Google Scholar] [CrossRef]
- Rharbi, Y.; Winnik, M.A. Solute exchange between surfactant micelles by micelle fragmentation and fusion. Adv. Colloid Interface Sci. 2001, 89, 25–46. [Google Scholar] [CrossRef]
- Coreta-Gomes, F.M.; Vaz, W.L.C.; Moreno, M.J. Effect of Acyl Chain Length on the Rate of Phospholipid Flip-Flop and Intermembrane Transfer. J. Membr. Biol. 2018, 251, 431–442. [Google Scholar] [CrossRef] [PubMed]
- Eaton, B.E.; Gold, L.; Zichi, D.A. Lets Get Specific—The Relationship Between Specificity and Affinity. Chem. Biol. 1995, 2, 633–638. [Google Scholar] [CrossRef]
- Gupta, A.B.; Mukherjee, S.; Pan, C.Q.; Velazquez-Campoy, A.; Sivaratnan, J.; Low, B.C. Spatial arrangement of LD motif-interacting residues on focal adhesion targeting domain of Focal Adhesion Kinase determine domain-motif interaction affinity and specificity. Biochim. Biophys. Acta-Gen. Subj. 2020, 1864, 129450. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, R.M.S.; Martins, P.A.T.; Ramos, C.V.; Cordeiro, M.M.; Leote, R.J.B.; Naqvi, K.R.; Vaz, W.L.C.; Moreno, M.J. Effect of dipole moment on amphiphile solubility and partition into liquid ordered and liquid disordered phases in lipid bilayers. Biochim. Biophys. Acta (BBA)-Biomembr. 2020, 1862, 183157. [Google Scholar] [CrossRef] [PubMed]
- Filipe, H.A.L.; Coreta-Gomes, F.M.; Velazquez-Campoy, A.; Almeida, A.R.; Peixoto, A.F.; Pereira, M.M.; Vaz, W.L.C.; Moreno, M.J. Synthesis and Characterization of a Lipidic Alpha Amino Acid: Solubility and Interaction with Serum Albumin and Lipid Bilayers. J. Phys. Chem. B 2013, 117, 3439–3448. [Google Scholar] [CrossRef]
- Kramer, S.D.; Braun, A.; Jakits-Deiser, C.; Wunderli-Allenspach, H. Towards the predictability of drug-lipid membrane interactions: The pH-dependent affinity of propranolol to phosphatidylinositol containing liposomes. Pharm. Res. 1998, 15, 739–744. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yang, Q.; Kamo, N.; Miyake, J. Effect of liposome type and membrane fluidity on drug-membrane partitioning analyzed by immobilized liposome chromatography. J. Chromatogr. A 2001, 913, 123–131. [Google Scholar] [CrossRef]
- Manuel, M.; Martins, J. Partitioning of 1-pyrenesulfonate into zwitterionic and mixed zwitterionic/anionic fluid phospholipid bilayers. Chem. Phys. Lipids 2008, 154, 79–86. [Google Scholar] [CrossRef]
- Martins, P.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Cardoso, R.M.S.; Valerio, J.; Moreno, M.J. Kinetics and Thermodynamics of Chlorpromazine Interaction with Lipid Bilayers: Effect of Charge and Cholesterol. J. Am. Chem. Soc. 2012, 134, 4184–4195. [Google Scholar] [CrossRef]
- Moreno, M.J.; Bastos, M.; Velazquez-Campoy, A. Partition of amphiphilic molecules to lipid bilayers by isothermal titration calorimetry. Anal. Biochem. 2010, 399, 44–47. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.J.; Prieto, M. Interaction of the Peptide-Hormone Adrenocorticotropin, ACTH(1- 24), with a Membrane Model System—A Fluorescence Study. Photochem. Photobiol. 1993, 57, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Saveyn, P.; Cocquyt, E.; Sinnaeve, D.; Martins, J.C.; Topgaard, D.; Van der Meeren, P. NMR study of the sorption behavior of benzyl alcohol derivatives into sonicated and extruded dioctadecyldimethylammonium chloride (DODAC) dispersions: The relevance of membrane fluidity. Langmuir 2008, 24, 3082–3089. [Google Scholar] [CrossRef]
- Thomae, A.V.; Koch, T.; Panse, C.; Wunderli-Allenspach, H.; Kramer, S.D. Comparing the lipid membrane affinity and permeation of drug-like acids: The intriguing effects of cholesterol and charged lipids. Pharm. Res. 2007, 24, 1457–1472. [Google Scholar] [CrossRef] [PubMed]
- Thomae, A.V.; Wunderli-Allenspach, H.; Kramer, S.D. Permeation of aromatic carboxylic acids across lipid bilayers: The pH-partition hypothesis revisited. Biophys. J. 2005, 89, 1802–1811. [Google Scholar] [CrossRef]
- Bender, F.C.; Whitbeck, J.C.; de Leon, M.P.; Lou, H.; Eisenberg, R.J.; Cohen, G.H. Specific association of glycoprotein B with lipid rafts during herpes simplex virus entry. J. Virol. 2003, 77, 9542–9552. [Google Scholar] [CrossRef]
- Kamlekar, R.K.; Simanshu, D.K.; Gao, Y.G.; Kenoth, R.; Pike, H.M.; Prendergast, F.G.; Malinina, L.; Molotkovsky, J.G.; Venyaminov, S.Y.; Patel, D.J.; et al. The glycolipid transfer protein (GLTP) domain of phosphoinositol 4-phosphate adaptor protein-2 (FAPP2): Structure drives preference for simple neutral glycosphingolipids. Biochim. Biophys. Acta 2013, 1831, 417–427. [Google Scholar] [CrossRef]
- Pina, D.G.; Johannes, L.; Castanho, M. Shiga toxin B-subunit sequential binding to its natural receptor in lipid membranes. Biochim. Biophys. Acta-Biomembr. 2007, 1768, 628–636. [Google Scholar] [CrossRef]
- Ruysschaert, J.M.; Lonez, C. Role of lipid microdomains in TLR-mediated signalling. Biochim. Biophys. Acta-Biomembr. 2015, 1848, 1860–1867. [Google Scholar] [CrossRef]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef]
- Schreiber, G.; Keating, A.E. Protein binding specificity versus promiscuity. Curr. Opin. Struct. Biol. 2011, 21, 50–61. [Google Scholar] [CrossRef] [PubMed]
- Claveria-Gimeno, R.; Vega, S.; Abian, O.; Velazquez-Campoy, A. A look at ligand binding thermodynamics in drug discovery. Expert Opin. Drug Discov. 2017, 12, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. Handling complexity in biological interactions: Allostery and cooperativity in proteins. J. Therm. Anal. Calorim. 2019, 138, 3229–3248. [Google Scholar] [CrossRef]
- Velazquez-Campoy, A.; Freire, E. ITC in the Post-Genomic era...? Priceless. Biophys. Chem. 2005, 115, 115–124. [Google Scholar] [CrossRef]
- Litman, T.; Zeuthen, T.; Skovsgaard, T.; Stein, W.D. Competitive, non-competitive and cooperative interactions between substrates of P-glycoprotein as measured by its ATPase activity. Biochim. Biophys. Acta 1997, 1361, 169–176. [Google Scholar] [CrossRef]
- Rabbani, G.; Baig, M.H.; Lee, E.J.; Cho, W.K.; Ma, J.Y.; Choi, I. Biophysical Study on the Interaction between Eperisone Hydrochloride and Human Serum Albumin Using Spectroscopic, Calorimetric, and Molecular Docking Analyses. Mol. Pharm. 2017, 14, 1656–1665. [Google Scholar] [CrossRef]
- Gelamo, E.L.; Silva, C.; Imasato, H.; Tabak, M. Interaction of bovine (BSA) and human (HSA) serum albumins with ionic surfactants: Spectroscopy and modelling. Biochim. Biophys. Acta 2002, 1594, 84–99. [Google Scholar] [CrossRef]
- Li, G.X.; Liu, B.S.; Zhang, Q.J.; Han, R. Investigation on the effect of fluorescence quenching of bovine serum albumin by cefoxitin sodium using fluorescence spectroscopy and synchronous fluorescence spectroscopy. Luminescence 2016, 31, 1054–1062. [Google Scholar] [CrossRef]
- Sengupta, B.; Sengupta, P.K. Binding of quercetin with human serum albumin: A critical spectroscopic study. Biopolymers 2003, 72, 427–434. [Google Scholar] [CrossRef]
- Hebert, P.C.; MacManus-Spencer, L.A. Development of a Fluorescence Model for the Binding of Medium- to Long-Chain Perfluoroalkyl Acids to Human Serum Albumin Through a Mechanistic Evaluation of Spectroscopic Evidence. Anal. Chem. 2010, 82, 6463–6471. [Google Scholar] [CrossRef]
- Vuignier, K.; Schappler, J.; Veuthey, J.L.; Carrupt, P.A.; Martel, S. Drug-protein binding: A critical review of analytical tools. Anal. Bioanal. Chem. 2010, 398, 53–66. [Google Scholar] [CrossRef] [PubMed]
- Cooper, M.A. Label-free screening of bio-molecular interactions. Anal. Bioanal. Chem. 2003, 377, 834–842. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Li, Y.; Xia, Y.L.; Ai, S.M.; Liang, J.; Sang, P.; Ji, X.L.; Liu, S.Q. Insights into Protein-Ligand Interactions: Mechanisms, Models, and Methods. Int. J. Mol. Sci. 2016, 17, 144. [Google Scholar] [CrossRef]
- Mackay, D.; Panjehshahin, M.R.; Bowmer, C.J. Analysis of the Binding of Fluorescent Ligands to Soluble- Proteins—Use of Simultaneous Nonlinear Least-Squares Regression to Obtain Estimates of Binding Parameters. Biochem. Pharmacol. 1991, 41, 2011–2018. [Google Scholar] [CrossRef]
- Abreu, M.S.C.; Estronca, L.M.B.B.; Moreno, M.J.; Vaz, W.L.C. Binding of a Fluorescent Lipid Amphiphile to Albumin and its Transfer to Lipid Bilayer Membranes. Biophys. J. 2003, 84, 386–399. [Google Scholar] [CrossRef]
- Cardoso, R.M.S.; Filipe, H.A.L.; Gomes, F.; Moreira, N.D.; Vaz, W.L.C.; Moreno, M.J. Chain Length Effect on the Binding of Amphiphiles to Serum Albumin and to POPC Bilayers. J. Phys. Chem. B 2010, 114, 16337–16346. [Google Scholar] [CrossRef]
- Haque, M.E.; Ray, S.; Chakrabarti, A. Polarity estimate of the hydrophobic binding sites in erythroid spectrin: A study by pyrene fluorescence. J. Fluoresc. 2000, 10, 1–6. [Google Scholar] [CrossRef]
- Srinivasan, B. A guide to the Michaelis-Menten equation: Steady state and beyond. FEBS J. 2021, 16124. [Google Scholar] [CrossRef]
- Velazquez-Campoy, A.; Goni, G.; Peregrina, J.R.; Medina, M. Exact analysis of heterotropic interactions in proteins: Characterization of cooperative ligand binding by isothermal titration calorimetry. Biophys. J. 2006, 91, 1887–1904. [Google Scholar] [CrossRef]
- Freire, E.; Kawasaki, Y.; Velazquez-Campoy, A.; Schon, A. Characterisation of Ligand Binding by Calorimetry. In Biophysical Approaches Determining Ligand Binding to Biomolecular Targets: Detection, Measurement and Modelling; Podjarny, A., Dejaegere, A.P., Kieffer, B., Eds.; Royal Society of Chemistry: Paris, France, 2011; pp. 275–299. [Google Scholar]
- Bastos, M.; Velazquez-Campoy, A. Isothermal titration calorimetry (ITC): A standard operating procedure (SOP). Eur. Biophys. J. Biophys. Lett. 2021, 50, 363–371. [Google Scholar] [CrossRef]
- Claveria-Gimeno, R.; Velazquez-Campoy, A.; Pey, A.L. Thermodynamics of cooperative binding of FAD to human NQO1: Implications to understanding cofactor-dependent function and stability of the flavoproteome. Arch. Biochem. Biophys. 2017, 636, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Claveria-Gimeno, R.; Vega, S.; Abian, O.; Velazquez-Campoy, A. Tinkering with Binding Polynomials in Isothermal Titration Calorimetry. In Microcalorimetry of Biological Molecules: Methods and Protocols; Ennifar, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1964, pp. 185–213. [Google Scholar]
- Freire, E.; Schon, A.; Velazquez-Campoy, A. Isothermal Titration Calorimetry: General Formalism using Binding Polynomials. Method. Enzymol. 2009, 455, 127–155. [Google Scholar] [CrossRef]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. A unified framework based on the binding polynomial for characterizing biological systems by isothermal titration calorimetry. Methods 2015, 76, 99–115. [Google Scholar] [CrossRef]
- Taneva, S.G.; Banuelos, S.; Falces, J.; Arregi, I.; Muga, A.; Konarev, P.V.; Svergun, D.I.; Velazquez-Campoy, A.; Urbaneja, M.A. A Mechanism for Histone Chaperoning Activity of Nucleoplasmin: Thermodynamic and Structural Models. J. Mol. Biol. 2009, 393, 448–463. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.D.; Timasheff, S.N. Cooperative Multiple Binding of Bisans and Daunomycin to Tubulin. Biochemistry 1994, 33, 11891–11899. [Google Scholar] [CrossRef] [PubMed]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill/Irwin: Boston, MA, USA, 2004. [Google Scholar]
- Alesio, J.L.; Slitt, A.; Bothun, G.D. Critical new insights into the binding of poly- and perfluoroalkyl substances (PFAS) to albumin protein. Chemosphere 2022, 287, 131979. [Google Scholar] [CrossRef]
- Estronca, L.M.B.B.; Moreno, M.J.; Vaz, W.L.C. Kinetics and thermodynamics of the association of dehydroergosterol with lipid bilayer membranes. Biophys. J. 2007, 93, 4244–4253. [Google Scholar] [CrossRef]
- Martins, P.A.T.; Domingues, N.; Pires, C.; Alves, A.M.; Palmeira, T.; Samelo, J.; Cardoso, R.; Velazquez-Campoy, A.; Moreno, M.J. Molecular crowding effects on the distribution of amphiphiles in biological media. Colloids Surf. B 2019, 180, 319–325. [Google Scholar] [CrossRef]
- Martins, P.A.; Gomes, F.; Vaz, W.L.C.; Moreno, M.J. Binding of Phospholipids to á-Lactoglobulin and their Transfer to Lipid Bilayers. Biochim. Biophys. Acta 2008, 1778, 1308–1315. [Google Scholar] [CrossRef]
- Abe, Y.; Fukui, S.; Koshiji, Y.; Kobayashi, M.; Shoji, T.; Sugata, S.; Nishizawa, H.; Suzuki, H.; Iwata, I. Enantioselective binding sites on bovine serum albumin to dansyl amino acids. Biochim. Biophys. Acta 1999, 1433, 188–197. [Google Scholar] [CrossRef]
- Epps, D.E.; Raub, T.J.; Kezdy, F.J. A General, Wide-Range Spectrofluorometric Method for Measuring the Site-Specific Affinities of Drugs Towards Human Serum- Albumin. Anal. Biochem. 1995, 227, 342–350. [Google Scholar] [CrossRef] [PubMed]
- Bischel, H.N.; MacManus-Spencer, L.A.; Zhang, C.J.; Luthy, R.G. Strong Associations of Short-Chain Perfluoroalkyl Acids with Serum Albumin and Investigation of Binding Mechanisms. Environ. Toxicol. Chem. 2011, 30, 2423–2430. [Google Scholar] [CrossRef] [PubMed]
- Allendorf, F.; Berger, U.; Goss, K.U.; Ulrich, N. Partition coefficients of four perfluoroalkyl acid alternatives between bovine serum albumin (BSA) and water in comparison to ten classical perfluoroalkyl acids. Environ. Sci.-Processes Impacts 2019, 21, 1852–1863. [Google Scholar] [CrossRef] [PubMed]
- Videira, R.A.; Antunesmadeira, M.D.; Custodio, J.B.A.; Madeira, V.M.C. Partition of Dde in Synthetic and Native Membranes Determined by Ultraviolet Derivative Spectroscopy. Biochim. Biophys. Acta-Biomembr. 1995, 1238, 22–28. [Google Scholar] [CrossRef]
- Andrieux, K.; Forte, L.; Lesieur, S.; Paternostre, M.; Ollivon, M.; Grabielle-Madelmont, C. Insertion and partition of sodium taurocholate into egg phosphatidylcholine vesicles. Pharm. Res. 2004, 21, 1505–1516. [Google Scholar] [CrossRef] [PubMed]
- Heerklotz, H. Interactions of surfactants with lipid membranes. Q. Rev. Biophys. 2008, 41, 205–264. [Google Scholar] [CrossRef]
- Lolicato, F.; Juhola, H.; Zak, A.; Postila, P.A.; Saukko, A.; Rissanen, S.; Enkavi, G.; Vattulainen, I.; Kepczynski, M.; Rog, T. Membrane-Dependent Binding and Entry Mechanism of Dopamine into Its Receptor. ACS Chem. Neurosci. 2020, 11, 1914–1924. [Google Scholar] [CrossRef]
- Shahoei, R.; Tajkhorshid, E. Menthol Binding to the Human alpha 4 beta 2 Nicotinic Acetylcholine Receptor Facilitated by Its Strong Partitioning in the Membrane. J. Phys. Chem. B 2020, 124, 1866–1880. [Google Scholar] [CrossRef]















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, M.J.; Loura, L.M.S.; Martins, J.; Salvador, A.; Velazquez-Campoy, A. Analysis of the Equilibrium Distribution of Ligands in Heterogeneous Media–Approaches and Pitfalls. Int. J. Mol. Sci. 2022, 23, 9757. https://doi.org/10.3390/ijms23179757
Moreno MJ, Loura LMS, Martins J, Salvador A, Velazquez-Campoy A. Analysis of the Equilibrium Distribution of Ligands in Heterogeneous Media–Approaches and Pitfalls. International Journal of Molecular Sciences. 2022; 23(17):9757. https://doi.org/10.3390/ijms23179757
Chicago/Turabian StyleMoreno, Maria João, Luís M. S. Loura, Jorge Martins, Armindo Salvador, and Adrian Velazquez-Campoy. 2022. "Analysis of the Equilibrium Distribution of Ligands in Heterogeneous Media–Approaches and Pitfalls" International Journal of Molecular Sciences 23, no. 17: 9757. https://doi.org/10.3390/ijms23179757