Effects of Cholesterol on Water Permittivity of Biomimetic Ion Pair Amphiphile Bilayers: Interplay between Membrane Bending and Molecular Packing
Abstract
:1. Introduction
2. Results and Discussion
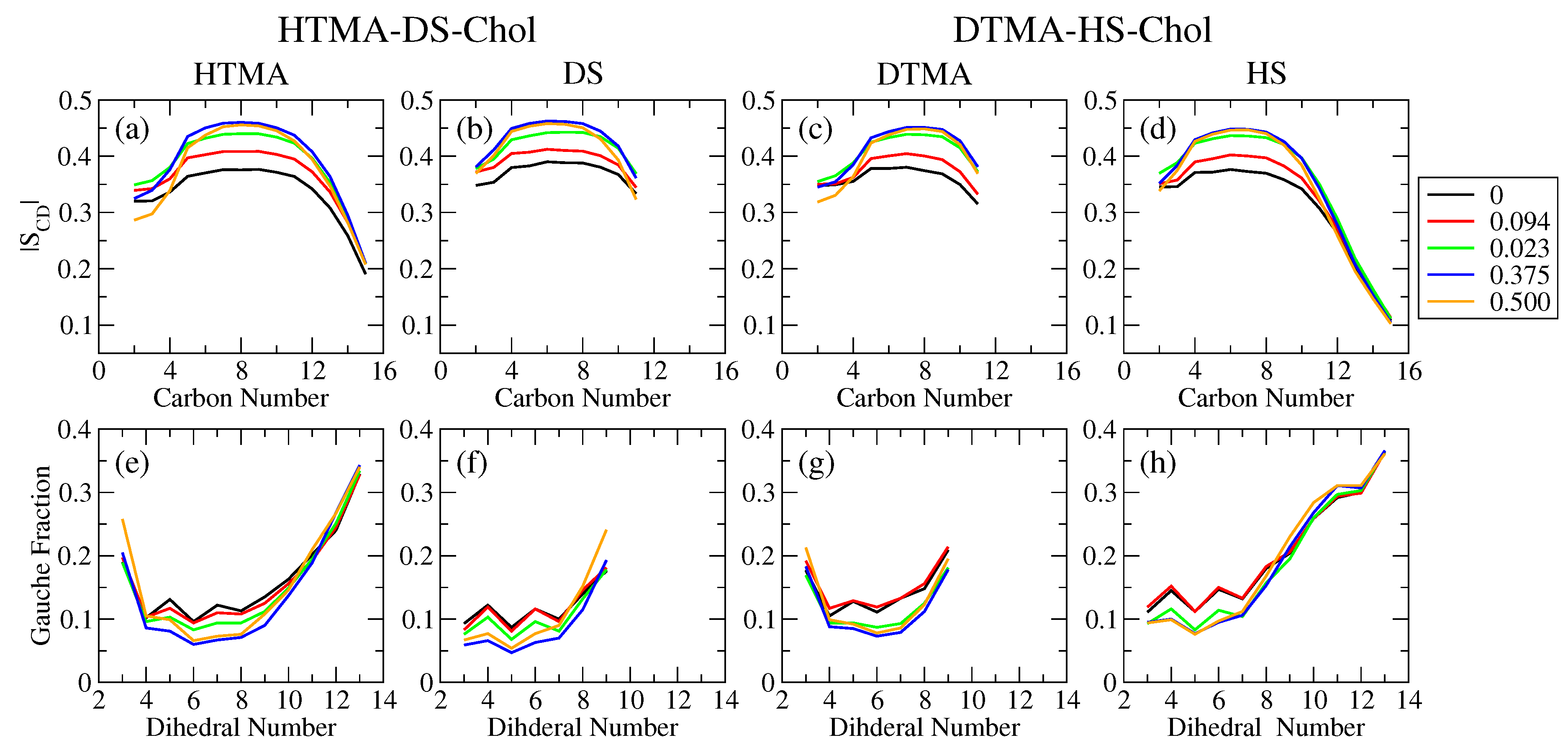
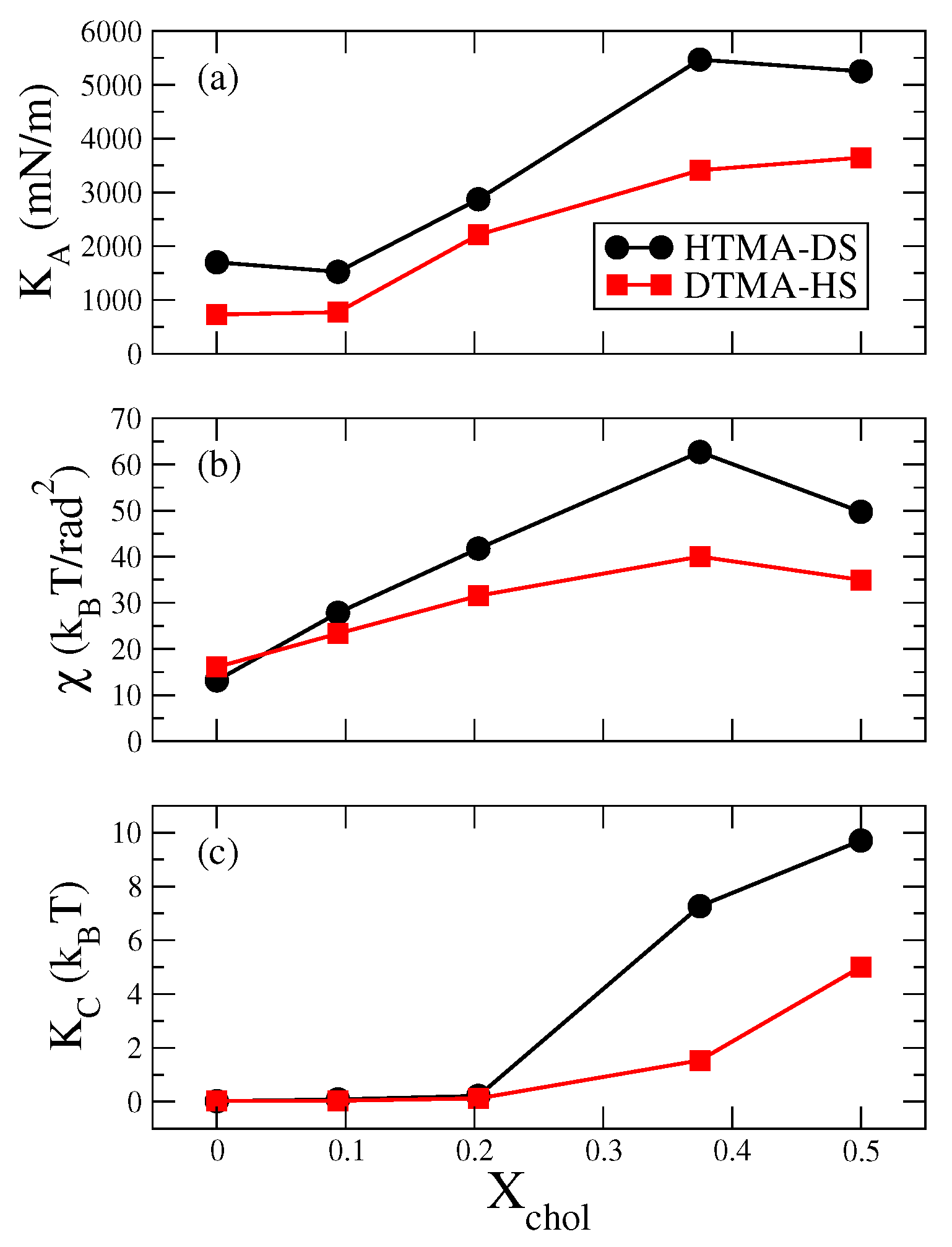
2.1. Bilayer Structural and Mechanical Properties
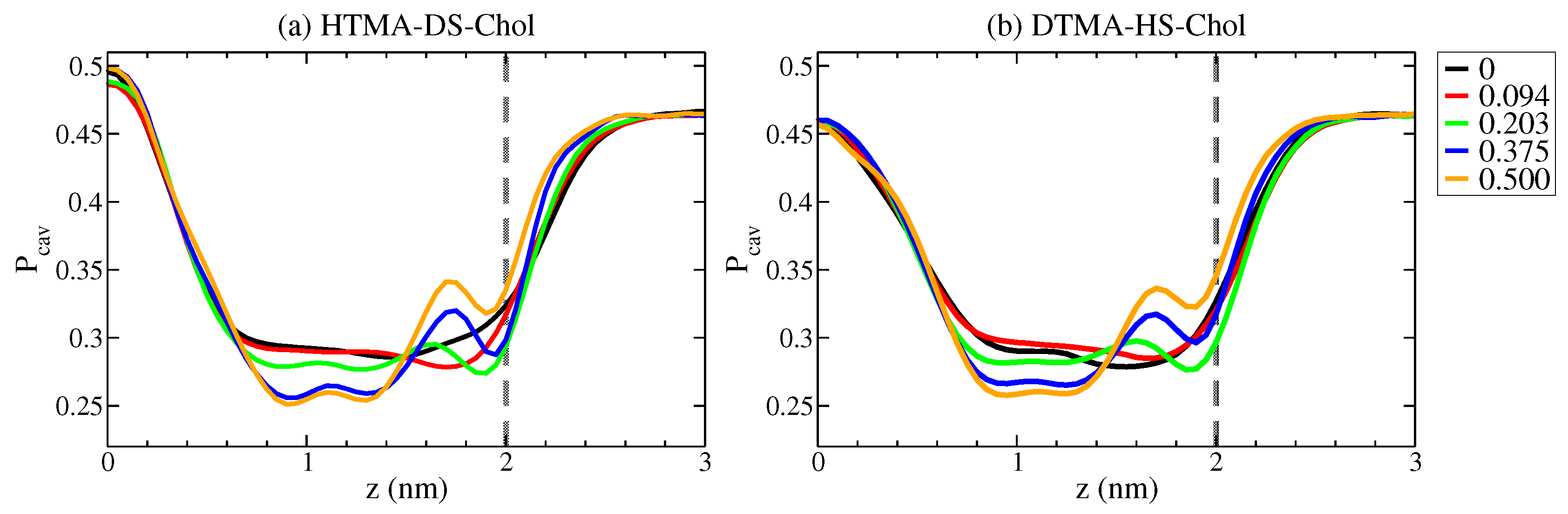
2.2. Free Energy of Water Crossing IPA-Chol Bilayer
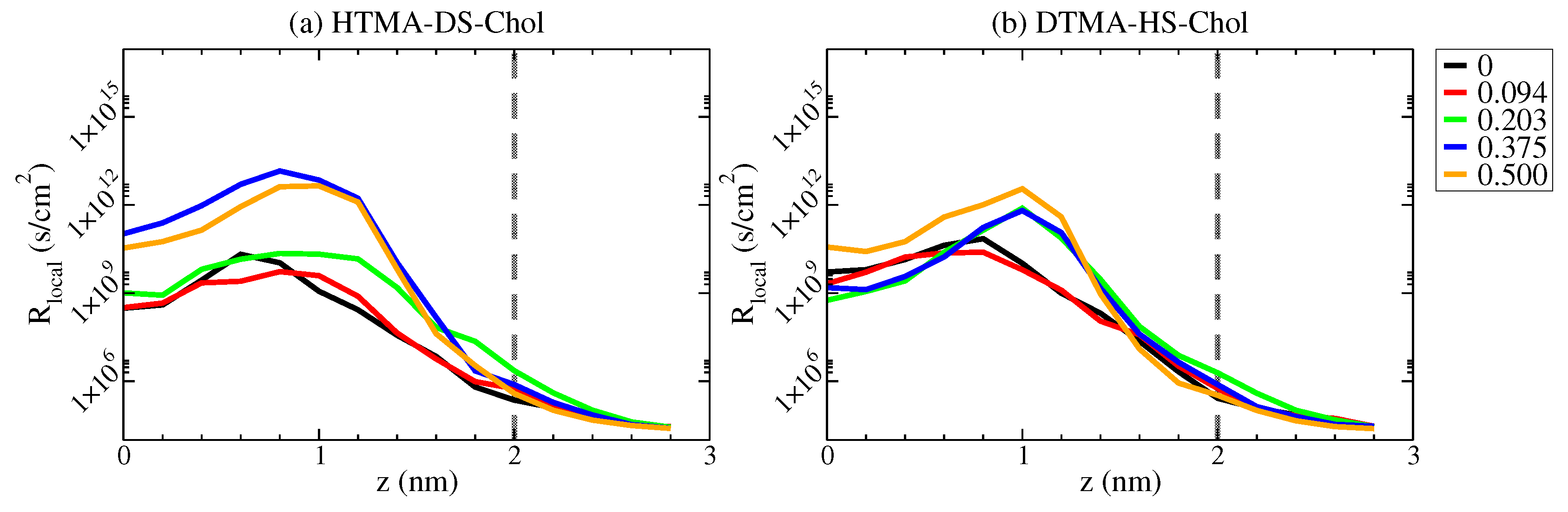
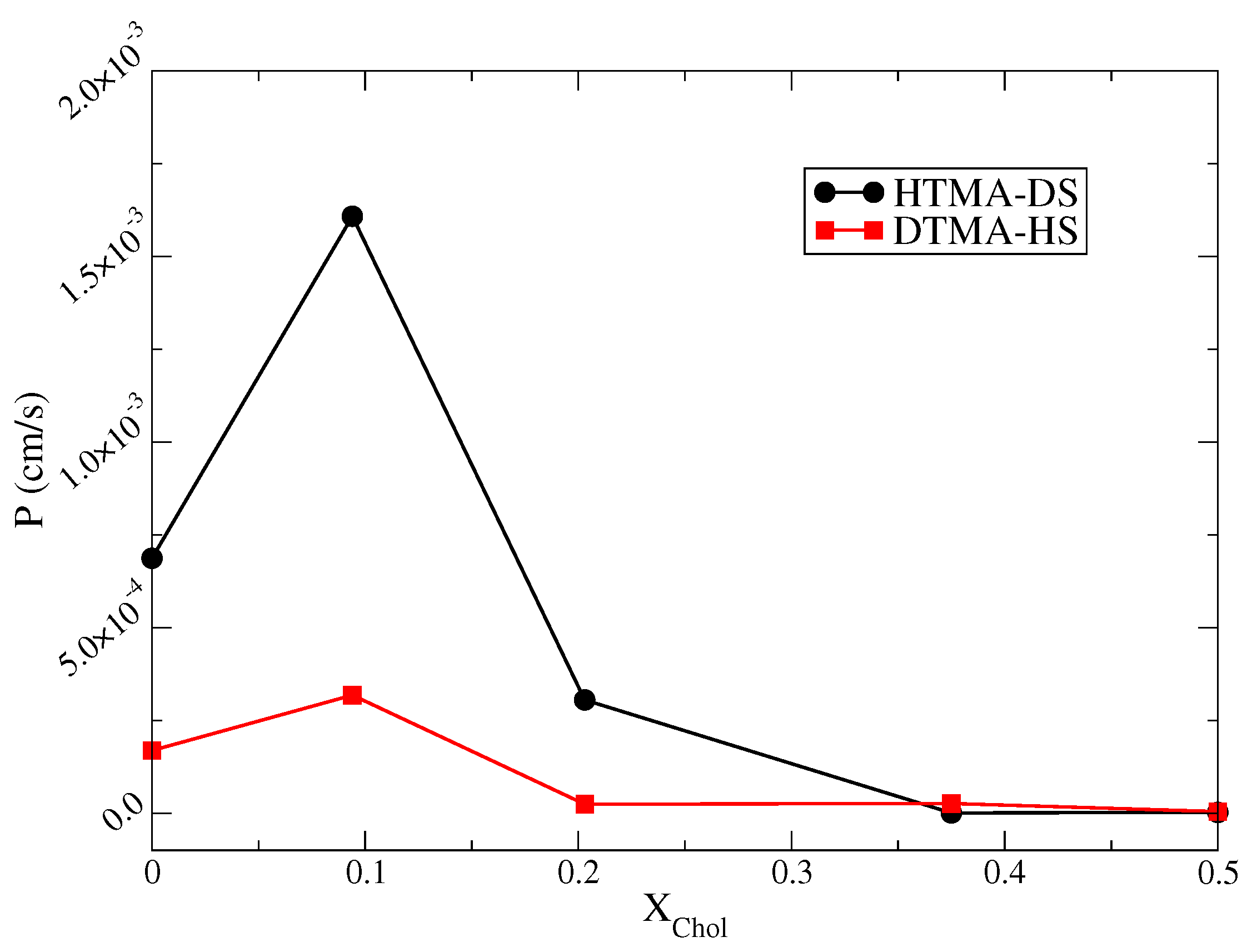
2.3. Water Permittivity of IPA-Chol Bilayer
3. Materials and Methods
3.1. Simulations Details
3.2. Mechanical Modulus
3.3. Permeation Free Energy Calculation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IPA | Ion Pair Amphiphile |
| MD | molecular dynamics |
| HTMA | hexadecyltrimethylammonium |
| DTMA | dodecyltrimethylammonium |
| HS | hexadecylsulfate |
| DS | dodecylsulfate |
| Chol | cholesterol |
References
- Lasic, D.D. Novel applications of liposomes. Trends Biotechnol. 1998, 16, 307–321. [Google Scholar] [CrossRef]
- Moghimi, S.M.; Hunter, A.C.; Murray, J.C. Nanomedicine: Current status and future prospects. FASEB J. 2005, 19, 311–330. [Google Scholar] [CrossRef] [PubMed]
- Yadav, D.; Sandeep, K.; Pandey, D.; Dutta, R.K. Liposomes for Drug Delivery. J. Biotechnol. Biomater. 2017, 7, 276. [Google Scholar] [CrossRef]
- Zylberberg, C.; Matosevic, S. Pharmaceutical liposomal drug delivery: A review of new delivery systems and a look at the regulatory landscape. Drug Deliv. 2016, 23, 3319–3329. [Google Scholar] [CrossRef] [PubMed]
- Soussan, E.; Cassel, S.; Blanzat, M.; Rico-Lattes, I. Drug Delivery by Soft Matter: Matrix and Vesicular Carriers. Angew. Chem. Int. Ed. Engl. 2009, 48, 274–288. [Google Scholar] [CrossRef] [PubMed]
- Kaler, E.; Murthy, A.; Rodriguez, B.; Zasadzinski, J. Spontaneous vesicle formation in aqueous mixtures of single-tailed surfactants. Science 1989, 245, 1371–1374. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.T.; Chang, C.H. Recent Strategies in the Development of Catanionic Vesicles. J. Oleo Sci. 2016, 65, 377–384. [Google Scholar] [CrossRef] [Green Version]
- Dhawan, V.V.; Nagarsenker, M.S. Catanionic systems in nanotherapeutics—Biophysical aspects and novel trends in drug delivery applications. J. Control. Release 2017, 266, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.A.; Zasadzinski, J.A. Electrostatic Control of Spontaneous Vesicle Aggregation. Langmuir 1997, 13, 5076–5081. [Google Scholar] [CrossRef]
- Kuo, A.T.; Chang, C.H.; Shinoda, W. Molecular Dynamics Study of Catanionic Bilayers Composed of Ion Pair Amphiphile with Double-Tailed Cationic Surfactant. Langmuir 2012, 28, 8156–8164. [Google Scholar] [CrossRef]
- Wu, C.J.; Kuo, A.T.; Lee, C.H.; Yang, Y.M.; Chang, C.H. Fabrication of positively charged catanionic vesicles from ion pair amphiphile with double-chained cationic surfactant. Colloid Polym. Sci. 2013, 292, 589–597. [Google Scholar] [CrossRef]
- Lee, C.H.; Yang, Y.M.; Chang, C.H. Enhancing physical stability of positively charged catanionic vesicles in the presence of calcium chloride via cholesterol-induced fluidic bilayer characteristic. Colloid Polym. Sci. 2014, 292, 2519–2527. [Google Scholar] [CrossRef]
- Kuo, A.T.; Chang, C.H. Cholesterol-induced condensing and disordering effects on a rigid catanionic bilayer: A molecular dynamics study. Langmuir 2014, 30, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.Y.; Chiu, C.C. Interplay between alkyl chain asymmetry and cholesterol addition in the rigid ion pair amphiphile bilayer systems. J. Chem. Phys. 2017, 146, 035102. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.H.; Tian, C.A.; Chiu, C.C. The Effects of Alkyl Chain Combinations on the Structural and Mechanical Properties of Biomimetic Ion Pair Amphiphile Bilayers. Bioengineering 2017, 4, 84. [Google Scholar] [CrossRef] [PubMed]
- De Meyer, F.J.M.; Benjamini, A.; Rodgers, J.M.; Misteli, Y.; Smit, B. Molecular Simulation of the DMPC-Cholesterol Phase Diagram. J. Phys. Chem. B 2010, 114, 10451–10461. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.H.; Tang, Y.L.; Chiu, T.C.; Yang, Y.M. Synthesis of Ion-Pair Amphiphiles and Calorimetric Study on the Gel to Liquid-Crystalline Phase Transition Behavior of Their Bilayers. J. Chem. Eng. Data 2015, 60, 1119–1125. [Google Scholar] [CrossRef]
- Tian, C.A.; Chiu, C.C. Importance of Hydrophilic Groups on Modulating the Structural, Mechanical, and Interfacial Properties of Bilayers: A Comparative Molecular Dynamics Study of Phosphatidylcholine and Ion Pair Amphiphile Membranes. Int. J. Mol. Sci. 2018, 19, 1552. [Google Scholar] [CrossRef]
- Liu, Y.S.; Wen, C.F.; Yang, Y.M. Cholesterol Effects on the Vesicular Membrane Rigidity and Drug Encapsulation Efficiency of Ethosome-Like Catanionic Vesicles. Sci. Adv. Mater. 2014, 6, 954–962. [Google Scholar] [CrossRef]
- Chang, W.H.; Chuang, Y.T.; Yu, C.Y.; Chang, C.H.; Yang, Y.M. Effects of Sterol-Like Additives on Phase Transition Behavior of Ion-Pair Amphiphile Bilayers. J. Oleo Sci. 2017, 66, 1229–1238. [Google Scholar] [CrossRef] [Green Version]
- Shinoda, W. Permeability across lipid membranes. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2254–2265. [Google Scholar] [CrossRef] [PubMed]
- Votapka, L.W.; Lee, C.T.; Amaro, R.E. Two Relations to Estimate Membrane Permeability Using Milestoning. J. Phys. Chem. B 2016, 120, 8606–8616. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Berendsen, H.J.C. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994, 98, 4155–4168. [Google Scholar] [CrossRef] [Green Version]
- Diamond, J.M.; Katz, Y. Interpretation of nonelectrolyte partition coefficients between dimyristoyl lecithin and water. J. Membr. Biol. 1974, 17, 121–154. [Google Scholar] [CrossRef] [PubMed]
- Palaiokostas, M.; Ding, W.; Shahane, G.; Orsi, M. Effects of lipid composition on membrane permeation. Soft Matter 2018, 14, 8496–8508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vos, O.; Venable, R.M.; Van Hecke, T.; Hummer, G.; Pastor, R.W.; Ghysels, A. Membrane Permeability: Characteristic Times and Lengths for Oxygen and a Simulation-Based Test of the Inhomogeneous Solubility-Diffusion Model. J. Chem. Theory Comput. 2018, 14, 3811–3824. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.T.; Comer, J.; Herndon, C.; Leung, N.; Pavlova, A.; Swift, R.V.; Tung, C.; Rowley, C.N.; Amaro, R.E.; Chipot, C.; et al. Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds. J. Chem. Inf. Model. 2016, 56, 721–733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cordeiro, R.M. Molecular Structure and Permeability at the Interface between Phase-Separated Membrane Domains. J. Phys. Chem. B 2018, 122, 6954–6965. [Google Scholar] [CrossRef]
- Qiao, B.; de la Cruz, M.O. Driving Force for Water Permeation Across Lipid Membranes. J. Phys. Chem. Lett. 2013, 4, 3233–3237. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Egberts, E.; Marrink, S.J.; Berendsen, H.J. Molecular dynamics simulation of a phospholipid membrane. Eur. Biophys. J. 1994, 22, 423–436. [Google Scholar] [CrossRef] [PubMed]
- Douliez, J.P.; Léonard, A.; Dufourc, E.J. Restatement of order parameters in biomembranes: calculation of C-C bond order parameters from C-D quadrupolar splittings. Biophys. J. 1995, 68, 1727–1739. [Google Scholar] [CrossRef] [Green Version]
- Pink, D.A.; Green, T.J.; Chapman, D. Raman scattering in bilayers of saturated phosphatidylcholines. Experiment and theory. Biochemistry 1980, 19, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Saito, H.; Shinoda, W. Cholesterol Effect on Water Permeability through DPPC and PSM Lipid Bilayers: A Molecular Dynamics Study. J. Phys. Chem. B 2011, 115, 15241–15250. [Google Scholar] [CrossRef]
- Khajeh, A.; Modarress, H. Effect of cholesterol on behavior of 5-fluorouracil (5-FU) in a DMPC lipid bilayer, a molecular dynamics study. Biophys. Chem. 2014, 187–188, 43–50. [Google Scholar] [CrossRef]
- Paloncýová, M.; DeVane, R.H.; Murch, B.P.; Berka, K.; Otyepka, M. Rationalization of Reduced Penetration of Drugs through Ceramide Gel Phase Membrane. Langmuir 2014, 30, 13942–13948. [Google Scholar] [CrossRef]
- Hartkamp, R.; Moore, T.C.; Iacovella, C.R.; Thompson, M.A.; Bulsara, P.A.; Moore, D.J.; McCabe, C. Composition Dependence of Water Permeation Across Multicomponent Gel-Phase Bilayers. J. Phys. Chem. B 2018, 122, 3113–3123. [Google Scholar] [CrossRef]
- Bemporad, D.; Essex, J.W.; Luttmann, C. Permeation of small molecules through a lipid bilayer: A computer simulation study. J. Phys. Chem. B 2004, 108, 4875–4884. [Google Scholar] [CrossRef]
- Kawamoto, S.; Klein, M.L.; Shinoda, W. Coarse-grained molecular dynamics study of membrane fusion: Curvature effects on free energy barriers along the stalk mechanism. J. Chem. Phys. 2015, 143, 243112. [Google Scholar] [CrossRef]
- Levine, Z.A.; Venable, R.M.; Watson, M.C.; Lerner, M.G.; Shea, J.E.; Pastor, R.W.; Brown, F.L.H. Determination of Biomembrane Bending Moduli in Fully Atomistic Simulations. J. Am. Chem. Soc. 2014, 136, 13582–13585. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: algorithms for highly efficient load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Nose, S. A molecular dynamics method for simulations in the canonical ensemble. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8596. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1469–1472. [Google Scholar] [CrossRef]
- Lee, S.; Tran, A.; Allsopp, M.; Lim, J.B.; Hénin, J.; Klauda, J.B. CHARMM36 United Atom Chain Model for Lipids and Surfactants. J. Phys. Chem. B 2014, 118, 547–556. [Google Scholar] [CrossRef] [PubMed]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; Mackerell, A.D.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926. [Google Scholar] [CrossRef]
- Feller, S.E.; Pastor, R.W. Constant surface tension simulations of lipid bilayers: The sensitivity of surface areas and compressibilities. J. Chem. Phys. 1999, 111, 1281–1287. [Google Scholar] [CrossRef]
- Shinoda, W.; Shinoda, K.; Baba, T.; Mikami, M. Molecular dynamics study of bipolar tetraether lipid membranes. Biophys. J. 2005, 89, 3195–3202. [Google Scholar] [CrossRef] [PubMed]
- Khelashvili, G.; Pabst, G.; Harries, D. Cholesterol Orientation and Tilt Modulus in DMPC Bilayers. J. Phys. Chem. B 2010, 114, 7524–7534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khelashvili, G.; Harries, D. How cholesterol tilt modulates the mechanical properties of saturated and unsaturated lipid membranes. J. Phys. Chem. B 2013, 117, 2411–2421. [Google Scholar] [CrossRef] [PubMed]
- Safran, S.A. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Sprik, M.; Ciccotti, G. Free energy from constrained molecular dynamics. J. Chem. Phys. 1998, 109, 7737–7744. [Google Scholar] [CrossRef]
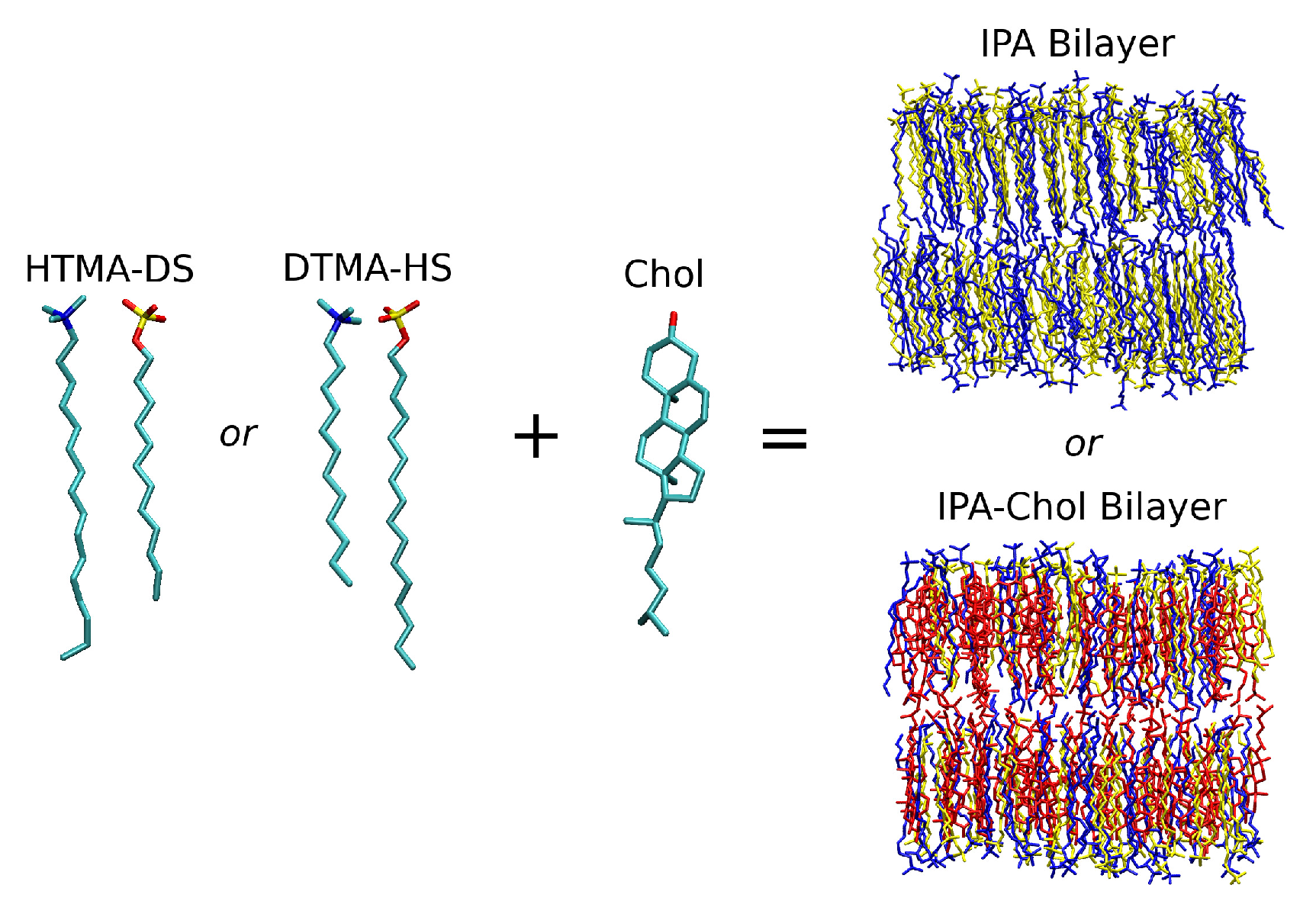


| System | X | N | N | N |
|---|---|---|---|---|
| 0 | 128 | 0 | ||
| HTMA-DS | 0.094 | 116 | 12 | |
| or | 0.203 | 102 | 26 | 3464 |
| DTMA-HS | 0.375 | 80 | 48 | |
| 0.5 | 64 | 64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien, W.-j.; Chen, K.-y.; Huang, F.-y.; Chiu, C.-c. Effects of Cholesterol on Water Permittivity of Biomimetic Ion Pair Amphiphile Bilayers: Interplay between Membrane Bending and Molecular Packing. Int. J. Mol. Sci. 2019, 20, 3252. https://doi.org/10.3390/ijms20133252
Tien W-j, Chen K-y, Huang F-y, Chiu C-c. Effects of Cholesterol on Water Permittivity of Biomimetic Ion Pair Amphiphile Bilayers: Interplay between Membrane Bending and Molecular Packing. International Journal of Molecular Sciences. 2019; 20(13):3252. https://doi.org/10.3390/ijms20133252
Chicago/Turabian StyleTien, Wu-jhao, Kun-you Chen, Fong-yin Huang, and Chi-cheng Chiu. 2019. "Effects of Cholesterol on Water Permittivity of Biomimetic Ion Pair Amphiphile Bilayers: Interplay between Membrane Bending and Molecular Packing" International Journal of Molecular Sciences 20, no. 13: 3252. https://doi.org/10.3390/ijms20133252





